Abstract
The heliostat field of Solar Central Receiver Systems takes up to 50% of the initial investment and can cause up to 40% of energetic loss in operation. Hence, it must be carefully optimized. Design procedures usually rely on particular heliostat distribution models. In this work, optimization of the promising biomimetic distribution model is studied. Two stochastic population-based optimizers are applied to maximize the optical efficiency of fields: a genetic algorithm, micraGA, and a memetic one, UEGO. As far as the authors know, they have not been previously applied to this problem. However, they could be a good option according to their structure. Additionally, a Brute-Force Grid is used to estimate the global optimum and a Pure-Random Search is applied as a baseline reference. Our empirical results show that many different configurations of the distribution model lead to very similar solutions. Although micraGA exhibits poor performance, UEGO achieves the best results in a reduced time and seems appropriate for the problem at hand.
1 Introduction
Solar Central Receiver Systems, SCRS in what follows, are an interesting and promising technology in the field of solar-based renewable energies. They were initially proposed in 1957 and, since then, they have been under continuous development (Gordon,
2013; p. 618). This kind of power facilities is especially characterized by its scalability, operating efficiency and output stability (Avila-Marin
et al.,
2013; Besarati and Goswami,
2014; Collado and Guallar,
2012,
2013).
In simple terms, SCRS consist of a set of high reflectance mirrors, called ‘heliostats’, and a radiation receiver which is usually on top of a tower. Heliostats track the apparent movement of the Sun throughout days to concentrate solar incident radiation over the receiver. Consequently, it is under high-density solar radiation. Then, a heat-interchange process is carried out in it to heat a working fluid. This fluid can be finally used in a classic turbine cycle to generate electric energy. Due to the high temperatures reached, thermodynamic performance is high (Besarati and Goswami,
2014; Collado and Guallar,
2012). In Fig.
1, a simple SCRS facility is depicted. Further information about them can be found in Alexopoulos and Hoffschmidt (
2017), Behar
et al. (
2013), Camacho
et al. (
2012), Müller-Steinhagen (
2013), Reddy
et al. (
2013), Stine and Geyer (
2001).
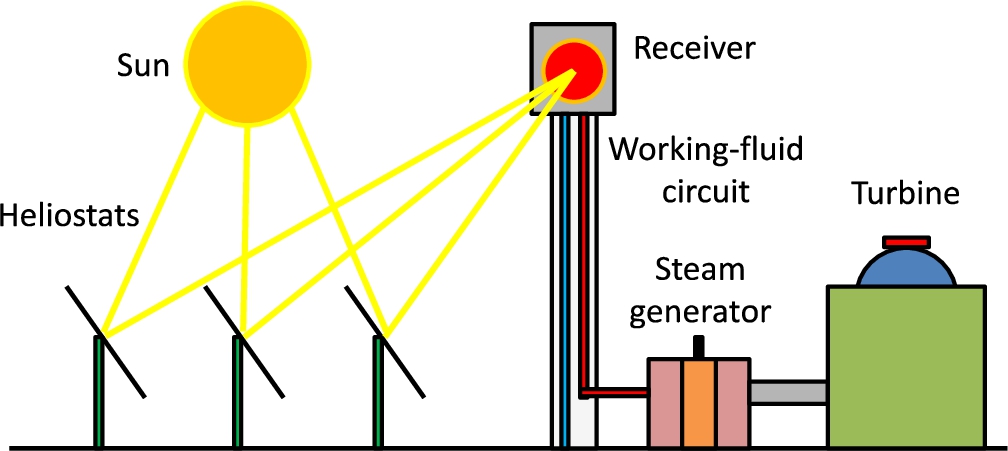
Fig. 1
Scheme of a SCRS system.
This work deals with optimizing the heliostat field of SCRS facilities, which is also known as ‘collector subsystem’. The set of heliostats and their configuration define this part of facilities. This subsystem can cause up to 40% of operating energetic loss and can take up to 50% of the initial investment according to Besarati and Goswami (
2014), Jones
et al. (
2007). Therefore, it must be carefully optimized when designing a SCRS power facility. Several optimization objectives are possible. For instance, optical efficiency maximization, as studied in Besarati and Goswami (
2014), Noone
et al. (
2012), is one of them. Production cost reduction, as mentioned in Ramos and Ramos (
2012), Sánchez and Romero (
2006), is another valid option. Finally, some variations and combinations of the previous ones, as studied in Zhang (
2007), are also common objective functions.
As summarized in Carrizosa
et al. (
2014), the design of heliostat fields is usually based on two basic strategies. The first one is to apply and optimize a certain heuristic distribution pattern. The classic radial staggered model, proposed by the University of Houston (Stine and Geyer,
2001; Chap. 10), and the biomimetic spiral, recently proposed by Noone
et al. (
2012), are two examples of patterns. In Mutuberria
et al. (
2015), where several patterns are compared, more examples and references can be found. The second strategy is to select final heliostat positions from a defined set (as iteratively done in Sánchez and Romero,
2006). However, a mixed approach is usually applied: An over-sized field is initially generated by following a particular distribution model to get a set of available positions over the ground. Then, the best ones are finally selected until the real power requirements are fulfilled. In fact, this strategy is quite common and it has been used, for instance, in Besarati and Goswami (
2014), Noone
et al. (
2012), Ramos and Ramos (
2012), Pitz-Paal
et al. (
2011), Sánchez and Romero (
2006). This latter approach permits more degrees of freedom to get optimal fields.
In this work, parametric optimization of the biomimetic spiral pattern is studied. The design objective is to maximize the optical efficiency of fields. This distribution scheme could be ultimately applied to both directly generate final fields and in a hybrid design methodology. Thus, it is important to rely on an efficient and reliable optimizer to adjust its design variables. In this context, two stochastic population-based algorithms, called micraGA and UEGO, are applied to solve the problem at hand. Their structure seems to be especially suitable to solve it. However, as far as the authors know, none of them had been previously used in this situation. Hence, the main goal of this work is to study their behaviour in it. Additionally, a Pure-Random Search algorithm is used to study the complexity of the problem and to get a baseline perspective of the quality of solutions. Finally, a Brute-Force Grid is applied to approximate where the optimal solution is deterministically. In contrast to the active trend of deploying large fields with several thousands of heliostats (e.g. 4120 units in Khi Solar One and 173500 ones in Ivanpah), this paper considers small and medium size fields. Specifically, facilities with several hundreds of heliostats, like CESA-I and PS10, with 300 and 624 units respectively, define the scope of interest. This is due to their lower requirements of space and initial investment, i.e. higher applicability. However, the size of the different problems is gradually increased, which makes it possible to discover general patterns. The results obtained seem scalable.
The rest of the paper is organized as follows: In Section
2, the optimization problem and the objective function are exposed. In Section
3, the different optimizers applied to the problem are described. In Section
4, the experiments carried out and the results obtained are shown. Finally, in Section
5, conclusions are drawn and future work is exposed.
2 Objective Function
The design of heliostat fields, as introduced, will be aimed at maximizing yearly irradiance weighted efficiency,
${\eta _{year,I}}$. It is a common objective function which is used, for instance, in Besarati and Goswami (
2014), Noone
et al. (
2012). It is focused on the optical efficiency of the heliostat field, while also considering the available solar radiation at every instant through the year. This magnitude can be formulated as Noone
et al. (
2012):
where
${I_{b}}(t)$ is the instantaneous beam irradiance and
$\eta (t)$ is the instantaneous optical efficiency. It must be noted that Eq. (
1) is defined in abstract terms. Hence, it must be configured by selecting the appropriate model for every encapsulated concept. These aspects are detailed in Noone
et al. (
2012), where the unweighted version of the equation is also included.
The optical efficiency of a field,
$\eta (t)$, measures its performance in redirecting and concentrating incident solar radiation over the receiver at every instant
t (Stine and Geyer,
2001; Chap. 10). In this context, an instant is equivalent to a certain solar position and incident radiation density on a particular day and time. It defines the heliostat field configuration. As an efficiency factor,
$\eta (t)$ is defined between 0 and 1 (minimum and maximum possible efficiency, respectively). It is internally formed by a selected set of sub-factors which model different sources of energy loss in heliostat fields. Discarding any of them is equivalent to assume it as 1, i.e. not causing energy loss. For the scope of this work,
η is defined for every heliostat as in Noone
et al. (
2012):
where
${\eta _{\mathit{cos}}}$,
${\eta _{sb}}$,
${\eta _{\mathit{itc}}}$,
${\eta _{aa}}$ and
${\eta _{\mathit{ref}}}$ are the cosine, shadowing and blocking, interception, atmospheric attenuation and reflectivity efficiency, respectively. These concepts will be summarized later in this section while also including the particular model applied to their calculation. Thus,
$\eta (t)$ in Eq. (
1) is referred to the average obtained from the values of every active heliostat. Further information about these efficiency factors can be found in Besarati and Goswami (
2014), Stine and Geyer (
2001), Noone
et al. (
2012). Additionally, the alternative definition of Eq. (
2) used in Collado and Guallar (
2012) is very descriptive. Its nomenclature not only includes time and the coordinates of heliostats but also the effect of their neighbours.
Instantaneous beam solar radiation,
${I_{b}}(t)$, weights pure optical efficiency. As introduced, it adds an energetic perspective to Eq. (
1). It modifies the instantaneous optical efficiency of a certain field considering the availability of solar radiation at every instant studied. This factor is also abstractly defined and the selected model will be described later in this section.
The instantaneous component,
t, encompasses a year, which is also divided into days. Days are finally considered as raw sets of instants, i.e. apparent solar positions. The way in which days are discretized is also abstract and configurable. For instance, in Noone
et al. (
2012), some interesting notes about considering a variable time step are presented. However, those strategies are out of the scope of this work and a constant time step will be used to compare the selected optimizers.
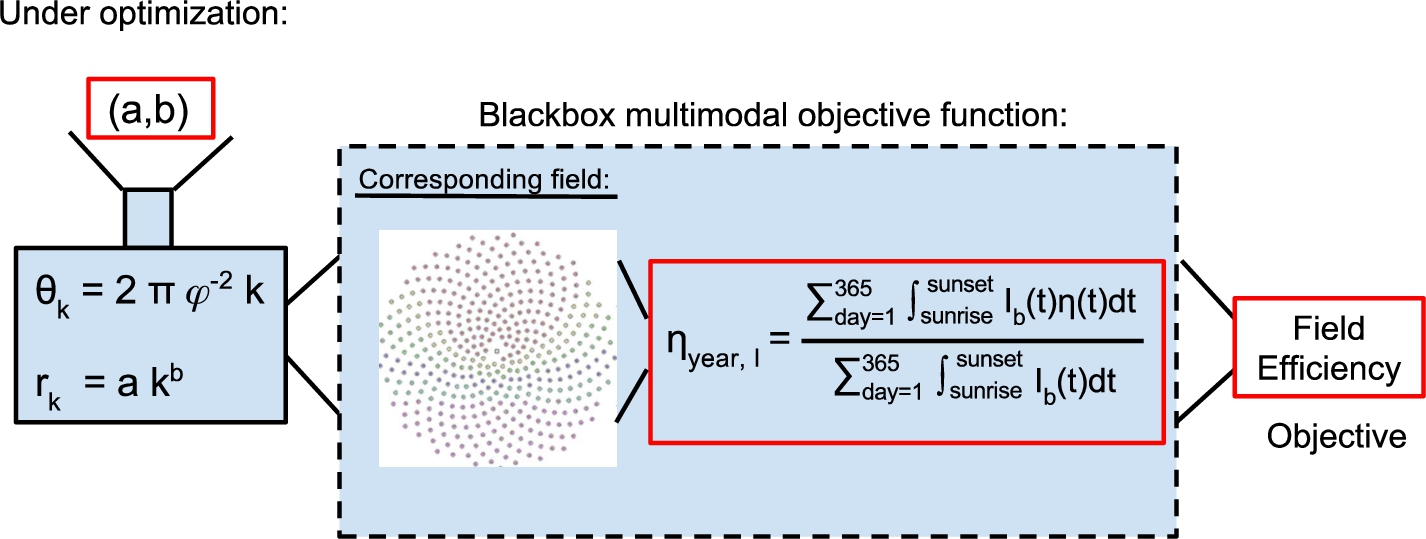
Fig. 2
Global scheme of the problem to solve.
Figure
2 gives an overview of the problem to solve. Eq. (
1), which directly depends on the heliostat field design, is the objective function to be maximized. It can be seen as simulation procedure of this part of SCRS facilities. A common context defined by the number of time steps per year, the configuration of every internal model, etc., is assumed. Therefore, it is necessary to define the design of candidate fields to be analysed with the underlying objective function while optimizing. As introduced, fields will be designed by directly applying the biomimetic spiral pattern proposed in Noone
et al. (
2012). Consequently, the optimizers applied will need to find the parameters of this pattern, ‘
a’ and ‘
b’, that generates a field with a maximum value of Eq. (
1). As usual in engineering problems, the objective function does not directly depend on the design variables. Next, the internal models selected for Eq. (
1) and the biomimetic pattern are described.
2.1 Sun Positioning
The configuration of heliostat fields is defined by the apparent solar position at every instant,
t. The model explained in Stine and Geyer (
2001; Chap. 3) has been selected to calculate the apparent solar position throughout the year. Its coordinate system and conventions have been followed too. Any apparent solar position is defined by its azimuth and altitude angles,
A and
α, respectively. They are calculated depending on solar declination (
δ), latitude (
ϕ) and hour angle (
ω):
2.2 Solar Radiation
The impact of the optical performance of a certain field depends on incident solar radiation density. Independently of their design, fields cannot concentrate much power on the receiver when there is no much solar energy to be profited. Therefore, it is important to weigh optical efficiency values with solar radiation density at every instant
t. The model used to estimate direct solar radiation density depends on the concept of ‘air mass’ (
$\mathit{AM}$) (explained in Stine and Geyer,
2001; Chap. 2) and the location height above sea level. The expression of this model, in (kW/m
${^{2}}$), is (Laue,
1970):
where
h is the location height above sea level in kilometers. It must be noted that
${I_{b}}$ depends on time because air mass varies with solar altitude.
2.3 Field Efficiency
The optical efficiency of heliostat fields depends on these concepts, which are defined for every single heliostat and averaged to compute Eq. (
2):
Cosine efficiency, ${\eta _{\cos }}$:
profitable reflective area of heliostats due to their orientation. According to the Law of Reflection, it is derived from the cosine of the angle formed by the incident solar beam with the heliostat normal direction:
where
S and
H are unit vectors expressing the solar and heliostat normal directions (the coordinate system used is described in Stine and Geyer,
2001; Sec. 8.5).
Shadowing and blocking efficiency, ${\eta _{sb}}$:
reflective area of heliostats neither shadowed nor blocked by any other one. As proposed in Ramos and Ramos (
2014), its computation is addressed as a polygon clipping problem. Once every heliostat has been oriented for the simulated instant, the
${\eta _{sb}}$ factor of a certain one,
${h_{i}}$, is computed after four steps. First, the four vertexes of the
${P_{s}}$ potentially shadowing heliostats are projected, in the direction of sunlight, on the plane defined by the reflective surface of
${h_{i}}$. By proceeding this way,
${P_{s}}$ polygons are generated over the plane of
${h_{i}}$. This step is depicted in Fig.
3. Second, the four vertexes of the
${P_{b}}$ potentially blocking heliostats are also projected on the plane of
${h_{i}}$, but in the direction of their target vector. Similarly,
${P_{b}}$ polygons are generated over the plane of
${h_{i}}$. Third, every generated polygon is subtracted from the rectangle of the reflective surface of
${h_{i}}$, which is on its infinite plane. Finally,
${\eta _{sb}}$ of
${h_{i}}$ is the ratio of the area of the polygon obtained after subtraction,
${A_{S}}$, to the original one,
${A_{T}}$, as expressed in Eq. (
7).
The heliostats previously labelled as ‘potentially shadowing/blocking’ are selected, for every heliostat
${h_{i}}$, by applying an adaptation of the ‘bounding sphere’ method mentioned in Noone
et al. (
2012). Specifically,
${h_{i}}$ is wrapped in a sphere and projected on the plane. After that, it is translated towards the Sun and the receiver. If the sphere of any other heliostat can intercept the translation trajectory, that one is considered a candidate. The type will be of ‘shadowing’ or ‘blocking’ when the translation is towards the Sun or the receiver, respectively. This procedure is depicted in Fig.
4:
${H_{2}}$ could block
${H_{1}}$ because the distance
d to the trajectory of
${H_{1}}$ towards the receiver is less than the sum of the radii of both spheres. Further information regarding aspects such as the way in which heliostats are oriented can be found in Stine and Geyer (
2001; Sec. 8.5). Polygon clipping methods are also out of the scope of this work. However, the algorithms of Greiner and Hormann (
1998) and Vatti (
1992) are good options for the interested reader. Whereas the algorithm of Greiner–Hormann was used in Ramos and Ramos (
2014), the method of Vatti has been used in this work through the implementation of Johnson (
2012).
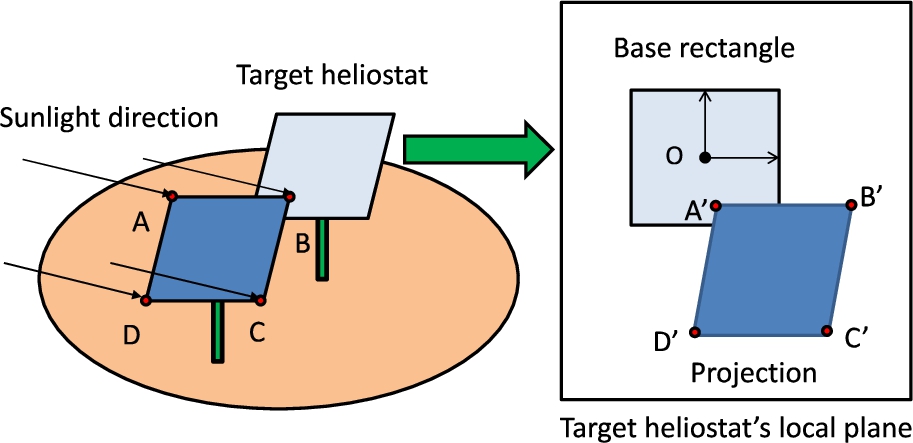
Fig. 3
Shadowing heliostat projection on the studied one.
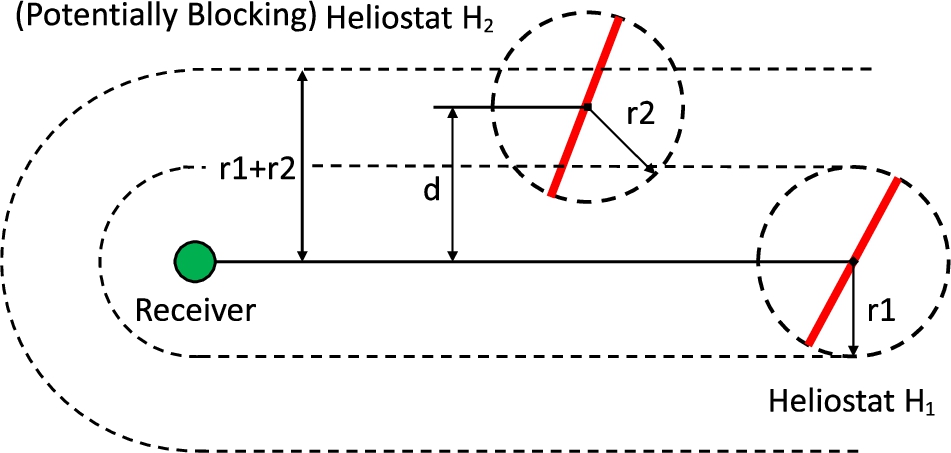
Fig. 4
Selection of candidate heliostats ‘bounding sphere’.
Interception efficiency, ${\eta _{\mathit{itc}}}$:
ratio of success in targeting the receiver. It is estimated once depending on the dimensions of the heliostats and the receiver as in Cristóbal (
2011), where the model proposed by Collado and Turégano (
1989) is implemented:
where
$l{w_{r}}$ and
$d{w_{r}}$ are the height and diameter of the receiver, respectively.
${\sigma _{r}}$ is the standard deviation of sunshape.
${a_{r}}$ is a compound parameter defined for convenience and computed as
$\sqrt{{A_{T}}}/(2\sqrt{2}{\sigma _{r}})$, where
${A_{T}}$ is the same area previously defined. Finally,
$pH$ is an auxiliary function and further information about it is available in Cristóbal (
2011), Collado and Turégano (
1989).
Atmospheric attenuation efficiency, ${\eta _{aa}}$:
effect of the atmosphere on radiation reflected by heliostats. It has been selected the same model applied in Noone
et al. (
2012). It depends on the distance between every heliostat and the receiver,
${d_{rec}}$, as expressed in Eq. (
9).
Reflectivity efficiency, ${\eta _{\mathit{ref}}}$:
energy loss caused by the physical properties of reflective surfaces. It is assumed to be a common constant of heliostats.
2.4 Biomimetic Distribution Model
The available heliostats are distributed according to the promising biomimetic layout proposed in Noone
et al. (
2012). It has been successfully used to design fields of several hundreds of heliostats in Besarati and Goswami (
2014), Noone
et al. (
2012), which is the main target of the present study. This distribution pattern is also characterized by achieving a good trade-off between land use and field efficiency. For instance, in Mutuberria
et al. (
2015), its good properties are also observed. The method is inspired by the spiral patterns of the phyllotaxis disc, like florets on the head of sunflowers. This pattern consists of two equations that define the position of every heliostat in polar coordinates (Noone
et al.,
2012):
${\theta _{k}}$ and
${r_{k}}$ are the azimuthal and radial distance, respectively.
k is the index of any heliostat as part of the spiral and
φ is the golden ratio. However,
a and
b are the parameters of the pattern which are adjusted to vary the density of fields. Hence, they will be determined through optimization. Finally, it must be noted that azimuth values are measured clockwise from North direction, in radians. Radial distances are measured from the tower base, in meters. For instance, the field shown in Fig.
2 follows this pattern.
3 Optimization Algorithms
The optimization problem described has been solved with four different algorithms: a genetic algorithm (called micraGA), a memetic global optimizer (called UEGO), a Pure-Random Search (that will be referred as PRS) and a Brute-Force Grid (named as BFG in what follows).
3.1 Genetic Algorithm: micraGA
Genetic algorithms, proposed by J. Holland in the late seventies (Holland,
1975), are frequently used for complex black-box optimization problems. This is because their principles are not linked to any particular problem but to the evolution of species. This kind of algorithms is also usually applied to heliostat field optimization. For instance, they have been successfully used in Besarati and Goswami (
2014), Ramos and Ramos (
2012), Pitz-Paal
et al. (
2011).
In this work, a genetic algorithm called micraGA has been designed to solve the problem summarized in Fig.
2. Each individual consists of: (i) a couple of values for variables
a and
b and (ii) the weighted efficiency of the corresponding field according to Eq. (
1). Three individuals can be seen in Fig.
5. Initial individuals are generated by randomly selecting their values for
a and
b in Eq. (10) within the search space. In case that random couples lead to inconsistent fields where some heliostats are too near each other, these couples are discarded and re-generated. The population size, defined by an input parameter, will be kept constant during the search. Once the initial population has been defined, this evolutionary procedure is repeated a given number of cycles:
A certain even number of sets of randomly selected individuals is formed. Both the number of sets and their cardinality are user-defined parameters. Their values will be commented later in Section
4. Then, the best individuals of all consecutive sets are paired to form a couple every two. This strategy, called ‘tournament selection’ (Redondo,
2009), is more likely to attenuate strong genetic drifts in the population.
A new descendant is generated from every previous couple. They result from averaging the values of the progenitors for
a and
b. This approach aims to obtain individuals that point to unknown local optima in the search space. Figure
5 contains a depiction of this step.
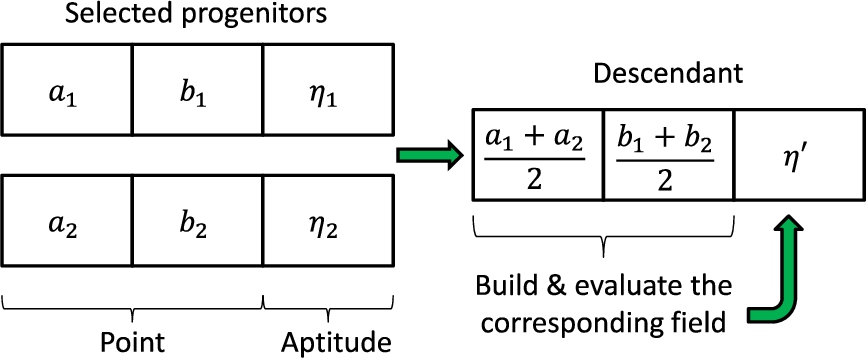
Fig. 5
Reproduction step of micraGA.
Every existing individual is altered by adding a random increment to its values for a and b. However, to get a cooling procedure, increments are previously divided by a parameter raised to the current number of cycle. The limits considered when generating random increments and the cooling factor are part of the input parameters of micraGA. Any mutation is discarded if the altered individual is worse than the initial one.
At the end of every cycle, the population for the next one is formed by selecting the best individuals from the current population and its descendants. Tournament selection is applied again for this purpose.
Finally, it must be noted that reproduction and mutation might lead to unfeasible individuals. However, in contrast to correctness required at population initialization, this kind of individuals is permitted during the search. This approach aims to maintain as many explored zones as possible to be able to reach isolated optimal solutions. Nevertheless, the aptitude of this kind of individuals is heavily penalized by setting it to 0.
3.2 Universal Evolutionary Global Optimizer: UEGO
The ‘Universal Evolutionary Global Optimizer’ (UEGO) is a memetic (Moscato,
1989; Dawkins,
1976) multi-modal optimization algorithm. It was presented in Jelasity (
1998) as a method especially suitable to be parallelized and highly adaptable to different problems (Jelasity,
1998; Ortigosa
et al.,
2001b,
2007; Redondo
et al.,
2009a,
2009b). The algorithm defines that of ‘species’ as its fundamental concept. Every species is the aggregation of a candidate solution and a certain attraction radius over the search space. The structure of UEGO is divided into two separate levels, a global and a local one. At the former one, an iterative management process of the set of species is defined. This procedure, which includes a cooling component to enhance convergence, is independent of the problem. However, the local level needs to be adjusted to the considered problem by selecting a local optimizer to use. This is an iconic property of memetic algorithms. This layered design is also determinant for the adaptability of UEGO to different problems.
For the problem at hand, species consist of: i) a couple of candidates values for
a and
b, ii) its aptitude according to Eq. (
1) and iii) its attraction radius. Figure
6 shows a species adapted to this problem. Algorithm
1 enumerates the steps of UEGO. As can be seen, its parameters are the maximum population size and executions of the objective function (
MSpec and
MEv, respectively), the number of search levels (
NLev) and the minimum attraction radius (
MR).
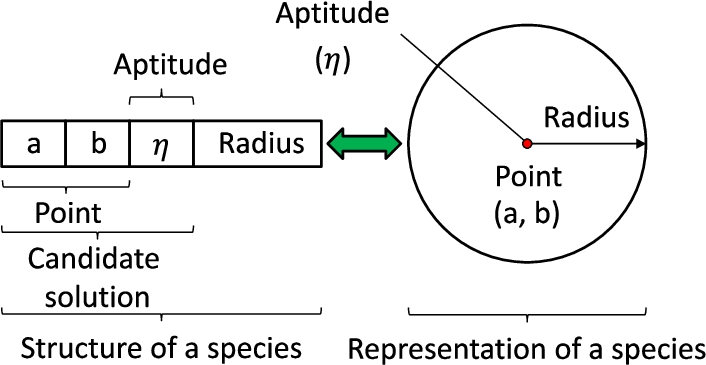
Fig. 6
UEGO species for the problem at hand.
According to Algorithm
1, at line 1, UEGO starts by randomly generating a species whose radius covers the whole search space. Next, it is locally optimized by applying the Solis & Wets’ SASS algorithm (Solis and Wets,
1981). This optimizer has been selected because it does not require any specific properties of the objective function. Besides, it has been previously and successfully coupled with UEGO (Redondo,
2009). Then, at line 3, the main loop of UEGO is repeated for the remaining levels. As shown at line 4, every level
i starts with the computation of three reference values. The first one,
$r[i]$, is the attraction radius that will be linked to every new species. Radii are progressively reduced, according to an exponential progression, until the minimum value defined by the user. The second one,
$\mathit{new}[i]$, is the number of objective function evaluations allowed to create new species. The last one,
$n[i]$, is the maximum number of objective function evaluations allowed to optimize species locally. Next, at line 5, new promising species are created within the zones defined by the existing ones. After that, at line 6, any overlapping species are fused depending on
$r[i]$ and the Euclidean distance between their centres, i.e. the
$(a,b)$ points in the search space. Figure
7 includes a depiction of this step. At line 7, if the maximum number of species has been exceeded, the most recent ones, which have the shortest radius, are removed. This approach makes premature convergence more difficult to occur because the search scope is kept wide. Later, at line 8, the existing species are locally optimized. It must be noted that this can cause that their centres are moved in the search space. Finally, the possibility of fusing nearby species is re-analysed at line 9.

Algorithm 1:
UEGO algorithm
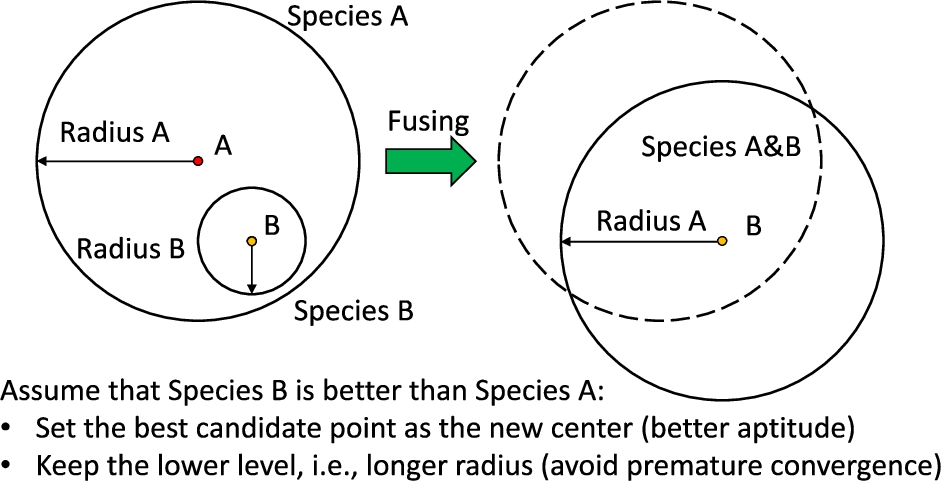
Fig. 7
Fusion of two species in UEGO.
Unfeasible solutions are allowed but penalized in the same way as in micraGA. Further information about UEGO and its configuration can be found in Redondo (
2009), Ortigosa
et al. (
2001a).
3.3 Pure-Random Search: PRS
Pure-Random Search, PRS in what follows, is the simplest global optimization algorithm (Brooks,
1958). It consists in randomly generating solutions in the search space while the best one achieved so far is kept as a reference. Despite its simplicity, when the number of iterations allowed increases to infinity, the probability of finding a global optimum tends to 1 (Brooks,
1958). However, this approach is more theoretically interesting than applicable.
For the problem at hand, PRS simply needs to generate a random couple of parameters
a and
b for Eq. (10) at each iteration. The corresponding field of that candidate solution is then evaluated according to Eq. (
1). In case that it outperforms the previous reference, the new one is registered as the best solution known. This procedure is repeated for an user-defined number of iterations. After that, PRS finally returns the reference as the solution.
In this work, PRS has been initially selected to get a baseline reference for analysing the results of population-based optimizers. It can also be used to appreciate the problem complexity.
3.4 Brute-Force Grid: BFG
Since all the previous methods are stochastic, they do not guarantee to obtain the same results after different executions. Furthermore, the optimal configuration of Eq. (10) is not formally known for the considered conditions. Consequently, a Brute-Force Grid (BFG) is applied to get a configurable and deterministic perspective of the search space.
BFG, given a discretization step in each dimension, systematically generates and evaluates all possible combinations of the variables under optimization. This approach seems to be successfully used by the tool HFLD in Wei
et al. (
2007) for parametric optimization of distribution models. It could have also been used in Noone
et al. (
2012) to generate the set of combinations of
a and
b.
On the one hand, this strategy is interesting due to its deterministic nature. Moreover, its accuracy can be precisely configured by adjusting the discretization steps. On the other hand, it will be extremely time-consuming for most configurations. Thus, its application to large problems or as part of complex field designs procedures might be unfeasible.
For the problem at hand, dimensions
a and
b of Eq. (10) are discretized for a given resolution. Then, all possible combinations are formed and evaluated according to Eq. (
1). The best one is finally selected as the optimal solution. BFG will be applied to get an approximated idea of the structure of the search space and where its optimal point is.
4 Experimentation and Results
The problem context has been implemented in C++. The objective function, which requires simulating the candidate fields throughout the year, has been parallelized due to its significant computational cost. The simulation of instants has been distributed among concurrent threads as proposed in Cruz
et al. (
2017). The POSIX-Threads (PThreads) library has been used for parallelization. The optimizers described in Section
3 have also been implemented in C++. The compiler used is g++ 4.8.1 with optimization level ‘O2’. The experiments have been carried out in a cluster node that features an Intel Xeon E5 2650 with 16 cores and 64 GB of shared RAM. The evaluation of the objective function can hence deploy up to 16 concurrent threads.
Regarding the problem definition, the latitude of the facility is 37.4
${^{\circ }}$ North. The height of the tower is 100 m with a cylindrical receiver of 10.5 m of height and 8.5 m in diameter. Since a north-field configuration is required, only those positions of the pattern at the north of the tower are considered. All heliostats are assumed to have a plain reflective surface of 100 m
${^{2}}$ (10 m × 10 m) whose center is at 5 m over the ground. The time step throughout days is constant. Specifically, for any studied field, Eq. (
1) is computed at every hour from sunrise to sunset. For the selected solar model and latitude, approximately 4000 instants can be uniformly generated in a year. However, the solar positioning model shows symmetry, which is inherited by radiation density estimation. Thus, simulations only evaluate about 2400 real instants.
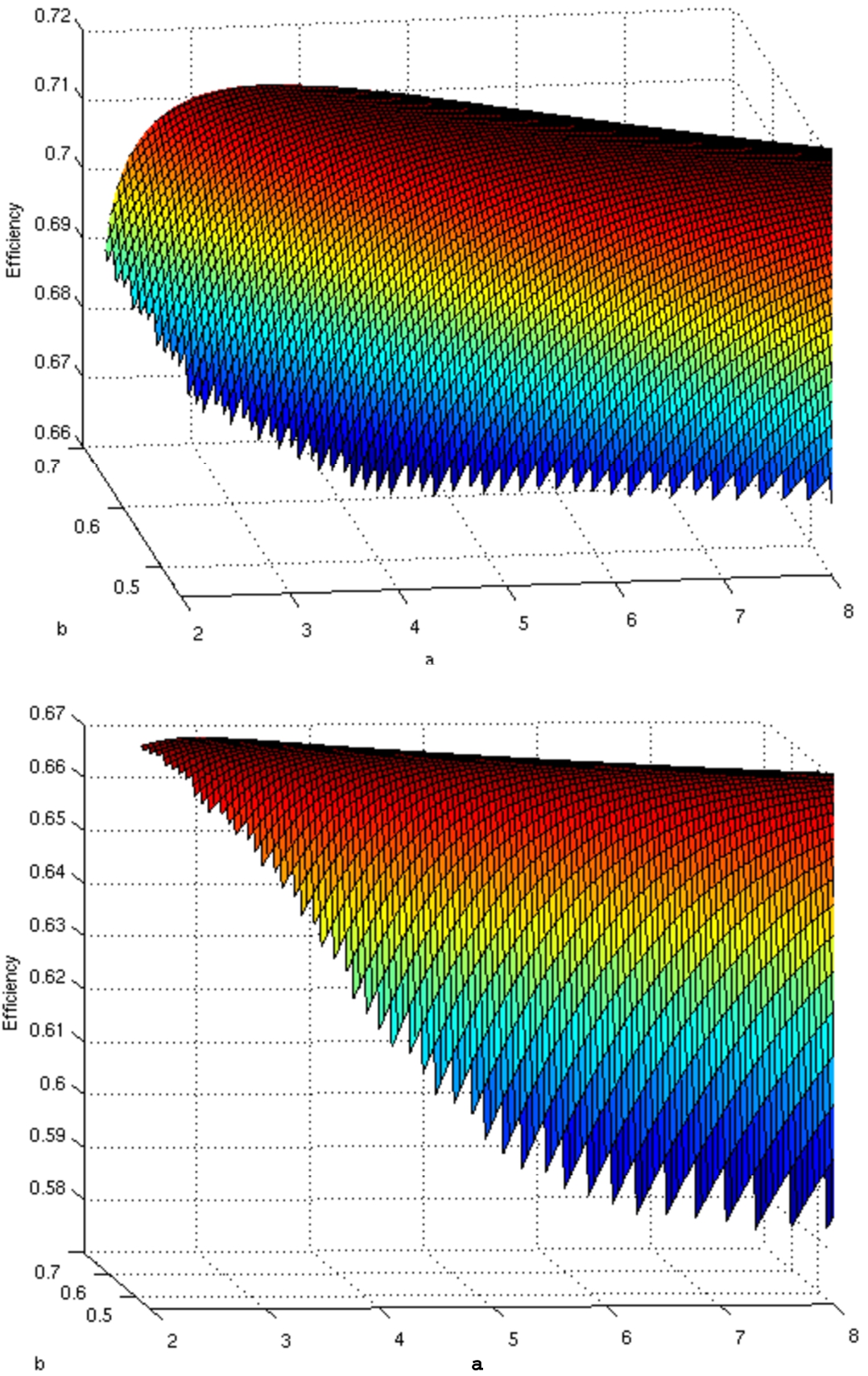
Fig. 8
Objective function’s approximated plot for 50 (left) and 500 (right) heliostats.
The considered problem sizes range from 50 to 500 heliostats to place. According to Besarati and Goswami (
2014),
a and
b, are defined in
$[2.0,8.0]$ and
$[0.45,0.70]$, respectively. For BFG, the discretization steps in
a and
b are 0.05 and 0.005, respectively. This configuration has also been used to plot the shape of the objective function shown in Fig.
8 for both the smallest and the biggest instances. As can be seen, the search space is quite homogeneous, which is mainly due to keeping it limited to a robust distribution model. UEGO and micraGA have been configured, after preliminary experimentation, with a robust set of parameters for all the studied problems. They have been configured to get the best results possible, with stability in spite of their stochastic nature, and as fast as possible. For UEGO, this is achieved with a limit of field evaluations equal to 1000, 20 levels of search, a limit of 15 species and a minimum radius equal to 0.0001. micraGA has been configured to have a population size of 70 and to select 70 progenitors from tournaments of 12 individuals at every cycle. micraGA will execute a total of 4 cycles. Its cooling procedure will divide mutation increments by
$9.{0^{(x-0.5)}}$, where
x is the cycle (when it is larger than 1). Mutation amplitude in
a is in range
$[-1.0,1.0]$ while it is in range
$[-0.15,0.15]$ in
b. Finally, PRS has been adjusted to take a similar time to UEGO and micraGA. Specifically, it is allowed to execute 1250 cycles. This time constraint would be interesting in case of using this process to generate preliminary fields in a more complex design method.
Table
1 contains the results obtained after experimentation. Each row represents a particular problem size while the sets of columns show the results achieved by every optimizer. The records of BFG contain the efficiency achieved and the runtime for every problem size. However, due to their non-deterministic nature, the records of UEGO, micraGA and PRS consist of the average efficiency achieved, the standard deviation and the runtime for every problem size. The experiments with non-deterministic methods have been repeated for 10 times. Additionally, the last row includes the average of all the instances. The best efficiency in every case is in bold font.
Table 1
Average results obtained with each optimizer.
|
BFG |
UEGO |
micraGA |
PRS |
| Hel. |
Ef. $({10^{-5}})$
|
T. (s) |
Ef. $({10^{-5}})$
|
St.D. $({10^{-5}})$
|
T. (s) |
Ef. $({10^{-5}})$
|
St.D. $({10^{-5}})$
|
T. (s) |
Ef. $({10^{-5}})$
|
St.D. $({10^{-5}})$
|
T. (s) |
| 50 |
70336.61 |
479 |
70336.62 |
0.00 |
54 |
70336.58 |
0.04 |
53 |
70336.24 |
0.43 |
62 |
| 100 |
69369.70 |
1235 |
69369.74 |
0.00 |
142 |
69369.24 |
0.71 |
148 |
69368.45 |
1.00 |
154 |
| 150 |
68671.19 |
2211 |
68671.20 |
0.00 |
271 |
68670.22 |
2.19 |
271 |
68669.97 |
1.00 |
278 |
| 200 |
68200.80 |
3457 |
68200.84 |
0.00 |
410 |
68197.08 |
4.33 |
422 |
68198.92 |
1.22 |
420 |
| 250 |
67798.31 |
4828 |
67798.38 |
0.00 |
600 |
67796.46 |
2.00 |
590 |
67795.90 |
1.35 |
594 |
| 300 |
67453.50 |
6487 |
67453.53 |
0.00 |
780 |
67451.34 |
3.03 |
800 |
67448.40 |
2.49 |
773 |
| 350 |
67178.22 |
8295 |
67178.30 |
0.00 |
975 |
67175.64 |
5.09 |
1010 |
67174.52 |
3.18 |
992 |
| 400 |
66929.81 |
10318 |
66929.92 |
0.00 |
1251 |
66925.94 |
5.74 |
1259 |
66925.12 |
2.03 |
1235 |
| 450 |
66727.91 |
12539 |
66727.96 |
0.00 |
1447 |
66724.96 |
4.25 |
1500 |
66725.76 |
1.45 |
1475 |
| 500 |
66538.51 |
14856 |
66538.57 |
0.00 |
1785 |
66534.14 |
4.12 |
1784 |
66531.64 |
5.96 |
1759 |
| Avg.: |
67920.46 |
6471 |
67920.51 |
0.00 |
772 |
67918.16 |
3.15 |
784 |
67917.49 |
2.01 |
774 |
As can be seen in Table
1, the achieved efficiencies are numerically very similar for the same instance. Besides, multiple combinations of
a and
b result in fields of similar efficiency. In Pitz-Paal
et al. (
2011), where heliostat field optimization is also studied, a similar situation was observed. Generally speaking, the real impact of such variations in efficiency would ultimately depend on the field size. In fact, the differences between those methods with a better average (UEGO and BFG) and the others tend to be higher with more heliostats. If we studied the final average efficiency of every method as that of a virtual field, the difference between the best and worst methods would be of a few thousands of euros a year (less than 6,000 euros). However, if these results were scaled to larger fields, the same degree of variation would represent an extra benefit of several thousands of euros (less than 60,000 euros). These values would not be determinant if compared to the total budget of the facility. Nevertheless, they could be achieved by simply selecting the most appropriate optimizer at design. Moreover, since analytical models might tend to overestimate efficiencies because of their simplifications, it is important to work with high precision.
UEGO gets the best average efficiency in all the studied cases. It is also very stable as can be observed in its values of standard deviation. In fact, it usually returns the same solution for each problem instance even after different executions. They all are also in the region where the optimal solution is expected to be according to the preliminary analysis with BFG. Therefore, UEGO is neither affected by its stochasticity nor by the multimodal structure of the objective function.
BFG achieves efficiencies quite near to those obtained by UEGO. However, its runtime is significantly higher. Hence, its integration in complex design procedures would be less practical. On the one hand, BFG is up to 10 times slower than UEGO with a relatively coarse discretization of the search space while even obtaining slightly worse results. On the other hand, BFG is deterministic and its resolution can be arbitrarily adjusted through its discretization steps. These properties make it theoretically interesting for studies such as the one presented in this work. However, as can be deduced from Table
1, BFG would need an enormous amount of time to handle larger problem instances, wider search spaces and higher accuracy. More sophisticated methods such as UEGO outperforms BFG with less computational effort.
Regarding micraGA, its performance is quite low when compared with UEGO. In fact, it is even marginally outperformed by PRS in two cases, the instances of 200 and 450 heliostats. This behaviour is consistent with the idea that the complexity of micraGA is between those of UEGO and PRS. Furthermore, it is not particularly stable if compared with the standard deviation obtained by PRS and especially by UEGO. micraGA does not converge adequately due to the structure of the search space. It would need a significantly higher runtime to get closer results to UEGO. Thus, since micraGA cannot outperform UEGO and it is complex if compared to PRS, it is not a good option to be further considered.
Finally, despite being the worst ones, the results obtained by PRS are quite interesting. In spite of its simplicity and lack of orientation during the search, depending on the precision needed, it could achieve acceptable results. This is mainly due to two reasons: i) its reduced logic overhead makes it possible to study numerous combinations in a similar runtime to UEGO and micraGA; ii) it is not affected by the structure of the search space. In fact, PRS could be interesting as part of a more complex heliostat field optimization method because of its simplicity. However, its instability and lack of robustness compared to UEGO make it not appropriate as a standalone method.
5 Conclusions and Future Work
In this work, the complexity of heliostat fields design has been studied. An optimization problem aimed at maximizing yearly irradiance weighted efficiency has been defined. The design procedure followed directly tries to optimize the parameters of the promising biomimetic distribution pattern. Four optimization algorithms have been studied to solve the problem, namely, BFG, UEGO, PRS and micraGA. The possibility of coupling their use within more complex methods is also discussed considering computational cost. Whereas Genetic Algorithms and BFG are state-of-art methods for the present problem, UEGO had not been applied to solve it before. PRS, as far as the authors know, could also be included in this set. Since the objective function is wrapped within a distribution robust pattern, it is heavily multimodal.
UEGO is the best option out of the considered ones. This method gets the best solutions in a stable and fast way for all the studied instances. Hence, it should be considered for heliostat field design based on the described distribution pattern. It also seems to be fast enough to be included as part of a more complex design procedure. The field efficiencies obtained by BFG are very similar to those achieved by UEGO. In fact, for a given resolution, BFG could obtain the best solution possible due to the extensive search that it performs. However, it would require significantly more runtime than UEGO. Thus, BFG does not seem to be appropriate for large fields, wide search spaces or to be included in a complex procedure of several stages. Regarding PRS, it turns out to be an interesting option considering its simplicity. Although it should not be applied to generate final fields, PRS could be appropriate in a multi-stage procedure depending on the precision requirements. Finally, the genetic optimizer proposed, micraGA, does not seem to be a good option. It does not explore the search space properly. Its results are of low quality and unstable if compared to those of UEGO. In fact, they are very similar to those of PRS in spite of being more sophisticated than that method.
There are some possible expansion points for future work. First, a better alternative to micraGA could be explored. Its design should aim at a trade-off between the complexity of UEGO with the best results and the simplicity of PRS with acceptable quality. Second, it could be interesting to compare the performance of UEGO and PRS in a multi-stage optimization process. Finally, extending this comparison context to encompass several distribution patterns and timing variations in the objective function would be of great interest.
Acknowledgements
This work has been funded by grants from the Spanish Ministry of Economy, Industry and Competitiveness (TIN2015-66680-C2-1-R and ENERPRO DPI 2014-56364-C2-1-R), Junta de Andalucía (P12-TIC301). Nicolás Calvo Cruz (FPU14/01728) is supported by an FPU Fellowship from the Spanish Ministry of Education. Juana López Redondo (RYC-2013-14174) and José Domingo Álvarez (RYC-2013-14107) are fellows of the Spanish ‘Ramón y Cajal’ contract program, co-financed by the European Social Fund.
References
Alexopoulos, S., Hoffschmidt, B. (2017). Advances in solar tower technology. WIREs Energy Environment, 6(1), 1–19.
Avila-Marin, A.L., Fernandez-Reche, J., Tellez, F.M. (2013). Evaluation of the potential of central receiver solar power plants: configuration, optimization and trends. Applied Energy, 112, 274–288.
Behar, O., Khellaf, A., Mohammedi, K. (2013). A review of studies on central receiver solar thermal power plants. Renewable and Sustainable Energy Reviews, 23(0), 12–39.
Besarati, S.M., Goswami, D.Y. (2014). A computationally efficient method for the design of the heliostat field for solar power tower plant. Renewable Energy, 69, 226–232.
Brooks, S.H. (1958). A discussion of random methods for seeking maxima. Operations Research, 6(2), 244–251.
Camacho, E., Berenguel, M., Rubio, F.R., Martínez, D. (2012). Control of Solar Energy Systems. Springer Science & Business Media.
Carrizosa, E., Domínguez-Bravo, C., Fernández-Cara, E., Quero, M. (2014).
An optimization approach to the design of multi-size heliostat fields. Technical report, Technical report IMUS.
Collado, F.J., Guallar, J. (2012). Campo: Generation of regular heliostat fields. Renewable Energy, 46, 49–59.
Collado, F.J., Guallar, J. (2013). A review of optimized design layouts for solar power tower plants with Campo code. Renewable and Sustainable Energy Reviews, 20, 142–154.
Collado, F.J., Turégano, J.A. (1989). Calculation of the annual thermal energy supplied by a defined heliostat field. Solar Energy, 42(2), 149–165.
Cristóbal, A.G. (2011).
Diseño del campo de helióstatos para torres solares de receptor central. Degree Dissertation, Universidad Carlos III de Madrid, Spain.
Cruz, N.C., Redondo, J.L., Berenguel, M., Álvarez, J.D., Becerra-Terón, A., Ortigosa, P.M. (2017). High performance computing for the heliostat field layout evaluation. The Journal of Supercomputing, 73, 259–276.
Dawkins, R. (1976). The Selfish Gene. Oxford University Press.
Gordon, J.M. (2013). Solar Energy: The State of the Art. Taylor & Francis.
Greiner, G., Hormann, K. (1998). Efficient clipping of arbitrary polygons. ACM Transactions on Graphics (TOG), 17(2), 71–83.
Holland, J.H. (1975). Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence. The MIT Press.
Jelasity, M. (1998). UEGO, an abstract niching technique for global optimization. In: Parallel Problem Solving from Nature-PPSN V. Springer, pp. 378–387.
Jones, S.A., Lumia, R., Davenport, R., Thomas, R.C., Gorman, D., Kolb, G.J., Donnelly, M.W. (2007). Heliostat cost reduction. In: ASME 2007 Energy Sustainability Conference. American Society of Mechanical Engineers, pp. 1077–1084.
Laue, E.G. (1970). The measurement of solar spectral irradiance at different terrestrial elevations. Solar Energy, 13(1), 43–57.
Moscato, P. (1989). On evolution, search, optimization, genetic algorithms and martial arts: Towards memetic algorithms.
Caltech Concurrent Computation Program, C3P Report, 826.
Müller-Steinhagen, H. (2013). Concentrating solar thermal power.
Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences,
371(1996).
Mutuberria, A., Pascual, J., Guisado, M.V., Mallor, F. (2015). Comparison of heliostat field layout design methodologies and impact on power plant efficiency. Energy Procedia, 69, 1360–1370.
Noone, C.J., Torrilhon, M., Mitsos, A. (2012). Heliostat field optimization: A new computationally efficient model and biomimetic layout. Solar Energy, 86(2), 792–803.
Ortigosa, P.M., García, I., Jelasity, M. (2001a). Reliability and performance of UEGO, a clustering-based global optimizer. Journal of Global Optimization, 19(3), 265–289.
Ortigosa, P.M., García, I., Jelasity, M. (2001b). Two approaches for parallelizing the UEGO algorithm. In: Optimization Theory. Springer, pp. 159–177.
Ortigosa, P.M., Redondo, J.L., García, I., Fernández, J.J. (2007). A population global optimization algorithm to solve the image alignment problem in electron crystallography. Journal of Global Optimization, 37(4), 527–539.
Pitz-Paal, R., Botero, N.B., Steinfeld, A. (2011). Heliostat field layout optimization for high-temperature solar thermochemical processing. Solar Energy, 85(2), 334–343.
Ramos, A., Ramos, F. (2012). Strategies in tower solar power plant optimization. Solar Energy, 86(9), 2536–2548.
Ramos, A., Ramos, F. (2014). Heliostat blocking and shadowing efficiency in the video-game era.
arXiv:1402.1690.
Reddy, V.S., Kaushik, S.C., Ranjan, K.R., Tyagi, S.K. (2013). State-of-the-art of solar thermal power plants – a review. Renewable and Sustainable Energy Reviews, 27, 258–273.
Redondo, J.L. (2009). Solving Competitive Location Problems via Memetic Algorithms. High Performance Computing Approaches, Vol. 258. Universidad, Almería.
Redondo, J.L., Fernández, J., García, I., Ortigosa, P.M. (2009a). A robust and efficient global optimization algorithm for planar competitive location problems. Annals of Operations Research, 167(1), 87–106.
Redondo, J.L., Fernández, J., García, I., Ortigosa, P.M. (2009b). Solving the multiple competitive facilities location and design problem on the plane. Evolutionary Computation, 17(1), 21–53.
Sánchez, M., Romero, M. (2006). Methodology for generation of heliostat field layout in central receiver systems based on yearly normalized energy surfaces. Solar Energy, 80(7), 861–874.
Solis, F.J., Wets, R.J.B. (1981). Minimization by random search techniques. Mathematics of Operations Research, 6(1), 19–30.
Vatti, B.R. (1992). A generic solution to polygon clipping. Communications of the ACM, 35(7), 56–63.
Wei, X., Lu, Z., Lin, Z., Zhang, H., Ni, Z. (2007). Optimization procedure for design of heliostat field layout of a 1mwe solar tower thermal power plant. In: Photonics Asia 2007. International Society for Optics and Photonics, pp. 684119–684119.
Zhang, H. (2007).
Multi-objective thermoeconomic optimisation of the design of heliostat field of solar tower power plants. Technical report.

