1 Introduction
Multiple attribute decision making (MADM) is a process of finding the best alternative that has the highest degree of satisfaction from a finite set of alternatives characterized with multiple attributes. Because of uncertainty and vagueness of human thinking, decision makers often consider preference values in terms of fuzzy set (Zadeh,
1965), hesitant fuzzy set (Torra,
2010), intuitionistic fuzzy set (Atanassov,
1986), Pythagorean fuzzy set (Yager,
2014), etc. However, these sets cannot properly express incomplete, indeterminate and inconsistent type information which generally occurs in MADM under uncertain environment. Smarandache (
1998) introduced neutrosophic set that can express incomplete, indeterminate and inconsistent type information with its three independent membership degrees: truth membership, indeterminacy membership, falsity membership. Since then, many researchers have successfully employed neutrosophic sets into MADM problem to develop several sophisticated strategies such as TOPSIS (Biswas
et al.,
2016a,
2018,
2019; Mondal
et al.,
2016; Ye,
2015a; Peng and Dai,
2018), AHP (Abdel-Basset
et al.,
2017,
2018a), COPRAS (Baušys
et al.,
2015; Şahin,
2019), DEMATEL (Abdel-Basset
et al.,
2018b), VIKOR (Baušys and Zavadskas,
2015; Liu and Zhang,
2015; Pramanik and Dalapati,
2018; Pramanik
et al.,
2018a,
2018b), MULTIMOORA (Stanujkic
et al.,
2017; Tian
et al.,
2017), TODIM (Ji
et al.,
2018a; Pramanik
et al.,
2017a,
2018c), WASPAS (Zavadskas
et al.,
2015; Nie
et al.,
2017), MAMVA (Zavadskas
et al.,
2017), ELECTREE (Peng
et al.,
2014; Zhang
et al.,
2016), similarity measure strategies (Pramanik
et al.,
2017b; Mondal
et al.,
2018a,
2018b; Ye,
2014a; Pramanik
et al.,
2017c,
2018d), aggregation operator strategies (Liu
et al.,
2016; Peng
et al.,
2015; Ye,
2014b; Ji
et al.,
2018b; Liu and Wang,
2016; Biswas
et al.,
2016c; Mondal
et al.,
2018c,
2019), cross entropy (Dalapati
et al.,
2017; Pramanik
et al.,
2018e,
2018f), etc.
Grey relational analysis (GRA) (Deng,
1989), a part of grey system theory, is another effective tool that has been successfully applied in solving a variety of MADM strategies (Zhang
et al.,
2005; Wei,
2010,
2011; Wei
et al.,
2011; Zhang and Liu,
2011; Pramanik and Mukhopadhyaya,
2011; Zhang
et al.,
2013). Recently, neutrosophic set has caught attention of the researchers for solving MADM using GRA strategy (Biswas
et al.,
2014a,
2014b; Pramanik and Mondal,
2015; Dey
et al.,
2016a,
2016b; Banerjee
et al.,
2017).
However, when decision makers are in doubt, they often hesitate to assign single value for rating alternatives, instead they prefer to assign a set of possible values. To deal with the issue, Torra (
2010) introduced hesitant fuzzy set, which permits the membership degree of an element to a given set to be represented by the set of possible numerical values in
$[0,1]$. This set, an extension of fuzzy set, is useful for handling uncertain information in MADM process. Xia and Xu (
2011) proposed some aggregation operators for hesitant fuzzy information and applied these operators to solve MADM. Wei (
2012) studied hesitant fuzzy MADM by developing some prioritized aggregation operators for hesitant fuzzy information. Xu and Zhang (
2013) developed TOPSIS method for hesitant fuzzy MADM with incomplete weight information. Li (
2014) extended the MULTIMOORA method for multiple criteria group decision making with hesitant fuzzy sets. Mu
et al. (
2015) investigated a novel aggregation principle for hesitant fuzzy elements.
In a hesitant fuzzy MADM, decision maker does not consider non-membership degree for rating alternatives. However, this degree is equally important to express imprecise information. Zhu
et al. (
2012) presented the idea of dual hesitant fuzzy set, in which membership degrees and non-membership degrees are in the form of sets of values in
$[0,1]$. Ye (
2014c) and Chen
et al. (
2014) proposed correlation method of dual hesitant fuzzy sets to solve MADM with hesitant fuzzy information. Singh (
2017) defined some distance and similarity measures for dual hesitant fuzzy set and utilized these measures in MADM.
Dual hesitant fuzzy set cannot properly capture indeterminate information in a decision making situation. Because of the inherent neutrosophic nature of human preferences, the rating values of alternatives and/or weights of attributes involved in the MADM problems are generally uncertain, imprecise, incomplete and inconsistent. Ye (
2015b) introduced single-valued neutrosophic hesitant fuzzy set (SVNHFS) by coordinating hesitant fuzzy set and single-valued neutrosophic set. SVNHFS is characterized by truth hesitancy, indeterminacy hesitancy and falsity-hesitancy membership functions which are independent in nature. Therefore, SVNHFS can express the three kinds of hesitancy information existing in MADM problems. Ye (
2015b) developed single valued neutrosophic hesitant fuzzy weighted averaging and single valued neutrosophic hesitant fuzzy weighted geometric operators for SVNHFS information and applied these two operators in MADM problems. Şahin and Liu (
2017) defined correlation co-efficient between SVNHFSs and used to MADM. Biswas
et al. (
2016a) proposed GRA strategy for solving MADM in SVNHFS environment. Wang and Li (
2018) proposed generalized SVNHF prioritized aggregation operators to solve MADM problem. Li and Zhang (
2018) developed SVNHF based choquet aggregation operators for solving MADM problems.
Liu and Shi (
2015) introduced interval neutrosophic hesitant fuzzy set (INHFS) which consists of three membership hesitancy functions: the truth, the indeterminacy and the falsity. The three membership functions of an element to a given set are individually expressed by a set of interval values contained in
$[0,1]$. Liu and Shi (
2015) proposed hybrid weighted average operator for interval neutrosophic hesitant fuzzy set and utilized the operators in MADM. Ye (
2016) put forward correlation coefficients of INHFSs and applied it to solve MADM problems. Biswas (
2018) proposed an extended GRA strategy for solving MADM in neutrosophic hesitant fuzzy environment with incomplete weight information. We observe that the SVNHFS as well as INHFS can be considered in many practical MADM problems in which the decision maker has to make a decision in neutrosophic hesitant fuzzy environment.
Up until now very few number of studies exist in the literature about GRA strategy of MADM under SVNHFS and INHFS environment. Therefore, we have an opportunity to extend the traditional methods or to propose new methods regarding GRA to deal with MADM in neutrosophic hesitant fuzzy environment.
In this study, our objectives are as follows:
-
1. To present the idea of MADM problem in SVNHFS and INHFS environments, where the preference values of alternatives are considered with either SVNHFSs or INHFSs and the weight information of attributes are assumed to be completely known, incompletely known, and completely unknown.
-
2. To develop some optimization models for determining weight information of attributes, when attributes’ weights are incompletely known, or completely unknown.
-
3. To propose GRA based strategy for handling MADM problem under SVNHFS and INHFS environments.
-
4. Finally, to present illustrative examples, one for SVNHFS and other for IVNHFs to show the feasibility and effectiveness of the proposed strategies.
To do so, the paper is organized as follows: Section
2 presents some basic concepts related to single valued neutrosophic set, interval neutrosophic set, hesitant fuzzy set, SVNHFS and INHFS. In Section
3, we define score function, accuracy function, Hamming distance measure for SVNHFS and INHFS. We propose NH-MADM strategy in SVNHFS environment in Section
4 and INH-MADM strategy in INHFS environment in Section
5. In Section
6, we illustrate the proposed NH-MADM and INH-MADM strategies with two examples. Finally, in Section
7 we present some concluding remarks and future scope of research of the study.
4 GRA Strategy for MADM with SVNHFS
In this section, we propose GRA based strategy to find out the best alternative in MADM under SVNHFS environment. Assume that
$A=\{{A_{1}},{A_{2}},\dots ,{A_{m}}\}$ be the discrete set of
m alternatives and
$C=\{{C_{1}},{C_{2}},\dots ,{C_{n}}\}$ be the set of
n attributes for an SVNHFSs based MADM problem. Suppose that the rating value of the
i-th alternative
${A_{i}}$ $(i=1,2,\dots ,m)$ over the attribute
${C_{j}}$ $(j=1,2,\dots ,n)$ is considered with SVNHFSs
${x_{ij}}=({t_{ij}},{i_{ij}},{f_{ij}})$, where
${t_{ij}}=\{{\gamma _{ij}}\mid {\gamma _{ij}}\in {t_{ij}},\hspace{0.1667em}0\leqslant {\gamma _{ij}}\leqslant 1\}$,
${i_{ij}}=\{{\delta _{ij}}\mid {\delta _{ij}}\in {i_{ij}},\hspace{0.1667em}0\leqslant {\delta _{ij}}\leqslant 1\}$ and
${f_{ij}}=\{{\eta _{ij}}\mid {\eta _{ij}}\in {f_{ij}},0\leqslant {\eta _{ij}}\leqslant 1\}$ indicate the possible truth, indeterminacy and falsity membership degrees of the rating
${x_{ij}}$ for
$i=1,2,\dots ,m$ and
$j=1,2,\dots ,n$. With these rating values, we construct a decision matrix
$X={({x_{ij}})_{m\times n}}$, where the entries assume the form of SVNHFSs. The decision matrix is constructed as follows:
We now propose MADM based on GRA to determine the most desirable alternative under the following cases:
Case 1a. Completely known attribute weights.
The weight vector of attributes prescribed by the decision maker is $w=({w_{1}},{w_{2}},\dots ,{w_{n}})$, where ${w_{j}}\in [0,1]$ and ${\textstyle\sum _{j=1}^{n}}{w_{j}}=1$.
However, in a real decision making, the information about the attribute weights is often incompletely known or completely unknown due to decision makers’ limited expertise about the public domain. In this case, we propose some models for determining the weight vector of the attributes under the following cases:
Case 2a. Incompletely known attribute weights.
In this case, we have to determine the attribute weights to find out the best alternative. The incomplete attribute weight information
H can be considered in the following form (Park
et al.,
2011; Park,
2004; Park
et al.,
1997):
-
1. A weak ranking:$\{{w_{i}}\geqslant {w_{j}}\}$, $i\ne j$;
-
2. A strict ranking:$\{{w_{i}}-{w_{j}}\geqslant {\epsilon _{i}}(>0)\}$, $i\ne j$;
-
3. A ranking of difference:$\{{w_{i}}-{w_{j}}\geqslant {w_{k}}-{w_{p}}\}$, $i\ne j\ne k\ne p$;
-
4. A ranking with multiples:$\{{w_{i}}\geqslant {\alpha _{i}}{w_{j}}$, $0\leqslant {\alpha _{i}}\leqslant 1,i\ne j$;
-
5. An interval form:$\{{\beta _{i}}\leqslant {w_{i}}\leqslant {\beta _{i}}+{\epsilon _{i}}(>0)$, $0\leqslant {\beta _{i}}\leqslant {\beta _{i}}+{\epsilon _{i}}\leqslant 1$.
We can take the weights of attributes as a subset of the above relationships for a particular decision making problem. We denote the considered weight information set by
H. The similarity measure of
${x_{ij}}$ to
${A_{j}^{+}}$ is defined as follows:
where
$D({x_{ij}}$,
${A_{j}^{+}})$ $(i=1,2,\dots ,m)$ denotes the Hamming distance between
${x_{ij}}$ to
${A_{j}^{+}}$. Similarly, the similarity measure of
${x_{ij}}$ to
${A_{j}^{-}}$ is determined as follows:
where
$D({x_{ij}}$,
${A_{j}^{-}})$ $(i=1,2,\dots ,m)$ denotes the Hamming distance between
${x_{ij}}$ to
${A_{j}^{-}}$. Then the weighted similarity measures of the alternative
${A_{i}}$ $(i=1,2,\dots ,m)$ to
${A^{+}}=({A_{1}^{+}},{A_{2}^{+}},\dots ,{A_{n}^{+}})$ and
${A^{-}}=({A_{1}^{-}},{A_{2}^{-}},\dots ,{A_{n}^{-}})$ are respectively determined as follows:
An acceptable weight vector
$w=({w_{1}},{w_{2}},\dots ,{w_{n}})$ should make all the similarities
$({S_{1}^{+}},{S_{2}^{+}},\dots ,{S_{m}^{+}})$ to ideal solution
$({A_{i1}^{+}},{A_{i2}^{+}},\dots ,{A_{in}^{+}})$ as large as possible and the similarities
$({S_{1}^{-}},{S_{2}^{-}},\dots ,{S_{m}^{-}})$ to ideal solution
$({A_{i1}^{-}},{A_{i2}^{-}},\dots ,{A_{in}^{-}})$ as small as possible under the condition
$w\in H$. Therefore, we can set the following multiple objective non-linear optimization model to determine the weight vector:
Since each alternative is non-inferior, there exists no preference relation among the alternatives. Then we can aggregate the above multiple objective optimization models with equal weights into the following single objective optimization model:
By solving the Model-2, we obtain the optimal solution
$w=({w_{1}},{w_{2}},\dots ,{w_{n}})$ that can be used as the weight vector of the attributes. Using this weight vector and following Step 3 to Step 5, we can easily determine the relative closeness coefficient
${S_{i}}$ $(i=1,2,\dots ,m)$ of each alternative to find out an optimal alternative.
Case 3a. Completely unknown attribute weights.
Here we construct the following non-linear programming model to determine the weights of attributes.
We now aggregate the multiple objective optimization models (see Eq. (
21)) to obtain the following single-objective optimization model:
To solve the Model-4, we consider the following Lagrange function:
where the real number
ϕ is called the Lagrange multiplier. Differentiating partially
L with respect to
${w_{j}}$ and
ϕ, we have the following equations:
It follows from Eq. (
24) that
Putting this value of
${w_{j}}$ in Eq. (
25), we have
where
$\phi <0$ and
$\sqrt{{\textstyle\sum _{j=1}^{n}}{\big({\textstyle\sum _{i=1}^{m}}S({x_{ij}},{A_{j}^{+}})\big)^{2}}}$ implies the sum of similarities with respect to the
j-th attribute. Combining Eq. (
26) and Eq. (
27), we obtain
Then, by normalizing
${w_{j}}$ $(j=1,2,\dots ,n)$, we make their sum into a unit and obtain the normalized weight of the
j-th attribute:
and consequently, we obtain the weight vector of the attribute as
$\bar{w}=({\bar{w}_{1}},{\bar{w}_{2}},\dots ,{\bar{w}_{n}})$.
Following Step 3 to Step 5, presented in the current section, we can easily determine the best alternative by using this weight vector.
5 GRA Strategy for MADM with INHFS
We consider a MADM problem in which
$A=\{{A_{1}},{A_{2}},\dots ,{A_{m}}\}$ is the set of alternatives and
$C=\{{C_{1}},{C_{2}},\dots ,{C_{n}}\}$ is the set of attributes. We assume that the rating value of the alternative
${A_{i}}$ $(i=1,2,\dots ,m)$ over the attribute
${C_{j}}$ $(j=1,2,\dots ,n)$ is represented by interval neutrosophic hesitant fuzzy element
${\tilde{n}_{ij}}=({\tilde{t}_{ij}},{\tilde{i}_{ij}},{\tilde{f}_{ij}})$, where
${\tilde{t}_{ij}}=\{{\tilde{\gamma }_{ij}}|{\tilde{\gamma }_{ij}}\in {\tilde{t}_{ij}}\}$,
${\tilde{i}_{ij}}=\{{\tilde{\delta }_{ij}}|{\tilde{\delta }_{ij}}\in {\tilde{i}_{ij}}\}$ and
${\tilde{f}_{ij}}=\{{\tilde{\eta }_{ij}}|{\tilde{\eta }_{ij}}\in {\tilde{f}_{ij}}\}$ are three sets of some interval values in the real unit interval
$[0,1]$. These values denote the possible truth, indeterminacy and falsity membership hesitant degrees with the following limits:
${\tilde{\gamma }_{ij}}=[{\gamma _{ij}^{L}},{\gamma _{ij}^{U}}]\subseteq [0,1]$,
${\tilde{\delta }_{ij}}=[{\delta _{ij}^{L}},{\delta _{ij}^{U}}]\subseteq [0,1]$,
${\tilde{\eta }_{ij}}=[{\eta _{ij}^{L}},{\eta _{ij}^{U}}]\subseteq [0,1]$ and
$0\leqslant \sup \tilde{\gamma }+\sup \tilde{\delta }+\sup \tilde{\eta }+\leqslant 3$, where
${\tilde{\gamma }^{+}}={\textstyle\bigcup _{\tilde{\gamma }\in \tilde{t}(x)}}\max \{{\gamma _{ij}^{U}}\}$,
${\tilde{\delta }^{+}}={\textstyle\bigcup _{\tilde{\delta }\in \tilde{i}(x)}}\max \{{\delta _{ij}^{U}}\}$, and
${\tilde{\eta }^{+}}={\textstyle\bigcup _{\tilde{\eta }\in \tilde{f}(x)}}\max \{{\eta _{ij}^{U}}\}$. Then we construct an interval neutrosophic hesitant fuzzy decision matrix
N as
We solve the interval neutrosophic hesitant fuzzy MADM considering the following two cases:
Case 1b. Completely known attribute.
Assume that $\Lambda =({\lambda _{1}},{\lambda _{2}},\dots ,{\lambda _{n}})$ be the weight vector such that ${\lambda _{j}}\in [0,1]$ and ${\textstyle\sum _{j=1}^{n}}{\lambda _{j}}=1$.
We now consider the following steps required for the proposed strategy:
Case 2b. Incompletely known attribute weights.
If the information about the attribute weights is incomplete, then we can follow the same procedures discussed in Case 2a of Section
4. Then we determine the similarity measure between
${\tilde{n}_{ij}}$ and
${\tilde{A}_{j}^{+}}$ as
where
$d({\tilde{n}_{ij}},{\tilde{A}_{j}^{+}})$ $(i=1,2,\dots ,m)$ denotes the Hamming distance between
${\tilde{n}_{ij}}$ and
${\tilde{A}_{j}^{+}}$. Similarly, we obtain the similarity measure between
${\tilde{n}_{ij}}$ and
${\tilde{A}_{j}^{-}}$ as
where
$d({\tilde{n}_{ij}}$,
${\tilde{A}_{j}^{-}})$ $(i=1,2,\dots ,m)$ denotes the Hamming distance between
${\tilde{n}_{ij}}$ to
${\tilde{A}_{j}^{-}}$. The weighted similarity measures of the alternative
${A_{i}}$ $(i=1,2,\dots ,m)$ to
${\tilde{A}^{+}}=({\tilde{A}_{1}^{+}},{\tilde{A}_{2}^{+}},\dots ,{\tilde{A}_{n}^{+}})$ and
${\tilde{A}^{-}}=({\tilde{A}_{1}^{-}},{\tilde{A}_{2}^{-}},\dots ,{\tilde{A}_{n}^{-}})$ are determined as follows:
We find a suitable weight vector
$\Lambda =({\lambda _{1}},{\lambda _{2}},\dots ,{\lambda _{n}})$ that makes all the similarities
$({s_{1}^{+}},{s_{2}^{+}},\dots ,{s_{m}^{+}})$ to ideal solution
$({\tilde{A}_{1}^{+}},{\tilde{A}_{2}^{+}},\dots ,{\tilde{A}_{n}^{+}})$ as large as possible and the similarities
$({s_{1}^{-}},{s_{2}^{-}},\dots ,{s_{m}^{-}})$ to ideal solution
$({\tilde{A}_{1}^{-}},{\tilde{A}_{2}^{-}},\dots ,{\tilde{A}_{n}^{-}})$ as small as possible with the condition
$\Lambda \in H$. Therefore, we can set the following multiple objective non-linear optimization model to determine the weight vector:
Since each alternative is non-inferior, then we construct the following single objective optimization model by aggregating the above multiple objective optimization models with equal weights:
Solving the Model-6, we have the optimal solution
$\Lambda =({\lambda _{1}},{\lambda _{2}},\dots ,{\lambda _{n}})$ that can be used as the weight vector of the attributes. Then we follow Step 3 to Step 5 to determine an optimal alternative.
Case 3b. Completely unknown attribute weights.
In this case we develop the following non-linear programming model to determine the attribute weights.
Similarly, we can aggregate all above multiple objective optimization model:
To solve the Model-4, we consider the following Lagrange function:
where the real number
ψ is the Lagrange multiplier. Then differentiating partially
L with respect to
${\lambda _{j}}$ and
ψ, we have
It follows from equation (
49) that
Putting this value of
${\lambda _{j}}$ in equation (
50), we have
where,
$\psi <0$ and
$\sqrt{{\textstyle\sum _{j=1}^{n}}{\big({\textstyle\sum _{i=1}^{m}}s({\tilde{n}_{ij}},{\tilde{A}_{j}^{+}})\big)^{2}}}$ implies the sum of similarities with respect to the
j-th attribute. Combining Eqs. (
26) and (
27), we obtain
To normalize
${\lambda _{j}}$ $(j=1,2,\dots ,n)$, we make their sum into a unit and obtain the normalized weight of the
j-th attribute:
Consequently, we obtain the weight vector of the attribute as
$\bar{\Lambda }=({\bar{\lambda }_{1}},{\bar{\lambda }_{2}},\dots ,{\bar{\lambda }_{n}})$. With this weight vector, we follow Step 3 to Step 5 to find out an optimal alternative.
We briefly present the steps of the proposed strategies in Fig.
1.
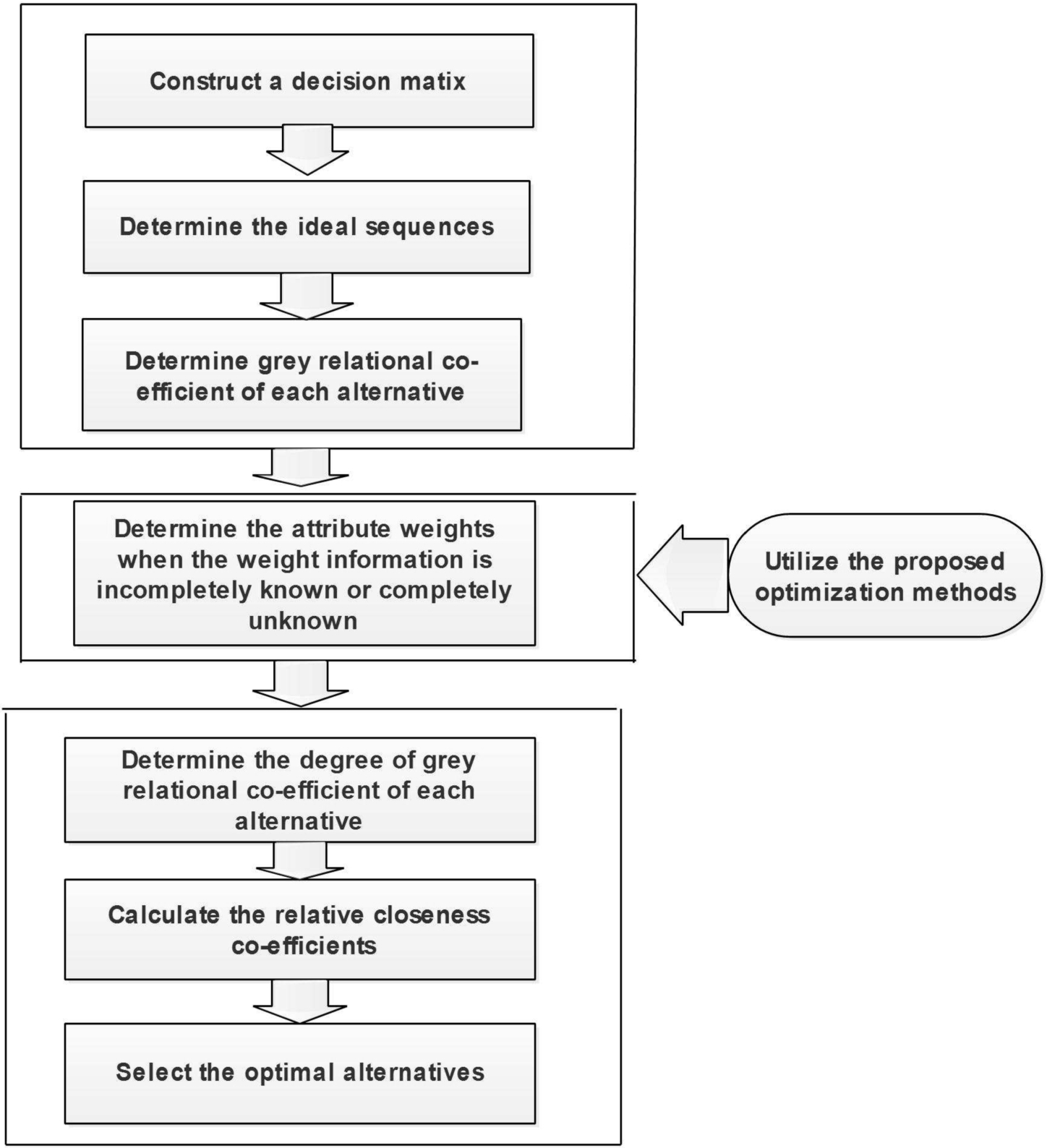
Fig. 1
The schematic diagram of the proposed strategy.

