1 Introduction
Multi-criteria decision-making (MCDM) methods and techniques have been used and developed by many researchers and applied to many real-world problems. The MCDM methods and techniques are usually categorized into two classes: multi-attribute decision-making (MADM) and multi-objective decision-making (MODM). The MODM methods are used to deal with continuous MCDM problems, and the MADM methods are utilized to handle discrete MCDM problems (Rezaei,
2015). However, MCDM is a common term to describe the MADM (discrete MCDM) methods, and because the focus of this study is on this class, we also use this terminology. In this class, we are usually confronted with a decision-matrix which contains information about a number of alternatives with respect to a number of criteria or attributes. The aim of the MCDM methods is to evaluate the alternatives and/or criteria.
Several MCDM methods have been proposed during the past decades. Here, we briefly review some important methods which are used for criteria weight determination and alternative evaluation based on the information of the decision-matrix, and readers are referred to some recent review articles on MCDM methods and their applications for further details (Behzadian
et al.,
2012; Abdullah and Adawiyah,
2014; Stefano
et al.,
2015; Gul
et al.,
2016; Mardani
et al.,
2017; Keshavarz Ghorabaee
et al.,
2017b). In the following, we present brief explanations of the SAW (Simple Additive Weighting), WASPAS (Weighted Aggregated Sum Product ASsessment), COPRAS (COmplex PRoportional ASsessment), TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution), VIKOR (from Serbian: VIseKriterijumska Optimizacija I Kompromisno Resenje) and EDAS (Evaluation based on Distance from Average Solution) methods which are used for the evaluation of alternatives. The range of the MCDM methods is wider than the mentioned methods. However, these methods are reviewed because we use them in the current study.
SAW is an old method which is likely the most common and very widely used method for the evaluation of alternatives. MacCrimmon (
1968) is one of the first researchers that summarized this method. In this method, the performance of each alternative is determined by multiplying the rating of each alternative on each criterion by the weight assigned to the criterion and then summing these products over all criteria (Hwang and Yoon,
1981). This is a simple, easy to use and easy to understand method, and has been used in many studies (Chen and Hwang,
1992). The researches of Wang (
2015), Wang
et al. (
2016a), Goodridge (
2016), Kalibatas and Kovaitis (
2017) and Muddineni
et al. (
2017), are some of the recent studies on the SAW method. Abdullah and Adawiyah (
2014) presented a review of the applications of simple additive weighting and its fuzzy variants from 2003 to 2013.
Zavadskas
et al. (
2012) proposed the WASPAS method based on a combination of the SAW or weighted sum model (WSM) and weighted product model (WPM). This method has the advantages of both of them. Many researchers have utilized this efficient method in their studies. In some recent studies, Bauðys and Juodagalvienë (
2017), Karabasevic
et al. (
2017), Nie
et al. (
2017), Peng and Dai (
2017) applied the WASPAS method to the MCDM problems. Mardani
et al. (
2017) presented a systematic review of applications and fuzzy developments of the WASPAS method.
The COPRAS method is an efficient MCDM method in which a ratio based on two measures (the summation of beneficial criteria performance and the summation of non-beneficial criteria performance) is used to evaluate alternatives (Zavadskas
et al.,
1994). We should define a set of beneficial and a set of non-beneficial criteria to use this method and determine the performance values of alternatives. This method has also been applied to many real-world MCDM problems. Wang
et al. (
2016b), Mulliner
et al. (
2016), Serrai
et al. (
2017), Rathi and Balamohan (
2017), Turanoglu Bekar
et al. (
2016) and Nakhaei
et al. (
2016) have done some studies on this method recently. A review of this method and its applications was presented by Stefano
et al. (
2015).
TOPSIS is a value-based compensatory method introduced by Hwang and Yoon (
1981). In this method, alternatives are ranked according to their distances from two reference points called ideal (positive-ideal) and nadir (negative-ideal) solutions. However, Opricovic and Tzeng (
2004) noted that the relative importance of these distances is not considered in the TOPSIS method. This method is one of the popular MCDM methods among researchers. Some recent applications of the TOPSIS method can be found in the studies done by Mao
et al. (
2018), Cayir Ervural
et al. (
2018), Chen
et al. (
2018), Shen
et al. (
2018), Polat
et al. (
2017) and Walczak and Rutkowska (
2017). A review of developments and applications of this method was made by Behzadian
et al. (
2012).
The VIKOR method, which was proposed by Opricovic (
1998), is a reference-based MCDM method that is able to solve decision problems with non-commensurable and conflicting criteria. The reference point of this method is an ideal solution, and alternatives are evaluated based on Manhattan and Chebyshev distances from this point. The VIKOR method is somewhat similar to the TOPSIS method, but there are some important differences that were explained by Opricovic and Tzeng (
2004). This method has also been used in many real-world MCDM problems such as military airport location selection (Sennaroglu and Varlik Celebi,
2018), risk evaluation of construction projects (Wang
et al.,
2018), maritime transportation (Soner
et al.,
2017), energy management (Sakthivel
et al.,
2017) and financial performance evaluation (Chang and Tsai,
2016). Gul
et al. (
2016) conducted a state-of-the-art literature review on VIKOR applications.
EDAS is an efficient and relatively new MCDM method introduced by Keshavarz Ghorabaee
et al. (
2015). The EDAS method measures the desirability of alternatives based on the distance from an average solution. Like some other MCDM methods, EDAS can be used to handle multi-criteria decision-making problems with non-commensurable and conflicting criteria. Despite the newness of the EDAS method, it has been applied to many practical MCDM problems like supplier selection (Keshavarz Ghorabaee
et al.,
2016b; Stević
et al.,
2017), life cycle sustainability assessment (Ren and Toniolo,
2018) and evaluation of architectural plans (Juodagalvienë
et al.,
2017).
Besides the MCDM methods used for evaluation of alternatives, there are some other methods for determination of objective weights of criteria. The Standard Deviation (SD) and Entropy are two common methods which determine the objective weights based on the within-criterion variation information, and assign smaller weights to a criterion if it has similar values across alternatives. These methods have been used in many studies (Keshavarz Ghorabaee
et al.,
2016a; Zhang
et al.,
2011; Liu
et al.,
2010). CRITIC (CRiteria Importance Through Inter-criteria Correlation) is another method which considers within- and between-criterion variation information (Diakoulaki
et al.,
1995). The correlation between criteria is used to measure variations between criteria. In this method, lower values of correlation have a positive effect on the weight of each criterion. Some researchers applied CRITIC to practical MCDM problems (Yalçı and Ünlü,
2017; Keshavarz Ghorabaee
et al.,
2017a; Adalı and Işık,
2017; Rostamzadeh
et al.,
2018).
In this paper, we introduce a new method that, unlike many other MCDM methods, can be used for simultaneous evaluation of criteria and alternatives (SECA) in a multi-criteria decision-making problem. A multi-objective non-linear mathematical model is developed to make the evaluation process. The model includes three objective functions. The first objective is related to maximization of the overall performance of alternatives, and the second and third objectives concern within- and between-criterion variation information. The within-criterion variation is measured by the standard deviation, and the between-criterion variation is considered using the correlation. By optimization of the developed mathematical model, the overall performance scores of alternatives and the objective weights of criteria can be determined simultaneously. A numerical example is used in this study for validation of the proposed method. Based on this example, the validity of objective criteria weights and the stability of the overall performance scores and ranking results are analysed. Moreover, a comparison is made between the ranking results of the proposed method with the results of the SAW, WASPAS, COPRAS, TOPSIS, VIKOR and EDAS methods.
The rest of this paper is organized as follows. Section
2 presents a new method for simultaneous evaluation of criteria and alternatives (SECA). In Section
3, we use a numerical example for validation of the proposed method by means of three analyses including “Analysis of criteria weights”, “Analysis of the performance of alternatives”, and “Comparative analysis”. In Section
4, we present conclusions.
2 Simultaneous Evaluation of Criteria and Alternatives (SECA)
In this section, a new method is proposed to handle multi-criteria decision-making problems. The aim of this method is to determine the overall performance scores of alternatives and the weights of criteria simultaneously. A multi-objective non-linear mathematical model is formulated in this section to reach this aim. To formulate the mathematical model, two types of reference points are described for criteria weights. The first type is based on within-criterion variation information defined by the standard deviation and the second is related to between-criterion variation information determined based on the correlation measure. The multi-objective model seeks to maximize the overall performance of each alternative and minimize the deviation of criteria weights from the reference points. For maximization of the overall performance of each alternative, a weighted sum model is used as an objective. Also, we take advantage of the sum of squared deviations from the reference points to define the other objectives of the model.
Suppose that we have an MCDM problem with
n alternatives and
m criteria, and the weight of each criterion (
${w_{j}}$,
$j\in \{1,2,\dots ,m\}$) is unknown. We can define the decision-matrix of this problem as follows:
where
${x_{ij}}$ denotes the performance value of
ith (
$i\in \{1,2,\dots ,n\}$) alternative on
jth (
$j\in \{1,2,\dots ,m\}$) criterion and
${x_{ij}}>0$.
Based on Eq. (
1), we can construct the normalized decision-matrix using the following equations
where
and
$\mathit{BC}$ and
$\mathit{NC}$ are the sets of beneficial and non-beneficial criteria, respectively.
Let
${\mathbf{V}_{j}}={[{x_{ij}^{N}}]_{n\times 1}}$ denotes the vector of
jth (
$j\in \{1,2,\dots ,m\}$) criterion. The standard deviation of the elements of each vector (
${\sigma _{j}}$) can get the within-criterion variation information. To capture the between-criterion variation information from the decision-matrix, we need to calculate the correlation between each pair of vectors of criteria. Let us denote by
${r_{jl}}$ the correlation between
jth and
lth vectors (
j and
$l\in \{1,2,\dots ,m\}$). Then the following summation (
${\pi _{j}}$) can reflect the degree of conflict between
jth criterion and the other criteria (Diakoulaki
et al.,
1995):
An increase in the variation within the vector of a criterion (
${\sigma _{j}}$), as well as an increase in the degree of conflict between a criterion and the other criteria (
${\pi _{j}}$), intensifies the objective importance of that criterion. Accordingly, we define the normalized values of
${\sigma _{j}}$ and
${\pi _{j}}$ as the reference points for the weights of criteria. These values can be calculated as follows:
Based on the above description, a multi-objective non-linear programming model is formulated as follows:
In Model (7), the first equation maximizes the overall performance of each alternative, and the second and third equations minimize the deviation of criteria weights from the reference points for each criterion. Eq. (
7.4) guarantees that the sum of weights is equal to 1. Eqs. (
7.5) and (
7.6) set the weights of criteria to some values in the interval
$[\varepsilon ,1]$. It should be noted that
ε is a small positive parameter considered as a lower bound for criteria weights. In this study, this parameter is set to 10
${^{-3}}$.
To optimize Model (7), we use some techniques of the multi-objective optimization and transform the model to Model (8) as follows:
According to the objective function of Model (8), the minimum of the overall performance score of alternatives (${\lambda _{a}}$) is maximized. Because the deviations from reference points should be minimized, they are subtracted from the objective function with a coefficient β ($\beta \geqslant 0$). This coefficient affects the importance of reaching the reference points of criteria weights.
The overall performance score of each alternative (${S_{i}}$) and the objective weight of each criterion (${w_{j}}$) are determined by solving Model (8).
3 Computational Analysis
Table 1
The decision-matrix of the numerical example.
|
${C_{1}}\in \mathit{BC}$ |
${C_{2}}\in \mathit{BC}$ |
${C_{3}}\in \mathit{BC}$ |
${C_{4}}\in \mathit{NC}$ |
${C_{5}}\in \mathit{NC}$ |
${C_{6}}\in \mathit{NC}$ |
${C_{7}}\in \mathit{NC}$ |
| ${A_{1}}$ |
23 |
264 |
2.37 |
0.05 |
167 |
8900 |
8.71 |
| ${A_{2}}$ |
20 |
220 |
2.2 |
0.04 |
171 |
9100 |
8.23 |
| ${A_{3}}$ |
17 |
231 |
1.98 |
0.15 |
192 |
10800 |
9.91 |
| ${A_{4}}$ |
12 |
210 |
1.73 |
0.2 |
195 |
12300 |
10.21 |
| ${A_{5}}$ |
15 |
243 |
2 |
0.14 |
187 |
12600 |
9.34 |
| ${A_{6}}$ |
14 |
222 |
1.89 |
0.13 |
180 |
13200 |
9.22 |
| ${A_{7}}$ |
21 |
262 |
2.43 |
0.06 |
160 |
10300 |
8.93 |
| ${A_{8}}$ |
20 |
256 |
2.6 |
0.07 |
163 |
11400 |
8.44 |
| ${A_{9}}$ |
19 |
266 |
2.1 |
0.06 |
157 |
11200 |
9.04 |
| ${A_{10}}$ |
8 |
218 |
1.94 |
0.11 |
190 |
13400 |
10.11 |
In this section, a computational analysis is made to validate the results of the proposed method. This analysis is presented in the three following sub-sections. Firstly, we compare the objective weights resulted from the proposed method with the results of some other methods, secondly the overall performance scores and ranks of alternatives are analysed and finally we make a comparative analysis based on some existing MCDM methods. It should be noted that the model is solved using the LINGO 11 software, and the code and instructions can be found in Keshavarz Ghorabaee (
2018).
To make the computational analysis, a numerical example is borrowed from the study of Keshavarz Ghorabaee
et al. (
2015). The decision-matrix of the example along with the type of each criterion is shown in Table
1, and the normalized decision-matrix, which is constructed using Eqs. (
2) and (
3), is represented in Table
2. As can be seen in these tables, there are ten alternatives (
${A_{1}}$ to
${A_{10}}$) which need to be evaluated with respect to seven criteria (
${C_{1}}$ to
${C_{7}}$).
Table 2
The normalized decision-matrix of the numerical example.
|
${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
${C_{5}}$ |
${C_{6}}$ |
${C_{7}}$ |
| ${A_{1}}$ |
1 |
0.9925 |
0.9115 |
0.8 |
0.9401 |
1 |
0.9449 |
| ${A_{2}}$ |
0.8696 |
0.8271 |
0.8462 |
1 |
0.9181 |
0.9780 |
1 |
| ${A_{3}}$ |
0.7391 |
0.8684 |
0.7615 |
0.2667 |
0.8177 |
0.8241 |
0.8305 |
| ${A_{4}}$ |
0.5217 |
0.7895 |
0.6654 |
0.2000 |
0.8051 |
0.7236 |
0.8061 |
| ${A_{5}}$ |
0.6522 |
0.9135 |
0.7692 |
0.2857 |
0.8396 |
0.7063 |
0.8812 |
| ${A_{6}}$ |
0.6087 |
0.8346 |
0.7269 |
0.3077 |
0.8722 |
0.6742 |
0.8926 |
| ${A_{7}}$ |
0.9130 |
0.9850 |
0.9346 |
0.6667 |
0.9813 |
0.8641 |
0.9216 |
| ${A_{8}}$ |
0.8696 |
0.9624 |
1 |
0.5714 |
0.9632 |
0.7807 |
0.9751 |
| ${A_{9}}$ |
0.8261 |
1 |
0.8077 |
0.6667 |
1 |
0.7946 |
0.9104 |
| ${A_{10}}$ |
0.3478 |
0.8195 |
0.7462 |
0.3636 |
0.8263 |
0.6642 |
0.8140 |
3.1 Analysis of Criteria Weights
In this sub-section, we solve Model (8) with the data provided in Table
2 and different values for the parameter
β (
$\beta =0.1$, 0.2, 0.3, 0.4, 0.5, 1, 2, 3, 4 and 5). By solving the model, 10 sets of criteria weights are determined. The weights of criteria related to changing the values of
β are presented in Table
3, and the variation of the weights is shown in Fig.
1.
According to Fig.
1, we can see that the weights of criteria are more stable when the values of the
β parameter are greater than 3 (
$\beta \geqslant 3$). Now, to validate the results, the weights of criteria are determined using some other methods. Here three methods including the SD, CRITIC and Entropy methods are chosen for the comparison analysis (Zardari
et al.,
2014). It should be noted that the normalization step in the CRITIC method is skipped because we use the normalized decision-matrix (Table
2) for computations. The weights of criteria determined by these methods are presented in Table
4.
Table 3
The sets of criteria weights determined by changing β.
|
β |
|
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
1 |
2 |
3 |
4 |
5 |
| ${w_{1}}$ |
0.001 |
0.001 |
0.035 |
0.068 |
0.081 |
0.133 |
0.148 |
0.153 |
0.156 |
0.158 |
| ${w_{2}}$ |
0.284 |
0.253 |
0.233 |
0.221 |
0.213 |
0.175 |
0.157 |
0.151 |
0.148 |
0.146 |
| ${w_{3}}$ |
0.001 |
0.083 |
0.115 |
0.131 |
0.142 |
0.129 |
0.126 |
0.126 |
0.125 |
0.125 |
| ${w_{4}}$ |
0.001 |
0.001 |
0.001 |
0.001 |
0.010 |
0.104 |
0.159 |
0.178 |
0.187 |
0.193 |
| ${w_{5}}$ |
0.289 |
0.239 |
0.212 |
0.196 |
0.186 |
0.145 |
0.125 |
0.118 |
0.115 |
0.113 |
| ${w_{6}}$ |
0.134 |
0.185 |
0.192 |
0.189 |
0.184 |
0.172 |
0.162 |
0.159 |
0.157 |
0.156 |
| ${w_{7}}$ |
0.289 |
0.238 |
0.211 |
0.194 |
0.183 |
0.143 |
0.122 |
0.116 |
0.112 |
0.110 |
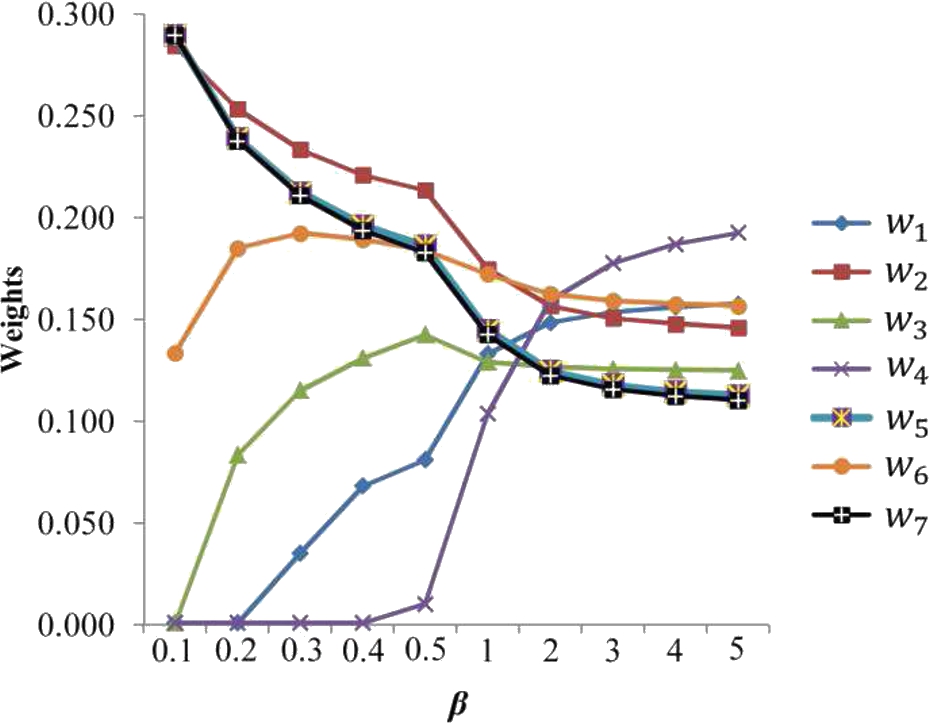
Fig. 1
The variation of the criteria weights related to β.
To make a comparison, the correlations between the results of the proposed method in different values of
β and the results of the other methods (SD, CRITIC and Entropy) are computed. If the value of correlation is greater than 0.6, we can say that there is a strong relationship between the results (Walters,
2009). In Table
5, we present the values of correlations between the results.
Table 4
The objective weights of criteria for comparison.
|
SD |
CRITIC |
Entropy |
| ${w_{1}}$ |
0.2206 |
0.1706 |
0.1991 |
| ${w_{2}}$ |
0.0888 |
0.1212 |
0.0199 |
| ${w_{3}}$ |
0.1148 |
0.1104 |
0.0397 |
| ${w_{4}}$ |
0.2934 |
0.2891 |
0.6596 |
| ${w_{5}}$ |
0.0801 |
0.0748 |
0.0162 |
| ${w_{6}}$ |
0.1295 |
0.1647 |
0.0521 |
| ${w_{7}}$ |
0.0727 |
0.0693 |
0.0134 |
Table 5
The correlation between the results of criteria weight determination.
| β |
SD |
CRITIC |
Entropy |
| 0.1 |
−0.7745 |
−0.6788 |
−0.5920 |
| 0.2 |
−0.8896 |
−0.7404 |
−0.7312 |
| 0.3 |
−0.9345 |
−0.7887 |
−0.8245 |
| 0.4 |
−0.9534 |
−0.8296 |
−0.8965 |
| 0.5 |
−0.9577 |
−0.8404 |
−0.9215 |
| 1 |
−0.6839 |
−0.5063 |
−0.7397 |
| 2 |
0.5552 |
0.7391 |
0.4719 |
| 3 |
0.8011 |
0.9238 |
0.7368 |
| 4 |
0.8604 |
0.9597 |
0.8040 |
| 5 |
0.8849 |
0.9725 |
0.8326 |
As it can be seen it Table
5, the values of correlations are greater than 0.6 for
$\beta \geqslant 3$ (the values are bold in the table). Accordingly,
$\beta =3$ can be a good threshold value for computations in the proposed method.
3.2 Analysis of the Performance of Alternatives
In this sub-section, we obtain the overall performance score of each alternative (
${S_{i}}$) by solving Model (8) based on the data provided in Table
2 and the same values of
β as we have used for the analysis of criteria weights. The overall performance scores obtained are presented in Table
6 and the corresponding ranks of alternatives are shown in Table
7. Also, the graphical view of performance scores is represented in Fig.
2.
As we can see in Fig.
2 (and Table
6), the performance of alternatives are more distinguishable and more stable when the values of
β are greater than 3 (
$\beta \geqslant 3$).
To analyse the stability of the ranks of criteria in different values of
β, the Spearman’s rank correlation coefficients (
${r_{s}}$) between each column of Table
7 are computed. The results are presented in Table
8.
Table 6
The overall performance scores of alternatives in different values of β.
|
β |
|
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
1 |
2 |
3 |
4 |
5 |
| ${S_{1}}$ |
0.9643 |
0.9631 |
0.9635 |
0.9641 |
0.9625 |
0.9500 |
0.9416 |
0.9388 |
0.9374 |
0.9365 |
| ${S_{2}}$ |
0.9239 |
0.9196 |
0.9157 |
0.9125 |
0.9113 |
0.9169 |
0.9203 |
0.9215 |
0.9220 |
0.9224 |
| ${S_{3}}$ |
0.8360 |
0.8295 |
0.8237 |
0.8193 |
0.8120 |
0.7547 |
0.7218 |
0.7108 |
0.7053 |
0.7020 |
| ${S_{4}}$ |
0.7890 |
0.7738 |
0.7593 |
0.7482 |
0.7378 |
0.6700 |
0.6335 |
0.6213 |
0.6152 |
0.6116 |
| ${S_{5}}$ |
0.8540 |
0.8370 |
0.8247 |
0.8162 |
0.8075 |
0.7441 |
0.7098 |
0.6983 |
0.6926 |
0.6892 |
| ${S_{6}}$ |
0.8400 |
0.8180 |
0.8031 |
0.7928 |
0..7836 |
0.7221 |
0.6893 |
0.6784 |
0.6729 |
0.6697 |
| ${S_{7}}$ |
0.9490 |
0.9421 |
0.9389 |
0.9373 |
0.9342 |
0.9055 |
0.8894 |
0.8840 |
0.8814 |
0.8798 |
| ${S_{8}}$ |
0.9416 |
0.9347 |
0.9310 |
0.9289 |
0.9252 |
0.8850 |
0.8633 |
0.8560 |
0.8524 |
0.8503 |
| ${S_{9}}$ |
0.9459 |
0.9242 |
0.9130 |
0.9064 |
0.9009 |
0.8694 |
0.8525 |
0.8469 |
0.8441 |
0.8424 |
| ${S_{10}}$ |
0.7982 |
0.7841 |
0.7644 |
0.7482 |
0.7378 |
0.6735 |
0.6426 |
0.6324 |
0.6272 |
0.6241 |
Table 7
The ranks of alternatives in different values of β.
|
|
β |
|
|
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
1 |
2 |
3 |
4 |
5 |
| Rank |
${A_{1}}$ |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
${A_{2}}$ |
5 |
5 |
4 |
4 |
4 |
2 |
2 |
2 |
2 |
2 |
|
${A_{3}}$ |
8 |
7 |
7 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
|
${A_{4}}$ |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
|
${A_{5}}$ |
6 |
6 |
6 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
|
${A_{6}}$ |
7 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
|
${A_{7}}$ |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
|
${A_{8}}$ |
4 |
3 |
3 |
3 |
3 |
4 |
4 |
4 |
4 |
4 |
|
${A_{9}}$ |
3 |
4 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
|
${A_{10}}$ |
9 |
9 |
9 |
10 |
10 |
9 |
9 |
9 |
9 |
9 |
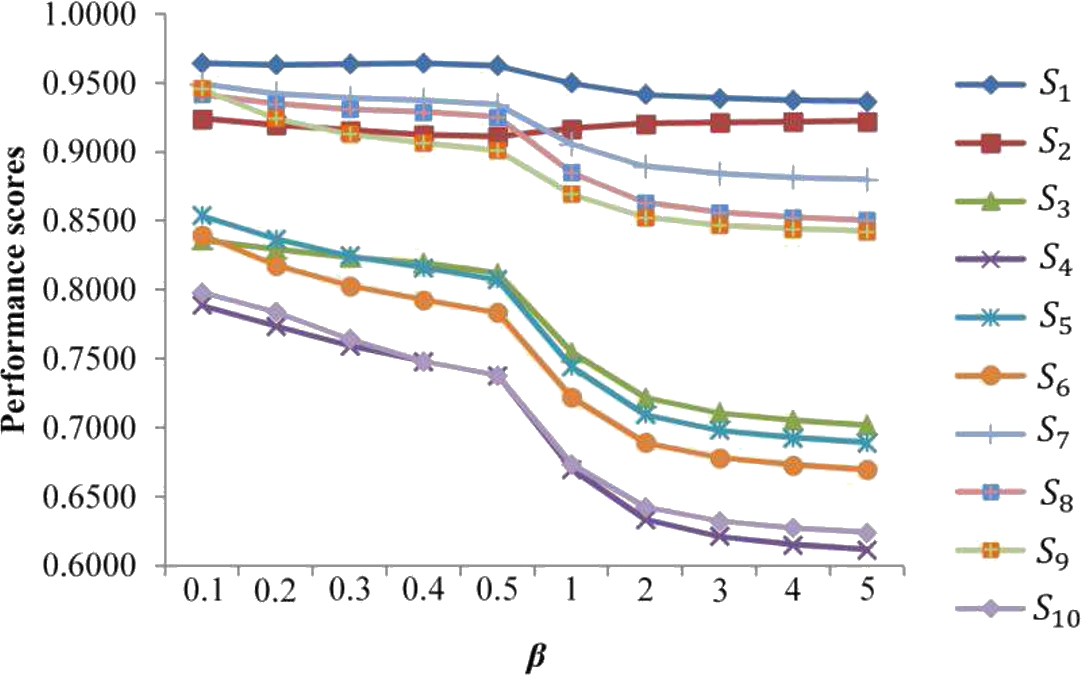
Fig. 2
Variations in the overall performance scores related to β.
Table 8
The correlation (${r_{s}}$) between the ranking results with different values of β.
|
|
β |
|
|
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
1 |
2 |
3 |
4 |
5 |
| β |
0.1 |
1 |
0.9758 |
0.9515 |
0.9240 |
0.9240 |
0.8788 |
0.8788 |
0.8788 |
0.8788 |
0.8788 |
|
0.2 |
0.9758 |
1 |
0.9879 |
0.9726 |
0.9726 |
0.9152 |
0.9152 |
0.9152 |
0.9152 |
0.9152 |
|
0.3 |
0.9515 |
0.9879 |
1 |
0.9848 |
0.9848 |
0.9515 |
0.9515 |
0.9515 |
0.9515 |
0.9515 |
|
0.4 |
0.9240 |
0.9726 |
0.9848 |
1 |
1 |
0.9605 |
0.9605 |
0.9605 |
0.9605 |
0.9605 |
|
0.5 |
0.9240 |
0.9726 |
0.9848 |
1 |
1 |
0.9605 |
0.9605 |
0.9605 |
0.9605 |
0.9605 |
|
1 |
0.8788 |
0.9152 |
0.9515 |
0.9605 |
0.9605 |
1 |
1 |
1 |
1 |
1 |
|
2 |
0.8788 |
0.9152 |
0.9515 |
0.9605 |
0.9605 |
1 |
1 |
1 |
1 |
1 |
|
3 |
0.8788 |
0.9152 |
0.9515 |
0.9605 |
0.9605 |
1 |
1 |
1 |
1 |
1 |
|
4 |
0.8788 |
0.9152 |
0.9515 |
0.9605 |
0.9605 |
1 |
1 |
1 |
1 |
1 |
|
5 |
0.8788 |
0.9152 |
0.9515 |
0.9605 |
0.9605 |
1 |
1 |
1 |
1 |
1 |
As can be seen in Table
7, we have a completely stable rank when the values of
β are greater than 1. Generally, we can say that
$\beta =3$ is also a good threshold for determination of the overall performance scores and ranks of alternatives.
3.3 Comparative Analysis
In this sub-section, the results of the proposed method are compared with those of some existing MCDM methods. We use six MCDM methods including SAW, WASPAS, COPRAS, TOPSIS, VIKOR and EDAS to make this comparison. Based on the results of the previous sections, the value of β is set to 3 for computations.
The methods which are used for comparative analysis need a set of weights to rank the alternatives. In the comparative analysis, we use the set of weights which has been determined by the proposed method with
$\beta =3$ (
${w_{1}}=0.153$,
${w_{2}}=0.151$,
${w_{3}}=0.126$,
${w_{4}}=0.178$,
${w_{5}}=0.118$,
${w_{6}}=0.159$ and
${w_{7}}=0.116$). Using the decision-matrix and this set of weights for criteria, the rank of alternatives is determined by the considered MCDM methods. The ranking results of the proposed method and the other methods are presented in Table
9. In the last row of this table, we can see the Spearman’s rank correlation coefficients (
${r_{s}}$) between the ranking result of SECA and the other methods.
According to Table
9, all of the correlation values are more than 0.8. Thus it can be said that there is a very strong relationship between the result of SECA and the MCDM methods considered for the comparative analysis (Walters,
2009). Based on these results we can conclude that the results of the proposed method are valid, and SECA can be considered as an efficient method to deal with the multi-criteria decision-making problems.
Table 9
The ranking results of different MCDM methods and the correlation values.
|
SAW |
WASPAS |
COPRAS |
TOPSIS |
VIKOR |
EDAS |
SECA |
| ${A_{1}}$ |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| ${A_{2}}$ |
2 |
2 |
2 |
2 |
5 |
2 |
2 |
| ${A_{3}}$ |
6 |
6 |
6 |
9 |
6 |
6 |
6 |
| ${A_{4}}$ |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
| ${A_{5}}$ |
7 |
7 |
7 |
8 |
7 |
7 |
7 |
| ${A_{6}}$ |
8 |
8 |
8 |
7 |
8 |
8 |
8 |
| ${A_{7}}$ |
3 |
3 |
3 |
3 |
2 |
3 |
3 |
| ${A_{8}}$ |
4 |
4 |
4 |
5 |
3 |
4 |
4 |
| ${A_{9}}$ |
5 |
5 |
5 |
4 |
4 |
5 |
5 |
| ${A_{10}}$ |
9 |
9 |
9 |
6 |
9 |
9 |
9 |
| ${r_{s}}$ |
1 |
1 |
1 |
0.867 |
0.927 |
1 |
– |
For using the proposed method, the suggested value of β is $\beta =3$. However, this parameter can be set according to the preferences of decision-makers and characteristics of the decision-making problem. The appropriate value of β can be estimated by making a sensitivity analysis based on the decision-matrix of the problem.
It should be noted that the elements of the decision-matrix should be greater than zero (${x_{ij}}>0$) to use SECA. If there are some elements with negative and/or zero values, they should be transformed.

