1 Introduction
Decision theory is a rapidly evolving field, particularly in the context of multi-criteria and multi-actor (or group) decision-making processes. This process entails ranking, selecting, or assigning a set of alternatives that are evaluated based on several conflicting criteria, typically performed by a group of individuals. The input data for this procedure can originate from various types of information, including quantitative and qualitative data. In many cases, this information may be subject to imprecision, ambiguity, or uncertainty due to measurement errors, imperfect knowledge, subjectivity, and other factors. Consequently, many decision-making models in the literature have been proposed to incorporate fuzzy set (FS) theory as a means of addressing this issue (Zadeh,
1965). In FS, each element of a set is characterized by a membership degree with a value in the unit interval
$[0,1]$, while the non-membership degree complements it. For instance, in the context of a stock selection problem, when evaluating the potential of a particular stock, an investor assigns a value of 0.89, signifying a favourable view on 89% of the stock’s potential, while holding a contrary opinion on 11%. The value 0.89 denotes the membership degree, whereas 0.11 represents the non-membership degree, with both initially defined as precise values. Subsequently, FS has expanded to include interval-valued FS (IVFS) (Zadeh,
1975), type-2 FS (T2FS) (Zadeh,
1965), and hesitant FS (HFS) (Torra and Narukawa,
2009), among others, to handle the issue of uncertain membership degrees instead of precise membership degrees. Some extensive reviews on the development of fuzzy set theory and its application in decision analysis can be referred to in the works of Dubois (
2011), Abdullah (
2013) and Kahraman
et al. (
2016).
In some other studies, researchers have argued that there are cases that go beyond the complementary nature of membership and non-membership degrees, involving indeterminate or incomplete information. Atanassov (
1986) introduced intuitionistic fuzzy set (IFS) as an extension of FS, where membership and non-membership degrees can exist independently within the unit interval, and the sum of the two degrees can be less than one. Additionally, a hesitancy degree was introduced to complement the membership and non-membership degrees. Similarly, IFS has undergone several developments, including the proposal of interval-valued IFS (IVIFS) (Atanassov and Gargov,
1989), type-2 IFS (T2IFS) (Zhao and Xiao,
2012), hesitant IFS (HIFS) (Beg and Rashid,
2014), among others, to represent uncertain membership and non-membership degrees (i.e. IF values). A substantial body of literature has reported on the expansion of multi-criteria and multi-actor decision-making models using these sets (Yusoff
et al.,
2011; Taib
et al.,
2016; Ecer
et al.,
2022).
Recently, Atanassov (
2020) introduced another extension of IFS, aiming to enhance the flexibility in interpreting and representing IF values. This extension is known as a Circular Intuitionistic Fuzzy Set (CIFS). In CIFS, each element of a set is characterized as a circle, with membership and non-membership degrees determining the centre and radius, denoted as
r, which represents the region of uncertainty. The primary distinction between CIFS and IVIFS lies in their representation of imprecision. IVIFS is depicted as a rectangle (bounded by lower and upper bounds of membership and non-membership degrees) within the IFS interpretation triangle (IFIT). In contrast, CIFS expresses its uncertainty region with equidistant boundaries from the centre. Fig.
1 provides a geometrical interpretation of IVIFS and CIFS.
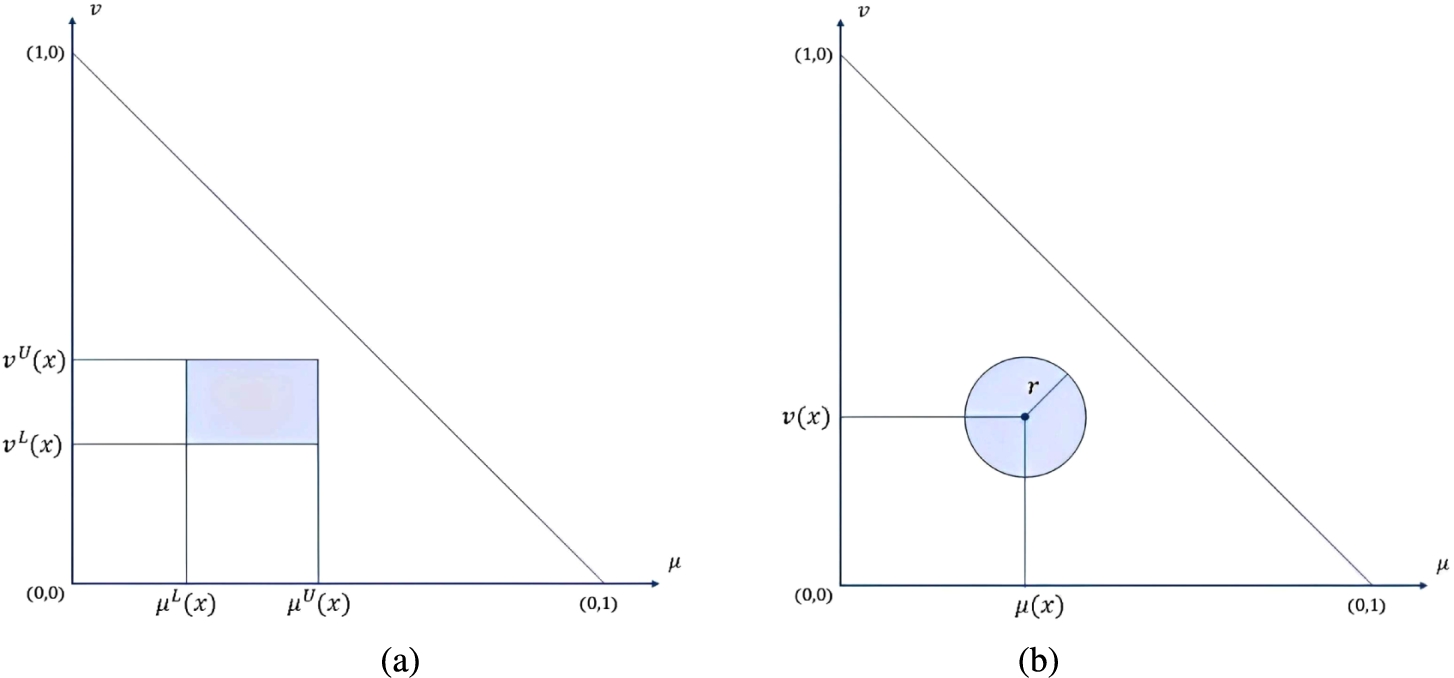
Fig. 1
Geometrical interpretation of (a) IVIFS and (b) CIFS.
The development of the CIFS theory is still in its early stages, and therefore, limited research has been conducted on it. In the initial paper, Atanassov (
2020) introduced CIFS, along with some fundamental operations and relations, where the radius was confined to the range of
$r\in [0,1]$. Subsequently, Atanassov expanded the range of the radius to
$[0,\sqrt{2}]$ in order to encompass the entire IFIT and also defined distance measures for CIFS (Atanassov and Marinov,
2021). Since then, there have been several studies aimed at advancing CIFS both in theory and practical applications. These include extensions of present worth analysis within the CIFS framework (Boltürk and Kahraman,
2022), distance and divergence measures tailored for CIFS (Khan
et al.,
2022), distance measure based on the theory of CIFS, considering the information of four aspects: membership degree, non-membership degree, radius and the assignment of hesitation degree (Xu and Wen,
2023), circular
q-rung orthopair fuzzy set and some algebraic properties (Yusoff
et al.,
2023), generalized CIFS (Pratama
et al.,
2023), circular pythagorean fuzzy sets (Bozyiğit
et al.,
2023) and its applications in decision-making models (Çakir and Taş,
2023), particularly in Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) (Kahraman and Alkan,
2021; Alkan and Kahraman,
2022; Chen,
2023), as well as Multicriteria Optimization and Compromise Solution (VIKOR) (Kahraman and Otay,
2021; Otay and Kahraman,
2021; Büyükselçuk and Sarı,
2023).
One of the intriguing developments in the context of CIFS in group decision-making problem was introduced by Kahraman and Alkan (
2021). Specifically, they proposed the inclusion of psychological behaviours within TOPSIS model under the CIFS environment, known as CIF-TOPSIS. These characteristics involve optimistic and pessimistic attitudes, which are represented as IF values derived from CIF values. The optimistic value is defined as the sum of the membership degree and the subtraction of the non-membership degree, both adjusted by the radius,
r. Conversely, the pessimistic value is defined in the opposite manner. In general, the optimistic value reflects the group’s inclination toward higher membership degrees (validity), while the pessimistic value indicates a tendency toward higher non-membership degrees (non-validity). However, these operations have shown certain limitations. Specifically, they may result in optimistic and pessimistic values falling outside the circular area. Ideally, all values should remain within the circular region to accurately represent the data. Furthermore, Kahraman and Alkan (
2021) restricted the radius,
r to the range
$[0,1]$ in CIF-TOPSIS, which covers only a certain region within the IFIT. This limitation may lead to incomplete representation and is not inclusive of the entire dataset.
In addition to the models mentioned above, ELECTRE (ELimination Et Choix Traduisant la REalité – elimination and choice expressing reality) is another well-established approach for handling multi-criteria and multi-actor decision-making problems. It was developed in the late 1960 by Roy (
1968). ELECTRE is a comprehensive outranking relation model with several variants designed for different decision problems, including ranking, selection, and assignment of alternatives. These variants include ELECTRE I (Roy,
1968), ELECTRE II (Roy and Bertier,
1973), ELECTRE III (Roy,
1978), ELECTRE IV (Hugonnard and Roy,
1982), and more. Numerous studies have explored the use of ELECTRE models based on fuzzy concepts and their development, including their application in FS (Mohamadghasemi
et al.,
2020), IFS (Rouyendegh,
2017; Qu
et al.,
2018). Notably, ELECTRE III, which relies on fuzzy outranking relations, has been widely utilized for its effectiveness in the ranking process. Numerous developments related to FS, IFS, and IVFS have been documented in the literature (Joshi,
2016; Hashemi
et al.,
2016; Peng
et al.,
2019; Ramya
et al.,
2023; Forestal and Pi,
2022). To the best of our knowledge, there has been no study proposing the integration of CIFS into ELECTRE models, particularly ELECTRE III.
Given the aforementioned limitations and research gaps, the research contribution of this paper is to achieve the following main objectives.
-
1. To explore the CIFS theory and integrate it with the ELECTRE III model for group decision analysis, extending the model’s capabillities.
-
2. To redefine the operations used to generate optimistic and pessimistic IF values from the group decision matrix and group weighting vector. Additionally, suggest conditional rules to ensure that every element of the set remains within the circular area.
-
3. To demonstrate the applicabillity of the proposed model through a case study of stock-picking process.
-
4. To conduct a comprehensive comparative analysis with existing models and then justify sensitivity analyses to explore the impact of α-values, which reflect the linear combination of optimistic and pessimistic attitudes, criteria weights, and thresholds.
We employ several models from the literature, including IF-ELECTRE III, IVIF-ELECTRE III (Hashemi
et al.,
2016), and CIF-TOPSIS (Kahraman and Alkan,
2021), in our comparisons. Additionally, we propose further analysis using a tranquility measure to gauge confidence in selecting the final ranking of alternatives, particularly in the comparison between CIF-TOPSIS and the proposed CIF-ELECTRE III model. These objectives collectively guide our research efforts to contribute to the field of decision-making in the context of CIFS, offering valuable insights and practical applications.
The remainder of this paper is structured as follows: Section
2 provides fundamental definitions and insights into IFS, CIFS, and ELECTRE III to clarify the proposed approach. In Section
3, we present a method for converting the group decision matrix and group weighting vector, based on CIF values, into optimistic and pessimistic forms of IF values. Section
4 introduces the proposed CIF-ELECTRE III model. We illustrate the application of this model with a numerical example in the context of stock selection in Section
5. Section
6 covers sensitivity analyses and a comparative discussion. In the conclusion (Section
7), we offer recommendations for future research.
2 Preliminaries
This section recalls some basic definitions and related concepts of IFS, CIFS, and ELECTRE III model prior to the development of the proposed CIF-ELECTRE III.
2.1 Intuitionistic Fuzzy Set
Definition 1 (Atanassov, 1986).
Let
X be a finite non-empty set. An Intuitionistic Fuzzy Set
A (denoted IFS
A) in
X is defined as:
where
$0\leqslant {\mu _{A}}(x)+{\nu _{A}}(x)\leqslant 1$ for every
$x\in X$ and
${\mu _{A}}:X\to [0,1]$ and
${\nu _{A}}:X\to [0,1]$ are membership and non-membership functions, respectively. Also
${\pi _{A}}(x)=1-({\mu _{A}}(x)+{\nu _{A}}(x))$ is the formula for hesitancy function corresponding to a pair of IF value
$\langle {\mu _{A}}(x),{\nu _{A}}(x)\rangle $.
Several metric methods in terms of score and accuracy functions have been presented to compare two or more IF values (see, for example, Garg,
2016). The formal definition of these functions is given as the following. For brevity, the notation
$\langle {\mu _{A}},{\nu _{A}}\rangle $ is used instead of
$\langle {\mu _{A}}(x),{\nu _{A}}(x)\rangle $ to represent a pair of IF value.
Definition 2 (Chen and Tan, 1994; Xu, 2007).
For IFS
A, let
$A=\langle {\mu _{A}},{\nu _{A}}\rangle $ be a pair of IF value, then a score function,
$s(A)$ and an accuracy function,
$h(A)$ of IFS
A can be defined as Eqs. (
2) and (
3), respectively:
where
$s(A)\in [-1,1]$ and
$h(A)\in [0,1]$.
Moreover, let
A and
B be two IF values, then relations of score function and accuracy functions between
A and
B can be given as follows:
2.2 Circular Intuitionistic Fuzzy Set
Definition 3 (Atanassov, 2020).
Let
X be a finite non-empty set. A Circular Intuitionistic Fuzzy Set
${A_{r}}$ (denoted CIFS
${A_{r}}$) in
X can be defined as:
where
$0\leqslant {\mu _{A}}(x)+{\nu _{A}}(x)\leqslant 1$ for every
$x\in X$, functions
${\mu _{A}}:X\to [0,1]$ and
${\nu _{A}}:X\to [0,1]$ are membership and non-membership degrees, respectively, and also
$r\in [0,1]$ is a radius of the circle around each element
$x\in X$.
Similarly, the hesitancy function ${\pi _{A}}$ can be defined as ${\pi _{A}}(x)=1-({\mu _{A}}(x)+{\nu _{A}}(x))$ for every $x\in X$. Under the IFS interpretation triangle (IFIT), each element of CIFS is represented by a circle with centre at $\langle {\mu _{A}}(x),{\nu _{A}}(x)\rangle $ and radius, $r\gt 0$. Note that, when $r=0$, CIFS is reduced to IFS (i.e. a single point). Alternatively, CIFS can also be defined as the following.
Let
${L^{\ast }}=\{(m,n)\hspace{0.1667em}|\hspace{0.1667em}m,n\in [0,1]\hspace{2.5pt}\text{and}\hspace{2.5pt}m+n\leqslant 1\}$, be an expression of
L-fuzzy set, then
${A_{r}}$ can be written in the form:
where:
Remark 1.
Note that Definition
3 with radius
$r\in [0,1]$ is not exhaustive as the IFS triangle is only partly covered.
Recently, Atanassov and Marinov (
2021) expanded the radius to
$r\in [0,\sqrt{2}]$ with consideration that if the centre is at
$\langle 0,1\rangle $ or
$\langle 1,0\rangle $, the smallest radius distance needed to completely cover the IFS triangle is
$\sqrt{2}$. The geometrical interpretation of CIFS for radii
$r=1$ and
$r=\sqrt{2}$ are depicted in Fig.
2 (a) and (b), respectively.
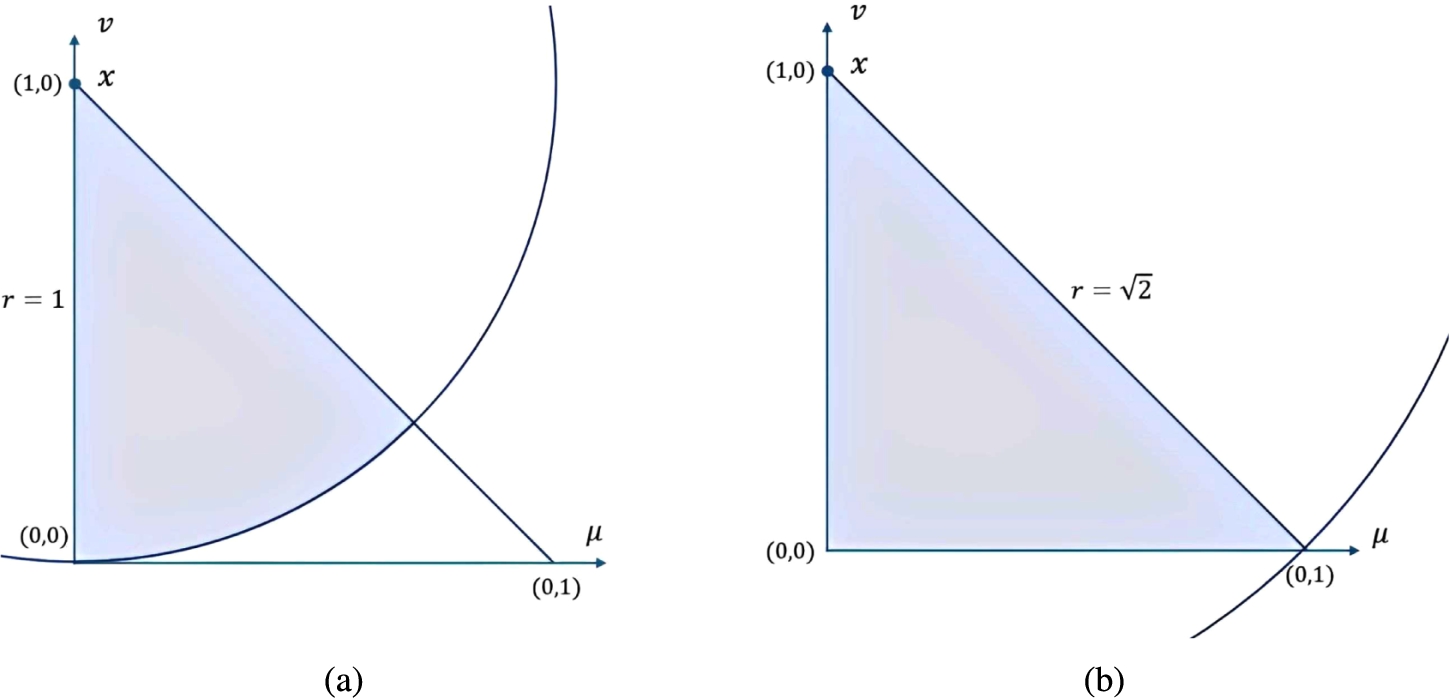
Fig. 2
Geometrical interpretation of CIFS for (a) $r=1$ and (b) $r=\sqrt{2}$.
Two different ways for constructing of CIFSs have been proposed recently (Atanassov,
2020): i) based on the geometrical interpretations of the standard IFSs (Atanassova,
2010), and ii) based on hesitant IFS (Torra,
2010; Chen
et al.,
2016). In the following, the algorithm for building the CIFS from IFSs is presented.
Definition 4 (Atanassov, 2020).
Let
${g_{j}}$ be an element formed by a set of
${k_{j}}$ intuitionistic fuzzy pairs
$\big\{({m_{j}^{1}},{n_{j}^{1}}),({m_{j}^{2}},{n_{j}^{2}}),\dots ,({m_{j}^{{k_{j}}}},{n_{j}^{{k_{j}}}})\big\}$, where
$j=1,2,\dots ,n$. The membership function
$\mu ({g_{j}})$ and non-membership function
$\nu ({g_{j}})$ of CIFS can be obtained as follows:
and the radius,
${r_{j}}$ is the maximum of the Euclidean distance such that:
where
${k_{j}}$ is the number of input sources for
${g_{j}}$. Then, for universe
$F=\{{g_{1}},{g_{2}},\dots ,{g_{n}}\}$, the CIFS can be represented in the following form:
The above expressions, under the group decision setting, can simply be assumed as the aggregated values of a group of actors
$h=1,2,\dots ,k$ with respect to each criterion
$j=1,2,\dots ,n$. The radius
r can be considered as the bounded uncertain region between the collective value of group (centre of a circle) and the individual actors’ values. Kahraman and Alkan (
2021) then proposed the conversion of CIF values to IF values by defining the concept of optimistic and pessimistic values, i.e. the attitudinal characters of the group of actors. By taking the effect of radius
r on both membership and non-membership degrees, the IF values for optimistic and pessimistic can be generated.
Definition 5 (Kahraman and Alkan, 2021).
Let
$A=\langle {\mu _{j}},{\nu _{j}};{r_{j}}\rangle $ be a CIF value. Then the conversion of CIF value to IF values can be obtained as follows:
where
${A^{o}}$ and
${A^{p}}$ are termed optimistic IF value and pessimistic IF value, respectively.
Remark 2.
Note that Definition
5 has a limitation as these optimistic and pessimistic IF values are not within the circular area (or radius
r) in the IFS triangle.
For example, the distance between the optimistic value and the centre of CIF value is obtained as:
Analogously, this also applies to the pessimistic value, where
$\sqrt{{({\mu _{j}^{p}}-{\mu _{j}})^{2}}+{({\nu _{j}^{p}}-{\nu _{j}})^{2}}}=\sqrt{{(-{r_{j}})^{2}}+{({r_{j}})^{2}}}={r_{j}}\sqrt{2}\ne {r_{j}}$.
2.3 ELECTRE III Model
ELECTRE III is a preference model for ranking purposes. In a general case, it is used for multi-criteria decision-making problem (single actor). However, it also can be directly extended to the case of multi-actor (or group) problem. The following are the important notations related to the basic data and the construction of ELECTRE III model.
Let $\mathcal{A}=\{{\mathfrak{a}_{1}},{\mathfrak{a}_{2}},\dots ,{\mathfrak{a}_{m}}\}$ be a set of m potential actions (or alternatives), $\mathcal{F}=\{{\mathfrak{g}_{1}},{\mathfrak{g}_{2}},\dots ,{\mathfrak{g}_{n}}\}$ be a set of criteria, and ${\mathfrak{g}_{j}}({\mathfrak{a}_{i}})$ is the performance of action ${\mathfrak{a}_{i}}\in \mathcal{A}$ on criterion ${\mathfrak{g}_{j}}\in \mathcal{F}$, thus an $m\times n$ performance (or decision) matrix $\mathcal{D}$ can be formed, with ${\mathfrak{g}_{j}}({\mathfrak{a}_{i}})$ in row i and column j $(i=1,2,\dots ,m;j=1,2,\dots ,n)$. In addition, let ${\mathfrak{w}_{j}}$ denotes a weight or relative importance of criterion ${\mathfrak{g}_{j}}$, for all ${\mathfrak{g}_{j}}\in \mathcal{F}$, where ${\mathfrak{w}_{j}}\in [0,1]$. Without loss of generality, we assume that ${\mathfrak{g}_{j}}({\mathfrak{a}_{i}})$ is based on the increasing direction of preference (i.e. the higher the preference value, the better the performance).
Moreover, under the group decision setting, let $\mathcal{E}=\{{\mathfrak{e}_{1}},{\mathfrak{e}_{2}},\dots ,{\mathfrak{e}_{k}}\}$ be a set of actors (or decision makers), then ${\mathcal{D}^{h}}$ represents an individual decision matrix of actor h $(h=1,2,\dots ,k)$.
The main feature of ELECTRE III compared to the other variants of ELECTRE family is a type of preference so-called pseudo-criterion. Pseudo-criterion is a multilevel threshold approach, as can be defined in the following.
Definition 6 (Roy and Vincke, 1984).
A pseudo-criterion is a function
${\mathfrak{g}_{j}}$ associated with two threshold functions defined as indifference
${q_{j}}(.)$ and preference
${p_{j}}(.)$, respectively. If
$(\mathfrak{a},{\mathfrak{a}^{\prime }})\in \mathcal{A}\times \mathcal{A}$ are alternatives, then:
where
P denotes a strict preference,
Q denotes a weak preference, and
I denotes indifferent. The weak preference is used to express the actor’s hesitation between indifference and strict preference.
The main process in ELECTRE III is the pairwise comparison of alternatives with respect to each criterion. These pairwise comparisons are presented in concordance and discordance indices. The concordance index
$C(\mathfrak{a},{\mathfrak{a}^{\prime }})$ of alternatives
$\mathfrak{a}$ and
${\mathfrak{a}^{\prime }}$ is the estimated value of pairs
$\mathfrak{a}$ and
${\mathfrak{a}^{\prime }}$ for each criterion. These estimates range from 0 to 1, where 1 indicates that
$\mathfrak{a}$ is better than
${\mathfrak{a}^{\prime }}$ for all criteria, and vice versa. The concordance index is calculated based on the weighted degree
${\mathfrak{w}_{j}}$ of each criterion as given in the following expression:
where
$W={\Sigma _{j=1}^{n}}{\mathfrak{w}_{j}}$ and
${c_{j}}(\mathfrak{a},{\mathfrak{a}^{\prime }})$ is the outranking degree of alternatives
$\mathfrak{a}$ and
${\mathfrak{a}^{\prime }}$ under criterion
${\mathfrak{g}_{j}}\in \mathcal{F}$, such that:
On the other hand, the concept of discordance utilizes a veto threshold such that the outranking of
${\mathfrak{a}^{\prime }}$ by
$\mathfrak{a}$ is refused if:
This resulted in the appearance of the discordance index
${d_{j}}(\mathfrak{a},{\mathfrak{a}^{\prime }})$ for each criterion
j. Like concordance, discordance index also has a value between 0 and 1.
Then, the credibility degree of outranking
$\mathfrak{a}$ over
${\mathfrak{a}^{\prime }}$ denoted as
$\sigma (\mathfrak{a},{\mathfrak{a}^{\prime }})$ is defined as follows:
where
$\mathcal{J}\subset \mathcal{F}$ is set of criteria for which
${d_{j}}(\mathfrak{a},{\mathfrak{a}^{\prime }})\gt C(\mathfrak{a},{\mathfrak{a}^{\prime }})$.
3 Group Decision Matrix and Group Weighting Vector Based on CIFS
This section is devoted to the conversion of group decision matrix and group weighting vector to optimistic and pessimistic forms. In the previous work, Kahraman and Alkan (
2021) proposed the formulation in Eqs. (
9) and (
10) to transform the CIF value to optimistic and pessimistic IF values, respectively. However, as stated in Remark
2, these values are not within the circular area of radius
r in the IFS interpretation triangle. Hence, this formulation needs to be redefined. In the following, the definitions of group decision matrix and group weighting vector based on CIFS and their conversion to optimistic and pessimistic IF values are presented.
Definition 7.
Let
$\mathcal{D}={[{\mathfrak{d}_{ij}}]_{m\times n}}$ be a group decision matrix (or CIF decision matrix) of dimension
$m\times n$ such that
i denotes alternative
$(i=1,2,\dots ,m)$ and
j criterion
$(j=1,2,\dots ,n)$. Each element of
$\mathcal{D}$ is represented by CIF value
${\mathfrak{d}_{ij}}=\langle {\mu _{ij}},{\nu _{ij}};{r_{ij}}\rangle $. The optimistic decision matrix and pessimistic decision matrix of
$\mathcal{D}$ denoted
${\mathcal{D}^{o}}$ and
${\mathcal{D}^{p}}$, respectively can be defined as follows:
where:
such that
${\mu _{ij}^{o}},{\nu _{ij}^{o}}\in [0,1]$ and
${\mu _{ij}^{p}},{\nu _{ij}^{p}}\in [0,1]$.
Upon checking the above definition,
${\mathfrak{d}_{ij}^{o}}$ and
${\mathfrak{d}_{ij}^{p}}$ clearly satisfy the condition of standard IFS, as can be demonstrated below:
Based on the Definiton
7, the concept of optimistic and pessimistic for weighting vector can be defined accordingly.
Definition 8.
Let
$\mathcal{W}={[{\mathfrak{w}_{j}}]_{n\times 1}}$ is vector dimension
$n\times 1$ where
j is a criterion
$(j=1,2,\dots ,n)$. Each element of
$\mathcal{W}$ is represented by CIF value
${\mathfrak{w}_{j}}=\langle {\mu _{j}},{\nu _{j}};{r_{j}}\rangle $. The optimistic weighting vector and pessimistic weighting vector of
$\mathcal{W}$, denoted
${\mathcal{W}^{o}}$ and
${\mathcal{W}^{p}}$, respectively, can be defined as follows:
where:
such that
${\mu _{j}^{o}},{\nu _{j}^{o}}\in [0,1]$ and
${\mu _{j}^{p}},{\nu _{j}^{p}}\in [0,1]$.
Likewise, the condition for standard IFS is fulfilled for
${\mathfrak{w}_{j}^{o}}$ and
${\mathfrak{w}_{j}^{p}}$ such that:
$0\leqslant {\mu _{j}^{o}}+{\nu _{j}^{o}}\leqslant 1$ and
$0\leqslant {\mu _{j}^{p}}+{\nu _{j}^{p}}\leqslant 1$. The difference between the proposed conversion IF values and the one used in Kahraman and Alkan (
2021) is depicted in Fig.
3.
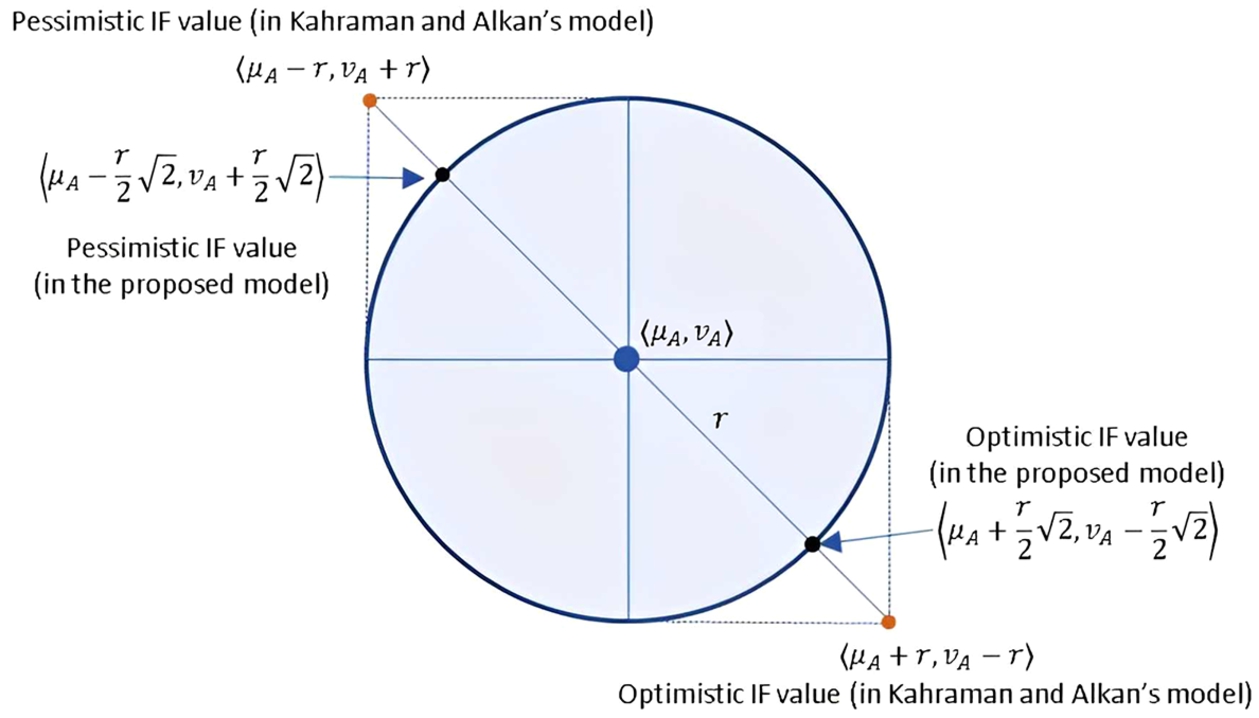
Fig. 3
Comparison of optimistic-pessimistic IF values for the proposed approach and Kahraman and Alkan’s approach.
Moreover, it can easily be shown that the distance between the optimistic IF value,
${\mathfrak{d}_{ij}^{o}}=\langle {\mu _{ij}^{o}},{\nu _{ij}^{o}}\rangle $, such that
${\mu _{ij}^{o}},{\nu _{ij}^{o}}\in [0,1]$, and the centre of the CIF value
${\mathfrak{d}_{ij}}=\langle {\mu _{ij}},{\nu _{ij}}\rangle $ is exactly
${r_{ij}}$, which satisfies the boundary condition:
Analogously, it can be shown for ${\mathfrak{d}_{ij}^{p}}=\langle {\mu _{ij}^{p}},{\nu _{ij}^{p}}\rangle $, such that ${\mu _{ij}^{p}},{\nu _{ij}^{p}}\in [0,1]$, its distance from the centre of the CIF value ${d_{ij}}=\langle {\mu _{ij}},{\nu _{ij}}\rangle $ is also ${r_{ij}}$. The same are true for ${\mathfrak{w}_{j}^{o}},{\mathfrak{w}_{j}^{p}}\in {O_{{r_{j}}}}({\mu _{j}},{\nu _{j}})$, which results in optimistic and pessimistic in the range of ${O_{{r_{j}}}}({\mu _{j}},{\nu _{j}})$. However, there are two cases in optimistic and pessimistic IF values that the above condition is not satisfied. Specifically, either one of the degrees is not within $[0,1]$ or both degrees are not elements of $[0,1]$. Let ${\mathfrak{d}_{ij}^{o}}=\langle {\mu _{ij}^{o}},{\nu _{ij}^{o}}\rangle $ be an optimistic IF value (or ${\mathfrak{d}_{ij}^{p}}=\langle {\mu _{ij}^{p}},{\nu _{ij}^{p}}\rangle $ be an pessimistic IF value), then:
Case (1): there is a possibility that $\varphi \leqslant {\mu _{ij}^{o}}\leqslant 1$, but ${\nu _{ij}^{o}}\lt 0$ occurs in the case of optimistic (or ${\mu _{ij}^{p}}\lt 0$, but $\varphi \leqslant {\nu _{ij}^{p}}\leqslant 1$ in the case of pessimistic), where $\varphi =\frac{{r_{ij}}}{2}\sqrt{2}$.
For example, ${\mathfrak{d}_{ij}}=\langle 0.4,0.3;0.5\rangle $, then ${\mathfrak{d}_{ij}^{o}}=\langle {\mu _{ij}^{o}},{\nu _{ij}^{o}}\rangle =\langle 0.75,-0.05\rangle $. This clearly contradicts the condition of IFS which is ${\nu _{ij}^{o}}\ne [0,1]$.
Case (2): there is possibility that ${\mu _{ij}^{o}}\gt 1$ and ${\nu _{ij}^{o}}\lt 0$ occur in case of optimistic (or in case of pessimistic: ${\mu _{ij}^{p}}\lt 0$ and ${\nu _{ij}^{p}}\gt 1$).
For example,
${\mathfrak{d}_{ij}}=\langle 0.7,0.3;0.5\rangle $, then
${\mathfrak{d}_{ij}^{o}}=\langle {\mu _{ij}^{o}},{\nu _{ij}^{o}}\rangle =\langle 1.05,-0.05\rangle $. This also contradicts the condition of IFS, which is
${\mu _{ij}^{o}},{\nu _{ij}^{o}}\notin [0,1]$. Fig.
4 demonstrates these two cases.
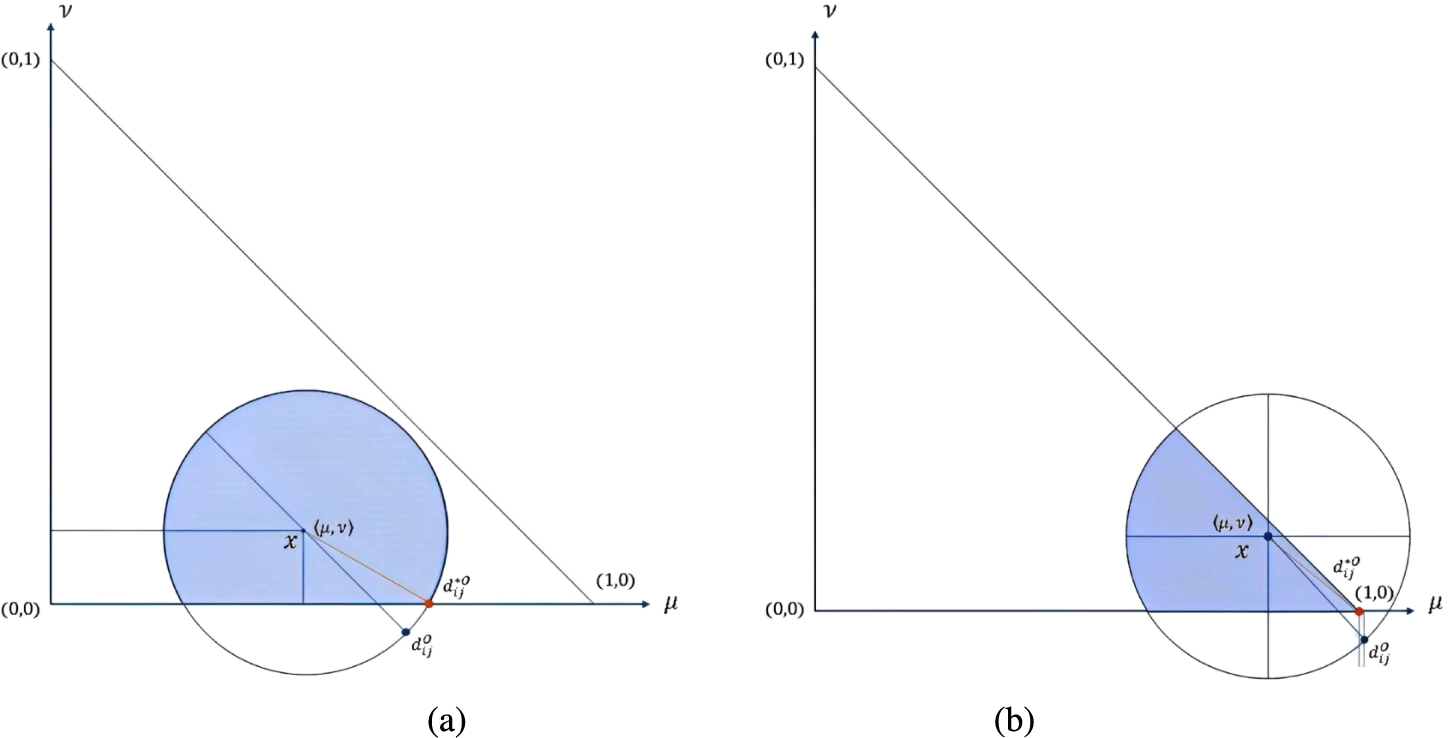
Fig. 4
Special cases for optimisitic decision element, when (a) ${\nu _{ij}^{o}}\lt 0$ and (b) ${\mu _{ij}^{o}}\gt 1$, ${\nu _{ij}^{o}}\lt 0$.
This leads to the following theorems for the elements of ${\mathcal{D}^{o}}$ and ${\mathcal{D}^{p}}$, as well as the ${\mathcal{W}^{o}}$ and ${\mathcal{W}^{p}}$.
Theorem 1.
Let ${\mathfrak{d}_{ij}^{o}}\in {\mathcal{D}^{o}},{\mu _{ij}}$, ${\nu _{ij}}\in [0,1]$ and ${r_{ij}}\in [0,\sqrt{2}]$, then ${\mathfrak{d}_{ij}^{o}}$ can be determined as follows:
-
1. If ${\mu _{ij}^{o}}$, ${\nu _{ij}^{o}}\in [0,1]$, then ${\mathfrak{d}_{ij}^{o}}=\big\langle {\mu _{ij}^{o}},{\nu _{ij}^{o}}\big\rangle $.
-
2. If ${\nu _{ij}^{o}}\lt 0$, then:
Proof.
It is clear that, for
${\mu _{ij}^{o}},{\nu _{ij}^{o}}\in [0,1]$, then
${\mathfrak{d}_{ij}^{o}}=\langle {\mu _{ij}^{o}},{\nu _{ij}^{o}}\rangle $, which is the point inside the IFS interpretation triangle. For
${\nu _{ij}^{o}}\lt 0$ (Case (1)), the point
${\mathfrak{d}_{ij}^{o}}=\langle {\mu _{ij}^{o}},{\nu _{ij}^{o}}\rangle $ occurs outside the IFS interpretation triangle. Thus, the revised IF value
${\mathfrak{d}_{ij}^{o\ast }}=\langle {\mu _{ij}^{o\ast }},{\nu _{ij}^{o\ast }}\rangle $ needs to be determined such that
${\mu _{ij}^{o\ast }},{\nu _{ij}^{o\ast }}\in [0,1]$. It can be shown that the point
${\mathfrak{d}_{ij}^{o\ast }}$ with
${\mu _{ij}^{o\ast }}={\mu _{ij}}+\sqrt{{r_{ij}^{2}}-{\nu _{ij}^{2}}}$ and
${\nu _{ij}^{o\ast }}=0$ is the only point that gives the highest score function
$s({\mathfrak{d}_{ij}^{o\ast }})$ inside the IFS triangle. Assume that there is another point
${\mathfrak{d}^{\prime }_{ij}}=\langle {\mu ^{\prime }_{ij}},{\nu ^{\prime }_{ij}}\rangle $ with
${\mu ^{\prime }_{ij}},{\nu ^{\prime }_{ij}}\in [0,1]$, such that
$s({\mathfrak{d}^{\prime }_{ij}})\gt s({\mathfrak{d}_{ij}^{o\ast }})$, then:
It follows from the fact that
${\mathfrak{d}^{\prime }_{ij}}=\langle {\mu ^{\prime }_{ij}},{\nu ^{\prime }_{ij}}\rangle $ is inside the
${O_{{r_{ij}}}}({\mu _{ij}},{\nu _{ij}})$, so:
From the Eqs. (
18) and (
19), it can be obtained that:
This implies
${\mu ^{\prime }_{ij}}\lt {\mu ^{\prime }_{ij}}-{\nu ^{\prime }_{ij}}$ and
${\nu ^{\prime }_{ij}}\lt 0$, which contradict the IFS condition. Therefore,
${\mathfrak{d}_{ij}^{o\ast }}=\big\langle {\mu _{ij}}+\sqrt{{r_{ij}^{2}}-{\nu _{ij}^{2}}},0\big\rangle $.
For ${\mu _{ij}^{o}}\gt 1$ and ${\nu _{ij}^{o}}\lt 0$ (Case (2)), it can be shown that ${\mathfrak{d}_{ij}^{o\ast }}=\langle 1,0\rangle $ is point with the highest score function inside the IFS triangle. Using the same assumption that $s({\mathfrak{d}^{\prime }_{ij}})\gt s({\mathfrak{d}_{ij}^{o\ast }})$, then ${\mu ^{\prime }_{ij}}-{\nu ^{\prime }_{ij}}\gt 1$. This again contradicts with the IFS condition, where ${\mu ^{\prime }_{ij}},{\nu ^{\prime }_{ij}}\in [0,1]$ and $s({\mathfrak{d}^{\prime }_{ij}})\in [0,1]$. Thus, ${\mathfrak{d}_{ij}^{o\ast }}=\langle 1,0\rangle $. □
Theorem 2.
Let ${\mathfrak{d}_{ij}^{p}}\in {\mathcal{D}^{p}},{\mu _{ij}}$, ${\nu _{ij}}\in [0,1]$ and ${r_{ij}}\in [0,\sqrt{2}\hspace{0.1667em}]$, then ${\mathfrak{d}_{ij}^{p}}$ can be determined as follows:
-
1. If ${\mu _{ij}^{p}}$, ${\nu _{ij}^{p}}\in [0,1]$, then ${\mathfrak{d}_{ij}^{p}}=\big\langle {\mu _{ij}^{p}},{\nu _{ij}^{p}}\big\rangle $.
-
2. If ${\mu _{ij}^{p}}\lt 0$, then:
Proof.
For
${\mu _{ij}^{p}},{\nu _{ij}^{p}}\in [0,1]$, then
${\mathfrak{d}_{ij}^{p}}=\langle {\mu _{ij}^{p}},{\nu _{ij}^{p}}\rangle $. It is straightforward. For
${\mu _{ij}^{p}}\lt 0$, the point
${\mathfrak{d}_{ij}^{p}}=\langle {\mu _{ij}^{p}},{\nu _{ij}^{p}}\rangle $ occurs outside the IFS triangle. It can be demonstrated that the point
${\mathfrak{d}_{ij}^{p\ast }}$ with
${\mu _{ij}^{p\ast }}=0$ and
${\nu _{ij}^{p\ast }}={\nu _{ij}}+\sqrt{{r_{ij}^{2}}-{\mu _{ij}^{2}}}$ is the only point that gives the lowest score function
$s({\mathfrak{d}_{ij}^{p\ast }})$ inside the IFS triangle. Suppose that there is other point
${\mathfrak{d}^{\prime\prime }_{ij}}=\langle {\mu ^{\prime\prime }_{ij}},{\nu ^{\prime\prime }_{ij}}\rangle $ with
${\mu ^{\prime\prime }_{ij}},{\nu ^{\prime\prime }_{ij}}\in [0,1]$ such that
$s({\mathfrak{d}^{\prime\prime }_{ij}})\lt s({\mathfrak{d}_{ij}^{p\ast }})$, then:
From the fact that
${\mathfrak{d}^{\prime\prime }_{ij}}=\langle {\mu ^{\prime\prime }_{ij}},{\nu ^{\prime\prime }_{ij}}\rangle $ is inside the
${O_{{r_{ij}}}}({\mu _{ij}},{\nu _{ij}})$, so:
From Eqs. (
20) and (
21), it can be obtained that:
This implies
${\mu ^{\prime\prime }_{ij}}\lt 0$ and
${\nu ^{\prime\prime }_{ij}}\lt -{\mu ^{\prime\prime }_{ij}}+{\nu ^{\prime\prime }_{ij}}$, which contradict the IFS condition. Therefore,
${\mathfrak{d}_{ij}^{p}}=\big\langle 0,{\nu _{ij}}+\sqrt{{r_{ij}^{2}}-{\mu _{ij}^{2}}}\big\rangle $.
For ${\mu _{ij}^{p}}\lt 0$ and ${\nu _{ij}^{p}}\gt 1$, it can be shown that ${\mathfrak{d}_{ij}^{p\ast }}=\langle 0,1\rangle $ is the point with the lowest score function inside the IFS triangle. By the same assumption, $s({\mathfrak{d}^{\prime\prime }_{ij}})\lt s({\mathfrak{d}_{ij}^{p\ast }})$, then ${\mu ^{\prime\prime }_{ij}}-{\nu ^{\prime\prime }_{ij}}\lt -1$. This again contradicts with the IFS condition, such that ${\mu ^{\prime\prime }_{ij}},{\nu ^{\prime\prime }_{ij}}\in [0,1]$ and $s({\mathfrak{d}^{\prime\prime }_{ij}})\in [-1,1]$. Thus, ${\mathfrak{d}_{ij}^{p\ast }}=\langle 0,1\rangle $. □
Theorem 3.
Let ${\mathfrak{w}_{j}^{o}}\in {\mathcal{W}^{o}}$ and ${\mathfrak{w}_{j}^{p}}\in {\mathcal{W}^{p}}$, also ${\mu _{j}},{\nu _{j}}\in [0,1]$ and ${r_{j}}\in [0,\sqrt{2}]$, then the rules for determining the value of ${\mathfrak{w}^{o}}$ and ${\mathfrak{w}^{p}}$ are as follows:
-
1. If ${\mu _{j}^{o}},{\nu _{j}^{o}},{\mu _{j}^{p}},{\nu _{j}^{p}}\in [0,1]$, then ${\mathfrak{w}_{j}^{o}}=\big\langle {\mu _{j}^{o}},{\nu _{j}^{o}}\big\rangle \hspace{2.5pt}\textit{and}\hspace{2.5pt}{\mathfrak{w}_{j}^{p}}=\big\langle {\mu _{j}^{p}},{\nu _{j}^{p}}\big\rangle $.
-
2. If ${\nu _{j}^{o}}\lt 0$, then
-
3. If ${\mu _{j}^{p}}\lt 0$, then
Proof.
The proof of this theorem is straightforward based on proofs of Theorem
1 and Theorem
2 with some adjustments. Instead of matrix, here vector is considered. □
The final outranking procedure in the CIF-ELECTRE III model is significantly influenced by the aformentioned definitions and theorems. For both the optimistic and pessimistic scenarios, separate scores underlie the ranking process. After identifying the optimistic and pessimistic scores, the composite ratio is defined. This ratio parameterizes the attitudinal character of the group of actors in order to determine the final score before the ranking process.
Definition 9.
Let
$\alpha \in [0,1]$,
${\phi ^{o}}({\mathfrak{a}_{i}})$ is an optimistic score of
${\mathfrak{a}_{i}}$ and
${\phi ^{p}}({\mathfrak{a}_{i}})$ is a pessimistic score of
${\mathfrak{a}_{i}}$ (showing how
${\mathfrak{a}_{i}}$ dominates all the other alternatives
${\mathfrak{a}^{\prime }_{i}}\in \mathcal{A}$), then the overall score degree of
${\mathfrak{a}_{i}}$ denoted
$\phi ({\mathfrak{a}_{i}})$ is defined as follow:
At the end, this composite ratio, $\alpha \in [0,1]$ determines the final ranking of alternatives. Moreover, it can be used as a sensitivity analysis to determine the stability level of the proposed model. Next, in the subsequent section, the CIF-ELECTRE III model based on several concepts proposed in this section is developed.
4 CIF-ELECTRE III Model for Group Decision Analysis
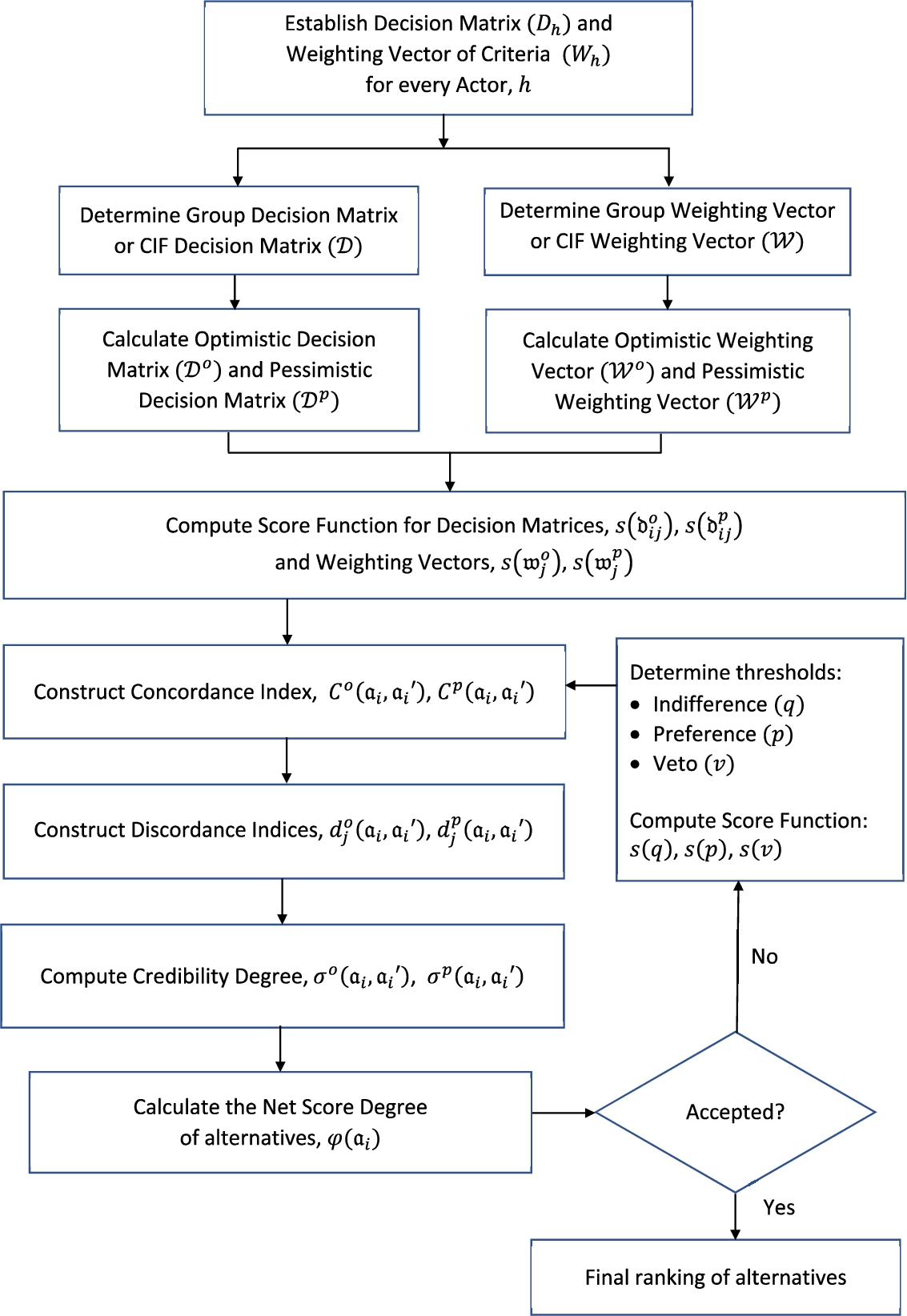
Fig. 5
Framework of CIF-ELECTRE III.
In this section, a novel CIF-ELECTRE III is presented. The framework of the proposed model is demonstrated in Fig.
5. The algorithm of the CIF-ELECTRE III is detailed in the following steps.
Step 1: Determine the list of potential alternatives, criteria, and actors to be implemented in the developed model. Let $\mathcal{A}=\{{\mathfrak{a}_{1}},{\mathfrak{a}_{2}},\dots ,{\mathfrak{a}_{m}}\}$ be a set of alternatives, $\mathcal{F}=\{{\mathfrak{g}_{1}},{\mathfrak{g}_{2}},\dots ,{\mathfrak{g}_{n}}\}$ be a set of criteria, and $\mathcal{E}=\{{\mathfrak{e}_{1}},{\mathfrak{e}_{2}},\dots ,{\mathfrak{e}_{k}}\}$ be a set of actors. Note that, in this model, only the homogeneous case of group decision-making is proposed where all actors are assumed to have equal degrees of importance.
Step 2: Generate the decision matrix
${\mathcal{D}_{h}}=[{\mathfrak{d}_{ij}^{h}}]$ for each actor
${\mathcal{E}_{h}}$,
$h=1,2,\dots ,k$, where
${\mathfrak{d}_{ij}^{h}}$ refers to the preference of actor for alternative
${\mathfrak{a}_{i}}$,
$i=1,2,\dots ,m$ with respect to criterion
${\mathfrak{g}_{j}}$,
$j=1,2,\dots ,n$. At this stage, each actor provides his/her preferences using the predefined linguistic scale such as in Table
1(a). For the computational purpose, the linguistic terms are directly converted to their associated IF values.
Step 3: Calculate the CIF decision matrix
$\mathcal{D}={[{\mathfrak{d}_{ij}}]_{m\times n}}$ (or group decision matrix) by aggregating the decision matrix
${\mathcal{D}_{h}}$ of all actors with respect to each criterion
${\mathfrak{g}_{j}}$. Note that
${\mathfrak{d}_{ij}}=\langle {\mu _{ij}},{\nu _{ij}};{r_{ij}}\rangle $ is the CIF value constructed from IF values
${\mathfrak{d}_{ij}^{h}}=\langle {m_{ij}^{h}},{n_{ij}^{h}}\rangle $ using the Eqs. (
6)–(
8).
Step 4: Calculate the optimistic decision matrix
${\mathcal{D}^{o}}=[{\mathfrak{d}_{ij}^{o}}]$ and the pessimistic decision matrix
${\mathcal{D}^{p}}=[{\mathfrak{d}_{ij}^{p}}]$, respectively using Eq. (
16). This step focuses on transforming the elements of group decision matrix from CIF values to IF values by considering not only the membership and non-membership degrees, but also the radius
r. The conditional rules (Theorems
1–
2) must be checked to guarantee that every element of matrix is confined under the circular area.
Step 5: Calculate the deterministic form of optimistic decision matrix
$s({\mathfrak{d}_{ij}^{o}})$ and pessimistic decision matrix
$s({\mathfrak{d}_{ij}^{p}})$ using the score function such in Eq. (
2). At the same time, determine the indifferent
$({q_{j}})$, preference
$({p_{j}})$ and veto
$({v_{j}})$ thresholds for every criterion
${\mathfrak{g}_{j}}$. This also can be done by using the predefined linguistic scale in Table
1(a). Similarly, generate the deterministic form for all the thresholds: indifferent
$s({q_{j}})$, preference
$s({p_{j}})$, and veto
$s({v_{j}})$ using Eq. (
2).
Step 6: Next, determine the weighting vector of criteria for each actor
${\mathfrak{e}_{h}}\in \mathcal{E}$ using the linguistic scale in Table
1(b). Similarly, obtain the group weighting vector
$\mathcal{W}={[{\mathfrak{w}_{j}}]_{n\times 1}}$ consisting of
${\mathfrak{w}_{j}}=\langle {\mu _{j}},{\nu _{j}};{r_{j}}\rangle $,
$j=1,2,\dots ,n$. The CIF values are constructed in the similar way using the aggregated IF values
${\mathfrak{d}_{j}^{h}}=\langle {m_{j}^{h}},{n_{j}^{h}}\rangle $ in Eqs. (
6)–(
8).
Step 7: Calculate the optimistic weighting vector
${\mathcal{W}^{o}}={[{\mathfrak{w}_{j}^{o}}]_{n\times 1}}$ and the pessimistic weighting vector
${\mathcal{W}^{p}}={[{\mathfrak{w}_{j}^{p}}]_{n\times 1}}$, respectively, from the CIF weighting vector
$\mathcal{W}$ using Eq. (
17). Similarly, the conditional rule (Theorem
3) must be checked to guarantee that every element of vector is confined under the circular area. Then, compute the deterministic format of weighting vectors
${\dddot{\mathcal{W}}^{o}}$ and
${\dddot{\mathcal{W}}^{p}}$ using the following expressions:
${\dddot{\mathcal{W}}^{o}}={[{\dddot{\mathfrak{w}}_{j}^{o}}]_{n\times 1}}$ for the optimistic weight, where
${\dddot{\mathfrak{w}}_{j}^{o}}=\frac{1+s({\mathfrak{w}_{j}^{o}})}{2}$ and
${\dddot{\mathcal{W}}^{p}}={({\dddot{\mathfrak{w}}_{j}^{p}})_{n\times 1}}$ for the pessimistic weight, where
${\dddot{\mathfrak{w}}_{j}^{p}}=\frac{1+s({\mathfrak{w}_{j}^{p}})}{2}$. Note that
$s({\mathfrak{w}_{j}^{o}})$ and
$s({\mathfrak{w}_{j}^{p}})$ are score functions of optimistic weight and pessimistic weight, respectively, that can be calculated using the Eq. (
2).
Step 8: Construct the optimistic concordance index
${C^{o}}({\mathfrak{a}_{i}},{\mathfrak{a}^{\prime }_{i}})$ and the pessimistic concordance index
${C^{p}}({\mathfrak{a}_{i}},{\mathfrak{a}^{\prime }_{i}})$, based on the outranking degree
${c_{j}}({\mathfrak{a}_{i}},{\mathfrak{a}^{\prime }_{i}})$ for every pair of alternatives
${\mathfrak{a}_{i}},{\mathfrak{a}^{\prime }_{i}}\in \mathcal{A}$ under criterion
${\mathfrak{g}_{j}}\in \mathcal{F}$. This can be done using Eqs. (
11)–(
12).
Step 9: Determine the optimistic discordance index
${d_{j}^{o}}({\mathfrak{a}_{i}},{\mathfrak{a}^{\prime }_{i}})$ and pessimistic discordance index
${d_{j}^{p}}({\mathfrak{a}_{i}},{\mathfrak{a}_{{i^{\prime }}}})$ for each set of alternatives
${\mathfrak{a}_{i}},{\mathfrak{a}^{\prime }_{i}}\in \mathcal{A}$ under criterion
${\mathfrak{g}_{j}}\in \mathcal{F}$ using Eqs. (
13)–(
14).
Step 10: Compute the credibility matrix
$\sigma ({\mathfrak{a}_{i}},{\mathfrak{a}^{\prime }_{i}})$ for both optimistic and pessimistic based on the degree of outranking using Eq. (
15).
Step 11: Finally, calculate the net score degree (i.e. a composite ratio score) using Eq. (
22), where the optimistic score degree
${\phi ^{o}}({\mathfrak{a}_{i}})$ and pessimistic score degree
${\phi ^{p}}({\mathfrak{a}_{i}})$ are given as follows:
The net score degree
$\phi ({\mathfrak{a}_{i}})$ represents a value function, where a higher value reflects higher attractiveness of the alternative
${\mathfrak{a}_{i}}\in \mathcal{A}$. This allows for a ranking of these options in decreasing importance.
5 Numerical Example
As a case study of the stock-picking process, this section shows how the suggested strategy was put into practice. Specifically, an investor intends to invest in one of the pre-screened stocks in Bursa Malaysia (i.e. under the technology sector). To finalize the decision, a set of criteria based on the fundamental analysis is considered for the further appraisal of stocks, i.e. using the forward-looking scenario analysis. The details of the decision-making process are demonstrated as follows.
Three financial analysts $\mathcal{E}=\{{\mathfrak{e}_{1}},{\mathfrak{e}_{2}},{\mathfrak{e}_{3}}\}$ with a vast experience in investment under the technology sector were selected to evaluate the five pre-screened stocks $\mathcal{A}=\{{\mathfrak{a}_{1}},{\mathfrak{a}_{2}},\dots ,{\mathfrak{a}_{5}}\}$. There were four criteria $\mathcal{F}=\{{\mathfrak{g}_{1}},{\mathfrak{g}_{2}},{\mathfrak{g}_{3}},{\mathfrak{g}_{4}}\}$ under the consideration, namely, market value of firm $({\mathfrak{g}_{1}})$, return on equity $({\mathfrak{g}_{2}})$, debt to equity $({\mathfrak{g}_{3}})$, and price per earnings ratio $({\mathfrak{g}_{4}})$. In this instance, the importance of each analyst was made to be equal.
Initially, using the predetermined linguistic scale such in Table
1(a), each analyst was asked to provide his/her preferences for all alternatives according to each criterion. The decision matrix of the performance rating by analysts is shown in Table
2.
Table 1
Linguistic scale for (a) rating of alternatives and (b) weighting of criteria.
| Linguistic terms |
IFVs for alternatives |
|
m |
n |
| VVG/VVH |
0.9 |
0.1 |
| VG/VH |
0.7775 |
0.0625 |
| G/H |
0.6775 |
0.1625 |
| MG/MH |
0.5775 |
0.2625 |
| F/M |
0.4775 |
0.3635 |
| MB/ML |
0.3775 |
0.4625 |
| B/L |
0.2188 |
0.5438 |
| VB/VL |
0.0688 |
0.6938 |
| VVB/VVL |
0.1 |
0.9 |
|
(a) |
|
| Linguistic terms |
IFVs for alternatives |
|
m |
n |
| VI |
0.9 |
0.1 |
| I |
0.5813 |
0.1058 |
| M |
0.3313 |
0.3563 |
| U |
0.1813 |
0.5063 |
| VU |
0.1 |
0.9 |
|
(b) |
|
Table 2
Linguistic decision matrix for each analyst.
| Criteria |
Decision makers |
${\mathfrak{a}_{1}}$ |
${\mathfrak{a}_{2}}$ |
${\mathfrak{a}_{3}}$ |
${\mathfrak{a}_{4}}$ |
${\mathfrak{a}_{5}}$ |
| ${\mathfrak{g}_{1}}$ |
${\mathfrak{e}_{1}}$ |
VG |
MG |
VG |
F |
B |
|
${\mathfrak{e}_{2}}$ |
VG |
G |
VG |
MB |
B |
|
${\mathfrak{e}_{3}}$ |
G |
MG |
VG |
F |
B |
| ${\mathfrak{g}_{2}}$ |
${\mathfrak{e}_{1}}$ |
VG |
VG |
MG |
MB |
B |
|
${\mathfrak{e}_{2}}$ |
G |
VG |
G |
F |
F |
|
${\mathfrak{e}_{3}}$ |
MG |
VG |
MG |
MG |
B |
| ${\mathfrak{g}_{3}}$ |
${\mathfrak{e}_{1}}$ |
G |
F |
VG |
F |
F |
|
${\mathfrak{e}_{2}}$ |
F |
G |
VVG |
MG |
MG |
|
${\mathfrak{e}_{3}}$ |
G |
MG |
VG |
F |
MG |
| ${\mathfrak{g}_{4}}$ |
${\mathfrak{e}_{1}}$ |
F |
G |
MG |
G |
F |
|
${\mathfrak{e}_{2}}$ |
F |
VG |
VG |
F |
MG |
|
${\mathfrak{e}_{3}}$ |
F |
G |
G |
F |
G |
At this stage, the linguistic data provided by analysts are converted to their corresponding IF values to compute the group decision matrix
$\mathcal{D}=[{\mathfrak{d}_{ij}}]$ (using Eqs. (
6)–(
8)). Table
3 shows the group decision matrix or the aggregated judgment of analysts. Note that,
${\mathfrak{d}_{ij}}=\langle {\mu _{ij}},{\nu _{ij}};{r_{ij}}\rangle $ is the CIF value constructed from IF value,
${\mathfrak{d}_{ij}^{h}}=\langle {m_{ij}^{h}},{n_{ij}^{h}}\rangle $, for
$h=1,2,3$.
Table 3
Group decision matrix $\mathcal{D}$.
|
${\mathfrak{g}_{1}}$ |
${\mathfrak{g}_{2}}$ |
${\mathfrak{g}_{3}}$ |
${\mathfrak{g}_{4}}$ |
| ${\mathfrak{a}_{1}}$ |
$(0.744,0.096;0.094)$ |
$(0.678,0.163;0.141)$ |
$(0.611,0.229;0.189)$ |
$(0.478,0.363;0)$ |
| ${\mathfrak{a}_{2}}$ |
$(0.611,0.229;0.094)$ |
$(0.778,0.063;0)$ |
$(0.578,0.263;0.141)$ |
$(0.711,0.129;0.094)$ |
| ${\mathfrak{a}_{3}}$ |
$(0.778,0.063;0)$ |
$(0.611,0.229;0.094)$ |
$(0.778,0.063;0)$ |
$(0.678,0.163;0.141)$ |
| ${\mathfrak{a}_{4}}$ |
$(0.444,0.396;0.094)$ |
$(0.478,0.363;0.141)$ |
$(0.511,0.329;0.094)$ |
$(0.544,0.296;0.189)$ |
| ${\mathfrak{a}_{5}}$ |
$(0.219,0.544;0)$ |
$(0.305,0.483;0.211)$ |
$(0.544,0.296;0.094)$ |
$(0.578,0.263;0.141)$ |
Table 4
Optimistic decision matrix, ${\mathcal{D}^{o}}$ and Pessimistic decision matrix, ${\mathcal{D}^{p}}$.
|
Optimistic decision matrix, ${\mathcal{D}^{o}}$
|
Pessimistic decision matrix, ${\mathcal{D}^{p}}$
|
|
${\mathfrak{g}_{1}}$ |
${\mathfrak{g}_{2}}$ |
${\mathfrak{g}_{3}}$ |
${\mathfrak{g}_{4}}$ |
${\mathfrak{g}_{1}}$ |
${\mathfrak{g}_{2}}$ |
${\mathfrak{g}_{3}}$ |
${\mathfrak{g}_{4}}$ |
| ${\mathfrak{a}_{1}}$ |
$(0.811,0.029)$ |
$(0.778,0.063)$ |
$(0.744,0.096)$ |
$(0.478,0.363)$ |
$(0.678,0.163)$ |
$(0.578,0.263)$ |
$(0.478,0.363)$ |
$(0.478,0.363)$ |
| ${\mathfrak{a}_{2}}$ |
$(0.678,0.163)$ |
$(0.778,0.063)$ |
$(0.678,0.163)$ |
$(0.778,0.063)$ |
$(0.544,0.296)$ |
$(0.778,0.063)$ |
$(0.478,0.363)$ |
$(0.644,0.196)$ |
| ${\mathfrak{a}_{3}}$ |
$(0.778,0.063)$ |
$(0.678,0.163)$ |
$(0.778,0.063)$ |
$(0.778,0.063)$ |
$(0.778,0.063)$ |
$(0.544,0.296)$ |
$(0.778,0.063)$ |
$(0.578,0.263)$ |
| ${\mathfrak{a}_{4}}$ |
$(0.515,0.329)$ |
$(0.578,0.263)$ |
$(0.578,0.263)$ |
$(0.678,0.163)$ |
$(0.378,0.463)$ |
$(0.378,0.463)$ |
$(0.444,0.396)$ |
$(0.411,0.429)$ |
| ${\mathfrak{a}_{5}}$ |
$(0.219,0.544)$ |
$(0.454,0.334)$ |
$(0.611,0.229)$ |
$(0.678,0.163)$ |
$(0.219,0.544)$ |
$(0.156,0.632)$ |
$(0.478,0.363)$ |
$(0.478,0.363)$ |
From the group decision matrix (Table
3),
${\mathcal{D}^{o}}$ and
${\mathcal{D}^{p}}$ can be formed using Eq. (
17). These two decision matrices are shown in the Tables
4. The analysts also were requested to determine the
$(q,p,v)$ tresholds to set the limits that need to be applied to the rating. Instead of individually determined, these were subjected to the consensus among analysts (see Table
5). Then, the deterministic format of optimistic and pessimistic decision matrices, as well as the tresholds, can be generated as shown in Table
6. Next, determine the group weighting vector of criteria,
$\mathcal{W}$ based on preferences by analysts (see Table
7). The linguistic scale, such as in Table
1(b), was used for this purpose. Following the same procedure (Eqs. (
6)–(
8) and Eq. (
18)), two weighting vectors can be obtained, namely, the optimistic weighting vector
${\mathcal{W}^{o}}$ and the pessimistic weighting vector
${\mathcal{W}^{p}}$. Then, the deterministic format of both optimistic and pessimistic weighting vectors,
${\dddot{\mathcal{W}}^{o}}$ and
${\dddot{\mathcal{W}}^{p}}$, can be obtained using Eq. (
2), as shown in the Table
8.
Table 5
Indifferent, preference and veto thresholds.
|
${\mathfrak{g}_{1}}$ |
${\mathfrak{g}_{2}}$ |
${\mathfrak{g}_{3}}$ |
${\mathfrak{g}_{4}}$ |
| q |
L |
L |
M |
M |
| p |
MH |
ML |
MH |
H |
| v |
VH |
H |
VH |
VH |
Table 6
Deterministic format of optimistic-pessimistic decision matrix and thresholds.
|
$s({\mathfrak{d}_{ij}^{o}})$ |
$s({\mathfrak{d}_{ij}^{p}})$ |
|
${\mathfrak{g}_{1}}$ |
${\mathfrak{g}_{2}}$ |
${\mathfrak{g}_{3}}$ |
${\mathfrak{g}_{4}}$ |
${\mathfrak{g}_{1}}$ |
${\mathfrak{g}_{2}}$ |
${\mathfrak{g}_{3}}$ |
${\mathfrak{g}_{4}}$ |
| ${\mathfrak{a}_{1}}$ |
0.782 |
0.715 |
0.648 |
0.115 |
0.515 |
0.315 |
0.115 |
0.115 |
| ${\mathfrak{a}_{2}}$ |
0.515 |
0.715 |
0.515 |
0.715 |
0.248 |
0.715 |
0.115 |
0.448 |
| ${\mathfrak{a}_{3}}$ |
0.715 |
0.515 |
0.715 |
0.715 |
0.715 |
0.248 |
0.715 |
0.315 |
| ${\mathfrak{a}_{4}}$ |
0.191 |
0.347 |
0.315 |
0.515 |
−0.085 |
−0.085 |
0.048 |
−0.018 |
| ${\mathfrak{a}_{5}}$ |
−0.325 |
0.120 |
0.382 |
0.515 |
−0.325 |
−0.476 |
0.115 |
0.115 |
| q |
−0.325 |
−0.325 |
0.115 |
0.115 |
−0.325 |
−0.325 |
0.115 |
0.115 |
| p |
0.315 |
−0.085 |
0.315 |
0.515 |
0.315 |
−0.085 |
0.315 |
0.515 |
| v |
0.715 |
0.515 |
0.715 |
0.715 |
0.715 |
0.515 |
0.715 |
0.715 |
Table 7
Linguistic preferences for criteria weights provided by analysts.
|
${\mathfrak{g}_{1}}$ |
${\mathfrak{g}_{2}}$ |
${\mathfrak{g}_{3}}$ |
${\mathfrak{g}_{4}}$ |
| ${\mathfrak{e}_{1}}$ |
VI |
I |
I |
U |
| ${\mathfrak{e}_{2}}$ |
VI |
I |
M |
M |
| ${\mathfrak{e}_{3}}$ |
I |
I |
I |
U |
Table 8
Optimistic weight and pessimistic weight for criteria.
|
${\mathfrak{g}_{1}}$ |
${\mathfrak{g}_{2}}$ |
${\mathfrak{g}_{3}}$ |
${\mathfrak{g}_{4}}$ |
| ${\mathfrak{w}_{j}}$ |
(0.794,0.102;0.213) |
(0.581,0.106;0) |
(0.498,0.189;0.236) |
(0.231,0.456;0.141) |
| ${\mathfrak{w}_{j}^{o}}$ |
(0.98,0) |
(0.581,0.106) |
(0.665,0.02) |
(0.33,0.355) |
| ${\mathfrak{w}_{j}^{p}}$ |
(0.643,0.252) |
(0.581,0.106) |
(0.331,0.356) |
(0.131,0.556) |
| ${\dddot{\mathcal{W}}^{o}}$ |
0.99 |
0.738 |
0.821 |
0.487 |
| ${\dddot{\mathcal{W}}^{p}}$ |
0.696 |
0.738 |
0.488 |
0.287 |
After that, determine the optimistic concordance index
${C^{o}}({\mathfrak{a}_{i}},{\mathfrak{a}^{\prime }_{i}})$ and pessimistic concordance index
${C^{p}}({\mathfrak{a}_{i}},{\mathfrak{a}^{\prime }_{i}})$ using Eqs. (
11)–(
12). Similarly, calculate the discordance indices for both optimistic and pessimistic decision matrices using Eqs. (
13)–(
14). The results are provided in Tables
9–
11, respectively. Then, the comparisons between the concordance and discordance indices are conducted, and the credibility index
$\sigma ({\mathfrak{a}_{i}},{\mathfrak{a}^{\prime }_{i}})$ can be determined using Eq. (
15). The value of
$\sigma ({\mathfrak{a}_{i}},{\mathfrak{a}^{\prime }_{i}})=1$ means that the concordance value is greater than any discordance value for each criterion, such that
$C({\mathfrak{a}_{i}},{\mathfrak{a}^{\prime }_{i}})\geqslant {d_{j}}({\mathfrak{a}_{i}},{\mathfrak{a}^{\prime }_{i}})$ for
$j\in \mathcal{F}$. While, if
$\sigma ({\mathfrak{a}_{i}},{\mathfrak{a}^{\prime }_{i}})=0$, then there is a case where discordance value on a criterion is greater than the concordance value. Next, the credibility matrices for optimistic
${\sigma ^{o}}({\mathfrak{a}_{i}},{\mathfrak{a}^{\prime }_{i}})$ and pessimistic
${\sigma ^{p}}({\mathfrak{a}_{i}},{\mathfrak{a}^{\prime }_{i}})$ are shown in Table
12. In the final step, by using
$\alpha =0.5$, the final ranking of alternatives can be generated, and the result is displayed in Table
13.
Table 9
Optimistic and pessimistic concordance indices.
| ${C^{o}}(\mathfrak{a},{\mathfrak{a}^{\prime }})$ |
${\mathfrak{a}_{1}}$ |
${\mathfrak{a}_{2}}$ |
${\mathfrak{a}_{3}}$ |
${\mathfrak{a}_{4}}$ |
${\mathfrak{a}_{5}}$ |
${C^{p}}(\mathfrak{a},{\mathfrak{a}^{\prime }})$ |
${\mathfrak{a}_{1}}$ |
${\mathfrak{a}_{2}}$ |
${\mathfrak{a}_{3}}$ |
${\mathfrak{a}_{4}}$ |
${\mathfrak{a}_{5}}$ |
| ${\mathfrak{a}_{1}}$ |
1 |
0.567 |
0.581 |
0.886 |
0.886 |
${\mathfrak{a}_{1}}$ |
1 |
0.566 |
0.159 |
1 |
1 |
| ${\mathfrak{a}_{2}}$ |
0.431 |
1 |
0.491 |
1 |
1 |
${\mathfrak{a}_{2}}$ |
0.709 |
1 |
0.464 |
1 |
1 |
| ${\mathfrak{a}_{3}}$ |
0.557 |
0.693 |
1 |
0.873 |
1 |
${\mathfrak{a}_{3}}$ |
0.604 |
0.66 |
1 |
1 |
1 |
| ${\mathfrak{a}_{4}}$ |
0.161 |
0.282 |
0.126 |
1 |
0.869 |
${\mathfrak{a}_{4}}$ |
0.345 |
0.236 |
0.059 |
1 |
0.952 |
| ${\mathfrak{a}_{5}}$ |
0.226 |
0.372 |
0.126 |
0.431 |
1 |
${\mathfrak{a}_{5}}$ |
0.351 |
0.280 |
0.103 |
0.388 |
1 |
Table 10
Optimistic discordance indices for each criterion.
|
Criteria 1 |
Criteria 2 |
Criteria 3 |
Criteria 4 |
|
${\mathfrak{a}_{1}}$ |
${\mathfrak{a}_{2}}$ |
${\mathfrak{a}_{3}}$ |
${\mathfrak{a}_{4}}$ |
${\mathfrak{a}_{5}}$ |
${\mathfrak{a}_{1}}$ |
${\mathfrak{a}_{2}}$ |
${\mathfrak{a}_{3}}$ |
${\mathfrak{a}_{4}}$ |
${\mathfrak{a}_{5}}$ |
${\mathfrak{a}_{1}}$ |
${\mathfrak{a}_{2}}$ |
${\mathfrak{a}_{3}}$ |
${\mathfrak{a}_{4}}$ |
${\mathfrak{a}_{5}}$ |
${\mathfrak{a}_{1}}$ |
${\mathfrak{a}_{2}}$ |
${\mathfrak{a}_{3}}$ |
${\mathfrak{a}_{4}}$ |
${\mathfrak{a}_{5}}$ |
| ${\mathfrak{a}_{1}}$ |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0.425 |
0.425 |
0 |
0 |
| ${\mathfrak{a}_{2}}$ |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
| ${\mathfrak{a}_{3}}$ |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
| ${\mathfrak{a}_{4}}$ |
0.713 |
0.046 |
0.546 |
1 |
0 |
0.713 |
0.046 |
0.546 |
1 |
0 |
0.046 |
0 |
0.213 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
| ${\mathfrak{a}_{5}}$ |
1 |
1 |
1 |
0.479 |
1 |
1 |
1 |
1 |
0.479 |
1 |
0 |
0 |
0.046 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
Table 11
Pessimistic discordance indices for each criterion.
| Criteria 1 |
Criteria 2 |
Criteria 3 |
Criteria 4 |
| ${\mathfrak{a}_{1}}$ |
${\mathfrak{a}_{2}}$ |
${\mathfrak{a}_{3}}$ |
${\mathfrak{a}_{4}}$ |
${\mathfrak{a}_{5}}$ |
${\mathfrak{a}_{1}}$ |
${\mathfrak{a}_{2}}$ |
${\mathfrak{a}_{3}}$ |
${\mathfrak{a}_{4}}$ |
${\mathfrak{a}_{5}}$ |
${\mathfrak{a}_{1}}$ |
${\mathfrak{a}_{2}}$ |
${\mathfrak{a}_{3}}$ |
${\mathfrak{a}_{4}}$ |
${\mathfrak{a}_{5}}$ |
${\mathfrak{a}_{1}}$ |
${\mathfrak{a}_{2}}$ |
${\mathfrak{a}_{3}}$ |
${\mathfrak{a}_{4}}$ |
${\mathfrak{a}_{5}}$ |
| 1 |
0 |
0 |
0 |
0 |
1 |
0.808 |
0.059 |
0 |
0 |
1 |
0 |
0.713 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
| 0 |
1 |
0.379 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0.713 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
| 0 |
0 |
1 |
0 |
0 |
0.253 |
0.919 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
| 0.713 |
0.046 |
1 |
1 |
0 |
0.808 |
1 |
0.697 |
1 |
0 |
0 |
0 |
0.879 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
| 1 |
0.646 |
1 |
0 |
1 |
1 |
1 |
1 |
0.794 |
1 |
0 |
0 |
0.713 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
Table 12
The credibility index for (a) optimistic and (b) pessimistic.

Based on the result, the first ranking is stock, ${\mathfrak{a}_{3}}$ followed by ${\mathfrak{a}_{2}}$, ${\mathfrak{a}_{1}}$, ${\mathfrak{a}_{4}}$, and ${\mathfrak{a}_{5}}$, respectively. Stock ${\mathfrak{a}_{3}}$ is ranked first due to the highest score which is 2.22 compared to the other alternatives and this indicates that it is a good stock to invest.
Table 13
Final ranking and score.
| Alternatives |
Score |
Rank |
| ${\mathfrak{a}_{1}}$ |
1.43 |
3 |
| ${\mathfrak{a}_{2}}$ |
2.09 |
2 |
| ${\mathfrak{a}_{3}}$ |
2.22 |
1 |
| ${\mathfrak{a}_{4}}$ |
−2.14 |
4 |
| ${\mathfrak{a}_{5}}$ |
−3.60 |
5 |
6 Sensitivity and Comparative Analyses
To check the robustness and stability of the proposed model, some sensitivity analyses, as well as a comparison analysis are carried out. These analyses are conducted to analyse various scenarios that might amend the result of the proposed model. First, a sensitivity analysis with respect to
α-value is conducted for
$\alpha \in [0,1]$. This value represents a ratio of combined decision for the attitudinal character of analysts (as a group), ranging from optimistic to pessimistic attitudes. Based on Eq. (
22), the closer
α to 1, the more optimist the analysts toward sureness or validity of membership degrees compared to non-membership degrees as the source of preferences. The result of this analysis with respect to
α-values can be seen in Table
14 and Fig.
6.
Table 14
The score alternatives with different α.
|
Degree of optimisitic attitude $(\alpha )$
|
|
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
| ${\mathfrak{a}_{1}}$ |
0.95 |
1.04 |
1.14 |
1.24 |
1.34 |
1.43 |
1.53 |
1.63 |
1.72 |
1.82 |
1.92 |
| ${\mathfrak{a}_{2}}$ |
2.59 |
2.49 |
2.39 |
2.29 |
2.19 |
2.09 |
1.99 |
1.89 |
1.79 |
1.69 |
1.59 |
| ${\mathfrak{a}_{3}}$ |
2.42 |
2.38 |
2.34 |
2.40 |
2.26 |
2.22 |
2.18 |
2.14 |
2.10 |
2.06 |
2.02 |
| ${\mathfrak{a}_{4}}$ |
−2.13 |
−2.13 |
−2.13 |
−2.13 |
−2.13 |
−2.14 |
−2.14 |
−2.14 |
−2.14 |
−2.14 |
−2.14 |
| ${\mathfrak{a}_{5}}$ |
−3.82 |
−3.78 |
−3.73 |
−3.69 |
−3.65 |
−3.60 |
−3.56 |
−3.52 |
−3.47 |
−3.43 |
−3.39 |
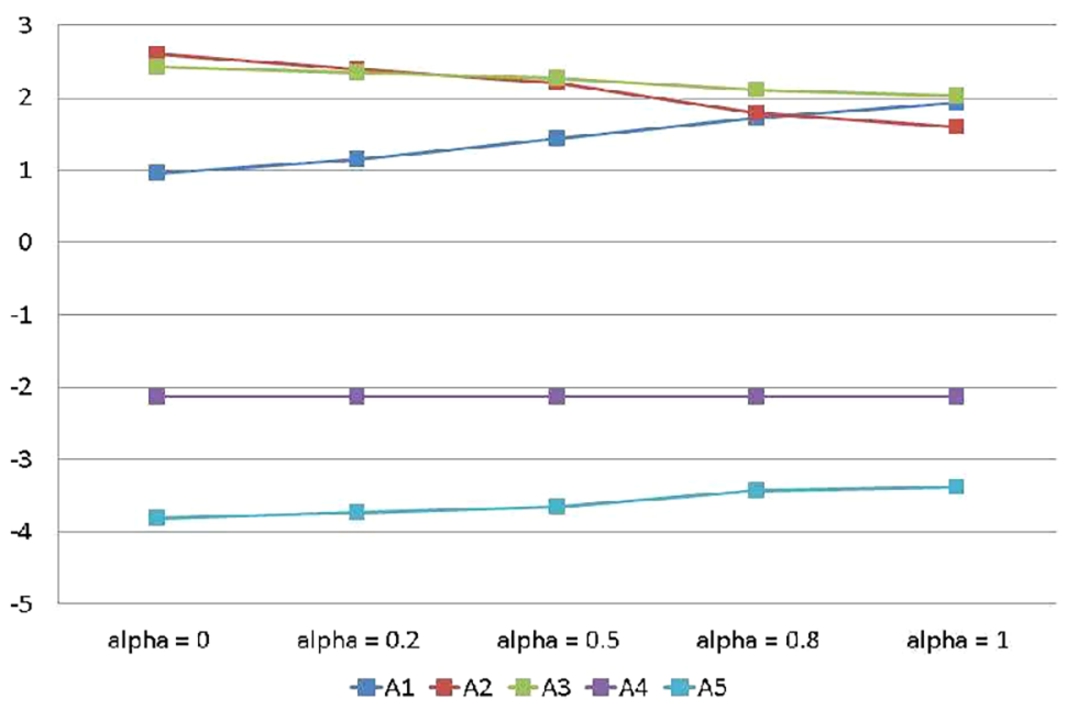
Fig. 6
Result of CIF-ELECTRE III.
In Table
14 and Fig.
6 below, it can be noticed that the ranking for top three alternatives is slightly reversed for
$\alpha \in [0,1]$, but the rest of the alternatives are consistent. For example,
${\mathfrak{a}_{2}}\succ {\mathfrak{a}_{3}}\succ {\mathfrak{a}_{1}}\succ {\mathfrak{a}_{4}}\succ {\mathfrak{a}_{5}}$ for
$\alpha \to 0$ (or toward pessimistic attitude). While for
$\alpha \to 1$ (or toward optimistic attitude), the ranking is
${\mathfrak{a}_{3}}\succ {\mathfrak{a}_{1}}\succ {\mathfrak{a}_{2}}\succ {\mathfrak{a}_{4}}\succ {\mathfrak{a}_{5}}$. However, it can be observed that
${\mathfrak{a}_{2}}$ is dominated by
${\mathfrak{a}_{3}}$ for
$\alpha \gt 0.2$. Hence, this analysis justifies
${\mathfrak{a}_{3}}$ as the best alternative. Moreover, to further validate this result, another sensitivity analyses with respect to criteria weights and thresholds are conducted (see Fig.
7). As can be noticed,
${\mathfrak{a}_{3}}$ and
${\mathfrak{a}_{2}}$ still ranked as the best alternatives. Nevertheless,
${\mathfrak{a}_{3}}$ dominates
${\mathfrak{a}_{2}}$ in most of the cases. To conclude, a change in
α-value influences the score of alternatives, but this does not contribute to major changes in the rankings. However, the inclusion of
α-value is significant to model the attitudinal character of group and to provide a vast analysis of different scenarios before making a final decision.
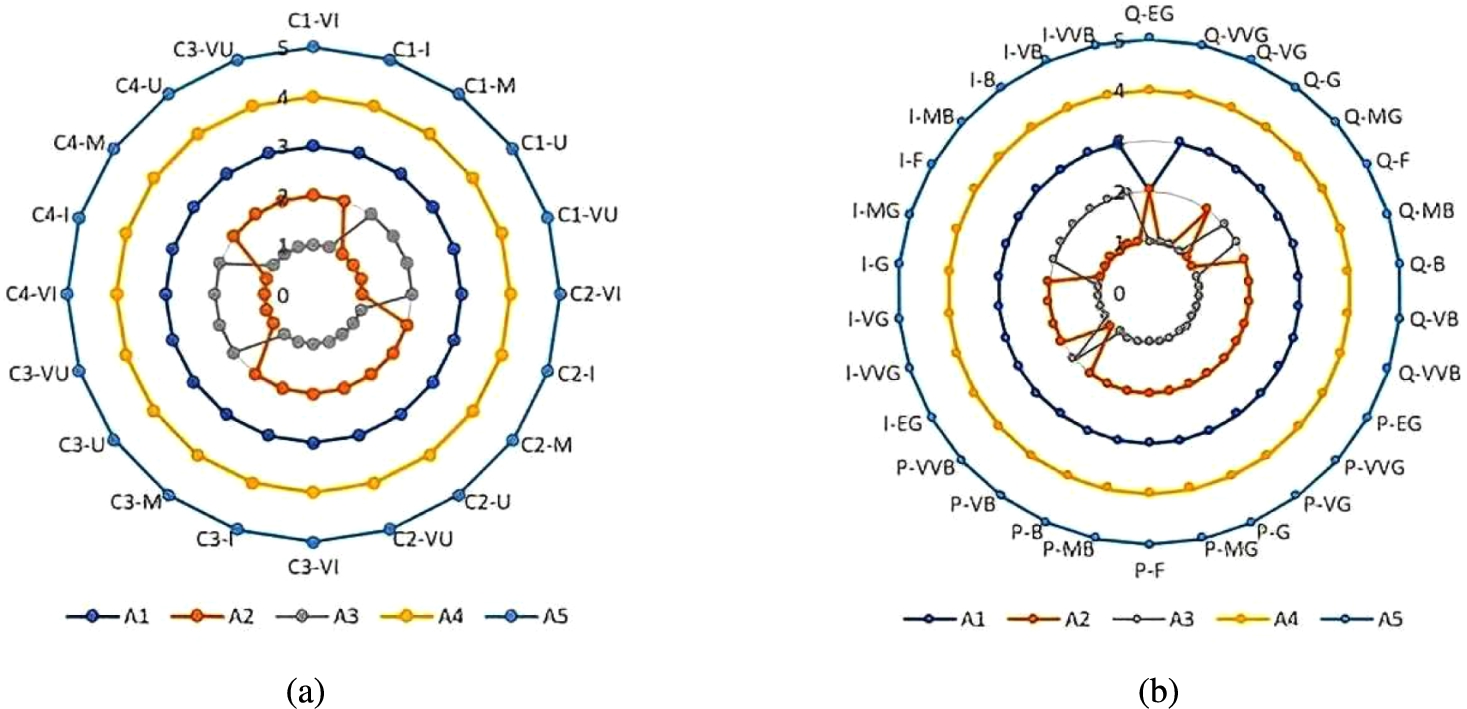
Fig. 7
Sensitivity analysis of CIF-ELECTRE III based on (a) criteria weights and (b) thresholds.
Table 15
Comparison of ELECTRE III under different sets and CIF-TOPSIS.
| Model |
Information |
Ranking |
| Proposed model |
$\alpha =0.1$ |
${\mathfrak{a}_{2}}\succ {\mathfrak{a}_{3}}\succ {\mathfrak{a}_{1}}\succ {\mathfrak{a}_{4}}\succ {\mathfrak{a}_{5}}$ |
|
$\alpha =0.5$ |
${\mathfrak{a}_{3}}\succ {\mathfrak{a}_{2}}\succ {\mathfrak{a}_{1}}\succ {\mathfrak{a}_{4}}\succ {\mathfrak{a}_{5}}$ |
|
$\alpha =0.9$ |
${\mathfrak{a}_{3}}\succ {\mathfrak{a}_{1}}\succ {\mathfrak{a}_{2}}\succ {\mathfrak{a}_{4}}\succ {\mathfrak{a}_{5}}$ |
| IF-ELECTRE III |
– |
${\mathfrak{a}_{3}}\succ {\mathfrak{a}_{2}}\succ {\mathfrak{a}_{1}}\succ {\mathfrak{a}_{4}}\succ {\mathfrak{a}_{5}}$ |
| IVIF-ELECTRE III |
– |
${\mathfrak{a}_{3}}\succ {\mathfrak{a}_{1}}\succ {\mathfrak{a}_{2}}\succ {\mathfrak{a}_{4}}\succ {\mathfrak{a}_{5}}$ |
| CIF-TOPSIS |
$\alpha =0.1$ |
${\mathfrak{a}_{3}}\succ {\mathfrak{a}_{2}}\succ {\mathfrak{a}_{1}}\succ {\mathfrak{a}_{5}}\succ {\mathfrak{a}_{4}}$ |
|
$\alpha =0.5$ |
${\mathfrak{a}_{3}}\succ {\mathfrak{a}_{2}}\succ {\mathfrak{a}_{1}}\succ {\mathfrak{a}_{4}}\succ {\mathfrak{a}_{5}}$ |
|
$\alpha =0.9$ |
${\mathfrak{a}_{3}}\succ {\mathfrak{a}_{1}}\succ {\mathfrak{a}_{2}}\succ {\mathfrak{a}_{4}}\succ {\mathfrak{a}_{5}}$ |
Furthermore, we compare the ranking results of our proposed model with ELECTRE III under two different sets: IF-ELECTRE III and IVIF-ELECTRE III (Hashemi
et al.,
2016). Additionally, we conduct a comparison with CIF-TOPSIS (Kahraman and Alkan,
2021).
In Table
15, it is evident that
${\mathfrak{a}_{3}}$ maintains its top ranking across all the compared models, followed by either
${\mathfrak{a}_{1}}$ or
${\mathfrak{a}_{2}}$. The only variation occurs in the pessimistic scenario, where
${\mathfrak{a}_{2}}$ attains the top rank in our proposed model (i.e.
$\alpha \leqslant 2$). This suggests that employing CIFS in ELECTRE III offers a justifiable approach and introduces a fresh perspective to modelling multi-criteria and multi-actor decision-making problems.
Moreover, for a more in-depth analysis of the effect of the final decision concerning the optimistic and pessimistic attitudes, we apply the tranquillity measure proposed by Yager (
1982) using the following formula:
where
${\gamma _{\max }}$ is the maximal grade of membership of any element of
$\mathcal{A}$ in
D and
$Card{D_{\gamma }}$ is the cardinality of the
γ-level set of
D. This function demonstrates the degree of tranquillity or confidence it provides when selecting the best alternative. Specifically, the closer
$T(D,\mathcal{A})$ to one, the higher the confidence in selecting the best alternative, while the closer it is to zero, the more anxiety there may be in choosing the best alternative, especially when there is small difference between alternatives or a tie. This analysis exclusively compares the results of CIF-TOPSIS and CIF-ELECTRE III. To do so, we conduct a normalization process for the final ranking in both models, specifically using linear scale transformation to convert the results to the unit interval [0,1]. The comparison of tranquillity values for the CIF-TOPSIS and CIF-ELECTRE III models is given in Table
16.
Table 16
Tranquillity measures on CIF-TOPSIS and CIF-ELECTRE III for $\alpha \in [0,1]$.
| $T(D,\mathcal{A})$ |
$\alpha =0$ |
$\alpha =0.1$ |
$\alpha =0.2$ |
$\alpha =0.3$ |
$\alpha =0.4$ |
$\alpha =0.5$ |
$\alpha =0.6$ |
$\alpha =0.7$ |
$\alpha =0.8$ |
$\alpha =0.9$ |
$\alpha =1$ |
| CIF-TOPSIS |
0.2649 |
0.2714 |
0.2778 |
0.2843 |
0.2907 |
0.2937 |
0.2946 |
0.2913 |
0.2879 |
0.2846 |
0.2812 |
| CIF-ELECTRE III |
0.3676 |
0.3589 |
0.3498 |
0.3417 |
0.3437 |
0.3457 |
0.3478 |
0.3500 |
0.3522 |
0.3463 |
0.3363 |
As shown in Table
16, the tranquillity measures for CIF-ELECTRE III consistently yield higher values compared to CIF-TOPSIS across all the specified
α values. This demonstrates that the decisions made with CIF-ELECTRE III are associated with a better psychological ease or confidence when selecting the best alternative.
7 Conclusion
In this paper, we propose an extension of the ELECTRE III model within the context of the CIFS environment for group decision analysis. We introduce several extensions to the group decision matrix (referred to as the CIF decision matrix) and the group weighting vector (referred to as the CIF weighting vector). These extensions specifically address CIFS conditions, focusing on optimistic and pessimistic attitudes. We construct these attitudinal attributes based on a set of conditional rules, ensuring that every element remains confined within a circular area defined by a radius r. We also introduce the concept of the net score degree, which serves as a unified formulation incorporating both optimistic and pessimistic scores for ranking alternatives. The net score degree is based on the parameter $\alpha \in [0,1]$, enabling a comprehensive analysis of group decision-making, considering both optimistic and pessimistic attitudes. To illustrate the applicability of the CIF-ELECTRE model, we provide a numerical example involving the stock-picking process. We conduct sensitivity analyses, considering variations in α-value, criteria weights, and thresholds, to validate the results of our proposed model. Furthermore, we perform a comparative analysis with ELECTRE III under IFS and IVIFS environments, as well as CIF-TOPSIS. In summary, our proposed model offers flexibility in data representation within the CIFS framework, allowing for the incorporation of a group of actors’ attitudes to address complex decision-making challenges.
However, our model has certain limitations and room for future development. Firstly, the model currently represents the attitudinal character of the entire group and does not account for individual actor attitudes. Secondly, it focuses exclusively on homogeneous group decision-making scenarios. Thirdly, in this model, CIF data is simplified to IF data for computational convenience. Future work could involve addressing individual actor attitudinal characteristics separately, accommodating heterogeneous group decision-making, and developing an algorithm that does not require converting CIF information to IF values. Lastly, it is essential to note that this study primarily deals with a simplified case involving a small group of just three experts. Discrepancies in final rankings may arise in large-scale group decision-making (LS-GDM) and more complex decision-making scenarios. Therefore, further application and analysis of our proposed method under LS-GDM are warranted.

