1 Introduction
Systems of nonlinear equations appear in the mathematical modelling of applications in the fields of physics, mechanics, chemistry, biology, computer science and applied mathematics.
Newton method is used for solving systems of nonlinear equations when the Jacobian matrix is Lipschitz continuous and nonsingular. The method is not well defined when the Jacobian matrix is singular. Levenberg-Marquardt algorithm was proposed to solve this problem, by introducing a regularization variable
var which switches between the Gradient Descent method and the Gauss-Newton method under the condition of evaluating a cost function. The difficulty of applying the Levenberg-Marquardt algorithm, in order to be efficient for a large number of applications, lies in determining a strategy for calculating the regularization variable at each iteration step. Thus, numerous solutions have been proposed for this calculation by: Musa
et al. (
2017), Karas
et al. (
2016), Umar
et al. (
2021). Ahookhosh Masoud implements an adaptive variable
var and studies the local convergence under Holder metric subregularity of the function defining the equation and Holder continuity of its gradient mapping (Masoud
et al.,
2019). He also evaluates the convergence under the assumption that the Lojasiewicz gradient inequality is valid. Liang Chen proposes a new Levenberg-Marquardt method by introducing a novel choice of the regularization variable
var, incorporating an extended domain for its exponent coefficient (Chen and Ma,
2023). He provides evidence that the new algorithm exhibits either superlinear or quadratic convergence, depending on the value of the exponent coefficient.
When the number of equations is very large, solving the identified least-square problem requires considerable resources, resulting in possible measurement redundancies. These realities lead us to conclude that an accurate assessment of the cost function and the gradient is not necessary to get the result of the problem. Jinyan Fan proposes a Levenberg-Marquardt algorithm using the trust region technique, where at each iteration an ap-proximate step is calculated in addition to the step towards the minimum of the function (Fan,
2012). The algorithm proposed by Stefania Bellavia is based on a control of the level of accuracy for the cost function and the gradient, increasing the approximation values when the accuracy is too low to continue the optimization (Bellavia
et al.,
2018).
Fog is a suspension of water droplets or ice crystals in the air. These particles are generally less than 50 microns in diameter and reduce visibility due to light scattering to less than 1 km. In the literature, the atmospheric propagation and the distribution of particles participating at effects such as light scattering corresponds to an atmospheric model. Intense research efforts are currently being developed to improve the possibility of detecting objects through fog. Kaiming He developed an algorithm predicated on the concept of dark channel prior (DCP) to mitigate the effects of fog (He
et al.,
2011). His observation elucidated that the majority of local patches in fog-free outdoor images encapsulate pixels exhibiting minimal intensity within at least one colour channel. In the context of foggy images, these low-intensity pixels serve as accurate estimators of light transmission. By implementing an atmospheric scattering model alongside a soft matting interpolation methodology, the image is defogged and restored to its original clarity. Kyungil Kim proposes an image enhancement technique for fog-affected indoor and outdoor images combining dark channel prior (DCP), contrast limited adaptive histogram equalization and discrete wavelet transform. Their algorithm employs a modified transmission map to increase processing speed (Kim
et al.,
2018). Sejal and Mitul (
2014) provide the results of enhancement algorithms based on homomorphic filtering (emphasizes contours and reduces the influence of low-frequency components such as airlight), respectively, on a method with a mask and local histogram equalization. A comprehensive study of existing enhancement algorithms for images acquired in fog is described by Xu
et al. (
2016). He also addresses the processing of image sequences acquired under the same bad weather conditions. Bolun Cai develops DehazeNet, a trainable system based on convolutional neural networks (CNNs), whose layers are designed to incorporate assumptions made in image dehazing. The algorithm takes in a foggy image and estimates the transmission map of the environment, which is used for reconstructing the defogged image using the mentioned arithmetic fog model (Cai
et al.,
2016). Adrian Galdran implements an image defogging method that eliminates degradation without requiring the model of the fog. The foggy image is first artificially underexposed through a sequence of gamma correction operations. The resulting images contain regions of increased contrast and saturation. A Laplacian multiscale fusion scheme gathers the areas of the highest quality from each image and combines them into a single fog-free image (Galdran,
2018). Boyun Li introduced the “You Only Look Yourself” algorithm, an unsupervised and untrained neural network. It utilizes three subnetworks to decompose the foggy image into three layers: scene radiance, transmission map, and atmospheric light. These individual layers are then merged in a self-supervised manner, eliminating the time-consuming data acquisition and image dehazing is done only based on the observed foggy image (Li
et al.,
2021).
The aim of our work is the enhancing visibility when fog reduces it. The method we propose uses a non-linear parametric model based on the extinction coefficient of the atmosphere and the sky light intensity. Both parameters are estimated thanks to the Levenberg-Marquard algorithm. An inverse transformation is applied to measured data (observations) to reconstruct the clear image. We described in Section
2 the “least squares problem” that determines an analytic function that traverses as well as possible a set of observations. Section
3 describes the Levenberg-Marquardt algorithm we use to estimate the components of the vector of unknown parameters of a model describing the process under analysis. The mathematical model for the acquisition process of homogeneous fog time images is described in Section
4, a more complex approach is given in Curilă
et al. (
2020). In Section
5 we propose an algorithm for improving fog degraded images (using simulated foggy images). Experimental results are presented in Section
6 and Section
7 presents discussions on the proposed method and the obtained results.
2 Non-Linear Least Squares Problem
Data modelling is an interpolation between some observations that belong to a continuous function, while the other observations approach the function with a certain tolerance (see Fig.
1). A model that has the parameters
${p_{i}}$,
$i=1,\dots ,K$ and which fits a
${L_{uv}}$ observations,
$u=1,\dots ,N$,
$v=1,\dots ,M$, provides an analytical function:
whose variables
p are adjustable. Here, we consider that
$L(u,v;\mathbf{p})$ depends non-linearly on the components of the vector
p.
The least squares problem’s scope is to estimate a mathematical model that fits a set of observations using the cost function minimization given by the sum of the squares of the errors between the data set and the model’s analytical function. The optimization algorithm is iterative because, as we mentioned, the model is non-linear in its parameters. At each step the parameters are modified to obtain a minimum of the cost function.
As the data is in most cases affected by noise, measurement errors are generated in the fitting process referred to as residues. Thus, for a fixed value of the vector
p at a given time, the residues will be estimated as follows
The objective is to find
${\mathbf{p}_{\min }}$, where the cost function
${\chi ^{2}}(\mathbf{p})$, given by the second-order norm of the residues
$\| {\chi _{uv}}{\| ^{2}}$, will take the minimum value.
With a certain number of ${L_{uv}}$ observations and a model that provides an analytical function that fits them, there are parameters for which the fitting is very well made (those parameters are unique), and for other parameter values the model’s analytical function $L(u,v;\mathbf{p})$ does not resemble the data at all.
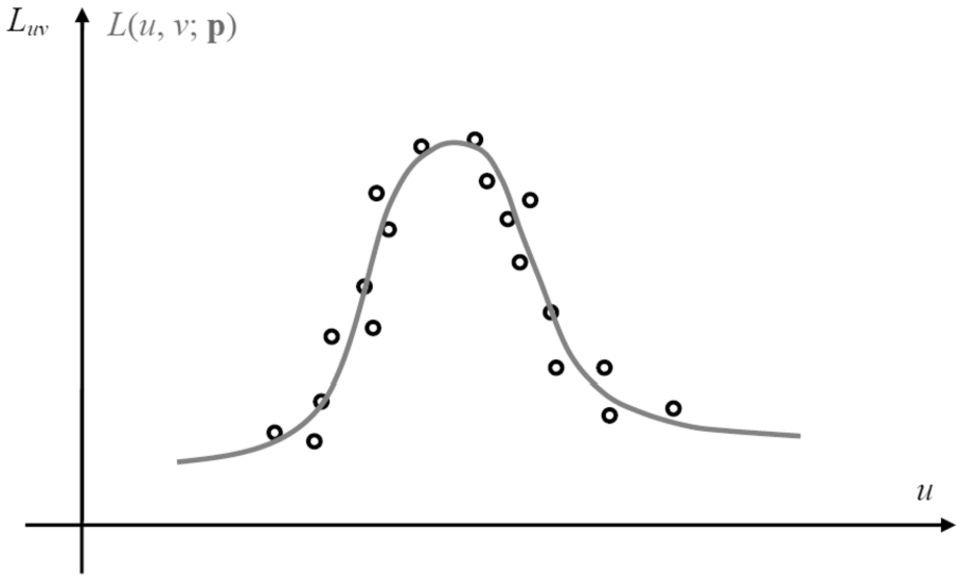
Fig. 1
The set of observations ${L_{uv}}$ (represented by O) and the model’s analytical function $L(u,v;\mathbf{p})$ (represented by a solid gray line).
Starting with an initial value of the vector p, we will implement an optimization algorithm that will adapt p by a difference $\Delta \mathbf{p}$ until the procedure stops based on predetermined constraints described below.
4 A Mathematical Model for Fog
It is assumed that a collimated beam of light with a unitary cross-section traverses the dispersive environment of thickness
$dz$ (fog dispersion, see Fig.
3) (Curilă
et al.,
2020). The radiative transfer through fog is expressed by Schwarzschild’s equation as follows:
where
${L_{\lambda }}(z)$ is the intensity of radiation,
${\beta _{\lambda }}$ is the extinction coefficient of the atmosphere and
${L_{S\lambda }}$ is the sky light intensity.
The fractional change in intensity of radiation, the first term of Eq. (
13), expresses a relationship between the light intensity and the properties of the dispersive environment.
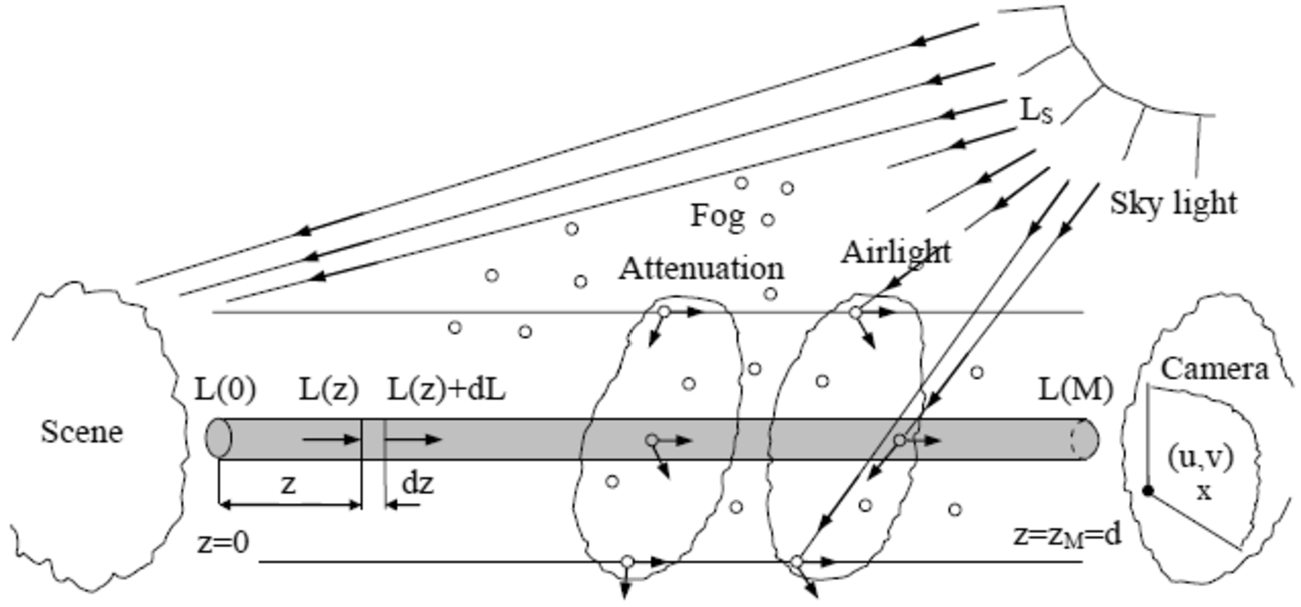
Fig. 3
Radiative transfer scheme.
As represented in the radiative transfer scheme, the aerosol particles capture the sky light and radiate it back in all directions. Some of the scattered light passes into the direct transmission path and raises the pixel intensity value acquired by the camera. Taking into account the increase
$(z,z+dz)$ of the direct transmission path, the fractional change in the radiation intensity due to the scattering of sky light is given by the second term of Eq. (
13). This process, the emission of thermal radiation via the direct transmission path, is typically called airlight. When the distance in the
z-direction grows, the minus sign in the above equation denotes a reduction in
${L_{\lambda }}(z)$, while the plus points to an increase.
Our approach uses a linear first-order Eq. (
13) whose solution was presented in Sokolik (
2021). This results in the following mathematical model of the image acquisition during homogeneous fog, which includes both object radiation attenuation and atmospheric veil superposition:
where
${L_{\lambda }}(M(u,v))$ is the intensity of the pixel,
${L_{\lambda }}(O(X,Y,Z))$ is the radiant intensity of corresponding point on the scene,
$d(u,v)$ is the distance map,
${\beta _{\lambda }}$ is the extinction coefficient and
${L_{S\lambda }}$ is the sky light intensity both mentioned above, and
${L_{S\lambda }}(1-{e^{-{\beta _{\lambda }}d(u,v)}})$ is the atmospheric veil.
The distance map expresses the distances between the camera and the points on the scene. This matrix recording was obtained by: a) FRIDA image database (as the first one in Fig.
4) (Tarel
et al.,
2010); b) using approximate measurements and perspective projection system for real images (the other two distance maps in the same figure). Real-life atmospheric impressions are simulated by choosing the type of fog and adding an atmospheric veil by suitably establishing the local distances. Next, we present distance maps for
LIMA-000011,
ship and
bridge images (Curilă
et al.,
2020; Tarel
et al.,
2010).
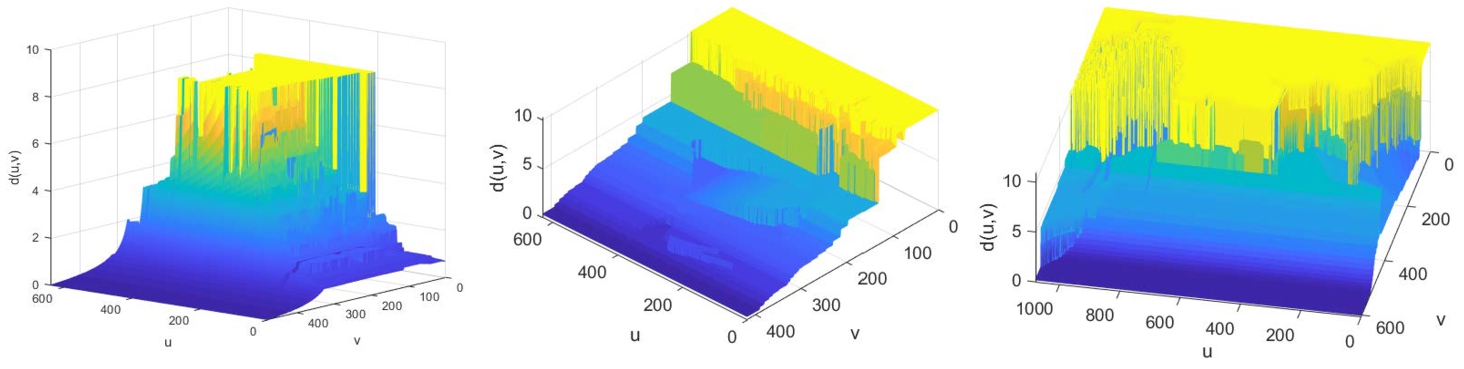
Fig. 4
The distance maps for the three aforementioned images, which are included in the test dataset.
5 Model Based Foggy Image Enhancement Using L-M (MBFIELM)
The algorithm we propose in this section relies on applying an inverse transformation to the degradation process during fog time image acquisition in order to obtain an enhanced image. We use the mathematical model described in Section
4 to estimate an analytic function that best approximates an image acquired in foggy conditions. We avoid arriving at an indeterminate problem, where the number of data is less than the number of unknowns, by setting the unknown parameters:
${\mu _{\lambda }}$ the mean of the radiant intensities of the scene points,
${\beta _{\lambda }}$ the extinction coefficient of the atmosphere and
${L_{S\lambda }}$ the sky light intensity (
$\mathbf{p}=[{\mu _{\lambda }}\hspace{2.5pt}{\beta _{\lambda }}\hspace{2.5pt}{L_{S\lambda }}]$). In this way, the following pseudo-model is generated for foggy images:
where
${p_{1}}={\mu _{\lambda }},{p_{2}}={\beta _{\lambda }},{p_{3}}={L_{S\lambda }}$,
${\mu _{\lambda }}=\text{mean}({L_{\lambda }}(O(X,Y,Z)))$.
The optimization algorithm that will estimate the pseudo-model
$L(u,v;{p_{1}},{p_{2}},{p_{3}})$ parameters is Levenberg-Marquardt (see Section
3.3).
We have the following description of the cost function that is minimized to determine the parameter vector
${\mathbf{p}_{\min }}=[{\mu _{\lambda \min }}\hspace{2.5pt}{\beta _{\lambda \min }}\hspace{2.5pt}{L_{S\lambda \min }}]$:
The estimated parameter
${\mu _{\lambda \min }}$ is not used in the degraded image enhancement equation, it only provides information about the mean of the radiant intensities of the scene. The enhanced image is determined by the following equation, applicable to each wavelength (red, green, blue):
6 Experimental Results
We validate the proposed algorithm using a dataset of sixteen simulated foggy images. Testing on real images would have meant having the set of reference images ${L_{0}}$ acquired in the absence of the dispersive environment (fog), the set of images acquired in foggy conditions ${L_{\text{fog\_real}}}$ and the corresponding set of distance maps d. The three data matrices, corresponding to an image enhancement, must be synchronized (for each pixel that records a point in the scene in the ${L_{0}}$ matrix, there must be a pixel that records the same point in the scene in the presence of fog in the ${L_{\text{fog\_real}}}$ matrix and in the d matrix we should find the distance between the camera and the point in the scene – with no offsets present). This synchronization requires a camera attached to a tripod that is not moved until both the reference image ${L_{0}}$ and the foggy image ${L_{\text{fog\_real}}}$ are acquired. The duration of the capture of the two moments can be very long. Furthermore, to test the robustness of the algorithm we should have made these pairs of acquisitions (reference image, foggy image) in different locations to capture different scenes while also ensuring that the distance map is synchronized.
Therefore, at this point, we are left with the quick solution of testing the enhancement algorithm on images with the presence of simulated fog
${L_{\text{fog\_simul}}}$ using the mathematical model in Eq. (
14) and the corresponding real reference image
${L_{0}}$. The set of
${L_{uv}}$ observations is determined by the simulated
${L_{\text{fog\_simul}}}$ image based on the reference image
${L_{0}}$ and the parameters
${\beta _{\text{red}}}$,
${L_{S\hspace{0.1667em}\text{red}}}$,
${\beta _{\text{green}}}$,
${L_{S\hspace{0.1667em}\text{green}}}$,
${\beta _{\text{blue}}}$,
${L_{S\hspace{0.1667em}\text{blue}}}$:
We applied the Levenberg-Marquardt optimization algorithm on the dataset of sixteen test images, a representative selection of which are evaluated here. We worked on each channel separately in the RGB (red-green-blue) colour space, as this is how the simulated fog was introduced. Table
1 shows the parameters used to simulate the images in foggy conditions (
${L_{\text{fog\_simul}}}$ –
LIma-000011,
ship,
bridge) and the parameters estimated by minimizing the cost function in Eq. (
16).
Table 1
| Image |
Parameters used in the simulation |
Estimated parameters |
| Red |
Green |
Blue |
Red |
Green |
Blue |
| LIma11 |
${L_{0\hspace{0.1667em}\text{r}}}$ |
${L_{0\hspace{0.1667em}\text{g}}}$ |
${L_{0\hspace{0.1667em}\text{b}}}$ |
${\mu _{\text{r}\min }}=92.4392$ |
${\mu _{\text{g}\min }}=93.8712$ |
${\mu _{\text{b}\min }}=84.3013$ |
|
${\beta _{\text{r}}}=0.3$ |
${\beta _{\text{g}}}=0.3$ |
${\beta _{\text{b}}}=0.3$ |
${\beta _{\text{r}\min }}=0.2820$ |
${\beta _{\text{g}\min }}=0.2711$ |
${\beta _{\text{b}\min }}=0.2705$ |
|
${L_{S\hspace{0.1667em}\text{r}}}=260$ |
${L_{S\hspace{0.1667em}\text{g}}}=260$ |
${L_{S\hspace{0.1667em}\text{b}}}=260$ |
${L_{S\hspace{0.1667em}\text{r}\min }}=263.8087$ |
${L_{S\hspace{0.1667em}\text{g}\min }}=264.7210$ |
${L_{S\hspace{0.1667em}\text{b}\min }}=264.5776$ |
| ship |
${L_{0\hspace{0.1667em}\text{r}}}$ |
${L_{0\hspace{0.1667em}\text{g}}}$ |
${L_{0\hspace{0.1667em}\text{b}}}$ |
${\mu _{\text{r}\min }}=57.9859$ |
${\mu _{\text{g}\min }}=91.5837$ |
${\mu _{\text{b}\min }}=108.4424$ |
|
${\beta _{\text{r}}}=0.4$ |
${\beta _{\text{g}}}=0.4$ |
${\beta _{\text{b}}}=0.4$ |
${\beta _{\text{r}\min }}=0.3710$ |
${\beta _{\text{g}\min }}=0.3177$ |
${\beta _{\text{b}\min }}=0.2752$ |
|
${L_{S\hspace{0.1667em}\text{r}}}=170$ |
${L_{S\hspace{0.1667em}\text{g}}}=170$ |
${L_{S\hspace{0.1667em}\text{b}}}=170$ |
${L_{S\hspace{0.1667em}\text{r}\min }}=172.4667$ |
${L_{S\hspace{0.1667em}\text{g}\min }}=173.7974$ |
${L_{S\hspace{0.1667em}\text{b}\min }}=175.0974$ |
| bridge |
${L_{0\hspace{0.1667em}\text{r}}}$ |
${L_{0\hspace{0.1667em}\text{g}}}$ |
${L_{0\hspace{0.1667em}\text{b}}}$ |
${\mu _{\text{r}\min }}=115.2789$ |
${\mu _{\text{g}\min }}=110.8441$ |
${\mu _{\text{b}\min }}=107.3712$ |
|
${\beta _{\text{r}}}=0.4$ |
${\beta _{\text{g}}}=0.4$ |
${\beta _{\text{b}}}=0.4$ |
${\beta _{\text{r}\min }}=0.3054$ |
${\beta _{\text{g}\min }}=0.3166$ |
${\beta _{\text{b}\min }}=0.3272$ |
|
${L_{S\hspace{0.1667em}\text{r}}}=220$ |
${L_{S\hspace{0.1667em}\text{g}}}=220$ |
${L_{S\hspace{0.1667em}\text{b}}}=220$ |
${L_{S\hspace{0.1667em}\text{r}\min }}=223.3607$ |
${L_{S\hspace{0.1667em}\text{g}\min }}=223.4535$ |
${L_{S\hspace{0.1667em}\text{b}\min }}=223.3768$ |
We will make a visual inspection of the degree of fit of the estimated foggy image
${L_{\text{fog\_estim}}}$, obtained with the mathematical model defined by Eq. (
14) using
${L_{0}}$ and the estimated parameters (
${\beta _{\text{red}\min }}$,
${L_{S\hspace{0.1667em}\text{red}\min }}$,
${\beta _{\text{green}\min }}$,
${L_{S\hspace{0.1667em}\text{green}\min }}$,
${\beta _{\text{blue}\min }}$,
${L_{S\hspace{0.1667em}\text{blue}\min }}$), to the simulated image
${L_{\text{fog\_simul}}}$, obtained with the same equation and the parameters
${L_{0\hspace{0.1667em}\text{red}}}$,
${\beta _{\text{red}}}$,
${L_{S\hspace{0.1667em}\text{red}}}$,
${L_{0\hspace{0.1667em}\text{green}}}$,
${\beta _{\text{green}}}$,
${L_{S\hspace{0.1667em}\text{green}}}$,
${L_{0\hspace{0.1667em}\text{blue}}}$,
${\beta _{\text{blue}}}$,
${L_{S\hspace{0.1667em}\text{blue}}}$, representing in 3D the absolute value of the difference of the two images:
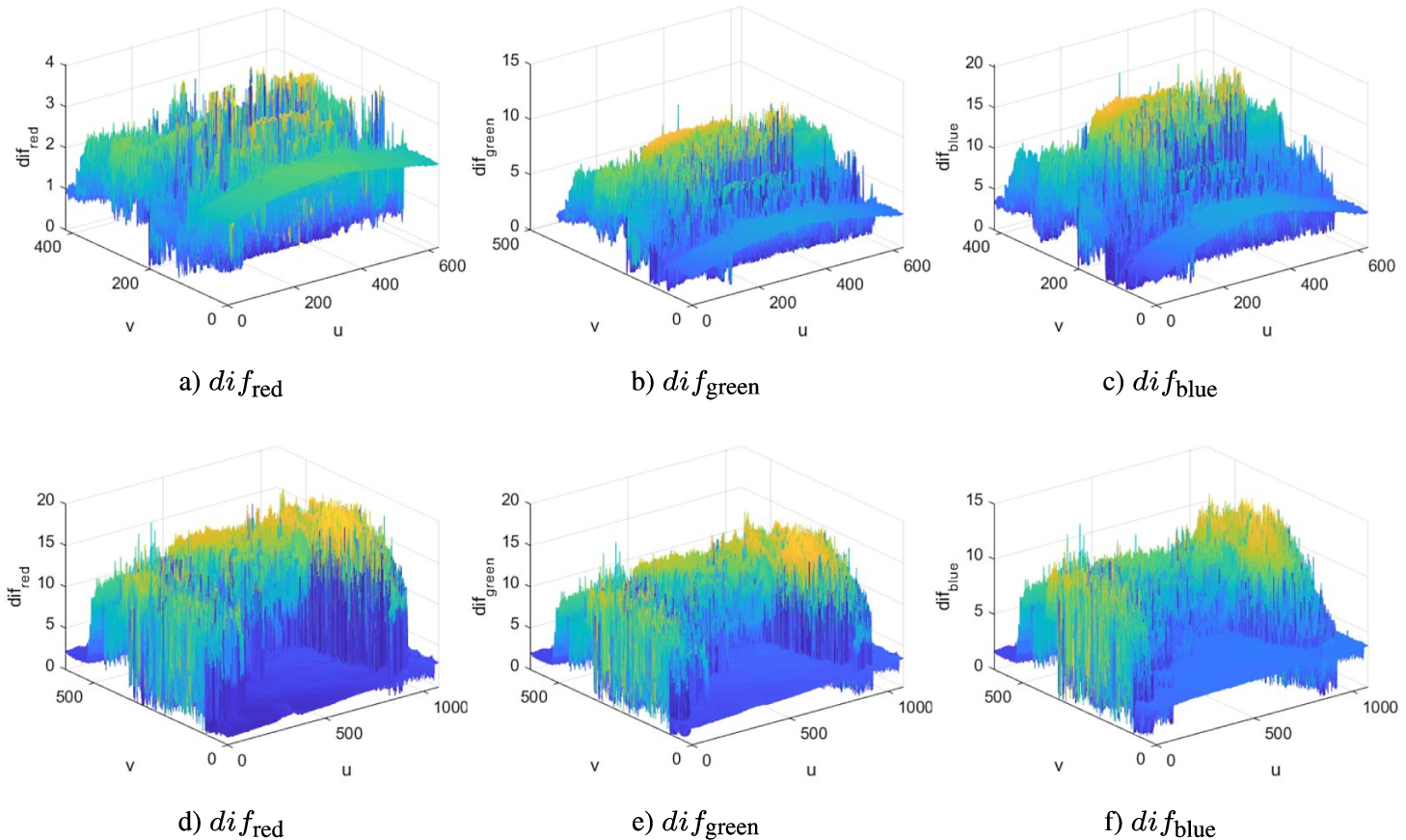
Fig. 5
Absolute value of the difference between the estimated foggy image ${L_{\text{fog\_estim}}}$ and the simulated image ${L_{\text{fog\_simul}}}$ (a, b, c the rgb components of the ship image; d, e, f the rgb components of the bridge image).
The better the fit, the smaller the difference
dif is, so the parameters
$[{\beta _{\lambda \min }}{L_{S\lambda \min }}]$ are better estimated and the enhancement algorithm gives a consistent result (ideally
$\textit{dif}=0$ and the enhanced image becomes
${L_{0}}$ – this result will never be obtained since the pseudo-model used in the optimization operation has as parameter
${p_{1}}$ an average of the
${L_{0}}$ luminances). As it can be seen from Fig.
5 for both images (
ship and
bridge), the mean value of the
dif is equal to 5 at almost all wavelengths. The exception is only in Fig.
5a) where for the red wavelength, in the case of the
ship image, the mean value of the
dif is equal to 2.
We assess the algorithm’s performance using both visual subjective inspection and a quantitative criterion. In order to compare our results with those from other algorithms in the relevant literature, we utilize an adapted metric to the quality of defogged images introduced by Liu
et al. (
2020).
Regarding the visual inspection, we present six representative images from the test dataset in the following order:
LIma-000011,
ship,
bridge,
LIma-000013,
LIma-000015 and
LIma-000006 (Tarel
et al.,
2010). The results of the
Model-Based Foggy Image Enhancement using Levenberg-Marquardt non-linear estimation (MBFIELM) are depicted in Fig.
6. The enhanced image
${L_{\text{enhanced}}}$ is obtained according to Eq. (
17).

Fig. 6
Visual inspection of the enhancing algorithm: a-reference images ${L_{0}}$ without dispersive environment, b-images with simulated fog ${L_{uv}}({L_{\text{fog\_simul}}})$, c-enhanced colour images ${L_{\text{enhanced}}}$.
The FRFSIM (Fog-Relevant Feature Similarity) indicator introduced by Wei Liu takes into account both
fog density, measured by the Dark channel feature and the Mean Subtracted Contrast Normalized (MSCN) feature, as well as
artificial distortion, measured by the Gradient feature (which refers to texture changes) and the Chroma
${_{\text{HSV}}}$ feature (which refers to colour distortion). Assessing the quality of the defogged image in relation to the reference image involves utilizing a single score that integrates four similarity maps: Dark Channel Similarity (DS), Mean Subtracted Contrast Normalized Similarity (MS), Gradient Similarity (GS) and Colour Similarity (CS), as detailed by Liu
et al. (
2020). First DS and MS are grouped into a single score to measure fog density, and then GS and CS are grouped into another score to measure texture and colour distortions artifacts. Both scores are merged into FRFSIM
$\in (0,1)$, index which takes on higher values as the quality of the defogged image increases.
Our method assumes the availability of a 3D component (distance map). In order to be able to compare our results with those of other methods that do not have this data, we define the following relative quantitative measure based on the FRFSIM indicator:
where FRFSIM1 represents the indicator calculated for the foggy image
${L_{uv}}$ relative to reference image
${L_{0}}$ and FRFSIM2 represents the indicator calculated for defogged image
${L_{\text{enhanced}}}$ relative to the same reference image
${L_{0}}$.
We used classical contrast enhancement algorithms, linear and non-linear contrast stretching and histogram equalization, working with simulated foggy images alongside with their corresponding reference images. In these cases, for the entire test dataset, the measure expressed by Eq. (
20) indicates either a decrese in the quality of the processed image or an irrelevant enhancement with a maximum
${\text{enhc}_{\text{FRFSIM}}}=4.8\% $.
Here, we present a comparative analysis of the results obtained by our algorithm versus the best results of foggy image enhancement algorithms discussed in Liu
et al. (
2020). The values of the
$\text{FRFSIM1}$ and
$\text{FRFSIM2}$ indicators for the enhancement algorithm based on the Levenberg-Marquardt method (MBFIELM) are displayed below in each of the six representative images of the test dataset in Fig.
6.
Also, the results of four sets of images taken from the article referenced above are presented below. Figures
7a1,
7a2,
7a3 and
7a4 represent reference images acquired under normal atmospheric conditions (no fog), Fig.
7b1 shows a real foggy image with
$\text{FRFSIM1}=0.2904$ (moderately foggy), the next four figures show images with different fog densities: Fig.
7b2 Slightly, Fig.
7b3 Moderately, Fig.
7b4 Highly, Fig.
7b5 Extremely, then two other foggy images: Fig.
7b6 with
$\text{FRFSIM1}=0.1278$ and Fig.
7b7 with
$\text{FRFSIM1}=0.3630$.

Fig. 7
Visual inspection of some results presented by Liu
et al. (
2020): a-reference images
${L_{0}}$, b-real foggy images
${L_{\text{fog\_real}}}$, c-enhanced colour images
${L_{\text{enhanced}}}$.
A first performance reported in Liu
et al. (
2020) on the defogged images is that of the DCP algorithm (He
et al.,
2011) with
$\text{FRFSIM2}=0.5105$ (Fig.
7c1) and DehazeNet algorithm (Cai
et al.,
2016) with
$\text{FRFSIM2}=0.5202$ (Fig.
7c2) compared to the foggy image with
$\text{FRFSIM1}=0.2904$. For the set of four images with different fog densities in the same article, the DCP algorithm is also highlighted with the following results: Fig.
7c3 with
$\text{FRFSIM2}=0.456$ compared to
$\text{FRFSIM1}=0.385$ (Slight fog), Fig.
7c4 with
$\text{FRFSIM2}=0.404$ compared to
$\text{FRFSIM1}=0.304$ (Moderate fog), Fig.
7c5 with
$\text{FRFSIM2}=0.377$ compared to
$\text{FRFSIM1}=0.228$ (High fog), Fig.
7c6 with
$\text{FRFSIM2}=0.327$ compared to
$\text{FRFSIM1}=0.215$ (Extreme fog) (Liu
et al.,
2020).
Next, there are two other images where the AMEF algorithm (Galdran,
2018) achieves the best results: Fig.
7c7 with
$\text{FRFSIM2}=0.3733$ compared to
$\text{FRFSIM1}=0.1278$ and Fig.
7c8 with
$\text{FRFSIM2}=0.4208$ compared to
$\text{FRFSIM1}=0.3630$ (Liu
et al.,
2020).
The performances of the enhancement algorithms, based on criterion two (Eq. (
20), are shown in Table
2.
Table 2
| No. |
Enhancement algorithm |
Images (reference-foggy-enhanced) |
${\text{enhc}_{\text{FRFSIM}}}$ [%] |
| 1 |
MBFIELM |
Fig.6a1–Fig. 6b1–Fig. 6c1 LIma-000011
|
33.041 |
| 2 |
MBFIELM |
Fig.6a2–Fig. 6b2–Fig. 6c2 ship
|
52.577 |
| 3 |
MBFIELM |
Fig.6a3–Fig. 6b3–Fig. 6c3 bridge
|
44.447 |
| 4 |
MBFIELM |
Fig.6a4–Fig. 6b4–Fig. 6c4 LIma-000013
|
32.41 |
| 5 |
MBFIELM |
Fig.6a5–Fig. 6b5–Fig. 6c5 LIma-000015
|
40.36 |
| 6 |
MBFIELM |
Fig.6a1–Fig. 6b1–Fig. 6c1 LIma-000006
|
14.821 |
| 7 |
DCP |
Fig.7a1–Fig. 7b1–Fig. 7c1 |
43.114 |
| 8 |
DehazeNet |
Fig.7a1–Fig. 7b1–Fig. 7c2 |
44.175 |
| 9 |
DCP |
Fig.7a2–Fig. 7b2–Fig. 7c3 |
15.570 |
| 10 |
DCP |
Fig.7a2–Fig. 7b3–Fig. 7c4 |
24.752 |
| 11 |
DCP |
Fig.7a2–Fig. 7b4–Fig. 7c5 |
39.522 |
| 12 |
DCP |
Fig.7a2–Fig. 7b5–Fig. 7c6 |
34.258 |
| 13 |
AMEF |
Fig.7a3–Fig. 7b6–Fig. 7c7 |
65.764 |
| 14 |
AMEF |
Fig.7a4–Fig. 7b7–Fig. 7c8 |
13.735 |
We utilise the
${\text{enhc}_{\text{FRFSIM}}}$ relative measure to rank the analysed foggy image enhancement algorithms. Thus, the best result, as shown in Table
2, is achieved by I) AMEF (No. 13,
${\text{enhc}_{\text{FRFSIM}}}=65.764$) followed by: II) MBFIELM (No. 2,
${\text{enhc}_{\text{FRFSIM}}}=52.577$), III) MBFIELM (No. 3,
${\text{enhc}_{\text{FRFSIM}}}=44.447$), IV) DehazeNet (No. 8,
${\text{enhc}_{\text{FRFSIM}}}=44.175$), V) DCP (No. 7,
${\text{enhc}_{\text{FRFSIM}}}=43.114$), VI) MBFIELM (No. 5,
${\text{enhc}_{\text{FRFSIM}}}=40.36$) etc. The larger FRFSIM2 is compared to FRFSIM1, the higher the quality of the defogged image. The
${\text{enhc}_{\text{FRFSIM}}}$ measure of the MBFIELM algorithm is significant (52.577%, 44.447%).
7 Discussion
This work focuses on a mathematical method to determine a two-dimensional analytic function that best approximates a set of measured data, called observations. Starting from the well-known “Least-squares problem”, we proposed, adapted and implemented the Levenberg-Marquardt algorithm that is used to determine the unknown parameters of the mathematical model describing the image acquisition process under foggy conditions. The non-linear form of the model, the observations and the unknown parameters lead to the iterative solution of an overdetermined equation system. The algorithm for improving the quality of these images, based on the determined parameters, involves applying an inverse transformation that removes the “atmospheric veil” from the measured data and compensates for the attenuation of the scene radiance. An effective enhancement in the region of interest is found for almost all test images, but small undesirable colour deviation problems occur in areas where the distances in the d-matrix are large (sky).
The mentioned classical algorithms used to improve image contrast do not obtain measures ${\text{enhc}_{\text{FRFSIM}}}$ that indicate an improvement in the quality of the processed image. This is due to the fact that these general algorithms do not take into account the physics of radiative transfer.
The algorithm we have proposed gives comparable results to the established algorithms such as AMEF, DehazeNet, and DCP. While it is outperformed by AMEF in certain cases, there are situations where it prevails over the mentioned algorithms (to see Table
2).
We should mention that in the implementation of the experiment we have encountered an obstacle that we have not overcome at this moment. Specifically, we could not test the MBFIELM algorithm on real foggy images. In a later approach we will extend the database used for testing the enhancement algorithm by obtaining all the resources needed to use images in real foggy conditions. Furthermore, we will work on how to choose the regularization variable in order to increase convergence performance.

