1 Introduction
A multi-criteria group decision-making (MCGDM) problem is defined as a decision problem where several experts (judges, decision makers (DMs), etc.) provide their evaluations on a set of alternatives regarding multiple criteria and seek to achieve a common solution that is most acceptable by the group of experts as a whole (Kabak and Ervural,
2017; Wang
et al.,
2021). One important issue in MCGDM is to depict the ratings of experts. As the socio-economic environment becomes increasingly complex, it becomes difficult for DMs to specify their preferences with crisp values. Zadeh (
1965) pioneered fuzzy sets (FSs), which are characterized by membership functions and considered as an effective tool to capture uncertain information. In order to capture DMs’ imprecise preferences, Atanassov (
1986) introduced the concept of intuitionistic fuzzy sets (IFSs), which are considered as an extension of Zadeh’s fuzzy sets (Zadeh,
1965). IFSs have been widely applied to address impreciseness and uncertainty information in MCGDM problems (Chen
et al.,
2020; Garg and Kumar,
2019; Ohlan,
2022; Seikh and Mandal,
2022; Wan
et al.,
2020; Zhao
et al.,
2021). For an overview of IFSs and their extensions in MCGDM, one can refer to Xu and Zhao (
2016).
Although FSs and IFSs have been extended to manage various MCGGDM problems, they failed to effectively handle a situation where the indeterminate and inconsistent information are involved. To manage such issues, Smarandache (
1999) pioneered neutrosophic sets that consider the truth, indeterminacy and falsity memberships, simultaneously. Neutrosophic sets are regarded as a flexible tool in coping with information involving uncertainty, incompleteness and inconsistency (Peng and Dai,
2020). However, without specific description, neutrosophic sets are hard to be applied in actual situations. Wang
et al. (
2010) introduced single-valued neutrosophic sets (SVNSs), which are considered as an extension of neutrosophic sets. Moreover, various extensions of neutrosophic sets, such as interval neutrosophic sets (Liu
et al.,
2022; Wang
et al.,
2005), trapezoidal neutrosophic sets (Liang
et al.,
2018b; Sarma
et al.,
2019), type-2 neutrosophic sets (Gokasar
et al.,
2022), multi-valued neutrosophic sets (MVNSs) (Ji
et al.,
2018; Ye
et al.,
2022), probability MVNSs (Liu and Cheng,
2019; Peng
et al.,
2018), interval-valued fermatean neutrosophic sets (Broumi
et al.,
2022) and complex fermatean neutrosophic sets (Broumi
et al.,
2023) have been proposed and applied to address various neutrosophic multi-criteria decision making (MCDM) problems, such as investment decision, personnel selection, disaster management and designing a stable sustainable closed-loop supply chain network (Kalantari
et al.,
2022). Among various forms of neutrosophic sets, SVNSs are considered as one of the most concise tools to capture DMs’ evaluations (Peng and Dai,
2020).
Over the past years, lots of studies have been witnessed focusing on MCDM and MCGDM based on SVNSs and their extensions, which can be roughly grouped into two categories (Nguyen
et al.,
2019; Peng and Dai,
2020). The first category is based on various neutrosophic aggregation operators, such as single-valued neutrosophic number (SVNN) generalized power averaging operator (Liu and Liu,
2018), SVNN weighted geometric averaging (WGA) operator (Refaat and El-Henawy,
2019), and SVNN ordered weighted harmonic averaging operator (Paulraj and Tamilarasi,
2022). The second category is based on kinds of neutrosophic measures (Hezam
et al.,
2023; Karabasevic
et al.,
2020; Kumar
et al.,
2020; Peng and Dai,
2018; Sun
et al.,
2019; Tian
et al.,
2020; Zhang
et al.,
2023). For example, Hezam
et al. (
2023) proposed a neutrosophic discrimination measure-based COPRAS framework, and applied it to evaluate the sustainable transport investment projects. Karabasevic
et al. (
2020) developed an extended TOPSIS method based on the SVNN Hamming distance measure, and applied it to e-commerce development strategies selection. Sun
et al. (
2019) developed a new distance measure for SVNNs, based on which an extended TODIM and ELECTRE III methods were proposed and applied in physician selection.
The above-mentioned approaches are effective when copying with MC(G)DM problems with SVNNs. However, specific numerical evaluations cannot always accurately reflect DMs’ behaviour and opinions because of the limitation of their cognition. Actually, DMs usually prefer to elicit their evaluations with linguistic terms, such as “poor”, “good” and “perfect” due to the prominent advantages of linguistic terms for characterizing ambiguous and inexact assessments (Zadeh,
1975). Recently, Li Y.
et al. (
2017) proposed linguistic single-valued neutrosophic sets (LSVNSs) which employ a triple-tuple linguistic structure to characterize the truth, indeterminacy and falsity memberships of LSVNSs. Since LSVNSs integrate the advantages of SVNSs and linguistic term sets (LTSs), various MC(G)DM methods on the basis of linguistic single-valued neutrosophic numbers (LSVNNs) have been proposed. For example, Fang and Ye (
2017) developed a linguistic neutrosophic MCGDM method based on the LSVNN weighted arithmetic averaging (WAA) and WGA operators. Garg and Nancy (
2018) proposed the LSVNN prioritized WAA and WGA operator-based MCGDM method. Moreover, several comprehensive MCGDM methods that integrate with the LSVNN power WAA and WGA operators and TOPSIS (Liang
et al.,
2018a), and the EDAS (Li
et al.,
2019) were developed. These linguistic neutrosophic MCGDM methods have been applied to the university human resource management evaluation and property management company selection, respectively.
Although great efforts have been made to improve and extend the application of linguistic neutrosophic MCGDM methods, there still exist some challenges. The existing methods seem to overlook the semantics of individual DMs and the consensual solution. In the existing methods, numerical values are identified through calculating the index values of linguistic terms. In this way, the numerical values cannot indicate experts’ personalized individual semantics with respect to linguistic terms.
When tackling linguistic MCGDM problems, it is argued and accepted that words indicate different meanings for various DMs in computing with words (Mendel
et al.,
2010). Considering the issue of personalized individual semantics (PISs) is necessary. For example, two referees are invited to express evaluations about a manuscript. Both of them provide comments with “good”. However, linguistic term “good” may indicate different numerical semantics for them. Recently, different attempts have been made to copy with this issue, which can be roughly classified into three groups, including type-2 fuzzy set model (Mendel and Wu,
2010), multi-granular linguistic model (Morente-Molinera
et al.,
2015), and consistency-driven models (Li
et al.,
2017). Compared with the first two types of models, the consistency-driven model can effectively characterize the specific semantics of individuals, and becomes a popular tool to manage PISs in linguistic GDM. Thus, various consistency-driven models have been designed to assign personalized numerical scales (PNSs) based on linguistic preference relations (LPRs) (Zhang and Li,
2022), incomplete LPRs (Li
et al.,
2022a), distribution LPRs (Tang
et al.,
2020), and hesitant fuzzy LPRs with self-confidence (Zhang
et al.,
2021). In these models, DMs’ PISs can be explored according to their linguistic preferences in terms of a set of alternatives. The traditional PIS models are valid in the situations where the evaluations are expressed with LPRs or their extensions. However, they will fail to work when DMs’ evaluations are in forms of linguistic MCGDM matrices.
Recently, Li
et al. (
2022a) designed a data-driven learning model to investigate the PISs of DMs in MCGDM. In this model, two objectives are achieved through maximizing the minimum overall deviation among alternatives between any two consecutive categories, and minimizing the overall deviation among alternatives in a category. Inspired by the idea of Li
et al. (
2022b), this study aims to propose an improved framework to handle PISs and GDM, where the evaluations are presented in forms of MCGDM matrices with LSVNNs. The main novelties and contributions are summarized as follows:
-
(1) A novel discrimination measure for SVNNs is proposed, based on which a discrimination-based optimization model is constructed to assign PNSs. The proposed framework is the first attempt to manage PISs in linguistic GDM, where DMs’ assessments are presented with linguistic neutrosophic MCGDM matrices.
-
(2) An extended consensus-based optimization model is constructed to identify the weights of DMs considering group consensus. The proposed approach can cautiously assign DMs’ weights to guarantee a level of agreement among members regarding the final solution, and reveal the differences among alternatives with the optimal discrimination degrees.
The rest of the paper is organized as follows. Section
2 introduces some concepts about 2-tuple linguistic model and numerical scale (NS) model, neutrosophic sets and LSVNSs. Section
3 presents the concept of distance and discrimination measures for LSVNNs and develops a discrimination-based optimization model to obtain PNSs. Section
4 presents a comprehensive linguistic neutrosophic MCGDM framework considering the PIS and group consensus. Section
5 presents an illustrative example, followed by the comparative analysis to valid the proposed framework. Finally, Section
6 concludes this study.
3 Optimization Model to Obtain PNSs in MCGDM with LSVNNs
This section presents the concepts of distance and discrimination measures of LSVNNs, based on which a programming model is constructed to derive the PNSs of each DM.
For convenience, assume that $M=\{1,2,\dots ,m\}$, $N=\{1,2,\dots ,n\}$ and $Q=\{1,2,\dots ,q\}$. Assume that $A=\{{a_{1}},{a_{2}},\dots ,{a_{m}}\}$ $(m\geqslant 2)$ is a set of alternatives; $C=\{{c_{1}},{c_{2}},\dots ,{c_{n}}\}$ $(n\geqslant 2)$ is a set of criteria and ${w_{j}}\in [0,1]$ is the corresponding weight of criterion ${c_{j}}$, satisfying ${\textstyle\sum _{j=1}^{n}}{w_{j}}=1$; and $E=\{{e_{1}},{e_{2}},\dots ,{e_{q}}\}$ $(q\geqslant 2)$ is a set of experts and each expert is assigned with a weight ${\lambda _{h}}\in [0,1]$, satisfying ${\textstyle\sum _{h=1}^{q}}{\lambda _{h}}=1$. Suppose that ${B^{h}}={[{b_{ij}^{h}}]_{m\times n}}$ $(h\in Q)$ are the decision matrices, where ${b_{ij}^{h}}=\langle {s_{{b_{ij}^{h}}}^{T}},{s_{{b_{ij}^{h}}}^{I}},{s_{{b_{ij}^{h}}}^{F}}\rangle $ is linguistic single-valued neutrosophic evaluation given by expert ${e_{h}}$.
Assume that the standardized matrices are denoted by
${R^{h}}={[{r_{ij}^{h}}]_{m\times n}}$ $(h\in Q)$. The original decision matrices
${B^{h}}={[{b_{ij}^{h}}]_{m\times n}}$ $(h\in Q)$ can then be normalized into
${R^{h}}={[{r_{ij}^{h}}]_{m\times n}}$ $(h\in Q)$ based on the primary transformation rule of Li Y.
et al. (
2017), where
3.1 Distance and Discrimination Measures for LSVNNs
Definition 8.
Let
${r_{j}}=\langle {s_{{r_{j}}}^{T}},{s_{{r_{j}}}^{I}}$,
${s_{{r_{j}}}^{F}}\rangle $ $(j=1,2)$ be any two LSVNNs. Then, the distance measure
$d({r_{1}},{r_{2}})$ between
${r_{1}}$ and
${r_{2}}$ is defined as follows:
where
$\textit{NS}({s_{\theta }})$ is the ordered NS of linguistic term
${s_{\theta }}$, as defined in Definition
2, and
$\rho >0$.
Remark 1.
Particularly,
$\rho =1,2$, Eq. (
7) is degenerated into the Hamming and Euclidean distance measures, respectively. Due to the distinct applicability of the distance measure under different values of
ρ, Eq. (
7) can help DMs flexibly select suitable parameter
ρ based on actual decision scenarios, thereby optimizing DMs’ discrimination measures.
Theorem 1.
Let ${r_{j}}=\langle {s_{{r_{j}}}^{T}},{s_{{r_{j}}}^{I}},{s_{{r_{j}}}^{F}}\rangle $ $(j=1,2,3)$ be any three LSVNNs. Then, the distance measure in Definition 8 satisfies the following properties:
-
(1) $0\leqslant d({r_{1}},{r_{2}})\leqslant 1$;
-
(2) $d({r_{1}},{r_{2}})=d({r_{2}},{r_{1}})$;
-
(3) If ${s_{{r_{1}}}^{T}}\leqslant {s_{{r_{2}}}^{T}}\leqslant {s_{{r_{3}}}^{T}}$, ${s_{{r_{1}}}^{I}}\geqslant {s_{{r_{2}}}^{I}}\geqslant {s_{{r_{3}}}^{I}}$ and ${s_{{r_{1}}}^{F}}\geqslant {s_{{r_{2}}}^{F}}\geqslant {s_{{r_{3}}}^{F}}$, then $d({r_{1}},{r_{2}})\leqslant d({r_{1}},{r_{3}})$ and $d({r_{2}},{r_{3}})\leqslant d({r_{1}},{r_{3}})$.
Proof.
It is obvious that Properties (1) and (2) hold. Thus, the proof of Property (3) is provided.
Since
$\textit{NS}({s_{\theta }})$ is ordered in terms of
${s_{\theta }}$, it has
$\textit{NS}({s_{{r_{1}}}^{T}})\leqslant \textit{NS}({s_{{r_{2}}}^{T}})\leqslant \textit{NS}({s_{{r_{3}}}^{T}})$,
$\textit{NS}({s_{{r_{1}}}^{I}})\geqslant \textit{NS}({s_{{r_{2}}}^{I}})\geqslant \textit{NS}({s_{{r_{3}}}^{I}})$ and
$\textit{NS}({s_{{r_{1}}}^{F}})\geqslant \textit{NS}({s_{{r_{2}}}^{F}})\geqslant \textit{NS}({s_{{r_{3}}}^{F}})$. Thus,
$S({r_{1}})\leqslant S({r_{2}})\leqslant S({r_{3}})$ based on Eq. (
5) and the following inequalities can be obtained:
$|\textit{NS}({s_{{r_{1}}}^{T}})-\textit{NS}({s_{{r_{2}}}^{T}}){|^{\rho }}\leqslant |\textit{NS}({s_{{r_{1}}}^{T}})-\textit{NS}({s_{{r_{3}}}^{T}}){|^{\rho }}$,
$|\textit{NS}({s_{{r_{1}}}^{I}})-\textit{NS}({s_{{r_{2}}}^{I}}){|^{\rho }}\leqslant |\textit{NS}({s_{{r_{1}}}^{I}})-\textit{NS}({s_{{r_{3}}}^{I}}){|^{\rho }}$ and
$|\textit{NS}({s_{{r_{1}}}^{F}})-\textit{NS}({s_{{r_{2}}}^{F}}){|^{\rho }}\leqslant |\textit{NS}({s_{{r_{1}}}^{F}})-\textit{NS}({s_{{r_{3}}}^{F}}){|^{\rho }}$. Therefore,
Thus, we have $d({r_{1}},{r_{2}})\leqslant d({r_{1}},{r_{3}})$. Similarly, it can be demonstrated that $d({r_{2}},{r_{3}})\leqslant d({r_{1}},{r_{3}})$. This completes the proof of Property (3). □
In GDM, a panel of experts are invited to provide their evaluations about a set of alternatives. It is required that an expert should be qualified with the ability to differentiate between cases which are similar but not identical (Herowati
et al.,
2017). Motivated by the idea of maximizing deviation method (Wang,
1997), the total deviation among all alternatives is considered an effective tool to measure the discrimination of an expert (Tian
et al.,
2019).
Definition 9.
Let
${R^{h}}={[{r_{ij}^{h}}]_{m\times n}}$ is a linguistic single-valued neutrosophic evaluation matrix, given by DM
${e_{h}}$. Then, the discrimination measure
$\textit{Dis}({e_{h}})$ of
${e_{h}}$ is defined as follows:
where
$\textit{Dis}({e_{h}})\in [0,1]$,
${w_{j}}\in [0,1]$ is the weight of criterion
${c_{j}}$, and
$d({r_{ij}^{h}},{r_{kj}^{h}})$ is the distance between LSVNNs
${r_{ij}^{h}}$ and
${r_{kj}^{h}}$, as per Eq. (
7).
Remark 2.
Although the discrimination measures defined in this study and Tian
et al. (
2019) are both used to measure experts’ discrimination degrees among alternatives, there are differences in application. The discrimination measure in Tian
et al. (
2019) is defined for measuring experts’ discrimination degrees among alternatives with evaluations in forms of interval type-2 fuzzy numbers. However, the discrimination measure defined in this study is suitable for experts who elicit qualitative ratings with LSVNSs.
Example 1.
Assume that
$S=\{{s_{0}},{s_{1}},\dots ,{s_{8}}\}$ is an LTS and
${R^{1}}={[{r_{ij}^{1}}]_{4\times 4}}$ is a linguistic single-valued neutrosophic evaluation matrix, given by DM
${e_{1}}$ based on
S, as shown in Table
1. The corresponding criterion weights are
${w_{j}}=0.25$ $(j=1,2,3,4)$. Assume that the NSs on
S are predetermined as
$\textit{NS}({s_{\theta }})=\frac{\theta }{8}$ $(\theta =0,1,\dots ,8)$. Then, according to Eq. (
8), the discrimination degree is
$\textit{Dis}({e_{1}})=0.1128$.
Table 1
LSVNN evaluations of Example
1.
|
${c_{1}}$ |
${c_{2}}$ |
${c_{3}}$ |
${c_{4}}$ |
| ${a_{1}}$ |
$\langle {s_{6}},{s_{2}},{s_{1}}\rangle $ |
$\langle {s_{5}},{s_{3}},{s_{1}}\rangle $ |
$\langle {s_{6}},{s_{1}},{s_{1}}\rangle $ |
$\langle {s_{4}},{s_{2}},{s_{2}}\rangle $ |
| ${a_{2}}$ |
$\langle {s_{4}},{s_{3}},{s_{1}}\rangle $ |
$\langle {s_{7}},{s_{3}},{s_{2}}\rangle $ |
$\langle {s_{6}},{s_{3}},{s_{2}}\rangle $ |
$\langle {s_{6}},{s_{2}},{s_{3}}\rangle $ |
| ${a_{3}}$ |
$\langle {s_{5}},{s_{3}},{s_{2}}\rangle $ |
$\langle {s_{4}},{s_{2}},{s_{3}}\rangle $ |
$\langle {s_{4}},{s_{3}},{s_{1}}\rangle $ |
$\langle {s_{5}},{s_{2}},{s_{2}}\rangle $ |
| ${a_{4}}$ |
$\langle {s_{5}},{s_{3}},{s_{3}}\rangle $ |
$\langle {s_{7}},{s_{2}},{s_{1}}\rangle $ |
$\langle {s_{6}},{s_{2}},{s_{3}}\rangle $ |
$\langle {s_{6}},{s_{2}},{s_{3}}\rangle $ |
3.2 Discrimination-Based Optimization Model to Obtain PNSs
As mentioned above, an expert is expected to be skilled and have the ability to discriminate the differences between cases. When experts are required to express linguistic ratings, their PISs of linguistic terms are embedded in the evaluations, which implicitly indicate the subtle differences among alternatives distinguished by experts. Therefore, an optimization model by maximizing the discrimination degree can be considered as a good solution to derive the PISs of DMs.
where
$d({r_{ij}^{h}},{r_{kj}^{h}})$ is the distance measure of LSVNNs, as per Eq. (
7).
By resolving Model (
9), a set of possible PNSs of linguistic terms for DM
${e_{h}}$ can be derived, i.e.
${\mathit{APS}^{h}}=\{({\textit{NS}^{h}}({s_{0}}),{\textit{NS}^{h}}({s_{1}}),\dots ,{\textit{NS}^{h}}({s_{\tau }}));\dots \hspace{0.1667em}\}$. The obtained NSs can guarantee the maximum discrimination degree with respect to alternatives.
Example 2 (Continuation of Example 1).
Assume that
${R^{1}}={[{r_{ij}^{1}}]_{4\times 4}}$ and
w are the same as Example
1. Then, the PNSs of linguistic terms for DM
${e_{1}}$ can be obtained as follows:
Without loss of generality,
ρ is set as
$\rho =1$. The discrimination-based optimization model can be established based on Model (
9).
By resolving Model (
10), the PNSs of linguistic terms for DM
${e_{1}}$ can be identified, i.e.
${\textit{NS}^{1}}({s_{0}})=0$,
${\textit{NS}^{1}}({s_{1}})=0.05$,
${\textit{NS}^{1}}({s_{2}})=0.125$,
${\textit{NS}^{1}}({s_{3}})=0.45$,
${\textit{NS}^{1}}({s_{4}})=0.5$,
${\textit{NS}^{1}}({s_{5}})=0.55$,
${\textit{NS}^{1}}({s_{6}})=0.875$,
${\textit{NS}^{1}}({s_{7}})=0.95$, and
${\textit{NS}^{1}}({s_{8}})=1$. Moreover, according to Eq. (
8), the discrimination degree is
$Di{s^{\prime }}({e_{1}})=0.1816$, which is higher than that derived from Example
1. Specifically, compared to the method of without considering PISs in Example
1, the approach of considering PISs increases the discrimination degree of DM
${e_{1}}$ by approximately 61%. Figure
1 vividly reveals the difference between the method of without considering and considering PISs.
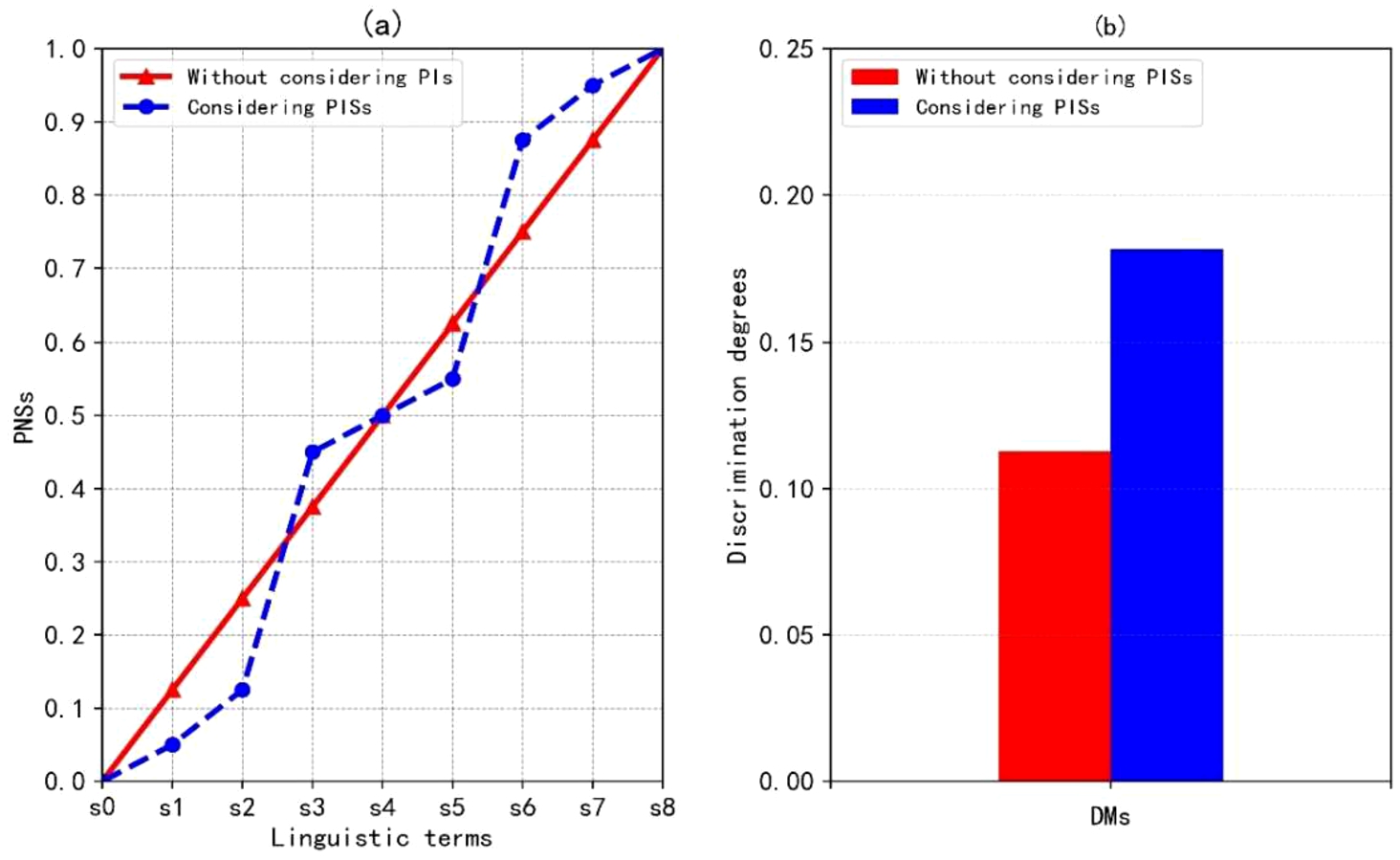
Fig. 1
Results derived from without considering and considering PISs.
5 Illustrative Example
This section presents an illustrative example adapted from Garg and Nancy (
2018) to demonstrate the application of the proposed approach.
5.1 Illustration of the Proposed MCGDM Method
A panel involving five experts are invited to express their evaluations and select the best internet service provider(s). After conducting the preliminary investigation, four internet service providers, namely, Bharti Airtel (${a_{1}}$), Relience Communications (${a_{2}}$), Vodafone India (${a_{3}}$) and Mahanagar Telecom Nigam (${a_{4}}$) are considered as alternatives. The criteria are Customer Service (${c_{1}}$), Bandwidth (${c_{2}}$), Package Deal (${c_{3}}$) and Total Cost (${c_{4}}$). The group of experts, represented as ${e_{h}}$ $(h=1,2,3,4,5)$ provide their ratings about alternatives ${a_{i}}$ $(i=1,2,3,4)$ in terms of each criterion ${c_{j}}$ $(j=1,2,3,4)$ with LSVNNs based on the LTS $S=\{{s_{0}}=\text{extremely poor},\hspace{2.5pt}{s_{1}}=\text{very poor},\hspace{2.5pt}{s_{2}}=\text{poor},\hspace{2.5pt}{s_{3}}=\text{slightly poor},\hspace{2.5pt}{s_{4}}=\text{fair},\hspace{2.5pt}{s_{5}}=\text{slightly good},\hspace{2.5pt}{s_{6}}=\text{good},\hspace{2.5pt}{s_{7}}=\text{very good},\hspace{2.5pt}{s_{8}}=\text{extremely good}\}$. Assume that the decision matrices of experts are denoted by ${B^{h}}={[{b_{ij}^{h}}]_{m\times n}}$ $(h=1,2,3,4,5)$ and the criterion weight vector is $w={(0.35,0.3,0.2,0.15)^{T}}$.
The proposed approach is employed to deal with the above linguistic neutrosophic MCGDM problem. Let the parameter $\rho =1$.
Table 3
LSVNN evaluations given by DM ${e_{1}}$.
|
${c_{1}}$ |
${c_{2}}$ |
${c_{3}}$ |
${c_{4}}$ |
| ${a_{1}}$ |
$\langle {s_{6}},{s_{1}},{s_{1}}\rangle $ |
$\langle {s_{5}},{s_{3}},{s_{3}}\rangle $ |
$\langle {s_{4}},{s_{3}},{s_{1}}\rangle $ |
$\langle {s_{6}},{s_{3}},{s_{1}}\rangle $ |
| ${a_{2}}$ |
$\langle {s_{5}},{s_{3}},{s_{3}}\rangle $ |
$\langle {s_{5}},{s_{4}},{s_{1}}\rangle $ |
$\langle {s_{6}},{s_{2}},{s_{1}}\rangle $ |
$\langle {s_{5}},{s_{2}},{s_{2}}\rangle $ |
| ${a_{3}}$ |
$\langle {s_{5}},{s_{3}},{s_{2}}\rangle $ |
$\langle {s_{4}},{s_{3}},{s_{2}}\rangle $ |
$\langle {s_{3}},{s_{4}},{s_{2}}\rangle $ |
$\langle {s_{6}},{s_{2}},{s_{2}}\rangle $ |
| ${a_{4}}$ |
$\langle {s_{5}},{s_{3}},{s_{3}}\rangle $ |
$\langle {s_{6}},{s_{2}},{s_{2}}\rangle $ |
$\langle {s_{4}},{s_{3}},{s_{2}}\rangle $ |
$\langle {s_{7}},{s_{1}},{s_{2}}\rangle $ |
Table 4
LSVNN evaluations given by DM ${e_{2}}$.
|
${c_{1}}$ |
${c_{2}}$ |
${c_{3}}$ |
${c_{4}}$ |
| ${a_{1}}$ |
$\langle {s_{4}},{s_{4}},{s_{1}}\rangle $ |
$\langle {s_{5}},{s_{3}},{s_{2}}\rangle $ |
$\langle {s_{6}},{s_{2}},{s_{2}}\rangle $ |
$\langle {s_{6}},{s_{1}},{s_{1}}\rangle $ |
| ${a_{2}}$ |
$\langle {s_{5}},{s_{2}},{s_{2}}\rangle $ |
$\langle {s_{4}},{s_{3}},{s_{3}}\rangle $ |
$\langle {s_{3}},{s_{4}},{s_{2}}\rangle $ |
$\langle {s_{5}},{s_{3}},{s_{2}}\rangle $ |
| ${a_{3}}$ |
$\langle {s_{6}},{s_{2}},{s_{1}}\rangle $ |
$\langle {s_{5}},{s_{4}},{s_{2}}\rangle $ |
$\langle {s_{6}},{s_{2}},{s_{4}}\rangle $ |
$\langle {s_{6}},{s_{2}},{s_{4}}\rangle $ |
| ${a_{4}}$ |
$\langle {s_{5}},{s_{2}},{s_{2}}\rangle $ |
$\langle {s_{7}},{s_{1}},{s_{2}}\rangle $ |
$\langle {s_{6}},{s_{2}},{s_{2}}\rangle $ |
$\langle {s_{6}},{s_{5}},{s_{2}}\rangle $ |
Step 1: Normalize the decision matrices of group members.
Table 5
LSVNN evaluations given by DM ${e_{3}}$.
|
${c_{1}}$ |
${c_{2}}$ |
${c_{3}}$ |
${c_{4}}$ |
| ${a_{1}}$ |
$\langle {s_{5}},{s_{3}},{s_{3}}\rangle $ |
$\langle {s_{5}},{s_{3}},{s_{1}}\rangle $ |
$\langle {s_{4}},{s_{3}},{s_{1}}\rangle $ |
$\langle {s_{6}},{s_{3}},{s_{1}}\rangle $ |
| ${a_{2}}$ |
$\langle {s_{4}},{s_{2}},{s_{7}}\rangle $ |
$\langle {s_{5}},{s_{4}},{s_{1}}\rangle $ |
$\langle {s_{6}},{s_{2}},{s_{1}}\rangle $ |
$\langle {s_{5}},{s_{2}},{s_{2}}\rangle $ |
| ${a_{3}}$ |
$\langle {s_{5}},{s_{3}},{s_{3}}\rangle $ |
$\langle {s_{4}},{s_{3}},{s_{2}}\rangle $ |
$\langle {s_{3}},{s_{4}},{s_{2}}\rangle $ |
$\langle {s_{6}},{s_{2}},{s_{2}}\rangle $ |
| ${a_{4}}$ |
$\langle {s_{4}},{s_{2}},{s_{5}}\rangle $ |
$\langle {s_{6}},{s_{2}},{s_{2}}\rangle $ |
$\langle {s_{4}},{s_{3}},{s_{2}}\rangle $ |
$\langle {s_{7}},{s_{1}},{s_{2}}\rangle $ |
Each member provides evaluation information with LSVNNs and the individual decision matrices are normalized based on Eq. (
6), as presented in Tables
3–
7.
Step 2: Identify PNSs of linguistic terms for each DM.
The PNSs
${\textit{APS}^{h}}$ $(h=1,2,3,4,5)$ of linguistic terms on LTS
S can be identified based on the discrimination-driven optimization model. Taking
${R^{1}}$ as an example, a programming model is established based on Model (
9) as follows:
By resolving the above model with the software MATLAB or LINGO, the PNS
${\textit{APS}^{1}}$ for DM
${e_{1}}$ can be obtained. Similarly,
${\textit{APS}^{h}}$ $(h=2,3,4,5)$ can be derived and the results are presented in Table
8. There are subtle differences about the semantics of linguistic terms among DMs.
Table 6
LSVNN evaluations given by DM ${e_{4}}$.
|
${c_{1}}$ |
${c_{2}}$ |
${c_{3}}$ |
${c_{4}}$ |
| ${a_{1}}$ |
$\langle {s_{4}},{s_{1}},{s_{3}}\rangle $ |
$\langle {s_{6}},{s_{2}},{s_{1}}\rangle $ |
$\langle {s_{5}},{s_{4}},{s_{2}}\rangle $ |
$\langle {s_{6}},{s_{1}},{s_{3}}\rangle $ |
| ${a_{2}}$ |
$\langle {s_{7}},{s_{2}},{s_{4}}\rangle $ |
$\langle {s_{7}},{s_{4}},{s_{2}}\rangle $ |
$\langle {s_{5}},{s_{3}},{s_{2}}\rangle $ |
$\langle {s_{6}},{s_{4}},{s_{3}}\rangle $ |
| ${a_{3}}$ |
$\langle {s_{6}},{s_{2}},{s_{1}}\rangle $ |
$\langle {s_{5}},{s_{4}},{s_{3}}\rangle $ |
$\langle {s_{6}},{s_{1}},{s_{2}}\rangle $ |
$\langle {s_{6}},{s_{3}},{s_{1}}\rangle $ |
| ${a_{4}}$ |
$\langle {s_{4}},{s_{2}},{s_{3}}\rangle $ |
$\langle {s_{5}},{s_{3}},{s_{2}}\rangle $ |
$\langle {s_{6}},{s_{5}},{s_{1}}\rangle $ |
$\langle {s_{7}},{s_{4}},{s_{2}}\rangle $ |
Table 7
LSVNN evaluations given by DM ${e_{5}}$.
|
${c_{1}}$ |
${c_{2}}$ |
${c_{3}}$ |
${c_{4}}$ |
| ${a_{1}}$ |
$\langle {s_{5}},{s_{1}},{s_{2}}\rangle $ |
$\langle {s_{6}},{s_{2}},{s_{3}}\rangle $ |
$\langle {s_{5}},{s_{3}},{s_{2}}\rangle $ |
$\langle {s_{6}},{s_{1}},{s_{1}}\rangle $ |
| ${a_{2}}$ |
$\langle {s_{7}},{s_{1}},{s_{1}}\rangle $ |
$\langle {s_{6}},{s_{2}},{s_{2}}\rangle $ |
$\langle {s_{5}},{s_{2}},{s_{2}}\rangle $ |
$\langle {s_{7}},{s_{1}},{s_{2}}\rangle $ |
| ${a_{3}}$ |
$\langle {s_{5}},{s_{2}},{s_{3}}\rangle $ |
$\langle {s_{5}},{s_{1}},{s_{1}}\rangle $ |
$\langle {s_{5}},{s_{2}},{s_{2}}\rangle $ |
$\langle {s_{5}},{s_{3}},{s_{1}}\rangle $ |
| ${a_{4}}$ |
$\langle {s_{4}},{s_{3}},{s_{1}}\rangle $ |
$\langle {s_{7}},{s_{2}},{s_{1}}\rangle $ |
$\langle {s_{5}},{s_{3}},{s_{2}}\rangle $ |
$\langle {s_{6}},{s_{1}},{s_{1}}\rangle $ |
Step 3: Determine the weight vector and obtain the collective evaluations of DMs.
Table 8
PNSs of linguistic terms.
|
$NS({s_{0}})$ |
$\textit{NS}({s_{1}})$ |
$\textit{NS}({s_{2}})$ |
$\textit{NS}({s_{3}})$ |
$\textit{NS}({s_{4}})$ |
$\textit{NS}({s_{5}})$ |
$\textit{NS}({s_{6}})$ |
$\textit{NS}({s_{7}})$ |
$\textit{NS}({s_{8}})$ |
| ${\textit{APS}^{1}}$ |
0 |
0.05 |
0.201 |
0.45 |
0.5 |
0.55 |
0.875 |
0.95 |
1 |
| ${\textit{APS}^{2}}$ |
0 |
0.05 |
0.125 |
0.45 |
0.5 |
0.651 |
0.875 |
0.95 |
1 |
| ${\textit{APS}^{3}}$ |
0 |
0.05 |
0.125 |
0.25 |
0.5 |
0.75 |
0.875 |
0.95 |
1 |
| ${\textit{APS}^{4}}$ |
0 |
0.05 |
0.375 |
0.45 |
0.5 |
0.55 |
0.875 |
0.95 |
1 |
| ${\textit{APS}^{5}}$ |
0 |
0.05 |
0.375 |
0.45 |
0.5 |
0.55 |
0.751 |
0.95 |
1 |
| ${\textit{APS}^{c}}$ |
0 |
0.05 |
0.262 |
0.406 |
0.5 |
0.605 |
0.854 |
0.95 |
1 |
A consensus-based optimization model can be established based on Model (
14) as follows:
By resolving the above model with the software MATLAB or LINGO, the weight vector of DMs is
$\lambda ={(0.244,0.113,0.219,0.252,0.172)^{T}}$. The collective PNSs
${\textit{APS}^{c}}$ for group members can be calculated based on the simple weighted average of
${\textit{APS}^{h}}$ $(h=1,2,3,4,5)$, as shown in Table
8. The collective evaluation matrix
${R^{c}}={[{r_{ij}^{c}}]_{4\times 4}}$ is calculated based on Eq. (
4). The result is presented in Table
9. Moreover, the group consensus
$\textit{GCL}$ can be calculated based on Eq. (
12), namely,
$\textit{GCL}=0.858$.
Step 4: Derive the overall evaluations of each alternative.
Table 9
Overall evaluations of alternatives in terms of each criterion.
|
${c_{1}}$ |
${c_{2}}$ |
| ${a_{1}}$ |
$\langle ({s_{5}},0.379),({s_{1}},0.2),({s_{2}},-0.41)\rangle $ |
$\langle ({s_{6}},-0.424),({s_{3}},-0.276),({s_{1}},0.418)\rangle $ |
| ${a_{2}}$ |
$\langle ({s_{6}},-0,121),({s_{2}},-0.327),({s_{2}},0.423)\rangle $ |
$\langle ({s_{6}},-0.249),({s_{3}},-0.015),({s_{2}},-0.367)\rangle $ |
| ${a_{3}}$ |
$\langle ({s_{6}},-0.409),({s_{2}},0.382),({s_{1}},0.491)\rangle $ |
$\langle ({s_{5}},0.001),({s_{2}},0.46),({s_{2}},-0.411)\rangle $ |
| ${a_{4}}$ |
$\langle ({s_{4}},0.305),({s_{2}},0.133),({s_{2}},0.255)\rangle $ |
$\langle ({s_{6}},-0.033),({s_{2}},-0.184),({s_{2}},-0.318)\rangle $ |
|
${c_{3}}$ |
${c_{4}}$ |
| ${a_{1}}$ |
$\langle ({s_{5}},0.375),({s_{2}},-0.069),({s_{2}},-0.484)\rangle $ |
$\langle ({s_{6}},0.058),({s_{1}},0.339),({s_{1}},0.266)\rangle $ |
| ${a_{2}}$ |
$\langle ({s_{5}},0.202),({s_{2}},0.19),({s_{2}},-0.084)\rangle $ |
$\langle ({s_{6}},-0.18,({s_{2}},-0.095),({s_{3}},-0.193)\rangle $ |
| ${a_{3}}$ |
$\langle ({s_{6}},-0.028),({s_{2}},-0.159),({s_{2}},-0.169)\rangle $ |
$\langle ({s_{6}},0.196),({s_{3}},-0.421),({s_{1}},0.32)\rangle $ |
| ${a_{4}}$ |
$\langle ({s_{6}},-0.291),({s_{2}},-0.041),({s_{1}},0.313)\rangle $ |
$\langle ({s_{6}},0.439),({s_{2}},-0.302),({s_{2}},-0.448)\rangle $ |
The overall evaluations
${r_{i}^{c}}$ $(i=1,2,3,4)$ are calculated based on Eq. (
4). The results are shown in Table
10.
Step 5: Determine the ranking of alternatives.
Table 10
Overall values of each alternative.
|
${r_{i}^{c}}$ |
$S({r_{i}^{c}})$ |
$H({r_{i}^{c}})$ |
Rankings |
| ${a_{1}}$ |
$\langle ({s_{6}},-0.435),({s_{2}},-0.399),({s_{1}},0.465)\rangle $ |
0.807 |
0.597 |
1 |
| ${a_{2}}$ |
$\langle ({s_{6}},-0.274),({s_{2}},0.057),({s_{2}},0.017)\rangle $ |
0.751 |
0.522 |
4 |
| ${a_{3}}$ |
$\langle ({s_{6}},-0.354),({s_{2}},0.291),({s_{2}},-0.453)\rangle $ |
0.765 |
0.600 |
3 |
| ${a_{4}}$ |
$\langle ({s_{6}},-0.337),({s_{2}},-0.086),({s_{2}},-0.295)\rangle $ |
0.776 |
0.571 |
2 |
The score and accuracy values
$S({r_{i}^{c}})$ $(i=1,2,3,4)$ and
$H({r_{i}^{c}})$ $(i=1,2,3,4)$ are calculated based on Eq. (
5), as presented in Table
10. Based on the comparison method for LSVNNs, the ranking of alternatives is
${a_{1}}\succ {a_{4}}\succ {a_{3}}\succ {a_{2}}$, and Bharti Airtel (
${a_{1}}$) can be considered as the best internet service provider.
5.2 Sensitivity Analysis
In order to investigate the influence of parameter
ρ on the final result, different values of
ρ are assigned, namely,
$\rho =1$,
$\rho =2$ and
$\rho \to \infty $. The PNSs of linguistic terms and discrimination degrees of each DM with different values of
ρ are presented in Figs.
3–
5, respectively. From Figs.
3(a)–
5(a), there are slight differences about the PNSs of linguistic terms when
ρ is assigned different values. From Figs.
3(b)–
5(b), although the discrimination levels are various when
ρ is assigned different values, the orders of discrimination levels of DMs remain unchanged, except
$\rho =2$. Moreover, from Table
11, the orders of alternatives almost have no change, except
$\rho =2$. The worst alternative is Relience Communications (
${a_{2}}$) in the three cases. In summary, different values of
ρ can generate various distance measures of LSVNNs. However, it seems to have little influence on the final ranking of alternatives. Thus, one can choose the Hamming distance measure of LSVNNs with
$\rho =1$ to assign the PNSs and drive the ranking of alternatives, which is simple and straightforward.
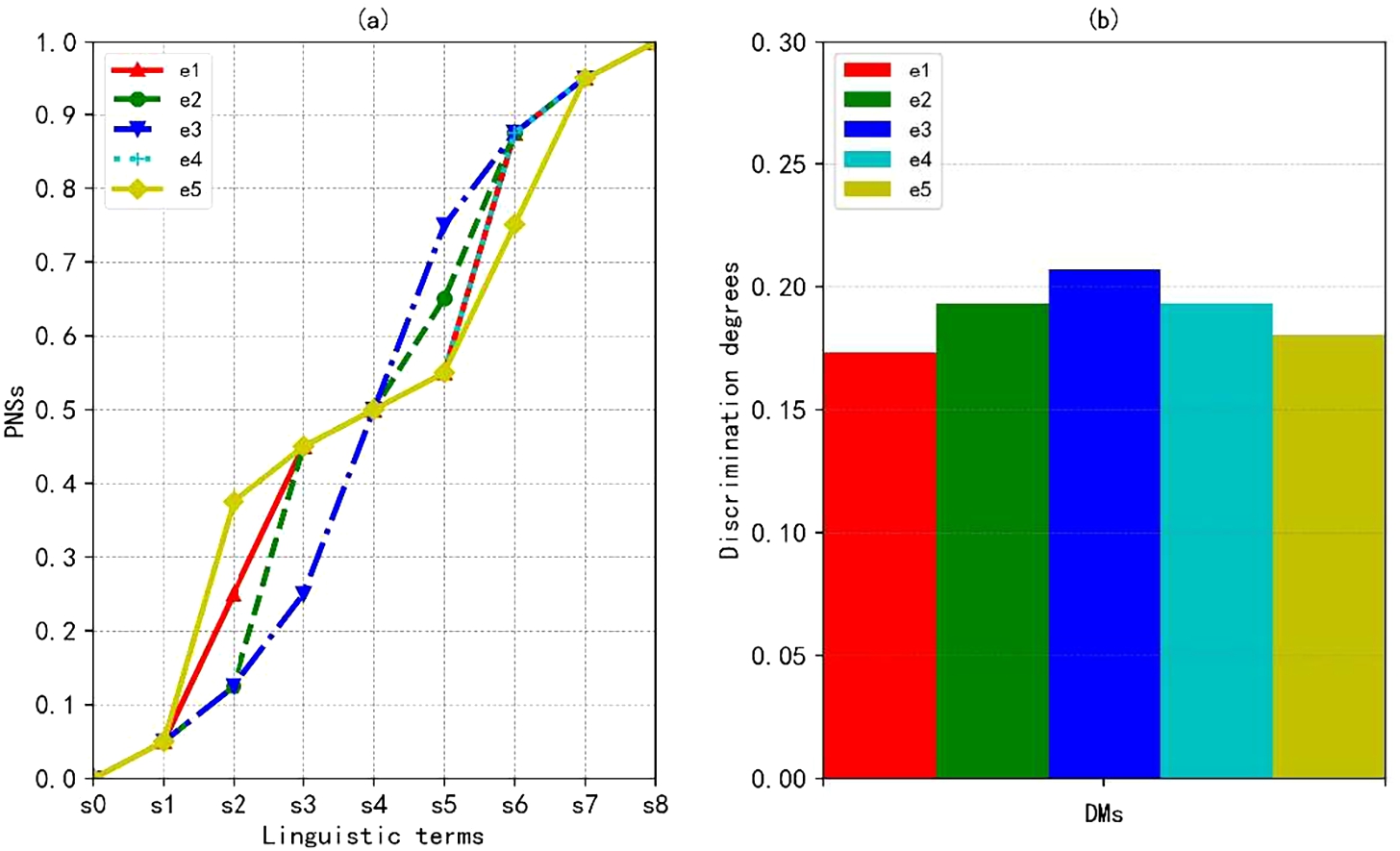
Fig. 3
PNSs of linguistic terms and discrimination degrees with $\rho =1$.
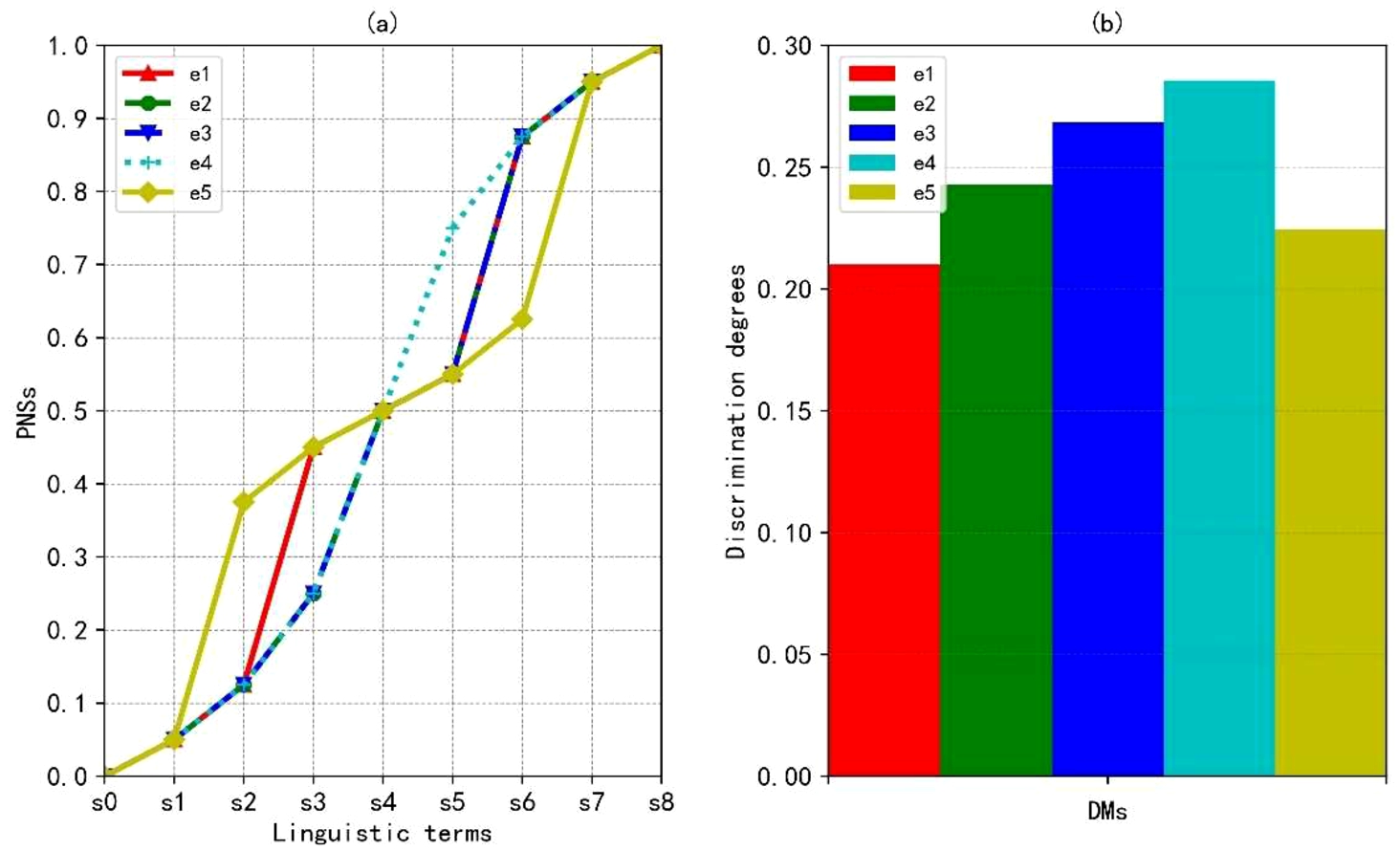
Fig. 4
PNSs of linguistic terms and discrimination degrees with $\rho =2$.
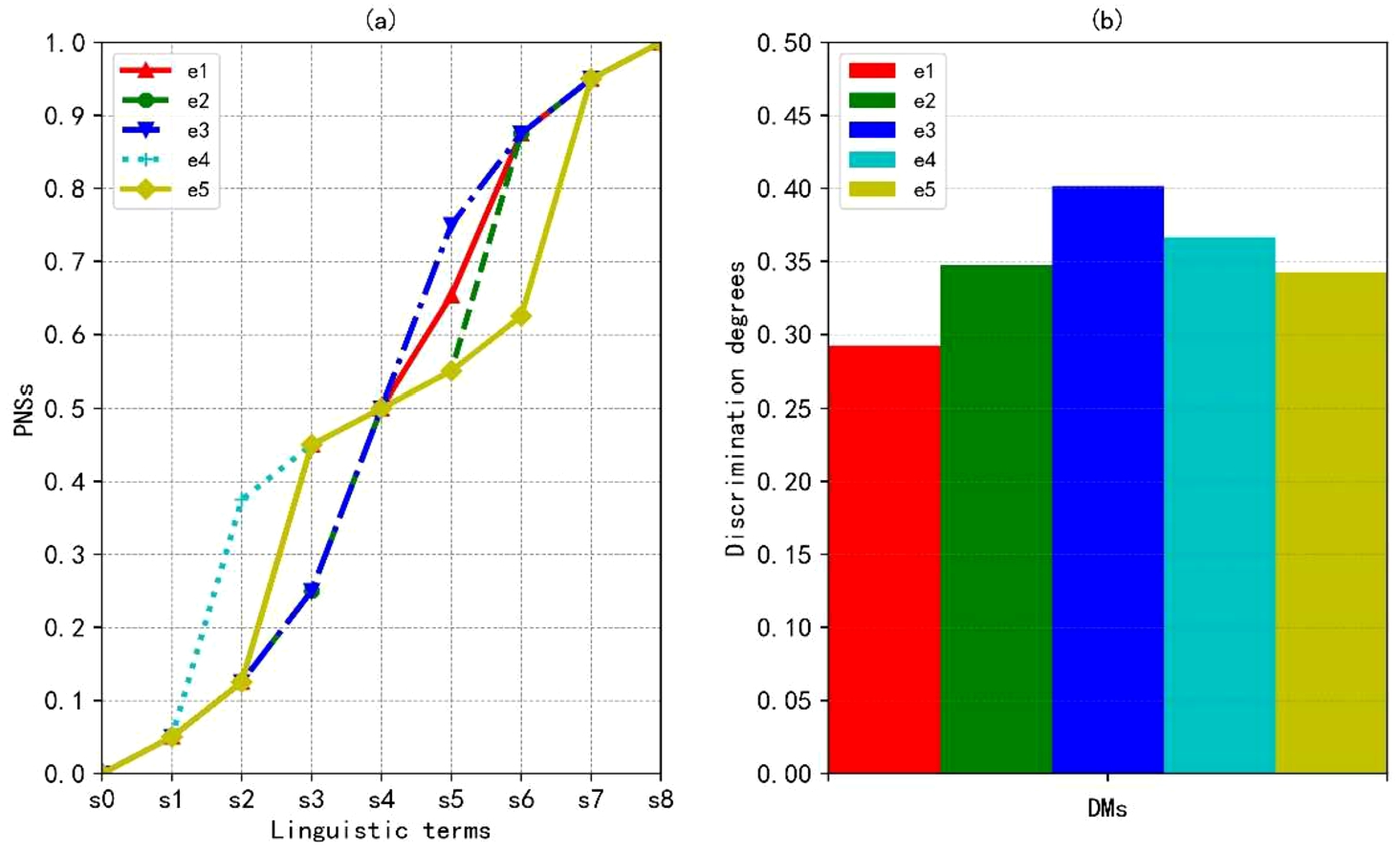
Fig. 5
PNSs of linguistic terms and discrimination degrees with $\rho \to \infty $.
5.3 Comparative Analysis
A comparative analysis is conducted between the existing MCGDM and the proposed approaches with LSVNNs. Two common MCGDM methods are employed in this comparison, and they are the LSVNN WAA and WGA operator-based method (M1 for short) (Fang and Ye,
2017) and the LSVNN prioritized WAA and WGA operator-based method (M2 for short) (Garg and Nancy,
2018).
The proposed approach is employed to solve the MCGDM problems in Fang and Ye (
2017) and Garg and Nancy (
2018), where the criterion weights keep the same as M1 and M2, respectively. The ranking results obtained by different methods are presented in Table
12. The sorting results obtained from the first group of comparative analysis are consistent, all of which are
${a_{4}}\succ {a_{2}}\succ {a_{3}}\succ {a_{1}}$. However, there are differences in the ranking results obtained from the second group of comparative analysis, which reflected in the order of alternatives
${a_{1}}$,
${a_{2}}$ and
${a_{4}}$. The possible reason for this difference is that the M1 needs to identify the orders of DMs and criteria before determining their weights. The aggregated results are highly related to the predefined orders. By contrast, the proposed approach identifies the weights of DMs based on a consensus-based optimization model, omitting the extra pre-procedure of determining the orders of DMs and criteria. Moreover, the alternatives are ranked based on the proposed PNSs-based score and accuracy functions. The different weight determination methods, aggregation rules and ranking methods may yield various results. The differences between M1, M2 and the proposed approach are summarized in Table
13.
Table 11
Rankings of alternatives with different values of ρ.
| ρ |
$S({r_{i}^{c}})$ |
Rankings |
| $\rho =1$ |
$S({r_{1}^{c}})=0.807$, $S({r_{2}^{c}})=0.751$, $S({r_{3}^{c}})=0.765$, $S({r_{4}^{c}})=0.776$
|
${a_{1}}\succ {a_{4}}\succ {a_{3}}\succ {a_{2}}$ |
| $\rho =2$ |
$S({r_{1}^{c}})=0.795$, $S({r_{2}^{c}})=0.757$, $S({r_{3}^{c}})=0.763$, $S({r_{4}^{c}})=0.797$
|
${a_{4}}\succ {a_{1}}\succ {a_{3}}\succ {a_{2}}$ |
| $\rho \to \infty $ |
$S({r_{1}^{c}})=0.802$, $S({r_{2}^{c}})=0.762$, $S({r_{3}^{c}})=0.775$, $S({r_{4}^{c}})=0.781$
|
${a_{1}}\succ {a_{4}}\succ {a_{3}}\succ {a_{2}}$ |
Table 12
Rankings of alternatives yielded by different methods.
| Methods |
Rankings |
Discrimination degrees |
| M1 (Fang and Ye, 2017) |
${a_{4}}\succ {a_{2}}\succ {a_{3}}\succ {a_{1}}$ |
$\textit{Dis}({e_{1}})=0.069$, $\textit{Dis}({e_{2}})=0.085$, and $\textit{Dis}({e_{3}})=0.121$
|
| The proposed approach |
${a_{4}}\succ {a_{2}}\succ {a_{3}}\succ {a_{1}}$ |
$\textit{Dis}({e_{1}})=0.159$, $\textit{Dis}({e_{2}})=0.123$, and $\textit{Dis}({e_{3}})=0.166$
|
| M2 (Garg and Nancy, 2018) |
${a_{2}}\succ {a_{4}}\succ {a_{1}}\succ {a_{3}}$ |
$\textit{Dis}({e_{1}})=0.159$, $\textit{Dis}({e_{2}})=0.214$, and $\textit{Dis}({e_{3}})=0.283$
|
| The proposed approach |
${a_{1}}\succ {a_{2}}\succ {a_{4}}\succ {a_{3}}$ |
$\textit{Dis}({e_{1}})=0.231$, $\textit{Dis}({e_{2}})=0.319$, and $\textit{Dis}({e_{3}})=0.386$
|
Table 13
Comparisons between the existing and the proposed methods.
| Methods |
Aggregation operators |
Ways of addressing LSVNNs |
PISs considered |
Group consensus considered |
| M1 (Fang and Ye, 2017) |
LSVNN WAA and WGA operators |
Consider indices of linguistic terms |
No |
No |
| M2 (Garg and Nancy, 2018) |
LSVNN prioritized WAA and WGA operators |
Consider indices of linguistic terms |
No |
No |
| Method in Li Y. et al. (2017) |
LSVNN geometric Heronian mean and prioritized geometric Heronian mean operators |
Consider indices of linguistic terms |
No |
No |
| Method in Liang et al. (2018a) |
LSVNN power WAA and WGA operators |
Consider indices of linguistic terms |
No |
No |
| Method in Li et al. (2019) |
LSVNN power WAA and WGA operators |
Consider indices of linguistic terms |
No |
No |
| The proposed approach |
LSVNN WAA operator |
NS-based 2-tuple linguistic model |
Yes |
Yes |
In order to highlight the characteristics of considering PISs, the discrimination degrees of decision matrices are calculated. Since the PISs of DMs are overlooked in M1 and M2, the fixed NSs for LTS
S are set, namely,
$\textit{FNS}({s_{\theta }})=\frac{\theta }{8}$ $(\theta =0,1,\dots ,8)$. Then, the discrimination degrees of decision matrices
${R^{h}}$ $(h=1,2,3)$ in Fang and Ye (
2017) and Garg and Nancy (
2018) are calculated by using Eq. (
8) based on the fixed and personalized NSs. The results are presented in Figs.
6 and
7. It shows that when expressing linguistic rating with LSVNNs, different DMs may present various linguistic semantics, as shown in Fig.
6(a) and Fig.
7(a). Therefore, it is necessary to take the PISs of each DM into account. Moreover, the proposed approach presents higher discrimination degrees than M1 and M2 that both fail to consider PISs of DMs, as shown in Fig.
6(b) and Fig.
7(b). Although the discrimination degrees obtained from the comparative analysis of each method are implicit, their significance can be achieved by describing the percentage of the improvement value brought by the proposed method compared to the results obtained by existing methods, as shown in Fig.
8. For example, in the first group of comparative analysis, the discrimination degree of
${e_{1}}$ calculated using the proposed method is greater than that using the M1 approach, and the discrimination degree is significantly improved by about 130.43% compared to the M1 method. In this way, the differences of alternatives in MCGDM problems with LSVNNs can be robustly distinguished by employing the proposed approach.
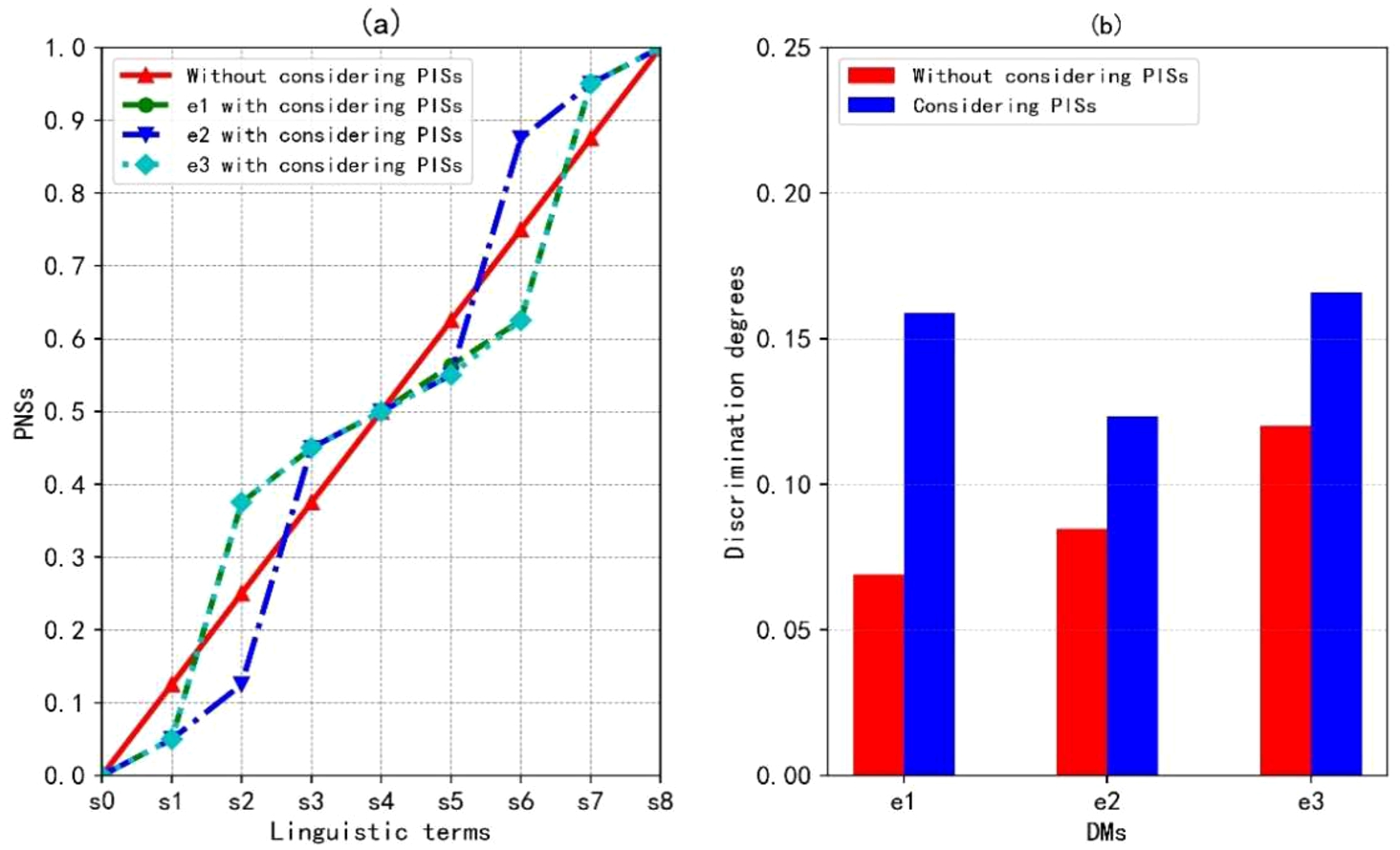
Fig. 6
Comparisons between M1 and the proposed approach.
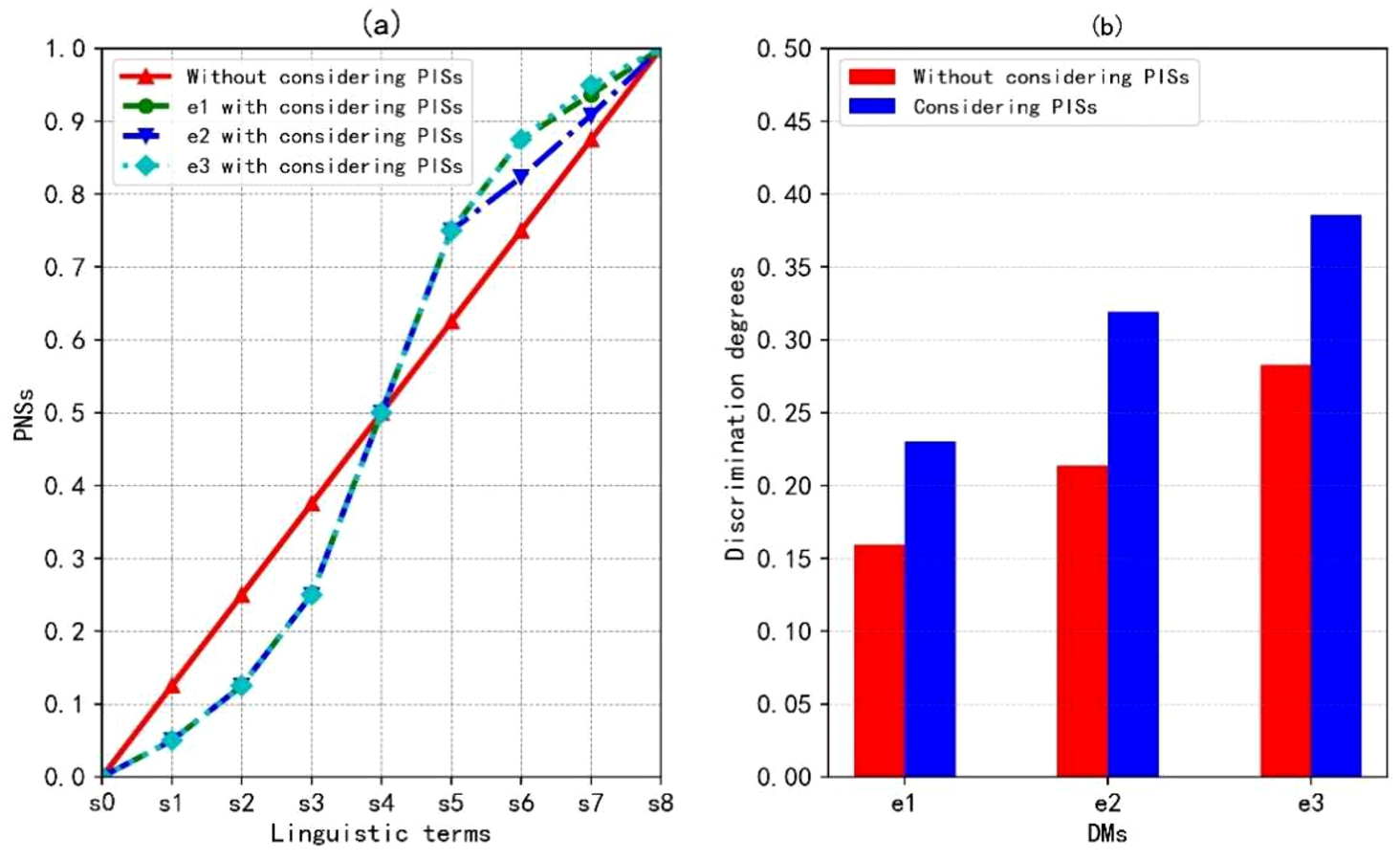
Fig. 7
Comparisons between M2 and the proposed approach.
Furthermore, comparisons are conducted between the existing LSVNN MCGDM methods and the proposed approach. The comparison results are summarized in Table
13. The results reflect that the existing methods aggregate LSVNNs based on the indices of linguistic variables of them. In this way, various virtual linguistic terms will be output and they may fail to be mapped to any original linguistic terms, reducing the readability. By contrast, the proposed approach considers the PISs of DMs and employs an NS-based 2-tuple linguistic model to address LSVNNs. The proposed approach can effectively avoid generating virtual linguistic terms. Meanwhile, the group consensus considered in the proposed approach can yield a final solution that is highly accepted by the group. In summary, the suggested method is better compared to other approaches.
Based on the discussion in the illustrative example, sensitivity and comparative analysis, the prominent features of the developed framework are summarized as follows:
-
(1) An effective solution for addressing PISs. The proposed PIS model can provide an effective solution to assign PNSs of linguistic terms for DMs, characterizing their personalized semantic preferences regarding linguistic MCGDM with LSVNNs.
-
(2) A cautious method to assign the weights of DMs considering group consensus. The developed consensus-driven optimization model is utilized to identify the weights of DMs, guaranteeing a high level of agreement among members in terms of the final solution.
-
(3) A robust method to determine the differences among alternatives. The proposed approach can not only consider the PISs of DMs, but also provide a robust method to reveal the differences among alternatives with the optimal discrimination degrees.
However, although the proposed approach equips outstanding characteristics in dealing with linguistic MCGDM problems with LSVNNs, DMs may have to derive the PNSs and weights of DMs by resolving some mathematic programming models. Compared to the existing methods without considering PISs, the proposed approach is intricate and time-consuming.
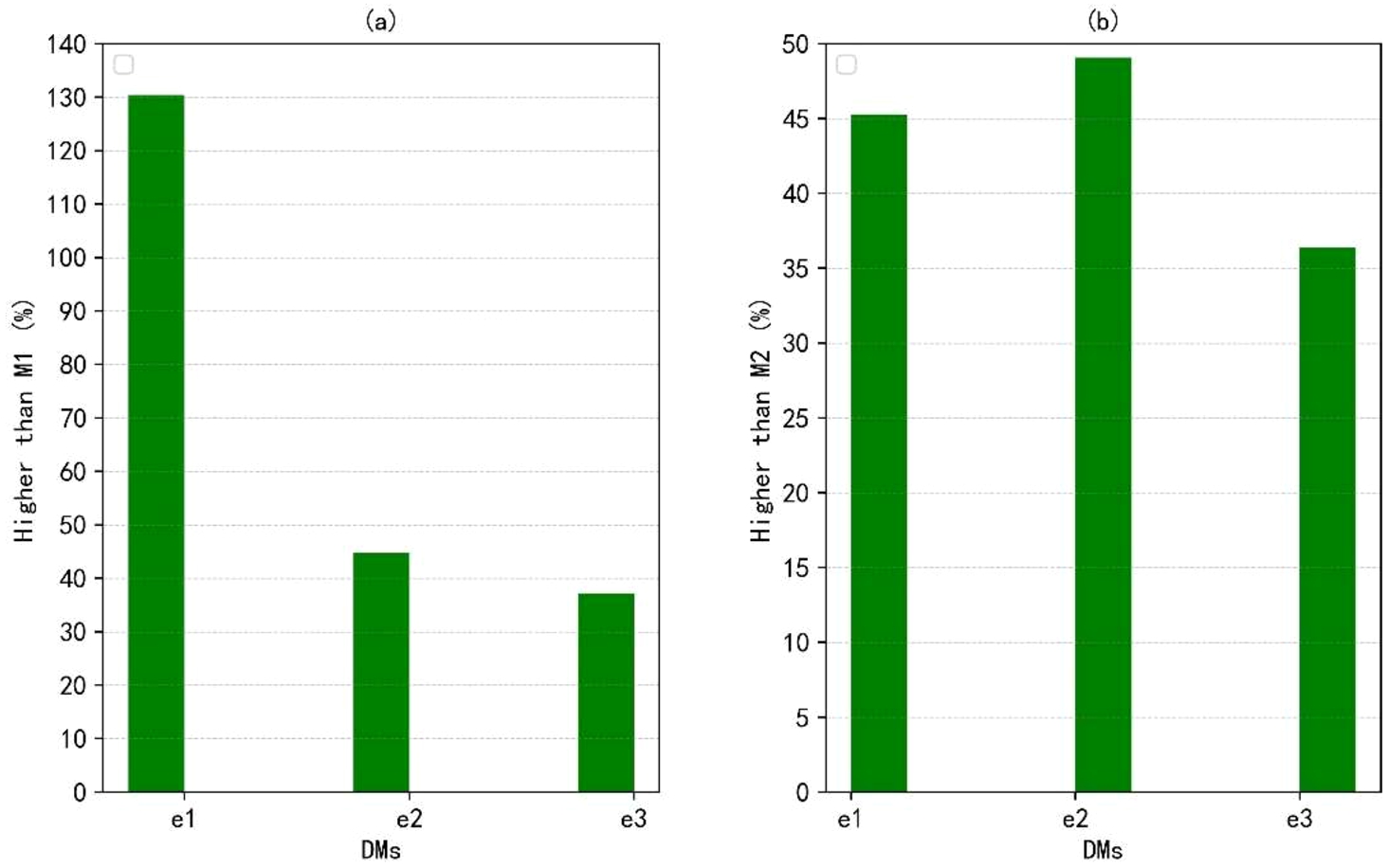
Fig. 8
Discrimination degrees derived from considering and without considering PISs.
6 Conclusions
LSVNNs are valuable for describing qualitative ratings involving uncertain, incomplete, and inconsistent information. When eliciting linguistic evaluations, words may be assigned different meanings for various people, that is, DMs have PISs with regard to linguistic terms. Considering PISs of DMs can lead to a realistic and effective methodology for addressing linguistic neutrosophic MCGDM problems. This study firstly develops a discrimination-based optimization model to assign PNSs of linguistic terms on LTS for DMs, and effectively describe their personalized semantic preferences regarding linguistic MCGDM with LSVNNs. Then, an optimization model on the basis of group consensus is constructed to identify the weights of DMs, which guarantees a high level of agreement among members in terms of the final solution. Subsequently, an LSVNN WAA aggregation operator and PNSs-based score and accuracy functions are utilized to determine the ranking of alternatives. Finally, by comparing with existing methods, the results demonstrate that the proposed approach which developed PIS can effectively derive PNSs of linguistic terms on LTS for DMs and lead to higher discrimination degrees than those without considering PISs.
In the future study, it would be an interesting topic to investigate the PIS-based approach for addressing incomplete MCGDM problems with LSVNNs. Moreover, complex MCGDM involving large-scale members and considering their social relationships has attracted much attention (Liao
et al.,
2021). It would be an interesting extension of the proposed framework for tackling social network large-scale MCGDM problems.

