Abstract
Ligand Based Virtual Screening methods are used to screen molecule databases to select the most promising compounds for a query. This is performed by decision-makers based on the information of the descriptors, which are usually processed individually. This methodology leads to a lack of information and hard post-processing dependent on the expert’s knowledge that can end up in the discarding of promising compounds. Consequently, in this work, we propose a new multi-objective methodology called MultiPharm-DT where several descriptors are considered simultaneously and whose results are offered to the decision-maker without effort on their part and without relying on their expertise.
1 Introduction
Drug development has always been an area of constant progress due to its direct application in society. This has been especially noticeable in recent years due to highly transmissible and deadly diseases such as Zika (Petersen
et al.,
2016), Ebola (Baize
et al.,
2014), and now COVID-19 (Mehta
et al.,
2020). Although a milestone in terms of development time has been achieved with the latter (Kim
et al.,
2020), the chances of failure are usually high and in fact, 90% of drugs that enter clinical trials fail to gain United States Food and Drug Administration (FDA) approval and are not marketed. Additionally, 75% of the costs are due to failures in the design pipeline (Tollman,
2001; Leelananda and Lindert,
2016). Consequently, the entire drug development process can take 12–15 years and exceed more than $1 billion (Hughes
et al.,
2011). To reduce costs, time and to improve the success rate, many new techniques and methodologies have been developed. One of these techniques is Virtual Screening (VS), which has been gaining ground in recent decades (Tanrikulu
et al.,
2013). VS is an in silico technique that allows the processing of large libraries with millions of compounds to find new compounds similar to a reference molecule based on one or several descriptors (Wang
et al.,
2009; Hamza
et al.,
2012; Boström
et al.,
2013; Kumar and Zhang,
2016). It is normally used as a filter to reduce the number of compounds to be studied in the later stages of drug development, one such example being High-Throughput Screening (HTS) to reduce costs and time (López-Ramos and Perruccio,
2010; Kar and Roy,
2013). This has increased the popularity of these techniques, which have shown great progress over the last two decades.
In terms of the VS methods, two categories are dependent on the available information of the compounds: Structure-Based Virtual Screening (SBVS) and Ligand-Based Virtual Screening (LBVS). The former is applied when the three-dimensional structure of the therapeutic target is available and it is exploited in order to propose hits, either obtained by experimental methods (X-ray crystallography (Lu
et al.,
2006) or Nuclear Magnetic Resonance (NMR) (Stark and Powers,
2011)) or through the construction of molecular models. An example of SBVS is the docking (Brooijmans and Kuntz,
2003; Morris and Lim-Wilby,
2008; Pagadala
et al.,
2017), a technique where the objective is to find the best coupling between two molecules: a receptor and a ligand. In contrast, LBVS is used when we exploit information derived only from one of several active or inactive ligands which usually happens when the three-dimensional structure of the drug target is not available. This includes Quantitative Structure-Activity Relationship (QSAR) (Karelson,
2000), shape matching techniques (comparison of global or partial shape between molecules) (Hawkins
et al.,
2007) and similarity search techniques using 2D/3D descriptors.
As far as we know, most LBVS methods proposed in the literature optimize the compounds by focusing on a single descriptor. A variety of descriptors can be considered: shape similarity, electrostatic similarity, aromatic potential, desolvation potential, or atomic property fields. For example, ROCS (OpenEye Scientific Software,
2021) or WEGA (Yan
et al.,
2013) find the most similar molecule to a given query in terms of shape similarity. In addition, the recently proposed OptiPharm has proved to be a very competitive piece of software when optimizing shape similarity or electrostatic potential (Puertas-Martín
et al.,
2019,
2020; OpenEye Scientific Software,
2020). Nevertheless, to increase the success of the predictions, the experts look for candidate compounds with similarities to the given query in more than one descriptor simultaneously. To do so, they face the query molecule to the whole database with one of the tools previously mentioned. They then carry out a post-processing phase that usually consists of sorting the compounds according to their scoring value, selecting the top of them, and analysing the subset of molecules by extracting or computing values related to the second descriptor of interest. This post-processing phase may be challenging and require much training and knowledge on the part of the expert (Tresadern
et al.,
2009; Maccari
et al.,
2011; Chu and Gochin,
2013; Kim
et al.,
2015; Kossmann
et al.,
2016; Woodring
et al.,
2017), basically because most of the time, there are descriptors in conflict, and an improvement in one leads to deterioration in the other.
A solution to these problems lies in multi-objective optimization. This has been used in different areas such as engineering (Marler and Arora,
2004), food (Ferrández
et al.,
2019), economics (Tapia and Coello,
2007) or energy (Cui
et al.,
2017). Within the VS field, solutions can be found using techniques such as QSAR, Docking, de novo design and even library design (Nicolaou and Brown,
2013), although, in the LBVS field there are few solutions found and, as far as we know, none applied to shape and electrostatic. In this work we propose:
-
• A new multi-objective software called MultiPharm able to optimize LVBS problems with many descriptors, simultaneously. For the sake of testing, we have solved a bi-objective optimization problem with shape and electrostatic similarity descriptors.
-
• A new decision-making methodology called MultiPharm-DT. Notice that there is usually no single optimal solution in multi-objective optimization but a group of alternative results with different trade-offs. Such a set of solutions is called the Pareto set (or efficient set) (Coello and Lamont,
2004), together with the corresponding set of scoring vectors, the Pareto front. With this new tool, the experts or decision-makers can solve a multi-objective LBVS problem and decide which Pareto optimal solution(s) fits their preferences more suitably, without any post-processing or additional effort from their side.
These new proposals may represent a real challenge since it is a non-convex multi-objective optimization problem and its resolution requires new methods beyond the generalization of single-objective global optimization techniques, as previously has been done (Pardalos
et al.,
2017).
The rest of the paper is organized as follows. Section
2 introduces the concepts of multi-objective optimization as well as the methodology currently used in the literature. This section also outlines a new proposal which includes a new methodology and a new tool. Section
3 describes the database used and the tool configurations. Section
4 shows the results obtained, detailing the different cases. Finally, the conclusions are summarized in the last section.
2 Methods
This section initially describes the multi-objective problem that we will address and defines some essential concepts about multi-objective optimization. Later we will briefly detail the two possible methodologies employed to deal with the problem. The first one is widely used in the literature, and it is based on optimizing only one descriptor followed by post-processing from the expert’s side. The second one consists of the simultaneous maximization of all the descriptors and helps reduce the expert’s effort.
2.1 The Multi-Objective Optimization Problem
This paper aims to maximize both the shape $T{c_{S}}$ and the electrostatic similarity $T{c_{E}}$ of two molecules (a query A and a target B), simultaneously.
The shape similarity score is calculated using a weighted Gaussian model (Grant and Pickup,
1995; Grant
et al.,
1996; Yan
et al.,
2013), which is widely used in other works (Yan
et al.,
2013; Cui
et al.,
2015; Lo
et al.,
2016) and can be expressed mathematically as follows:
where
${v_{ij}}$ is the sum of the intersections of the atoms and
${w_{i}}$ and
${w_{j}}$ are weights associated with the atoms
i and
j, respectively. From this function, the Tanimoto coefficient (Real and Vargas,
1996) is computed to normalize the score:
where
${V_{AA}}$ and
${V_{BB}}$ are the overlaps of the molecules
A and
B with themselves, respectively. This function returns a value in the range
$[0,1]$ where 0 means that there is no overlap and 1 means that there is a complete overlap between both molecules.
The electrostatic similarity (Böttcher and Bordewijk,
1978) between
A and
B is obtained by calculating the (
3):
In a similar fashion to (
1), the Tanimoto metric is used to normalize the value. For (
4), the range value is
$[-0.33,1]$ where 0 means there is no electrostatic overlap, 1 means the overlap is complete and
$-0.33$ means the overlap is complete but the loads of the molecules are opposite.
For optimization purposes, we look for the target’s pose that maximizes both the shape and electrostatic score values. To do so, we consider that the query remains in the same position during the whole optimization process. A pose $\boldsymbol{p}$ represents the rotation and translation of the target from its original position, and it is defined as a quaternion of the form $\boldsymbol{p}=\{\theta ,{\boldsymbol{c}_{\mathbf{1}}},{\boldsymbol{c}_{\mathbf{2}}},\boldsymbol{\Delta }\}$, where θ is the angle that a molecule is rotated with respect to the axis created by the points ${\boldsymbol{c}_{\mathbf{1}}}=({c_{1x}},{c_{1y}},{c_{1z}})$ and ${\boldsymbol{c}_{\mathbf{2}}}=({c_{2x}},{c_{2y}},{c_{2z}})$. $\boldsymbol{\Delta }=({\Delta _{x}},{\Delta _{y}},{\Delta _{z}}$) is a displacement vector.
The multi-objective optimization problem can be then defined as:
The need to tackle this problem from a multi-objective perspective can be seen in Fig.
1. It shows an example where the query molecule DB01155 and the target DB01208 are considered as input. Figure
1(a) shows the pose obtained when the shape similarity is maximized. As can be seen, a high value of
$T{c_{S}}=0.832$ is obtained. However, when we evaluate such a pose with the electrostatic similarity, we realize the obtained value is quite small (
$T{c_{E}}=0.556$). In Fig.
1(b) we show the opposite case, i.e. we optimize the electrostatic similarity and evaluate the shape similarity with the obtained pose. As can be seen, we obtain high values of
$T{c_{E}}=0.892$ but a negligible value for shape similarity
$T{c_{S}}=0.318$. All this clearly means that there exist instances where both objectives are in conflict and then, multi-objective techniques are needed.
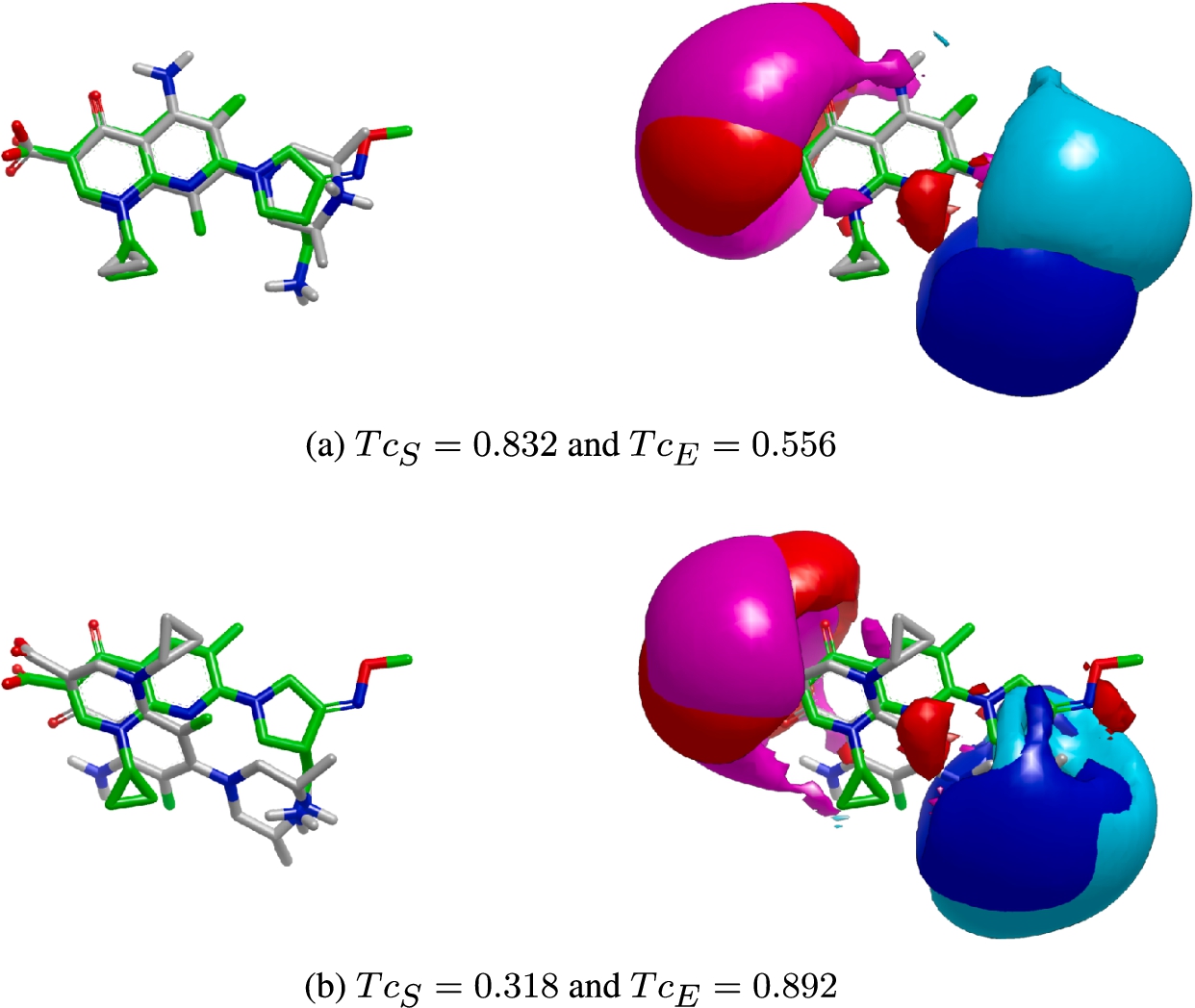
Fig. 1
Example of the conflict existing between the shape and electrostatic optimization. We have considered the query molecule DB01155 represented in green and fixed in 3D space, and the target molecule DB01208 depicted in gray. We show the overlap of their structures on the left and their electrostatic charges on the right. To the latter, the positive charge for the query (resp. target) is represented in blue (resp. cyan) and the negative in red (resp. magenta). (a) Shows the optimal pose obtained when the shape similarity is maximized. With such a pose we obtain a $T{c_{S}}=0.832$ value. Additionally, we have evaluated the electrostatic similarity at the optimal pose, reaching a $T{c_{E}}=0.556$ value. (b) Shows the optimal pose when the electrostatic similarity is maximized, obtaining a $T{c_{E}}=0.892$ figure. We have also evaluated the shape similarity at the optimal pose. The corresponding value has been $T{c_{S}}=0.318$.
When multiple objectives are present, the concept of an optimal solution, as in the single-objective problems, does not exist (Pardalos
et al.,
2017). Then, before addressing the optimization problem, it is necessary to explain what solving a multi-objective problem means. In a single-objective context it is easy to determine when a pose
$\boldsymbol{p}$ is better than another
${\boldsymbol{p}^{\prime }}$. It clearly happens when
$T{c_{i}}(\boldsymbol{p})>T{c_{i}}({\boldsymbol{p}^{\prime }})$, being
$i\in \{S,E\}$. In a multi-objective framework, the quality of two poses is determined by the concept of dominance. Its definitions are as follows:
Definition 1.
For two feasible poses $\boldsymbol{p},{\boldsymbol{p}^{\prime }}\in S$, we say that $\boldsymbol{p}$ dominates ${\boldsymbol{p}^{\prime }}$ and $Tc(\boldsymbol{p})$ dominates $Tc({\boldsymbol{p}^{\prime }})$ if and only if $T{c_{i}}(\boldsymbol{p})\geqslant T{c_{i}}{(\boldsymbol{p})^{\prime }}$ for all $i=S,E$, and there is at least one $j\in \{S,E\}$ such that $T{c_{j}}(\boldsymbol{p})>T{c_{j}}{(\boldsymbol{p})^{\prime }}$.
Figure
2 illustrates the concept of dominance. Notice how the objective space is represented, i.e. we have mapped a set of solutions
$\boldsymbol{p}$ to the objective space
$Tc(\boldsymbol{p})=(T{c_{S}},T{c_{E}})$.
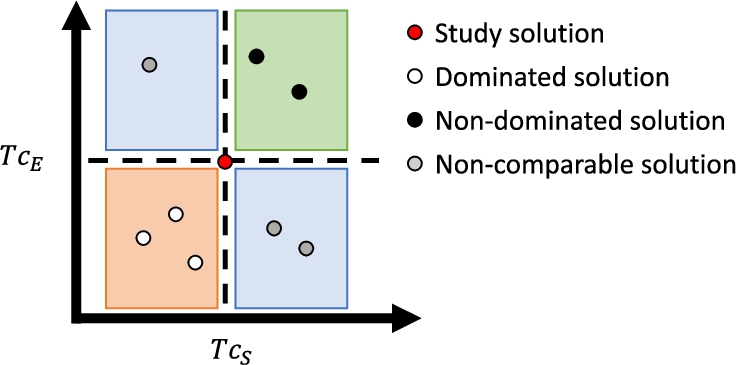
Fig. 2
Concept of dominance. Let us consider the solution in red as a reference. The solutions represented by black dots have better similarity values in the two objective functions than the red one. Consequently, the black solutions dominate the red one. Likewise, the solutions in white are dominated, since they have worse similarity values in both descriptors than the red one. Finally, the gray solutions have better similarity values in one property and worse in the other, so they are non-comparable solutions regarding the reference solution.
Definition 2.
A pose $\boldsymbol{p}\in S$ is said to be efficient or a Pareto optimal solution if and only if there is not another pose ${\boldsymbol{p}^{\prime }}\in S$ dominating $\boldsymbol{p}$, i.e. none of the objective functions can be improved without worsening at least one of the others. The set ${S_{E}}$ of all the Pareto optimal solutions is called the efficient set or the Pareto optimal set. The image of a Pareto optimal solution $Tc(\boldsymbol{p})$ is called the Pareto optimal objective vector and the set of all the Pareto optimal objective vectors $Tc({S_{E}})$ is denominated the Pareto optimal front.
Therefore, solving a multi-objective problem like the one in (
5) means finding the whole non-dominated subset formed by all the efficient poses, whose corresponding
$Tc=(T{c_{S}},T{c_{E}})$ represents the optimal Pareto front (Deb
et al.,
2016). However, obtaining an exact description of the efficient set (or Pareto front) is impossible for the problem at hand since those sets are continuous and include an infinite number of points. Furthermore, the computing cost may be high, which is an important point in the current context. As such, in this work, we will focus on providing a finite set of points comprising a Pareto Front Approximation (PFA) as a solution of (
5) (see Fig.
3).
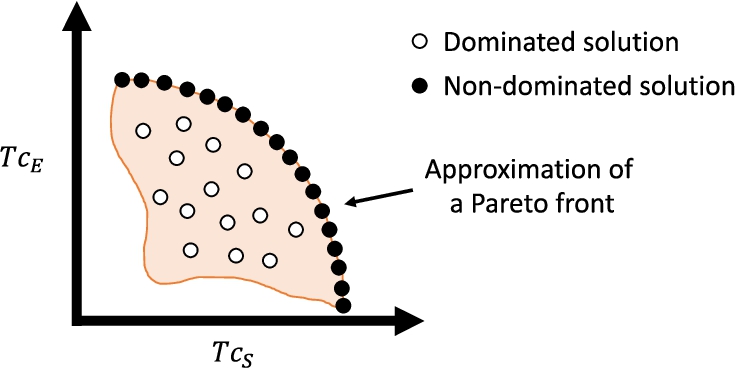
Fig. 3
An example of an approximation of the Pareto front for two objective functions ($T{c_{S}}$ and $T{c_{E}}$). White points are solutions dominated by the black points. All the black points belong to the Pareto front. None of the black points can be considered better than each other.
2.2 Single-Objective Approach
This subsection describes the methodology used in the literature that is characterized by the use of single-objective software for the selection of candidate compounds. As will be seen, regardless of the case, not only is a significant effort required to determine which molecules to select for evaluation, but the selection is highly dependent on the available information and expert knowledge, which can rule out promising results.
The most widely used methodology in the literature consists of facing the query molecule to the whole database by optimizing the shape similarity. This procedure, denoted as Mono-Shape throughout this paper, is illustrated through an example in Fig.
4(a), where the
Query molecule is DB09074, and the database consists of the rigid compounds from the well-known FDA. Initially, the
Query is compared to each compound
${\textit{Target}_{S}}$ from the database to obtain their optimum position and corresponding shape similarity value
$T{c_{S}}$. Afterward, a post-processing procedure starts, whose complexity and required effort depends on the experience of the decision-maker. In this respect, there can be many different workflows. As part of this work, three of them will be explained.
The first workflow ($W{F_{1}^{\textit{Mono-Shape}}}$) is trivial and consists of the decision-maker only being interested in similarity of shape. In such a case, the compounds are sorted ($R{k_{S}}$) in descending order by $T{c_{S}}$, and the molecule with the greatest $T{c_{S}}$ is proposed as the best prediction. In our example, this molecule would be DB11799 with $T{c_{S}}=0.69$.
However, if the decision-maker’s preferences include molecules with both high shape and electrostatic similarities, which we named the second workflow (
$W{F_{2}^{\textit{Mono-Shape}}}$), the post-processing is rather time-consuming. This workflow is widely used in the literature and for more details on the specific procedures, several papers can be consulted (Chu and Gochin,
2013; Kim
et al.,
2015; Kossmann
et al.,
2016; Woodring
et al.,
2017). After sorting the molecules by the
$T{c_{s}}$ value, it continues by selecting and evaluating the
N best compounds to measure the corresponding electrostatic similarity value
$T{c_{E}^{\textit{Eval}}}$. Notice that the evaluation of the electrostatic similarity considers the pose obtained with the shape similarity optimization. The decision-maker usually determines the number
N of analysed molecules and usually is not greater than 10% of the database sizes (Hevener
et al.,
2012; Kaoud
et al.,
2012; Kossmann
et al.,
2016). Even so, the number of compounds to be analysed might be considerably high, meaning the selection of promising solutions might demand a lot of experience, knowledge, and time from the expert’s side. In our example, for
$N=100$ and after a visual inspection of the aligned poses, the expert could select the molecule DB13801 with a
$T{c_{S}}=0.48$ and
$T{c_{E}^{\textit{Eval}}}=0.32$ grounded on several criteria (additional chemical substructural similarities and potential known pharmacophores for the chosen drug target, among others).
Finally, another possible way to proceed might be to compute the average value between $T{c_{S}}$ and $T{c_{E}^{\textit{Eval}}}$ and propose the one with the greatest mean value ($T{c_{\textit{meanSE}}}$) as the best prediction, which is called the third workflow ($W{F_{3}^{\textit{Mono-Shape}}}$). It is intended to alleviate a problem that frequently occurs in $W{F_{2}^{\textit{Mono-Shape}}}$. As part of this, compounds can have a very high value in shape similarity but very low in electrostatic similarity.
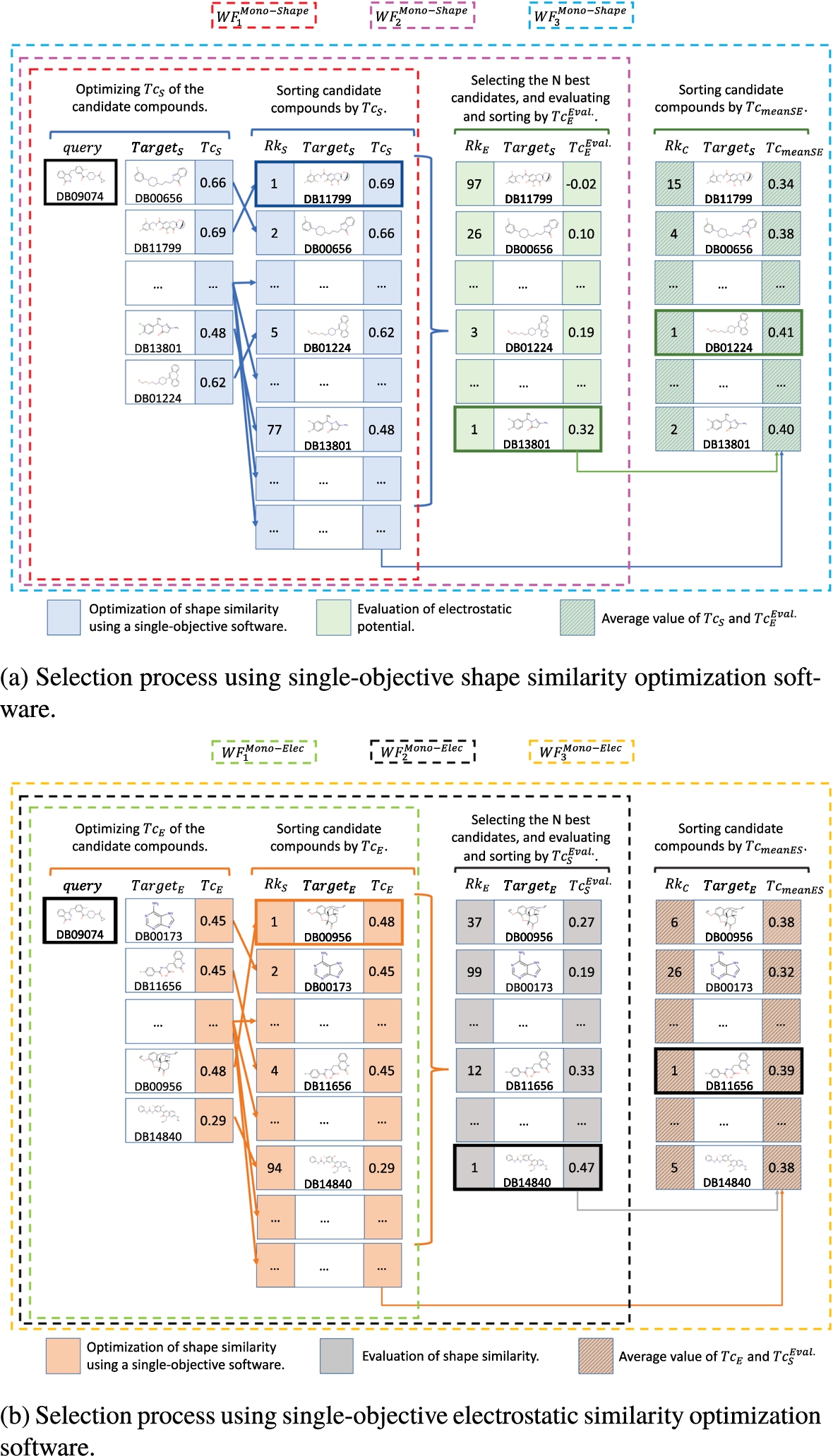
Fig. 4
Selection process using single-objective software. Each compound in the database is optimized to maximize the value of a descriptor ($W{F_{1}}$). Subsequently, the compounds are sorted and the best N are selected. This subset is evaluated with the second descriptor ($W{F_{2}}$). Finally, the average value of both descriptors ($W{F_{3}}$) is calculated. Depending on the interests of the decision-maker, the compounds can be selected from one workflow or another.
Let us now itemize the obtained predictions when we optimize the electrostatic similarity instead of the shape similarity, denoted as Mono-Elec. We can now consider the expert has a single-objective tool available to maximize the electrostatic similarity of two molecules. As previously, to illustrate the procedure, the same query and database are selected (see Fig.
4(b)). Similarly, the query molecule faced the whole database by optimizing the electrostatic similarity of each target, and a list of candidate molecules sorted according to their
$T{c_{E}}$ values is obtained. From this point on, the experts can make different decisions based on their knowledge, available information, or preferences. They might consider that only a descriptor is of interest and hence select the molecule with the greatest
$T{c_{E}}$, (
$W{F_{1}^{\textit{Mono-Elec}}}$). In our example, this molecule would be DB00956 with a
$T{c_{E}}=0.48$. They might also require molecules with high similarities in both descriptors. As previously considered, the experts might select the top
N molecules and evaluate the obtained pose with the shape similarity descriptor, to ultimately select the one with the greatest evaluated value, (
$W{F_{2}^{\textit{Mono-Elec}}}$). In our example, for
$N=100$ the expert would propose DB14840 with
$T{c_{E}}=0.29$ and
$T{c_{S}^{\textit{Eval}}}=0.47$. Either that, or they might compute the average value (
$W{F_{3}^{\textit{Mono-Elec}}}$) and propose the molecule DB11656 as the best prediction with
$T{c_{\textit{meanES}}}=0.39$.
To summarize both methodologies, Mono-Shape and Mono-Elec, it has been shown that the decision-maker needs a great deal of knowledge and experience to be able to carry out many decisions ($W{F_{1}}$, $W{F_{2}}$, $W{F_{3}}$), solve different single-objective optimization problems and accomplish different analyses in search of good predictions. The key point is that all of them may lead to different candidate molecules that could be of interest to the experts. However, the larger the number of candidate molecules obtained, the bigger the number of optimization problems to solve, and the greater the post-processing effort required by the decision-makers, meaning it becomes unfeasible for a human expert to apply their experience and chemical knowledge to such large scale contexts.
2.3 The Multi-Objective Approach: MultiPharm-DT
This section describes the methodology proposed in this work. For this purpose, it has been divided into two parts. Firstly, we will detail the tool, called MultiPharm, which has been developed to support this methodology. Secondly, MultiPharm-DT will be explained. It is the compound selection strategy based on a decision tool that implements the expert’s preferences.
2.3.1 MultiPharm, the Multi-Objective Optimization Tool
This subsection is devoted to explaining MultiPharm, a new tool designed to deal with LBVS multi-objective optimization problems. As a result, it can obtain a set of predictions without any post-processing from the expert’s side.
MultiPharm can solve any LBVS multi-objective optimization problem with up to
m objective functions that depend on the position of the molecules. In other words, it can deal with any objective function used to measure the similarity between two given molecules. Its structure is defined in Fig.
5 and the procedures implemented are explained below.
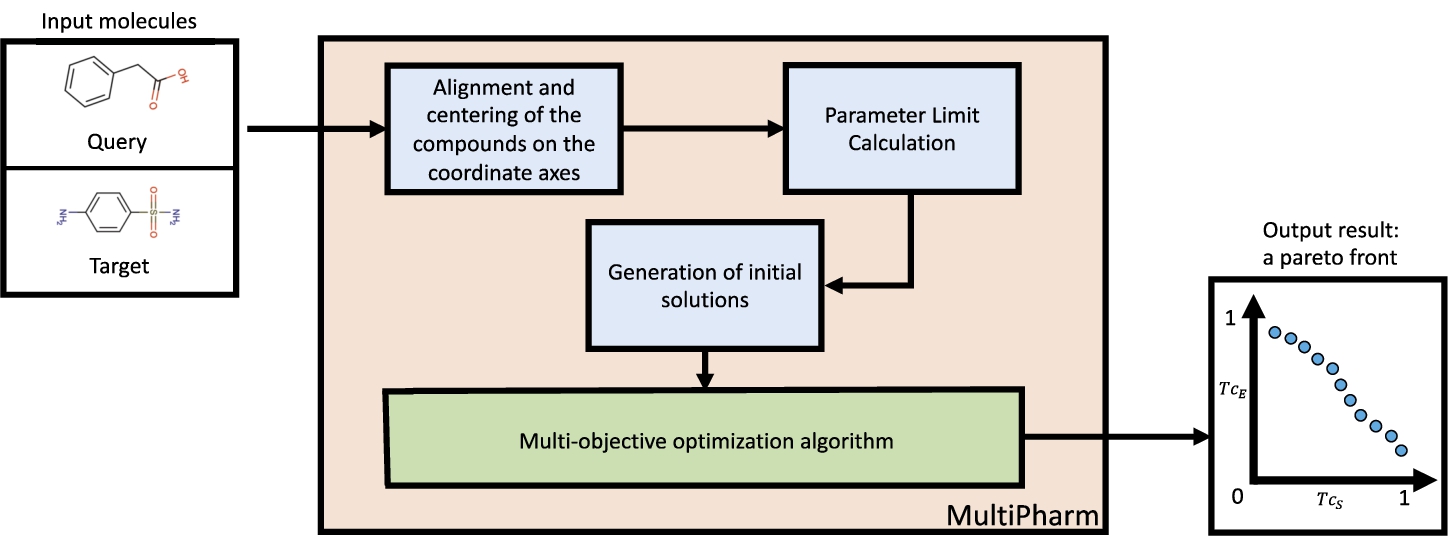
Fig. 5
MultiPharm tool structure. Two molecules are received as input parameters. After applying alignment mechanisms to them and calculating the boundaries of the optimization parameters, a set of initial poses is generated. After that, the position of the target molecule is modified by a multi-objective optimization algorithm to optimize the shape and electrostatic similarities with the query molecule. The result obtained is a set of poses with different similarity values in each descriptor.
Alignment and centering compounds. The first step consists of preprocessing the input molecules. The processing performed on the compounds databases before applying VS techniques to them is well known. Consequently, the position of the molecules is entirely random and it influences the solutions. To avoid this, MultiPharm places the centroids of the pair of molecules at the origin of coordinates. Subsequently, it aligns the compounds using PCA such that the longest axis is aligned with the X-axis and the shortest axis of the molecules with the Z-axis. In this way, the initial solutions generated have a good starting point and do not depend on the position of the compounds in the database.
Parameter limit calculation. Since each pair of input compounds can have different sizes, the corresponding limits of the decision parameters are dynamically computed for each particular instance. θ is the rotation angle applied to the axis formed by the 3D points in space ${c_{1}}$ and ${c_{2}}$. θ is always defined in the range $[0,2\pi ]$ radians to allow the molecule to rotate freely. In contrast, ${c_{1}}$ and ${c_{2}}$ depends on the target molecule. Specifically, the box containing the target molecule is calculated, and within it, the two points are randomly generated. Finally, Δ is calculated as the difference between the boxes containing the query and the target molecules. This procedure avoids poses in which there is no overlap between the two compounds.
Initial solutions. Once the parameters are defined and limited, we generate the initial solutions. We carry out an empirical study to obtain a good set of starting poses for this problem, which consists of creating 300 solutions from the centred and aligned molecules’ initial position. After that, we divide them into 4 groups: three of them with 80 solutions obtained when rotating the target molecule by different angles at each axis $(X,Y,Z)$ and one group of 60 poses randomly generated, to include variety and hence, avoid being trapped in local optima.
Multi-objective optimization algorithm. MultiPharm is a wrapper for a multi-objective optimization algorithm. It means that it can include any of the multi-objective optimization algorithms proposed in the literature, such as NSGA-II and SPEA-II (Zitzler
et al.,
2001; Deb
et al.,
2002; Durillo and Nebro,
2011). However, for the problem at hand, and taking previous experiences (Puertas-Martín
et al.,
2019,
2020) into account, we consider that MOEA/D (Zhang and Li,
2007) is an excellent alternative to prove the efficacy of the multi-objective methodology. As such, it is implemented as part of the MultiPharm tool.
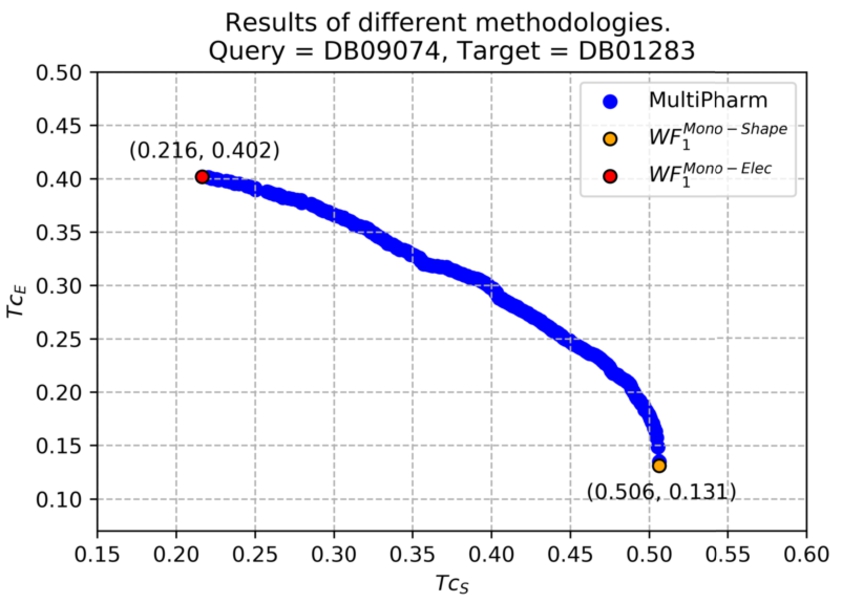
Fig. 6
An example where results obtained by comparing the query DB09074 and the target DB01283 are shown. In yellow (resp. red) is the value obtained by optimizing the electrostatic potential similarity (resp. shape) with single-objective software. It is observed that only two solutions (poses) are obtained. However, the multi-objective tool provides a greater number of solutions in which a balance between both properties is sought. In addition, single-objective solutions are shown. They are located at the extreme points of the Pareto front.
MOEA/D stands for Multi-Objective Evolutionary Algorithm based on Decomposition. It transforms the multi-objective problem into several scalar optimization problems using a decomposition method. All these subproblems are simultaneously solved considering a set of uniformly distributed weight vectors. With each generation, the population is formed by the best solution found for each subproblem. This population evolves throughout the optimization procedure taking the neighborhood information into account. We refer the interested reader to Zhang and Li (
2007), Li and Zhang (
2008) for an in-depth description of the optimization algorithm.
2.3.2 Output Result: a Pareto Front
MultiPharm obtains, as a result, a Pareto front (and of course, its corresponding efficient set). Figure
6 shows the Pareto front obtained as a real example where the query molecule was DB09074 and the target molecule was DB00504. Notice that each blue circle represents the value of
$T{c_{S}}$ and
$T{c_{E}}$ that can be obtained if the target molecule is at a particular pose
p. As can be seen, there is a pose where the
$T{c_{S}}$ achieves its maximum value and another one where it reaches the maximum
$T{c_{E}}$. As we illustrate in the figure, those solutions coincide with the ones obtained when a single-objective problem is considered, i.e. with the solutions of
$W{F_{1}^{\textit{Mono-Shape}}}$ and
$W{F_{1}^{\textit{Mono-Elec}}}$ methodologies, respectively.
2.4 The Decision Tool: MultiPharm-DT
The execution of MultiPharm over a database will obtain a Pareto front for each pair (query, target). It could be too much information for the expert, even considerably more than the one managed with the single-objective perspective. In this work, we have also implemented a decision tool, called MultiPharm-DT, to reduce the quantity of information given to the expert. Although one could consider many different selection criteria, we opted to implement a mechanism that obtains the Pareto front of the paretos as part of MultiPharm-DT.
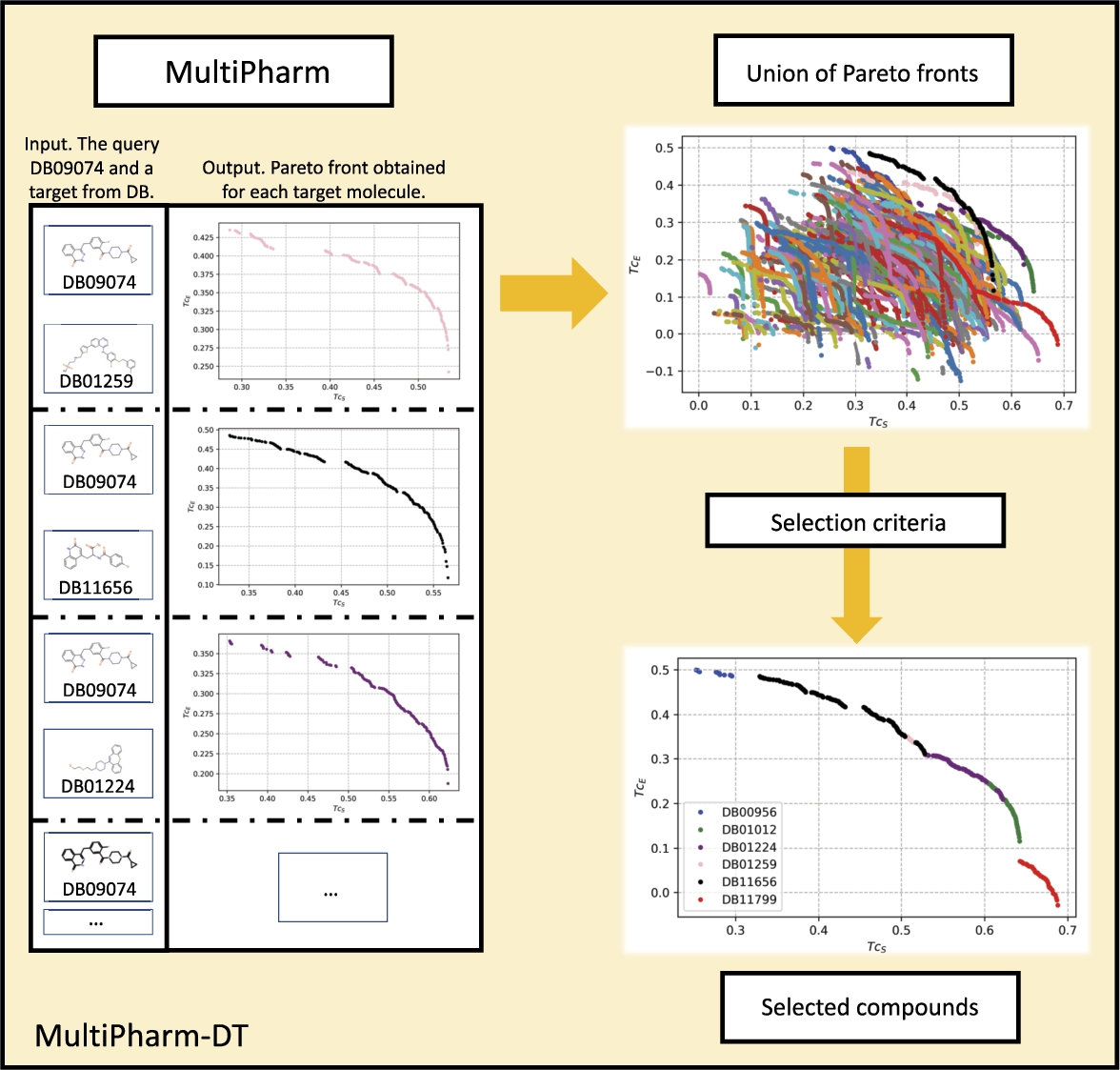
Fig. 7
Selection process for the most similar compounds following the multi-objective methodology. The query molecule is compared with the whole database, consequently obtaining a Pareto front for each target molecule. Subsequently, all the fronts are mixed and it is left to the decision-maker’s discretion which compounds to select. For this example, the compounds with non-dominated poses have been selected.
Figure
7 helps to illustrate this mechanism. As can be seen, MultiPharm-DT merges all the particular Pareto fronts. At this point, the experts can compare them, see the similarities of the compounds from the database with the query molecule, and extract information in different ways. Apart from the union of the paretos, MultiPharm-DT applies a decision mechanism and provides a filtered solution. The expert is able to select the most appropriate compound for their preferences at a glance. That means they will select the compound DB00956 if they are looking for a molecule with high electrostatic similarity. If their preferences are inclined towards shape similarity, they will choose the compound DB11799. However, if they are interested in proposing compounds with a balance between the two descriptors, they will choose from the compounds DB01012, DB01224, DB01259 or DB11656. Finally notice that for each compound, the multi-objective methodology offers a set of possible poses, as mentioned in subsection
The Multi-Objective Optimization Problem, which could also be of great interest to the decision-maker.
3 Materials
3.1 Database
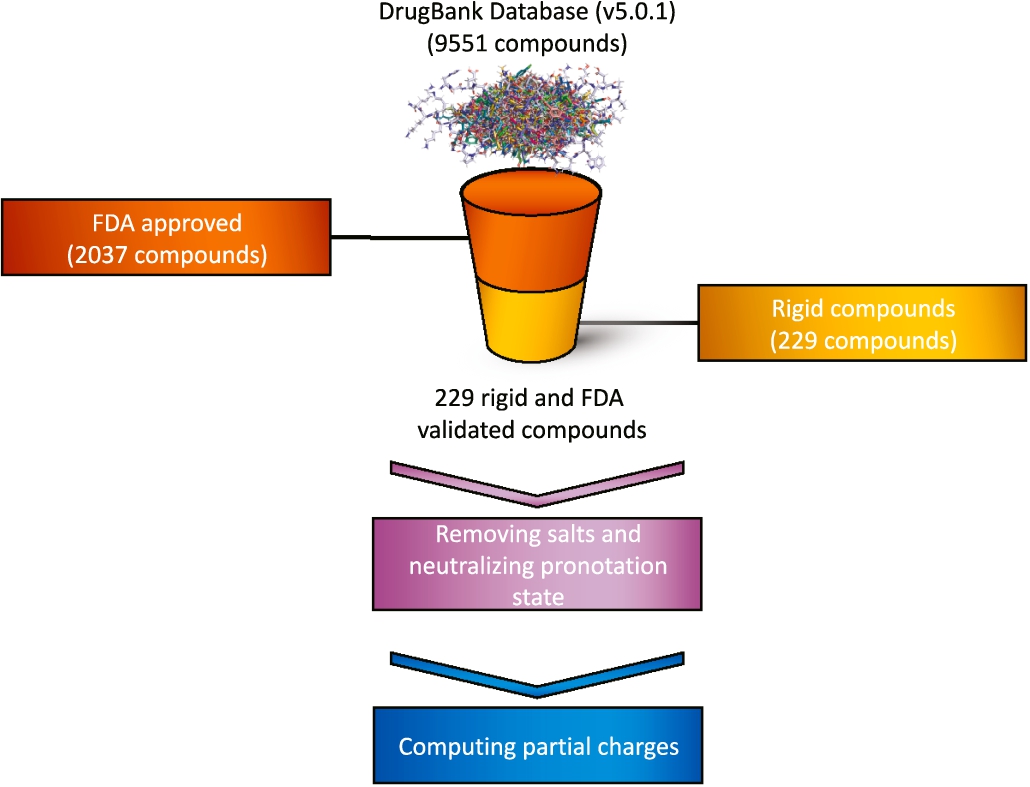
Fig. 8
Only validated and rigid compounds are selected from the original database. The compounds are then processed by removing salts, neutralizing the pronotation state and computing the partial charges.
The database used in this work was obtained from DrugBank v5.0.1 (Wishart
et al.,
2018) and mol2 files necessary for the VS calculations were set up by using AmberTools (Case
et al.,
2017). This took the form of removing salts and neutralizing their protonation state, computing partial charges by MMFF94 force field, adding hydrogen atoms and minimizing energies (default parameters) (Halgren,
1995) (see Fig.
8). From this database, we selected those compounds that were rigid and validated by the FDA, a federal agency of the United States Department of Health and Human Services. This subset was classified by its number of atoms in groups. A compound (query) was selected randomly from each group, as shown in Fig.
9. Consequently, 32 molecules were selected for analysis against the rest of the database. And in order to compare software and methodologies on an equal footing, hydrogen atoms were considered for shape and electrostatic similarity.
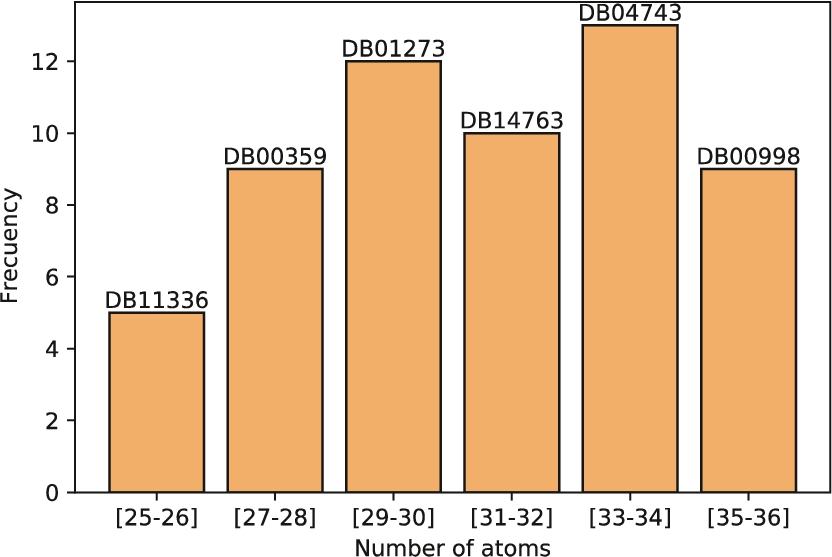
Fig. 9
Molecules are grouped by their number of atoms. Queries molecules are randomly selected from each group. This process has been performed on the whole database although in this figure only molecules containing between 25 and 36 atoms are shown.
3.2 Hardware Setup
All the experiments in this work have been executed using 18x Bullx R424-E3, which consists of 2 Intel Xeon E5 2650 (16 cores), 64 GB of RAM memory and 128 GB SSD (
http://hpca.ual.es/en/infraestructure).
3.3 Software Configuration
To compare the two methodologies, we decided to use OptiPharm in its two versions (Puertas-Martín
et al.,
2019; Puertas-Martín
et al.,
2020) and MultiPharm. OptiPharm is a recent piece of software designed to work with the LBVS problem which implements an evolutionary global optimization algorithm that can solve any optimization problem related to the similarity of two compounds, a query and target molecules. It implements procedures to adjust the latter to the query molecule, remaining unchanged throughout the optimization process. OptiPharm has proved to be very competitive when maximizing the shape similarity, as well as the electrostatic. For a more comprehensive explanation of the software and the obtained results, reading the original works (Puertas-Martín
et al.,
2019; Puertas-Martín
et al.,
2020) is recommended. It is also available in the free-to-use server BRUSELAS (Banegas-Luna
et al.,
2019).
OptiPharm and MultiPharm can be parameterized in order to adapt them to different problems and the preferences of the user. Focusing on the quality of the solutions, the configuration established for OptiPharm is the same as published in other works. This will be called OptiPharm Robust (OpR) and its input parameters are:
N = 200,000 function evaluations,
$M=5$ starting poses,
${t_{\max }}=5$ iterations and
${l_{\max }}=1$ as the smallest possible radius. Conversely, MultiPharm is set up with the default parameters (Zhang and Li,
2007; Li and Zhang,
2008). But in order to compare both pieces of software on equal terms, the number of MultiPharm evaluations is set to the same value as the OptiPharm configuration, i.e. the number of evaluations is 200,000. In addition, the number of solutions that will form a Pareto front is set at 300.
4 Results and Discussion
Before proceeding with the results, it is necessary to explain how we will compare both methodologies, i.e. MultiPharm-DT versus Mono-Shape and Mono-Elec. Our goal is to prove that we can obtain more predictions of interest with the multi-objective methodology, but (i) without the participation of the expert, (ii) with less computational effort and (iii) with more accuracy. To do so, the 32 query molecules are faced against the database. The results are summarized in Table
2. To understand such a table, we will focus on a particular row, more precisely, on the one corresponding to the query molecule DB09516. The pertinent results appear in Fig.
10 and Table
1.
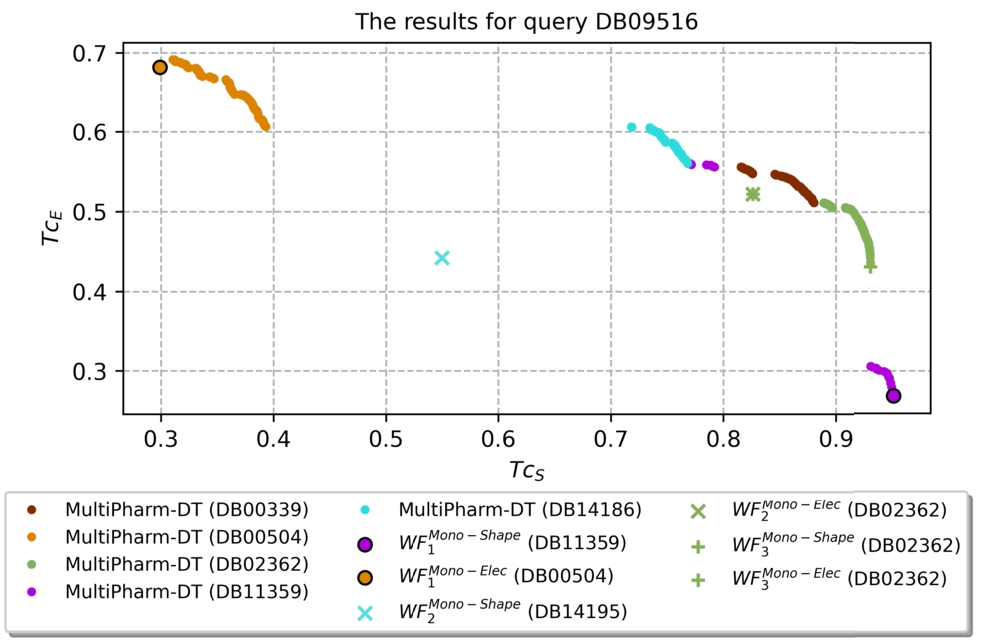
Fig. 10
The predictions obtained by the single-objective and multi-objective software for the query DB09516.
Table 1
Summary of the results obtained for both single and multi-objective methods for the query compound DB09516. The most similar compound is shown for Mono-Shape and Mono-Elec, and the list of compounds with non-dominated MultiPharm-DT solutions (poses).
|
$W{F_{1}^{\textit{Mono-Shape}}}$ |
$W{F_{1}^{\textit{Mono-Elec}}}$ |
MultiPharm-DT |
| Query |
Target |
$T{c_{S}}$ |
$T{c_{E}^{\textit{Eval}}}$ |
Target |
$T{c_{S}^{\textit{Eval}}}$ |
$T{c_{E}}$ |
Compounds |
| DB09516 |
DB11359 |
0.951 |
0.268 |
DB00504 |
0.310 |
0.692 |
DB00339, DB00504, DB02362, DB11359, DB14186 |
In the figure, we show the solution found by each workflow ($W{F_{i}^{\textit{Mono-Shape}}}$ and $W{F_{i}^{\textit{Mono-Elec}}}$ with $i=1,2,3$), and also the filtered Pareto front obtained by MultiPharm-DT. As expected, the predictions obtained by $W{F_{1}^{\textit{Mono-Shape}}}$ and $W{F_{1}^{\textit{Mono-Elect}}}$ coincide with the extreme points of the Pareto front. It shows that we are analysing the single-objective methodology with a reliable algorithm, OptiPharm, and hence the comparison with the multi-objective methodology is fair.
Nevertheless, the predictions achieved by MultiPharm-DT dominate the ones obtained by $W{F_{i}^{\textit{Mono-Shape}}}$ and $W{F_{i}^{\textit{Mono-Elec}}}$ with $i=2,3$. As can be seen, $W{F_{2}^{\textit{Mono-Elec}}}$, $W{F_{3}^{\textit{Mono-Elec}}}$ and $W{F_{3}^{\textit{Mono-Shape}}}$ offer the compound DB02362 as a solution, which is also provided by MultiPharm-DT. However, MultiPharm-DT is more accurate and finds a pose p that allows higher score values to be reached, as can be appreciated in the figure. Finally, the workflow $W{F_{2}^{\textit{Mono-Shape}}}$ obtains the DB14195 compound as the best prediction. This solution is not in competition with any of the molecules provided by MultiPharm-DT, i.e. it is dominated.
The performance observed in the previous paragraph for the DB09516 query follows the normal trend for all the experiments; the only solutions that can compete with the ones obtained by MultiPharm-DT are those provided by $W{F_{1}^{\textit{Mono-Shape}}}$ and $W{F_{1}^{\textit{Mono-Elec}}}$. For the remaining cases ($W{F_{i}^{\textit{Mono-Shape}}}$ and $W{F_{i}^{\textit{Mono-Elec}}}$ with $i=2,3$), MultiPharm-DT always offers a better alternative that dominates them. All of this reveals the advantages of considering a multi-objective methodology when we require compounds that maximize several descriptors simultaneously. Notice that during the optimization procedure, MultiPharm-DT evolves the initial poses towards new ones considering the values of $T{c_{S}}$ and $T{c_{E}}$ simultaneously. However, the single-objective methodology only optimizes the pose taking a single descriptor into account. Accordingly, even in those cases where both methods offer the same compound as part of the solution, MultiPharm-DT always reaches better scoring function values. For this reason, in the following results and for the sake of simplicity, we will only show $W{F_{1}^{\textit{Mono-Shape}}}$ and $W{F_{1}^{\textit{Mono-Elec}}}$. Nevertheless, the interested reader may consult the Supplementary Material section, which provides all the information about the predictions obtained for all the workflows.
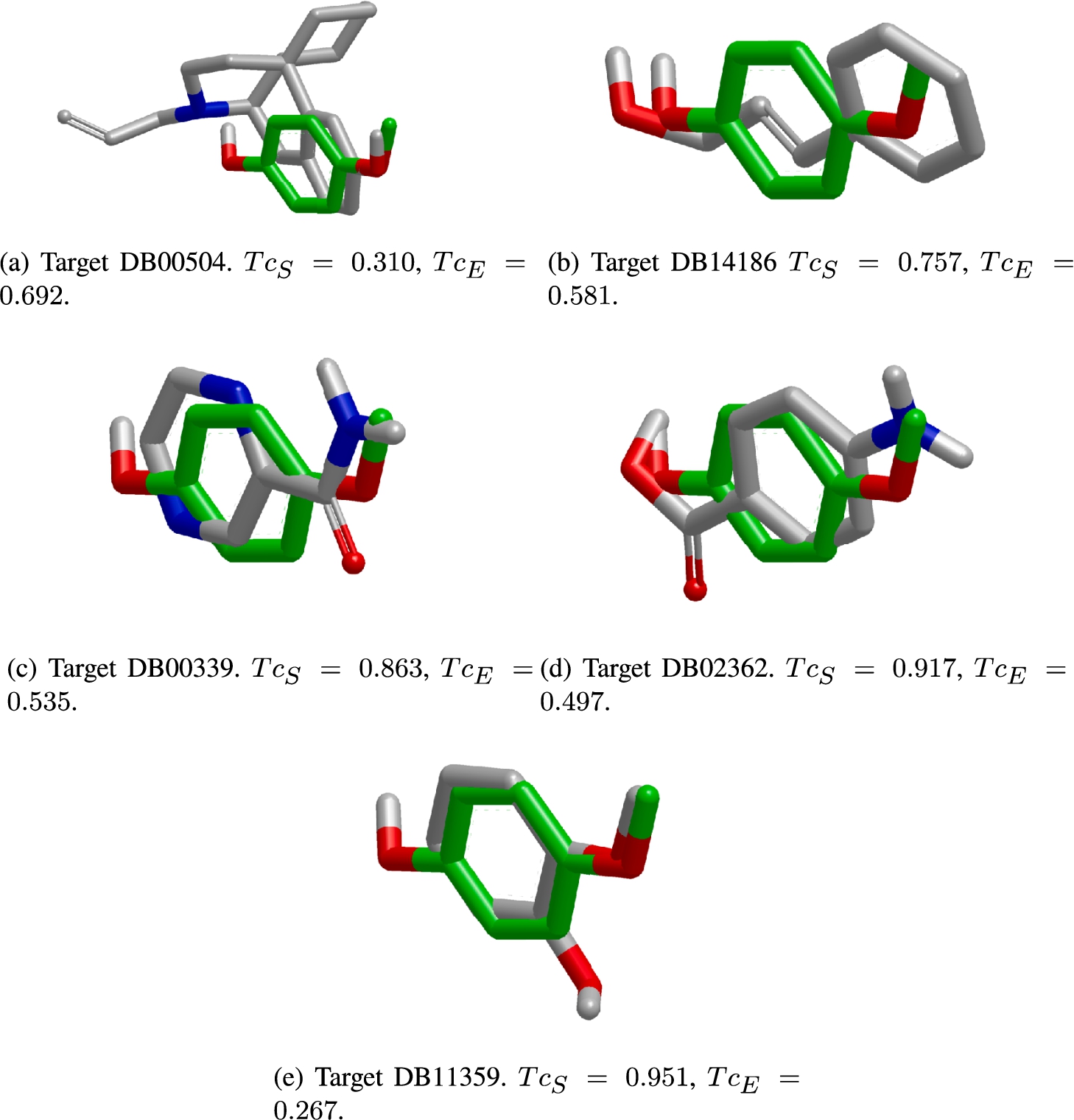
Fig. 11
The predicted compounds obtained for query DB09516 sorted by $T{c_{S}}$ in ascending order. All poses are found by the multi-objective tool. Note that subfigures (a) and (e) are also found with the single-objective methods Mono-Elec and Mono-Shape, respectively.
The information depicted in Fig.
10 is also summarized in Table
1. In such a table, we only include the predictions provided by
$W{F_{1}^{\textit{Mono-Shape}}}$,
$W{F_{1}^{\textit{Mono-Elec}}}$ and MultiPharm-DT, for the reasons previously argued. Furthermore, for the sake of completeness, the
$T{c_{S}}$ and
$T{c_{E}^{\textit{Eval}}}$ (resp.
$T{c_{E}}$ and
$T{c_{S}^{\textit{Eval}}}$) for
$W{F_{1}^{\textit{Mono-Shape}}}$ (resp.
$W{F_{1}^{\textit{Mono-Elec}}}$) are also mentioned. Notice that we do not provide any objective function value for MultiPharm-DT because many are available depending on the selected pose. Additionally, for each predicted target, a pose is obtained and represented using the VIDA (OpenEye Scientific Software,
2018) program (see Fig.
11).
Once the specific case is explained, we provide some statistics for the complete set of experiments. All the results appears in Table
2, which follows the same structure and information as Table
1.
As can be seen in the table, for 23 out of 32 cases, MultiPharm-DT obtains a set of predictions that include those obtained by $W{F_{1}^{\textit{Mono-Shape}}}$ and/or $W{F_{1}^{\textit{Mono-Elec}}}$. We remark in bold the coincidences in the predictions. For 14 out of those 23, it provides many more alternative compounds as part of the solution. Finally, for the remaining 9 queries, MultiPharm-DT obtains a set of predictions that only include one of the two predictions provided by $W{F_{1}^{\textit{Mono-Shape}}}$ or $W{F_{1}^{\textit{Mono-Elec}}}$. On average, MultiPharm-DT obtains 4.5 different predictions, which is a valuable number for a decision-maker.
It is important to remember that given a particular query, MultiPharm-DT generates a Pareto front. After that, the decision-makers have different poses to choose the one that best fits their interest, i.e. the one with a better balance between the scoring functions. On the contrary, the single-objective workflows only provide the pose that maximizes one descriptor, without considering the other one.
4.1 Comparison of Results for $W{F_{1}}$ and MultiPharm-DT
In this subsection, an exhaustive analysis of the results from Table
2 is performed, showing the values of
$T{c_{S}}$ and
$T{c_{E}}$ that could not be displayed in the table due to the large number of poses offered by MultiPharm-DT. Thus, 3 groups can be distinguished. In the first group there are 9 queries characterized by a high similarity value in both descriptors. In addition, MultiPharm-DT finds the same compounds as
$W{F_{1}^{\textit{Mono-Shape}}}$ and
$W{F_{1}^{\textit{Mono-Elec}}}$. Two examples are the DB00536 and DB01242 queries. The most similar target for the first one has similarity values of
$T{c_{S}}=0.967$ and
$T{c_{E}}=0.800$ while regarding the target for the second query, the values are
$T{c_{S}}=0.987$ and
$T{c_{E}}=0.919$ (Fig.
12).
Table 2
Results obtained for 32 query compounds from the rigid and validated database.
|
$W{F_{1}^{\textit{Mono-Shape}}}$ |
$W{F_{1}^{\textit{Mono-Elec}}}$ |
MultiPharm-DT |
| Query |
Target |
$T{c_{S}}$ |
$T{c_{E}^{\textit{Eval}}}$ |
Target |
$T{c_{S}^{\textit{Eval}}}$ |
$T{c_{E}}$ |
Compounds |
| DB00209 |
DB00427 |
0.726 |
−0.043 |
DB09076 |
0.816 |
0.385 |
DB09076, DB00990, DB08942, DB00894, DB00639, DB11699, DB00427, DB05812 |
| DB00259 |
DB09269 |
0.891 |
−0.084 |
DB14186 |
0.606 |
0.694 |
DB02362 |
| DB00354 |
DB04825 |
0.641 |
0.183 |
DB05246 |
0.437 |
0.343 |
DB05246, DB04825
|
| DB00359 |
DB00323 |
0.785 |
0.015 |
DB09280 |
0.557 |
0.277 |
DB00259, DB08981, DB04657, DB00323, DB04948, DB11699 |
| DB00481 |
DB06249 |
0.827 |
0.141 |
DB11153 |
0.357 |
0.055 |
DB06249, DB00458, DB00674, DB05239, DB04825 |
| DB00536 |
DB03904 |
0.967 |
0.508 |
DB03904 |
0.800 |
0.807 |
DB03904 |
| DB00696 |
DB06077 |
0.633 |
0.113 |
DB08903 |
0.345 |
0.409 |
DB08903, DB06077, DB00831, DB00354 |
| DB00758 |
DB00205 |
0.748 |
−0.025 |
DB00754 |
0.512 |
0.353 |
DB06802, DB00754, DB00674, DB01069, DB00564, DB13225, DB00794, DB01033, DB00420, DB14763 |
| DB00956 |
DB00318 |
0.966 |
0.692 |
DB00318 |
0.823 |
0.827 |
DB00318 |
| DB00998 |
DB13284 |
0.808 |
0.287 |
DB09269 |
0.521 |
0.421 |
DB09269, DB01069, DB13284, DB04840, DB11560, DB13501 |
| DB01192 |
DB00956 |
0.911 |
0.504 |
DB09214 |
0.581 |
0.437 |
DB00956, DB09214
|
| DB01242 |
DB00458 |
0.987 |
0.913 |
DB00458 |
0.919 |
0.985 |
DB00458 |
| DB01273 |
DB00909 |
0.844 |
0.087 |
DB00184 |
0.556 |
0.311 |
DB00909, DB00184, DB11823, DB11156, DB14763 |
| DB01336 |
DB00696 |
0.550 |
−0.008 |
DB09321 |
0.805 |
0.045 |
DB09131, DB09076, DB00526, DB09321, DB00696, DB00209, DB15328 |
| DB01419 |
DB06816 |
0.624 |
0.112 |
DB06767 |
0.390 |
0.072 |
DB01579, DB06816, DB14845, DB06767, DB00656, DB14506 |
| DB01608 |
DB00477 |
0.883 |
0.600 |
DB00477 |
0.631 |
0.830 |
DB00477 |
| DB04743 |
DB00427 |
0.789 |
−0.014 |
DB13801 |
0.615 |
0.392 |
DB08981, DB01007, DB06147, DB06413, DB00967, DB13801, DB09214 |
| DB06637 |
DB00544 |
0.961 |
−0.038 |
DB11359 |
0.785 |
0.829 |
DB13100, DB00763, DB00544, DB11359, DB00936 |
| db06799 |
DB00592 |
0.848 |
0.066 |
DB01367 |
0.232 |
0.472 |
DB01367, DB00431, DB00592
|
| DB09074 |
DB11799 |
0.688 |
−0.022 |
DB00956 |
0.476 |
0.274 |
DB11656, DB01259, DB11799, DB01224, DB00956, DB01012 |
| DB09241 |
DB14200 |
0.768 |
0.013 |
DB14180 |
0.654 |
0.073 |
DB09473, DB11183, DB11156, DB14200, DB00674, DB08797, DB01213, DB09513, DB14530, DB11221, DB14180, DB01273, DB11150, DB00805 |
| DB09280 |
DB00216 |
0.640 |
−0.020 |
DB09104 |
0.640 |
0.067 |
DB00216, DB11656, DB06077, DB09104, DB00469, DB00956, DB01012, DB00805 |
| DB09472 |
DB14499 |
0.895 |
0.978 |
DB14499 |
0.980 |
0.882 |
DB14499 |
| DB09516 |
DB11359 |
0.951 |
0.268 |
DB00504 |
0.682 |
0.299 |
DB00504, DB14186, DB00339, DB02362, DB11359
|
| DB11151 |
DB11153 |
1.000 |
0.991 |
DB11153 |
0.989 |
0.678 |
DB14506 |
| DB11336 |
DB00261 |
0.812 |
−0.004 |
DB00173 |
0.645 |
0.549 |
DB14186, DB01399, DB04657, DB13284, DB04840, DB00173, DB11156 |
| DB11363 |
DB11799 |
0.647 |
−0.174 |
DB06767 |
0.479 |
0.075 |
DB14723, DB01259, DB09280, DB06816, DB06767, DB09104, DB04868, DB13801, DB00469 |
| DB11496 |
DB08797 |
0.954 |
−0.129 |
DB00356 |
0.787 |
0.947 |
DB00356 |
| DB12404 |
DB00967 |
0.694 |
0.217 |
DB01283 |
0.635 |
0.389 |
DB11656, DB01283, DB01069, DB00967
|
| DB14702 |
DB09418 |
0.872 |
0.876 |
DB09418 |
0.948 |
0.670 |
DB09418 |
| DB14723 |
DB11799 |
0.650 |
0.128 |
DB00805 |
0.493 |
0.290 |
DB00998, DB11799, DB01283, DB00605, DB00469, DB00805
|
| DB14763 |
DB00205 |
0.828 |
0.334 |
DB00205 |
0.558 |
0.714 |
DB00205 |
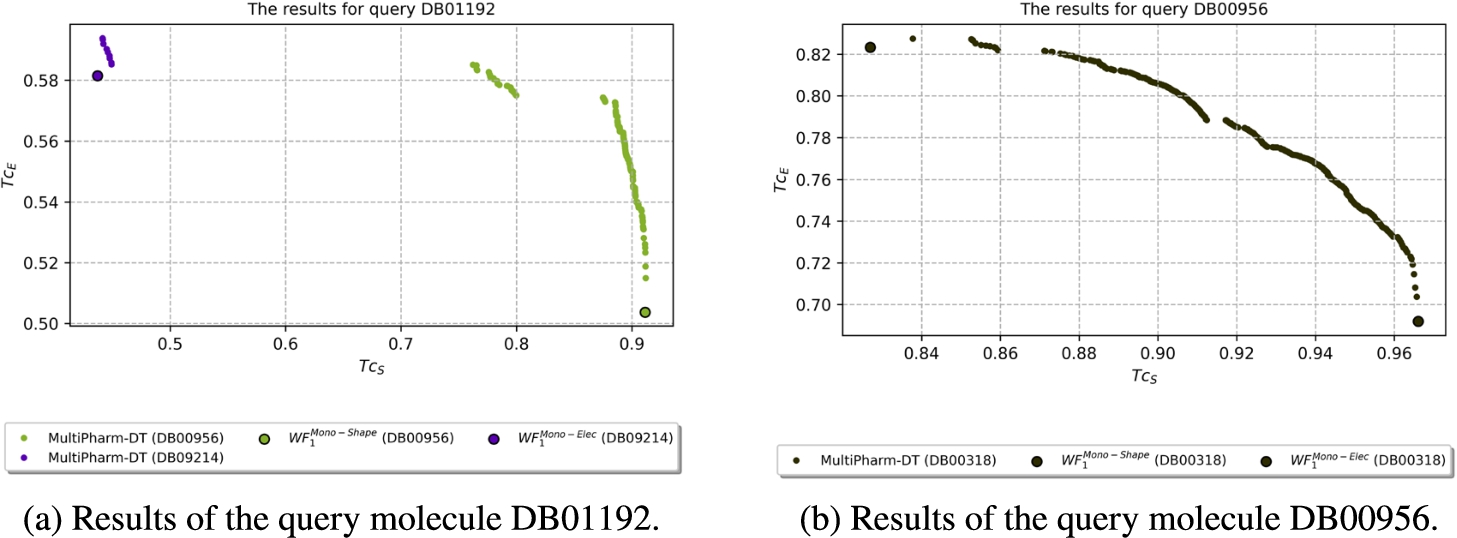
Fig. 12
Results where $W{F_{1}}$ and MultiPharm-DT return the same compounds.
The second group of compounds consists of 14 queries. It is characterized by MultiPharm finding more compounds in addition to those from
$W{F_{1}^{\textit{Mono-Shape}}}$ and
$W{F_{1}^{\textit{Mono-Elec}}}$. Figure
13 shows an example of 6 different queries. These queries are of great interest and are where the potential of MultiPharm-DT can truly be seen. Normally, the compounds found by
$W{F_{1}^{\textit{Mono-Shape}}}$ and
$W{F_{1}^{\textit{Mono-Elec}}}$ are very good in terms of the descriptor they optimize but not the other. However, with MultiPharm, in addition to getting these two compounds, it is possible to find a set where the balance of both descriptors is much better and by giving a slightly lower value to one descriptor, the similarity of the other improves considerably.
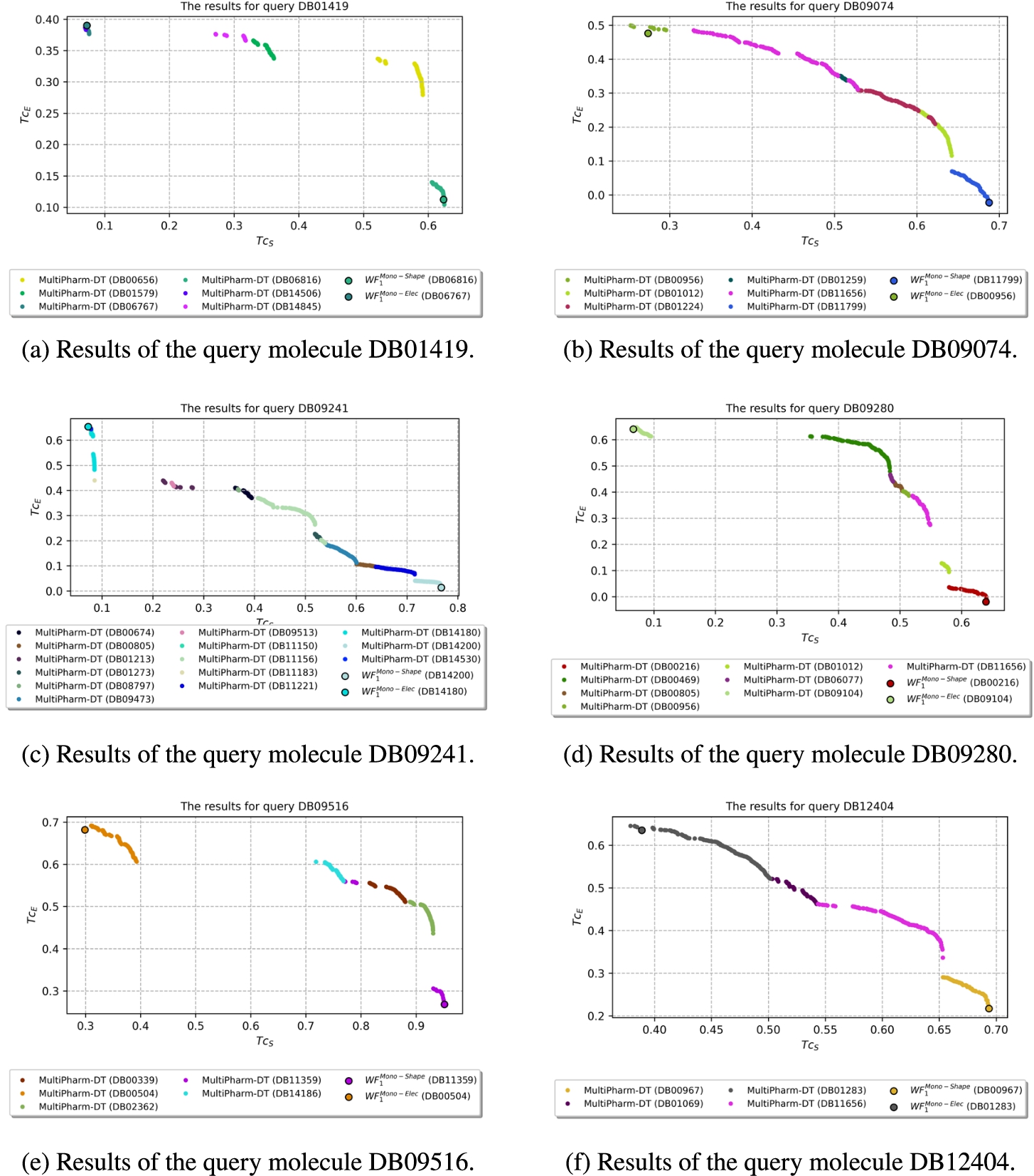
Fig. 13
Results where MultiPharm-DT get more compounds than with $W{F_{1}}$ methodology.
Finally, the third group consists of the remaining 9 queries, where MultiPharm finds several molecules, but among them, only one belongs either to
$W{F_{1}^{\textit{Mono-Shape}}}$ or
$W{F_{1}^{\textit{Mono-Elec}}}$. Four of these cases are represented in Fig.
14 and in fact, in Fig.
14(c) it can be seen that among the MultiPharm compounds, the DB13801 molecule, and not the DB00427 molecule, is found by
$W{F_{1}^{\textit{Mono-Elec}}}$.
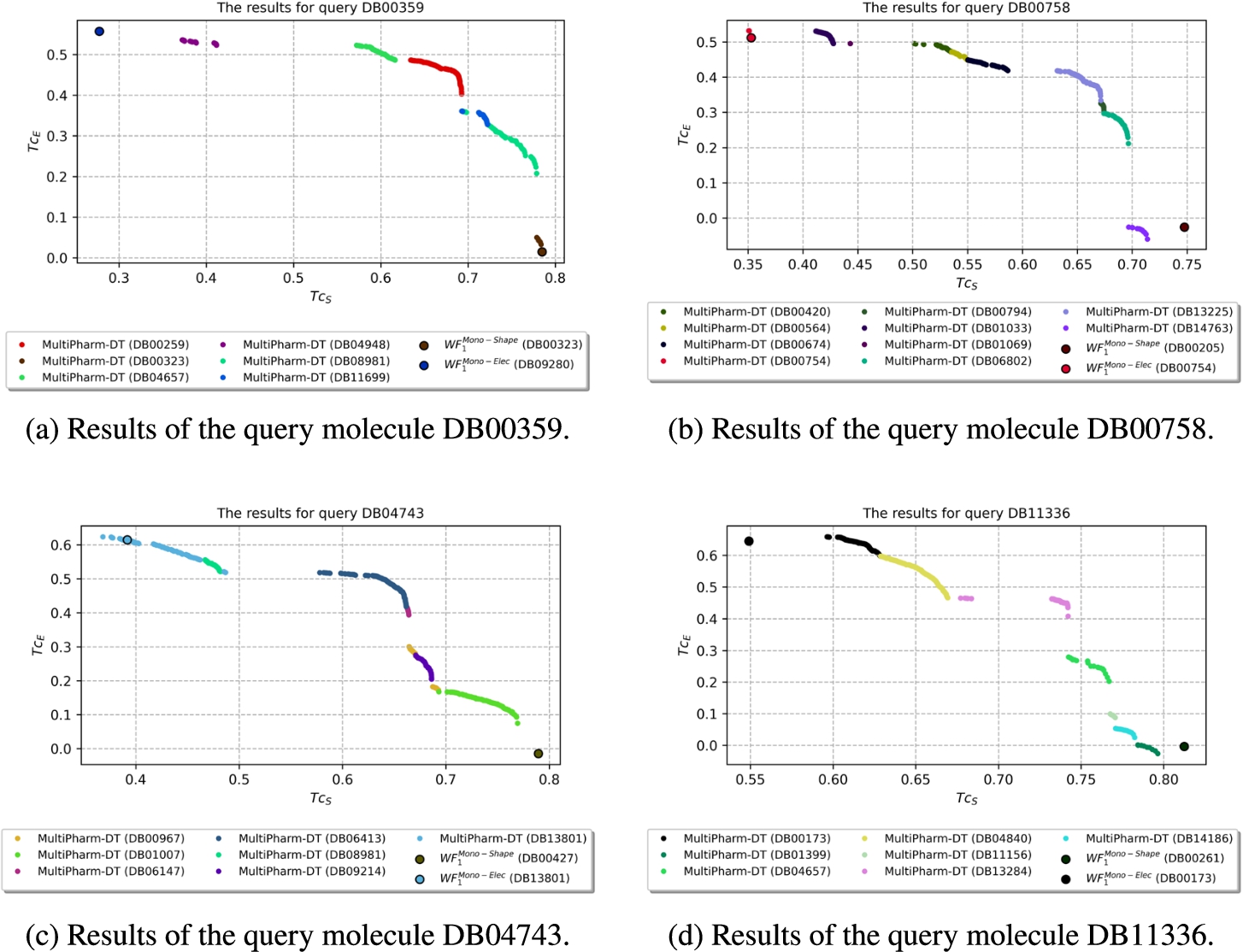
Fig. 14
Results where $W{F_{1}}$ and MultiPharm-DT return various different compounds.
In view of all the above results, it can be seen that this new methodology with MultiPharm-DT is able to widen the knowledge about the compounds to be selected since different poses with similarity values in both descriptors are known for each compound. Indeed, it improves the quality of the decisions and allows good compounds to be selected without the knowledge or action of a decision-maker, which greatly facilitates the appropriate choice of compounds.
Finally, as a general comment, it is important to mention that MultiPharm-DT provides more valuable predictions than the single-objective workflows, in terms of quantity and quality. Interestingly, this is in a single run without the expert’s participation. Furthermore, without considering the expert’s effort, obtaining the solutions for the single-objective methodology will cost 200,000 evaluations per workflow (a total of 400,000 evaluations) while MultiPharm-DT only requires 200,000. It is clear to see then that the advantages of using MultiPharm-DT, in terms of computing time, are sizeable.
5 Conclusions
In this work, we propose a new methodology for solving LBVS problems that require the optimization of several descriptors simultaneously. It is composed of a new tool, named MultiPharm, and a decision mechanism, named MultiPharm-DT. As a result, a set of predictions is obtained that can be directly offered to the decision-makers without any participation on their side.
This new method has been compared with the one currently being followed in the literature, which entails solving an optimization problem that includes a single descriptor and analysing the obtained solutions taking a second descriptor into account. This system requires a concerted effort on the part of the decision-maker to select the best compounds because they have to relate both descriptors via post-processing that becomes more costly as the number of compounds to be processed increases.
To test this new approach, a set of rigid, FDA-approved compounds has been used. In addition, shape and electrostatic similarities have been used although it is possible to use MultiPharm with a larger number of descriptors. As the results have shown, multi-objective solutions provide more information on compound similarity and a larger number of quality candidate compounds without performing any post-processing. In terms of computational time, multi-objective optimization is much faster than trying to replicate the same behaviour with single-objective.
In the future, new algorithms will be included in this novel tool so that the expert can select the most suitable algorithm for their problem. Following this line, new objective functions will be added to improve decision-making knowledge. Finally, it would be wise to employ the flexibility of the compounds so that they are not treated as rigid compounds, regardless of their nature.
6 Supplementary Material
Figures
The development of this work has generated a large number of results. Consequently, all the results obtained can be found in the compressed attachment, classified in 4 folders:
-
• All. Pareto fronts obtained by MultiPharm for all compounds.
-
• Clean. MultiPharm-DT solutions.
-
• Comparative. The MultiPharm-DT compounds and those obtained by $W{F_{1}}$ are shown.
-
• AllWorkflows. The MultiPharm-DT compounds and those obtained by $W{F_{1}}$, $W{F_{2}}$ and $W{F_{3}}$ are shown.
Software
-
• Project name: MultiPharm.
-
-
• Operating system(s): Windows, Linux and MacOS.
-
• Programming language: Java.
-
• License: Mozilla Public License 2.0.
-
• Any restrictions to use by non-academics: licence needed, contact with the authors.
Databases
The databases belong to their authors and access to them depends on any applicable restrictions.
Acknowledgements
This research was partially supported by the supercomputing infrastructure at Poznan Supercomputing Centre, the e-infrastructure program of the Research Council of Norway, the supercomputer centre at UiT – the Arctic University of Norway and by the computing facilities at the Extremadura Research Centre for Advanced Technologies (CETA–CIEMAT), funded by the European Regional Development Fund (ERDF). CETA–CIEMAT belongs to CIEMAT and the Government of Spain. The authors also acknowledge the computing resources and technical support provided by the Plataforma Andaluza de Bioinformática at the University of Málaga. Powered@NLHPC research was partially supported by the supercomputing infrastructure at the NLHPC (ECM-02).
References
Baize, S., Pannetier, D., Oestereich, L., Rieger, T., Koivogui, L., Magassouba, N.F., Soropogui, B., Sow, M.S., Këita, S., De Clerck, H., Tiffany, A., Dominguez, G., Loua, M., Traoré, A., Kolié, M., Malano, E.R., Heleze, E., Bocquin, A., Mély, S., Raoul, H., Caro, V., Cadar, D., Gabriel, M., Pahlmann, M., Tappe, D., Schmidt-Chanasit, J., Impouma, B., Diallo, A.K., Formenty, P., Van Herp, M., Günther, S. (2014). Emergence of Zaire Ebola virus disease in Guinea. New England Journal of Medicine, 371(15), 1418–1425.
Banegas-Luna, A.J., Cerón-Carrasco, J.P., Puertas-Martín, S., Pérez-Sánchez, H. (2019). BRUSELAS: HPC generic and customizable software architecture for 3D ligand-based virtual screening of large molecular databases. Journal of Chemical Information and Modeling, 59(6), 2805–2817.
Boström, J., Grant, J.A., Fjellström, O., Thelin, A., Gustafsson, D. (2013). Potent fibrinolysis inhibitor discovered by shape and electrostatic complementarity to the drug tranexamic acid. Journal of Medicinal Chemistry, 56(8), 3273–3280.
Böttcher, C.J.F., Bordewijk, P. (1978). Theory of Electric Polarization. Elsevier Science Limited, Amsterdam.
Brooijmans, N., Kuntz, I.D. (2003). Molecular recognition and docking algorithms. Annual Review of Biophysics and Biomolecular Structure, 32(1), 335–373.
Case, D.A., Cerutti, D.S., Cheatham, T.E., Darden, T.A., Duke, R.E., Giese, T.J., Gohlke, H., Goetz, A.W., Greene, D., Homeyer, N., Izadi, S., Kovalenko, A., Lee, T.S., LeGrand, S., Li, P., Lin, C., Liu, J., Luchko, T., Luo, R., Mermelstein, D., Merz, K.M., Monard, G., Nguyen, H., Omelyan, I., Onufriev, A., Pan, F., Qi, R., Roe, D.R., Roitberg, A., Sagui, C., Simmerling, C.L., Botello-Smith, W.M., Swails, J., Walker, R.C., Wang, J., Wolf, R.M., Wu, X., Xiao, L., York, D.M., Kollman, P.A. (2017).
AMBER. University of California, San Francisco.
Chu, S., Gochin, M. (2013). Identification of fragments targeting an alternative pocket on HIV-1 gp41 by NMR screening and similarity searching. Bioorganic & Medicinal Chemistry Letters, 23(18), 5114–5118.
Coello, C.A.C., Lamont, G.B. (2004). Applications of Multi-Objective Evolutionary Algorithms. World Scientific, Singapore.
Cui, L., Wang, Y., Liu, Z., Chen, H., Wang, H., Zhou, X., Xu, J. (2015). Discovering new acetylcholinesterase inhibitors by mining the Buzhongyiqi decoction recipe data. Journal of Chemical Information and Modeling, 55(11), 2455–2463.
Cui, Y., Geng, Z., Zhu, Q., Han, Y. (2017). Multi-objective optimization methods and application in energy saving. Energy, 125, 681–704.
Deb, K., Sindhya, K., Hakanen, J. (2016). Multi-objective optimization. In: Decision Sciences. CRC Press, United States, pp. 145–184.
Deb, K., Pratap, A., Agarwal, S., Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6(2), 182–197.
Durillo, J.J., Nebro, A.J. (2011). jMetal: a java framework for multi-objective optimization. Advances in Engineering Software, 42, 760–771.
Ferrández, M.R., Puertas-Martín, S., Redondo, J.L., Ivorra, B., Ramos, A.M., Ortigosa, P.M. (2019). High-performance computing for the optimization of high-pressure thermal treatments in food industry. The Journal of Supercomputing, 75(3), 1187–1202.
Grant, J.A., Pickup, B.T. (1995). A Gaussian description of molecular shape. The Journal of Physical Chemistry, 99(11), 3503–3510.
Grant, J.A., Gallardo, M.A., Pickup, B.T. (1996). A fast method of molecular shape comparison: a simple application of a gaussian description of molecular shape. Journal of Computational Chemistry, 17(14), 1653–1666.
Halgren, T.A. (1995). Potential energy functions. Current Opinion in Structural Biology, 5(2), 205–210.
Hamza, A., Wei, N.-N., Zhan, C.-G. (2012). Ligand-based virtual screening approach using a new scoring function. Journal of Chemical Information and Modeling, 52(4), 963–974.
Hawkins, P.C.D.D., Skillman, A.G., Nicholls, A. (2007). Comparison of shape-matching and docking as virtual screening tools. Journal of Medicinal Chemistry, 50(1), 74–82.
Hevener, K.E., Mehboob, S., Su, P.-C., Truong, K., Boci, T., Deng, J., Ghassemi, M., Cook, J.L., Johnson, M.E. (2012). Discovery of a novel and potent class of F. Tularensis enoyl-reductase (FabI) inhibitors by molecular shape and electrostatic matching. Journal of Medicinal Chemistry, 55(1), 268–279.
Hughes, J.P., Rees, S., Kalindjian, S.B., Philpott, K.L. (2011). Principles of early drug discovery. British Journal of Pharmacology, 162(6), 1239–1249.
Kaoud, T.S., Yan, C., Mitra, S., Tseng, C.-C., Jose, J., Taliaferro, J.M., Tuohetahuntila, M., Devkota, A., Sammons, R., Park, J., Park, H., Shi, Y., Hong, J., Ren, P., Dalby, K.N. (2012). From in silico discovery to intracellular activity: targeting JNK-protein interactions with small molecules. ACS Medicinal Chemistry Letters, 3(9), 721–725.
Kar, S., Roy, K. (2013). How far can virtual screening take us in drug discovery? Expert Opinion on Drug Discovery, 8(3), 245–261.
Karelson, M. (2000). Molecular descriptors in QSAR/QSPR. Wiley-Interscience, New York.
Kim, E.-S.S., Cho, H., Lim, C., Lee, J.-Y.Y., Lee, D.-I.I., Kim, S., Moon, A., Kim, E.-S.S., Cho, H., Lim, C., Lee, J.-Y.Y., Lee, D.-I.I., Moon, A. (2015). A natural piper-amide-like compound NED-135 exhibits a potent inhibitory effect on the invasive breast cancer cells. Chemico-Biological Interactions, 237, 58–65.
Kim, Y.C., Dema, B., Reyes-Sandoval, A. (2020). COVID-19 vaccines: breaking record times to first-in-human trials. npj Vaccines, 5(1), 34.
Kossmann, B.R., Abdelmalak, M., Lopez, S., Tender, G., Yan, C., Pommier, Y., Marchand, C., Ivanov, I. (2016). Discovery of selective inhibitors of Tyrosyl-DNA phosphodiesterase 2 by targeting the enzyme DNA-binding cleft. Bioorganic and Medicinal Chemistry Letters, 26(14), 3232–3236.
Kumar, A., Zhang, K.Y.J. (2016). Application of shape similarity in pose selection and virtual screening in CSARdock2014 exercise. Journal of Chemical Information and Modeling, 56(6), 965–973.
Leelananda, S.P., Lindert, S. (2016). Computational methods in drug discovery. Beilstein Journal of Organic Chemistry, 12, 2694–2718.
Li, H., Zhang, Q. (2008). Multiobjective optimization problems with complicated Pareto sets, MOEA/D and NSGA-II. IEEE Transactions on Evolutionary Computation, 13(2), 284–302.
Lo, Y.-C., Senese, S., Damoiseaux, R., Torres, J.Z. (2016). 3D chemical similarity networks for structure-based target prediction and scaffold hopping. ACS Chemical Biology, 11(8), 2244–2253.
López-Ramos, M., Perruccio, F. (2010). HPPD: ligand- and target-based virtual screening on a herbicide target. Journal of Chemical Information and Modeling, 50(5), 801–814.
Lu, I.-L., Huang, C.-F., Peng, Y.-H., Lin, Y.-T., Hsieh, H.-P., Chen, C.-T., Lien, T.-W., Lee, H.-J., Mahindroo, N., Prakash, E., et al.(2006). Structure-based drug design of a novel family of PPARgamma partial agonists: virtual screening, X-ray crystallography, and in vitro/in vivo biological activities. Journal of Medicinal Chemistry, 49(9), 2703–2712.
Maccari, G., Jaeger, T., Moraca, F., Biava, M., Flohé, L., Botta, M. (2011). A fast virtual screening approach to identify structurally diverse inhibitors of trypanothione reductase. Bioorganic and Medicinal Chemistry Letters, 21(18), 5255–5258.
Marler, R.T., Arora, J.S. (2004). Survey of multi-objective optimization methods for engineering. Structural and Multidisciplinary Optimization, 26(6), 369–395.
Mehta, P., McAuley, D.F., Brown, M., Sanchez, E., Tattersall, R.S., Manson, J.J. (2020). COVID-19: consider cytokine storm syndromes and immunosuppression. The Lancet, 395(10229), 1033–1034.
Morris, G.M., Lim-Wilby, M. (2008). Molecular docking. In: Kukol, A. (Ed.), Molecular Modeling of Proteins, Vol. 443. Humana Press, Clifton, N.J., pp. 365–382.
Nicolaou, C.A., Brown, N. (2013). Multi-objective optimization methods in drug design. Drug Discovery Today: Technologies, 10(3), 427–435.
Pagadala, N.S., Syed, K., Tuszynski, J. (2017). Software for molecular docking: a review. Biophysical Reviews, 9(2), 91–102.
Pardalos, P.M., Žilinskas, A., Žilinskas, J. (2017). Non-Convex Multi-Objective Optimization. Springer International Publishing, New York.
Petersen, L.R., Jamieson, D.J., Powers, A.M., Honein, M.A. (2016). Zika virus. New England Journal of Medicine, 374(16), 1552–1563.
Puertas-Martín, S., Redondo, J.L., Ortigosa, P.M., Pérez-Sánchez, H. (2019). OptiPharm: an evolutionary algorithm to compare shape similarity. Scientific Reports, 9(1), 1398.
Puertas-Martín, S., Redondo, J.L., Pérez-Sánchez, H., Ortigosa, P.M. (2020). Optimizing electrostatic similarity for virtual screening: a new methodology. Informatica, 31(4), 821–839.
Real, R., Vargas, J.M. (1996). The probabilistic basis of Jaccard’s index of similarity. Systematic Biology, 45(3), 380–385.
Stark, J.L., Powers, R. (2011). Application of NMR and molecular docking in structure-based drug discovery.
NMR of Proteins and Small Biomolecules, 1–34.
Tanrikulu, Y., Krüger, B., Proschak, E. (2013). The holistic integration of virtual screening in drug discovery. Drug Discovery Today, 18(7-8), 358–364.
Tapia, M.G.C., Coello, C.A.C. (2007). Applications of multi-objective evolutionary algorithms in economics and finance: a survey. In: 2007 IEEE Congress on Evolutionary Computation. IEEE, Singapore, pp. 532–539.
Tollman, P. (2001). A Revolution in R & D: How Genomics and Genetics are Transforming the Biopharmaceutical Industry. Boston Consulting Group, Boston, US.
Tresadern, G., Bemporad, D., Howe, T. (2009). A comparison of ligand based virtual screening methods and application to corticotropin releasing factor 1 receptor. Journal of Molecular Graphics and Modelling, 27(8), 860–870.
Wang, Z., Lu, Y., Seibel, W., Miller, D.D., Li, W. (2009). Identifying novel molecular structures for advanced melanoma by ligand-based virtual screening. Journal of Chemical Information and Modeling, 49(6), 1420–1427.
Wishart, D.S., Feunang, Y.D., Guo, A.C., Lo, E.J., Marcu, A., Grant, J.R., Sajed, T., Johnson, D., Li, C., Sayeeda, Z., Assempour, N., Iynkkaran, I., Liu, Y., Maciejewski, A., Gale, N., Wilson, A., Chin, L., Cummings, R., Le, D., Pon, A., Knox, C., Wilson, M. (2018). DrugBank 5.0: a major update to the DrugBank database for 2018. Nucleic Acids Research, 46(D1), 1074–1082.
Woodring, J.L., Bachovchin, K.A., Brady, K.G., Gallerstein, M.F., Erath, J., Tanghe, S., Leed, S.E., Rodriguez, A., Mensa-Wilmot, K., Sciotti, R.J., Pollastri, M.P. (2017). Optimization of physicochemical properties for 4-anilinoquinazoline inhibitors of trypanosome proliferation. European Journal of Medicinal Chemistry, 141, 446–459.
Yan, X., Li, J., Liu, Z., Zheng, M., Ge, H., Xu, J. (2013). Enhancing molecular shape comparison by weighted Gaussian functions. Journal of Chemical Information and Modeling, 53(8), 1967–1978.
Zhang, Q., Li, H. (2007). MOEA/D: a multiobjective evolutionary algorithm based on decomposition. IEEE Transactions on Evolutionary Computation, 11(6), 712–731.
Zitzler, E., Laumanns, M., Thiele, L. (2001). SPEA2: improving the strength pareto evolutionary algorithm.
Evolutionary Methods for Design Optimization and Control with Applications to Industrial Problems, 95–100.

