Abstract
Machine Translation has become an important tool in overcoming the language barrier. The quality of translations depends on the languages and used methods. The research presented in this paper is based on well-known standard methods for Statistical Machine Translation that are advanced by a newly proposed approach for optimizing the weights of translation system components. Better weights of system components improve the translation quality. In most cases, machine translation systems translate to/from English and, in our research, English is paired with a Slavic language, Slovenian. In our experiment, we built two Statistical Machine Translation systems for the Slovenian-English language pair of the Acquis Communautaire corpus. Both systems were optimized using self-adaptive Differential Evolution and compared to the other related optimization methods. The results show improvement in the translation quality, and are comparable to the other related methods.
1 Introduction
A translation is a challenging and creative act. A Machine Translation (MT) (Dorr
et al.,
1999; Bungum and Gambäck,
2010) can ease the work of a translator, or even replace it as a rough translation, or as a draft which serves as an aid to the translation. Nowadays, Statistical Machine Translation (SMT) (Lopez,
1993; Specia,
2010; Bungum and Gambäck,
2010) is by far the most studied and used MT method (Albat,
2007). SMT was based originally on single words, but has now progressed to the level of word sequences, called phrases. Currently the most successful SMT approach is phrase-based translation (Specia,
2010).
Translations in SMT are generated on the basis of statistical models, i.e. translation and language models, where different models’ weights provide various translations. The translation model is used to translate words or phrases from the source language to the target language text, and the language model ensures that the translated text is more fluent. These models know nothing about each other, so the problem appears to be how to find a set of weights that would provide the best translation quality. This problem can be regarded as an optimization problem. Optimization refers to the process of finding the optimal models’ weights, where the optimal weights are those which maximize the translation quality.
The translation quality is measured using translation error metrics, and the Bilingual Evaluation Understudy (BLEU) (Papineni
et al.,
2002) metric is one of the more popular and inexpensive automated metrics for achieving a high correlation with human judgments of quality (Callison-Burch
et al.,
2006). It is worth noting that MT evaluation is a complex problem, and that methods such as BLEU are not without criticism.
The quality of MT depends on the languages. For some language pairs, SMT brings good results, especially if the target language is English. The morphological richness of languages has a direct impact on the quality. Significantly lower quality is obtained for language pairs when translating from English into a morphologically rich language. Agglutinative target languages (Hungarian or Turkish) are even more problematic for statistical approaches. Although the approach proposed in this paper is general, our research was done on a difficult language pair where one language is highly analytical (English) and the other, morphologically rich (Slovenian) (Sepesy Maučec and Brest,
2010).
Numerous algorithms exist for solving general optimization problems with real valued numbers. One of these algorithms is the Differential Evolution algorithm (DE) (Storn and Price,
1997; Price
et al.,
2005; Neri and Tirronen,
2010; Das
et al.,
2016), which is a simple and effective algorithm for global optimization. It has been proved to be efficient at solving different optimization problems involving real valued numbers which interact non-linearly with each other (Das and Suganthan,
2011; Das
et al.,
2011; Zhou
et al.,
2011; Bošković
et al.,
2011; Glotić and Zamuda,
2015; Mlakar
et al.,
2014; Bošković and Brest,
2016). The DE algorithm is an evolutionary based algorithm where each individual from the population is described as a vector of models’ weights.
Currently, the more popular way to find optimal models’ weights is to use Minimum Error Rate Training (MERT) (Och,
2003; Bertoldi
et al.,
2009) and, in this paper, we used the jDE (Brest
et al.,
2006a) algorithm where each individual has its own crossover rate and scale factor. The authors in Brest
et al. (
2006a), Zhang and Sanderson (
2009) observed through experiments that the efficiency of the DE algorithm is improved when control parameters respond to the evolution with a self-adapting mechanism. This enables the jDE algorithm to solve our problem more efficiently and reduce the number of main control parameters. Translations are then evaluated using the BLEU metric.
Recently, Evolutionary Algorithms have attracted increasing attention for enhancing the performance of Natural Language Processing (NLP) (Bungum and Gambäck,
2010) techniques. NLP is a field concerned with the interaction between computer and human using natural language – spoken (Du Bois
et al.,
2005; Kasparaitis and Anbinderis,
2014) and written (Koehn,
2005; Steinberger
et al.,
2006). In this paper, the focus is on the written language.
The SMT system should produce translations in a reasonable time. Some MT applications are working almost in real-time. Since the training and optimization processes are both a part of an offline training where we have a static corpus and no time constraints, the training time is not so relevant. Once the SMT system is built it is ready to use, and then the actual translating depends mostly on the size of the text which is to be translated.
The main goal of this paper is to find the optimal models’ weights. The work presented in this paper is different from previous studies in several aspects. Firstly, this is the first study of using the jDE algorithm to optimize models’ weights within SMT. We believe that the self-adaptive nature of the jDE algorithm in comparison to a DE algorithm improves the efficiency of the optimization algorithm. Secondly, the evaluation is usually based on only one optimizer run (Koehn
et al.,
2009; Bojar
et al.,
2015). In this paper, each optimizer (MERT, MIRA, DE, and jDE) was run many times, and the results were compared statistically to meet the conventional significance level.
The remainder of the paper is organized as follows. Section
2 presents some background on the related work. Our experiment is described in Section
3, and the results are presented in Section
4, along with the statistical analysis using a MultEval (Clark
et al.,
2011) tool. We conclude this paper with Section
5 where we give our opinion about the obtained results and future work.
2 Background
The availabilities of linear models and discriminative optimization algorithms have been a huge boon to SMT, allowing this field to move beyond the constraints of generative noisy channels (Och and Ney,
2002). The ability to optimize these models according to an error metric has become a standard assumption in SMT, due to the wide-spread adoption of MERT. The problems with MERT can be addressed through the use of surrogate loss functions. The Margin Infused Relaxed Algorithm (MIRA) (Watanabe
et al.,
2007; Chiang
et al.,
2008,
2009; Cherry and Foster,
2012; Hasler
et al.,
2011) employs a structured hinge loss. In order to improve generalization, the average of all weights seen during learning is used on unseen data. Chiang
et al. (
2008) took advantage of the MIRA to modify each update to suit SMT better. Pairwise Ranking Optimization (PRO) (Hopkins and May,
2011) aims to handle large feature sets inside the traditional MERT architecture. This architecture is desirable, as most groups have infrastructures to
n-best decode their tuning sets in parallel. A simple approach of using Evolutionary Algorithms in SMT was shown in our previous work (Dugonik
et al.,
2014).
SMT deals with mapping sentences in one natural language (source) into another natural language (target). This process can be represented as a stochastic process. There are many SMT variants, depending on how the translation is modelled. Commonly, we are translating the text sentence by sentence. We want to find the best possible translation
${e^{\ast }}$ out of all possible translations
e for a given source sentence
f. The system selects the translation with the highest probability
$P(e|f)$. Applying the Bayes rule, the probability
$P(e|f)$ is decomposed into probabilities
$P(f|e)$,
$P(e)$ and
$P(f)$:
The denominator
$P(f)$ does not influence argmax and can be disregarded.
This approach has three major aspects:
-
• Translation model $P(f|e)$: specifies the set of possible translations for some target sentence and assigns probabilities to these translations.
-
• Language model $P(e)$: models the fluency of the proposed target sentence and assigns distributions over strings (higher probabilities are assigned to sentences which are more representative of a natural language).
-
• Search process (argmax operation): this process is called decoding, and its job is to find possible target translations.
SMT systems usually decompose entire sentences into a sequence of strings called phrases. These phrases are not linguistic phrases but phrases found using statistical methods from a corpus. The SMT system looks for general patterns (
n-grams) which appear in everyday language. An
n-gram is a contiguous sequence of
n items from a given sequence of text or speech. In the phrase-based model, the source sentence
f is broken down into
I phrases
$\bar{{f_{i}}}$, and each source phrase
$\bar{{f_{i}}}$ is translated into a target phrase
$\bar{{e_{i}}}$. From the produced translations it can be seen that the target sentence is not fluent, hence the idea to introduce weights and scale the contribution of each model:
We can generalize the setup of the SMT system to many different models, and we can scale the contribution of each of them:
where
${h_{1}},\dots ,{h_{r}}$ are the models of a search algorithm, e.g. translation model, language model, reordering model, word penalty, etc.,
r denotes the number of models, and
${\lambda _{i}},\dots ,{\lambda _{r}}$ are models’ weights. The weights are scaling factors, and are optimized with a loss function which evaluates the translation quality, for example, the BLEU evaluation metric. These models are trained separately and then combined, assuming that they are independent of each other. But the contributions of different models influence each other. The problem is to find a set of weights that will provide the best translation quality:
The area of possible weight settings is too large for the exploration of all possible values. Usually a tuning set is used to optimize weights. The simplest method is to try out with a large number of possible settings and pick what works best. Assuming we wish to optimize our decoder’s BLEU score, the natural objective of learning would be to find such $\boldsymbol{\lambda }={\boldsymbol{\lambda }_{\boldsymbol{i}}},\dots ,{\boldsymbol{\lambda }_{\boldsymbol{r}}}$ that the BLEU score is maximal.
Optimization refers to the process of finding the optimal weights for this linear model where optimal weights are those which maximize the translation quality on the tuning set. During decoding, the decoder scores translations using a linear model. The features of this linear model are the probabilities of multiple models. Each feature contributes information over one aspect of the characteristics of a good translation, e.g. the language model ensures that the translation is more fluent. Each feature can be given a weight that sets its importance. We see the problem as an optimization problem that will be tackled using the jDE algorithm.
2.1 Differential Evolution
The DE algorithm is a simple and effective evolutionary algorithm for global optimization. This algorithm is a population-based algorithm, and uses the differences between individuals. These differences are defined with simple and fast arithmetic operations. The DE algorithm uses a population
P of
Np individuals, where each individual is represented as a
D-dimensional vector. The elements of the vector are real-valued numbers from specified intervals. These intervals and the dimension (
D) are determined by the problem being solved. The following control parameters are specified by the user and affect the behaviour of the algorithm:
-
• mutation parameter (F),
-
• crossover parameter (Cr),
-
• population size (Np).
These parameters are fixed during the evolutionary process. If nothing is known about the problem, the initial population is chosen randomly:
where
min and
max are the lower and upper bounds determined by the problem. The function
$\mathit{rand}(\mathit{min},\mathit{max})$ returns a uniformly distributed random number within the range
$[\mathit{min},\mathit{max})$.
The crucial idea behind the DE algorithm is a strategy for generating new individuals. Based on the type of problem we can choose between various strategies of the DE algorithm which determine the mutation and crossover methods. The classic DE algorithm, shown in Algorithm
1, uses the
rand/1/
bin strategy. The algorithm generates new individual
${\mathbf{m}_{i}}$ by adding a weighted difference vector between two individuals from the population to a third individual from the population:
The integers
$r1$,
$r2$ and
$r3$ are chosen randomly from the interval
$\{1,\textit{Np}\}$ and are different from each other and the current index
i. F is a constant factor which controls the amplification of the differential variation.
Cr is a crossover probability which controls the fraction of parameters that are copied from the mutant vector
${\mathbf{m}_{i}}$. The function
$\textit{rand}(0,1)$ returns a uniformly distributed random number within the range [0,1). The integer value
jrand is the index of a randomly taken individual from the mutant vector
${\mathbf{m}_{i}}$ to ensure that the newly generated individual
${\mathbf{c}_{i}}$ does not duplicate
${\mathbf{x}_{i}}$. If the newly created individual
${\mathbf{c}_{i}}$ yields better fitness value than the current individual
${\mathbf{x}_{i}}$, then
${\mathbf{c}_{i}}$ survives into the next generation. The process of mutation, crossover, and selection is repeated until the optimum is located or a prespecified termination criterion is satisfied. In addition, the best individual is evaluated for every generation
g in order to keep track of the progress that is made during the optimization process.
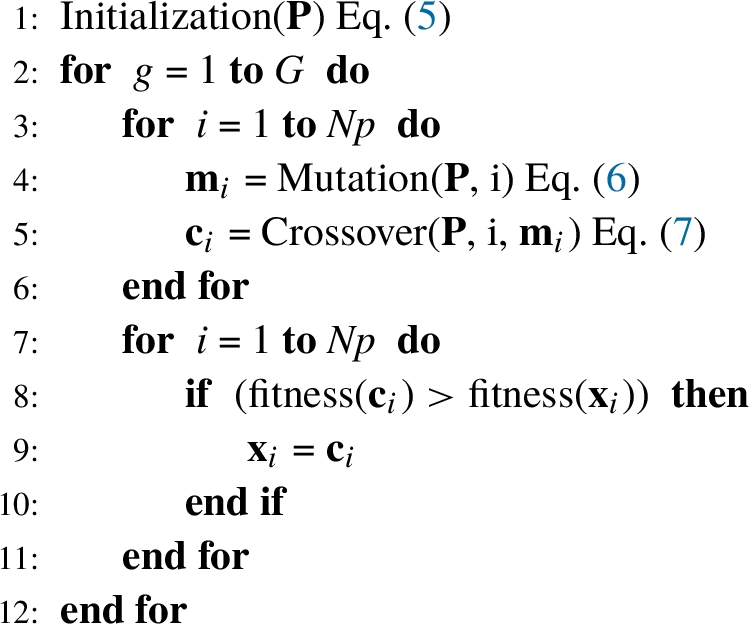
Algorithm 1
The Differential Evolution Algorithm
2.2 jDE Algorithm
The classic DE algorithm has three control parameters,
F,
$Cr$ and
$Np$, that are fixed during the evolution. They are usually problem-dependent, and with different values during the evolutionary process, allow the algorithm to perform better. For this purpose, the jDE algorithm (Brest
et al.,
2006a,
2006b) recalculates two control parameters using the following equations:
${F_{\mathit{min}}}=0.1$ and
${F_{\mathit{max}}}=0.9$ determine the lower and upper bounds for the parameter
F, and the function
$\mathit{rand}()$ returns a uniform random value within the interval
$[0,1]$.
${\tau _{1}}$ and
${\tau _{2}}$ represent probabilities for recalculating
F and
$Cr$.
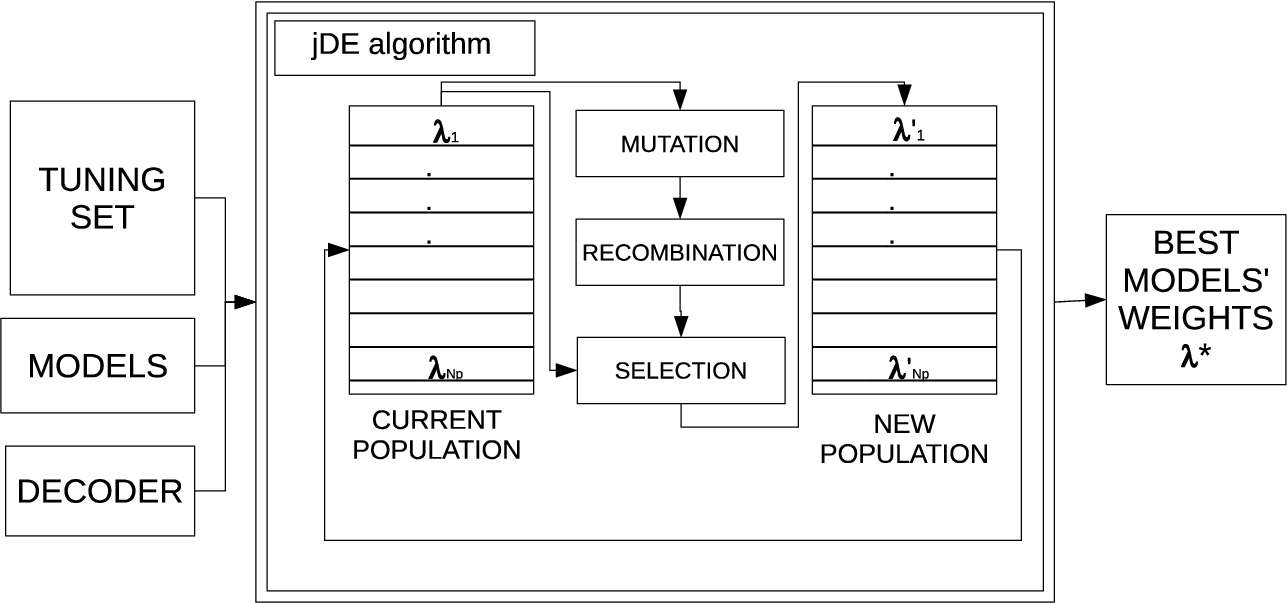
Fig. 1
The optimization process for finding the best models’ weights using the jDE algorithm.
As seen in Fig.
1, the jDE algorithm has three inputs: The tuning set, models, and the Moses decoder (Koehn
et al.,
2007). The output of the algorithm is the best models’ weights
${\boldsymbol{\lambda }^{\ast }}$. The tuning set consists of a source and target sentences. This algorithm is a population-based algorithm, and the population
P consists of individuals where an individual
$\boldsymbol{\lambda }$ is represented by the vector of models’ weights:
$\boldsymbol{\lambda }=\{{\lambda _{1}},{\lambda _{2}},\dots ,{\lambda _{D}}\}$. In the initial population, weights in vectors are generated randomly between lower (
$min$) and upper (
$max$) bounds, and the scale factor
F and crossover rate
$Cr$ are set initially to 0.5 and 0.9, respectively. The algorithm generates a new trial vector for each vector in the population using mutation and crossover, and the
F or
Cr are recalculated if certain conditions are met. During the selection, this trial vector is then compared to the current vector in the population. The trial vector survives to the next generation if the trial vector is better than the current vector from the population. In order to evaluate a vector, the SMT system translates the source sentences into the target sentences using weights from this vector. The translated sentences are then compared with the target sentences from the tuning set using the BLEU metric, which returns a real number where a higher number implies greater similarity. The algorithm repeats this process until it reaches the maximum number of generations. In the last generation, the best individual is taken from the population and its weights are used for translating in real-time.
3 Experiment
In our experiment, we built two SMT systems for translating from Slovenian to English and vice versa. All of the codes and data necessary to begin work on an SMT system are available as a public source, Moses toolkit (Koehn
et al.,
2007), and the freely available JRC-Acquis parallel corpora (Steinberger
et al.,
2006) used as a benchmark in the SMT community (Koehn
et al.,
2009).
Moses toolkit is an open-source toolkit for SMT which contains the SMT decoder and a wide variety of tools for training, tuning and applying the system to many translation tasks. The SMT system is frequency-based, where frequencies are trained on translated texts that are preprocessed and collected into a parallel corpus. Parallel corpora vary in size tremendously. Most of the language pairs, for example, Finnish to Irish, will have a far smaller parallel corpora available. Parallel corpora exist for all European languages and for many other pairs, such as Mandarin to English. However, one of the major challenges faced is the scarce availability of parallel corpora, so we need some methods for creating parallel corpora automatically and efficiently because manual creation of a large parallel corpus can be very costly in terms of effort and time. Currently, parallel corpora are an object of interest.
Table 1
The aligned and selected JRC ACQUIS corpus.
|
Aligned |
Selected |
|
Slovenian |
English |
Slovenian |
English |
| Sentences |
1,170,663 |
700,000 |
| Words |
25,964,572 |
30,382,264 |
14,262,144 |
17,093,472 |
The used JRC-Acquis corpus must not be seen as a legal reference corpus. Instead, the purpose of the JRC-Acquis is to provide a large parallel corpus of documents for (computational) linguistics research purposes. To align the sentences in a source and language text automatically, we used the HunAlign aligner (Varga
et al.,
2005). After successful aligning, we selected 700,000 sentences which were used in our experiment. The exact size of the corpora is shown in Table
1. The used corpus was tokenized, lowercased, and sentences longer than 80 words were removed. It is important to obtain a representative sample as much as is possible. The translation quality of neighbouring sentences correlates positively, therefore, we chose sentences from different parts of the corpus to create the training and test sets.
The training set was divided further into training and tuning sets. Sentences shorter than 8 and longer than 60 words were removed from the tuning and test sets. The final sizes of all sets are seen in Table
2. The language model is estimated from a monolingual corpora, typically using relative frequency estimates which are then smoothed. For languages such as English, typically, billions and more words are used. Deploying such large models can pose significant engineering challenges. This is because the language model can easily be so large that it will not fit into the memory of conventional machines. Also, the language model can be queried millions of times when translating sentences, which precludes storing it on disk.
Table 2
Divided JRC ACQUIS corpus.
|
Slovenian ↔ English |
|
Train |
Tuning |
Test |
| Sentences |
560,133 |
644 |
1,987 |
| Words |
11,614,065 |
13,213,582 |
15,065 |
16,944 |
70,245 |
74,922 |
For each language (Slovenian and English) we built language and translation models. The language model was a 5-gram language model with improved Kneser-Ney smoothing using the IRST Language Modeling (IRSTLM) (Federico
et al.,
2008) toolkit. The translation models were built using
grow-diag-final-and alignment from GIZA++ (Och and Ney,
2000). We also extended both SMT systems with four advanced models: The distortion model, the lexicalized reordering model (
msd-bidirectional-fe reordering), the word and phrase penalty models. Each SMT system had six models and 14 weights:
-
• 1 weight for the word penalty model (${\lambda _{1}}$),
-
• 1 weight for the phrase penalty model (${\lambda _{2}}$),
-
• 4 weights for the translation model (${\lambda _{3}},{\lambda _{4}},{\lambda _{5}},{\lambda _{6}}$),
-
• 6 weights for the lexical reordering model (${\lambda _{7}},{\lambda _{8}},{\lambda _{9}},{\lambda _{10}},{\lambda _{11}},{\lambda _{12}}$),
-
• 1 weight for the distortion model (${\lambda _{13}}$), and
-
• 1 weight for the language model (${\lambda _{14}}$).
The translation quality is considered to be the correspondence between a machine and professional human (reference) translation. There are many metrics, i.e. BLEU, Translation Error Rate (TER) (Snover
et al.,
2006), Word Error Rate (WER) (Saon
et al.,
2006), etc. The more popular metric in SMT is the BLEU metric, because it is quick, inexpensive, language-independent, and one of the first metrics to achieve a high correlation with human judgments. The central idea behind BLEU is that the closer a machine translation is to a reference translation, the better it is. The primary task in the BLEU metric is to compare the
n-grams of the machine translation with the
n-grams of the reference translation and count the number of matches which are position-independent. The foundation of the BLEU metric is the modified
n-gram precision measure. This captures two aspects of the translation: Adequacy and fluency. The unigram scores are found to account for how much the information is retained (adequacy), and the longer
n-gram scores account for the fluency of the translation, i.e. if the target language is English, to what extent it reads like “good” English. The BLEU metric’s output is always a real-valued number between 0 and 1. This value indicates how similar the machine and reference translations are. Values closer to 1 represent the more similar texts, however, few machine translations will attain a score of 1 because, in that case, the machine translation must be identical to the reference translations.
4 Results and Discussion
4.1 Results
We performed the experiment in order to compare the jDE algorithm with the state-of-the-art methods MERT and MIRA, and with the DE algorithm. For each optimizer we performed 30 independent runs on the tuning set described earlier. To evaluate optimizers, we used the test set, which consists of a source and target language texts. The source language text was translated using the decoder and models with the non-optimized and optimized weights. The translated text was then compared with the target language text and evaluated using the BLEU metric, as seen in Fig.
2.
The comparison of the results of SMT systems with the jDE optimization against the SMT systems without optimization is shown in Table
3. The jDE algorithm achieved BLEU scores of 60.57 for the Slovenian to English SMT system and 51.95 for the English to Slovenian SMT system, followed by MERT, the DE algorithm, and MIRA. Note that an improvement of 2-3 BLEU points is usually hard to obtain, and we will outline this further in Section
4.2.
Fig. 2
Evaluating the translation quality using the test set.
Table 3
Comparison between baseline system and the system optimized with the jDE algorithm on the test set.
|
BLEU ↑ |
|
Slovenian → English |
English → Slovenian |
| Baseline (non-optimized) |
58.00 |
50.47 |
| Optimized with jDE |
60.57 |
51.95 |
We compared the newly proposed jDE optimizer with the other state-of-the-art optimizers. Table
4 shows a comparison between MERT, MIRA, the DE algorithm, and the jDE algorithm. The
best and
mean BLEU scores were obtained from 30 optimizer runs. The jDE algorithm achieved the
best BLEU scores in the case of the Slovenian to English SMT, while DE and jDE were the best performing algorithms for English to Slovenian translation. MERT and MIRA obtained worse results for SMT systems in both translation directions.
Table 4
Best and mean BLEU score of 30 runs for the Slovenian ↔ English SMT systems.
|
MERT |
MIRA |
DE |
jDE |
|
Best |
Mean |
Best |
Mean |
Best |
Mean |
Best |
Mean |
| Slovenian → English |
60.56 |
60.04 |
60.32 |
60.06 |
60.52 |
59.70 |
60.57 |
60.12 |
| English → Slovenian |
51.85 |
51.28 |
51.40 |
51.02 |
51.86 |
51.52 |
51.95 |
51.51 |
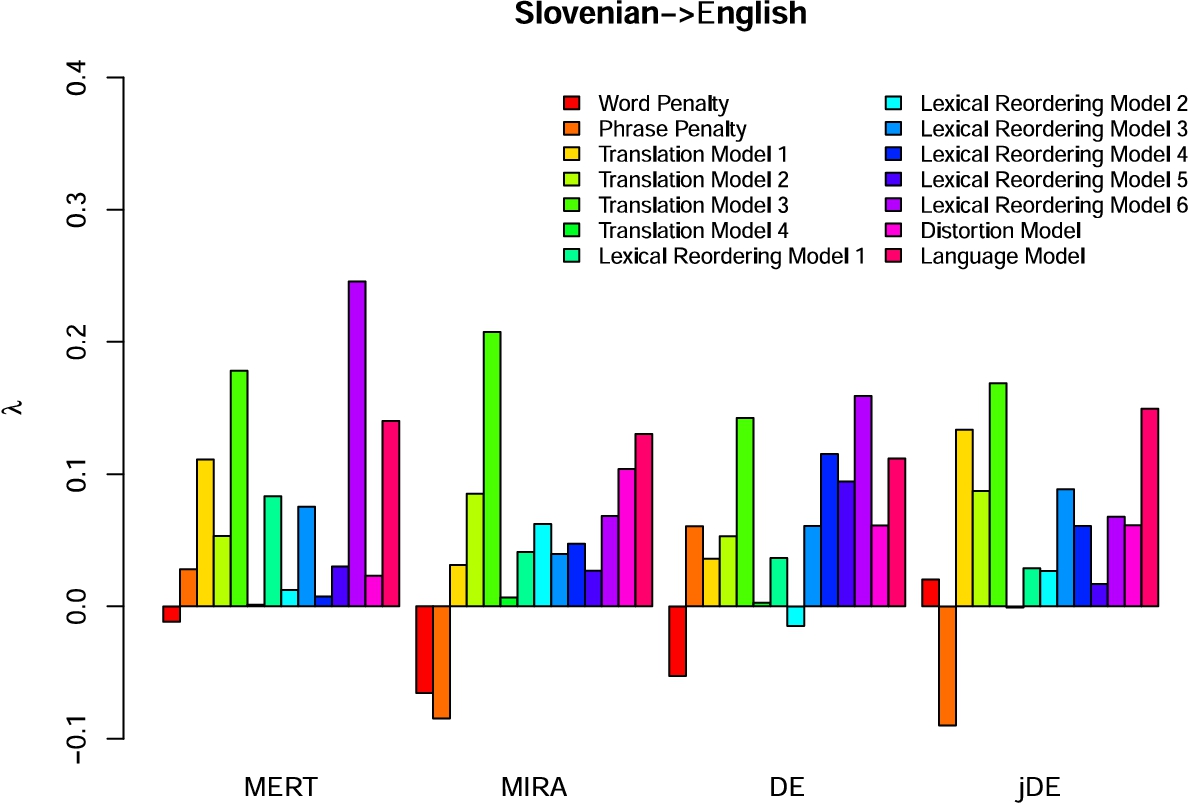
Fig. 3
The best values of weights after the optimization for Slovenian-English SMT system using MERT, MIRA, DE and jDE.
The obtained values of weights for the Slovenian-English SMT system for MERT, MIRA, DE and jDE are shown in Fig.
3. Despite the difference in BLEU score, some of the parameters are very different. The phrase penalty parameter for MIRA and jDE was negative, while for MERT and DE it was positive. Also, for jDE, we can notice that phrase penalty, translation and language models contributed most to the translation.
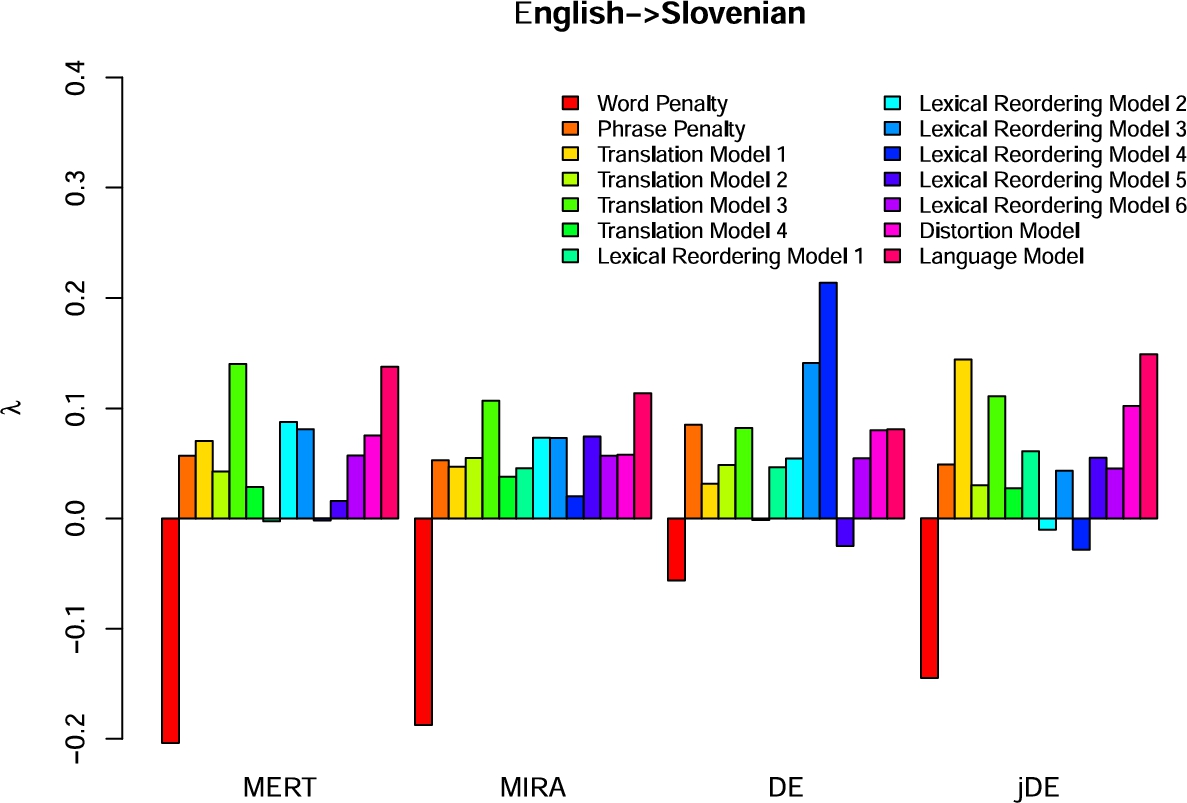
Fig. 4
The best values of weights after the optimization for the English-Slovenian SMT system using MERT, MIRA, DE and jDE.
The obtained values of weights for the English-Slovenian SMT system for MERT, MIRA, DE and jDE are shown in Fig.
4. The 4-th parameter for the lexical reordering model was much higher in DE than in the other systems, and the parameter for the phrase penalty model was much lower in DE than in the other systems. Also, it can be seen, that for all systems, except DE, the word penalty model contributed the most to the translation.
Since the optimization process was a part of an offline training with a static corpus, described in Section
3, and no time constraints, the optimization time was not so relevant. Once the SMT system was built, the actual time for translating was the same for all optimizations. For a text of 15,000 words it took approximately 5 minutes on a single CPU (i5). As we can see in Table
5, both DE and jDE used the same settings, and, with these, they both made 750 evaluations, and time for one evaluation was around 2.5 minutes on two CPU’s (i5), resulting in a total optimization time of 1,875 minutes for each.
Table 5
Tuning process statistics for the SMT systems using DE and jDE.
|
DE |
jDE |
| Number of generations |
50 |
50 |
| Population size |
15 |
15 |
| Tuning set size [words] |
15,000 |
15,000 |
| Number of evaluations |
750 |
750 |
| Tuning time [min] |
1,875.2 |
1,875.3 |
The goal of the experimental testing was to assess the true translation quality of an SMT system on a text from a certain domain. However, this is an abstract concept, because it has to be computed on all possible sentences in that domain. In practice, we will always be able just to measure the performance of an SMT system on a specific sample. In our experiment, we compared an SMT system without the optimization (baseline) with an SMT system which was optimized with MERT, MIRA, the DE algorithm, and the jDE algorithm. We translated the same test set, and measured the translation quality using the BLEU metric. One important element of a solid experimental framework is a statistical significance test that allows us to judge if a change in the score that comes from a change in the system truly reflects a change in overall translation quality (Koehn,
2004). To measure the reliability of the conclusion that one system is better than the other, or that the difference in test scores is statistically significant, we used the MultEval (Clark
et al.,
2011) tool, which is a recognized tool for MT significance testing within the field of SMT. MultEval takes translations from several optimizers and provides two popular metric scores (BLEU, TER), as well as Standard Deviations via bootstrap resampling, and
p-values via approximate randomization. With this, we can mitigate some of the risk of using unstable optimizers, and it is intended to help in evaluating the impact of in-house experimental variations on the translation quality.
The statistical comparison using the MultEval tool is shown in Tables
6 and
7, where the jDE algorithm was used as a baseline. This means that we are looking to see if MERT, MIRA and the DE algorithm differ statistically significantly according to the jDE algorithm. Again, we can see that the jDE algorithm achieved the higher BLEU scores and the lowest TER scores for both SMT systems.
Table 6
Statistical test using MultEval for the Slovenian-English SMT system.
| Metric |
Optimizer |
Avg |
Std |
p-value |
| BLEU ↑ |
jDE |
60.12 |
0.24 |
– |
|
MERT |
60.03 |
0.25 |
0.001 |
|
MIRA |
60.06 |
0.19 |
0.004 |
|
DE |
59.71 |
0.49 |
0.001 |
| TER ↓ |
jDE |
28.36 |
0.20 |
– |
|
MERT |
28.53 |
0.20 |
0.001 |
|
MIRA |
28.51 |
0.12 |
0.001 |
|
DE |
28.65 |
0.32 |
0.001 |
Table 7
Statistical test using MultEval for the English-Slovenian SMT system.
| Metric |
Optimizer |
Avg |
Std |
p-value |
| BLEU ↑ |
jDE |
51.51 |
0.44 |
– |
|
MERT |
51.28 |
0.48 |
0.001 |
|
MIRA |
51.03 |
0.29 |
0.001 |
|
DE |
51.52 |
0.32 |
0.001 |
| TER ↓ |
jDE |
36.26 |
0.45 |
– |
|
MERT |
36.57 |
0.56 |
0.001 |
|
MIRA |
36.61 |
0.29 |
0.001 |
|
DE |
36.33 |
0.36 |
0.001 |
4.2 Discussion
According to the author in Koehn (
2004), it is difficult to evaluate the translation quality decently, since it is not entirely clear what the focus of the evaluation should be. Of course, a good translation has to capture the meaning of the target language text. However, differences in emphasis are introduced based on the interpretation of the translator. At the same time, the output should be fluent so that it can be read easily. These two goals (adequacy and fluency) are the main criteria in an MT evaluation. A human translator may be asked to evaluate the adequacy and fluency of the translation output, but this is a laborious and expensive task. Therefore, it is hard to interpret what the BLEU score, for example, 60.57, means. It is not intuitive, and depends on the number of reference translations used. In our experiment, the example of the differences in BLEU scores between reference translations and SMT systems with and without optimization, can be seen in Table
8. It is interesting to note that, in all translations, there is a partial translation “for the detection” (or “for detection”), which corresponds to “pri odkrivanju” in the original text, while this part was not translated in the reference translation. We can also see that all the translations except the one with MIRA have the determiner “the”. Differences in the word order could be noticed as well.
The authors in Koehn
et al. (
2009) used the same JRC-Acquis corpus, and built SMT systems for 462 language pairs including the Slovenian-English language pair. As we can see from their results, the BLEU score for the Slovenian-English translation system was 61 and for English-Slovenian was 50.7. The exact division of the corpus into train, tuning and test sets is not published, so we could not make a direct comparison.
Table 8
Example of one translation from Slovenian to English given by different systems.
| System |
Translation |
| Original |
za nekatere referenčne laboratorije skupnosti pri odkrivanju bioloških tveganj na veterinarskem področju javnega zdravstvenega varstva |
| Reference |
to certain community reference laboratories in the veterinary public health field of biological risks |
| Baseline |
to certain community reference laboratories for the detection of biological risk in the veterinary field of public health protection |
| MERT |
to certain community reference laboratories for the detection of biological risk in the veterinary field of public health protection |
| MIRA |
to certain community reference laboratories for detection of biological risk in the veterinary public health field |
| DE |
to certain community reference laboratories for the detection of biological risk public health in the veterinary field |
| jDE |
to certain community reference laboratories for the detection of biological risk in the veterinary public health field |
4.3 Optimization Settings
The following settings were used for the optimization: D = 14, min = −1, max = 1, Np = 15, G = 50, F = 0.5, Cr = 0.9, ${\tau _{1}}$ = 0.1, and ${\tau _{2}}$ = 0.1. Values for F and Cr were set only within the initial population, and were self-adapting during the evolution process. The maximum number of generations G was the stopping criterion for the algorithm.
5 Conclusion
Weights in SMT systems can affect the quality of the translations significantly. In this paper, the two phrase-based SMT systems were built successfully, and their weights were optimized using the jDE algorithm. They were tested on the unseen set, and the results were comparable. However, based on extensive experiments, the jDE algorithm obtained better BLEU scores compared to the state-of-the-art algorithms MERT, MIRA and the DE algorithm. The jDE algorithm achieved the best BLEU scores of 60.57 for the Slovenian to English SMT system and 51.95 for the English to Slovenian SMT system, followed by MERT and the DE algorithm, and MIRA. We are confident of the promising characteristics of algorithms based on Differential Evolution and good attributes of the jDE self-adaptive mechanism.
Recently, the neural machine translation has emerged as a new paradigm in MT. It also has many parameters that could be optimized to yield better performance.

