4.1 The Process of MAGDM Based on the IT-ICOWD Measure
The IT-ICOWD measure is of high feasibility in a broad range of situations, especially in solving multiple attribute group decision making where the attribute assessment values are represented by interval-valued 2-tuple linguistic information.
Here we propose an approach to MAGDM with interval-valued 2-tuple linguistic information by the IT-ICOWD measure. Moreover, we can determine the order-inducing variables of the IT-ICOWD measure, the weighting vector of decision makers and the weighting vector of attributes.
Let
$X=\{{X_{1}},{X_{2}},\dots ,{X_{m}}\}$ be a discrete set of alternatives,
$C=\{{C_{1}},{C_{2}},\dots ,{C_{n}}\}$ be an attributes set, and
$w={({w_{1}},{w_{2}},\dots ,{w_{n}})^{T}}$ be the weighting vector satisfying
${w_{j}}\in [0,1]$, associated with weight of
${C_{j}}$, and
${\textstyle\sum _{j=1}^{n}}{w_{j}}=1$. Let
$E=\{{e_{1}},{e_{2}},\dots ,{e_{t}}\}$ be a decision maker collection, and
$\omega ={({\omega _{1}},{\omega _{2}},\dots ,{\omega _{t}})^{T}}$ be the weighting vector of decision makers, where
${\textstyle\sum _{k=1}^{t}}{\omega _{k}}=1$,
${\omega _{k}}\in [0,1]$. The decision makers
${e_{k}}$ $(k=1,2,\dots ,t)$ are required to give his/her assessment values of alternative
${X_{i}}$ with respect to attribute
${C_{j}}$ in linguistic term sets
${S^{{T_{k}}}}$ (
${S^{{T_{k}}}}$ may have different granularity), therefore, the decision matrix
${\tilde{R}^{k}}$ can be built as
${\tilde{R}^{k}}={({\tilde{r}_{ij}^{k}})_{m\times n}}={([{r_{ij}^{k}},{r^{\prime \hspace{0.1667em}k}_{ij}}])_{m\times n}}$, where
${\tilde{r}_{ij}^{k}}$ is linguistic variable
${s_{ij}^{k}}$,
${s_{ij}^{k}}\in {S^{{T_{k}}}}$,
${S^{{T_{k}}}}=\{{s_{i}^{{T_{k}}}}\mid i\in \{0,1,\dots ,{T_{k}}-1\}\}$. The decision makers also establish the ideal alternative by giving the ideal levels of each characteristic, which is shown in Table
3, where
${\tilde{\varphi }^{k}}$ is the ideal alternative and
${\tilde{\varphi }_{j}^{k}}=[{\varphi _{j}^{k}},{\varphi ^{\prime \hspace{0.1667em}k}_{j}}]$ is the
j-th ideal characteristic of
${\tilde{\varphi }^{k}}$.
Table 3
Ideal alternative.
|
${C_{1}}$ |
${C_{2}}$ |
$\dots \hspace{0.1667em}$ |
${C_{j}}$ |
$\dots \hspace{0.1667em}$ |
${C_{n}}$ |
| ${\tilde{\varphi }^{k}}$ |
${\tilde{\varphi }_{1}^{k}}$ |
${\tilde{\varphi }_{2}^{k}}$ |
$\dots \hspace{0.1667em}$ |
${\tilde{\varphi }_{j}^{k}}$ |
$\dots \hspace{0.1667em}$ |
${\tilde{\varphi }_{n}^{k}}$ |
The process with the IT-ICOWD measure in MAGDM involves the following steps.
Step 1. Transform the decision matrix ${\tilde{R}^{k}}={({\tilde{r}_{ij}^{k}})_{m\times n}}$ $(k=1,2,\dots ,t)$ and the ideal alternative ${\tilde{\phi }^{k}}$ into interval-valued 2-tuple linguistic decision matrix ${\hat{R}^{k}}={({\hat{r}_{ij}^{k}})_{m\times n}}={([({r_{ij}^{k}},0),({r^{\prime \hspace{0.1667em}k}_{ij}},0)])_{m\times n}}$ $(k=1,2,\dots ,t)$ and interval-valued 2-tuple linguistic the ideal alternative ${\hat{\phi }^{k}}={({\hat{\phi }_{j}^{k}})_{1\times n}}=([({\phi _{1}^{k}},0),({\phi ^{\prime \hspace{0.1667em}k}_{1}},0)],[({\phi _{2}^{k}},0),({\phi ^{\prime \hspace{0.1667em}k}_{2}},0)],\dots ,[({\phi _{n}^{k}},0),({\phi ^{\prime \hspace{0.1667em}k}_{n}},0)])$ respectively.
Step 2. Calculate the distance between each assessment value
${\hat{r}_{ij}^{k}}$ provided by the decision maker
${e_{k}}$ and his/her ideal assessment value
${\hat{\phi }_{j}^{k}}$ by Eq. (
28):
where
$k=1,2,\dots ,t$,
$i=1,2,\dots ,m$,
$j=1,2,\dots ,n$,
$\lambda ={\textstyle\int _{0}^{1}}Q(y)\hspace{0.1667em}dy$ is the attitudinal character of
Q.
Step 3. Let
${\bar{d}_{ij}}=\Delta (\frac{1}{t}{\textstyle\sum _{k=1}^{t}}{\Delta ^{-1}}({d_{\lambda }}({\hat{r}_{ij}^{k}},{\hat{\phi }_{j}^{k}})))$, i.e.
${({\bar{d}_{ij}})_{m\times n}}$ is the mean distance matrix of
${d_{\lambda }}({\hat{r}_{ij}^{k}},{\hat{\phi }_{j}^{k}})$,
$k=1,2,\dots ,t$, and
${(\Lambda ({d_{\lambda }}({\hat{r}_{ij}^{k}},{\hat{\phi }_{j}^{k}}),\bar{d}))_{m\times n}}={(\Delta (|{\Delta ^{-1}}({d_{\lambda }}({\hat{r}_{ij}^{k}},{\hat{\phi }_{j}^{k}}))-{\Delta ^{-1}}(\bar{d})|))_{m\times n}}$ is the absolute distance matrix between
${d_{\lambda }}({\hat{r}_{ij}^{k}},{\hat{\phi }_{j}^{k}})$ and
${\bar{d}_{ij}}$. Then, the similarity measure can be defined as follows:
The closer
${\mathit{Sim}_{{^{k}}}}$ is to 1, the more representative and reliable the information provided by the
k-th expert is. That is the absolute distance matrix with the more similarity measure should be more important. Thus, we can use the similarity measure
${\mathit{Sim}_{k}}$ as the order-inducing variables of the assessment values to be aggregated in the process of group decision making. Thus, the weighting vector
$\omega ={({\omega _{1}},{\omega _{2}},\dots ,{\omega _{t}})^{T}}$ can be determined by the following formula:
Moreover, according to the principle that the closer a preference value is to the mid one(s), the more the weight, the weighting vector
$w={({w_{1}},{w_{2}},\dots ,{w_{n}})^{T}}$ can be determined by the following formula:
Step 4. Utilize the
IT-
ICOWD measure
to aggregate all the 2-tuple linguistic distance matrices into the collective 2-tuple linguistic distance matrix
$\tilde{R}={({\tilde{r}_{ij}})_{m\times n}}={(({r_{ij}},{a_{ij}}))_{m\times n}}$, where
$\omega ={({\omega _{1}},{\omega _{2}},\dots ,{\omega _{t}})^{T}}$ is the weighting vector of decision makers. Here, it should be mentioned that
${r_{ij}}\in {S^{{T_{k}}}}$ and
${a_{ij}}\in [-\frac{1}{2{T_{k}}},\frac{1}{2{T_{k}}})$.
Step 5. Utilize the
T-GOWA operator (Liu
et al.,
2011)
to aggregate all of the preference values
${\tilde{r}_{ij}}$ $(j=1,2,\dots ,n)$ in the
i-th line of
$\tilde{R}$, and then derive the collective overall preference values
${\tilde{r}_{i}}=({r_{i}},{a_{i}})$ $(i=1,2,\dots ,m)$ of the alternative
${X_{i}}$ $(i=1,2,\dots ,m)$, where
$w={({w_{1}},{w_{2}},\dots ,{w_{n}})^{T}}$ is the weighting vector of attribute.
Step 6. According to the comparison law, rank the ${\tilde{r}_{i}}=({r_{i}},{a_{i}})$ $(i=1,2,\dots ,m)$ in descending order.
Step 7. Rank all of the alternatives ${X_{i}}$ $(i=1,2,\dots ,m)$, and then select the best one(s) in accordance with the collective overall preference values ${\tilde{r}_{i}}=({r_{i}},{a_{i}})$ $(i=1,2,\dots ,m)$. The best choice is the one with the smallest distance.
Step 8. End.
4.2 Illustrative Example
In this section, we employ a practical MAGDM problem to illustrate the efficiency of the proposed method in dealing with problems of interval-valued 2-tuple linguistic information. Suppose that an investment company wants to find an optimal investment. There are four possible alternatives to invest the money:
${X_{1}}$: car industry; ${X_{2}}$: food company; ${X_{3}}$: computer company${X_{4}}$: arms industry.
The investment company must make a decision according to the following four attributes:
${C_{1}}$: risk analysis; ${C_{2}}$: growth analysis; ${C_{3}}$: social-political impact analysis; ${C_{4}}$: environment impact analysis.
In order to eliminate influence among them, three decision makers are invited to provide their preferences for each possible alternative on each attributes in anonymity and in different linguistic term sets respectively, which are seven terms: ${S^{7}}=\{{s_{0}^{7}},{s_{1}^{7}},{s_{2}^{7}},{s_{3}^{7}},{s_{4}^{7}},{s_{5}^{7}},{s_{6}^{7}}\}$, five terms: ${S^{5}}=\{{s_{0}^{5}},{s_{1}^{5}},{s_{2}^{5}},{s_{3}^{5}},{s_{4}^{5}}\}$ and nine terms: ${S^{9}}=\{{s_{0}^{9}},{s_{1}^{9}},{s_{2}^{9}},{s_{3}^{9}},{s_{4}^{9}},{s_{5}^{9}},{s_{6}^{9}},{s_{7}^{9}},{s_{8}^{9}}\}$.
The linguistic decision matrices ${\tilde{R}^{k}}={({\tilde{r}_{ij}^{k}})_{4\times 4}}$ $(k=1,2,3)$ and the ideal alternative ${\tilde{\phi }^{k}}$ are provided as follows:
Linguistic decision matrix ${\tilde{R}^{1}}$ provided by ${D_{1}}$
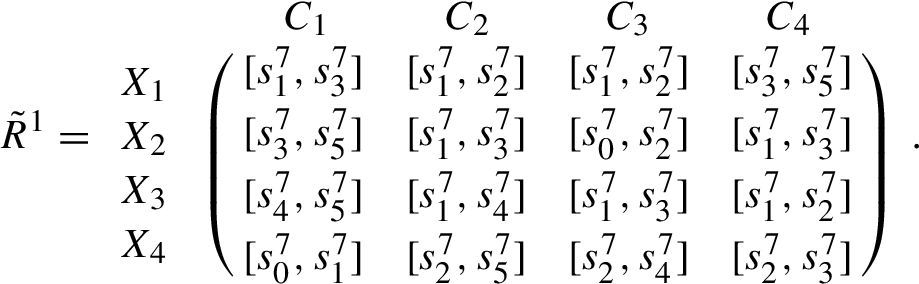
Linguistic decision matrix ${\tilde{R}^{2}}$ provided by ${D_{2}}$
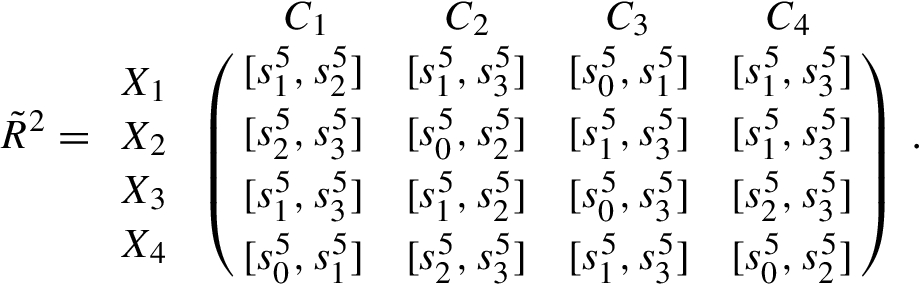
Linguistic decision matrix ${\tilde{R}^{3}}$ provided by ${D_{3}}$
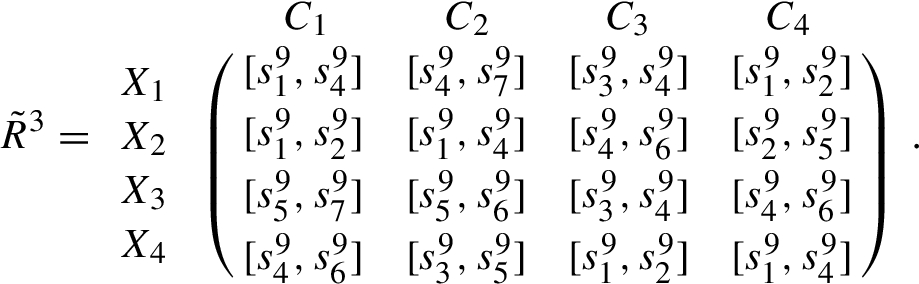
Table 4
Ideal alternative.
|
${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
| ${\tilde{\phi }^{1}}$ |
$({s_{4}^{7}},{s_{6}^{7}})$ |
$({s_{4}^{7}},{s_{5}^{7}})$ |
$({s_{3}^{7}},{s_{4}^{7}})$ |
$({s_{4}^{7}},{s_{5}^{7}})$ |
| ${\tilde{\phi }^{2}}$ |
$({s_{3}^{5}},{s_{4}^{5}})$ |
$({s_{2}^{5}},{s_{4}^{5}})$ |
$({s_{2}^{5}},{s_{3}^{5}})$ |
$({s_{3}^{5}},{s_{4}^{5}})$ |
| ${\tilde{\phi }^{3}}$ |
$({s_{6}^{9}},{s_{8}^{9}})$ |
$({s_{5}^{9}},{s_{7}^{9}})$ |
$({s_{6}^{9}},{s_{7}^{9}})$ |
$({s_{5}^{9}},{s_{6}^{9}})$ |
Then, we utilize the method developed to obtain the best alternative(s).
Step 1. Transform the decision matrix ${\tilde{R}^{k}}={({\tilde{r}_{ij}^{k}})_{4\times 4}}$, $k=1,2,3$ and the ideal alternative ${\tilde{\phi }^{k}}$ into interval-valued 2-tuple linguistic decision matrix ${\hat{R}^{k}}={({\hat{r}_{ij}^{k}})_{4\times 4}}={([({r_{ij}^{k}},0),({r^{\prime \hspace{0.1667em}k}_{ij}},0)])_{4\times 4}}$ and interval-valued 2-tuple linguistic ideal alternative ${\hat{\phi }^{k}}={({\hat{\phi }_{j}^{k}})_{1\times 4}}=([({\phi _{1}^{k}},0),({\phi ^{\prime \hspace{0.1667em}k}_{1}},0)],[({\phi _{2}^{k}},0),({\phi ^{\prime \hspace{0.1667em}k}_{2}},0)],\dots ,[({\phi _{4}^{k}},0),({\phi ^{\prime \hspace{0.1667em}k}_{4}},0)])$, shown as follows:
Interval-valued 2-tuple linguistic decision matrix ${\hat{R}^{1}}$ provided by ${D_{1}}$
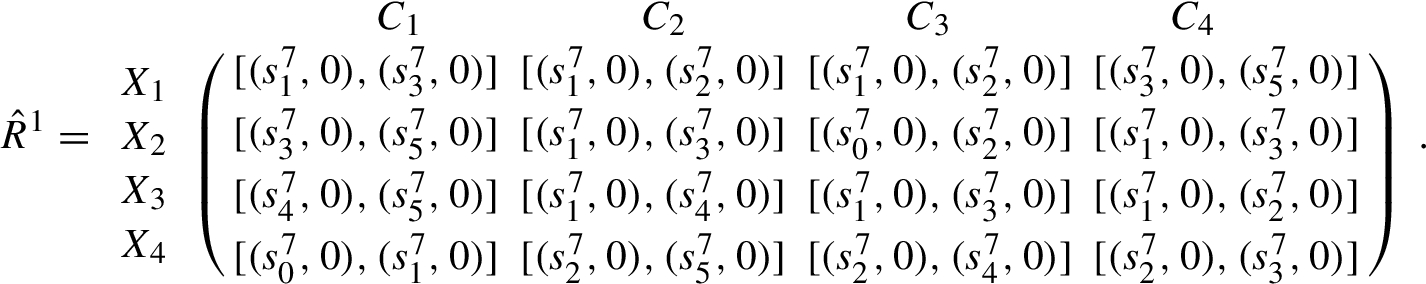
Interval-valued 2-tuple linguistic decision matrix ${\hat{R}^{2}}$ provided by ${D_{2}}$
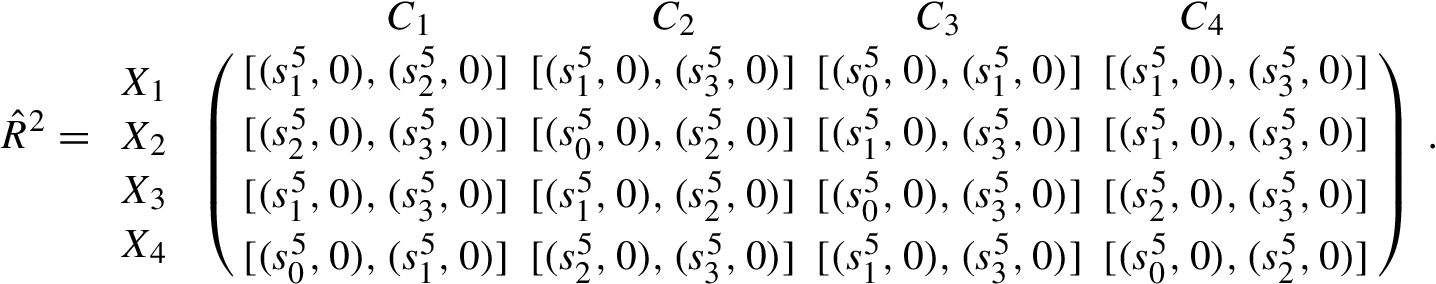
Interval-valued 2-tuple linguistic decision matrix ${\hat{R}^{3}}$ provided by ${D_{3}}$
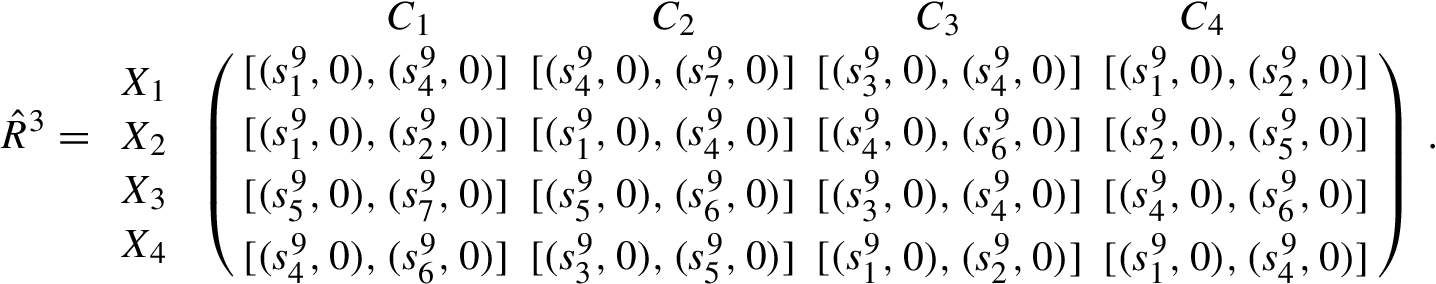
Interval-valued 2-tuple linguistic ideal alternative ${\hat{\phi }^{k}}$ $(k=1,2,3)$
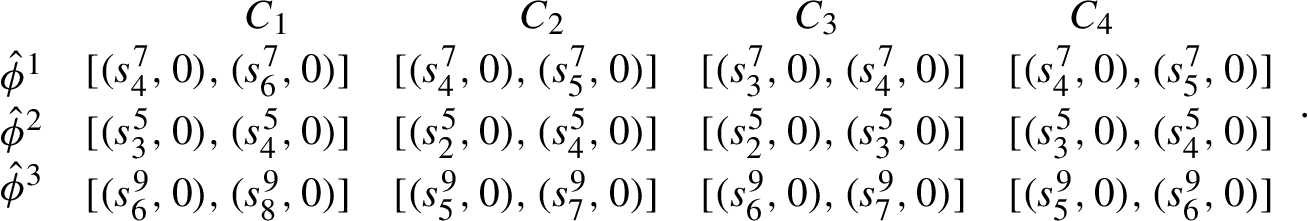
Step 2. Calculate the distance of each assessment value
${\hat{r}_{ij}^{k}}$ provided by the decision maker
${e_{k}}$ and his/her ideal assessment value
${\hat{\phi }_{j}^{k}}$ by Eq. (
44), where
$Q(y)={y^{2}}$,
$\lambda =\frac{1}{3}$. The results are listed as follows:
Distance matrix of decision maker ${D_{1}}$
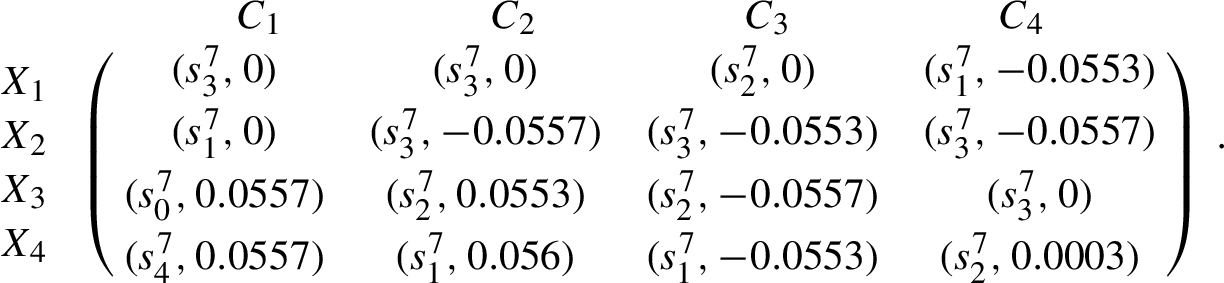
Distance matrix of decision maker ${D_{2}}$
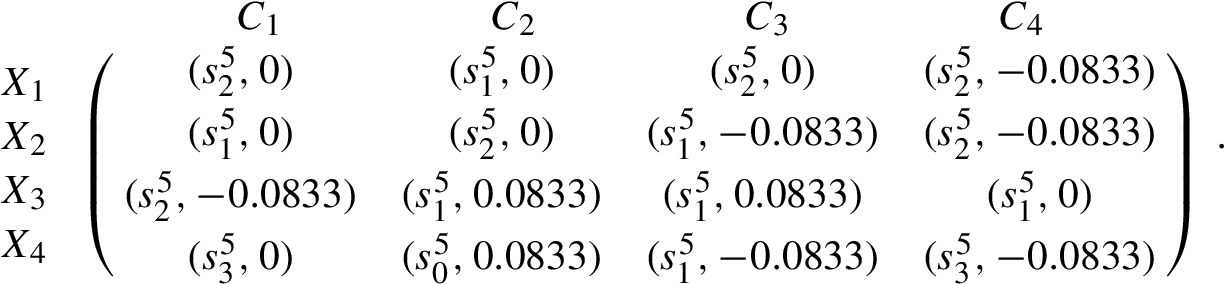
Distance matrix of decision maker ${D_{3}}$

Step 3. Calculate the mean distance matrix $\bar{d}$ and the absolute distance matrix $\Lambda ({d_{\lambda }}({\hat{r}_{ij}^{k}},{\hat{\phi }_{j}^{k}}),\bar{d})$, $k=1,2,3$, where $\bar{d}$ chooses the linguistic term sets ${S^{5}}$. The results are shown as follows:
The mean distance matrix
$\bar{d}$
The absolute distance matrix of decision maker
${D_{1}}$
The absolute distance matrix of decision maker
${D_{2}}$
The absolute distance matrix of decision maker
${D_{3}}$
Then, we can get the similarity measure by Eq. (
45) and the weighting vector
ω by Eq. (
46):
Moreover, we can obtain the weighting vector
w by Eq. (
47):
Step 4. Utilize the IT-ICOWD measure to aggregate 2-tuple linguistic distance matrix into the collective 2-tuple linguistic distance matrix $\tilde{R}={({\tilde{r}_{ij}})_{4\times 4}}={(({r_{ij}},{a_{ij}}))_{4\times 4}}$, where $\tau =3$. We can use the similarity measure ${\mathit{Sim}_{k}}$ as the order-inducing variables. Note that ${r_{ij}}\in {S^{{T_{k}}}}$ and ${a_{ij}}\in [-\frac{1}{2{T_{k}}},\frac{1}{2{T_{k}}})$.
The collective 2-tuple linguistic distance matrix $\tilde{R}$

Step 5. Utilize the
T-GOWA operator to derive the collective overall preference value
${\tilde{r}_{i}}=({r_{i}},{a_{i}})$ $(i=1,2,3,4)$ of the alternative
${X_{i}}$ $(i=1,2,3,4)$:
Assume that the parameter τ in the T-GOWA operator is equal to the parameter τ in the IT-ICOWD measure.
Step 6. According to the comparison law, rank the
${\tilde{r}_{i}}=({r_{i}},{a_{i}})$ $(i=1,2,3,4)$ in descending order:
Step 7. Rank all of the alternatives
${X_{i}}$ $(i=1,2,3,4)$ as follows:
and the best alternative is thus
${X_{3}}$. i.e. the best alternative is the computer company.
Furthermore, it is possible to analyse how the different particular cases of the
IT-
ICOWD measure influence for the aggregation results. Here we consider the
IT-
ICOWHD measure, the
IT-
ICOWED measure, the
IT-
ICOWGD measure, the
IT-
ICMAXD measure, the
IT-
ICMIND measure, the Step
-IT-ICOWD measure (
$k=2$), the
IT-ICND measure, the
IT-ICNHD measure, the
IT-ICNED measure, the
IT-ICNGD measure, the Median
IT-
ICOWD measure and the Olympic
IT-
ICOWD measure. The results are clearly demonstrated in Table
5. Now, we are able to propose the order of the companies for each case. The results are clearly demonstrated in Table
6. Note that the best and the most optimal investment is the one possessing the lowest distance.
Table 5
Aggregated results.
|
IT-ICOWHD
|
IT-ICOWED
|
IT-ICOWGD
|
IT-ICMAXD
|
| ${X_{1}}$ |
$({s_{2}^{5}},-0.1167)$ |
$({s_{2}^{5}},-0.0864)$ |
$({s_{1}^{5}},0.0839)$ |
$({s_{2}^{5}},0.0214)$ |
| ${X_{2}}$ |
$({s_{1}^{5}},0.118)$ |
$({s_{2}^{5}},-0.1042)$ |
$({s_{1}^{5}},0.0864)$ |
$({s_{2}^{5}},0.0287)$ |
| ${X_{3}}$ |
$({s_{1}^{5}},0.0179)$ |
$({s_{1}^{5}},0.0572)$ |
$({s_{1}^{5}},-0.0431)$ |
$({s_{2}^{5}},-0.072)$ |
| ${X_{4}}$ |
$({s_{2}^{5}},-0.122)$ |
$({s_{2}^{5}},-0.0558)$ |
$({s_{1}^{5}},0.0519)$ |
$({s_{2}^{5}},0.1233)$ |
|
IT-ICMIND
|
Step-IT-ICOWD
|
IT-ICND |
IT-ICNHD |
| ${X_{1}}$ |
$({s_{1}^{5}},0.0888)$ |
$({s_{2}^{5}},-0.0977)$ |
$({s_{2}^{5}},-0.0657)$ |
$({s_{2}^{5}},-0.1151)$ |
| ${X_{2}}$ |
$({s_{1}^{5}},0.0565)$ |
$({s_{1}^{5}},0.1106)$ |
$({s_{2}^{5}},-0.0792)$ |
$({s_{1}^{5}},0.1179)$ |
| ${X_{3}}$ |
$({s_{1}^{5}},-0.0779)$ |
$({s_{1}^{5}},0.033)$ |
$({s_{1}^{5}},0.0783)$ |
$({s_{1}^{5}},0.014)$ |
| ${X_{4}}$ |
$({s_{1}^{5}},0.021)$ |
$({s_{2}^{5}},-0.0204)$ |
$({s_{2}^{5}},-0.0044)$ |
$({s_{2}^{5}},-0.12)$ |
|
IT-ICNED |
IT-ICNGD |
Median IT-ICOWD
|
Olympic IT-ICOWD
|
| ${X_{1}}$ |
$({s_{2}^{5}},-0.0849)$ |
$({s_{1}^{5}},-0.0853)$ |
$({s_{2}^{5}},-0.0887)$ |
$({s_{2}^{5}},-0.0887)$ |
| ${X_{2}}$ |
$({s_{2}^{5}},-0.1036)$ |
$({s_{1}^{5}},0.086)$ |
$({s_{2}^{5}},-0.0933)$ |
$({s_{2}^{5}},-0.0933)$ |
| ${X_{3}}$ |
$({s_{1}^{5}},0.0532)$ |
$({s_{1}^{5}},-0.0465)$ |
$({s_{2}^{5}},-0.1233)$ |
$({s_{2}^{5}},-0.1233)$ |
| ${X_{4}}$ |
$({s_{2}^{5}},-0.054)$ |
$({s_{1}^{5}},0.0544)$ |
$({s_{2}^{5}},-0.375)$ |
$({s_{2}^{5}},-0.0375)$ |
Table 6
Ordering of the companies.
|
Ordering |
|
Ordering |
|
IT-ICOWHD
|
${X_{3}}\succ {X_{2}}\succ {X_{4}}\succ {X_{1}}$ |
IT-ICND |
${X_{3}}\succ {X_{2}}\succ {X_{1}}\succ {X_{4}}$ |
|
IT-ICOWED
|
${X_{3}}\succ {X_{2}}\succ {X_{1}}\succ {X_{4}}$ |
IT-ICNHD |
${X_{3}}\succ {X_{2}}\succ {X_{4}}\succ {X_{1}}$ |
|
IT-ICOWGD
|
${X_{3}}\succ {X_{4}}\succ {X_{1}}\succ {X_{2}}$ |
IT-ICNED |
${X_{3}}\succ {X_{2}}\succ {X_{1}}\succ {X_{4}}$ |
|
IT-ICMAXD
|
${X_{3}}\succ {X_{1}}\succ {X_{2}}\succ {X_{4}}$ |
IT-ICNGD |
${X_{3}}\succ {X_{4}}\succ {X_{1}}\succ {X_{2}}$ |
|
IT-ICMIND
|
${X_{3}}\succ {X_{4}}\succ {X_{2}}\succ {X_{1}}$ |
Median IT-ICOWD
|
${X_{3}}\succ {X_{2}}\succ {X_{1}}\succ {X_{4}}$ |
| Step-IT-ICOWD
|
${X_{3}}\succ {X_{2}}\succ {X_{1}}\succ {X_{4}}$ |
Olympic IT-ICOWD
|
${X_{3}}\succ {X_{2}}\succ {X_{1}}\succ {X_{4}}$ |
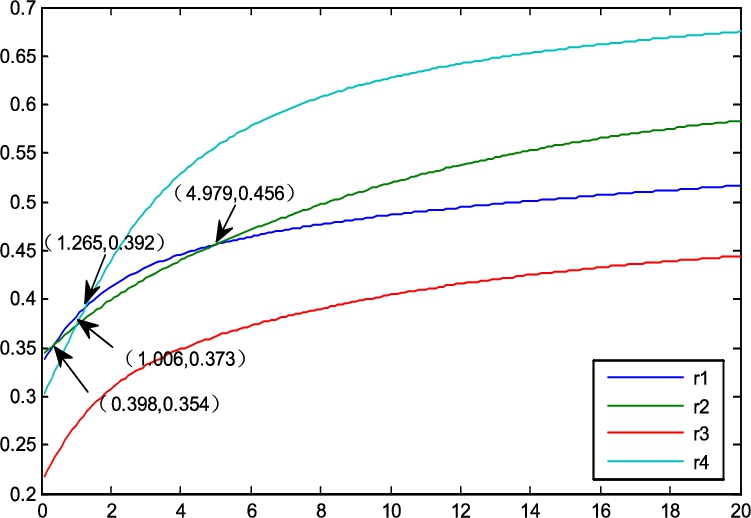
Fig. 1
Variations of the aggregation results with parameter τ.
As we can see, the company order varies with category of IT-ICOWD measures.
Moreover, we can also analyse how different parameter
τ affects the aggregation results. Considering different values of parameter
$\tau \in (0,20)$ provided by the decision makers, here we take
$\lambda =\frac{1}{3}$. The results are shown in Fig.
1.
Similarly, the company order varies with parameter
τ. From Fig.
1, we can conclude that
-
(1) when $\tau \in (0,0.398]$, alternative’s rank is ${X_{3}}\succ {X_{4}}\succ {X_{1}}\succ {X_{2}}$, and the best alternative is ${X_{3}}$;
-
(2) when $\tau \in (0.398,1.006]$, alternative’s rank is ${X_{3}}\succ {X_{4}}\succ {X_{2}}\succ {X_{1}}$, and the best alternative is ${X_{3}}$;
-
(3) when $\tau \in (1.006,1.265]$, alternative’s rank is ${X_{3}}\succ {X_{2}}\succ {X_{4}}\succ {X_{1}}$, and the best alternative is ${X_{3}}$.
-
(4) when $\tau \in (1.265,4.979]$, alternative’s rank is ${X_{3}}\succ {X_{2}}\succ {X_{1}}\succ {X_{4}}$, and the best alternative is ${X_{3}}$;
-
(5) when $\tau \in (4.979,20]$, alternative’s rank is ${X_{3}}\succ {X_{1}}\succ {X_{2}}\succ {X_{4}}$, and the best alternative is ${X_{3}}$.
4.3 Discussion of Comparative Analysis
In order to evaluate the performance and effectiveness of the proposed distance measure with the existing one, this paper conducts a comparative study in this subsection, including the comparison with well-applied distance measures and algorithm-based aggregation tools.
(1) Comparison with the existing distance measure.
Compared with the previous distance measure, we can conclude that the IT-ICOWD measure is very useful to deal with deviated problem in aggregation on continuous valued interval 2-tuple linguistic information. The prominent characteristic of the IT-ICOWD measure is that it combines the GOWA operator with the distance measure and the IT-ICOWA operator in the same formula. The decision maker is able to consider the MAGDM problem more clearly according to his/her risk attitude in aggregation process because the parameter λ, which lies in the interval $[0,1]$, can be considered as the measure of the decision maker’s attitudinal character.
(2) Comparison with the aggregation tool based algorithm.
In Liu
et al. (
2014b), Liu
et al. proposed the interval 2-tuple hybrid weighted distance (
IT-HWD) measure to aggregate the interval-valued 2-tuple linguistic information. To facilitate a comparison with the proposed approach, we adopt the algorithm proposed by Liu
et al. (
2014b) and solve the same illustrative example described above. The steps are as follows:
Step 1. Interval-valued 2-tuple linguistic decision matrix
${\hat{R}^{k}}={({\hat{r}_{ij}^{k}})_{4\times 4}}=([({r_{ij}^{k}},0),{({r^{\prime \hspace{0.1667em}k}_{ij}},0)])_{4\times 4}}$ $(k=1,2,3)$ and interval-valued 2-tuple linguistic ideal alternative
${\hat{\phi }^{k}}={({\hat{\phi }_{j}^{k}})_{1\times 4}}=([({\phi _{1}^{k}},0),({\phi ^{\prime \hspace{0.1667em}k}_{1}},0)],[({\phi _{2}^{k}},0),({\phi ^{\prime \hspace{0.1667em}k}_{2}},0)],\dots ,[({\phi _{4}^{k}},0),({\phi ^{\prime \hspace{0.1667em}k}_{4}},0)])$ are listed as shown in Section
4.2.
Step 2. According to the interval 2-tuple linguistic distance (Liu
et al.,
2014b) between two interval 2-tuple linguistic information, the distance of each assessment value
${\hat{r}_{ij}^{k}}$ provided by the decision maker
${e_{k}}$ and his/her ideal assessment value
${\hat{\phi }_{j}^{k}}$ are calculated. The results are listed as follows:
Distance matrix of decision maker ${D_{1}}$
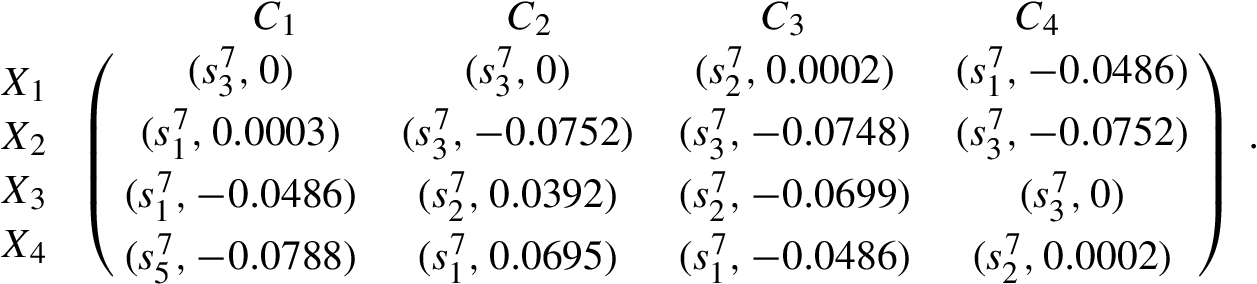
Distance matrix of decision maker ${D_{2}}$
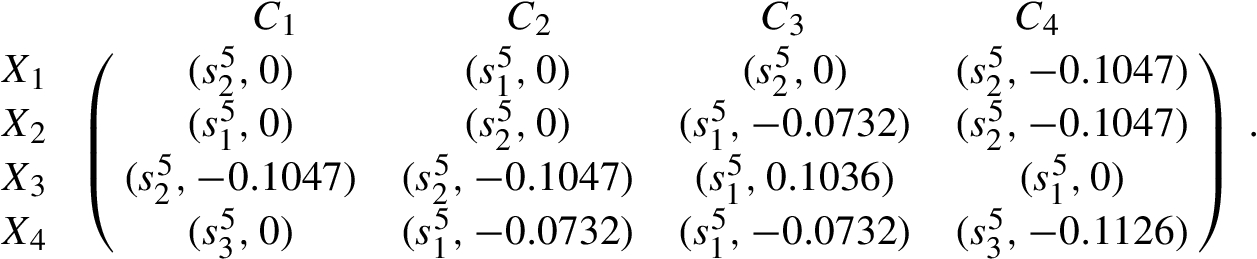
Distance matrix of decision maker ${D_{3}}$

Step 3. Calculate the collective 2-tuple linguistic distance matrix $\tilde{R}={({\tilde{r}_{ij}})_{4\times 4}}={(({r_{ij}},{a_{ij}}))_{4\times 4}}$ by using the IT-HWD measure, which is proposed by Liu’s algorithm. Here, in order to eliminate the unnecessary impacts, we also suppose the objective weight vector $\omega ={(0.3193,0.3736,0.3071)^{T}}$, the subjective weight vector $W={(0.3,0.4,0.3)^{T}}$ and the parameter $\lambda =3$.
The collective 2-tuple linguistic distance matrix $\tilde{R}$

It is noted that the balancing coefficient is $n=3$ and ${r_{ij}}\in {S^{5}}$.
Step 4. Utilize the
T-GOWA operator to derive the collective overall preference value
${\tilde{r}_{i}}=({r_{i}},{a_{i}})$ $(i=1,2,3,4)$ of the alternative
${X_{i}}$ $(i=1,2,3,4)$:
Assume that the parameter λ in the T-GOWA operator is equal to the parameter λ in the IT-HWD measure.
Step 5. According to the comparison law, rank the
${\tilde{r}_{i}}=({r_{i}},{a_{i}})$ $(i=1,2,3,4)$ in descending order:
Step 6. Rank all of the alternatives
${X_{i}}$ $(i=1,2,3,4)$ as follows:
Therefore, the best alternative is ${X_{3}}$, i.e. the best alternative is the computer company.
From the comparison with interval 2-tuple linguistic distance of Liu
et al. (
2014b), the newly proposed approach and Liu’s have their own merits. For one thing, the interval 2-tuple linguistic distance (Liu
et al.,
2014b) is defined by endpoints of interval-valued 2-tuple linguistic information. This measure varies with the uncertain linguistic environment in GDM and makes it more flexible in diverse circumstances. For another, the approach proposed in this paper is able to provide more decision-related information such as order-inducing variables in the
IT-ICOWD measure, the weighting vector of decision makers and the weighting vector of attributes. This enables decision-making process more evidential and reliable, and these intermediate results can be applied for multiple times when necessary. However, this benefit requires more efforts in computation, opposed to Liu’s approach. Therefore, decision makers who request a deterministic answer as well as reasonable and solid evidence would prefer the novel
IT-ICOWD measure regardless of computational complexity.

