Abstract
The new nonlocal delayed feedback controller is used to control the production of drugs in a simple bioreactor. This bioreactor is based on the enzymatic conversion of substrate into the required product. The dynamics of this device is described by a system of two nonstationary nonlinear diffusion-reaction equations. The control loop defines the changes of the substrate concentration delivered into the bioreactor at the external boundary of the bioreactor depending on the difference of measurements of the produced drug delivered into the body and the flux of the drug prescribed by a doctor in accordance with the therapeutic protocol. The system of PDEs is solved by using the finite difference method, the control loop parameters are defined from the analysis of stationary linearized equations. The stability of the algorithm for the inverse boundary condition is investigated. Results of computational experiments are presented and analysed.
1 Introduction
Mathematical problems of biological systems are attracting a lot of attention from specialists in many fields. In this paper, from mathematical point of view we restrict to models described by non-stationary and non-linear diffusion–reaction equations. The dynamics of their solutions can be very complicated, the interaction of different physical processes can lead to development of spatial and temporal patterns and instabilities (Murray,
2002).
The delayed feedback control mechanism is used in many technological applications (Pyragas,
2006; Novičenko,
2015). The recent developments of this technique for optimal control of processes in smart bioreactors is one of the most interesting new theoretical and computational challenges (Ivanauskas
et al.,
2017; Kok Kiong
et al.,
1999; Yordanova and Ichtev,
2017). Our main aim is to propose a new feedback control algorithm for advanced bioreactors by using nonlocal formulations of the control functionals. This method enables automatic adaptation of rates of produced drugs to the treatment procedures specified by medical doctors. Such a technology gives a very convenient, flexible and robust tool for patients. The analysis is based on virtual simulation of real physical processes and demonstrates a potential of virtual mathematical modelling technique in biomedicine applications.
The rest of this paper is organized as follows. In Section
2 a system of two nonstationary nonlinear diffusion-reaction equations is formulated. This model describes the dynamics of the substrate
S (prodrug) and the product
P (drug). The three classical boundary conditions (two for
P and one for
S) are specified at the boundary of domain. The last fourth boundary condition defines the flux of
P at
$x=0$. Thus a nonclassical combination of boundary conditions is used. The inverse problem is formulated to find the equivalent boundary condition for the substrate function
$S(X,t)$.
In Section
3 the proportional nonlocal controller is proposed in a control loop of the delayed feedback system. The parameters of control function are defined by solving the stationary (limit) system of equations, when the nonlinear interaction term is linearized around some constant value. At the boundary of domain, both the substrate value
$S(X,t)$ and the flux
${D_{S}}{S^{\prime }_{x}}(X,t)$ can be used in the control loop. In addition, the total amount of the produced drug can be controlled by the proposed feedback control algorithm.
The finite volume method is used to approximate the diffusion process in Section
4. The second order symmetrical difference scheme is applied. The time derivatives and reaction terms are approximated by the symmetrical Euler method. The predictor-corrector method is applied to linearize the obtained discrete nonlinear substrate equation.
In Section
5 results of computational experiments are presented. First it is investigated how accurately the unknown boundary condition is recovered by the proposed control loop, when the test functions of the product flux are computed apriori by using some smooth boundary conditions of the substrate. The stability of the algorithm with respect to perturbations of the given drug flux is investigated. Next, two test problems are solved for different known treatment protocols. In both cases the produced drug rates are very close to the required fluxes of the drug. Also, the robustness of the proposed control method is investigated, when the parameters of bioreactors are perturbed. Final conclusions are presented in Section
6.
2 Mathematical Models
In this paper, we consider a simple model used to simulate dynamics of various bioreactors (Hillen and Painter,
2009). It is based on a system of two equations:
where
t and
x are time and space variables,
$S(x,t)$ and
$P(x,t)$ are real valued functions.
S defines the concentration of the substrate of the enzyme and
P is the concentration of a product. This type of bioreactors is interesting for medical applications, since the enzymatic reaction converts a substrate of the enzyme
S (which is a prodrug material) into the active drug
P. Such technology can be considered as a smart technology producing the drug on demand. In the presented model the reaction conversation is described as the most simple Michaelis-Menten process. An extended review of models on nonlinear reactions in bioreactors is given in Murray (
2003), Čiegis and Bugajev (
2012), a very good practical user guide on such models is presented in Hillen and Painter (
2009). We note that this model is also considered in paper Ivanauskas
et al. (
2017). The enzyme is uniformly distributed in the reactor, and the substrate S diffuses in the bioreactor with the diffusion coefficient
${D_{S}}$. The product of the reaction
P diffuses inside the bioreactor with the diffusion coefficient
${D_{P}}$.
It is interesting also to consider more complicated bio-reaction processes (Hillen and Painter,
2009). The second simplification of the presented model is due to the fact that a transport process is described only by the diffusion. For many bioreactors the convection process also significantly influences the behaviour of the devices. Such extensions of the model will be considered in the next paper.
In order to define a full mathematical model we formulate initial conditions
and three boundary conditions:
The last boundary condition specifies the flux of
P at the boundary
$x=0$:
where
$Q(t)$ defines the flux of the drug prescribed by a doctor in accordance with the therapeutic protocol.
Such a combination of boundary conditions is not defining a classical well-posed boundary value problem. In order to use such bioreactors in real life applications, we propose to find the equivalent boundary condition for the substrate function
where
$s(t)$ is unknown function. Then for
S we get a well-posed non-stationary boundary value problem.
In general the inverse problems belong to the class of ill-posed problems (Aster
et al.,
2012). A more flexible for applications mathematical model is obtained if for
$s(t)$ we consider the variational problem (Tikhonov and Arsenin,
1977): find
$s(t)$ such that
where
W defines a feasible set of boundary conditions and
${P_{s}}$ defines a product function, when
$s(t)$ is used as a boundary condition in (
5). In the next section we investigate the stability of the obtained inverse problem and show that it can be treated as a well-posed model with a bounded stiffness constant.
The additional boundary condition (
5) defines a concentration of the substrate at the boundary of the bioreactor
$x=X$. Depending on technological requirements, it is possible also to consider the boundary condition when the incoming flux of the substrate concentration is specified
Again we get a well-posed initial-boundary value problem for
S, if the function
$q(t)$ is given. For the system of equations (
1)–(
4) this function should be obtained by solving the inverse problem.
3 The Delayed Feedback Control Loop
In this section we use the delayed feedback control loop technology (controllers) to achieve the desired regime of drug production (Kok Kiong
et al.,
1999). Instead of solving directly the inverse problem for the boundary condition (
5) (or (
7)) we consider the approach based on the nonlocal delayed feedback control method. Our aim is to select some efficient manipulated variable and to formulate an equivalent well-posed boundary value problem in order to produce the required flux of drugs at the boundary
$x=0$. Thus we are interested to develop a dynamic control system based on proportional delayed feedback controllers.
A classical proportional–integral–derivative controller (PID controller) is used in paper (Ivanauskas
et al.,
2017). The authors have attempted to minimize the error over the drug production by adjustment of a control variable
$S(X,t)$ to a new value determined by a weighted sum:
where
$e(t)=Q(t)-{Q_{R}}(t)$ is the difference between a desired amount of produced drugs
$Q(t)$ and a measured process variable
${Q_{R}}(t)$.
${K_{p}}$,
${K_{i}}$ and
${K_{d}}$ denote non-negative coefficients for the proportional, integral, and derivative terms of the error. The selection of
$S(X,d)$ as a control variable seems quite questionable in this model. The stability analysis of the proposed PID controller is not presented in Ivanauskas
et al. (
2017) and optimal values of coefficients
${K_{p}}$,
${K_{i}}$ and
${K_{d}}$ are selected experimentally.
Our approach to construct the proportional controller is based on the following ideas. The reformulated initial boundary value problem (
1)–(
3), (
5) defines a system of two parabolic type equations. Since for the reaction term we have the estimate
and due to the maximum principle valid for the parabolic problems, the flux of function
P at
$x=0$ depends monotonically on the boundary value
s of the substrate concentration
S.
We are interested to control a so-called steady-state error. Thus the asymptotic analysis of stationary (limit) system of equations is done and the nonlinear interaction term is linearized around some constant value of
S. Due to the maximum principle it is recommended to linearize this term around a zero value of
S. The following system of two linear differential equations for functions
$\tilde{S}(x)$ and
$\tilde{P}(x)$ is considered:
The solution of problem (
9) is given by
Substituting it into (
10) and integrating we get the flux of
$\tilde{P}$ at
$x=0$:
Using this information a simple definition of the proportional controller algorithm is obtained. In order to follow the dynamics of drug flux prescribed by a doctor, the required supply of the substrate into the bioreactor is defined as:
For most applied bioreactors the estimate
$\lambda X\ll 1$ is satisfied. Then we can derive the following estimate of the control parameter
This information gives a possibility for bio-engineers to select optimal parameters of applied bioreactors.
3.1 The Control Algorithm Based on the Boundary Value of Substrate S
The smart bioreactors have a possibility to perform the electrochemical monitoring of the enzymatic reaction. Let us assume that we can measure the concentration of the produced drug flux
${Q_{R}}(t)$. Then the delayed feedback control loop can be used to regulate the substrate supply. In order to define the boundary condition at the time moment
t we can apply one iteration of the boundary value error correction and also include the information on a change of
$Q(t)$ values over time:
where
τ defines a time step. The obtained control algorithm can be considered as a representative of delayed feedback control algorithms (Pyragas,
2006; Novičenko,
2015). Such algorithms are often used in practical computations, but in order to guarantee the stability of the control technique the parameter
μ should be adapted to the behaviour of the system and it is not sufficient to consider the solution of a stationary nonlinear system.
In many cases it is important also to control the total amount of the drug produced during the bioreaction. This additional objective function can be included into the control algorithm by adding the correction into the definition of function
$Q(t)$:
In this algorithm the surplus/deficit of the produced drug is distributed uniformly over time and compensated dynamically during the prolonged remaining working time of the bioreactor. Here
τ defines a time step of the numerical integration algorithms. It should not be interpreted as a time delay of the system reaction to the changes of the boundary condition (
5). In the following sections we investigate such a delay in more details.
3.2 The Control Algorithm Based on the Flux of Substrate S
Let us consider the second case of boundary conditions used in the control system
The solution of problem (
9) with these boundary conditions is given by
Substituting it into (
10) and integrating we get the flux of
$\tilde{P}$ at
$x=0$:
In the control loop, the boundary condition at the time moment
t is defined as
3.3 Approximation of the Flux of P
We consider Taylor series expansion of function
P at point
$x=0$:
Integrating this equation in the interval
$(a,b)$,
$0<a<b<X$, and using the boundary condition
$P(0,t)=0$, we get the estimate
Thus for
$b\ll 1$, the flux of
P at
$x=0$ can be approximated by the integral term:
As it follows from the Taylor series expansion, the approximation error can be estimated as
where
This error should be taken into account when the interval
$(a,b)$ is selected to construct the bioreactor.
As an example we present errors
$e(a,b)$ obtained for approximation of the flux of
$P(x)={e^{x}}-1$ at point
$x=0$, when
${P^{\prime }}(0)=1$:
4 Finite Volume Scheme
In this section we consider the discrete approximation of the problem (
1). Let
${\Omega _{t}}$ be a
t-grid
where
τ is the discretization step. Also we introduce a uniform spatial grid
We consider numerical approximation
${U_{j}^{n}}$ to the exact solution values of function
$U({x_{j}},{t^{n}})$ at the grid points
$({x_{j}},{t^{n}})$.
For functions defined on the grid
${\Omega _{x}}\times {\Omega _{t}}$ we introduce the backward difference quotient and the averaging operator with respect to
t and two difference operators with respect to
x:
We approximate the differential problem (
1)–(
4) by the symmetrical Euler discrete scheme
where
${Q_{Rh}}$ defines a measured value of the product. The proposed discrete model includes the dynamic control condition (
19).
The nonlinear boundary value problem (
18) is linearized by using the predictor – corrector technique. The approximation error is of order two with respect to time and space, i.e. it is bounded by
$C({\tau ^{2}}+{h^{2}})$. It follows from Hundsdorfer and Verwer (
2003), Čiegis and Tumanova (
2010) that for the standard boundary conditions the scheme (
18)–(
20) is also convergent of order two in the
${L_{\infty }}$ norm.
Next we consider in more details the boundary condition (
19). If function
${Q_{Rh}}$ is defined as a direct discrete approximation of the flux of
$P(x,t)$ at
$x=0$, then
If the flux is approximated using integral formula (
17), then applying the trapezoidal quadrature formula we get the product flux approximation:
where
Both boundary conditions with approximations (
21) and (
22) are nonlocal conditions. Since the nonlocal terms are approximated on
$(n-1)$-th level, the standard factorization algorithm is used to solve the obtained systems of linear equations (see, e.g. Leonavičienė
et al. (
2016) for more details on discrete approximations of problems with nonlocal boundary conditions). The stability analysis of the dynamical process will be considered in the next section.
The accuracy of the proposed control algorithm depends on the accuracy of approximation (
22). It was shown above that the approximation error of this formula and quadrature formula is bounded by
$C({h^{2}}+b)$. The discretization error can be controlled by selecting a sufficiently small space grid step
h. The error due to approximation of the flux by the integral formula is bounded by
$Cb$. This error will make a small perturbation of the real flux of the produced drug, since the control technique depends on the approximate flux value
${S_{Rh}}$.
5 Results and Discussion
In this section we present results of some computational experiments. The model constants are selected as in Ivanauskas
et al. (
2017):
Our aim is to validate the new control scheme and to compare the most simple control algorithm with a more complicated control scheme, which includes the dynamic compensation control.
The results of computational experiments have shown that the control quality of boundary condition (
16) is the same as of (
13). Thus we have restricted to presenting results only for the condition (
13).
First we illustrate the important fact that the drug production process reacts with a fixed delay to the changes of the substrate boundary condition (
5). In Fig.
1 the dynamics of product
P molar flow rate at
$x=0$ is shown (a scale factor
${10^{8}}$ is used) when the boundary condition for the substrate
S is a stepwise function (a scale factor
${10^{3}}$ is used):
Such scaling of
S and
P functions is used in presentation of results in all computational examples.
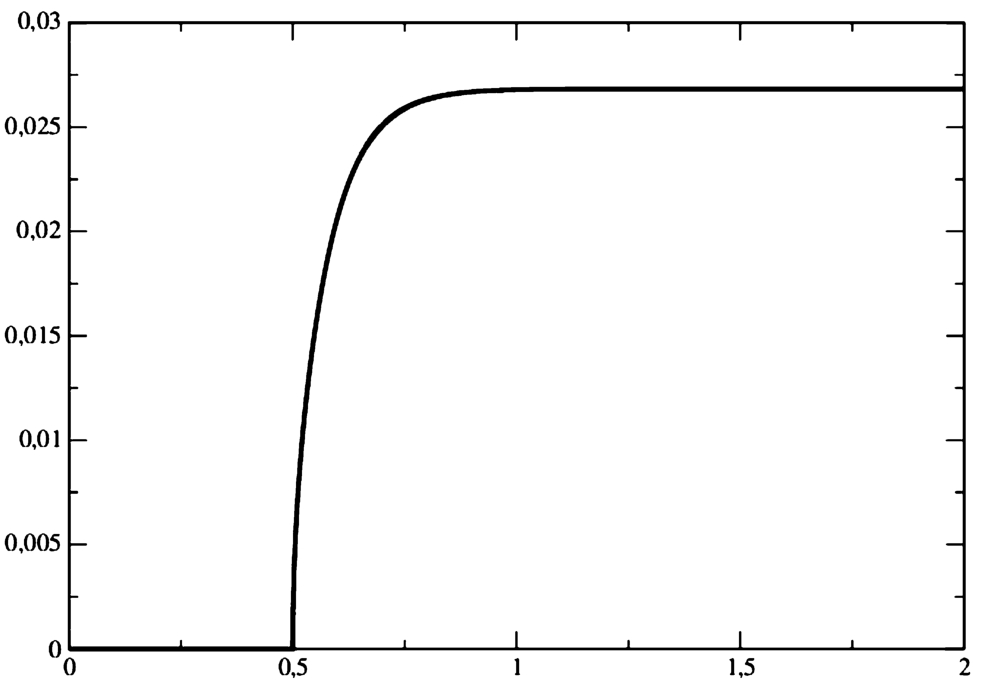
Fig. 1
Product (
P) molar flow rate at
$x=0$, when for the boundary condition (
23) is applied for the substrate (
S).
It follows from the presented results that the response of the product flow rate to the stepwise change of the substrate concentration is delayed approximately 0.25 seconds.
Next we give a brief theoretical justification of the obtained result. and restrict to differential case of models. One general technique to analyse the stability for non-stationary differential problems is to apply the eigenvalue criterion for the space depending operators. Thus we solve the eigenvalue problem
The eigenvalues of this problem are given by
The delay time of the biosystem is defined by the smallest eigenvalue
and
${\lambda _{0}}$ depends on the length of the bioreactor as
$1/{X^{2}}$ for the given typical values of parameters.
The influence of time delay to the stability and efficiency of the control algorithm will be much more important when a convection transport mechanism is included into the mathematical model. Such models will be investigated in a separate paper.
Remark 1.
One important recommendation follows, that the treatment procedures defined by doctors should follow smooth changes of the drug concentration.
5.1 Inverse Reconstruction of the Boundary Condition
In this section we consider the accuracy of the proposed delayed feedback control algorithm. We use this algorithm to reconstruct two typical in real-world applications boundary conditions for the substrate
S. The first one defines a piecewise linear function
The second test boundary condition is defined as
Then the direct problem (
1)–(
3), (
5) is solved and the fluxes of produced drug
${Q_{1}}(t)$ and
${Q_{2}}(t)$ are computed. The numerical approximations of these functions are computed using the discrete scheme (
18), (
20) and the boundary condition
${S_{J}^{n}}={s_{1,2}^{n}}$. Functions
${Q_{1}}(t)$ and
${Q_{2}}(t)$ are shown in Fig.
2.
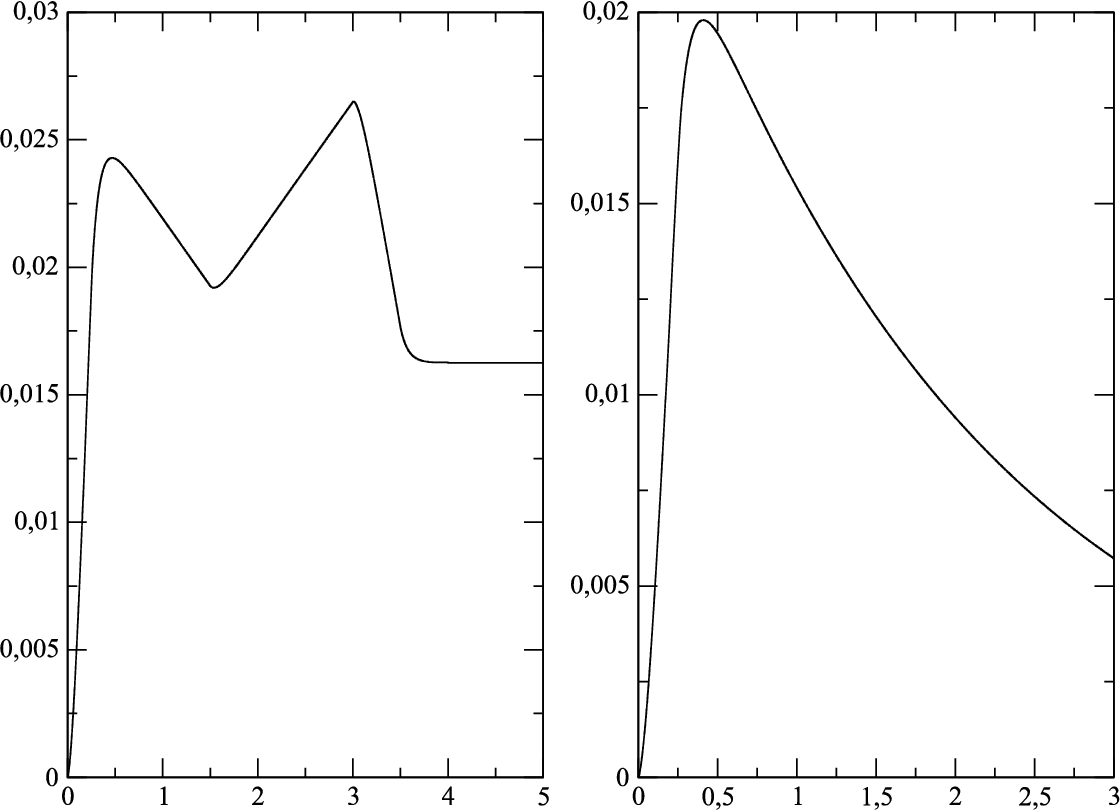
Fig. 2
The fluxes of the produced drug for the specified boundary conditions (
24) and (
25): a)
${Q_{1}}(t)$, b)
${Q_{2}}(t)$.
Then the feedback control algorithm (
12) is applied to reconstruct boundary conditions
${s_{1}}(t)$ and
${s_{2}}(t)$. The control parameter
$1/\mu =181.88$ is computed from formula (
11). The reconstructed functions
${s_{R1}}(t)$ and
${s_{R2}}(t)$ are shown in Fig.
3.
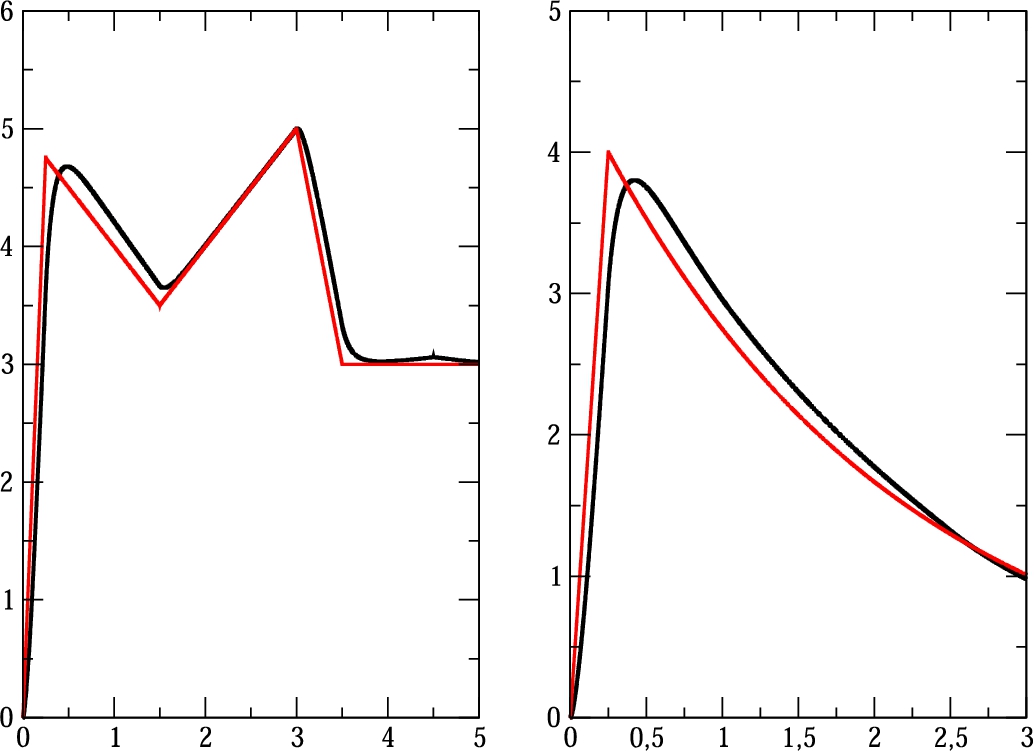
Fig. 3
Reconstructed boundary conditions ${s_{R1}}(t)$ and ${s_{R2}}(t)$: black colour denotes reconstructed solution and red colour denotes the exact boundary condition.
The main conclusion from these results is that reconstructed boundary conditions are approximating the exact boundary conditions sufficiently accurately. It is also clearly seen that the proposed dynamical control of total amount of produced drugs influences the control procedure.
5.1.1 Sensitivity of the Inverse Reconstruction Procedure to Perturbations of $Q(t)$
In general the inverse problems belong to the class of ill-posed problems (Aster
et al.,
2012). Yet, for the given mathematical model the obtained above theoretical stability estimates of the stationary solutions show that well-posedness of the proposed feedback control algorithm can be expected. We also note that the obtained system of two nonlinear PDEs with the prescribed four classical boundary conditions defines a stable mathematical model. Thus the discrete scheme is stable with respect to approximation errors.
In order to test the sensitivity of the inverse reconstruction procedure with respect to perturbations of the function $Q(t)$ we have perturbed exact functions $Q(t)$ using the random number noise. Here our aim is not to regularize the control algorithm by using some averaging or smoothing procedure, but to test if the error of reconstructed flux ${Q_{R}}(t)$ is not increasing essentially due to perturbations of the data.
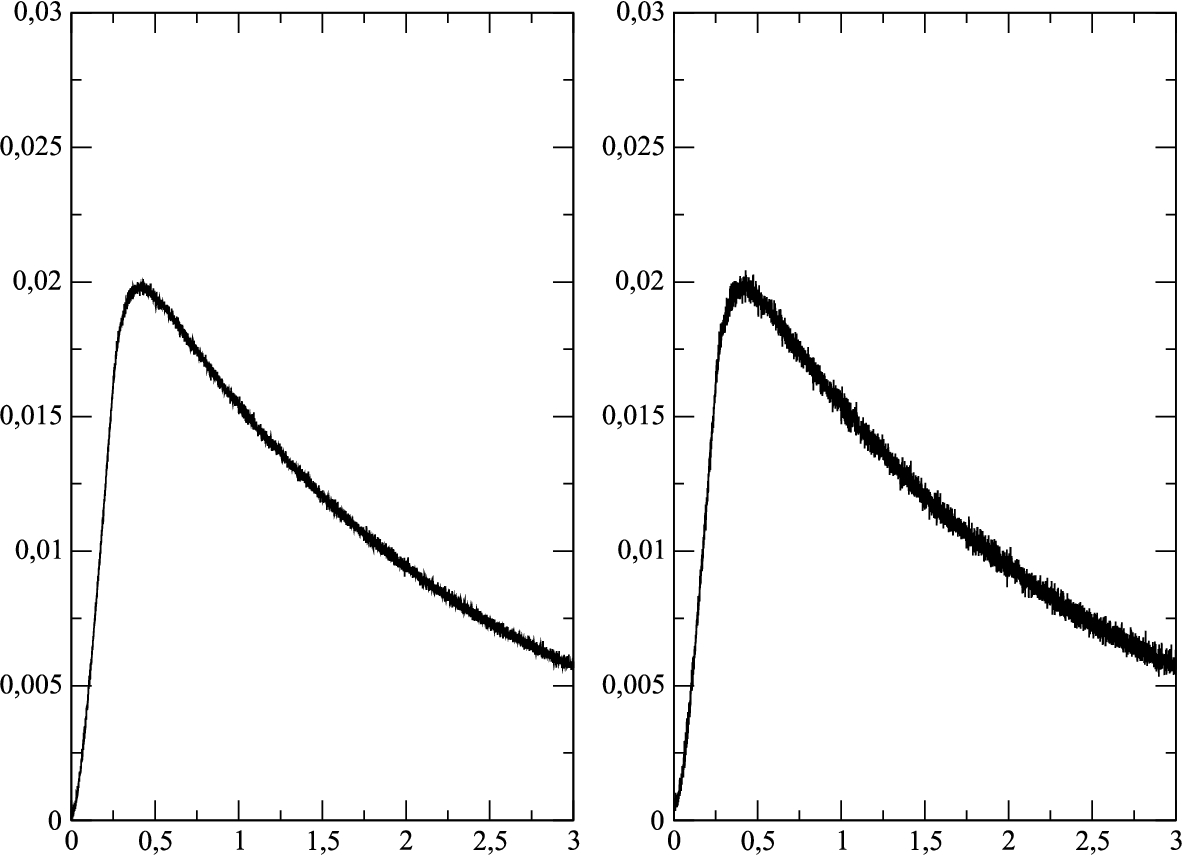
Fig. 4
Reconstructed drug fluxes ${Q_{R2}}$ for perturbed exact fluxes with different perturbation levels of the random noise generator: a) $\eta =0.001$, b) $\eta =0.002$.
In Fig.
4, the reconstructed drug fluxes
${Q_{R2}}(t)$ are presented for two different perturbation levels
$\eta =0.001$ and
$\eta =0.002$. It follows from the presented results that the level of the noise is not increased for the reconstructed drug fluxes
${Q_{R}}$.
5.1.2 Stability Analysis of the Control Scheme
In this section we have investigated the stability of the control algorithm. The standard test is to analyse the reaction of the controlled function
${Q_{R}}(t)$ to the step change of
$Q(t)$:
In Fig.
5, the reconstructed drug flux
${Q_{R}}(t)$ is presented. It is clear that it reaches the stationary solution fast and the amplitudes of oscillations are quite well damped. The overshoot of the solution is due to attempt of the control procedure to keep the specified total amount of the product.
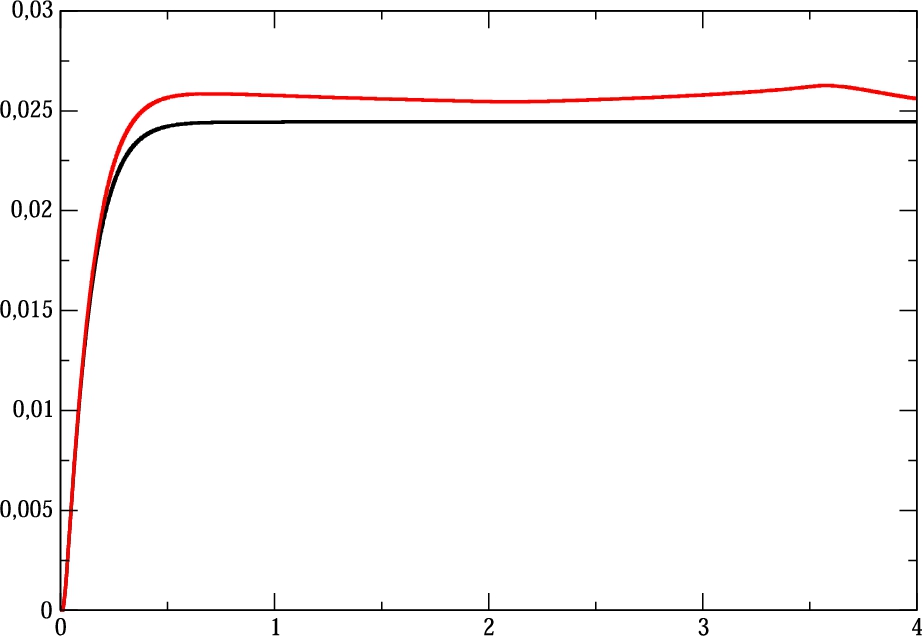
Fig. 5
Reconstructed drug flux ${Q_{R}}$ for the benchmark monitoring step function $Q(t)$.
5.2 Feedback Control of Different Treatment Protocols
In this section the proposed feedback control algorithm is applied for two different treatment protocols, when a short-time treatment process is considered.
The first protocol uses the piecewise linear changes of the drug flow over time, i.e.
${Q_{1}}(t)$ is a scaled version of (
24). In Fig.
6(a) the results are presented when the proportional control algorithm (
12)–(
13) is used to define the substrate supply rate. Control parameter
$1/\mu =181.88$ is computed from formula (
11). The produced drug rate is quite close to the required treatment protocol.
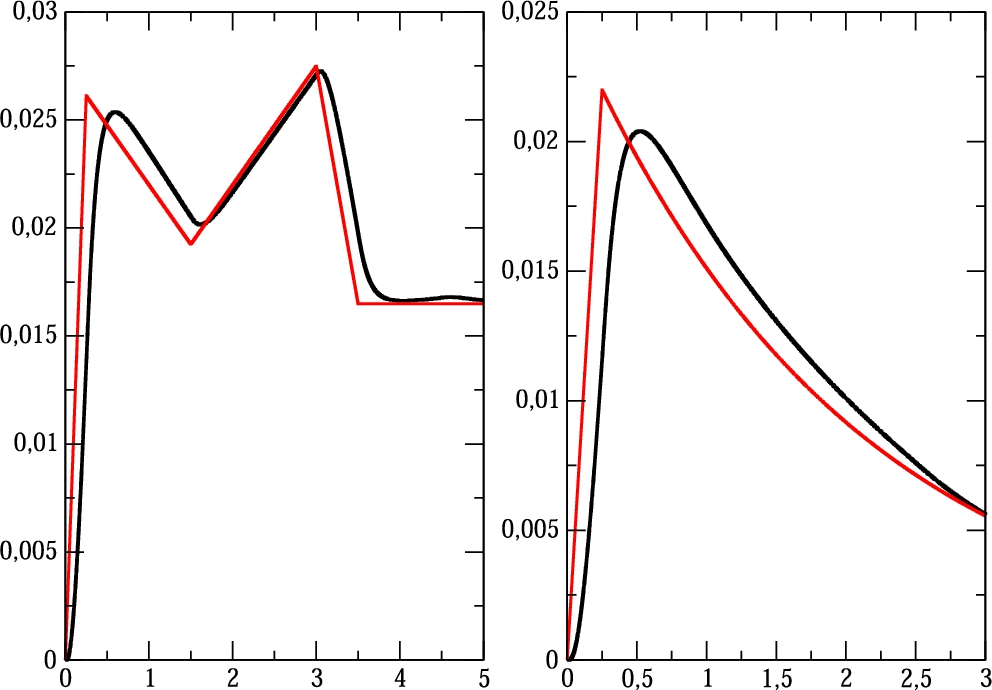
Fig. 6
Application of the proportional control algorithm: a) piecewise linear treatment protocol, red colour function defines the theoretical treatment function $Q(t)$, black colour function defines the produced drug rate ${Q_{R}}(t)$, b) exponential treatment protocol.
The second treatment protocol defines the drug flow which changes exponentially over time. In Fig.
6(b) the results are presented when the proportional control algorithm (
12) is applied. It follows that the produced drug rate is quite accurate for the proportional control algorithm, and the obtained experimental function
${Q_{R}}(t)$ is again adjusted to the required total amount of drugs specified by medical doctor.
5.2.1 Robustness of the Control Method
Robustness of the proposed feedback control method is investigated experimentally. We tested the accuracy of the proposed control algorithm for a fixed value of the control parameter μ and different parameters of the model which are distributed within some compact set. Using the maximum principle which is valid for the given mathematical model we propose to use the maximum value of the control parameter μ computed for the given set of parameters. In computational experiments we have fixed the the control parameter $1/\mu =181.88$ and used it for different values of $V\in [0.0005,0.0011]$ and ${K_{M}}\in [0.2,0.3]$. The obtained results have proved that in all cases the produced drug rate ${Q_{R}}(t)$ was close to the required treatment protocol $Q(t)$.
6 Conclusions
In this paper we have proposed a new delayed feedback control algorithm for a mathematical model which describes the drug delivery system. The system simulates the enzyme-containing bioreactor and the prodrug is converted into an active drug during the reaction. The finite volume method is used to approximate the given nonstationary reaction-diffusion equations. It approximates the system of partial differential equations with the second order in space and time.
The proposed delayed feedback control algorithm is based on solution of two inverse boundary condition problems. The stability of this algorithm is investigated for the case of the stationary solution. This analysis enables us to formulate all parameters of the control algorithm. Results of computational experiments show that the proposed control algorithm is accurate and robust.
Two drug treatment protocols, linear stepwise and exponential, are used to investigate the efficiency of the inverse control algorithm. It is proved that the produced drug flows approximate both investigated treatment protocols with high accuracy. Thus the proposed feedback control algorithm can be recommended to be used in medical practices.
Acknowledgements
Authors would like to thank Prof. J. Janno for fruitful discussions on ill-posedness of the obtained inverse problems.
References
Aster, R., Borchers, B., Thurber, C. (2012). Parameter Estimation and Inverse Problems. Elsevier.
Čiegis, R., Tumanova, N. (2010). Numerical solution of parabolic problems with nonlocal boundary conditions. Numerical Functional Analysis and Optimization, 31(12), 1318–1329.
Čiegis, R., Bugajev, A. (2012). Numerical approximation of one model of the bacterial self-organization. Nonlinear Analysis: Modelling and Control, 17(3), 253–270.
Hillen, T., Painter, K.J. (2009). A users guide to PDE models for chemotaxis. J. Math. Biol., 58(1–2), 183–217.
Hundsdorfer, W., Verwer, J.G. (2003). Numerical Solution of Time-Dependent Advection-Difusion-Reaction Equations.
Springer Series in Computational Mathematics, Vol. 33. Springer, Berlin, Heidelberg, New York, Tokyo.
Ivanauskas, F., Laurinavičius, V., Sapagovas, M., Nečiporenko, A. (2017). Reaction-diffusion equation with nonlocal boundary condition subject to PID-controlled bioreactor. Nonlinear Analysis: Modelling and Control, 22(2), 261–272.
Kok Kiong, T., Wang, Q.-G., Hang, C.C. (1999). Advances in PID Control. Springer-Verlag, London, UK.
Leonavičienė, T., Bugajev, A., Jankevičiūtė, G., Čiegis, R. (2016). On stability analysis of finite difference schemes for generalized Kuramoto-Tsuzuki equation with nonlocal boundary conditions. Mathematical Modelling and Analysis, 21(5), 630–643.
Murray, J.D. (2002). Mathematical Biology I: An Introduction. Springer, Berlin.
Murray, J.D. (2003). Mathematical Biology II: Spatial Models and Biomedical Applications. Springer, Berlin.
Novičenko, V. (2015). Delayed feedback control of synchronization in weakly coupled oscillator networks. Physical Review E, 92, 022919.
Pyragas, K. (2006). Delayed feedback control of chaos. Philosophical Transactions of The Royal Society A, 364, 2309.
Tikhonov, A.N., Arsenin, V.Y. (1977). Solutions of Ill Posed Problems. V.H. Winston and Sons, New York.
Yordanova, S., Ichtev, A. (2017). A model-free neuro-fuzzy predictive controller for compensation of nonlinear plant inertia and time delay. Informatica, 28(4), 749–766.

