1 Introduction
The parallel-batching scheduling models are well-known in many practical applications of the real-life manufacturing systems. In these models, parallel-batching machines allow several jobs to be processed simultaneously in a batch, and the processing time of a batch is equal to the largest processing time of the jobs in that batch (Arroyo and Leung,
2017). The total size of a batch cannot exceed the capacity of the parallel-batching machine, and all jobs in each batch have the same completion time (Abedi
et al.,
2015). Recent research on parallel-batching scheduling problems can be found in Xuan and Tang (
2007), Wang and Tang (
2008), Tang and Gong (
2009), Tang and Liu (
2009), Fan
et al. (
2012), Hazir and Kedad-Sidhoum (
2014), Liu
et al. (
2014), Li and Yuan (
2014), Jia and Leung (
2015), Li
et al. (
2015), He
et al. (
2016), Li
et al. (
2017), Ham (
2017), and Ozturk
et al. (
2017), etc.
In many practices, production scheduling problems involve deteriorating jobs, where a job to be processed later requires longer processing time (Wang and Wang,
2014). As a practical scheduling problem in a steel plant, the longer an ingot waits until the start of the preheating processing time, the more time the steel-making process will take to preheat the ingots (Li
et al.,
2007). Recently, Yin
et al. (
2017) addressed the parallel-machine scheduling problems of deteriorating jobs with potential machine disruptions, and developed pseudo-polynomial-time solution algorithms and fully polynomial-time approximation schemes to solve two different cases. Lalla-Ruiz and Voß (
2016) investigated the parallel machine scheduling problem with step deteriorating jobs, and proposed two novel mathematical models based on the Set Partitioning Problem. Tang
et al. (
2017) addressed a single-machine scheduling problems with two agents and deteriorating jobs, and proposed multiple efficient algorithms for certain special cases. More recent papers considering scheduling jobs with deteriorating jobs include Lu (
2016), Yang
et al. (
2015), Yue and Wan (
2016), Su and Wang (
2017), Zhang
et al. (
2017), Wang and Li (
2017), and Bai
et al. (
2014).
We have also investigated the serial-batching scheduling problems with deteriorating jobs in our previous research (Pei
et al.,
2015a,
2015b,
2017a,
2017b,
2017c, Liu
et al.,
2017). There are some key differences among the previous research and this paper: (1) we focus on parallel-batching scheduling in this paper, while we mainly studied the serial-batching scheduling in our previous papers; (2) Different from other researchers’ previous research (Li
et al., 2011), various groups are further investigated, and the time-dependent setup time is required for processing each group and batch; (3) A new deteriorating function of job processing time is considered for the parallel-batching scheduling, and both single-machine and parallel-machine cases are studied.
To the best of our knowledge, there is no previous research considering these features simultaneously. The main contributions of this paper can be summarized as follows:
-
(1) We study novel integrated scheduling problems by taking into account the combinatorial features of various groups, parallel-batching, deteriorating jobs, and time-dependent setup time simultaneously under the settings of both single-machine and parallel-machine.
-
(2) For solving the single-machine scheduling problem, the structural properties on jobs sequencing in the same and different batches, jobs number argument, and batches sequencing are first proposed. Then, a scheduling rule is developed to solve this problem based on these structural properties.
-
(3) For solving the parallel-machine scheduling problem, we develop a novel hybrid AIS-VNS algorithm incorporating Artificial Immune System algorithm (AIS) and Variable Neighbourhood Search (VNS), and the optimal structural properties and scheduling rules for the single-machine setting are integrated in this hybrid algorithm.
The remainder of this paper is organized as follows. The notations and problem description are given in Section
2. The single-machine and parallel-machine scheduling problems are studied in Sections
3 and
4, respectively. Finally, we conclude the paper in Section
5.
2 Notation and Problem Description
The notation used throughout this paper is first described in Table
1.
Table 1
The list of the notation.
| Notation |
Definition |
| n |
The number of job groups |
| ${G_{i}}$ |
The job set of group i , $i=1,2,\dots ,n$
|
| ${N_{i}}$ |
The number of jobs in ${G_{i}}$, $i=1,2,\dots ,n$
|
| N |
The total number of jobs, i.e. $N={N_{1}}+{N_{2}}+\cdots +{N_{n}}$
|
| ${J_{ij}}$ |
Job j in ${G_{i}}$, $i=1,2,\dots ,n$, $j=1,2,\dots ,{N_{i}}$
|
| ${p_{ij}}$ |
The normal processing time of ${J_{ij}}$, $i=1,2,\dots ,n$, $j=1,2,\dots ,{N_{i}}$
|
| b |
The deteriorating rate of processing jobs |
| ${p_{ij}^{A}}$ |
The actual processing time of ${J_{ij}}$, $j=1,2,\dots ,{N_{i}}$, $i=1,2,\dots ,n$
|
| ${m_{i}}$ |
The number of batches in ${G_{i}}$, $i=1,2,\dots ,n$
|
| ${b_{ik}}$ |
Batch k in ${G_{i}}$, $k=1,2,\dots ,{m_{i}}$, $i=1,2,\dots ,n$
|
| ${A_{ik}}$ |
The normal processing time of ${b_{ik}}$, ${A_{ik}}=\max \{{p_{ij}}:{J_{ij}}\in {b_{ik}}\}$, $k=1,2,\dots ,{m_{i}}$, $i=1,2,\dots ,n$
|
| ${n_{ik}}$ |
The number of jobs in ${b_{ik}}$, $k=1,2,\dots ,{m_{i}}$, $i=1,2,\dots ,n$
|
| ${\theta _{b}}$ |
The deteriorating rate of batches’ setup times |
| ${\theta _{g}}$ |
The deteriorating rate of groups’ setup times |
| ${s_{b}^{ik}}$ |
The setup time of ${b_{ik}}$, $k=1,2,\dots ,{m_{i}}$, $i=1,2,\dots ,n$
|
| ${s_{g}^{i}}$ |
The setup time of ${G_{i}}$, $i=1,2,\dots ,n$
|
| c |
The capacity of the batching machine |
| $S({b_{ik}})$ |
The starting time of ${b_{ik}}$, $k=1,2,\dots ,{m_{i}}$, $i=1,2,\dots ,n$
|
| $C({b_{ik}})$ |
The completion time of ${b_{ik}}$, $k=1,2,\dots ,{m_{i}}$, $i=1,2,\dots ,n$
|
| $P({b_{ik}})$ |
The actual processing time of ${b_{ik}}$, $k=1,2,\dots ,{m_{i}}$, $i=1,2,\dots ,n$
|
| $C({G_{i}})$ |
The completion time of ${G_{i}}$, $i=1,2,\dots ,n$
|
| $P({G_{i}})$ |
The total actual processing time of ${G_{i}}$, $i=1,2,\dots ,n$
|
| ${C_{max}}$ |
The makespan |
Given a set of
N non-preemptively deteriorating jobs to be processed, all jobs are classified into
n groups in advance, and each group contains a certain number of jobs, that is,
${G_{i}}=\{{J_{i1}},{J_{i2}},\dots ,{J_{{N_{i}}}}\}$,
$i=1,2,\dots ,n$. In this paper, we address parallel-batching scheduling problems of a single and parallel-batching machines respectively, considering deteriorating jobs and time-dependent setup time based on various groups and minimizing the makespan as the objective. In the single-machine scheduling problem, all jobs in each group are batched and processed on a single parallel-batching machine. In the parallel-machine scheduling, all jobs in each group are first assigned into parallel machines and then processed on each machine. During the parallel-batching processing, all the jobs within a batch are processed simultaneously (Jia
et al.,
2015), and the completion times of all jobs are equal to that of their belonged batch. It is also required that the maximum number of jobs in a batch cannot exceed the capacity of the parallel-batching machine.
In this paper, we further extend the application of Cheng and Ding (
2000) and Cheng
et al. (
2004) in the parallel-batching scheduling problem combining various groups. If
${J_{ij}}$ is scheduled at the time
t, then its actual processing time is defined as Cheng and Ding (
2000), Cheng
et al. (
2004)
where
${p_{ij}}$ is the normal processing time of
${J_{ij}}$,
$b>0$ is the deteriorating rate of processing jobs, and
t is the starting time for processing
${J_{ij}}$.
Furthermore, the normal processing time of ${b_{ik}}$ is defined as ${A_{ik}}=\max \{{p_{ij}}:{J_{ij}}\in {b_{ik}}\}$, $k=1,2,\dots ,{m_{i}}$, $i=1,2,\dots ,n$. Then, its actual processing time can be obtained by ${A_{ik}}+bt$ where t is the starting time for processing ${b_{ik}}$.
Setup time is required before processing one group or batch, and the setup times of
${G_{i}}$ and
${b_{ik}}$ are defined as follows:
where
${\theta _{g}}$ and
${\theta _{b}}$ are the deteriorating rates of setup time for batches and groups, and
t and
${t^{\prime }}$ are the starting time of processing
${G_{i}}$ and
${b_{ik}}$, respectively.
In the remaining sections of the paper, all the problems are denoted by the three-field notation schema
$\alpha |\beta |\gamma $ introduced by Graham
et al. (
1979).
3 Problem $1|p\text{-}\mathit{batch},{G_{i}},{p_{ij}^{A}}={p_{ij}}+bt|{C_{\max }}$
In this section, we first focus on the single-machine scheduling case. The completion time of the makespan is first given, and the structural properties on jobs sequencing in the same and different batches, jobs number argument, and batches sequencing are proposed. Then, a scheduling rule is developed to solve this problem.
Lemma 1.
For the problem $1|p\textit{-}\mathit{batch},{G_{i}},{p_{ij}^{A}}={p_{ij}}+bt|{C_{\max }}$, given any schedule $\pi =({G_{1}},{G_{2}},\dots ,{G_{n}})$ with all groups arriving at time ${t_{0}}>0$, if the starting time of ${G_{1}}$ $(f=1,2,\dots ,n)$ is ${t_{0}}$, then the makespan is
Proof.
The proof of this lemma can be completed by the mathematical induction. Firstly for
$n=1$, it can be derived that
It can be seen that Eq. (
1) holds for
$n=1$. Suppose that for all
$2\leqslant d\leqslant n-1$, if Eq. (
1) is satisfied, then it can be obtained that
Then,
Thus, Eq. (
1) still holds for
$n=d+1$, and it can be also derived that Eq. (
1) holds for
${G_{n}}$. The proof is completed. □
Lemma 2.
For the problem $1|p\textit{-}\mathit{batch},{G_{i}},{p_{ij}^{A}}={p_{ij}}+bt|{C_{\max }}$, all batches in the same group ${G_{i}}$ $(i=1,2,\dots ,n)$ should be sequenced in non-decreasing order of ${A_{ik}}$ $(k=1,2,\dots ,{m_{i}})$ in the optimal schedule.
Proof.
Here we assume that ${\pi ^{\ast }}$ and π are an optimal schedule and a job schedule, respectively. The difference of these two schedules is the pairwise interchange of these two batches ${b_{dl}}$ and ${b_{d(l+1)}}$ ($l=1,2,\dots ,{m_{i}}-1$, $d=1,2,\dots ,n$), that is, ${\pi ^{\ast }}=({W_{1}},{b_{dl}},{b_{d(l+1)}},{W_{2}})$, $\pi =({W_{1}},{b_{d(l+1)}},{b_{dl}},{W_{2}})$, where ${b_{dl}}$,${b_{d(l+1)}}\in {G_{d}}$, ${m_{d}}\geqslant 2$. ${W_{1}}$ and ${W_{2}}$ represent two partial sequences, and ${W_{1}}$ or ${W_{2}}$ may be empty. It is assumed that ${A_{dl}}>{A_{d(l+1)}}$.
We first give the completion time of
${b_{v}}$ in
${\pi ^{\ast }}$,
Then, the completion time of
${b_{v}}$ in
π is
Since ${A_{dl}}>{A_{d(l+1)}}$, it can be obtained that $C({b_{d(l+1)}}({\pi ^{\ast }}))>C({b_{dl}}(\pi ))$, which conflicts with the optimal schedule. Hence, it should be ${A_{dl}}\leqslant {A_{d(l+1)}}$.
The proof is completed. □
Based on Lemma
2, the following properties of the jobs sequencing in the different batch can be further derived.
Lemma 3.
For the problem $1|p\textit{-}\mathit{batch},{G_{i}},{p_{ij}^{A}}={p_{ij}}+bt|{C_{\max }}$, all jobs in the same group ${G_{i}}$ $(i=1,2,\dots ,n)$ should be sequenced in non-decreasing order of ${p_{ij}}$ $(j=1,2,\dots ,{N_{i}})$ in the optimal schedule.
The proof is similar to that of Lemma
2, and we omit it.
Next we derive the properties on the argument of jobs number in all batches from the same group.
Lemma 4.
For the problem $1|p\textit{-}\mathit{batch},{G_{i}},{p_{ij}^{A}}={p_{ij}}+bt|{C_{\max }}$, it should be ${n_{il}}\leqslant {n_{i(l+1)}}$ for all batches from a certain group ${G_{i}}$, where $i=1,2,\dots ,n$, $l=1,2,\dots ,{m_{i}}-1$.
The proof can be completed based on jobs transferring operations. It is similar to that of Lemma
2, and we omit it.
Then, the following property on the argument of batches number can be further obtained.
Lemma 5.
For the problem $1|p\textit{-}\mathit{batch},{G_{i}},{p_{ij}^{A}}={p_{ij}}+bt|{C_{\max }}$, there should be $\lceil \frac{{N_{i}}}{c}\rceil $ batches and all batches are full of jobs except possibly the first batch for any group ${G_{i}}$ in the optimal schedule, where $i=1,2,\dots ,n$.
Then, based on Lemmas
2–
5, we develop the following optimal jobs batching policy of each group for the problem
$1|p\text{-}\mathit{batch},{G_{i}},{p_{ij}^{A}}={p_{ij}}+bt|{C_{\max }}$.
| Optimal Policy 1 |
-
Step 1. Set $i=1$.
-
Step 2. All jobs are indexed in the non-decreasing order of ${p_{ij}}$ in ${G_{i}}$, $j=1,2,\dots ,{N_{i}}$, and a job list is generated such that ${p_{i1}}\leqslant {p_{i2}}\leqslant \cdots \leqslant {p_{i{N_{i}}}}$.
-
Step 3. Place the first ${N_{i}}-(\lceil \frac{{N_{i}}}{c}\rceil -1)c$ jobs in the first batch of ${G_{i}}$.
-
Step 4. If there are more than c jobs in the job list, then place c jobs in the batch and iterate. Then, all batches are generated in ${G_{i}}$.
-
Step 5. If $i<n$, then set $i=i+1$, go to step 2. Otherwise, end.
|
According to the optimal jobs batching policy of each group, we can further obtain the following property for the optimal sequencing of each group.
Lemma 6.
For the problem $1|p\textit{-}\mathit{batch},{G_{i}},{p_{ij}^{A}}={p_{ij}}+bt|{C_{\max }}$, considering two consecutive groups ${G_{r}}$ and ${G_{r+1}}$, if $\rho ({G_{r}})\leqslant \rho ({G_{r+1}})$, where $\rho ({G_{r}})=\frac{{\textstyle\sum _{k=1}^{{m_{r}}}}{(1+{\theta _{b}})^{{m_{r}}-k}}{(1+b)^{{m_{r}}-k}}{A_{rk}}}{(1+{\theta _{g}}){(1+{\theta _{b}})^{{m_{r}}}}{(1+b)^{{m_{r}}}}}$, $r=1,2,\dots ,n-1$, then it is optimal to process ${G_{r}}$ before ${G_{r+1}}$.
Proof.
Let
${\pi ^{\ast }}$ and
π be an optimal schedule and a job schedule, and their difference is the pairwise interchange of these two job sets
${G_{r}}$ and
${G_{r+1}}$ $(r=1,2,\dots ,n-1)$, that is,
${\pi ^{\ast }}=({W_{1}},{G_{r}},{G_{r+1}},{W_{2}})$,
$\pi =({W_{1}},{G_{r+1}},{G_{r}},{W_{2}})$, where both
${G_{r}}$ and
${G_{r+1}}$ may include one or multiple batches,
${W_{1}}$ and
${W_{2}}$ represent two partial sequences, and
${W_{1}}$ or
${W_{2}}$ may be empty. Here we assume that
$\rho ({G_{r}})>\rho ({G_{r+1}})$, i.e.
and we denote the starting time of processing
${G_{r}}$ as
T.
For
${\pi ^{\ast }}$, the completion time of
${G_{r+1}}$ is
For
π, the completion time of
${G_{r}}$ is
Then, it can be derived that
It conflicts with the optimal schedule. Consequently, the proof is completed. □
Based on the above lemmas and the optimal jobs batching policy, the following Algorithm
1 can be developed to solve the problem
$1|p\text{-}\mathit{batch},{G_{i}},{p_{ij}^{A}}={p_{ij}}+bt|{C_{\max }}$.
Execute Optimal Policy 1.
Calculate $\rho ({G_{r}})=\frac{{\textstyle\sum _{k=1}^{{m_{r}}}}{(1+{\theta _{b}})^{{m_{r}}-k}}{(1+b)^{{m_{r}}-k}}{A_{rk}}}{(1+{\theta _{g}}){(1+{\theta _{b}})^{{m_{r}}}}{(1+b)^{{m_{r}}}}}$, $r=1,2,\dots ,n-1.$
Sequence all groups in the non-increasing order of $\rho ({G_{l}})$, i.e. $\rho ({G_{1}})\leqslant \rho ({G_{2}})\leqslant \cdots \leqslant \rho ({G_{n}})$.
Algorithm 1
To demonstrate the Algorithm
1 for the single-machine problem, a simple simulation case is given. There exist three groups, with
$c=2$,
${\theta _{b}}=0.1$ and
${\theta _{g}}=0.1$. The related parameters of the instance are provided in Table
2.
Table 2
The related parameters of the instance
| Group $(i)$
|
1 |
2 |
3 |
| Job $(j)$
|
1 |
2 |
3 |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
| ${p_{ij}}$ |
0.2 |
0.1 |
0.3 |
0.1 |
0.3 |
0.2 |
0.3 |
0.2 |
0.1 |
0.1 |
The optimal schedule generated by Algorithm
1 is shown as following figure.
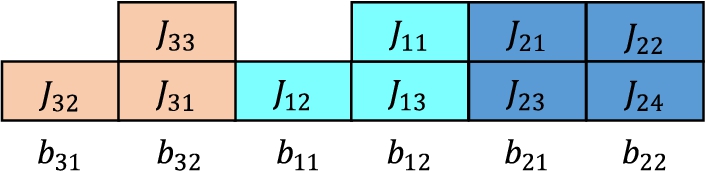
Fig. 1
The schemes of the simulation case on a single machine.
Theorem 1.
For the problem $1|p\textit{-}\mathit{batch},{G_{i}},{p_{ij}^{A}}={p_{ij}}+bt|{C_{\max }}$, and Algorithm 1 can generate an optimal schedule in $O(NlogN)$ time.
Proof.
An optimal solution can be generated by Algorithm
1 based on Lemmas
1–
6 and Corollary 1. The time complexity of step 1 is at most
$O(N\log N)$, the time complexity of step 2 is
$O(1)$, and for step 3 the time complexity of obtaining the optimal group sequence is
$O(N\log N)$. Since we have
$n\leqslant N$, the time complexity of Algorithm
1 is at most
$O(N\log N)$. □
4 Problem $P|p\text{-}\mathit{batch},{G_{i}},{p_{ij}^{A}}={p_{ij}}+bt|{C_{\max }}$
Our studied problem
$P|p\text{-}\mathit{batch},{G_{i}},{p_{ij}^{A}}={p_{ij}}+bt|{C_{\max }}$ can be simplified to the problem of
${P_{m}}||{C_{\max }}$ by relaxing that each parallel-batching machine only processes one job at a time and there is no deteriorating effect. Since Lenstra
et al. (
1977) proved that the problem of
${P_{m}}||{C_{\max }}$ is NP-hard, then the problem of
$P|p\text{-}\mathit{batch},{G_{i}},{p_{ij}^{A}}={p_{ij}}+bt|{C_{\max }}$ is also NP-hard. Thus, we put forward an AIS-VNS algorithm to solve it in this section and furthermore conduct some computational experiments to testify the performance of the proposed algorithm.
Since Variable Neighbourhood Search (VNS) was first proposed by Mladenović and Hansen (
1997), it has been widely used in solving optimization problems. In Hansen and Mladenović (
2001), they summarized the following observations: (1) A local optimal solution with respect to one neighbourhood structure is not necessary for another. (2) A local optimal solution with respect to all neighbourhood structures is the global optimal solution. (3) Different local optimal solutions with respect to different neighbourhood structures are relative to each other. The improved VNS algorithms have been put forward in previous works, for example, Wen
et al. (
2011) extended the search and improved solution quality through the combination of heuristic algorithm, VNS and genetic algorithm. Duarte
et al. (
2015) explored the adaptation of the Variable Neighbourhood Search (VNS) metaheuristic to solve multi-objective combinatorial optimization problems. Similarly, Artificial Immune System algorithm (AIS) is also an effective metaheuristic algorithm that has drawn much attention in recent years. Ying and Lin (
2014) presents a novel hybrid AIS to solve the wafer sorting scheduling problem. Different mechanisms such as the clonal selection theory, the immune response along with its affinity maturation process and the immune network hypothesis can be found in Panigrahi
et al. (
2007), Castro and Zuben (
2000), Komaki
et al. (
2015), and Hashemipour and Soleimani (
2016). This research improves AIS through the introduction of VNS operators.
4.1 Coding and Encoding
In order to improve efficiency of the algorithm, we divide this problem into three stages: (1) schedule within each group to minimize the group processing time; (2) assign groups to machines; (3) sequence the groups on each machine to be processed. The proposed Optimal Policy 1 can solve the problem in the first stage. Moreover, in the third stage, the optimal processing sequence is determined by Algorithm
1. Hence, in the second stage, we use an array of group to represent a solution to our problem. Given a solution
$X=\{2,1,3,1,3,1\}$, these six groups are scheduled on three machines. The object suggests that jobs
$\{2,4,6\}$,
$\{1\}$, and
$\{3,5\}$ are assigned to manufacturers 1, 2, and 3, respectively, and the fitness of
X is calculated by Optimal Policy 1 and Algorithm
1.
4.2 Description of VNS Algorithm
In order to improve the efficiency of AIS, the VNS algorithm is applied as local search strategy to strengthen the optimization ability of the algorithm, the VNS algorithm can be described as follows Castro and Zuben (
2000):
| VNS algorithm |
Define neighbourhood structures ${N_{s}}(s=1,\dots ,{s_{\max }})$.
Execute the sth Local Search for X to obtain a solution ${X^{\prime }}$.
If solution ${X^{\prime }}$ is better than X, then set $x={X^{\prime }}$’, $s=1$ and go to step 3. Otherwise, set $s=s+1$, go to step 5.
If $s\leqslant {s_{\max }}$, then go to step 3; else, stop the iteration.
|
In the VNS strategy, three types of local search operators are selected to define the neighbourhood structures ${N_{s}}$.
Swap operator. Given a solution X, two groups’ positions x and y are selected randomly from the solution. A neighbour of X is obtained by swapping the positions x and y. The detail of swap operator in the VNS is described as follows:
| The detail of swap operator in the VNS |
Randomly generating two different numbers x and y from 1 to n.
Select two groups’ position x and y from the solution X.
Swap the sequence of the positions x and y in X.
Generate a neighbour of X.
|
Mutation operator. Given a solution X, two groups’ positions x and y are selected randomly from the solution. A neighbour of X is obtained by randomly generating a number from 1 to n in the positions x and y. The detail of mutation operator in the VNS is described as follows:
| The detail of mutation operator in the VNS |
Randomly generating two different numbers x and y from 1 to n.
Select two groups’ position x and y from the solution X.
Randomly generate a number from 1 to n in the positions x and y, respectively.
Generate a neighbour of X.
|
2-opt operator. Given a solution X, two groups’ positions x and y are selected randomly from the solution. A neighbour of X is obtained by reversal of the sequence between x and y. The detail of 2-opt operator in the VNS is described as follows:
| The detail of 2-opt operator in the VNS |
Randomly generating two different numbers x and y from 1 to n.
Reverse the sequence between the two groups’ position x and y in the solution X.
Generate a neighbour of X.
|
Figure
2 shows the schemes of these three operators.

Fig. 2
The schemes of swap operator (a), mutation operator (b), and 2-opt operator (c).
4.3 The Algorithm Framework of AIS-VNS
A cross operator and a variation operator are applied in AIS-VNS algorithm, $X=\{{x_{1}},\dots ,{x_{i}},\dots ,{x_{n}}\}$ and $Y=\{{y_{1}},\dots ,{y_{i}},\dots ,{y_{n}}\}$ are used to denote two solutions, and the two operators are defined as follows.
| Cross operator |
Randomly select a groups’ position x from the solution X.
Replace the sequence in X before x with the sequence after x in Y.
|
| Variation operator |
Randomly select a groups’ position x from the solution X.
Generating a number from 1 to n in position x.
|
We improve AIS through the introduction of VNS operators and the algorithm framework of AIS-VNS is described in Table
3. The flow chart of AIS-VNS is also given in Fig.
3.
Table 3
The Pseudocode of AIS-VNS.
| Pseudocode of AIS-VNS |
| 1. |
Initialize parameters, including poplong, PR, tmax, CM, pmax and pmin
|
| 2. |
Set $it=0$, $\mathit{con}=0$, $\mathit{gbest}=a$ large enough positive constant, randomly generate a population $\mathit{pop}=\{{X_{1}},\dots ,{X_{l}},\dots ,{X_{\mathit{poplong}}}\}$ with poplong antibodies, and each solution includes n elements, ${X_{l}}=\{{x_{l1}},\dots ,{x_{li}},\dots ,{x_{ln}}\}$
|
| 3. |
While $(it\leqslant \mathit{tmax})$
|
| 4. |
Calculate fitness for each antibody $\mathit{popfit}=\{{\mathit{fit}_{1}},\dots ,{\mathit{fit}_{l}},\dots ,{\mathit{fit}_{\mathit{poplong}}}\}$
|
| 5. |
If $\mathit{gbest}>{\min _{1\leqslant l\leqslant \mathit{poplong}}}{\mathit{fit}_{l}}$, then |
| 6. |
Set $\mathit{gbest}={\min _{1\leqslant l\leqslant \mathit{poplong}}}{\mathit{fit}_{l}}$
|
| 7. |
End if |
| 8. |
For population pop, $l=1$ to poplong
|
| 9. |
If $\mathit{pmin}<\frac{{\mathit{fit}_{l}}}{\mathit{gbest}}<\mathit{pmax}$, then |
| 10. |
Set $\mathit{con}=\mathit{con}+1$
|
| 11. |
End if |
| 12. |
End for |
| 13. |
If $\mathit{con}\leqslant \mathit{CM}\ast \mathit{poplong}$ then |
| 14. |
For population pop, $l=1$ to $\mathit{poplong}$
|
| 15. |
Set $\mathit{pro}=\frac{1/{\mathit{fit}_{l}}}{{\textstyle\sum _{k=1}^{\mathit{prolong}}}1/{\mathit{fit}_{k}}}$
|
| 16. |
End for |
| 17. |
else |
| 18. |
For population pop, $l=1$ to poplong
|
| 19. |
Set $\mathit{pro}=\frac{{\mathit{fit}_{l}}}{{\textstyle\sum _{k=1}^{\mathit{prolong}}}{\mathit{fit}_{k}}}$
|
| 20. |
End for |
| 21. |
End if |
| 22. |
For population pop, $l=1$ to poplong
|
| 23. |
Generate a random number $\mathit{rand}()$ in $[0,1]$
|
| 24. |
If $\mathit{rand}()\leqslant \mathit{PR}$ then |
| 25. |
Select ${X_{k}}$ from pop with probability ${\mathit{pro}_{k}}$, and perform variation operator for ${X_{k}}$ to get ${Y_{l}}$
|
| 26. |
Else |
| 27. |
Select ${X_{e}}$ and ${X_{k}}$ from pop with probability ${\mathit{pro}_{e}}$ and ${\mathit{pro}_{k}}$, and perform cross operator for them to get ${Y_{l}}$
|
| 28. |
End if |
| 29. |
Perform VNS operators to update ${Y_{l}}$
|
| 30. |
End for |
| 31. |
For population pop, $l=1$ to poplong
|
| 32. |
Set ${X_{l}}={Y_{l}}$
|
| 33. |
End for |
| 34. |
End while |
| 35. |
Output gbest
|
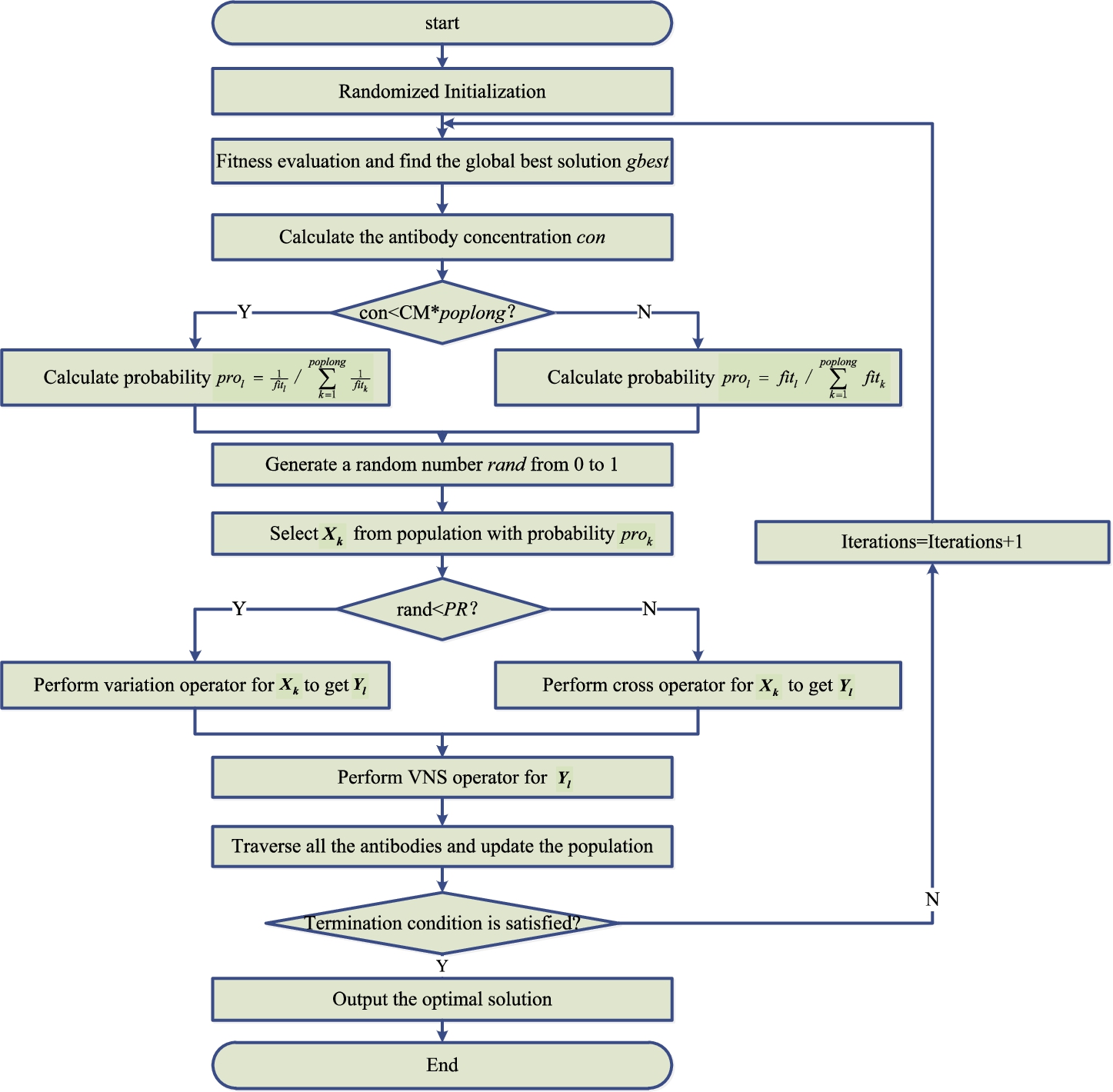
Fig. 3
The flow chart of AIS-VNS.
4.4 Computational Experiments and Comparison
In this section, we present computational experiments to evaluate the performance of our proposed algorithm AIS-VNS, compared with AIS (Castro and Timmis,
2002), VNS (Lei,
2015), and PSO (Ercan,
2008). The test problems were randomly generated based on the real production in Table
4. Based on the number of machines and groups, 16 instances are generated in our computational experiments.
Table 4
Parameters setting.
| Notation |
Definition |
Value |
| n |
The number of groups |
20, 50, 100, 150 |
| M |
The number of machines |
3, 5, 7, 9 |
| ${\theta _{b}}$ |
The deteriorating rate of batches’ setup times |
0.01 |
| ${\theta _{g}}$ |
The deteriorating rate of groups’ setup times |
0.01 |
| c |
The capacity of the batching machine |
3 |
| ${N_{i}}$ |
The number of jobs in ${G_{i}}$, $i=1,2,\dots ,n$
|
$U[1,6]$ |
| ${p_{ij}}$ |
The normal processing time of ${J_{ij}}$, $i=1,2,\dots ,n,$ $j=1,2,\dots ,{N_{i}}$
|
$U[0.1,0.2]$ |
| $CM$ |
The concentration limit in AIS |
0.9 |
| $PR$ |
The variation probability in AIS |
0.9 |
Table
5 lists the results of the average objective value (Avg.Obj) and the maximum objective value (Max.Obj) for the problem.
Table 5
The average objective value (Avg.Obj) and the minimum objective value (Max.Obj) for each algorithm.
| n |
M |
AIS-VNS |
AIS |
VNS |
PSO |
| Ave.Obj |
Max.Obj |
Ave.Obj |
Max.Obj |
Ave.Obj |
Max.Obj |
Ave.Obj |
Max.Obj |
| 20 |
3 |
10.571 |
12.399 |
10.623 |
12.518 |
10.622 |
12.663 |
10.742 |
12.628 |
| 20 |
5 |
4.683 |
5.198 |
4.751 |
5.248 |
4.970 |
5.691 |
4.805 |
5.270 |
| 20 |
7 |
3.289 |
3.547 |
3.425 |
4.065 |
3.666 |
4.745 |
3.441 |
4.076 |
| 20 |
9 |
2.570 |
2.814 |
2.667 |
2.880 |
2.846 |
3.318 |
2.746 |
2.876 |
| 50 |
3 |
217.085 |
296.108 |
220.559 |
300.668 |
217.848 |
301.268 |
226.132 |
330.299 |
| 50 |
5 |
32.665 |
40.856 |
33.121 |
40.914 |
33.461 |
48.288 |
35.945 |
47.115 |
| 50 |
7 |
12.561 |
14.954 |
12.976 |
14.931 |
12.618 |
15.653 |
14.409 |
17.915 |
| 50 |
9 |
8.137 |
8.858 |
8.452 |
9.115 |
8.622 |
10.016 |
9.529 |
11.228 |
| 100 |
3 |
3.490e+4 |
4.777e+4 |
3.577e+4 |
4.815e+4 |
3.513e+4 |
4.791e+4 |
3.774e+4 |
5.025e+4 |
| 100 |
5 |
624.447 |
838.807 |
639.009 |
838.911 |
657.050 |
1020.680 |
782.191 |
1020.226 |
| 100 |
7 |
109.115 |
135.965 |
113.689 |
140.236 |
116.997 |
139.878 |
133.772 |
177.172 |
| 100 |
9 |
43.686 |
46.131 |
45.642 |
51.037 |
46.434 |
54.854 |
61.520 |
73.883 |
| 150 |
3 |
4.909e+6 |
7.376e+6 |
5.005e+6 |
7.701e+6 |
4.918e+6 |
7.445e+6 |
5.486e+6 |
8.058e+6 |
| 150 |
5 |
1.391e+4 |
1.889e+4 |
1..432e+4 |
1.967e+4 |
1.419e+4 |
1.905e+4 |
2.001e+4 |
3.147e+4 |
| 150 |
7 |
899.797 |
1075.621 |
959.789 |
1188.779 |
1063.756 |
1475.763 |
1303.263 |
2050.683 |
| 150 |
9 |
244.268 |
276.081 |
260.709 |
302.718 |
247.808 |
295.556 |
321.250 |
500.599 |
In this experiment, the average of the current optimal solutions for 1 to 400 iterations is used to plot the convergence curves. The convergence behaviours of each algorithm for each instance are shown in Fig.
4.
$(A,B)$ is used to denote various instances. For example, the instance with 20 jobs and 3 machines is represented by (20, 3).
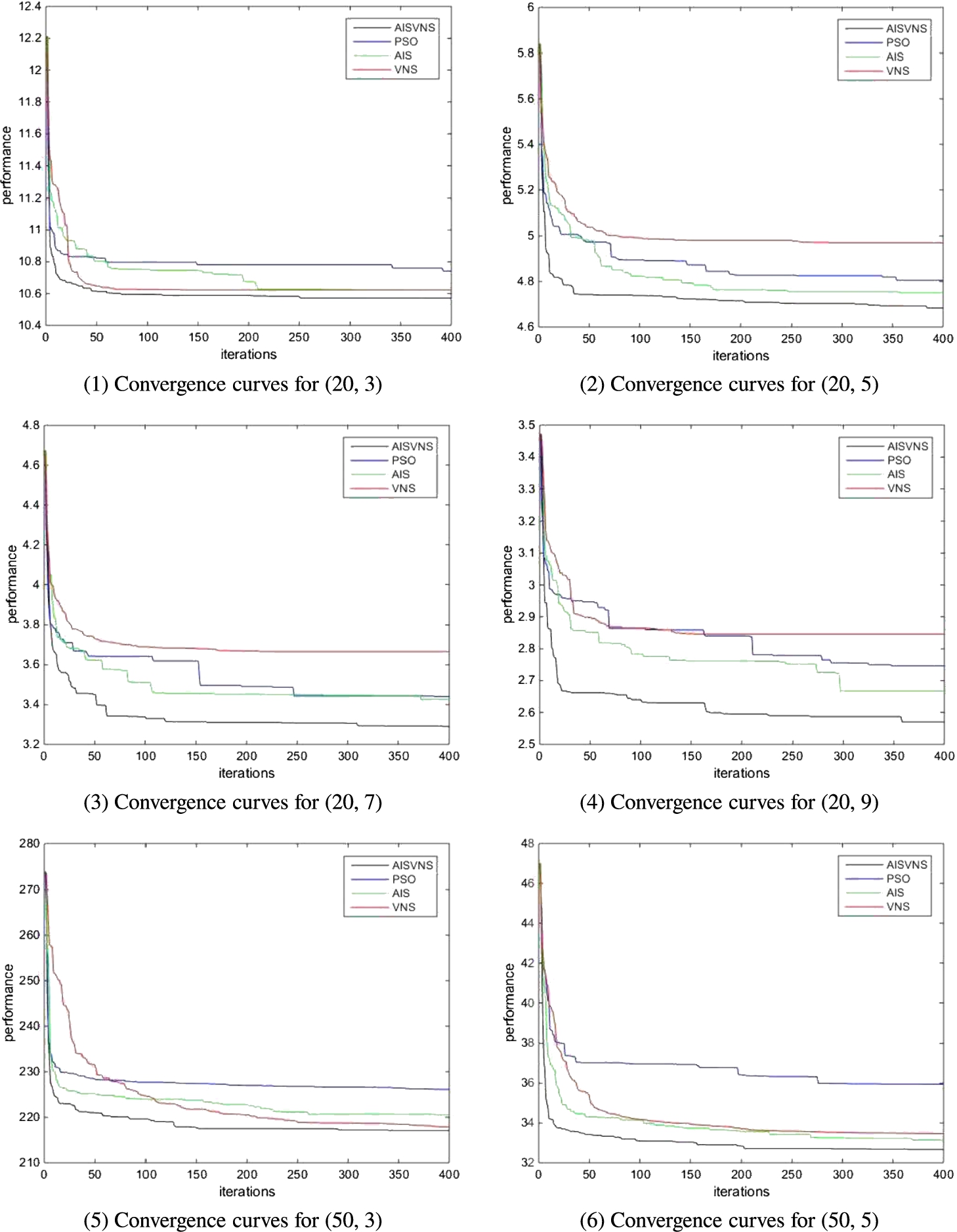
Fig. 4
Convergence curves for each instance.
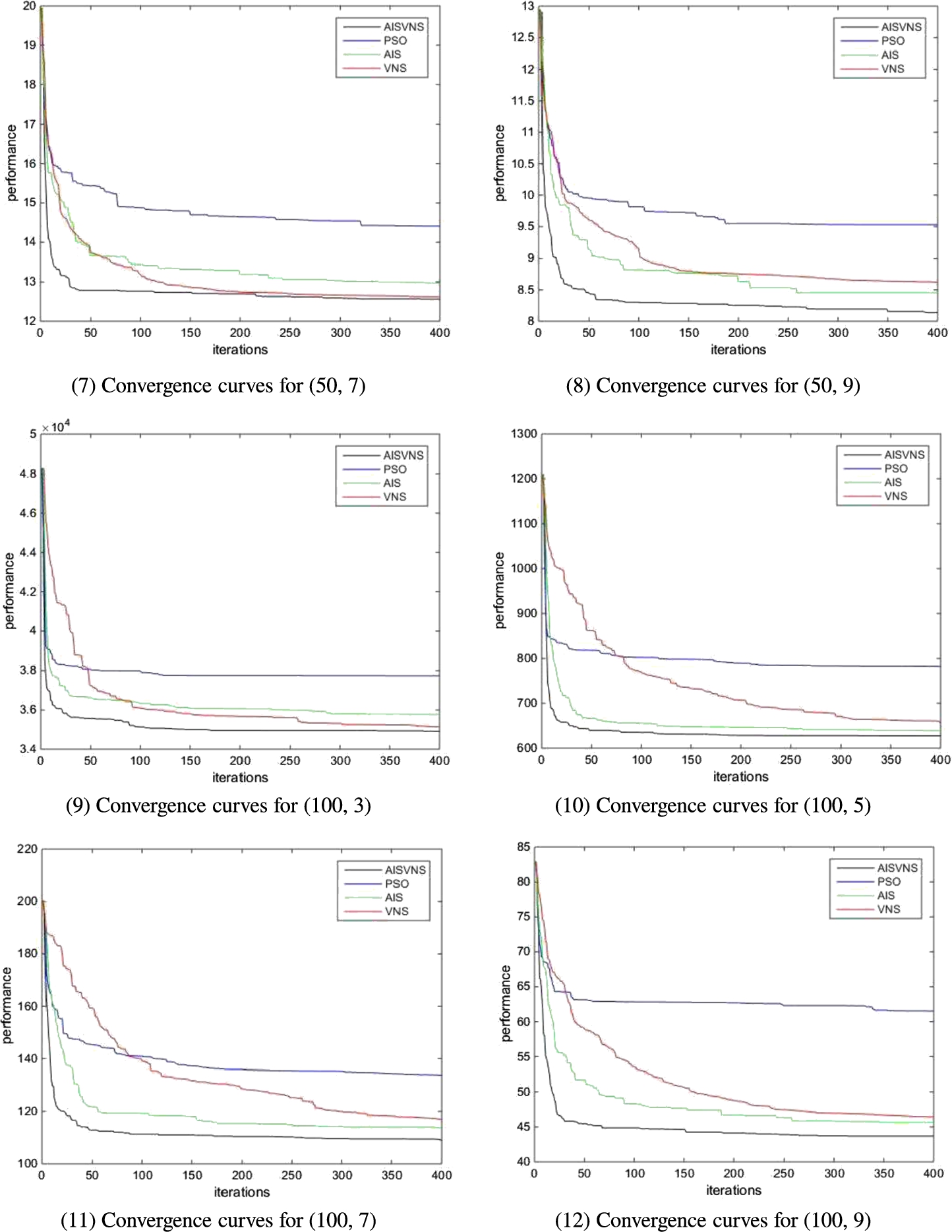
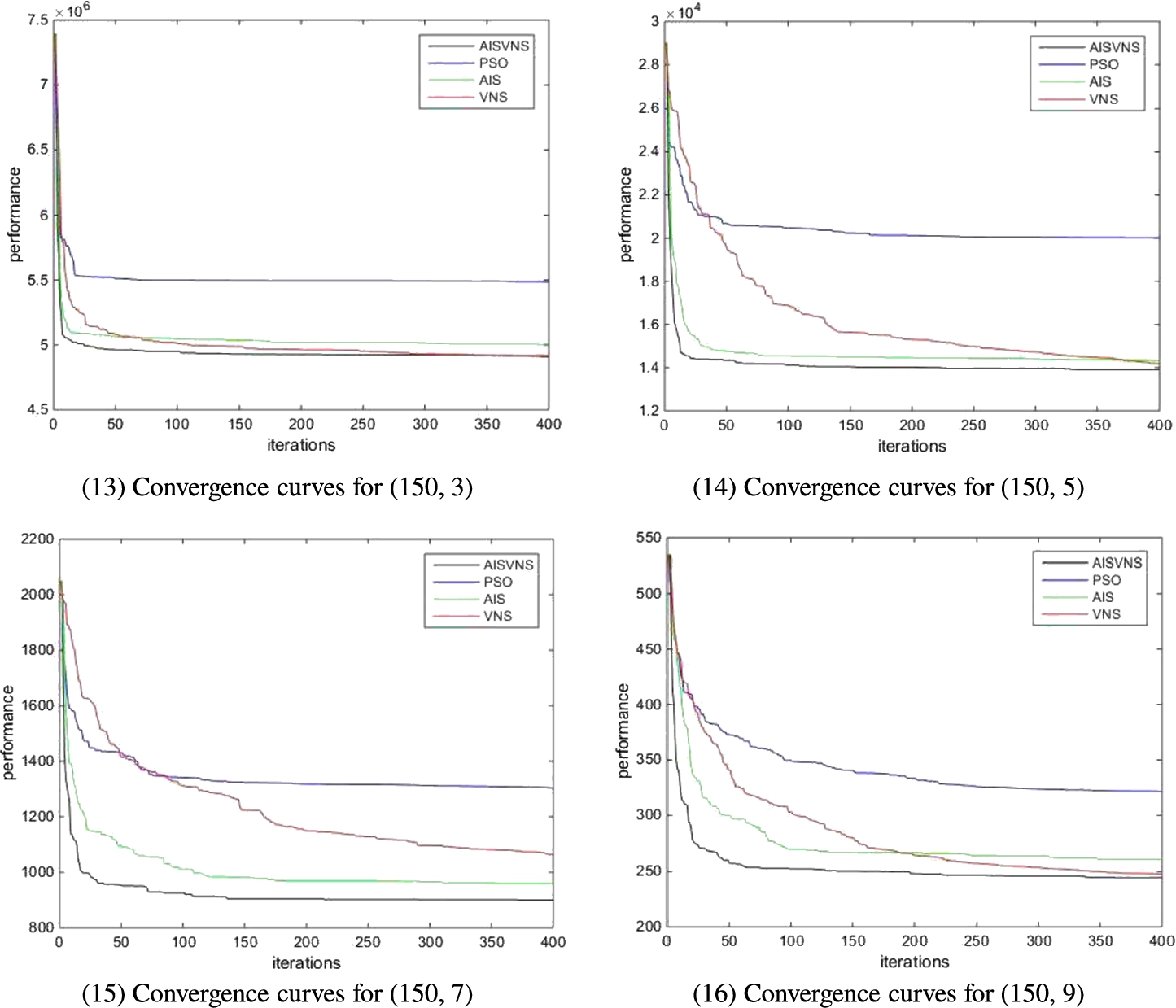
All the algorithms were implemented in C++ and run on a Lenovo computer running Windows 10 with a dual-core CPU Intel i3-3240@3.40 GHz and 4 GB RAM. As can be observed from Fig.
4, AIS-VNS outperforms all the other three methods across the 16 instances in solution quality and convergence. With respect to solution quality, it is worth mentioning that proposed algorithm obtains the best solution within 400 iterations for all the instances. Moreover, AIS-VNS also has better performance than the other algorithms in the form of convergence speed. Since proposed algorithm can converge to a reasonable solution before the 50 iterations in many instances, such as instance 1, 7, 10, 11, 12, 13, 14, 15. It is important to remark that all the available results for AIS-VNS are obtained in reasonable time. For example, per single running time is between 6 and 10 seconds when the number of jobs is 100. Thus, we can infer that the running time of AIS-VNS does not exceed 1 second in a single running. Based on the above experimental results and analysis, we can infer that the proposed AIS-VNS is stable and robust in terms of solution quality and convergence speed in solving the presented problems.

