1 Introduction
Modelling of business processes can be considered on two distinct levels. One concerning visual specification and another related to the verification of processes. BPMN is a predominant visual notation used for processes specification and is used as the starting point for the research presented in the paper. Because BPMN is not provided with a formal semantics, interpretation of a certain business model may be ambiguous. Thus, to verify a model in a formal way, it must be translated onto another formalism. A survey of transformation methods developed for BPMN is presented in Section
2. The most popular formalism used as the aim of such transformations are Petri nets (Lohmann
et al.,
2009). However, some modelling patterns (Russell
et al.,
2006) are hard to handle in Petri nets, e.g. multi-choice, in which execution of a number of branches is chosen. Moreover, it can lead the resulting net to become hard to read or to use Petri net classes, for which analysis may be infeasible. A critical analysis of the approach based on translation of BPMN diagrams onto YAWL (and finally coloured Petri nets) can be found in Börger (
2012). It seems that new methods of expressing BPMN models in a formal way are still worth attention.
In this paper, we introduce a translation from BPMN to the Alvis modelling language (Szpyrka
et al.,
2011a) in order to verify BPMN models formally. Alvis combines the advantages of formal methods and practical modelling languages. Alvis provides a user-friendly syntax from engineers’ point of view, and the visual modelling language (communication diagrams) that is used to define communication among agents. The main difference between Alvis and industry programming languages is a possibility of formal verification of Alvis models using model checking techniques. A short position paper concerning this approach was previously presented during the Intelligent Distributed Computing 2011 conference (Szpyrka
et al.,
2011b). Since then, we extended and evaluated the model. Thus in this paper a complete discussion of our approach is given. One of the main advantages of this approach is the similarity between BPMN and Alvis models. The Alvis model resembles the original BPMN one from the graph structure point of view. Thus, after a verification of the Alvis model, it is easy to link the model properties to the properties of the original BPMN model. Moreover, due to the high level programming language used to define behaviour of Alvis components (agents), it is easy to encode more complex BPMN constructions in the Alvis code layer in order to avoid complex structure of the graphical layer.
The paper focuses on the control-flow perspective of BPMN, i.e. it deals with the order in which activities and events are allowed to occur. An Alvis states are represented using a labelled transition system (LTS) graph. Execution of any language statement is expressed as a transition between formally defined states (Szpyrka
et al.,
2014). In other words, an LTS graph precisely mimics all activities and events of the corresponding BPMN model. The LTS graph is used to verify model properties using model checking techniques (Baier and Katoen,
2008).
The rest of the paper is organized as follows. In Section
2 the BPMN notation is briefly described. Moreover, related works in the area of BPMN mode are presented. In Section
3, a short presentation of selected Alvis features that are essential from the considered problem point of view is given. The transformation method from BPMN to Alvis is described in Section
4. A BPMN use case describing a student project evaluation process is presented in Section
5. Using the case study the verification approach for the BPMN models using Alvis is demonstrated. Conclusion and future work are described in the final section.
2 Related Works in BPMN Formalization
A business process (White and Miers,
2008) (BP) can be defined as a collection of related, structured tasks that produce a specific service or product (serve a particular goal) for a particular customer. Business Process Model and Notation (BPMN) (Allweyer,
2010), developed by the Business Process Management Initiative, is a visual notation for modelling business processes. The notation uses a set of predefined graphical elements to depict a business process and how it is performed. For the purpose of this research, only a subset of BPMN elements is considered. The current version of BPMN (version 2.0) (OMG,
2011) defines three basic types of sub-models to cover various aspects of processes (process, choreography and collaboration sub-models) and provides five diagram types to express different issues of these sub-models:
-
1. Private (internal) process model – describing the ways in which operations within the organization are carried out to accomplish the intended objectives,
-
2. Public (collaborative) process model – showing the operations on the higher abstraction levels in the context of collaboration between the B2B participants,
-
3. Choreography model – defining the expected behaviour between interacting business participants in the process, especially focusing on activities of message exchanging between them,
-
4. Collaboration model – focusing on interaction between participants and exchanged messages,
-
5. Conversation model – specifying the logical relation of message exchanges.
In our research, the internal BP Model is considered. There are four basic categories of elements used to model such processes: flow objects (activities, gateways, and events), connecting objects (sequence flows, message flows, and associations), swimlines, and artifacts.
A task is a type of activity and is represented in the diagram with a rounded-corner rectangle. A model defines the ways in which individual tasks are carried out. Gateways, represented with diamond shapes, determine forking and merging of the sequence flow between flow objects in a process, depending on some conditions. Events denote something that happens in the process and they are represented with circles. The icon within the circle depicts the event type, e.g. an envelope for message event, a clock for timer event.
BPMN does not specify how to define lower level logic. Such logic can be specified in other forms, such as rules, especially modelled in decision tables. Such decision tables can be specified using Decision Model and Notation (DMN) (OMG,
2015), a recent specification from OMG. Although the DMN specification is extensive, it does not clarify all the methodological issues concerning modelling using DMN. Some additional considerations how to use DMN and take advantage of the FEEL expressions can be found in Silver (
2016). The DMN decision tables itself can be formally analysed, e.g. directly using geometric algorithms for detection of overlapping rules and of missing rules (Calvanese
et al.,
2016) or translated into other representation such as XTT2 for checking such properties as completeness, consistency or subsumption of rules (Nalepa
et al.,
2011a).
From our point of view, a major challenge is that as BPMN models are generally not formalized, they can not be verified using formal language verifiers. Thus, such models have to be transformed into a formal language, and then some properties of such models can be verified. Before introducing our original approach we discuss related works in this area.
One of such approaches (Lam,
2010) transforms BPMN models to the New Symbolic Model Verifier (NuSMV) language in order to do a model-checking analysis. This approach has formal foundations and addresses the correctness issue of the transformation. It requires to encode properties of a model using Computation Tree Logic (CTL) formulas.
There are many solutions which focus on checking of selected properties of the BPMN model using approaches based on Petri nets. Raedts et al. presented an approach (Raedts
et al.,
2007) which transforms BPMN models to Petri nets, and these to the mCRL2 process algebraic language. It allows for using the mCRL2 tool-set for verification of the model e.g. revealing the states from where no transitions are enabled (the so-called deadlocks). However, the revealed deadlocks are not directly pointed out in the source BPMN model. So, they have to be manually identified in the BPMN models, what can slow the process of result interpretation.
A similar approach (Dijkman
et al.,
2007), proposed by Dijkman et al., focuses on mapping the BPMN model to Petri Net Markup Language (PNML). After transformation, the ProM tool can semantically analyse the model and check it for absence of dead tasks and incomplete process executions. The approach does not support the OR-join gateways.
Ou-Yang and Lin proposed a Petri-net-based approach (Ou-Yang and Lin,
2008) which evaluates the feasibility of a BPMN model, e.g. to reveal deadlocks and infinite loops. The approach consists in manual translating of the BPMN model to the Modified BPEL4WS representation, and then to Coloured Petri-net XML (CPNXML). The CPNXML representation can be then verified using CPN Tools. The approach has some major limitations, such as limited assessment criteria, and lack of support of the multiple merge and split conditions.
Similar research concerns the translation of BPMN models to Yet Another Workflow Language (YAWL) (van derAalst and terHofstede,
2005) was presented in Decker
et al. (
2008) and formally specified in Ye
et al. (
2008). The model after translation can be checked using a YAWL-based verification tool. The recent research in this field, conducted by Wynn
et al. (
2009), allows for verification of YAWL models with advanced constructs, such as cancellations or OR-joins. It uses mapping of a model to an extended Petri net in order to verify the following properties: soundness, weak soundness, irreducible cancellation regions, and immutable OR-joins. The research concerns the processes modelled in YAWL, but according to the authors, it can be easily applicable to BPMN models. As the abovementioned YAWL approaches consider only the one way (BPMN to YAWL) transformation, the errors revealed in the YAWL model can not be easily tracked in the original BPMN model. Badica et al. consider formalized models using Role Activity Diagrams for BP business process verification (Badica and Badica,
2011a) as well as including logic-based ones in similar multi-agent approaches (Badica and Badica,
2011b). Other formalized approaches in modelling complex heterogeneous information systems include (Stepaniuk
et al.,
2005).
Table 1
Related BPMN verification solutions
| Paper |
Formal language |
Limitations |
| (Aguilar et al., 2011) |
Promela |
– only properties manually defined using LTL formula can be checked |
|
|
– no visualization of the formal language |
| (Lam, 2010) |
NuSMV → CTL |
– only properties manually defined using CTL formula can be checked |
|
|
– no visualization of the formal language |
| (Raedts et al., 2007) |
Petri nets → mCRL2 |
– lack of support for OR-joins |
| (Dijkman et al., 2007) |
Petri nets → PNML |
– lack of support for OR-joins |
| (Ou-Yang and Lin, 2008) |
BPEL4WS → CPNXML |
– limited assessment criteria |
|
|
– lack of support of the multiple merge and split conditions |
| (Decker et al., 2008), (Ye et al., 2008) |
YAWL → Petri nets |
– lack of support for OR-joins |
| (Wynn et al., 2009) |
YAWL → Petri nets |
– errors revealed in the YAWL model can not be easily, tracked in the BPMN model |
Several limitations of the existing solutions are summarized in Table
1. In the existing solutions, including our approach, only a subset of BPMN models is capable to be verified (or possible for transformation). Thus, most of the solutions do not support more advanced BPMN constructs. Our solution supports OR-joins as well as multiple merge and split conditions. Moreover, to the best of our knowledge, only our solution takes into account the interaction with external participants (presented as black box pools in BPMN models).
The main drawback of other solutions is that it is difficult to map the resulting model back to the BPMN one. It is not straightforward to find the corresponding structure in the BPMN model when an error is revealed in the model after translation. From the structure point of view the Alvis model resembles the original BPMN one, thus after verification of the Alvis model, it is easy to link the model properties to the properties of the original BPMN model.
3 Alvis Modelling Language
Alvis (Szpyrka
et al.,
2011a,
2014; Matyasik
et al.,
2016) combines the advantages of formal methods and practical modelling languages. The main differences between Alvis and more classical formal methods, like Petri nets and process algebras, include the syntax that is more user-friendly from engineers’ point of view, and the visual modelling language (communication diagrams Szpyrka
et al.,
2016) that is used to define communication among agents. The main difference between Alvis and industry programming languages is a possibility of formal verification of Alvis models using model checking techniques.
An Alvis model is a system of
agents that usually run concurrently, communicate with each other, compete for shared resources etc. An agent denotes any distinguished part of the system under consideration with a defined identity persisting in time. To describe all dependencies among agents Alvis uses two model layers: graphical and code one. The
code layer is used to define the behaviour of individual agents. Each agent is described with source code implemented using Alvis statements (Szpyrka
et al.,
2011a). From the code layer point of view, agents are divided into
active and
passive ones.
Active agents perform some activities and each of them can be treated as a thread of control in a concurrent or distributed system.
Passive agents do not perform any individual activity, but provide a mechanism for the mutual exclusion and data synchronization. The
graphical layer (communication diagram Szpyrka
et al.,
2016) is used to define interconnections (communication channels) among agents. Communication diagram is a hierarchical graph whose nodes may represent both kinds of agents (
active or
passive) and parts of the model from the lower level. The diagrams allow programmers to combine sets of agents into modules that are also represented as agents (called
hierarchical ones). A survey of Alvis graphical items and code statements is given in Fig.
1.
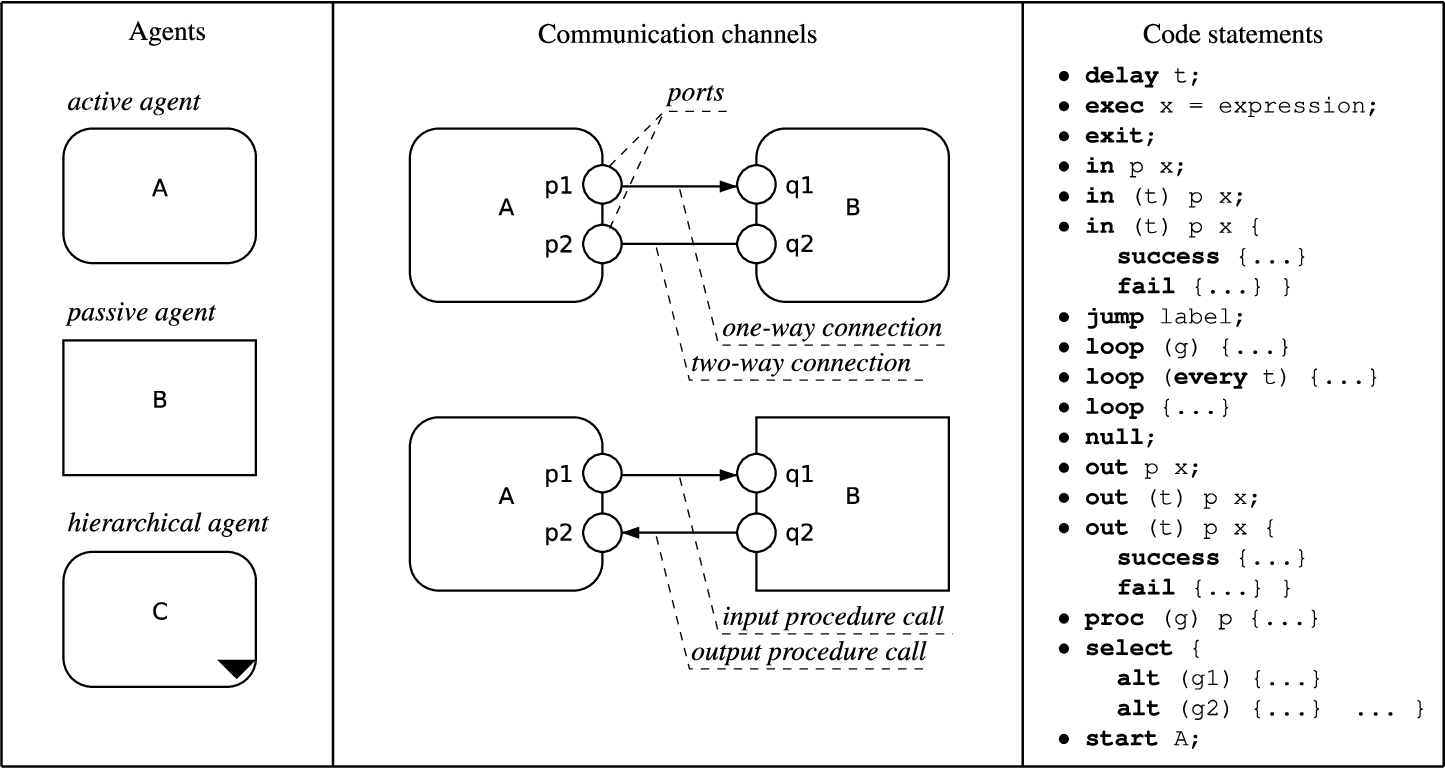
Fig. 1
Elements of Alvis modelling language.
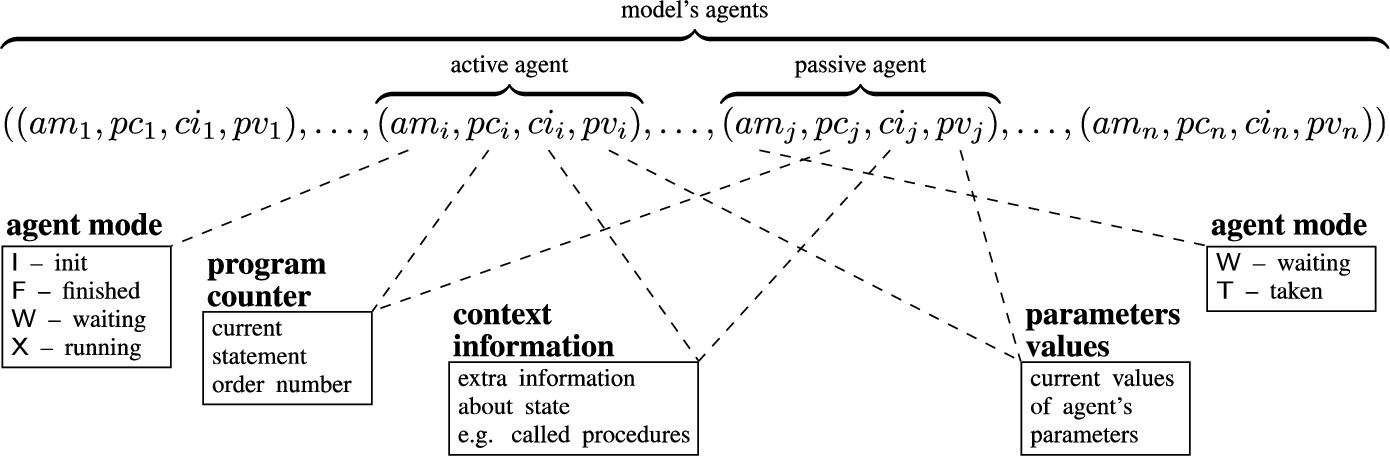
Fig. 2
Representation of an Alvis model state.
A state of an Alvis model is represented as a sequence of agents states. To describe the current state of an agent a four-tuple is used (Szpyrka
et al.,
2014): agent mode, program counter, context information list and parameters’ values tuple (see Fig.
2). An active agent can be in one of the following modes:
finished (F),
init (I),
running (X) and
waiting (W), while a passive agent can be either in
waiting (W) or in
taken (T) mode. The program counter points out the current statement of an agent, i.e. the next statement to be executed or the statement that has been executed by an agent but needs a feedback from another agent to be completed. The context information list contains additional information about the current state of an agent, e.g. if an agent is in the
waiting mode,
$ci$ contains information about events the agent is waiting for. Finally, a parameters’ values tuple contains the current values of the agent parameters.
States of an Alvis model and transitions among them are represented using a labelled transition system (LTS graph for short). An LTS graph is an ordered graph with nodes representing states of the considered system and edges representing transitions among states. LTS graphs are a universal method of a state space representation and are omnipresent in formal modelling languages. Different languages like Petri nets, time automata, process algebras etc. use different methods of describing nodes and edges in LTS graphs. They also use different names for them, e.g. reachability graphs in Petri nets, but the general structure of these graphs is still the same. In spite of the availability of dedicated tools designed for specific formalisms, there are also universal tools for verification of LTS graphs regardless of the formalism that is the source of such an LTS graph generation. Usually, such tools use model checking techniques for an LTS graph verification (Baier and Katoen,
2008).
Alvis LTS graphs can be verified using the CADP toolbox (Garavel
et al.,
2007). CADP offers a wide set of functionalities, ranging from step-by-step simulation to massively parallel model-checking. Alvis Compiler provides a possibility to export an LTS graph into the CADP Aldebaran format. Then, such a graph can be converted into BCG (Binary Coded Graphs) format that is one of acceptable input formats for CADP Toolbox. The conversion method is provided by one of CADP tools. The BCG format is independent from any particular model-based verification technique; it can be used either by tools performing graph comparison and reduction modulo equivalence relations, or by tools checking properties expressed in temporal logics. One of CADP tools called
evaluator provides on-the-fly model checking of regular alternation-free
μ-calculus formulas (Emerson,
1997a; Mateescu and Sighireanu,
2000). The Alvis language is supported by Alvis Toolkit software that, among other things, provides Alvis Editor used for developing models and Alvis Compiler used to generate LTS graphs.
4 BPMN to Alvis Translation
The most fundamental rule of the transformation algorithm is to treat each activity, event and black box pools in a BPMN model as an active agent in Alvis (Szpyrka
et al.,
2011a). Thus, an Alvis model structure is similar to the corresponding BPMN model and errors found in an Alvis model can be easily located in the corresponding BPMN one. Moreover, a split gateway is merged with its preceding activity and a merge gateway is merged with its succeeding activity. Other BPMN elements are usually represented in Alvis as agents’ ports and/or sequences of Alvis statements used to describe behaviour of the corresponding agents.
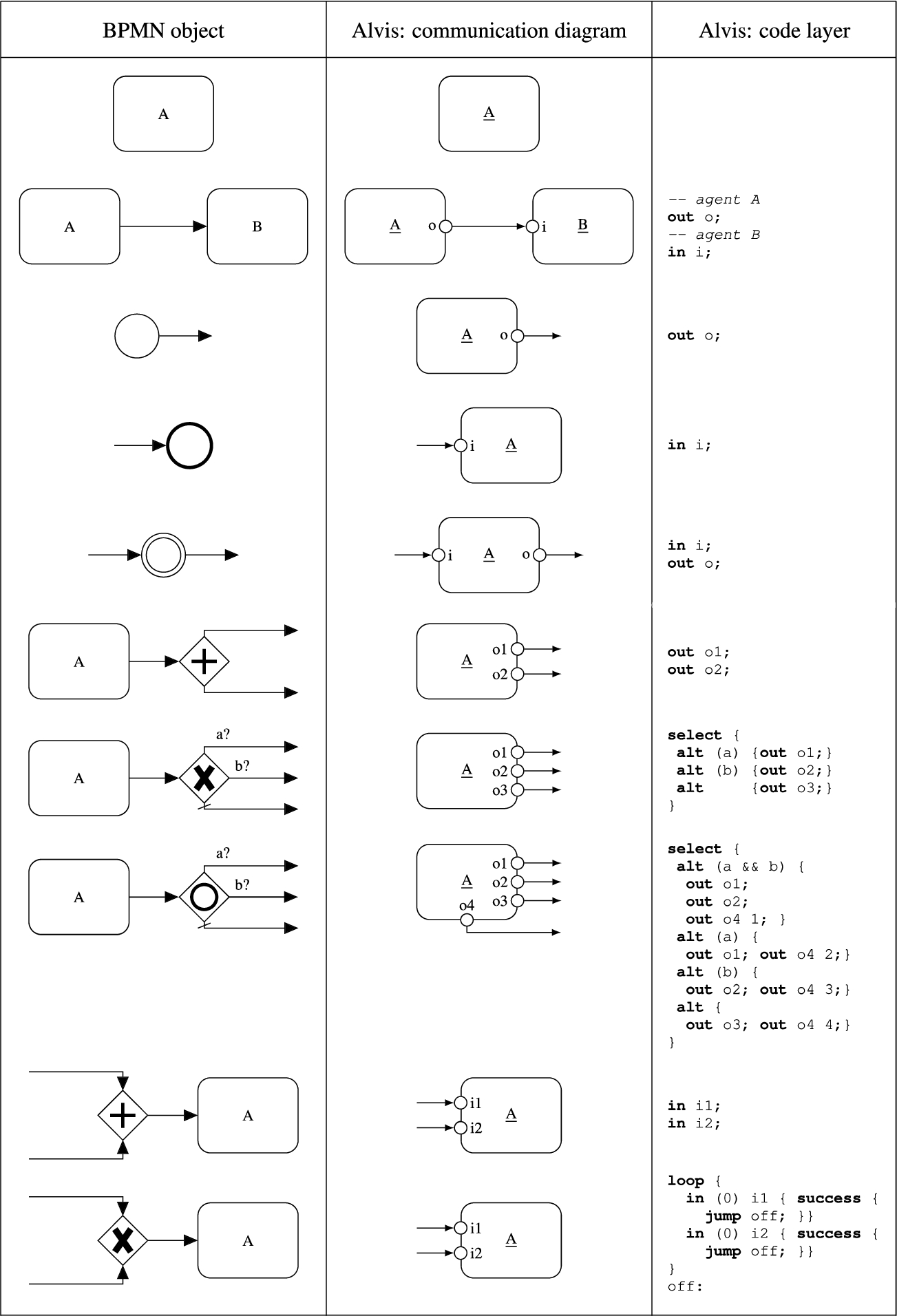
Fig. 3
Mapping BPMN objects onto Alvis (part 1).
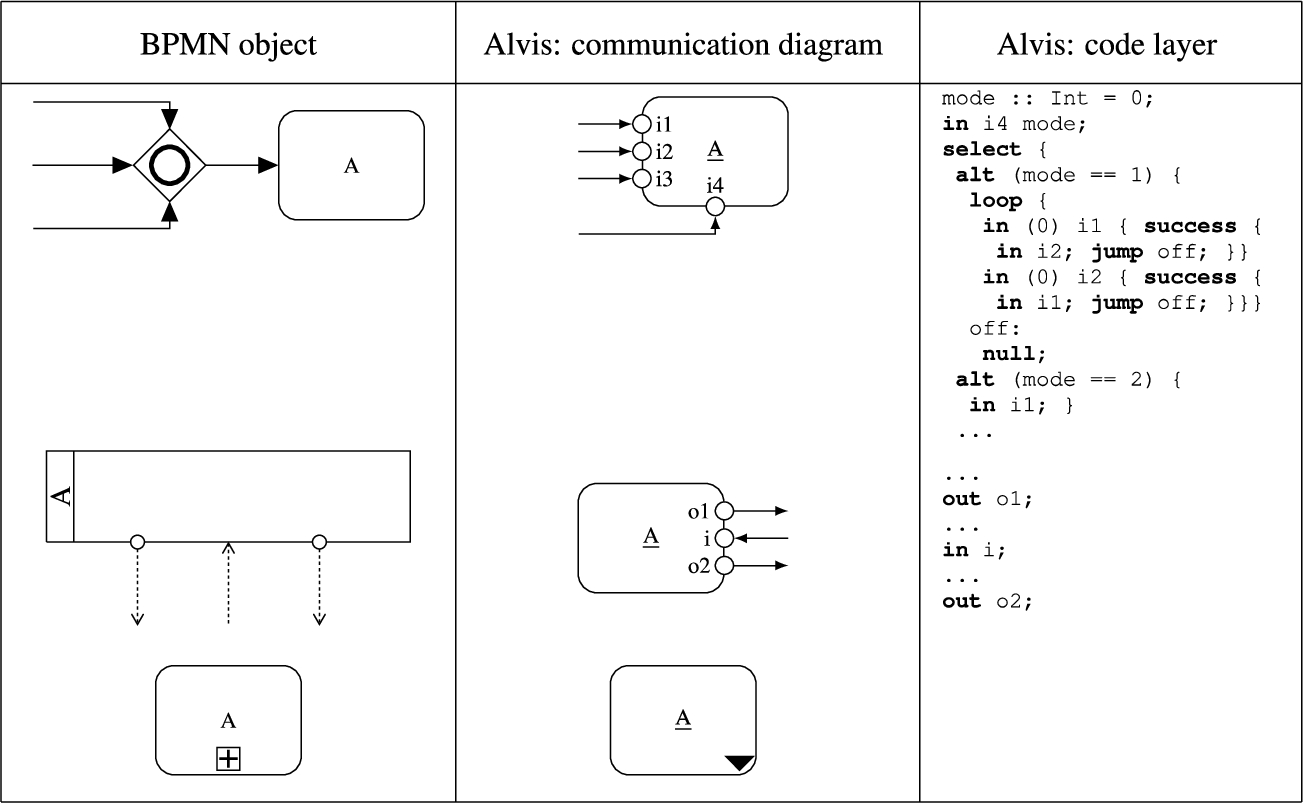
Fig. 4
Mapping BPMN objects onto Alvis (part 2).
Figures
3 and
4 depict the mapping from BPMN objects to parts of an Alvis model. The figures present both parts of the communication diagram and essential pieces of code from the code layer. Active agents are labelled with the name of the corresponding task or pool. In case of events the agent name may be composed of the name of the event e.g. message, timer etc. and its order number. We use
i and
o, with an index if necessary, to denote input and output ports respectively. However, if a flow is labelled, the label may be used as the corresponding port name.
The process flow between two activities is represented by a valueless signal sent between the corresponding agents. A start event is mapped onto an active agent with a single output port. It should be emphasized that more than one connection can lead from the port. Similarly, an end event is mapped onto an active agent with a single input port. An intermediate event is mapped onto an agent with two ports. The period between executing the
in and
out statements denotes the
waiting for the event. Intermediate events anchored to activities are mapped to ports belonging to the corresponding agent. Such an example is shown in Section
5.
Let us suppose that an activity is followed by a single split gateway. Any split gateway (and the preceding activity) is mapped onto an agent with an output port for each flow leading from the gateway. However, the assigned piece of code depends on the gateway type. In case of a parallel gateway a valueless signal is sent via each output port. In case of an exclusive gateway conditions are checked and a valueless signal is sent via one port only. To cope with an inclusive gateway an extra output port is used (see Fig.
3 port
$o4$). Each possible behaviour of the considered split inclusive gateway is denoted by an integer that is sent via the port
$o4$ to the agent that represents the corresponding merge inclusive gateway. Thus, the agent “
knows” how many and which signals must be collected to proceed.
Suppose, an activity is proceeded by a single merge gateway. Any merge gateway (and the following activity) is mapped onto an agent with an input port for each flow leading to the gateway. In case of a parallel gateway a valueless signal is collected via each input port. In case of an exclusive gateway the agent uses a loop to check to which port a signal has been provided and collects it. Finally, in case of an inclusive gateway the agent first collects the extra value and stores it in the mode parameter. Then, it collects all necessary signals.
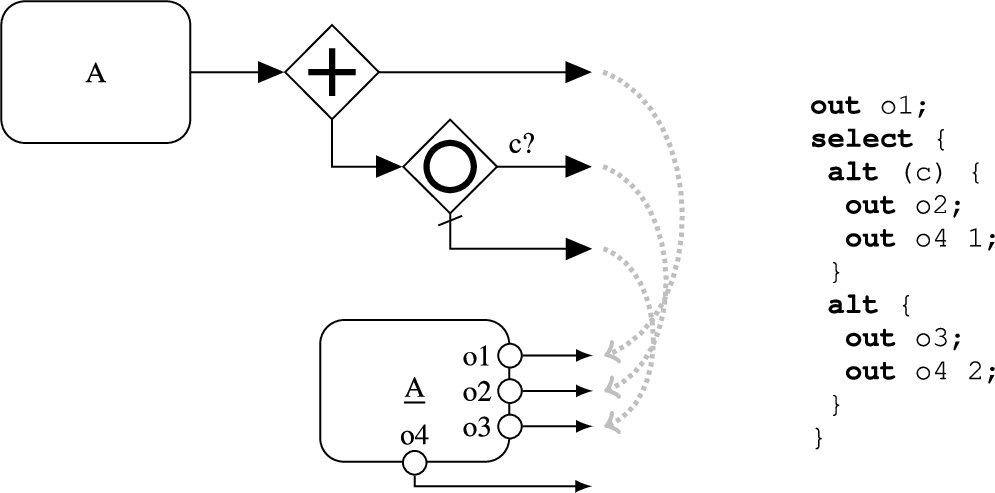
Fig. 5
Mapping two consecutive gateways onto Alvis.
A black box pool is mapped onto an agent with a set of input and output ports that correspond to sent and received messages. Subprocesses are mapped onto hierarchical agents. Moreover, the
loop statement may be used to represent an activity with a loop. Activities with a
multiple instantiation attribute can be represented as a set of agents enclosed between a parallel split and merge gateways, if the number of instances may be determined at the design time. We do not deal with multi-instance activities where the number of instances is only determined at runtime. Similarly to considerations presented in Dijkman
et al. (
2008), if the purpose of the mapping is to check for deadlocks in the process model, we can treat a multiple-instance activity as a single-instance one.
Finally, let us explain how to cope with a sequence of gateways. An example of mapping two consecutive gateways onto Alvis is shown in Fig.
5. Both gateways are considered together. There are three flows leading from these gateways thus the corresponding agent contains three output ports plus an extra output port for the inclusive split gateway. The presented excerpt of Alvis code is the result of combination of the pieces of code for parallel and inclusive split gateways.
5 Case Study
A BPMN use case describing a student project evaluation process is used in this section to illustrate the BPMN to Alvis translation method. The diagram shown in Fig.
6 depicts the evaluation process of a student’s project for the Internet technologies course. This is a slightly reworked version of the BPMN model presented in Szpyrka
et al. (
2011b). The process is applied to the website evaluation. At the beginning, the syntax is automatically checked. Every website code in XHTML needs to be a
well-formed XML and
valid w.r.t. XHTML DTD. If the syntax of the project file is correct, preliminary content checking is performed. Then, if the project contains expected elementary tags (e.g. at least several headings, an image and a table), it can be evaluated and a grade can be given according to some specified evaluation rules (Nalepa
et al.,
2011b). On the other hand, if the project contains any syntax error or lacks some basic required content, it is requested to be completed. After receiving the completed project, the whole process starts from the syntax checking again. However, if the completed project is not received in time, the process is terminated (thus, the author does not get a credit).
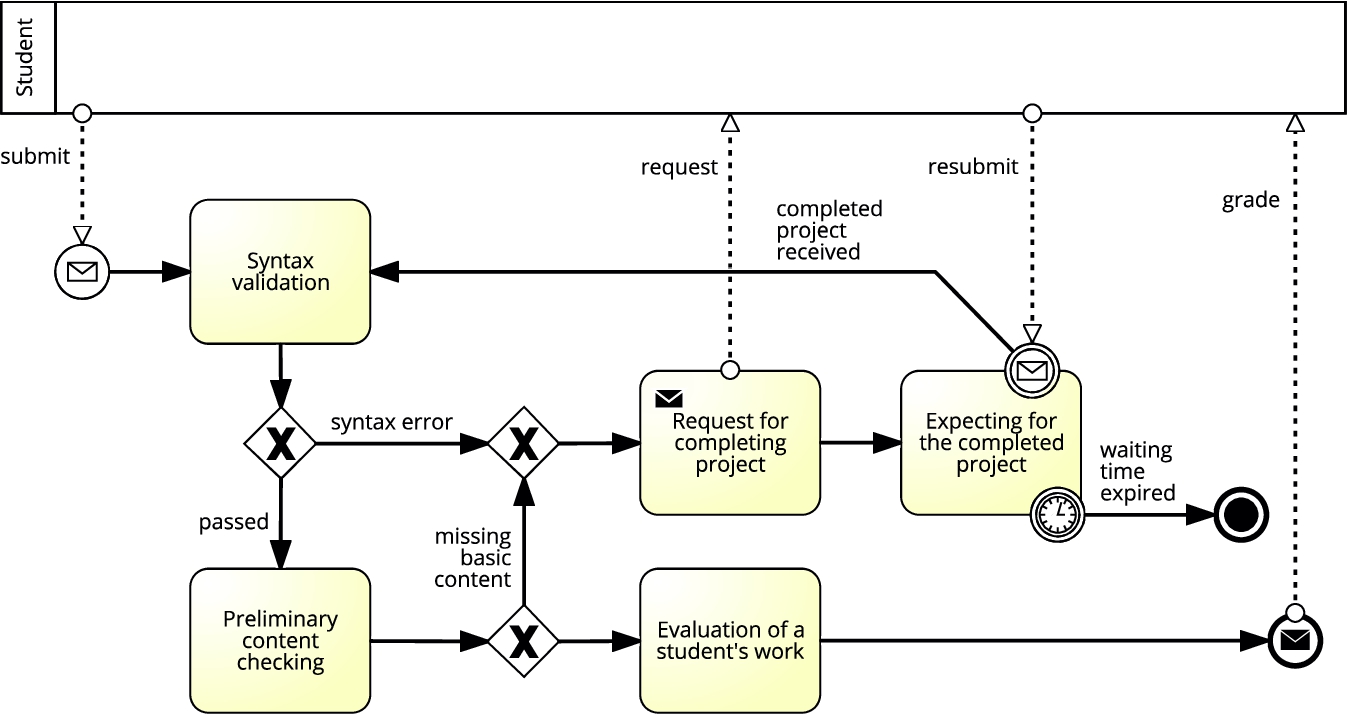
Fig. 6
An example of the student’s project evaluation process.
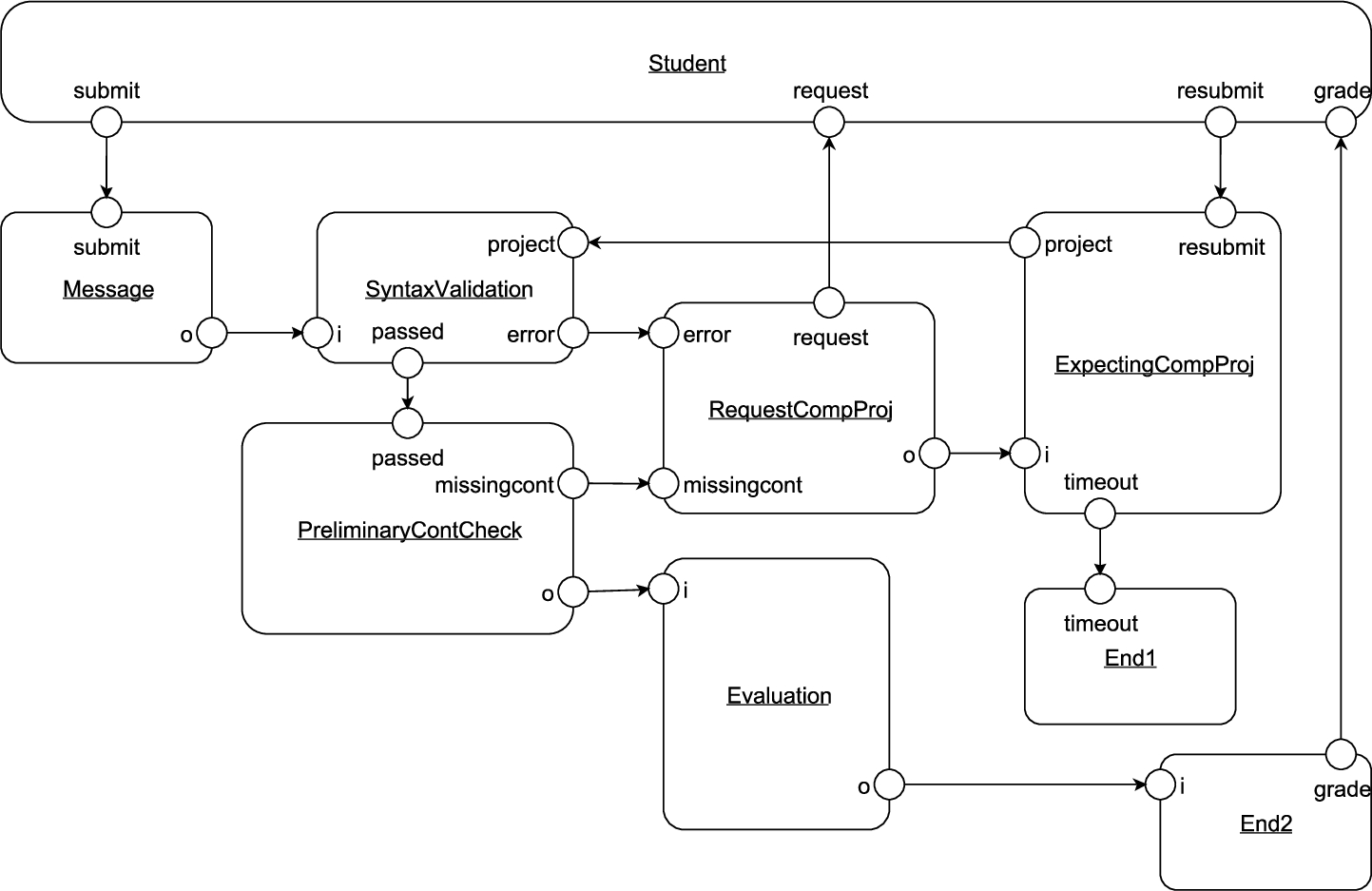
Fig. 7
Alvis model of the student’s project evaluation process (communication diagram).
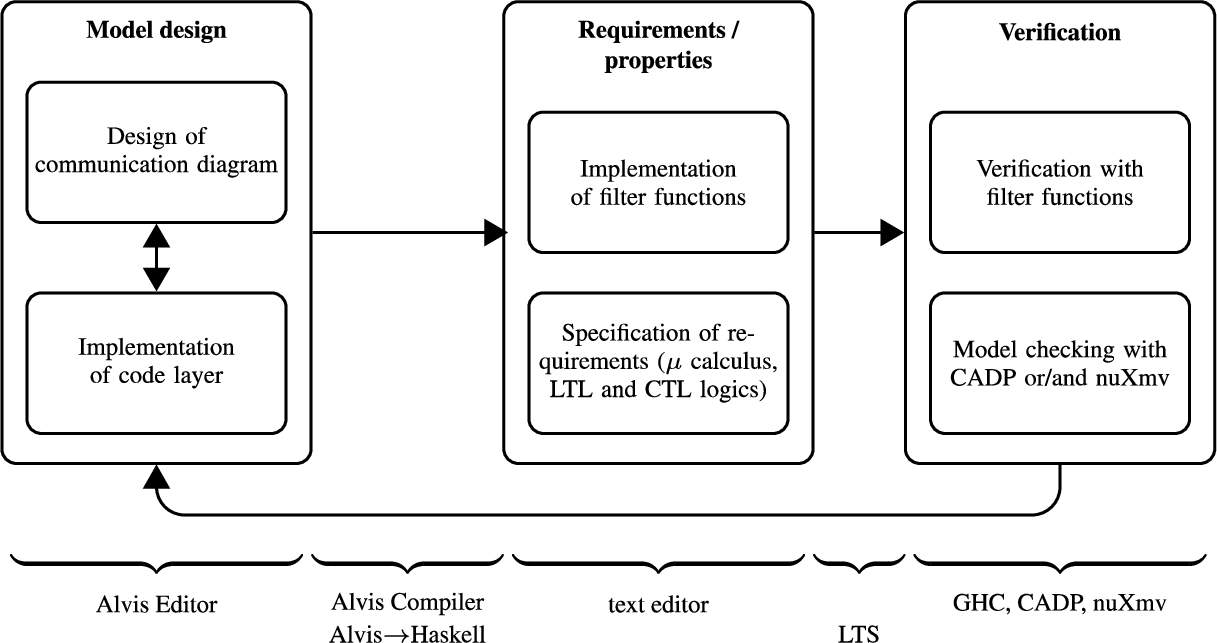
Fig. 8
Modelling and verification process with Alvis.

Fig. 9
Alvis model of the student’s project evaluation process (code layer).
The communication diagram for the corresponding Alvis model is given in Fig.
7. Abbreviation of activities’ names are used as agents names. The code layer for the model is shown in Fig.
9. Taking into account the transformation method presented in Figs.
3 and
4 some modifications are introduced to the communication diagram. The modelled process starts with a student’s activity (submitting a project) and may end with a student’s activity (collecting the grade), thus, the starting agent (
Message) contains an input port (
submit) and one of the ending agents (
End1) contains an output port (
grade).
Let us focus on the code layer. The pick function is used to choose at random one value from its argument (a list of items). The function is used to introduce the indeterminism into the Alvis model. If an agent belongs to a loop in the BPMN model, its piece of code that results from the transformation method is put inside a loop statement. The behaviour of a student is based on the following assumption. A student submits a project once and waits either for a grade or for a request for project resubmitting. The project can be resubmitted only once.
6 Model Verification
The scheme of the modelling and verification process with Alvis is shown in Fig.
8 (Szpyrka
et al.,
2013). From a user point of view, it starts from designing a model using prototype modelling environment called
Alvis Editor. The designed model is stored using XML file format. Then it is translated into Haskell (O’Sullivan
et al.,
2008) source code and its Haskell representation is used to generate the LTS graph. The generated LTS graphs can be verified using the CADP Toolbox.
We use Haskell as a middle-stage representation of an Alvis model in a similar way as CPN Tools use SML to generate reachability graphs for coloured Petri nets. The main difference between these approaches is that Alvis users have access to the generated Haskell source files and may include some extra Haskell code into them. The internal representation of an LTS graph is a Haskell list of model states. Lists are the most used data structures in Haskell (O’Sullivan
et al.,
2008) and the language provides a lot of built-in functions to manipulate them. The most important one, from the Alvis point of view, is the
filter function that takes a predicate and a list and then returns the list of elements that satisfy the predicate. In the considered approach predicates are called
filtering functions. They are usually implemented using the Haskell pattern matching mechanism. It should be emphasized that filtering functions give only some extra possibilities of the LTS graph exploration.
Finally, the source code is compiled with GHC compiler. The results of the received program execution are the LTS graph for the given model (
Aldebaran or
dot format) and the report of the model verification with included filtering functions. Analysis of Alvis models can be realized using the CADP
evaluator tool. In such approach, a specification of requirements is given as a set of
μ-calculus formulas (Mateescu and Sighireanu,
2000; Emerson,
1997b; Kozen,
1983), and the tool is used to check whether the LTS graph satisfies them. It should be emphasized that this is an action based approach. A
μ-calculus formula concerns actions labels while states of considered model are represented using their numbers only.
The input language of the CADP evaluator tool is an extension of the alternation-free μ-calculus. The logic is built from three types of formulas: action, regular and state formulas. An action formula is built from action names, regular expressions substituted for action names, Boolean constants $\mathit{true}$ and $\mathit{false}$ and the propositional logic operators: not, or, and, implies and equ (equivalence). Regular formulas represent regular expressions over action sequences. The μ logic uses nil to denote the empty word and the following regular expression operators: . (dot) – concatenation operator, | – choice operator, ∗ – the transitive and reflexive closure operator, and + – the transitive closure operator. Finally, a state formula is built of: propositional variables, Boolean constants $\mathit{true}$ and $\mathit{false}$, the propositional logic operators, the possibility ($\langle \hspace{0.2778em}\rangle $) and necessity ($[\hspace{0.2778em}]$) modal operators and minimal (μ) and maximal (ν) fixed point operators.
Approaches based on translation to Petri nets usually focus on fairness or liveness properties. However, these properties are mostly studied as ones of infinite runs, which in practice do not occur in real-life business processes. Analysis of presence or absence of some actions or relationships between occurrences of some actions seem to be more important for such cases. To illustrate the possibilities of verification of a model’s properties with the
evaluator let us consider a few properties encoded in
μ:
-
• $[{\mathit{true}^{\ast }}]\langle \mathit{true}\rangle \mathit{true}$ – it is always possible to do next step (no deadlocks).
-
• $[{\mathit{true}^{\ast }}.\text{''}\mathit{out}(\mathit{Student}.\mathit{submit})\text{''}.{\mathit{true}^{\ast }}.\text{''}\mathit{out}(\mathit{Student}.\mathit{submit})\text{''}]\mathit{false}$ – it is not possible to submit the project twice.
-
• $[{\mathit{true}^{\ast }}.\text{''}\mathit{out}(\mathit{Student}.\mathit{submit})\text{''}]\mu X.(\langle \mathit{true}\rangle \mathit{true}\wedge [\lnot (\text{''}\mathit{out}(\mathit{RequestCompProj}.\mathit{request})\text{''}\vee \text{''}\mathit{out}(\mathit{End}2.\mathit{grade})\text{''})]X)$ – after submitting a project a grade or request for resubmitting is received in a finite number of steps.
The
evaluator tool takes an LTS graph encoded in the BGC format and a file with a
μ calculus formula and checks whether the formula holds for the system. The tool is equipped with diagnostic generation algorithms, which construct both examples and counterexamples for a given formula. The CADP Toolbox can handle LTS graphs with
${2^{44}}$ elements.
The first property is false, while the second and third hold for the Alvis model. The result is required for the model because we expect that any sequence of actions leads to a final state so the presence of final states is desirable.

Fig. 10
Filtering LTS graph with Haskell.
The second approach to models verification takes advantage of the Haskell language features and lets the user to improve the generated model. Alvis Compiler generates a Haskell source file for a model and user-defined filter functions may be included into this file. Because of the very simple to use and flexible Haskell pattern matching mechanism, it is easy to select states that meet a given specification. Some of the functions are universal and can be included into any model, so it is possible to import them from an external Haskell module. However, most of these functions are based on the considered model
State type and must be defined for a model individually. Examples of such filtering functions are given in Fig.
10. The first one selects deadlocks, i.e. states with empty list of output arcs. The second function select states with the
Student agent in
finished mode. One of the states found by this function is included into the listing from Fig.
10.
The presented Haskell approach to LTS graph verification is mostly oriented on states, but in fact the method is not limited neither to states only nor to actions. We can use both at the same time, for example, searching for some specified parts of an LTS graph. Moreover, the Haskell approach can be used to implement user defined verification algorithms that are not provided by verification toolbox. For example, this is a good path to test user-defined non-standard verification procedures fast. Moreover, Haskell expressiveness allows to fit even quite complex algorithms in a few lines of code as compared to imperative languages.
The similarity between the structure of a BPMN diagram and the structure of the corresponding Alvis communication diagram allows relatively easy to identify parts of the original diagram, which are responsible for the occurrence of errors. Let us consider the last
μ property, but slightly modified:
i.e. after submitting a project a grade is received in a finite number of steps.
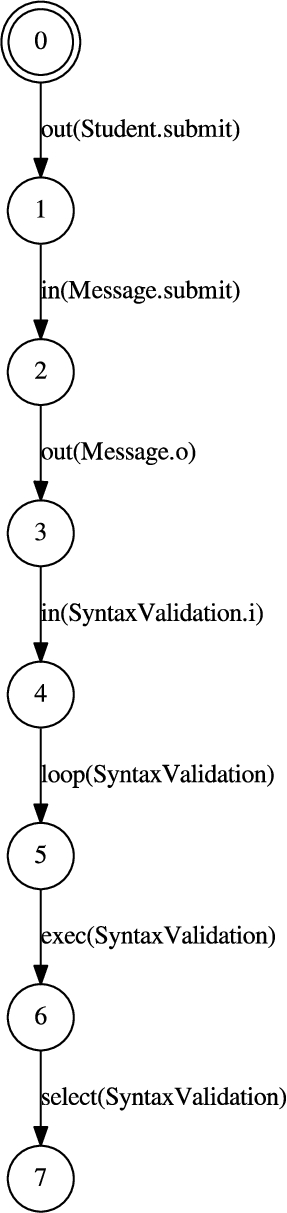
Fig. 11
Counterexample (initial part).
The property does not hold for the model and suitable counterexample may be generated by the CADP toolbox. The counterexample takes the form of a path from the corresponding LTS graph. Its initial part is shown in Fig.
11. Analysing the counterexample returned by CADP (especially labels of edges), we can identify all the agents that are involved in the path. The labels contain both names of agents and names of statements. Moreover, in the case of a communication between agents, the labels include not only the type of communication statement (
in or
out), but also the name of the port used for communication. Thus, we have information about all the agents involved in the path, performed statements, and communication between them. The considered counterexample may be represented graphically as shown in Fig.
12. The gray trace points out agents and their ports involved in the counterexample.
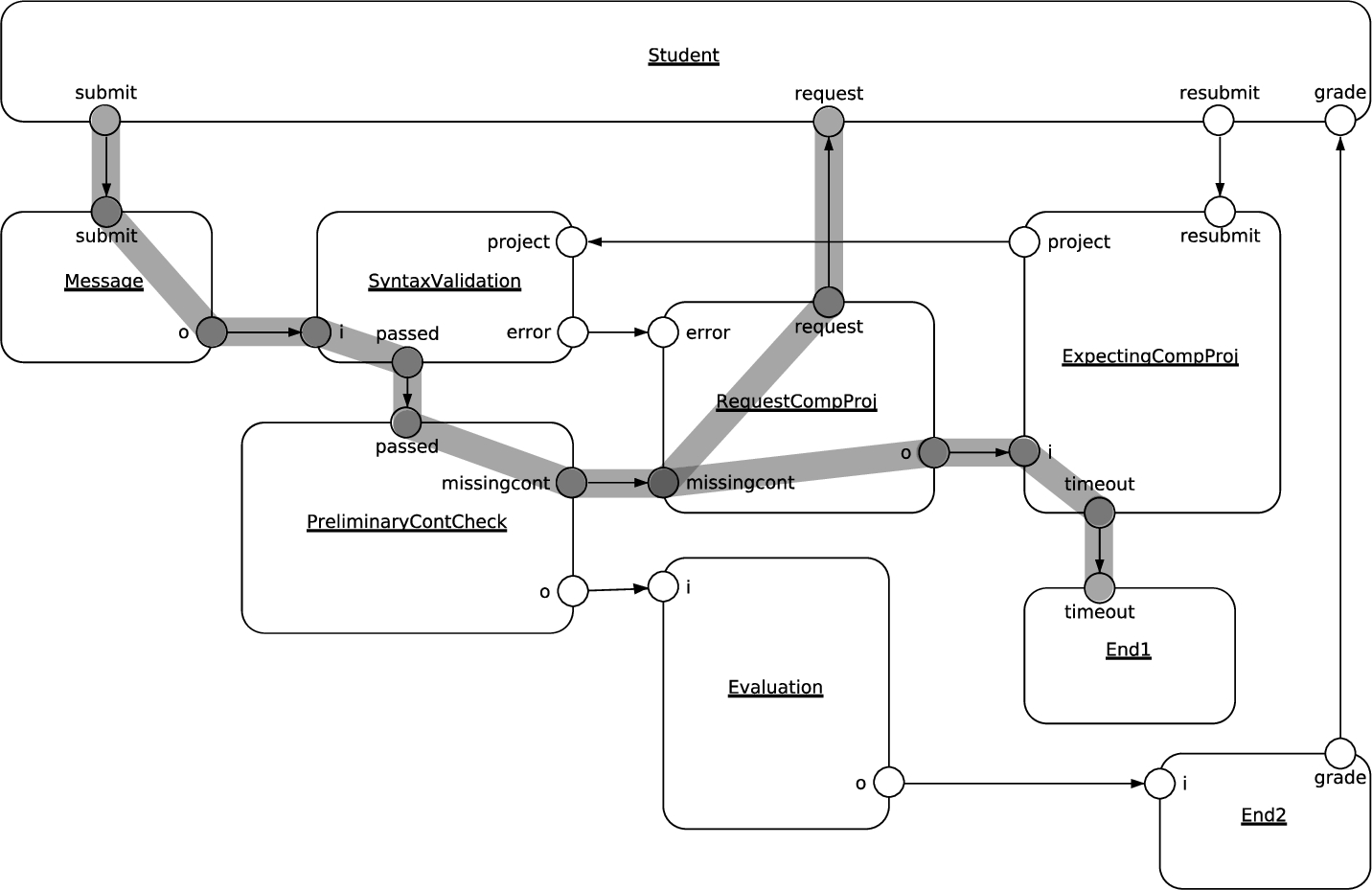
Fig. 12
Communication diagram with the trace of the counterexample.

Fig. 13
Part of translation log file.
Because agents correspond to tasks in a BPMN diagram, and gateways and events are represented by ports and snippets of source code, we can accurately reproduce the gray trace in the original BPMN diagram. The translation method shown in Figs.
3 and
4 applied to the given example may be described with a log file that contains dependencies between components of both diagrams (BPMN and Alvis). A snippet of such a log file is shown in Fig.
13. Based on the translation log BPMN elements involved in the counterexample are identified as shown in Fig.
14.
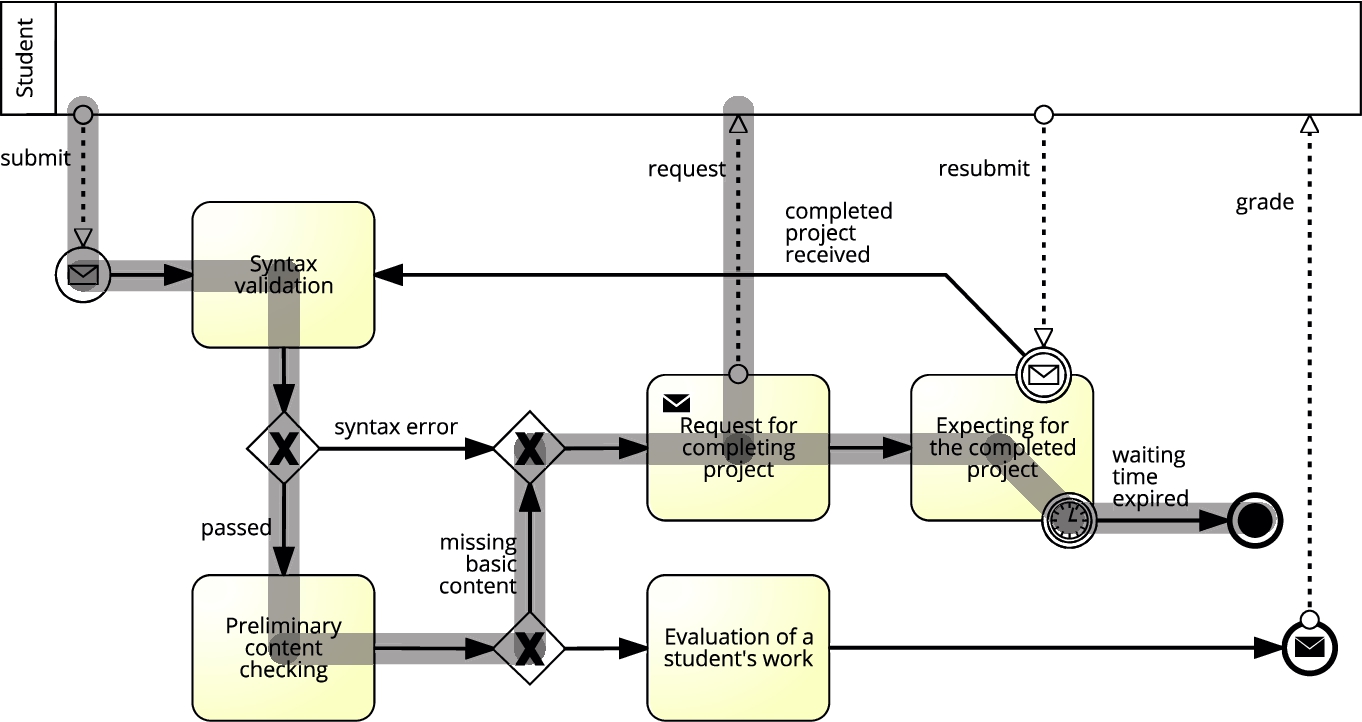
Fig. 14
BPMN diagram with the trace of the counterexample.
The considered counterexample represents the scenario when after the request for project resubmitting the waiting time expired so the grade is not provided. In the general case, based on the numbers of states returned by CADP, we can filter the states from the complete LTS graph. Analysis of the states, especially the current parameter values, may also explain the cause of the undesirable behaviour of the model.
7 Summary
Business process models find applications in many systems. In some mission-critical cases, e.g. control systems, process models should be formally analysed. The analysis of the formal aspects of a model allows for its optimization and verification. Furthermore, it may be useful in the assessment of the quality of the models. To perform such an analysis, translations of the process model to a formal specification should be considered. The original contribution of this paper is the introduction of a method for translation of models from BPMN to the Alvis language.
As opposed to some low-level representations, such as Petri nets, structure of the Alvis model is close to the original BPMN model. In comparison to the related works, our approach allows for verification of models containing OR-joins and external participants. The advantage of our solution is that errors revealed in the Alvis model can be easily tracked in the BPMN model. This is why it can be especially useful for practical modelling of BPMN models. The presented method is evaluated using an illustrative example of a process model. In spite of the fact that the considered example contains only selected BPMN items, the translation method can be extended, e.g. to cope with subprocesses, iterations, multiplicity etc.
The transformation of a BPMN model into an Alvis model allows for performing its formal verification. For this purpose, we use the Alvis model to automatically generate an LTS graph (Labelled Transition System). There are two possible approaches to the formal verification of an LTS graph. An LTS graph is generated with Haskell implemented algorithms and a designer has access to its source code so user-defined Haskell function for the LTS graph analysis can be included into the model. Moreover, external tools like CADP toolbox or nuXmv can be used to verify the model using model checking techniques.
As future work, we consider a more complex modelling and verification approach which uses formalized attributive language for representing rules in decision tables or networks, such as the XTT2 rule language (Nalepa
et al.,
2011c). XTT2 rules (and tables) can be formally analysed using the so-called HalVA verification framework (Nalepa
et al.,
2011a). In this approach table-level verification would be performed with HalVA (Kluza
et al.,
2011) and the global verification would be provided with translation to Alvis model. Furthermore, the process models integrated with rules can be visually designed using our customized editor (Kluza
et al.,
2012), and possibly executed in a hybrid runtime environment (Nalepa
et al.,
2013; Jasiul
et al.,
2014).

