1 Introduction
In recent years, as data has significantly grown, there is an increasing inclination among people to store data in cloud servers. Cloud computing (Sun, 2020; Alouffi et al., 2021), viewed as an efficient way of data storage and processing, is gradually becoming an indispensable infrastructure in various industry applications. However, data transmitting and storing in the cloud have also raised security concerns about data confidentiality. Therefore, to enhance the demand for data privacy protection is a significant issue. To ensure the security of data transmission in the cloud, encryption technology has become an essential topic in order to prevent unauthorized individuals from accessing sensitive information. Public key encryption (Lee et al., 2019; Deverajan et al., 2021; Zhou et al., 2021) is a well-known technique employed to ensure data confidentiality.
Since data in a cloud environment is encrypted for confidentiality, it becomes a challenge to find a specific data in cloud effectively. To address this issue, the concept of public key encryption with keyword search (PKEKS) (Boneh et al., 2004) has been proposed to achieve an effective search functionality for encrypted data. However, a PKEKS scheme has a limitation in the sense that it can only search for ciphertexts encrypted under identical receiver (entity) with the same public key. To overcome this limitation, the concept of public key encryption with equality test (PKEET) (Yang et al., 2010) has been introduced. A PKEET scheme allows users to perform comparative searches on ciphertexts encrypted under different public keys without revealing sensitive data.
Recently, a new type of attack has been actively discussed, known as side-channel attacks (Kubota et al., 2021; Ngo et al., 2021). A side-channel attack refers to a situation that attackers do not attempt to directly break the cryptographic algorithm in a security system, but exploit side-channel information, such as power consumption or timing, to gain access to critical system information. For example, as shown in Fig. 1, a user employs her/his secret key $\mathit{SK}$ to perform the decryption algorithm by inputting the ciphertext $\mathit{CT}$ at the device. Upon the completion of the decryption, the plaintext M is obtained. During the decryption process, an attacker could launch side-channel attacks to obtain crucial partial information about the user’s secret key $\mathit{SK}$. By doing so, the attacker can acquire partial information of the user’s secret key in every decryption process. After several rounds, the attacker may potentially reconstruct the complete sensitive data or the user’s secret key $\mathit{SK}$ by analysing these side-channel signals.
It is worth noting that a cryptographic mechanism known as leakage-resilient public key encryption (LR-PKE) (Akavia et al., 2009) has indeed been studied and published. It can withstand such side-channel attacks mentioned above. However, this mechanism’s application in diverse cloud computing environments remains constrained due to the absence of the property of equality test of ciphertext. Furthermore, to ensure the authenticity and integrity of information is also an important issue. Simultaneously, the development of cryptographic mechanisms that can efficiently merge digital signature and encryption has emerged as a pivotal topic in this field. In light of these challenges, this paper endeavours to propose a novel scheme, called leakage-resilient public key signcryption with equality test (LR-PKSCET), which not only offers robust security against side-channel attacks but also seamlessly integrates the processes of digital signing and encryption. In light of the increasing incidence of fraudulent activities, we will leverage the proposed LR-PKSCET as the foundation for developing an anti-scam system application. Our specific contributions include the following.
-
– The framework and security notions of LR-PKSCET: We establish the framework of LR-PKSCET that includes six distinct algorithms, and present the associated security notions of LR-PKSCET. The security notions encompass leakage resilience, indistinguishability, one-wayness, and existential unforgeability.
-
– A concrete LR-PKSCET scheme: Under the framework of LR-PKSCET, we propose a concrete LR-PKSCET scheme that meets the defined security notions.
-
– Security analysis: By using hash function properties and discrete logarithm problem, we provide a rigorous security proof of the proposed scheme under the associated security notions.
-
– Comparison with other schemes: Compared to existing schemes, our proposed LR-PKSCET scheme distinguishes itself as the first to withstand side-channel attacks.
-
– LR-PKSCET’s application: We extend the applicability of the proposed scheme to anti-scam systems that aims to mitigate the ongoing occurrence of a myriad of scam cases.
The remaining sections of this paper include the following parts. Section 2 introduces related work. Preliminaries are given in Section 3. Section 4 shows the LR-PKSCET framework and its associated security definitions. The concrete LR-PKSCET scheme is presented in Section 5. Formal proofs of ensuring the security of the LR-PKSCET scheme are given in Section 6. Performance analysis is carried out in Section 7. Section 8 introduces an application. Lastly, Section 9 offers the concluding remarks.
2 Related Work
The concept of the PKEET scheme was first introduced by Yang et al. (2010) as an extension of the existing public key encryption with keyword search (Boneh et al., 2004). The primary goal of their research was to enable the comparison of encrypted data, or ciphertexts, generated under different public keys. Based on the Yang et al.’s work (2010), a significant amount of related research on PKEET has been continuously conducted and published. Tang (2011) designed a PKEET scheme with a proxy, where the proxy can obtain tokens from different users and use them to perform equality test of associated ciphertexts. Based on this authorization concept, Tang (2012a) introduced a PKEET scheme that incorporated user-specified authorization. Subsequently, Tang (2012b) further extended the PKEET scheme (Tang, 2012a) to offer the support for fine-grained authorization. Huang et al. (2014) introduced a novel PKEET scheme which enables the comparison of ciphertexts without requiring decryption. As a result, their scheme achieves the verification of equivalence among ciphertexts encrypted using the PKEET scheme. Building on this foundation, Huang et al. (2015) expanded Huang et al.’s scheme (2014) to propose a public key encryption with authorized equality test that allowed authorized proxy to perform equality test on selected ciphertexts. This enhancement augmented the versatility and functionality of the PKEET scheme. Another significant advancement in this field was made by Ma et al. (2015). They introduced a PKEET scheme with four distinct authorization policies, thereby increasing the adaptability of PKEET. However, these proposed PKEET schemes were all shown to be secure only under the random oracle model. To overcome this limitation, Lee et al. (2020) presented a generic construction of a PKEET scheme in the standard model which provides enhanced security guarantees. Additionally, for the lattice-based cryptography, Duong et al. (2019) introduced a PKEET scheme in the standard model which was built on lattice concepts from an identity-based encryption scheme (Agrawal et al., 2010). On the other hand, to simultaneously ensure the confidentiality, authenticity, and integrity of messages, Le et al. (2021) proposed a lattice-based signcryption with equality test in the standard model.
In the real-world scenarios of public key systems, the significance of secret keys is widely acknowledged. However, it is worth noting that the secret keys are often stored in the devices, making them susceptible to potential side-channel attacks (Kubota et al., 2021; Ngo et al., 2021). To avoid the scenario that secret keys can be computed when facing such attacks, the leakage-resilient cryptography (Dziembowski and Pietrzak, 2008; Faust et al., 2010) has emerged as a crucial topic. The core ambition of leakage-resilient cryptography was the formulation of algorithms with the capability to effectively counteract side-channel attacks. For data confidentiality, Akavia et al. (2009) introduced a leakage-resilient public key encryption (LR-PKE) scheme that effectively safeguards sensitive information even in the presence of potential side-channel threats. Subsequently, several studies (Naor and Segev, 2009, 2012; Li et al., 2013) related to LR-PKE have also been published to enhance both security and efficiency. However, the aforementioned LR-PKE schemes are specifically designed to provide security only in a bounded leakage model. To overcome this limitation, Kiltz and Pietrzak (2010) proposed the first LR-PKE scheme to provide security in continuous leakage models. Furthermore, Galindo et al. (2016) also presented a LR-PKE that drew inspiration from ElGamal and offered security in the continuous leakage model. For addressing the issue of ensuring the security of public key encryption when the randomness of ciphertexts becomes non-uniform due to faulty implementations or adversarial actions, Huang et al. (2022) introduced the concept of leakage-resilient hedged public-key encryption that offered a heightened level of comprehensive security. On the other hand, Tseng et al. (2022) introduced a leakage-resilient signcryption to achieve the objectives of message confidentiality, authenticity, and integrity.
3 Preliminaries
3.1 Bilinear Map
This section outlines the properties of a bilinear map, which serves as the fundamental basis for the proposed LR-PKSCET scheme discussed in this paper. We choose two multiplicative cyclic groups, denoted by G and ${G_{T}}$, both of a prime order q. Let g be a generator of G. A bilinear map $\hat{e}$: $G\times G\to {G_{T}}$ satisfies the following properties.
3.2 Generic Bilinear Group Model
The generic bilinear group (GBG) model, introduced by Boneh et al. (2005), is served as a security analysis technique for cryptographic schemes. This model is used in the security game of a cryptographic scheme where an adversary and a challenger interact with each other. Initially, the challenger creates the bilinear parameters G, ${G_{T}}$, q, g, $\hat{e}$ defined above. During the adversary’s operations in the bilinear parameters, the adversary can request three types of queries from the challenger. The three types of queries consist of the multiplicative query ${Q_{G}}$ of G, the multiplicative query ${Q_{{G_{T}}}}$ of ${G_{T}}$, and the bilinear pairing query ${Q_{\hat{e}}}$ of $\hat{e}$. Additionally, the challenger establishes two injective random mappings, 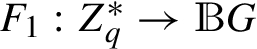 and
and 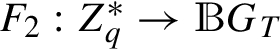 , to encode all the elements of G and ${G_{T}}$ into distinct bit strings. These mappings must satisfy the conditions
, to encode all the elements of G and ${G_{T}}$ into distinct bit strings. These mappings must satisfy the conditions 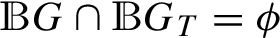 and
and 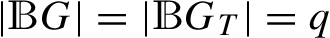 . The behaviours of the three associated queries ${Q_{G}}$, ${Q_{{G_{T}}}}$, and ${Q_{\hat{e}}}$, for m and n in ${Z_{q}^{\ast }}$, are defined as follows:
. The behaviours of the three associated queries ${Q_{G}}$, ${Q_{{G_{T}}}}$, and ${Q_{\hat{e}}}$, for m and n in ${Z_{q}^{\ast }}$, are defined as follows:
-
– ${Q_{G}}({F_{1}}(m),{F_{1}}(n))\to {F_{1}}(m+n\hspace{0.1667em}\hspace{0.1667em}\mathrm{mod}\hspace{0.1667em}\hspace{0.1667em}q)$.
-
– ${Q_{{G_{T}}}}({F_{2}}(m),{F_{2}}(n))\to {F_{2}}(m+n\hspace{0.1667em}\hspace{0.1667em}\mathrm{mod}\hspace{0.1667em}\hspace{0.1667em}q)$.
-
– ${Q_{\hat{e}}}({F_{1}}(m),{F_{1}}(n))\to {F_{1}}(m\cdot n\hspace{0.1667em}\hspace{0.1667em}\mathrm{mod}\hspace{0.1667em}\hspace{0.1667em}q)$.
3.3 Security Assumptions and Entropy
To establish the security of the LR-PKSCET scheme, we depend on the computational complexity of the discrete logarithm problem (DL) and the properties of hash functions (HF). More precisely, our security analysis is based on the following two related assumptions.
-
– DL assumption: The DL problem aims to find the unknown value $x\in {Z_{q}^{\ast }}$ from a given ${g^{x}}$. If there exists a probabilistic polynomial-time (PPT) adversary, the probability of this adversary successfully determining $x\in {Z_{q}^{\ast }}$ is considered negligible.
-
– HF assumption: Given a hash function $\mathit{HF}$, which possesses collision-resistant and one-way properties, the probability of a PPT adversary successfully finding two values ${Y_{1}},{Y_{2}}$. such that $\mathit{HF}({Y_{1}})=\mathit{HF}({Y_{2}})$, is considered negligible.
To assess the probability of successfully obtaining a secret key through side-channel attacks, we utilize entropy concept to measure the probability of successful reconstruction. In the following, we introduce two types of min-entropies for conducting this analysis.
To measure entropy, there are two cases to be considered: one with a single secret key and the other with multiple secret keys. For these two cases, we will refer to the results of Dodis et al. (2008) (Lemma 1) and Galindo and Virek (2013) (Lemma 2), respectively.
Lemma 1.
Consider a single secret key M and let Φ represent the maximum length of the bit strings that might be leaked from the secret key M. We define $f:M\to {\{0,1\}^{\Phi }}$ as the leakage function. In this context, we obtain ${\widetilde{H}_{\infty }}(M|f(M))\geqq {H_{\infty }}(M)-\Phi $.
Lemma 2.
Consider n multiple secret keys, denoted as ${M_{1}},{M_{2}},\dots ,{M_{n}}$. Let $F\in {Z_{q}}[{M_{1}},{M_{2}},\dots ,{M_{n}}]$ be a polynomial with degree at most d. For each $i=1,2,\dots ,n$, let $P{D_{i}}$ be a probability distribution of ${M_{i}}={m_{i}}$ such that ${H_{\infty }}(P{D_{i}})\geqq \log q-\Phi $, where $0\leqq \Phi \leqq \log q$. If ${m_{i}}\stackrel{P{D_{i}}}{\gets }{Z_{q}}$ are independent, the inequality $\Pr [F({M_{1}}={m_{1}},{M_{2}}={m_{2}},\dots ,{M_{n}}={m_{n}})=0]\leqq (d/q){2^{\Phi }}$ holds. If $\Phi \lt \log q(1-\varepsilon )$, $\Pr [F({M_{1}}={m_{1}},{M_{2}}={m_{2}},\dots ,{M_{n}}={m_{n}})=0]$ is negligible, where ε is a positive decimal.
4 Framework and Security Notions for LR-PKSCET
We illustrate the framework of our LR-PKSCET scheme in Fig. 2, which includes a cloud server and two entities (also works more than two member entities). The two member entities ${\mathit{ME}_{\zeta }}$ and ${\mathit{ME}_{\eta }}$ can respectively generate their own entity secret keys denoted by $({\textit{ESK}_{\zeta }^{I}},{\textit{ESK}_{\zeta }^{II}})$ and $({\textit{ESK}_{\eta }^{I}},{\textit{ESK}_{\eta }^{II}})$ and entity public keys denoted by $({\textit{EPK}_{\zeta }^{I}},{\textit{EPK}_{\zeta }^{II}})$ and $({\textit{EPK}_{\eta }^{I}},{\textit{EPK}_{\eta }^{II}})$. The entity ${\mathit{ME}_{\zeta }}$ utilizes her/his entity secret keys $({\textit{ESK}_{\zeta }^{I}},{\textit{ESK}_{\zeta }^{II}})$ along with the entity public keys $({\textit{EPK}_{\eta }^{I}},{\textit{EPK}_{\eta }^{II}})$ of the entity ${\mathit{ME}_{\eta }}$ to perform the process of signing and encryption on the message $\mathit{msg}$ using the Signcryption algorithm. The output ciphertext ${\mathit{CT}_{\eta }}$ will be sent to the entity ${\mathit{ME}_{\eta }}$. Upon receiving ${\mathit{CT}_{\eta }}$, the entity ${\mathit{ME}_{\eta }}$ can utilize her/his entity secret keys $({\textit{ESK}_{\eta }^{I}},{\textit{ESK}_{\eta }^{II}})$ along with the entity public keys $({\textit{EPK}_{\zeta }^{I}},{\textit{EPK}_{\zeta }^{II}})$ of the entity ${\mathit{ME}_{\zeta }}$ to perform a decryption and verification process using the Unsigncryption algorithm. The process above allows the entity ${\mathit{ME}_{\zeta }}$ to obtain the message $\mathit{msg}$. On the other hand, the entities ${\mathit{ME}_{\zeta }}$ and ${\mathit{ME}_{\eta }}$ can respectively transmit their ciphertexts ${\mathit{CT}_{\zeta }}$, ${\mathit{CT}_{\eta }}$, and trapdoors ${\mathit{TD}_{\zeta }}$, ${\mathit{TD}_{\eta }}$ to the cloud server. The cloud server is capable of testing whether the two ciphertexts contain the same plaintext.
4.1 Framework for LR-PKSCET
In this subsection, we provide a formal definition of the proposed scheme’s framework, which is defined according to the frameworks of PKSCET (Le et al., 2021) and LR-PKSC (Tseng et al., 2022). To facilitate understanding of the formal definition, a symbol table is provided in Table 1.
Table 1
Symbols.
| Symbol | Meaning |
| $\textit{DE}$ | The designated entity of the system |
| λ | The security parameter |
| $\textit{SP}$ | The system parameters |
| ${\textit{ESK}^{I}}$ | The first entity secret key |
| ${\textit{ESK}^{II}}$ | The second entity secret key |
| ${\textit{EPK}^{I}}$ | The first entity public key |
| ${\textit{EPK}^{II}}$ | The second entity public key |
| ${\textit{ESK}_{S,i-1}^{I}}$ | The first entity secret key of sender in the $i-1$th round |
| ${\textit{ESK}_{S,i-1}^{II}}$ | The second entity secret key of sender in the $i-1$th round |
| ${\textit{ESK}_{R,j-1}^{I}}$ | The first entity secret key of receiver in the $j-1$th round |
| ${\textit{ESK}_{R,j-1}^{II}}$ | The second entity secret key of receiver in the $j-1$th round |
| ${\textit{ESK}_{k-1}^{II}}$ | The second entity secret key in the $k-1$th round |
| $\textit{TD}$ | The trapdoor |
| $\mathit{msg}$ | The message |
| $\textit{CT}$ | The ciphertext |
Definition 1.
An LR-PKSCET scheme is composed of six algorithms, namely, Initialization, EntityKeyGen, Signcryption, Unsigncryption, Authorization, and Test as follows.
-
– Initialization: The designated entity $DE$ of this scheme (system) is responsible for executing the algorithm with a security parameter λ and outputs the system parameters $\mathit{SP}$.
-
– EntityKeyGen: By executing the algorithm with the system parameters $\mathit{SP}$, the member entity $\mathit{ME}$ generates two entity secret keys ${\textit{ESK}^{I}}$, ${\textit{ESK}^{II}}$ and two entity public keys ${\textit{EPK}^{I}}$, ${\textit{EPK}^{II}}$.
-
– Signcryption: By executing the algorithm in the $i\mathrm{th}$ round with the system parameters $\mathit{SP}$, two entity secret keys ${\textit{ESK}_{S,i-1}^{I}}$, ${\textit{ESK}_{S,i-1}^{II}}$ (the $i-1\mathrm{th}$ round) of the member entity ${\mathit{ME}_{S}}$, identified as the sender, a message $\mathit{msg}$, and two entity public keys ${\textit{EPK}_{R}^{I}}$, ${\textit{EPK}_{R}^{II}}$ of the member entity ${\mathit{ME}_{R}}$, identified as the receiver, the sender ${\mathit{ME}_{S}}$ generates a ciphertext $\mathit{CT}$.
-
– Unsigncryption: By executing the algorithm in the $j\mathrm{th}$ round with the system parameters $\mathit{SP}$, two entity secret keys ${\textit{ESK}_{R,j-1}^{I}}$, ${\textit{ESK}_{R,j-1}^{II}}$ (the $j-1\mathrm{th}$ round) of a member entity ${\mathit{ME}_{R}}$ identified as the receiver, a ciphertext $\mathit{CT}$, and two entity public keys ${\textit{EPK}_{S}^{I}}$, ${\textit{EPK}_{S}^{II}}$ of a member entity ${\mathit{ME}_{S}}$ identified as the sender, the sender ${\mathit{ME}_{S}}$ generates a message $\mathit{msg}$.
-
– Authorization: By executing the algorithm in the $k\mathrm{th}$ round with the system parameters $\mathit{SP}$ and the entity secret key ${\textit{ESK}_{k-1}^{II}}$ (the $k-1\mathrm{th}$ round) of a member entity $\mathit{ME}$, the member entity $\mathit{ME}$ generates a trapdoor $\mathit{TD}$.
-
– Test: By executing the algorithm with the system parameters $\mathit{SP}$, the ciphertext-trapdoor pair $({\mathit{CT}_{\zeta }},{\mathit{TD}_{\zeta }})$ of a member entity ${\mathit{ME}_{\zeta }}$ and the ciphertext-trapdoor pair $({\mathit{CT}_{\eta }},{\mathit{TD}_{\eta }})$ of a member entity ${\mathit{ME}_{\eta }}$, the cloud server $\mathit{CS}$ generates 1 or 0.
4.2 Security Notions for LR-PKSCET
By the technique introduced in Galindo and Virek (2013), we initiate six unique leakage functions: ${\textit{LF}_{SC,i}^{A}}$, ${\textit{LF}_{SC,i}^{B}}$, ${\textit{LF}_{\mathit{USC},j}^{A}}$, ${\textit{LF}_{\mathit{USC},j}^{B}}$, ${\textit{LF}_{\mathit{Auth},k}^{A}}$ and ${\textit{LF}_{\mathit{Auth},k}^{B}}$. Specifically, ${\textit{LF}_{SC,i}^{A}}$ and ${\textit{LF}_{SC,i}^{B}}$ are utilized to extract leaked information of ${\textit{ESK}_{S}^{I}}$ and ${\textit{ESK}_{S}^{II}}$, denoted as ${\textit{ESK}_{S}^{I}}=({\textit{ESK}_{S,i,A}^{I}},{\textit{ESK}_{S,i,B}^{I}})$ and ${\textit{ESK}_{S}^{II}}=({\textit{ESK}_{S,i,A}^{II}},{\textit{ESK}_{S,i,B}^{II}})$ which are used in the Signcryption algorithm during the $i\mathrm{th}$ round. Similarly, ${\textit{LF}_{\mathit{USC},j}^{A}}$ and ${\textit{LF}_{\mathit{USC},j}^{B}}$ are applied to extract leaked information of ${\textit{ESK}_{R}^{I}}$ and ${\textit{ESK}_{R}^{II}}$, denoted as ${\textit{ESK}_{R}^{I}}=({\textit{ESK}_{R,j,A}^{I}},{\textit{ESK}_{R,j,B}^{I}})$ and ${\textit{ESK}_{R}^{II}}=({\textit{ESK}_{R,j,A}^{II}},{\textit{ESK}_{R,j,B}^{II}})$ which are used in the Unsigncryption algorithm during the $j\mathrm{th}$ round. The last two leakage functions ${\textit{LF}_{\mathit{Auth},k}^{A}}$ and ${\textit{LF}_{\mathit{Auth},k}^{B}}$ are utilized to extract leaked information of ${\textit{ESK}_{R}^{II}}$, denoted as ${\textit{ESK}_{R}^{II}}=({\textit{ESK}_{R,k,A}^{II}},{\textit{ESK}_{R,k,B}^{II}})$ which is used in the Authorization algorithm during the $k\mathrm{th}$ round. Let Φ represent the maximum length of the bit strings that might be leaked from the secret keys. As a result, the size of $|{\textit{LF}_{SC,i}^{A}}|$, $|{\textit{LF}_{SC,i}^{B}}|$, $|{\textit{LF}_{\mathit{USC},j}^{A}}|$, $|{\textit{LF}_{\mathit{USC},j}^{B}}|$, $|{\textit{LF}_{\mathit{Auth},k}^{A}}|$, and $|{\textit{LF}_{\mathit{Auth},k}^{B}}|$ are all bounded by Φ, where the notation $|\cdot |$ signifies the length of a bit string. Also, for convenience we will adopt the following six symbols:
-
– ${\Lambda LF_{SC,i}^{A}}={\textit{LF}_{SC,i}^{A}}({\textit{ESK}_{S,i,A}^{I}},{\textit{ESK}_{S,i,A}^{II}})$;
-
– ${\Lambda LF_{SC,i}^{B}}={\textit{LF}_{SC,i}^{B}}({\textit{ESK}_{S,i,B}^{I}},{\textit{ESK}_{S,i,B}^{II}})$;
-
– ${\Lambda LF_{\mathit{USC},j}^{A}}={\textit{LF}_{\mathit{USC},j}^{A}}({\textit{ESK}_{R,j,A}^{I}},{\textit{ESK}_{R,j,A}^{II}})$;
-
– ${\Lambda LF_{\mathit{USC},j}^{B}}={\textit{LF}_{\mathit{USC},j}^{B}}({\textit{ESK}_{R,j,B}^{I}},{\textit{ESK}_{R,j,B}^{II}})$;
-
– ${\Lambda LF_{\mathit{Auth},k}^{A}}={\textit{LF}_{\mathit{Auth},k}^{A}}({\textit{ESK}_{R,k,A}^{II}})$;
-
– ${\Lambda LF_{\mathit{Auth},k}^{B}}={\textit{LF}_{\mathit{Auth},k}^{B}}({\textit{ESK}_{R,k,B}^{II}})$.
Next, we define indistinguishable security, one-way security, and existential unforgeability to serve as the security notion that can withstand adversaries with the capabilities of side-channel attacks.
Definition 2.
If the advantage of an adversary ${\mathcal{A}_{I}}$ to break a LR-PKSCET scheme in the following security game under side-channel and chosen-ciphertext attacks is negligible, we say that the scheme has leakage resilience and indistinguishable security.
-
– Setup: The challenger $\mathcal{CH}$ is responsible for executing the Initialization algorithm with a security parameter λ and outputs the system parameters $\mathit{SP}$ which will be made public.
-
– Phase 1: The adversary ${\mathcal{A}_{I}}$ has the capability to make various adaptive queries as follows.
-
✓ EntityKeyGen query: ${\mathcal{A}_{I}}$ sends a query containing member entity’s information $\mathit{ME}$. Subsequently, $\mathcal{CH}$ processes the EntityKeyGen algorithm to acquire two entity secret keys ${\textit{ESK}^{I}}$, ${\textit{ESK}^{II}}$ and two entity public keys ${\textit{EPK}^{I}}$, ${\textit{EPK}^{II}}$, and returns them back to ${\mathcal{A}_{I}}$.
-
✓ Signcryption query: ${\mathcal{A}_{I}}$ sends a query containing two entity secret keys ${\textit{ESK}_{S,i}^{I}}$, ${\textit{ESK}_{S,i}^{II}}$ of a member entity ${\mathit{ME}_{S}}$ identified as the sender, a message $\mathit{msg}$, and two entity public keys ${\textit{EPK}_{R}^{I}}$, ${\textit{EPK}_{R}^{II}}$ of a member entity ${\mathit{ME}_{R}}$ identified as the receiver. Subsequently, $\mathcal{CH}$ processes the Signcryption algorithm to acquire a ciphertext $\mathit{CT}$, and returns it back to ${\mathcal{A}_{I}}$.
-
✓ Signcryption leak query: ${\mathcal{A}_{I}}$ sends a query containing an index i, and two leaked functions ${\textit{LF}_{SC,i}^{A}}$ and ${\textit{LF}_{SC,i}^{B}}$. Subsequently, $\mathcal{CH}$ returns two leaked information ${\Lambda LF_{SC,i}^{A}}$ and ${\Lambda LF_{SC,i}^{B}}$ back to ${\mathcal{A}_{I}}$.
-
✓ Unsigncryption query: ${\mathcal{A}_{I}}$ sends a query containing two entity secret keys ${\textit{ESK}_{R,j}^{I}}$, ${\textit{ESK}_{R,j}^{II}}$ of a member entity ${\mathit{ME}_{R}}$ identified as the receiver, a ciphertext $\mathit{CT}$, and two entity public keys ${\textit{EPK}_{S}^{I}}$, ${\textit{EPK}_{S}^{II}}$ of a member entity ${\mathit{ME}_{R}}$ identified as the sender. Subsequently, $\mathcal{CH}$ processes the Unsigncryption algorithm to acquire a message $\mathit{msg}$, and returns it back to ${\mathcal{A}_{I}}$.
-
✓ Unsigncryption leak query: ${\mathcal{A}_{I}}$ sends a query containing an index j, and two leaked functions ${\textit{LF}_{\mathit{USC},j}^{A}}$ and ${\textit{LF}_{\mathit{USC},j}^{B}}$. Subsequently, $\mathcal{CH}$ returns two sets of leaked information $\Lambda {\textit{LF}_{\mathit{USC},j}^{A}}$ and ${\Lambda LF_{\mathit{USC},j}^{B}}$ back to ${\mathcal{A}_{I}}$.
-
✓ Authorization query: ${\mathcal{A}_{I}}$ sends a query containing the entity secret key ${\textit{ESK}_{k}^{II}}$ of a member entity $\mathit{ME}$. Subsequently, $\mathcal{CH}$ processes the Authorization algorithm to acquire a trapdoor $\mathit{TD}$, and returns it back to ${\mathcal{A}_{I}}$.
-
✓ Authorization leak query: ${\mathcal{A}_{I}}$ sends a query containing an index k, and two leaked functions ${\textit{LF}_{\mathit{Auth},k}^{A}}$ and ${\textit{LF}_{\mathit{Auth},k}^{B}}$. Subsequently, $\mathcal{CH}$ returns two sets of leaked information ${\Lambda LF_{\mathit{Auth},k}^{A}}$ and ${\Lambda LF_{\mathit{Auth},k}^{B}}$ back to ${\mathcal{A}_{I}}$.
-
-
– Challenge: ${\mathcal{A}_{I}}$ chooses a specific member entity ${\mathit{ME}_{R}^{\ast }}$, and provides two target plaintexts, ${\mathit{msg}_{0}}$ and ${\mathit{msg}_{1}}$, to $\mathcal{CH}$. Subsequently, $\mathcal{CH}$ chooses a random bit $b\in \{0,1\}$ and utilizes the Signcryption algorithm in the $i\mathrm{th}$ round with the corresponding parameters ${\mathit{msg}_{b}^{\ast }}$, ${\textit{EPK}_{R}^{I}}$, ${\textit{EPK}_{R}^{II}}$, ${\textit{ESK}_{S,i}^{I}}$ and ${\textit{ESK}_{S,i}^{II}}$ to generate the target ciphertext ${\mathit{CT}^{\ast }}$. Then, $\mathcal{CH}$ sends ciphertext ${\mathit{CT}^{\ast }}$ to ${\mathcal{A}_{I}}$. One restriction is that ${\mathit{ME}_{R}^{\ast }}$ is not allowed to appear in the EntityKeyGen queries.
-
– Phase 2: The adversary ${\mathcal{A}_{I}}$ can make further queries as in the Phase 1 except that the selected target, namely ${\mathit{ME}_{R}^{\ast }}$, ${\mathit{msg}_{b}^{\ast }}$, ${\textit{ESK}_{S,i}^{I}}$ and ${\textit{ESK}_{S,i}^{II}}$ are not allowed to appear in the EntityKeyGen, the Unsigncryption and the Authorization queries.
-
– Guess phase: ${\mathcal{A}_{I}}$ produces the value ${b^{\prime }}$ and succeeds in the game if ${b^{\prime }}$ is equal to b. The advantage of winning the game is represented by $\textit{Adv}({\mathcal{A}_{I}})=|\text{Pr}[{b^{\prime }}=b]-1/2|$.
Definition 3.
If the advantage of an adversary ${\mathcal{A}_{II}}$ to break a LR-PKSCET scheme in the following game under side-channel and chosen-ciphertext attacks is negligible, we say that the scheme has leakage resilience and one-way security.
-
– Setup: This stage is the same as that in Definition 2.
-
– Phase 1: This stage is the same as that in Definition 2.
-
– Challenge: ${\mathcal{A}_{II}}$ chooses a specific member entity ${\mathit{ME}_{R}^{\ast }}$ to $\mathcal{CH}$. Subsequently, $\mathcal{CH}$ chooses a random message ${\mathit{msg}^{\ast }}$ and utilizes the Signcryption algorithm with ${\mathit{msg}^{\ast }}$, ${\textit{EPK}_{R}^{I}}$, ${\textit{EPK}_{R}^{II}}$, ${\textit{ESK}_{S,i}^{I}}$ and ${\textit{ESK}_{S,i}^{II}}$ to generate the target ciphertext ${\mathit{CT}^{\ast }}$. Then, $\mathcal{CH}$ sends ciphertext ${\mathit{CT}^{\ast }}$ to ${\mathcal{A}_{II}}$. One restriction is that ${\mathit{ME}_{R}^{\ast }}$ is not allowed to appear in the EntityKeyGen and the Authorization queries.
-
– Phase 2: The adversary ${\mathcal{A}_{II}}$ can make further queries as in the Phase 1 except that the selected target, namely ${\mathit{ME}_{R}^{\ast }}$, ${\mathit{msg}^{\ast }}$, ${\textit{ESK}_{S,i}^{I}}$ and ${\textit{ESK}_{S,i}^{II}}$ are not allowed to appear in the EntityKeyGen and the Unsigncryption queries.
-
– Guess phase: ${\mathcal{A}_{II}}$ produces the message ${\mathit{msg}^{\prime }}$ and succeeds in the game if ${\mathit{msg}^{\prime }}$ is equal to ${\mathit{msg}^{\ast }}$. The advantage of winning the game is represented by $\textit{Adv}({\mathcal{A}_{II}})=|\text{Pr}[{\mathit{msg}^{\prime }}={\mathit{msg}^{\ast }}]|$.
Definition 4.
If the advantage of an adversary ${\mathcal{A}_{\mathit{III}}}$ to break a LR-PKSCET scheme in the following game under side-channel and chosen-message attacks is negligible, we say that the scheme has leakage resilience and existential unforgeability.
-
– Setup: This stage is the same as that in Definition 2.
-
– Phase 1: This stage is the same as that in Definition 2.
-
– Forgery: The adversary ${\mathcal{A}_{\mathit{III}}}$ successfully forges a ciphertext ${\mathit{CT}^{\ast }}=({\mathit{ME}_{S}^{\ast }},{\mathit{ME}_{R}^{\ast }},{U^{\ast }},{V^{\ast }},{R^{\ast }},{S^{\ast }},{\sigma ^{\ast }})$ for a message ${M^{\ast }}$, and we declare ${\mathcal{A}_{\mathit{III}}}$ as the winner of this game if the following conditions are satisfied.
-
✓ The Unsigncryption algorithm is capable of generating the message ${M^{\ast }}$.
-
✓ The Signcryption queries are not allowed to query the message ${M^{\ast }}$, ${\mathit{ME}_{S}^{\ast }}$ or ${\mathit{ME}_{R}^{\ast }}$.
-
✓ The EntityKeyGen queries are not allowed to query the member entity ${\mathit{ME}_{S}^{\ast }}$.
-
5 The Proposed LR-PKSCET Scheme
In this section, we show a leakage-resilient public key signcryption with equality test (LR-PKSCET) scheme that includes the following six algorithms.
The following describes how to obtain the message $\mathit{msg}$ and verify the signature σ in the Unsigncryption algorithm.
-
– Initialization: The designated entity $\textit{DE}$ of this scheme (system) is responsible for executing the algorithm with a security parameter λ and outputs the system parameters $\mathit{SP}$ by the following steps.
-
✓ Follow the guidelines provided in Section 3 to generate the bilinear parameters G, ${G_{T}}$, q, $\hat{e}$, g.
-
✓ Pick two random values $x,y\in {Z_{q}^{\ast }}$, and then compute $X={g^{x}}$ and $Y={g^{y}}$.
-
✓ Select five hash functions, namely, ${\mathit{HF}_{1}}:{G_{T}}\to G$, ${\mathit{HF}_{2}}:G\times G\times {G_{T}}\to {\{0,1\}^{m+n}}$, ${\mathit{HF}_{3}}:{\{0,1\}^{m}}\to G$, ${\mathit{HF}_{4}}:{\{0,1\}^{m+n}}\to {Z_{q}^{\ast }}$, ${\mathit{HF}_{5}}:{\{0,1\}^{\ast }}\times {\{0,1\}^{m+n}}\times {\{0,1\}^{m}}\times G\times G\times G\to {\{0,1\}^{t}}$, where m, n and t represent fixed lengths.
-
✓ Define the system parameters $SP=\{G,{G_{T}},q,\hat{e},g,X,Y,{\mathit{HF}_{1}},{\mathit{HF}_{2}},{\mathit{HF}_{3}},{\mathit{HF}_{4}},{\mathit{HF}_{5}}\}$.
-
-
– EntityKeyGen: By executing the algorithm with the system parameters $\mathit{SP}$, the member entity $\mathit{ME}$ generates two entity secret keys ${\textit{ESK}^{I}}$, ${\textit{ESK}^{II}}$ and two entity public keys ${\textit{EPK}^{I}}$, ${\textit{EPK}^{II}}$ using the following steps.Next, the member entity $\mathit{ME}$ chooses two random renewed values, a and b, to calculate the initial entity secret keys ${\textit{ESK}_{0}^{I}}=({\textit{ESK}_{0,A}^{I}},{\textit{ESK}_{0,B}^{I}})=({\textit{ESK}^{I}}\cdot {g^{a}},{g^{-a}})$ and ${\textit{ESK}_{0}^{II}}=({\textit{ESK}_{0,A}^{II}},{\textit{ESK}_{0,B}^{II}})=({\textit{ESK}^{II}}\cdot {g^{b}},{g^{-b}})$.
-
✓ Choose two random values $\alpha ,\beta \in {Z_{q}^{\ast }}$, and then compute ${\textit{ESK}^{I}}={g^{\alpha }}$ and ${\textit{ESK}^{II}}={g^{\beta }}$.
-
✓ Utilize ${\textit{ESK}^{I}}$ and ${\textit{ESK}^{II}}$ to establish ${\textit{EPK}^{I}}=\hat{e}(g,{g^{\alpha }})$ and ${\textit{EPK}^{II}}=\hat{e}(g,{g^{\beta }})$, respectively.
-
-
– Signcryption: By executing the algorithm in the $i\mathrm{th}$ round with the system parameters $\mathit{SP}$, two entity secret keys ${\textit{ESK}_{S,i-1}^{I}}$, ${\textit{ESK}_{S,i-1}^{II}}$ (the $i-1\mathrm{th}$ round) of the member entity ${\mathit{ME}_{S}}$, identified as the sender, a message $\mathit{msg}$, and two entity public keys ${\textit{EPK}_{R}^{I}}$, ${\textit{EPK}_{R}^{II}}$ of the member entity ${\mathit{ME}_{R}}$, identified as the receiver, the sender ${\mathit{ME}_{S}}$ generates a ciphertext $\mathit{CT}$ by the following steps.
-
✓ Pick two random values $h\in {\{0,1\}^{n}}$ and $v\in {Z_{q}^{\ast }}$, and compute $U={g^{u}}$ and $V={g^{v}}$, where $u={\mathit{HF}_{4}}(\mathit{msg},h)$.
-
✓ Compute $R={\mathit{HF}_{2}}({({\textit{EPK}_{R}^{I}})^{v}},U,V)\oplus (\mathit{msg}||h)$ and $S={\mathit{HF}_{1}}({({\textit{EPK}_{R}^{II}})^{v}})\cdot {\mathit{HF}_{3}}{(\mathit{msg})^{u}}$.
-
✓ Choose a random values $c\in {Z_{q}^{\ast }}$ which are used to update the entity secret keys.
-
✓ Compute two entity secret keys ${\textit{ESK}_{S,i}^{I}}=({\textit{ESK}_{S,i,A}^{I}},{\textit{ESK}_{S,i,B}^{I}})=({\textit{ESK}_{S,i-1,A}^{I}}\cdot {g^{c}},{\textit{ESK}_{S,i-1,B}^{I}}\cdot {g^{-c}})$ and ${\textit{ESK}_{S,i}^{II}}=({\textit{ESK}_{S,i,A}^{II}},{\textit{ESK}_{S,i,B}^{II}})=({\textit{ESK}_{S,i-1,A}^{II}}\cdot {g^{c}},{\textit{ESK}_{S,i-1,B}^{II}}\cdot {g^{-c}})$.
-
✓ Compute $\delta ={\mathit{HF}_{5}}({\mathit{ME}_{S}},{\mathit{ME}_{R}},U,V,R,S,\mathit{msg})$, and then set $T{S^{I}}={\textit{ESK}_{S,i,A}^{I}}\cdot {(X\cdot {Y^{\delta }})^{u}}$ and $T{S^{II}}={\textit{ESK}_{S,i,A}^{II}}\cdot {(X\cdot {Y^{\delta }})^{v}}$.
-
✓ Generate a signature $\sigma ={\textit{ESK}_{S,i,B}^{I}}\cdot T{S^{I}}\cdot {\textit{ESK}_{S,i,B}^{II}}\cdot T{S^{II}}$.
-
✓ Set a ciphertext $CT=({\mathit{ME}_{S}},{\mathit{ME}_{R}},U,V,R,S,\sigma )$.
-
-
– Unsigncryption: By executing the algorithm in the $j\mathrm{th}$ round with the system parameters $\mathit{SP}$, two entity secret keys ${\textit{ESK}_{R,j-1}^{I}}$, ${\textit{ESK}_{R,j-1}^{II}}$ (the $j-1\mathrm{th}$ round) of the member entity ${\mathit{ME}_{R}}$, identified as the receiver, a ciphertext $\mathit{CT}$, and two entity public keys ${\textit{EPK}_{S}^{I}}$, ${\textit{EPK}_{S}^{II}}$ of the member entity ${\mathit{ME}_{S}}$, identified as the sender, the sender ${\mathit{ME}_{S}}$ generates a message ${\mathit{msg}^{\prime }}$ by the following steps.
-
✓ Choose a random values $d\in {Z_{q}^{\ast }}$ which are used to update the entity secret keys.
-
✓ Compute two entity secret keys ${\textit{ESK}_{R,j}^{I}}=({\textit{ESK}_{R,j,A}^{I}},{\textit{ESK}_{R,j,B}^{I}})=({\textit{ESK}_{R,j-1,A}^{I}}\cdot {g^{d}},{\textit{ESK}_{R,j-1,B}^{I}}\cdot {g^{-d}})$ and ${\textit{ESK}_{R,j}^{II}}=({\textit{ESK}_{R,j,A}^{II}},{\textit{ESK}_{R,j,B}^{II}})=({\textit{ESK}_{R,j-1,A}^{II}}\cdot {g^{d}},{\textit{ESK}_{R,j-1,B}^{II}}\cdot {g^{-d}})$.
-
✓ Set ${\mathit{TU}^{I}}=\hat{e}({\textit{ESK}_{R,j,A}^{I}},V)$ and ${\mathit{TU}^{II}}=\hat{e}({\textit{ESK}_{R,j,A}^{II}},V)$.
-
✓ Compute $R\oplus {\mathit{HF}_{2}}({\mathit{TU}^{I}}\cdot \hat{e}({\textit{ESK}_{R,j,B}^{I}},V),U,V)$ to obtain ${\mathit{msg}^{\prime }}$ and ${h^{\prime }}$.
-
✓ Set ${u^{\prime }}={\mathit{HF}_{4}}({\mathit{msg}^{\prime }},{h^{\prime }})$. If the two equations $U={g^{{u^{\prime }}}}$ and $S={\mathit{HF}_{1}}({\mathit{TU}^{II}}\cdot \hat{e}({\textit{ESK}_{R,j,B}^{II}},V))\cdot {\mathit{HF}_{3}}{({\mathit{msg}^{\prime }})^{{u^{\prime }}}}$ hold, compute ${\delta ^{\prime }}={\mathit{HF}_{5}}({\mathit{ME}_{S}},{\mathit{ME}_{R}},U,V,R,S,{\mathit{msg}^{\prime }})$. Otherwise, return the result “failure”.
-
✓ If $\hat{e}(g,\sigma )={\textit{EPK}^{I}}\cdot {\textit{EPK}^{II}}\cdot \hat{e}(U\cdot V,X\cdot {Y^{{\delta ^{\prime }}}})$ holds, return the message ${\mathit{msg}^{\prime }}$. Otherwise, return the result “failure”.
-
-
– Authorization: By executing the algorithm in the $k\mathrm{th}$ round with the system parameters $\mathit{SP}$ and the entity secret key ${\textit{ESK}_{S,k-1}^{II}}$ (the $k-1\mathrm{th}$ round) of a member entity $\mathit{ME}$, the member entity $\mathit{ME}$ generates a trapdoor $\mathit{TD}$ using the following steps.
-
✓ Choose a random value $e\in {Z_{q}^{\ast }}$, and update the entity secret key ${\textit{ESK}_{k}^{II}}=({\textit{ESK}_{k,A}^{II}},{\textit{ESK}_{k,B}^{II}})=({\textit{ESK}_{k-1,A}^{II}}\cdot {g^{e}},{\textit{ESK}_{k-1,B}^{II}}\cdot {g^{-e}})$.
-
✓ Set $TT={\textit{ESK}_{k,A}^{II}}$, and compute $TD=TT\cdot {\textit{ESK}_{k,B}^{II}}$.
-
-
– Test: By executing the algorithm with the system parameters $\mathit{SP}$, the ciphertext-trapdoor pair $({\mathit{CT}_{\zeta }},{\mathit{TD}_{\zeta }})$ of the member entity ${\mathit{ME}_{\zeta }}$ and the ciphertext-trapdoor pair $({\mathit{CT}_{\eta }},{\mathit{TD}_{\eta }})$ of the member entity ${\mathit{ME}_{\eta }}$, the cloud server $\mathit{CS}$ generates 1 or 0 by the following steps.
-
✓ Compute ${R_{\zeta }}={S_{\zeta }}/{\mathit{HF}_{1}}(\hat{e}({\mathit{TD}_{\zeta }},{V_{\zeta }})$ and ${R_{\eta }}={S_{\eta }}/{\mathit{HF}_{1}}(\hat{e}({\mathit{TD}_{\eta }},{V_{\eta }})$.
-
✓ If the equation $\hat{e}({R_{\eta }},{U_{\zeta }})=\hat{e}({R_{\zeta }},{U_{\eta }})$ holds, output 1. Otherwise, output 0.
-
\[\begin{aligned}{}R\hspace{0.1667em}\oplus \hspace{0.1667em}& {\mathit{HF}_{2}}\big({\mathit{TU}^{I}}\cdot \hat{e}\big({\textit{ESK}_{R,j,B}^{I}},V\big),U,V\big)\\ {} & ={\mathit{HF}_{2}}\big({\big({\textit{EPK}_{R}^{I}}\big)^{v}},U,V\big)\oplus (\mathit{msg}\hspace{0.1667em}\| \hspace{0.1667em}h)\\ {} & \hspace{1em}\oplus {\mathit{HF}_{2}}\big(\hat{e}\big({\textit{ESK}_{R,j,A}^{I}},V\big)\cdot \hat{e}\big({\textit{ESK}_{R,j,B}^{I}},V\big),U,V\big)\\ {} & =(\mathit{msg}\hspace{0.1667em}\| \hspace{0.1667em}h)\oplus {\mathit{HF}_{2}}\big({\big({\textit{EPK}_{R}^{I}}\big)^{v}},U,V\big)\oplus {\mathit{HF}_{2}}\big(\hat{e}\big({\textit{ESK}_{R}^{I}},V\big),U,V\big)\\ {} & =(\mathit{msg}\hspace{0.1667em}\| \hspace{0.1667em}h)\oplus {\mathit{HF}_{2}}\big(\hat{e}{\big(g,{g^{\alpha }}\big)^{v}},U,V\big)\oplus {\mathit{HF}_{2}}\big(\hat{e}\big({g^{\alpha }},{g^{v}}\big),U,V\big)\\ {} & =(\mathit{msg}\hspace{0.1667em}\| \hspace{0.1667em}h)\oplus {\mathit{HF}_{2}}\big(\hat{e}{(g,g)^{\alpha v}},U,V\big)\oplus {\mathit{HF}_{2}}\big(\hat{e}{(g,g)^{\alpha v}},U,V\big)\\ {} & =(\mathit{msg}\hspace{0.1667em}\| \hspace{0.1667em}h),\end{aligned}\]
\[\begin{aligned}{}\hat{e}(g,\sigma )& =\hat{e}\big(g,{\textit{ESK}_{S,i,B}^{I}}\cdot T{S^{I}}\cdot {\textit{ESK}_{S,i,B}^{II}}\cdot T{S^{II}}\big)\\ {} & =\hat{e}\big(g,{\textit{ESK}_{S,i,B}^{I}}\cdot {\textit{ESK}_{S,i,A}^{I}}\cdot {\big(X\cdot {Y^{\delta }}\big)^{u}}\cdot {\textit{ESK}_{S,i,B}^{II}}\cdot {\textit{ESK}_{S,i,A}^{II}}\cdot {\big(X\cdot {Y^{\delta }}\big)^{v}}\big)\\ {} & =\hat{e}\big(g,{\textit{ESK}_{S}^{I}}\cdot {\big(X\cdot {Y^{\delta }}\big)^{u}}\cdot {\textit{ESK}_{S}^{II}}\cdot {\big(X\cdot {Y^{\delta }}\big)^{v}}\big)\\ {} & =\hat{e}\big(g,{g^{\alpha }}\cdot {\big(X\cdot {Y^{\delta }}\big)^{u}}\cdot {g^{\beta }}\cdot {\big(X\cdot {Y^{\delta }}\big)^{v}}\big)\\ {} & =\hat{e}\big(g,{g^{\alpha }}\big)\cdot \hat{e}\big(g,{g^{\beta }}\big)\cdot \hat{e}\big(g,{\big(X\cdot {Y^{\delta }}\big)^{u}}\big)\cdot \hat{e}\big(g,{\big(X\cdot {Y^{\delta }}\big)^{v}}\big)\\ {} & ={\textit{EPK}^{I}}\cdot {\textit{EPK}^{II}}\cdot \hat{e}\big({g^{u}},\big(X\cdot {Y^{\delta }}\big)\big)\cdot \hat{e}\big({g^{v}},\big(X\cdot {Y^{\delta }}\big)\big)\\ {} & ={\textit{EPK}^{I}}\cdot {\textit{EPK}^{II}}\cdot \hat{e}\big(U,\big(X\cdot {Y^{\delta }}\big)\big)\cdot \hat{e}\big(V,\big(X\cdot {Y^{\delta }}\big)\big)\\ {} & ={\textit{EPK}^{I}}\cdot {\textit{EPK}^{II}}\cdot \hat{e}\big(U\cdot V,X\cdot {Y^{\delta }}\big).\end{aligned}\]
Next, we present the equation derivation process used in the $Test$ algorithm.
\[\begin{aligned}{}{R_{\zeta }}& ={S_{\zeta }}/{\mathit{HF}_{1}}\big(\hat{e}({\mathit{TD}_{\zeta }},{V_{\zeta }})\big)\\ {} & ={\mathit{HF}_{1}}\big({\big({\textit{EPK}_{\zeta }^{II}}\big)^{{v_{\zeta }}}}\big)\cdot {\mathit{HF}_{3}}{({\mathit{msg}_{\zeta }})^{{u_{\zeta }}}}/{\mathit{HF}_{1}}\big(\hat{e}\big(T{T_{\zeta }}\cdot {\textit{ESK}_{k,B}^{II}},{g^{{v_{\zeta }}}}\big)\big)\\ {} & ={\mathit{HF}_{1}}\big(\hat{e}{\big(g,{g^{{\beta _{\zeta }}}}\big)^{{v_{\zeta }}}}\big)\cdot {\mathit{HF}_{3}}{({\mathit{msg}_{\zeta }})^{{u_{\zeta }}}}/{\mathit{HF}_{1}}\big(\hat{e}\big({\textit{ESK}_{\zeta ,k,A}^{II}}\cdot {\textit{ESK}_{\zeta ,k,B}^{II}},{g^{{v_{\zeta }}}}\big)\big)\\ {} & ={\mathit{HF}_{1}}\big(\hat{e}\big({g^{{v_{\zeta }}}},{g^{{\beta _{\zeta }}}}\big)\big)\cdot {\mathit{HF}_{3}}{({\mathit{msg}_{\zeta }})^{{u_{\zeta }}}}/{\mathit{HF}_{1}}\big(\hat{e}\big({\textit{ESK}_{\zeta }^{II}},{g^{{v_{\zeta }}}}\big)\big)\\ {} & ={\mathit{HF}_{1}}\big(\hat{e}\big({g^{{v_{\zeta }}}},{g^{{\beta _{\zeta }}}}\big)\big)\cdot {\mathit{HF}_{3}}{({\mathit{msg}_{\zeta }})^{{u_{\zeta }}}}/{\mathit{HF}_{1}}\big(\hat{e}\big({g^{{\beta _{\zeta }}}},{g^{{v_{\zeta }}}}\big)\big)\\ {} & ={\mathit{HF}_{3}}{({\mathit{msg}_{\zeta }})^{{u_{\zeta }}}},\end{aligned}\]
\[\begin{aligned}{}{R_{\eta }}& ={S_{\eta }}/{\mathit{HF}_{1}}\big(\hat{e}({\mathit{TD}_{\eta }},{V_{\eta }})\big)\\ {} & ={\mathit{HF}_{1}}\big({\big({\textit{EPK}_{\eta }^{II}}\big)^{{v_{\eta }}}}\big)\cdot {\mathit{HF}_{3}}{({\mathit{msg}_{\eta }})^{{u_{\eta }}}}/{\mathit{HF}_{1}}\big(\hat{e}\big(T{T_{\eta }}\cdot {\textit{ESK}_{\eta ,k,B}^{II}},{g^{{v_{\eta }}}}\big)\big)\\ {} & ={\mathit{HF}_{1}}\big(\hat{e}{\big(g,{g^{{\beta _{\eta }}}}\big)^{{v_{\eta }}}}\big)\cdot {\mathit{HF}_{3}}{({\mathit{msg}_{\eta }})^{{u_{\eta }}}}/{\mathit{HF}_{1}}\big(\hat{e}\big({\textit{ESK}_{\eta ,k,A}^{II}}\cdot {\textit{ESK}_{\eta ,k,B}^{II}},{g^{{v_{\eta }}}}\big)\big)\\ {} & ={\mathit{HF}_{1}}\big(\hat{e}\big({g^{{v_{\eta }}}},{g^{{\beta _{\eta }}}}\big)\big)\cdot {\mathit{HF}_{3}}{({\mathit{msg}_{\eta }})^{{u_{\eta }}}}/{\mathit{HF}_{1}}\big(\hat{e}\big({\textit{ESK}_{\eta }^{II}},{g^{{v_{\eta }}}}\big)\big)\\ {} & ={\mathit{HF}_{1}}\big(\hat{e}\big({g^{{v_{\eta }}}},{g^{{\beta _{\eta }}}}\big)\big)\cdot {\mathit{HF}_{3}}{({\mathit{msg}_{\eta }})^{{u_{\eta }}}}/{\mathit{HF}_{1}}\big(\hat{e}\big({g^{{\beta _{\eta }}}},{g^{{v_{\eta }}}}\big)\big)\\ {} & ={\mathit{HF}_{3}}{({\mathit{msg}_{\eta }})^{{u_{\eta }}}},\end{aligned}\]
\[\begin{aligned}{}\hat{e}({R_{\eta }},{U_{\zeta }})& =\hat{e}\big({\mathit{HF}_{3}}{({\mathit{msg}_{\eta }})^{{u_{\eta }}}},{g^{{u_{\zeta }}}}\big)=\hat{e}{\big({\mathit{HF}_{3}}({\mathit{msg}_{\eta }}),g\big)^{{u_{\eta }}\cdot {u_{\zeta }}}},\\ {} \hat{e}({R_{\zeta }},{U_{\eta }})& =\hat{e}\big({\mathit{HF}_{3}}{({\mathit{msg}_{\zeta }})^{{u_{\zeta }}}},{g^{{u_{\eta }}}}\big)=\hat{e}{\big({\mathit{HF}_{3}}({\mathit{msg}_{\zeta }}),g\big)^{{u_{\zeta }}\cdot {u_{\eta }}}}.\end{aligned}\]
6 Security Analysis
In this section, we will prove three theorems to establish the security of the proposed LR-PKSCET scheme in terms of indistinguishable security, one-way security and existential unforgeability, while ensuring that the proposed scheme possesses leakage resilience to withstand side-channel attacks.
Theorem 1.
Under the assumptions of DL and HF, the proposed LR-PKSCET scheme possesses leakage resilience and indistinguishable security in the security game (Definition 2) using the GBG model.
Proof.
Let’s begin the security game with the interaction between a challenger $\mathcal{CH}$ and an adversary ${\mathcal{A}_{I}}$.
-
– Setup: The challenger $\mathcal{CH}$ utilizes a security parameter λ to execute the Initialization algorithm to generate the system parameters $SP=\{G$, ${G_{T}}$, q, $\hat{e}$, g, X, Y, ${\mathit{HF}_{1}}$, ${\mathit{HF}_{2}}$, ${\mathit{HF}_{3}}$, ${\mathit{HF}_{4}}$, ${\mathit{HF}_{5}}\}$. Furthermore, $\mathcal{CH}$ creates eight lists $\mathcal{L}G$, $\mathcal{L}{G_{T}}$, $\mathcal{L}{\mathit{HF}_{1}}$, $\mathcal{L}{\mathit{HF}_{2}}$, $\mathcal{L}{\mathit{HF}_{3}}$, $\mathcal{L}{\mathit{HF}_{4}}$, $\mathcal{L}{\mathit{HF}_{5}}$, $\mathcal{L}\textit{MEkeys}$ as below.
-
✓ The list $\mathcal{L}G$ contains pairs of
, where each element in G is represented by a multivariate polynomial
, and its corresponding encoded bit-string is denoted by
. Here, r, t, and v respectively represent the query type, the t-th query, and the v-th element in G. Initially, the challenger $\mathcal{CH}$ adds three pairs
,
and
to the list $\mathcal{L}G$.
-
✓ The list $\mathcal{L}{G_{T}}$ contains pairs of
, where each element in ${G_{T}}$ is represented by a multivariate polynomial
, and its corresponding encoded bit-string is denoted by
. Furthermore, the symbols r, t, and v have the same meanings as those in the list $\mathcal{L}G$ above.
Each element present in the lists $\mathcal{L}G$ and $\mathcal{L}{G_{T}}$ is represented both as a multivariate polynomial and a bit-string. To facilitate the conversion between these representations, we introduce two conversion rules, namely Rule-1 and Rule-2. These rules illustrate the process of transforming a multivariate polynomial into its corresponding bit-string and vice versa.-
• Under Rule-1, when encountering the multivariate polynomial
in the list $\mathcal{L}G/\mathcal{L}{G_{T}}$, the procedure involves converting it to the corresponding bit-string
, which will be the output. However, if the multivariate polynomial is not present in the list, a random bit-string
related to
is chosen. This newly selected string will be appended to the list $\mathcal{L}G/\mathcal{L}{G_{T}}$, and then returned as the output.
-
• Under Rule-2, when encountering the bit-string
in the list $\mathcal{L}G/\mathcal{L}{G_{T}}$, the procedure involves converting it to the corresponding multivariate polynomial
, which will be the output. However, if the bit-string is not present in the list, a random polynomial
related to
is chosen. This newly selected polynomial will be appended to the list $\mathcal{L}G/\mathcal{L}{G_{T}}$, and then returned as the output.
-
-
✓ The list $\mathcal{L}{\mathit{HF}_{1}}$ contains pairs of
, where
and
are the necessary information for the execution of ${\mathit{HF}_{1}}$.
-
✓ The list $\mathcal{L}{\mathit{HF}_{2}}$ contains pairs of
, where
and
are the necessary information for the execution of ${\mathit{HF}_{2}}$.
-
✓ The list $\mathcal{L}{\mathit{HF}_{3}}$ contains pairs of
, where $\mathit{msg}$ and
are the necessary information for the execution of ${\mathit{HF}_{3}}$.
-
✓ The list $\mathcal{L}{\mathit{HF}_{4}}$ contains pairs of
, where $\mathit{msg}||h$ and
are the necessary information for the execution of ${\mathit{HF}_{4}}$.
-
✓ The list $\mathcal{L}{\mathit{HF}_{5}}$ contains pairs of
, where
and
are the necessary information for the execution of ${\mathit{HF}_{5}}$.
-
✓ The list $\mathcal{L}\mathit{MEkeys}$ contains pairs of
, where $\mathit{ME}$,
and
, respectively, are presented as the information of member entity, entity secret keys and entity public keys.
-
-
– Phase 1: The adversary ${\mathcal{A}_{I}}$ has the capability to make at most ${\psi _{1}}$ queries as follows.
-
✓ ${Q_{G}}$ query: By providing
and $ACT$ as inputs to this query, the execution of the following steps will produce a response denoted by
.
-
✓ ${Q_{{G_{T}}}}$ query: By providing
,
and $ACT$ as inputs to this query, the execution of the following steps will produce a response denoted by
.
-
✓ ${Q_{\hat{e}}}$ query: By providing
and
as inputs to this query, the execution of the following steps will produce a response denoted by
.
-
✓ EntityKeyGen query: By providing member entity’s information $\mathit{ME}$ as inputs to this query, the challenger $\mathcal{CH}$ uses $\mathit{ME}$ to search the list $\mathcal{L}\mathit{MEkeys}$. Once the matching pair
is located, $\mathcal{CH}$ transforms the pair into
, respectively, and subsequently returns them to ${\mathcal{A}_{I}}$.
-
✓ Signcryption query: By inputting two entity secret keys ${\textit{ESK}_{S,i}^{I}}$, ${\textit{ESK}_{S,i}^{II}}$ of the member entity ${\mathit{ME}_{S}}$, identified as the sender, a message $\mathit{msg}$, and two entity public keys ${\textit{EPK}_{R}^{I}}$, ${\textit{EPK}_{R}^{II}}$ of the member entity ${\mathit{ME}_{R}}$, identified as the receiver, the execution of the following steps will produce a ciphertext $\mathit{CT}$.
-
• Use ${\mathit{ME}_{S}}$ and ${\mathit{ME}_{R}}$ to find
and
in the list $\mathcal{L}\mathit{MEkeys}$, respectively.
-
• Choose the variate
from the list $\mathcal{L}{\mathit{HF}_{4}}$ by using $\mathit{msg}||h$, where h is a random value.
-
• Set
and pick a random variate
in G.
-
• Choose the variate
from the list $\mathcal{L}{\mathit{HF}_{2}}$ by using
.
-
• Execute Rule-1 to transform
into
.
-
• Compute
, and execute Rule-2 to transform
into
.
-
• Choose the variate
from the list $\mathcal{L}{\mathit{HF}_{1}}$ by using
, and choose the variate
from the list $\mathcal{L}{\mathit{HF}_{3}}$ by using $\mathit{msg}$.
-
• Set
.
-
• Choose the variate
from the list $\mathcal{L}{\mathit{HF}_{5}}$ by using
.
-
• Set
.
-
• Set
.
-
-
✓ Signcryption leak query: By providing an index i, and two leaked functions ${\textit{LF}_{SC,i}^{A}}$ and ${\textit{LF}_{SC,i}^{B}}$ as inputs to this query, the challenger $\mathcal{CH}$ provides two sets of leaked information ${\Lambda LF_{SC,i}^{A}}={\textit{LF}_{SC,i}^{A}}({\textit{ESK}_{S,i,A}^{I}},{\textit{ESK}_{S,i,A}^{II}})$ and ${\Lambda LF_{SC,i}^{B}}={\textit{LF}_{SC,i}^{B}}({\textit{ESK}_{S,i,B}^{I}},{\textit{ESK}_{S,i,B}^{II}})$ back to ${\mathcal{A}_{I}}$.
-
✓ Unsigncryption query: By inputting two entity secret keys ${\textit{ESK}_{R,j}^{I}}$, ${\textit{ESK}_{R,j}^{II}}$ of the member entity ${\mathit{ME}_{R}}$, identified as the receiver, a ciphertext $\mathit{CT}$ message $\mathit{msg}$, and two entity public keys ${\textit{EPK}_{S}^{I}}$, ${\textit{EPK}_{S}^{II}}$ of the member entity ${\mathit{ME}_{S}}$, identified as the sender, the execution of the following steps will produce a message $\mathit{msg}$.
-
• Choose the variate
from the list $\mathcal{L}{\mathit{HF}_{2}}$ by using
.
-
• Execute Rule-1 to transform
and
into
and
.
-
• Compute
, and obtain ${\mathit{msg}^{\prime }}$ and ${h^{\prime }}$.
-
• Choose the variate
from the list $\mathcal{L}{\mathit{HF}_{1}}$ by using
.
-
• Choose the variate
from the list $\mathcal{L}{\mathit{HF}_{3}}$ by using ${\mathit{msg}^{\prime }}$.
-
• Choose the variate
from the list $\mathcal{L}{\mathit{HF}_{4}}$ by using ${\mathit{msg}^{\prime }}||{h^{\prime }}$.
-
• If both equations
and
hold, find
from the list $\mathcal{L}{\mathit{HF}_{5}}$ by using
.
-
• If
holds, return the message ${\mathit{msg}^{\prime }}$.
-
-
✓ Unsigncryption leak query: By providing an index j, and two leaked functions ${\textit{LF}_{\mathit{USC},j}^{A}}$ and ${\textit{LF}_{\mathit{USC},j}^{B}}$ as inputs to this query, the challenger $\mathcal{CH}$ provides two sets of leaked information $\Lambda {\textit{LF}_{\mathit{USC},j}^{A}}={\textit{LF}_{\mathit{USC},j}^{A}}({\textit{ESK}_{R,j,A}^{I}},{\textit{ESK}_{R,j,A}^{II}})$ and ${\Lambda LF_{\mathit{USC},j}^{B}}={\textit{LF}_{\mathit{USC},j}^{B}}({\textit{ESK}_{R,j,B}^{I}},{\textit{ESK}_{R,j,B}^{II}})$ back to ${\mathcal{A}_{I}}$.
-
✓ Authorization query: By providing member entity’s information $\mathit{ME}$ as inputs to this query, the challenger $\mathcal{CH}$ uses $\mathit{ME}$ to search the list $\mathcal{L}\mathit{MEkeys}$. Once the matching pair
is located, $\mathcal{CH}$ transforms the pair into
respectively. Then, $\mathcal{CH}$ sets
, and subsequently returns it to ${\mathcal{A}_{I}}$.
-
✓ Authorization leak query: By providing an index k, and two leaked functions ${\textit{LF}_{\mathit{Auth},k}^{A}}$ and ${\textit{LF}_{\mathit{Auth},k}^{B}}$ as inputs to this query, the challenger $\mathcal{CH}$ provides two sets of leaked information ${\Lambda LF_{\mathit{Auth},k}^{A}}={\textit{LF}_{\mathit{Auth},k}^{A}}({\textit{ESK}_{R,j,A}^{II}})$ and ${\Lambda LF_{\mathit{Auth},k}^{B}}={\textit{LF}_{\mathit{Auth},k}^{B}}({\textit{ESK}_{R,j,B}^{II}})$ back to ${\mathcal{A}_{I}}$.
-
-
– Challenger: ${\mathcal{A}_{I}}$ chooses a specific member entity ${\mathit{ME}_{R}^{\ast }}$, and provides two target plaintexts, ${\mathit{msg}_{0}}$ and ${\mathit{msg}_{1}}$, to $\mathcal{CH}$. Subsequently, $\mathcal{CH}$ chooses a random bit $b\in \{0,1\}$ and utilizes the Signcryption algorithm with the corresponding parameters ${\mathit{msg}_{b}^{\ast }}$, ${\textit{EPK}_{R}^{I}}$, ${\textit{EPK}_{R}^{II}}$, ${\textit{ESK}_{S,i}^{I}}$ and ${\textit{ESK}_{S,i}^{II}}$ to generate the target ciphertext ${\mathit{CT}^{\ast }}$. Then, $\mathcal{CH}$ sends the resulting ciphertext ${\mathit{CT}^{\ast }}$ to ${\mathcal{A}_{I}}$.
-
– Phase 2: The adversary ${\mathcal{A}_{I}}$ can make further queries at most ${\psi _{2}}$ times as in the Phase 1 except that the selected target, namely ${\mathit{ME}_{R}^{\ast }}$, ${\mathit{msg}_{b}^{\ast }}$, ${\textit{ESK}_{S,i}^{I}}$ and ${\textit{ESK}_{S,i}^{II}}$, may not appear in the EntityKeyGen, the Unsigncryption and the Authorization queries.
-
– Guess phase: ${\mathcal{A}_{I}}$ produces the value ${b^{\prime }}$ and succeeds in the game if ${b^{\prime }}$ is equal to b. The advantage of winning the game is represented by $\textit{Adv}({\mathcal{A}_{I}})=|$ Pr[${b^{\prime }}=b]$–$1/2|$.
In the following, we explore the advantage that ${\mathcal{A}_{I}}$ wins the security game. We discuss ${\mathcal{A}_{I}}$’s advantage in two scenarios: (1) ${\mathcal{A}_{I}}$ refrains from employing leak queries; (2) ${\mathcal{A}_{I}}$ utilizes Signcryption leak query, Unsigncryption leak query and Authorization leak query.
-
– Scenario I: ${\mathcal{A}_{I}}$ possesses ${\mathit{Adv}_{{\mathcal{A}_{I}}}^{nlq}}\leqq |\text{Pr}[\text{Case}\hspace{2.5pt}1]+\text{Pr}[\text{Case}\hspace{2.5pt}2]-1/2|\leqq |384{({\psi _{1}}+{\psi _{2}})^{2}}/q+1/2-1/2|=O({({\psi _{1}}+{\psi _{2}})^{2}}/q)$ in winning the security game, where Pr[Case 1] and Pr[Case 2] are described below.
-
✓ Pr[Case 1] refers to the probability of encountering a collision in either $\mathcal{L}G$ or $\mathcal{L}{G_{T}}$. Let’s focus on the collision probability within the list $\mathcal{L}G$. Assume that we have j elements in $\mathcal{L}G$, denoted by ${v_{i}}\in {Z_{q}^{\ast }}$ for $i\in [1,j]$, where j random values are considered. In the event of a collision, we observe
–
, where
and
represent any two polynomials from the list $\mathcal{L}G$. This implies that
and
have the same value, which resembles a collision in a hash function. Therefore, if one could efficiently find such a collision, it would imply the ability to solve the discrete logarithm problem. Utilizing Lemma 2, we can evaluate the probability of a collision occurring within $\mathcal{L}G$, estimated as $(3/q)\left(\genfrac{}{}{0pt}{}{|\mathcal{L}G|}{2}\right)$, based on the fact that the maximum degree of a polynomial in $\mathcal{L}G$ is 3, as observed from the Signcryption query where the highest-degree term
has degree 3. Similarly, the probability of a collision occurring within the list $\mathcal{L}{G_{T}}$ is $(6/q)\left(\genfrac{}{}{0pt}{}{|\mathcal{L}{G_{T}}|}{2}\right)$. Thus, we have $\text{Pr}[\text{Case}\hspace{2.5pt}1]\leqq (3/q)\left(\genfrac{}{}{0pt}{}{|\mathcal{L}G|}{2}\right)+(6/q)\left(\genfrac{}{}{0pt}{}{|\mathcal{L}{G_{T}}|}{2}\right)\leqq (6/q){(|\mathcal{L}G|+|\mathcal{L}{G_{T}}|)^{2}}\leqq 384{({\psi _{1}}+{\psi _{2}})^{2}}/q$ due to the fact that $|\mathcal{L}G|+|\mathcal{L}{G_{T}}|\leqq 8({\psi _{1}}+{\psi _{2}})$.
-
✓ Pr[Case 2] refers to the probability of encountering a correct guess ${b^{\prime }}=b$ and so $\text{Pr}[\text{Case}\hspace{2.5pt}2]\leqq 1/2$.
-
-
– Scenario II: ${\mathcal{A}_{I}}$ possesses ${\mathit{Adv}_{{\mathcal{A}_{I}}}^{lq}}\leqq O({({\psi _{1}}+{\psi _{2}})^{2}}/q\cdot {2^{2\Phi }})+O({({\psi _{1}}+{\psi _{2}})^{2}}/q)=O({({\psi _{1}}+{\psi _{2}})^{2}}/q\cdot {2^{2\Phi }})$ in successfully winning the security game by the following cases.
-
✓ ${\mathcal{A}_{I}}$ issues the Signcryption leak query: Through this query, ${\mathcal{A}_{I}}$ acquires ${\Lambda LF_{SC,i}^{A}}$ and ${\Lambda LF_{SC,i}^{B}}$ from two leaked functions ${\textit{LF}_{SC,i}^{A}}$ and ${\textit{LF}_{SC,i}^{B}}$, where ${\Lambda LF_{SC,i}^{A}}$ is defined as ${\textit{LF}_{SC,i}^{A}}({\textit{ESK}_{S,i,A}^{I}}$, ${\textit{ESK}_{S,i,A}^{II}})$, and ${\Lambda LF_{SC,i}^{B}}$ corresponds to ${\textit{LF}_{SC,i}^{B}}({\textit{ESK}_{S,i,B}^{I}}$, ${\textit{ESK}_{S,i,B}^{II}})$. Here, ${\textit{ESK}_{S}^{I}}$ and ${\textit{ESK}_{S}^{II}}$ can be obtained from the equations ${\textit{ESK}_{S,0,A}^{I}}\cdot {\textit{ESK}_{S,0,B}^{I}}={\textit{ESK}_{S,1,A}^{I}}\cdot {\textit{ESK}_{S,1,B}^{I}}=\cdots ={\textit{ESK}_{S,i-1,A}^{I}}\cdot {\textit{ESK}_{S,i-1,B}^{I}}={\textit{ESK}_{S,i,A}^{I}}\cdot {\textit{ESK}_{S,i,B}^{I}}$, and ${\textit{ESK}_{S,0,A}^{II}}\cdot {\textit{ESK}_{S,0,B}^{II}}={\textit{ESK}_{S,1,A}^{II}}\cdot {\textit{ESK}_{S,1,B}^{II}}=\cdots ={\textit{ESK}_{S,i-1,A}^{II}}\cdot {\textit{ESK}_{S,i-1,B}^{II}}={\textit{ESK}_{S,i,A}^{II}}\cdot {\textit{ESK}_{S,i,B}^{II}}$. By employing key update techniques in Galindo and Virek (2013) with the constraint that $|{\Lambda LF_{SC,i}^{A}}|$ and $|{\Lambda LF_{SC,i}^{B}}|$ are both less than Φ, the adversary ${\mathcal{A}_{I}}$’s ability is restricted to acquiring a maximum of $2\Phi $ bits of ${\textit{ESK}_{S}^{I}}$ and ${\textit{ESK}_{S}^{II}}$.
-
✓ ${\mathcal{A}_{I}}$ issues the Unsigncryption leak query: Through this query, ${\mathcal{A}_{I}}$ acquires $\Lambda {\textit{LF}_{\mathit{USC},j}^{A}}$ and ${\Lambda LF_{\mathit{USC},j}^{B}}$ from two leaked functions ${\textit{LF}_{\mathit{USC},j}^{A}}$ and ${\textit{LF}_{\mathit{USC},j}^{B}}$, where $\Lambda {\textit{LF}_{\mathit{USC},j}^{A}}$ is defined as ${\textit{LF}_{\mathit{USC},j}^{A}}({\textit{ESK}_{R,j,A}^{I}},{\textit{ESK}_{R,j,A}^{II}})$, and ${\Lambda LF_{\mathit{USC},j}^{B}}$ corresponds to ${\textit{LF}_{\mathit{USC},j}^{B}}({\textit{ESK}_{R,j,B}^{I}},{\textit{ESK}_{R,j,B}^{II}})$. Here, ${\textit{ESK}_{R}^{I}}$ and ${\textit{ESK}_{R}^{II}}$ can be obtained from the equations ${\textit{ESK}_{R,0,A}^{I}}\cdot {\textit{ESK}_{R,0,B}^{I}}={\textit{ESK}_{R,1,A}^{I}}\cdot {\textit{ESK}_{R,1,B}^{I}}=\cdots ={\textit{ESK}_{R,j-1,A}^{I}}\cdot {\textit{ESK}_{R,j-1,B}^{I}}={\textit{ESK}_{R,j,A}^{I}}\cdot {\textit{ESK}_{R,j,B}^{I}}$, and ${\textit{ESK}_{R,0,A}^{II}}\cdot {\textit{ESK}_{R,0,B}^{II}}={\textit{ESK}_{R,1,A}^{II}}\cdot {\textit{ESK}_{R,1,B}^{II}}=\cdots ={\textit{ESK}_{R,j-1,A}^{II}}\cdot {\textit{ESK}_{R,j-1,B}^{II}}={\textit{ESK}_{R,j,A}^{II}}\cdot {\textit{ESK}_{R,j,B}^{II}}$. By employing key update techniques in Galindo and Virek (2013) with the constraint that $|\Lambda {\textit{LF}_{\mathit{USC},j}^{A}}|$ and $|{\Lambda LF_{\mathit{USC},j}^{B}}|$ are both less than Φ, the adversary ${\mathcal{A}_{I}}$’s ability is restricted to acquiring a maximum of $2\Phi $ bits of ${\textit{ESK}_{R}^{I}}$ and ${\textit{ESK}_{R}^{II}}$.
-
✓ ${\mathcal{A}_{I}}$ issues the Authorization leak query: Through this query, ${\mathcal{A}_{I}}$ acquires ${\Lambda LF_{\mathit{Auth},k}^{A}}$ and ${\Lambda LF_{\mathit{Auth},k}^{B}}$ from two leaked functions ${\textit{LF}_{\mathit{Auth},k}^{A}}$ and ${\textit{LF}_{\mathit{Auth},k}^{B}}$, where ${\Lambda LF_{\mathit{Auth},k}^{A}}$ is defined as ${\textit{LF}_{\mathit{Auth},k}^{A}}({\textit{ESK}_{R,j,A}^{II}})$, and ${\Lambda LF_{\mathit{Auth},k}^{B}}$ corresponds to ${\textit{LF}_{\mathit{USC},j}^{B}}({\textit{ESK}_{R,j,B}^{II}})$. Here, ${\textit{ESK}_{R}^{II}}$ can be obtained from the equation ${\textit{ESK}_{R,0,A}^{II}}\cdot {\textit{ESK}_{R,0,B}^{II}}={\textit{ESK}_{R,1,A}^{II}}\cdot {\textit{ESK}_{R,1,B}^{II}}=\cdots ={\textit{ESK}_{R,k-1,A}^{II}}\cdot {\textit{ESK}_{R,k-1,B}^{II}}={\textit{ESK}_{R,k,A}^{II}}\cdot {\textit{ESK}_{R,k,B}^{II}}$. By employing key update techniques in Galindo and Virek (2013) with the constraint that $|{\Lambda LF_{\mathit{Auth},k}^{A}}|$ and $|{\Lambda LF_{\mathit{Auth},k}^{B}}|$ are both less than Φ, the adversary ${\mathcal{A}_{I}}$’s ability is restricted to acquiring a maximum of $2\Phi $ bits of ${\textit{ESK}_{R}^{II}}$.
-
Based on the aforementioned discussions, three events are defined as follows:
-
– In the first event $\mathcal{E}{\textit{ESK}^{I}}$, ${\mathcal{A}_{I}}$ has the capability to derive ${\textit{ESK}^{I}}$ from ${\Lambda LF_{SC,i}^{A}}$, ${\Lambda LF_{SC,i}^{B}}$, $\Lambda {\textit{LF}_{\mathit{USC},j}^{A}}$ and ${\Lambda LF_{\mathit{USC},j}^{B}}$. Furthermore, the complementary event of $\mathcal{E}{\textit{ESK}^{I}}$ is denoted as $\overline{{\mathcal{E}\textit{ESK}^{I}}}$.
-
– In the second event $\mathcal{E}{\textit{ESK}^{II}}$, ${\mathcal{A}_{I}}$ has the capability to derive ${\textit{ESK}^{II}}$ from ${\Lambda LF_{SC,i}^{A}}$, ${\Lambda LF_{SC,i}^{B}}$, $\Lambda {\textit{LF}_{\mathit{USC},j}^{A}}$, ${\Lambda LF_{\mathit{USC},j}^{B}}$, ${\Lambda LF_{\mathit{Auth},k}^{A}}$ and ${\Lambda LF_{\mathit{Auth},k}^{B}}$. Furthermore, the complementary event of $\mathcal{E}{\textit{ESK}^{II}}$ is denoted as $\overline{{\mathcal{E}\textit{ESK}^{II}}}$.
-
– In the third event $\mathcal{E}CG$, ${\mathcal{A}_{I}}$ has a correct guess.
Considering these three events, we can compute the probability Pr[${\mathcal{A}_{I}}$] of ${\mathcal{A}_{I}}$ winning this game.
\[\begin{aligned}{}\mathrm{P}\mathrm{r}[{\mathcal{A}_{I}}]& =\mathrm{P}\mathrm{r}[\mathcal{E}CG]\\ {} & =\mathrm{P}\mathrm{r}\big[\mathcal{E}CG\wedge \big(\mathcal{E}{\textit{ESK}^{I}}\vee \mathcal{E}{\textit{ESK}^{II}}\big)\big]+\mathrm{P}\mathrm{r}\big[\mathcal{E}CG\wedge \big(\overline{\mathcal{E}{\textit{ESK}^{I}}}\wedge \overline{\mathcal{E}{\textit{ESK}^{II}}}\big)\big]\\ {} & \leqq \mathrm{P}\mathrm{r}\big[\mathcal{E}{\textit{ESK}^{I}}\vee \mathcal{E}{\textit{ESK}^{II}}\big]+\mathrm{P}\mathrm{r}\big[\mathcal{E}CG\wedge \big(\overline{\mathcal{E}{\textit{ESK}^{I}}}\wedge \overline{\mathcal{E}{\textit{ESK}^{II}}}\big)\big]\end{aligned}\]
Because of Lemma 2, we obtain $\text{Pr}[\mathcal{E}{\textit{ESK}^{I}}\wedge \mathcal{E}{\textit{ESK}^{II}}]\leqq {\textit{Adv}_{{\mathcal{A}_{I}}}^{nlq}}\cdot {2^{2\Phi }}\leqq O({({\psi _{1}}+{\psi _{2}})^{2}}/q\cdot {2^{2\Phi }})$. Since $\text{Pr}[\mathcal{E}CG\wedge (\overline{\mathcal{E}{\textit{ESK}^{I}}}\wedge \overline{\mathcal{E}{\textit{ESK}^{II}}})]$ indicates the advantage of correct guess while having no knowledge of ${\textit{ESK}^{I}}$ and ${\textit{ESK}^{II}}$, we have $\text{Pr}[\mathcal{E}CG\wedge (\overline{\mathcal{E}{\textit{ESK}^{I}}}\wedge \overline{\mathcal{E}{\textit{ESK}^{II}}})]=\textit{Adv}{{\mathcal{A}_{I}}^{nlq}}=O({({\psi _{1}}+{\psi _{2}})^{2}}/q)$. Finally, we have $\text{Pr}[{\mathcal{A}_{I}}]=\text{Pr}[\mathcal{E}CG]\leqq O({({\psi _{1}}+{\psi _{2}})^{2}}/q\cdot {2^{2\Phi }})+O({({\psi _{1}}+{\psi _{2}})^{2}}/q)=O({({\psi _{1}}+{\psi _{2}})^{2}}/q\cdot {2^{2\Phi }})$. □
Theorem 2.
Under the assumptions of DL and HF, the proposed LR-PKSCET scheme possesses leakage resilience and one-way security in the security game (Definition 3) using the GBG model.
Proof.
Let’s begin the security game with the interaction between a challenger $\mathcal{CH}$ and an adversary ${\mathcal{A}_{II}}$.
-
– Setup: This stage is the same as that in the proof of Theorem 1.
-
– Phase 1: This stage is the same as that in the proof of Theorem 1.
-
– Challenge: ${\mathcal{A}_{II}}$ chooses a specific member entity ${\mathit{ME}_{R}^{\ast }}$ to $\mathcal{CH}$. Subsequently, $\mathcal{CH}$ chooses a random message ${\mathit{msg}^{\ast }}$ and utilizes the Signcryption algorithm with the corresponding parameters ${\mathit{msg}^{\ast }}$, ${\textit{EPK}_{R}^{I}}$, ${\textit{EPK}_{R}^{II}}$, ${\textit{ESK}_{S}^{I}}$ and ${\textit{ESK}_{S}^{II}}$ to generate the target ciphertext ${\mathit{CT}^{\ast }}$. Then, $\mathcal{CH}$ sends ${\mathit{CT}^{\ast }}$ to ${\mathcal{A}_{II}}$.
-
– Phase 2: The adversary ${\mathcal{A}_{II}}$ can make further queries at most ${\psi _{2}}$ times as in the Phase 1 except that the selected target, namely ${\mathit{ME}_{R}^{\ast }}$, ${\mathit{msg}^{\ast }}$, ${\textit{ESK}_{S,i}^{I}}$ and ${\textit{ESK}_{S,i}^{II}}$, may not appear in the EntityKeyGen and the Unsigncryption queries.
-
– Guess phase: ${\mathcal{A}_{II}}$ produces the message ${\mathit{msg}^{\prime }}$ and wins the game if ${\mathit{msg}^{\prime }}$ is the same as $\mathit{msg}$. The advantage of winning the game is represented by $\textit{Adv}({\mathcal{A}_{II}})=|\text{Pr}[{\mathit{msg}^{\prime }}=\mathit{msg}]|$.
In the following, we explore the advantage that ${\mathcal{A}_{II}}$ wins in the security game. We discuss ${\mathcal{A}_{II}}$’s advantage in two scenarios: (1) ${\mathcal{A}_{II}}$ refrains from employing leak queries; (2) ${\mathcal{A}_{II}}$ utilizes Signcryption leak query and Unsigncryption leak query.
□
-
– Scenario I: ${\mathcal{A}_{II}}$ possesses ${\mathit{Adv}_{{A_{II}}}^{nlq}}\leqq |\text{Pr}[\text{Case}\hspace{2.5pt}1]+\text{Pr}[\text{Case}\hspace{2.5pt}2]|\leqq |384{({\psi _{1}}+{\psi _{2}})^{2}}/q+2/q|=O({({\psi _{1}}+{\psi _{2}})^{2}}/q)$ in winning the security game, where Pr[Case 1] and Pr[Case 2] are described below.
-
✓ Pr[Case 1] refers to the probability of encountering a collision in either $\mathcal{L}G$ or $\mathcal{L}{G_{T}}$. We can obtain $\text{Pr}[\text{Case}\hspace{2.5pt}1]\leqq 384{({\psi _{1}}+{\psi _{2}})^{2}}/q$ using a proof similar to that in the proof of Theorem 1.
-
✓ Pr[Case 2] refers to the probability of encountering a correct output ${\mathit{msg}^{\prime }}=\mathit{msg}$. Certainly, ${\mathcal{A}_{II}}$ will be provided with a target ciphertext ${\mathit{CT}^{\ast }}=({\mathit{ME}_{S}^{\ast }},{\mathit{ME}_{R}^{\ast }},{U^{\ast }},{V^{\ast }},{R^{\ast }},{S^{\ast }},{\sigma ^{\ast }})$, and ${\mathcal{A}_{II}}$ will utilize the Unsigncryption algorithm to derive the message ${\mathit{msg}^{\prime }}$. Notably, the message ${\mathit{msg}^{\prime }}$ is computed using the expression ${R^{\ast }}\oplus {\mathit{HF}_{2}}(\hat{e}({\textit{ESK}_{R}^{I}},{V^{\ast }}),{U^{\ast }},{V^{\ast }})$. Let’s denote
. The polynomial
exhibits a maximum degree of 2. By Lemma 2, the probability $\text{Pr}[\text{Case}\hspace{2.5pt}2]\leqq 2/q$ can be achieved.
-
-
– Scenario II: By employing a similar approach to the proof of Theorem 1, we have that ${\mathcal{A}_{II}}$ possesses ${\mathit{Adv}_{{\mathcal{A}_{II}}}^{lq}}\leqq O({({\psi _{1}}+{\psi _{2}})^{2}}/q\cdot {2^{2\Phi }})+O({({\psi _{1}}+{\psi _{2}})^{2}}/q)=O({({\psi _{1}}+{\psi _{2}})^{2}}/q\cdot {2^{2\Phi }})$ in winning the security game.
Theorem 3.
Under the assumptions of DL and HF, the proposed LR-PKSCET scheme possesses leakage resilience and existential unforgeability in the security game (Definition 4) using the GBG model.
Proof.
Let’s begin the security game with the interaction between a challenger $\mathcal{CH}$ and an adversary ${\mathcal{A}_{\mathit{III}}}$.
-
– Setup: This stage is the same as that in the proof of Theorem 1.
-
– Phase 1: This stage is the same as that in the proof of Theorem 1.
-
– Forgery: The adversary ${\mathcal{A}_{\mathit{III}}}$ successfully forges a ciphertext ${\mathit{CT}^{\ast }}=({\mathit{ME}_{S}^{\ast }},{\mathit{ME}_{R}^{\ast }},{U^{\ast }},{V^{\ast }},{R^{\ast }},{S^{\ast }},{\sigma ^{\ast }})$ for a message ${\mathit{msg}^{\ast }}$, and we declare ${\mathcal{A}_{\mathit{III}}}$ as the winner of this game if the following conditions are satisfied.
-
✓ The Unsigncryption algorithm is capable of generating the message ${\mathit{msg}^{\ast }}$.
-
✓ The Signcryption queries do not include the message ${\mathit{msg}^{\ast }}$, and that also do not contain the two member entities ${\mathit{ME}_{S}^{\ast }}$ and ${\mathit{ME}_{R}^{\ast }}$.
-
✓ The EntityKeyGen queries do not include the member entity ${\mathit{ME}_{S}^{\ast }}$.
-
In the following, we explore the advantage that ${\mathcal{A}_{\mathit{III}}}$ wins the security game. We discuss ${\mathcal{A}_{\mathit{III}}}$’s advantage in two scenarios: (1) ${\mathcal{A}_{\mathit{III}}}$ refrains from employing leak queries; (2) ${\mathcal{A}_{\mathit{III}}}$ utilizes Signcryption leak query, Unsigncryption leak query and Authorization leak query.
□
-
– Scenario I: ${\mathcal{A}_{\mathit{III}}}$ possesses ${\mathit{Adv}_{{A_{\mathit{III}}}}^{nlq}}\leqq |\text{Pr}[\text{Case}\hspace{2.5pt}1]+\text{Pr}[\text{Case}\hspace{2.5pt}2]|\leqq |384{\psi _{1}^{2}}/q+3/q|=O({\psi _{1}^{2}}/q)$ in winning the security game, where Pr[Case 1] and Pr[Case 2] are described below.
-
✓ Pr[Case 1] refers to the probability of encountering a collision in either $\mathcal{L}G$ or $\mathcal{L}{G_{T}}$. We can obtain $\text{Pr}[\text{Case}\hspace{2.5pt}1]\leqq 384{({\psi _{1}}+{\psi _{2}})^{2}}/q$ using a proof similar to that in the proof of Theorem 1.
-
✓ Pr[Case 2] refers to the probability of forging a valid pair $({\mathit{msg}^{\ast }},{\mathit{CT}^{\ast }}=({\mathit{ME}_{S}^{\ast }},{\mathit{ME}_{R}^{\ast }},{U^{\ast }},{V^{\ast }},{R^{\ast }},{S^{\ast }},{\sigma ^{\ast }}))$. The valid pair satisfies
in the Unsigncryption algorithm. Let’s denote
–
. The polynomial
exhibits a maximum degree of 3. By Lemma 2, the probability $\text{Pr[Case 2]}\leqq 3/q$ can be achieved.
-
-
– Scenario II: By employing a similar approach to the proof of Theorem 1, we have that ${\mathcal{A}_{\mathit{III}}}$ possesses ${\mathit{Adv}_{{\mathcal{A}_{\mathit{III}}}}^{lq}}\leqq O({\psi _{1}^{2}}/q\cdot {2^{2\Phi }})+O({\psi _{1}^{2}}/q)=O({\psi _{1}^{2}}/q\cdot {2^{2\Phi }})$ in winning the security game.
7 Comparisons
We compare the proposed LR-PKSCET scheme with the existing PKEET scheme (Ma et al., 2015), PKSCET scheme (Le et al., 2021), LR-PKE scheme (Galindo et al., 2016), and LR-PKSC scheme (Tseng et al., 2022). Table 2 summarizes these comparisons on three properties: possession of signature and encryption, permission of secret keys leakage, and with the property of equality test. Firstly, let’s consider the PKEET scheme (Ma et al., 2015), which focuses on the equality test functionality, but falls short in the other two properties. On the other hand, the PKSCET scheme (Le et al., 2021) possesses the property of performing both signature and encryption, along with the desirable equality test functionality. Unfortunately, it does not allow secret keys leakage. Conversely, the LR-PKE scheme (Galindo et al., 2016) addresses the issue of secret keys leakage, but does so without possessing both signature and encryption capabilities or the equality test functionality. In contrast, the LR-PKSC scheme (Tseng et al., 2022) combines the advantage of possessing both signature and encryption capabilities along with the ability to allow secret keys leakage. However, it falls short in providing the equality test functionality. In conclusion, the proposed LR-PKSCET emerges as a versatile solution that includes all three properties – having signature and encryption capabilities, permission of secret key leakage, and with the equality test functionality.
Table 2
Comparison of our LR-PKSCET with existing PKEET, PKSCET, LR-PKE and LR-PKSC.
| Schemes | Possession of signature and encryption | Permission of secret keys leakage | With the property of equality test |
| Ma et al.’s PKEET scheme (2015) | No | No | Yes |
| Le et al.’s PKSCET scheme (2021) | Yes | No | Yes |
| Galindo et al.’s LR-PKE scheme (2016) | No | Yes | No |
| Tseng et al.’s LR-PKSC scheme (2022) | Yes | Yes | No |
| Our LR-PKSCET scheme | Yes | Yes | Yes |
Next, we introduce a pair of symbols aimed at evaluating the computational effort of the algorithms of our LR-PKSCET scheme:
We derive the pertinent result from simulations (Xiong and Qin, 2015) to obtain an approximate 20 ms for $C{E_{bp}}$ and 7 ms for $C{E_{exp}}$. These simulations are conducted under a computer environment of an Intel Core i7 CPU with 1.80 GHz. The input of simulations encompasses a finite field denoted as ${F_{q}}$, along with the groups G and ${G_{T}}$. Here, q denotes a prime number with 512 bits, and it concurrently serves as the order of the two groups G and ${G_{T}}$. The simulations involve a mobile device environment that employs an Intel 624-MHz PXA270 CPU. We obtain $C{E_{bp}}$ and $C{E_{exp}}$ to be approximately 96 ms and 31 ms, respectively. For a more comprehensive understanding, Table 3 presents an overview of the computational effort of our LR-PKSCET scheme linked to distinct algorithmic processes, including Initialization, EntityKeyGen, Signcryption, Unsigncryption, Authorization and Test on a mobile device MD and a PC.
Table 3
Computational cost of our LR-PKSCET.
| Algorithms | Computational effort | Running time on a MD | Running time on a PC |
| Initialization | 2 $C{E_{exp}}$ | 62 ms | 14 ms |
| EntityKeyGen | 2 $C{E_{bp}}+6C{E_{exp}}$ | 378 ms | 82 ms |
| Signcryption | 10 $C{E_{exp}}$ | 310 ms | 70 ms |
| Unsigncryption | 5 $C{E_{bp}}+5C{E_{exp}}$ | 635 ms | 135 ms |
| Authorization | 2 $C{E_{exp}}$ | 62 ms | 14 ms |
| Test | 4 $C{E_{bp}}$ | 384 ms | 80 ms |
8 Application
As mentioned in Section 1, our LR-PKSCET scheme can be applied to anti-scam systems. As depicted in Fig. 3, we present a situation that exemplifies the utilization of the LR-PKSCET scheme to counteract telephone scams. The scenario encompasses four key roles: anti-scam centre, interlocutor, user, and cloud server. Now, we provide a breakdown of the responsibilities and functions associated with each role within the presented scenario.
-
✓ The anti-scam centre $(\textit{ASC})$ continuously collects keywords related to telephone scams and subjects these keywords to a signcryption process (by using Signcryption algorithm). Also, the $\textit{ASC}$ employs its own secret key to perform Authorization algorithm to generate a trapdoor ${\mathit{TD}_{ACS}}$. Subsequently, the $\textit{ASC}$ transmits the generated ciphertexts and the trapdoor ${\mathit{TD}_{ACS}}$ to the cloud server through public and secure channels, respectively.
-
✓ The interlocutor could potentially be a scammer, who initiates a call to the user with the intention of orchestrating a fraudulent scheme over the phone.
-
✓ The user is vulnerable to potential scammers. When an interlocutor’s call is received, the mobile application automatically transforms the spoken content into text. Relevant keywords are extracted from this transcribed text, and then these keywords will also be subjected to the signcryption procedure. On the other hand, the user also employs its own secret key to generate a trapdoor ${\mathit{TD}_{U}}$. Subsequently, the user transmits the generated ciphertexts and the trapdoor ${\mathit{TD}_{U}}$ to the cloud server through public and secure channels, respectively.
-
✓ The cloud server $(\mathit{CS})$ is responsible for performing equality tests of ciphertexts using the Test algorithm, which determines whether two ciphertexts contain the same plaintext. During this test process, the $\mathit{CS}$ remains unaware of the actual plaintext content. Upon detecting a specific number of matches, the $\mathit{CS}$ will promptly dispatch a warning message to the user. This message serves to alert the user that the ongoing conversation could be linked to a scam activity. As a result, the user may be able to avoid this scam activity.
According to the scenario described above, the proposed LR-PKSCET scheme demonstrates a collaborative approach to counter telephone scams effectively. The synergy among the $\textit{ASC}$, interlocutor, user, and $\mathit{CS}$ displays the potential to enhance security measures in the realm of telecommunication.
9 Conclusions and Future Work
In this paper, we have presented a novel solution to the critical challenge of enhancing the security of PKSCET against side-channel attacks. Our proposed leakage-resilient public key signcryption with equality test (LR-PKSCET) scheme not only successfully combines the benefits of public key signcryption and equality test properties but also offers robust resistance against side-channel attacks. Through rigorous analysis and security proofs, we have demonstrated that the LR-PKSCET scheme achieves several essential security attributes, including leakage resilience, indistinguishability, one-wayness, and existential unforgeability. By incorporating the proposed LR-PKSCET scheme into an anti-scam system, we offer a practical application that addresses a pressing societal concern. The integration of our scheme into such a system has the potential to significantly reduce the frequency and impact of scam cases, thereby safeguarding users from financial and personal losses. While our proposed scheme is based on classical bilinear pairing and achieves indistinguishable chosen-ciphertext attacks (IND-CCA) security, we recognize the increasing importance of post-quantum cryptography (PQC). Although some research efforts have been made in designing PQC-based public key signcryption with equality test (PKSCET), these schemes still lack the functionality to side-channel attacks. As part of our future work, we aim to design a PQC-based LR-PKSCET scheme that maintains IND-CCA security and addresses the challenges posed by the quantum era.

