Abstract
Existing fuzzy inference systems are generally based on ordinary fuzzy sets, which do not let the second and third dimensions of the other fuzzy sets extensions to be employed. This paper suggests a decision-making approach by utilizing the fuzzy inference systems (FIS) based on spherical fuzzy sets (SFS). We prefer spherical fuzzy sets to consider the indecision degree together with membership and non-membership degrees in the proposed FIS. During the defuzzification of SF inference system, the indecision degree is distributed over membership and non-membership degree in balance regarding to indecision degree by using a special transformation function. By applying the proposed approach on FIS, it aims to cover hesitancies and uncertainties caused by insufficient assessments of the decision makers more effectively. The proposed decision-making approach is tested with a real-world application in the field of maintenance work order prioritization for scheduling. Finally, the result of the suggested approach based on SFS is compared with the risk assessment matrix technique (RAM) existing in the literature and Picture Fuzzy Inference Systems (PiFIS). It is observed that the proposed Spherical Fuzzy Inference System (SFIS) is more efficient than RAM and PiFIS methods.
1 Introduction
One of the most effective methods to show uncertainty scenario-based situations is fuzzy set theory, which Zadeh introduced in 1965. A fuzzy set is a type of object whose membership is not clearly specified. Fuzzy sets describe reality better than traditional mathematical binary representations. Because membership in fuzzy sets is gradual, the idea is important for representing the limited amount of precision in mental thinking (Zadeh,
1965). According to Zadeh, characterizing linguistic variables in fuzzy logic increased the application of fuzzy in various situations that could directly transport the mathematical representation of uncertainty in real-world scenarios from the human brain. He introduced in 1975 type-2 fuzzy sets which allow to define membership function as an interval to solve more uncertain problems (Zadeh,
1975; Atanassov,
1986,
2000; Jana
et al.,
2023; Mendel
et al.,
2014).
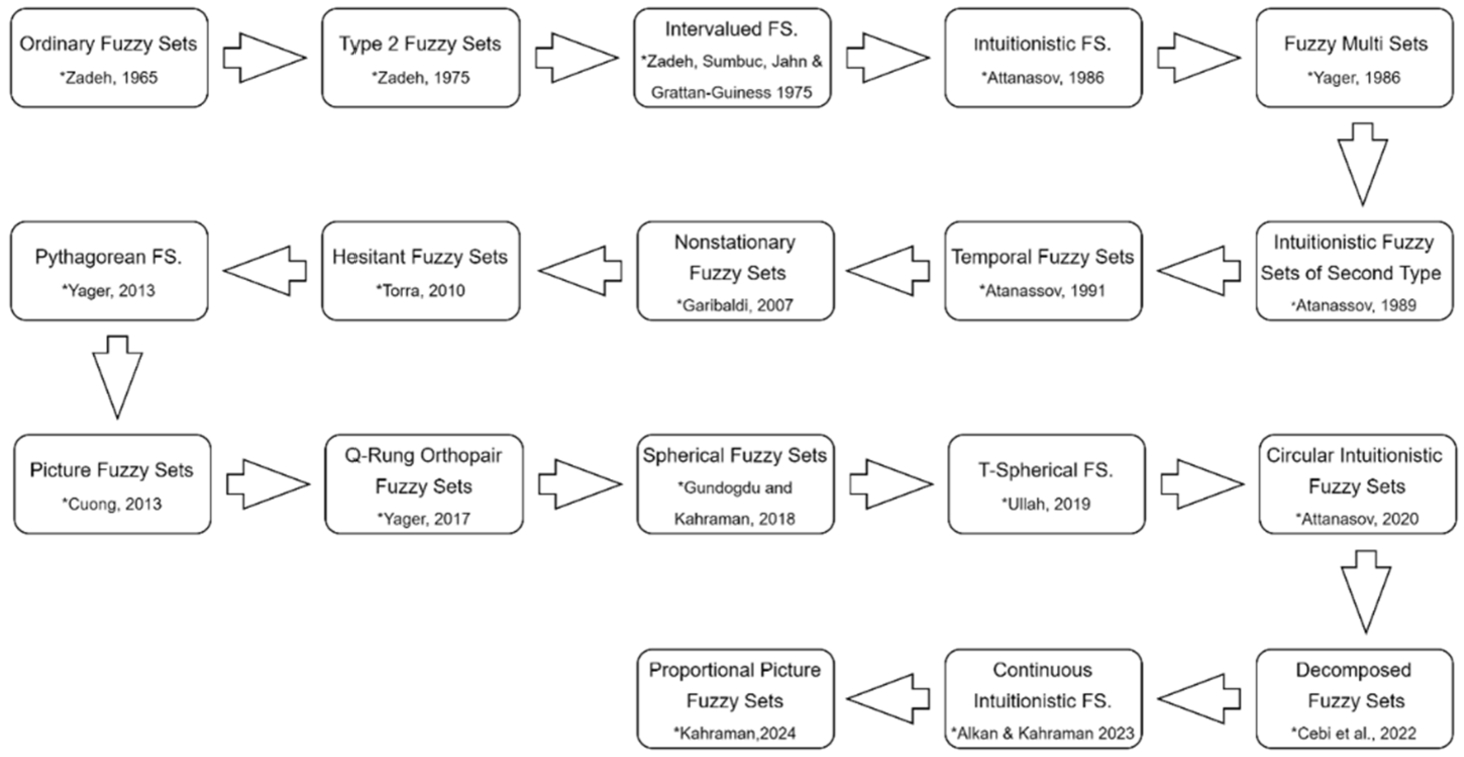
Fig. 1
Historical progress of fuzzy set extensions.
The ordinary fuzzy sets are extended to several new types of fuzzy sets. In Fig.
1, the historical progress of the extensions of the ordinary fuzzy sets is demonstrated. Atanassov (
1986) expanded the idea of uncertainty by proposing intuitionistic fuzzy sets (IFSs) which consider a non-membership degree, which is not necessarily a complementary degree to 1. Yager (
2013) introduced Pythagorean fuzzy sets to extend the limits of relationship between membership and non-membership functions. Cuong and Kreinovich (
2013) introduced the third dimension on membership function of fuzzy sets that states hesitancy degree of the membership function. As an extension of Picture fuzzy sets (PiFS) and Pythagorean fuzzy sets (PyFS), Kahraman and Kutlu Gundogdu introduced spherical fuzzy sets in 2018. SFSs create a membership function on a spherical surface with a bigger domain with respect to PiFS. Spherical fuzzy sets (SFSs) are an extension of ordinary fuzzy sets that incorporate an additional dimension to better handle uncertainty and hesitancy in decision-making processes. In an ordinary fuzzy set, each element has a membership degree that indicates the extent to which the element belongs to the set. In intuitionistic fuzzy sets, membership and non-membership degrees are determined by assigning from a triangular area, while in picture and spherical fuzzy sets, assignment is made from a volume bounded by a triangular prism and a one-eight of unit sphere, respectively. However, this single membership degree may not be sufficient to capture the full range of uncertainty and hesitancy that decision-makers experience. SFSs address this limitation by introducing three degrees for each element: membership, non-membership, and hesitancy (or indecision). These three degrees must satisfy the constraint that their squared sum is less than or equal to one. This additional dimension allows SFSs to provide a more nuanced representation of uncertainty and hesitancy compared to ordinary fuzzy sets (Ashraf
et al.,
2019; Gundogdu and Kahraman,
2018,
2019,
2020; Shishavan
et al.,
2020; Kahraman
et al.,
2007,
2019).
Spherical fuzzy sets with some operational rules and aggregation procedures based on Archimedean t-norm and t-conorms were improved by Ashraf and Abdullah in 2019 to obtain much bigger domain than typical SFS (Ashraf
et al.,
2019; Gundogdu and Kahraman,
2018,
2019). In Fig.
1, the historical progress of fuzzy sets with other new improvements is illustrated (Cebi
et al.,
2023; Alkan and Kahraman,
2023; Kahraman,
2024; Torra,
2010; Yager,
2017; Atanassov,
2020; Ullah
et al.,
2018; Wang
et al.,
2017).
A fuzzy inference system (FIS) is a framework built on fuzzy set theory and fuzzy logic that focuses primarily on fuzzy reasoning to set up the computational foundations for solving real-world problems. In order to accommodate the knowledge of experts, a FIS is a reasoning process that employs fuzzy production rules, often known as if-then rules. Therefore, each FIS could be completed by applying the knowledge and experience of the experts to create a rule base and then obtain the necessary controlling actions (Chen,
1988; Chen and Tan,
1994; Chaudhari and Patil,
2014; Muriana
et al.,
2016; Rong
et al.,
2013; Martínez
et al.,
2020).
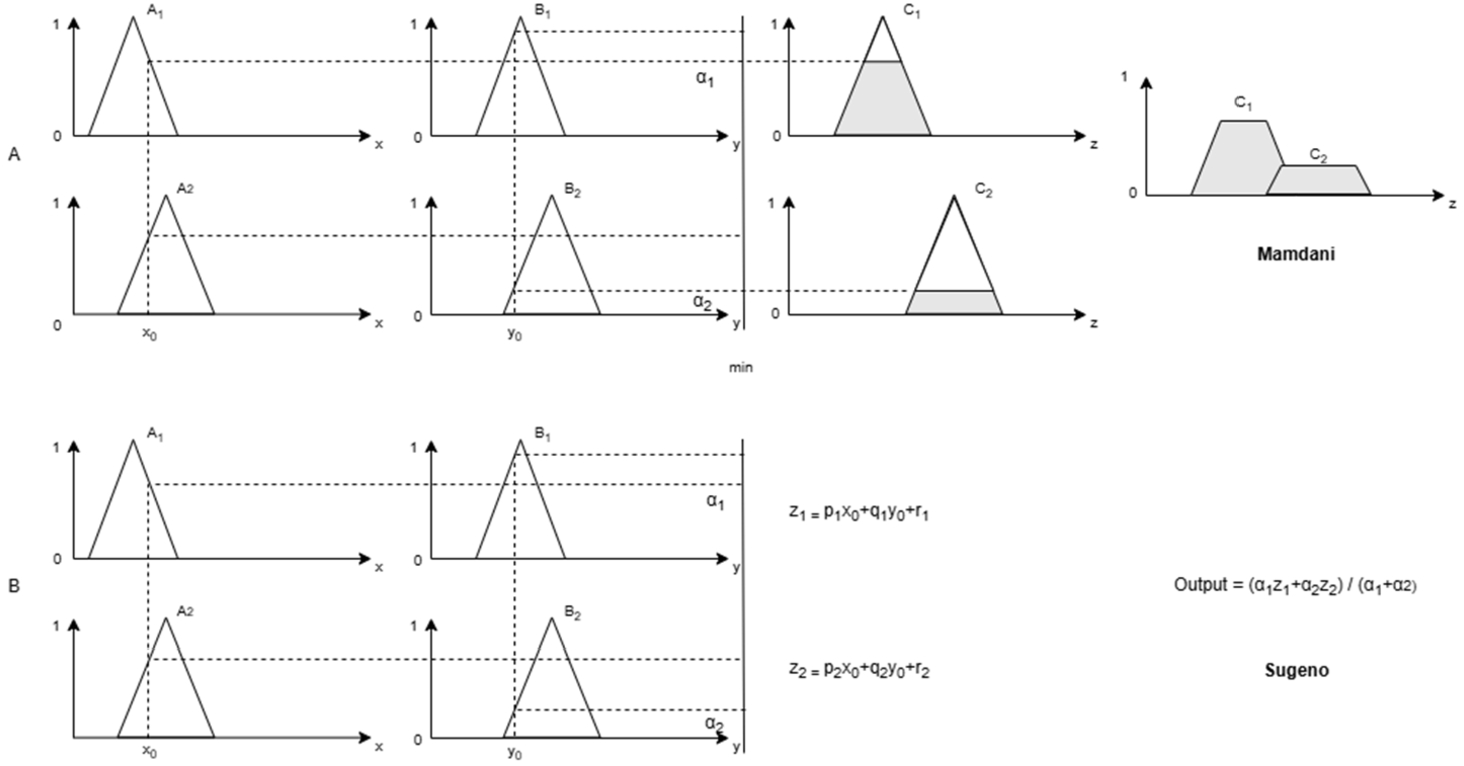
Fig. 2
Rules of A) Mamdani and B) Sugeno FIS (Sugeno,
1985).
There are two types of popular fuzzy inference systems used in literature: Mamdani type and Sugeno type. Mamdani type fuzzy inference systems produce fuzzy output as seen in Fig.
2A. After the process of aggregation of the outputs, the aggregated fuzzy output is defuzzified (Chen,
1988; Chen and Tan,
1994; Mamdani,
1974; Mamdani and Assilian,
1975). The type of Fuzzy Inference System (FIS) in this study is based on Mamdani type decomposition of membership and non-membership functions.
The main difference between Sugeno type FIS and Mamdani type FIS is the process of producing outputs. Sugeno type FIS is based on the weighted average of the outputs to determine the crisp output as observed in Fig.
2B, whereas Mamdani type FIS is based on the defuzzification of a fuzzy output. Therefore, Sugeno FIS does not employ the defuzzification process. In Sugeno FIS, the user must define the coefficients of the inputs where it is evaluated as its disadvantage (Sugeno,
1985).
Ilbahar
et al. (
2018) proposed Pythagorean Fuzzy Proportional Risk Assessment which combines Pythagorean fuzzy analytic hierarchy process and a fuzzy inference system to evaluate the risks in the field of occupational health and safety.
In order to improve the inference performance of the conventional fuzzy inference system, Son
et al. (
2016) presented a novel fuzzy inference system based on picture fuzzy sets called Picture fuzzy inference system (PiFIS). The three degrees of picture fuzzy sets are used to create the positive and negative defuzzification values, which are employed to provide clear outputs. Defuzzification parameters were determined by using learning algorithms to reach a well-approximated model. Donyatalab and Farid (
2021) improved a new fuzzy inference system based on spherical fuzzy sets. One of the other beneficial contributions to literature is the transformation function definition, which is a type of defuzzification function and explained with Gaussian Spherical Fuzzy Linguistic Scales. The scale parameter establishes the relationship among the membership and non-membership functions and indecision function. In their study, the scale parameter is chosen empirically by the decision makers. The brand-new spherical fuzzy inference system (SFIS) with S-FIS attributes was introduced by them.
According to the literature in terms of application field, it is seen that the studies on maintenance prioritization mainly focus on preventive maintenance, the criticality of the equipment to be maintained, and Failure Modes and Effects Analysis (FMEA). In this study, it is going to be studied on the subject of prioritization of corrective work orders, which does not exceed the acceptable risk level during the deferral period of the equipment after notified as a defective, which is one of the issues that the literature does not evaluate in depth.
Islam
et al. (
2021) used risk-based maintenance technique for crude oil refineries based on fuzzy approach. The assets were prioritized according to their risk value. Their paper compared conventional Risk Based Maintenance (RBM) with fuzzy RBM and also implemented classic Risk Based Maintenance (RBM). In their case study, refining assets were prioritized according to their criticality. Ratnayakea and Antosz (
2017) proposed a fuzzy inference system (FIS) as a solution to maintenance prioritization problem of potential failures and demonstrated the application of fuzzy logic for the minimization of suboptimal classifications. The rule base fuzzy inference systems and related membership functions were developed. The recommended method offered to be used as a manufacturing company’s present computer-aided maintenance management system (CMMS). Unlike Islam
et al.’s research, they designed their classification algorithm by using fuzzy inference systems.
Lee
et al. (
2007) introduced a metric in their study that can be used to numerically assess the effects of different maintenance priorities. On the basis of the proposed index, a search algorithm can be used to determine the maintenance work order priorities that will increase productivity over the optimization horizon. Their findings demonstrated that by properly utilizing online production data in dynamic maintenance scheduling, visible production benefits can be obtained through the optimization of maintenance priorities. In contradistinction to Islam
et al. and Ratnayekea
et al., the scope of the study proposed a dynamic method to overcome the corrective maintenance work order prioritization rather than failure possibilities and equipment criticality.
In this paper, we introduce a novel fuzzy inference system based on spherical fuzzy sets (SFS). The originality of our approach lies in the proposal of a special defuzzification transformation function that allows decision-makers to operate in a wider workspace by distributing the hesitancy more fairly over membership values. The conventional transformation functions used in the literature distribute hesitancies especially over membership function or equal to membership or non-membership sites. This function provides a fair distribution of hesitancy degree over other two degrees by caring their magnitude. This innovative method aims to address hesitations and uncertainties brought on by inadequate assessments of decision-makers more effectively than existing methods. By applying our proposed approach to fuzzy inference systems, we demonstrate its superiority over traditional methods such as the risk assessment matrix technique (RAM) and Picture Fuzzy Inference Systems (PiFIS) in a real-world application of maintenance work order prioritization for scheduling.
The need for a novel fuzzy inference system based on spherical fuzzy sets (SFS) arises from the limitations of existing methods in handling uncertainty and hesitancy in decision-making processes. Traditional fuzzy sets and their extensions, such as intuitionistic and Pythagorean fuzzy sets, do not adequately address the complexities of real-world scenarios where decision-makers often face significant indecision. Spherical fuzzy sets introduce an additional dimension that incorporates membership, non-membership, and hesitancy degrees, providing a more nuanced representation of uncertainty. This enhanced capability is crucial for applications like maintenance workorder prioritization, where accurate risk assessment and effective handling of hesitancy can lead to better scheduling and resource allocation. By distributing hesitancy more fairly over membership values, the proposed system aims to improve decision-making accuracy and efficiency, ultimately leading to optimized maintenance costs and increased asset availability.
Finally, the performance of the decision support system is tested with the data taken from computerized maintenance management system to prioritize the maintenance work orders.
The rest of the paper is structured as follows: Section
2 provides the preliminaries of spherical fuzzy sets. The main purpose of Section
3 is to describe the methodology, and the stepwise procedure of fuzzy inference systems based on spherical fuzzy sets. Section
4 illustrates a real-world application of the methodology in the field of maintenance work order prioritization for scheduling. Section
5 involves concluding remarks and future directions.
2 Preliminaries
In this section, the most common types of FIS including the Mamdani and the Sugeno fuzzy inferences are introduced in Section
2.1. Section
2.2 gives the main definition of the spherical fuzzy sets. Section
2.3 represents the novel spherical fuzzy transformation function for dimension reduction of uncertainty. Section
2.4 defines the basic notions of picture fuzzy sets.
2.1 Types of Fuzzy Inference Systems
The most common two types of fuzzy inference systems are Mamdani fuzzy inference and Sugeno (or Takagi-Sugeno) fuzzy inference.
A Mamdani fuzzy inference operates as a special calculator that takes two inputs, x and y, and gives an output, z. Each input x, y and output z have N, M, K membership functions, respectively.
The system has
R rules in the form:
where
$k=1\dots R$,
$i=1\dots N$,
$j=1\dots M$ and
$l=1\dots L$.
Figure
2a shows Mamdani fuzzy inference system to have better understanding of the model.
The steps of Mamdani FIS are as follows:
-
1. Fuzzification of Inputs: Crisp or linguistic inputs should be reformed as fuzzy values by using transformation techniques. Thus, both inputs and outputs are represented on fuzzy sets.
-
2. Set Fuzzy Rules: A FIS with i inputs and l linguistic terms generate
$r={l^{i}}$ rules. If the dimensions and the complexity of the system grow, the number of rules increases exponentially (Chen,
1988; Chen and Tan,
1994).
-
3. Apply Fuzzy Sets Operators to Inputs: The fuzzified inputs are combined with assigned set operations. AND and OR set operations are used to derive outputs from different inputs among linguistic terms.
-
4. Implication: Defined rules must be applied individually. Each rule determines the cut point of membership value for the corresponding output membership function.
-
5. Apply Aggregation Operator to Fuzzy Outputs: The results for each rule aggregated to obtain the final aggregate membership value, which consists of the aggregated fuzzy domains.
The aggregated membership function of the output is formulated as follows:
-
6. Defuzzification: A defuzzification function is used to figure out the exact value from a group of fuzzy values. The centroid method is preferred to determine the crisp output value in this study.
2.2 Spherical Fuzzy Sets
Definition 1.
A spherical fuzzy set (SFS) in a non-empty set
X is
where
${\mu _{A}}(x)$,
${v_{A}}(x)$,
${h_{A}}(x)$ are membership, non-membership and hesitancy degrees (in some cases neutral membership) of each element
$x\in X$, respectively, and satisfies the constraints
Then the refusal degree of an element is calculated as
In cases
${R_{A}}(x)=0$, SFS returns to traditional Pythagorean fuzzy sets. This means that SFS is an extension of PyFS where refusal degree is appended to definition.
Definition 2.
For
$A,B\in \text{SFS}(X)$, the union, intersection, complement, and inclusion operations are defined as follows.
Definition 3.
For
$A,B\in \text{SFS}(X)$, some operators on SFS are:
2.3 Spherical Fuzzy Transformation Function for Dimension Reduction
Transformation functions are developed to convert different fuzzy extensions between each other often from a higher dimensional, to a lower dimensional, especially to an ordinary fuzzy set. For instance, Atanasov proposed a transformation function which transforms any intuitionistic fuzzy sets to ordinary fuzzy sets (Atanassov,
1986,
2000). A transformation function is a function that maps between two types of fuzzy sets. Furthermore, any mapping function that does not preserve the original fuzzy sets’ characteristics until the completion of the transformation process is unacceptable. It is defined as some qualities that must be met to establish a suitable mapping function as a transformation function (Donyatalab and Farid,
2021).
The special transformation function for defuzzification in the context of spherical fuzzy sets (SFS) is designed to convert the three-dimensional membership, non-membership, and hesitancy degrees into a two-dimensional fuzzy set. This transformation is crucial for simplifying the defuzzification process while maintaining the integrity of the original fuzzy set’s characteristics.
Below is a detailed explanation of how this function operates:
Transformation Function Definition: The transformation function maps the spherical fuzzy set (SFS) to an ordinary fuzzy set (FS). This function is defined to ensure that the original characteristics of the SFS are preserved during the transformation process.
Properties of the Transformation Function: The transformation function must satisfy certain properties to be considered valid. These properties include maintaining the relationships between membership, non-membership, and hesitancy degrees.
Application of the Transformation Function: The function distributes the hesitancy degree over the membership and non-membership degrees. This distribution is done in a balanced manner, ensuring that the indecision degree is fairly represented in the resulting fuzzy set.
The transformation function allows decision-makers to operate in a wider workspace simply by effectively addressing hesitations and uncertainties. It ensures that the defuzzification process is both accurate and efficient, providing a more nuanced representation of uncertainty and hesitancy compared to ordinary fuzzy sets.
In this section, a transformation function from spherical fuzzy sets to ordinary fuzzy sets are defined previously. Then, the required features for this transformation function are introduced by demonstrating how these features are met.
Definition 4.
Let
X is the universal set and
$x\in X$, then
$\tilde{A}=\{\langle x,{\mu _{\tilde{A}}}(x),{v_{\tilde{A}}}(x),{h_{\tilde{A}}}(x)\rangle \hspace{0.1667em}|\hspace{0.1667em}x\in X\}$ be SFS, so that
${\mu _{\tilde{A}}}(x)$,
${v_{\tilde{A}}}(x)$,
${h_{\tilde{A}}}(x)$ and
${R_{\tilde{A}}}(x)$ are membership, non-membership, hesitancy and refusal degrees, respectively. Every
$\Theta \in {[0,1]^{[0,1]x[0,1]\times [0,1]}}$ is a mapping function
$\Theta :SFS(X)\to FS(X)$. Thus, transformation function
$(\Theta )$ proposed as follows:
Definition 5.
Let X is the universal set and
$x\in X$, then
$A=\{\langle x,\hspace{2.5pt}{\mu _{\tilde{A}}}(x),{v_{\tilde{A}}}(x),{h_{\tilde{A}}}(x)\rangle \mid x\in X\}$ and
$\tilde{B}=\{\langle x,{\mu _{\tilde{B}}}(x),{v_{\tilde{B}}}(x),{h_{\tilde{B}}}(x)\rangle \mid x\in X\}$ be two SFS, so that
${\mu _{\tilde{A}}}(x)$,
${v_{\tilde{A}}}(x)$,
${h_{\tilde{A}}}(x)$ and
${R_{\tilde{A}}}(x)$ are membership, non-membership, hesitancy and refusal degrees, respectively. Transformation function (Θ), which is defined in Definition
4, will satisfy the following properties:
-
P(1): ${\mu _{\Theta (\tilde{A})}}(x)\geqslant {\mu _{\tilde{A}}}(x)$;
-
P(2): $\Theta (\tilde{A})\subseteq \Theta (\tilde{B})$, if $\tilde{A}\subseteq \tilde{B}$;
-
P(3): $\Theta ({\tilde{A}^{C}})=\Theta (\tilde{A})$, if ${\mu _{\tilde{A}}}(x)={v_{\tilde{A}}}(x)$;
-
P(4): $\Theta (\Theta (\tilde{A}))=\Theta (\tilde{A})$.
We demonstrated that the function (Θ) in Definitiom
4 providing (P1), (P2), (P3) and (P4) is a transformation function of SFSs.
We do not consider the hesitancy degree when describing the above-defined and proven transformation function (Θ) in FS. A non-membership degree is deemed dependent on membership, therefore membership in an SFS is far more feasible in an equal position. Another reason is that a portion of the membership degree associated with reluctance is out of our control when considering uncertainty and fuzzifying in FS and will not be considered, therefore it is added to the membership (Donyatalab and Farid,
2021).
2.4 Picture Fuzzy Sets
Definition 6.
A picture fuzzy set (PiFS) in a non-empty set X is
where
${\mu _{A}}(x)$,
${v_{A}}(x)$,
${h_{A}}(x)$ are membership, non-membership and hesitancy degrees of each element
$x\in X$, respectively, and satisfies the constraints
Then the refusal degree of an element is calculated as
In cases
${R_{\tilde{A}}}(x)=0$ PiFS, returns to traditional Intuitionistic fuzzy sets. This means that PiFS is an extension of IFS where refusal degree is appended to definition.
Definition 7.
For
$\tilde{A}$,
$\tilde{B}\in \text{PiFS}(X)$, the union, intersection, complement, and inclusion operations are defined as follows.
Definition 8.
For
$\tilde{A},\tilde{B}\in \text{PiFS}(X)$, some operators on PiFS are:
3 Methodology and Stepwise Procedure
The proposed approach, Risk Assessment by using Spherical Fuzzy Inference Systems (SFIS), consists of 8 steps. The main steps of the proposed approach are as follows:
Step 1: Set Convenient Linguistic and Numerical Scales for Decision Makers (DM)
In this step, the criteria of risk assessment and scales of the evaluation are determined, which should be compatible with the application industry. (Labella
et al.,
2021). Our general approach for formulating risk is to consider it as a function of likelihood and severity. It is also common to include determinability in this formula.
Risk = f(Likelihood, Severity)
Severity can be formed based on several factors. In this study, possible consequences of Assets, People, Environment and Reputation are the components of the severity (Chen,
1988).
Decision makers take the amount of total cost levels, which can be caused by equipment repair, equipment replacement and production loss, into consideration for Asset Criteria. The assessment scale can be numerical or ordinal. They evaluate injury levels for People Criteria from slight effect without lost time injury to multiple fatalities. Environmental Criteria take into account the location and amount of the spill relative to the facility boundaries and the authority of complaints such as local residents, NGO’s, governmental organizations. To assess reputation criteria, they evaluate the level of appearance and interest of media such as being local, provincial, national and international.
Figures
3a–
3c show the graphical representation of Severity, Likelihood and Risk in terms of linguistic membership function.
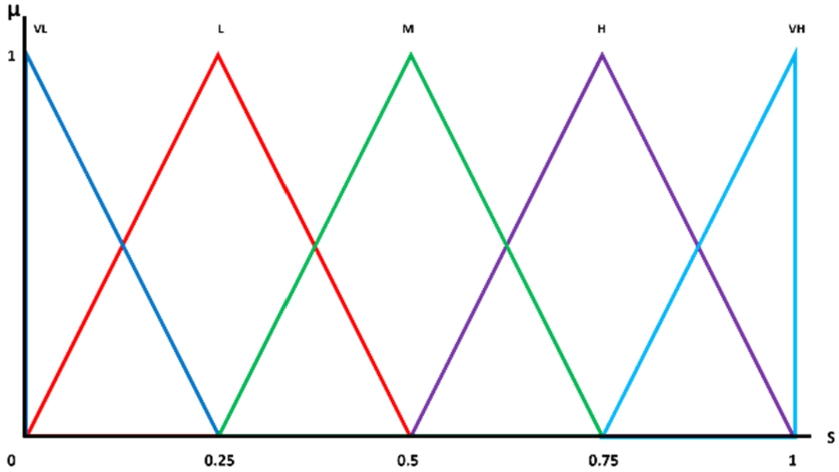
Fig. 3a
Linguistic scales of severity.

Fig. 3b
Linguistic scales of likelihood.
Step 2: Gather Risk Assessment Data from Decision Makers
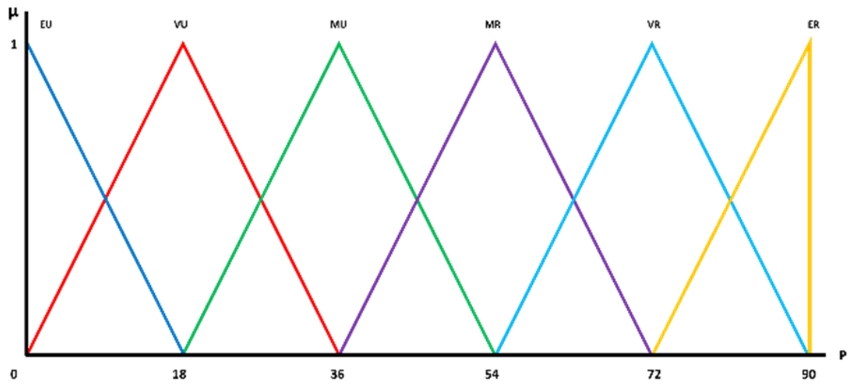
Fig. 3c
Linguistic scales of maintenance due dates.
Decision makers assess the risk scenario over a matrix or guided survey questions. They are directed to guess the most likely and pessimistic scenario of the case that should be also feasible.
Step 3: Fuzzification of Inputs and Outputs
Crisp or linguistic inputs are reformed as fuzzy values by using transformation techniques. Thus, both inputs and outputs are represented by fuzzy sets as seen in Figure
4.
Step 4: Set Rules
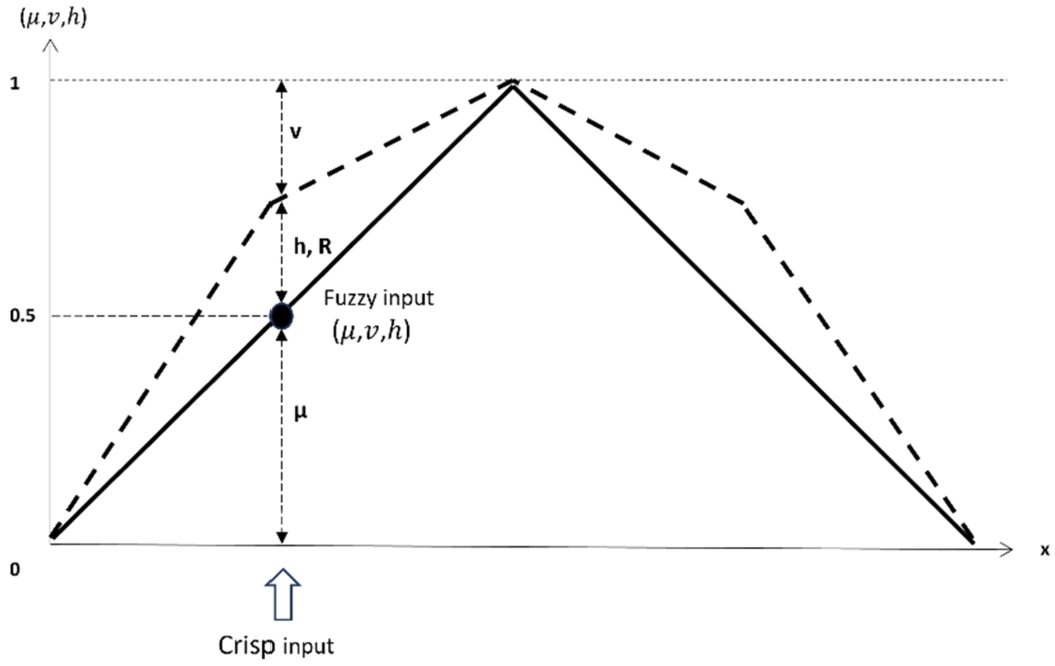
Fig. 4
The membership graph of SFS where (μ, v, h) are the membership, non-membership and hesitancy degrees.
A FIS with 4 inputs and 5 linguistic terms generates 625 rules. If the number of inputs can be decreased to 2, it generates only 25 rules. An example of a defined rule is shown below.
Step 5: Apply AND/OR Operators
The fuzzified inputs are combined with “AND” operator to derive outputs from different inputs among linguistic terms.
Before applying operators (Step 5) or defuzzification (Step 8), Spherical Fuzzy Sets are transformed into two dimensional fuzzy sets with a transformation function. Transformation function distributes hesitancies and refusals over membership and non-membership functions to apply operators easily.
The proposed transfer function in this study enables a fairer distribution of hesitancies by comparison to the transfer function of Donyatalab and Farid (
2021). As seen in Fig.
5, hesitancy is distributed more in the middle and less at the edges of membership degree. This means that if the membership and non-membership are evaluated equally or there is strict certainty, then hesitancy should be distributed equally. When the certainty is lower, hesitancy is distributed to the membership nonlinearly.
Step 6: Implication
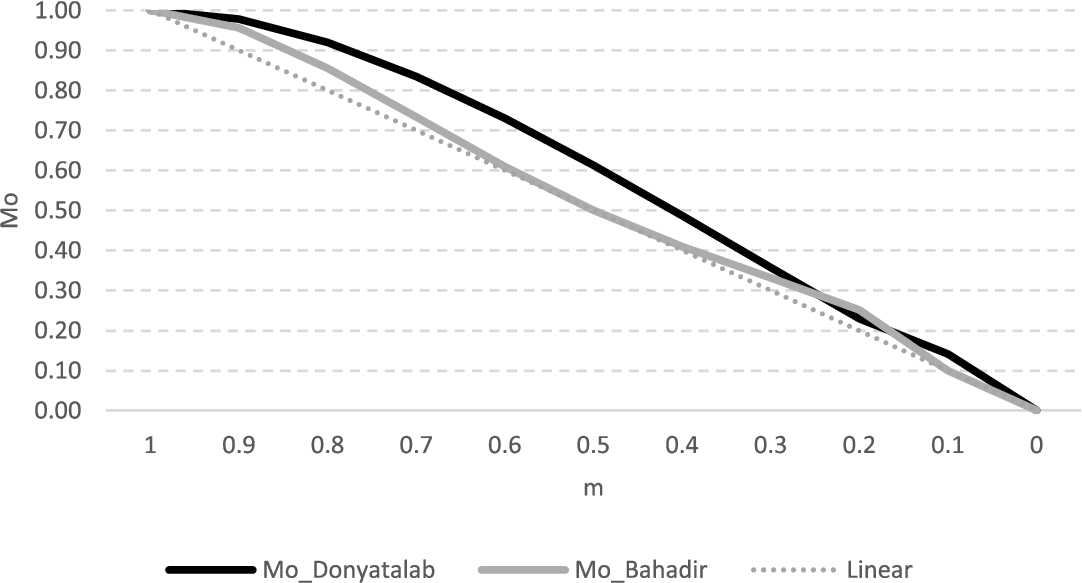
Fig. 5
Comparison between membership degrees of proposed transformation functions.
Defined rules must be applied individually. Each rule determines the cut point of membership value for the corresponding output membership function. Figure
6 depicts Mamdani implication by AND operator. It cuts the output membership functions from a minimum level of inputs.
Step 7: Apply Aggregation Operator to Fuzzy Outputs

Fig. 6
Determining cut points of output by implication rules.
The results for each rule aggregated to obtain the final aggregate membership value, which consists of the aggregated fuzzy domains (Donyatalab
et al.,
2019). This step acts as OR function of cut points in Fig.
7.
Step 8: Defuzzification
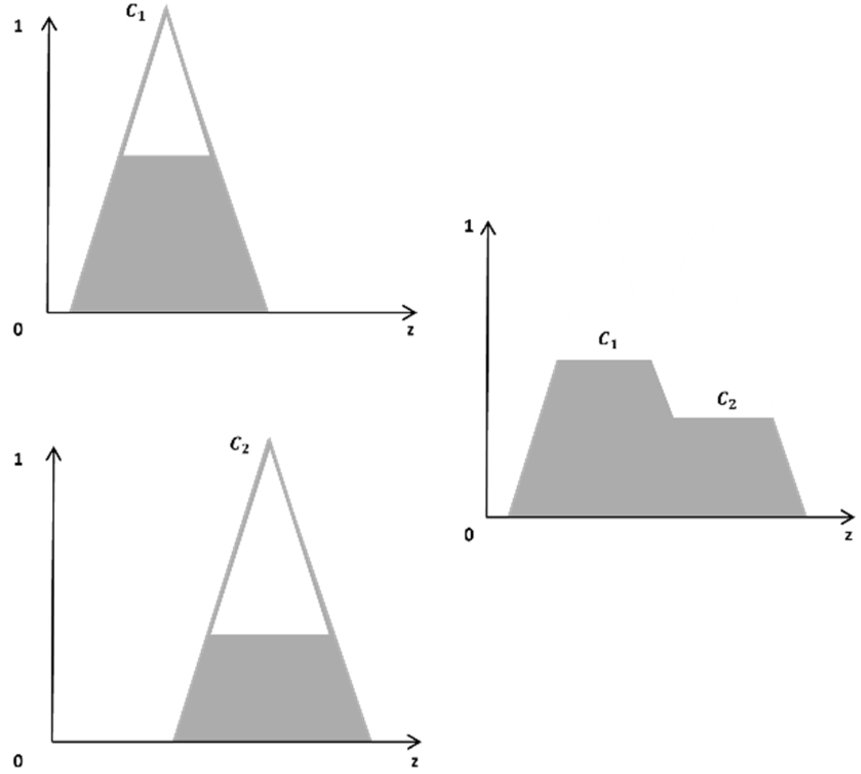
Fig. 7
Aggregating fuzzy outputs.
A defuzzification function is used to figure out the exact value from a group of fuzzy values. The centroid method is preferred to determine the crisp output value in this study. Figure
8 gives a graphical representation of defuzzification by using centroid method to calculate maintenance due dates.
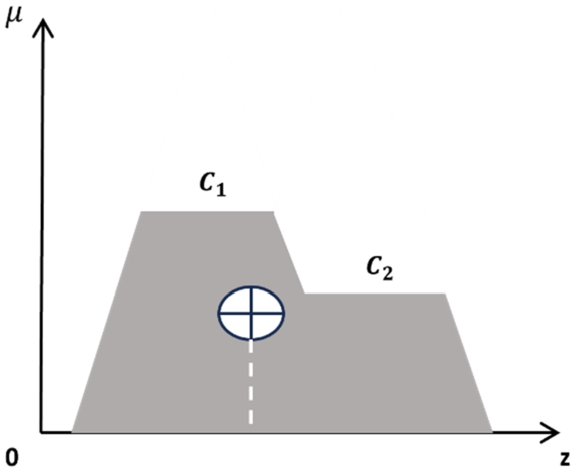
Fig. 8
Defuzzified maintenance due dates.
It is hard to represent spherical fuzzy inference systems on two dimensional area. Because it requires four dimensional space to visualize domain, membership, non-membership, indecision degrees. Figure
9 depicts the steps between applying operators to defuzzification on 3D surfaces. It provides a 3D representation of the spherical fuzzy inference systems (SFIS) and illustrates the steps involved in applying operators to defuzzification on 3D volume. Each input is a three-dimensional spherical fuzzy set. The inputs are fuzzified and represented on 3D volume, where each point in the volume corresponds to a combination of membership, non-membership, and hesitancy degrees. The fuzzified inputs on 3D volumes are combined using the AND operator to reach the projection of the defuzzified output. This step ensures that the combined effect of all inputs is considered in the decision-making process. The transformation function calculates a two-dimensional output, which is a combination of the transformed membership function and the domain (z). This function distributes the hesitancy degree over the membership and non-membership degrees in a balanced manner, ensuring that the indecision degree is fairly represented in the resulting fuzzy set. By using aggregation operator OR, all outputs are aggregated on z domain. This step combines the results of all rules to obtain the final aggregate membership value. Finally, aggregated output is defuzzified to obtain a crisp value. The centroid method is used in this study to calculate the maintenance due dates, providing a precise and actionable output.
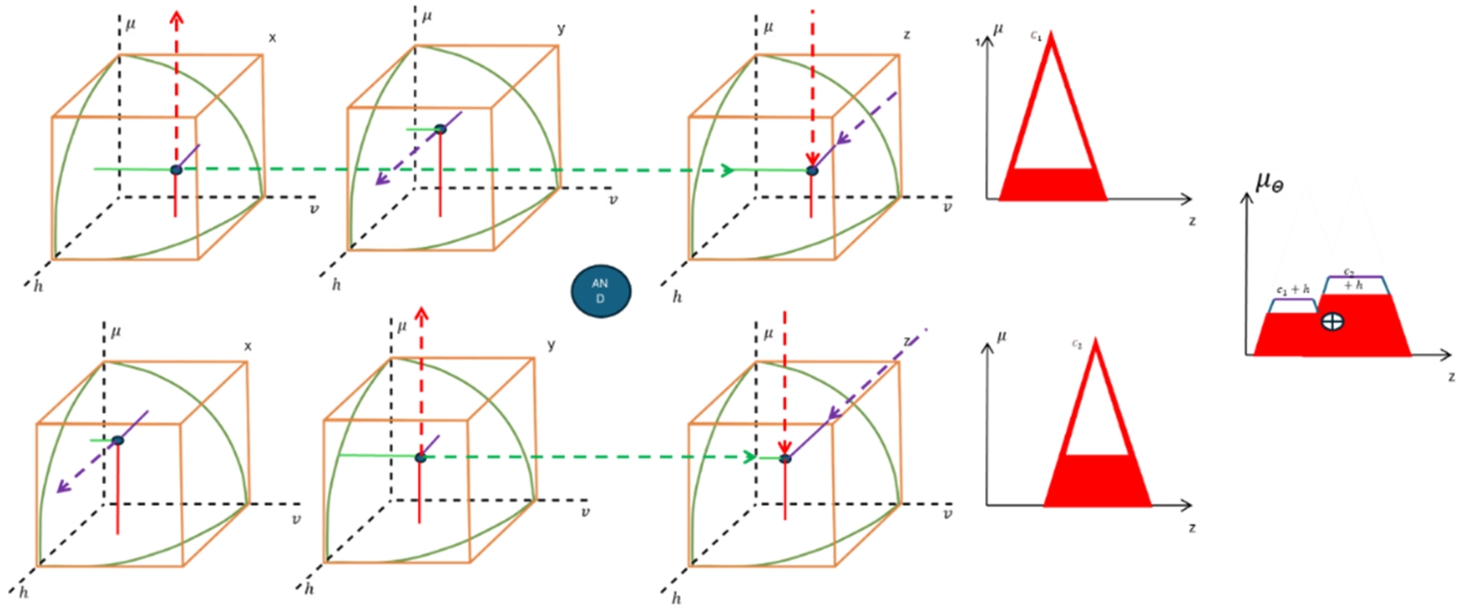
Fig. 9
3D representation of spherical fuzzy inference systems.
4 Application to Maintenance Work Order Prioritization for Scheduling
In this section, the proposed method is used to assess the risks of a corrective maintenance need in an oil&gas refinery and a completion due date for it is determined. The results of the study are compared to the risk assessment with a matrix method.
The production units of oil&gas refining companies should be available as much as possible and should sustain their continuous operation. In that way, market demands can be met, and the companies would gain market advantage against competitors and increase their profitability. Besides, the refining companies would like to keep costs at the optimum level while providing the highest level of availability. For this purpose, they try to minimize maintenance expenses while keeping service levels maximum by using central maintenance organizations. To achieve this, it should be ensured that no maintenance technician remains idle, and they are provided to work during labour hours. In this context, it is important to create a backlog at a certain level for the technicians to use their labour hours more effectively and prioritize the maintenance to minimize the risk of just-in-time asset availability.
Performing a risk assessment for prioritization of maintenance among the work order list is one the most useful methods by which the risks of postponing maintenance can be evaluated (Li
et al.,
2017). The main purpose at that point is to ensure high-risk maintenance work orders to be executed within an acceptable risk period. The tradeoff is to keep the number of resources at the optimum amount by delaying the completion deadlines of maintenance with lower risk. In this way, maintenance costs will also be optimized. It is foreseen that maintenance costs can be reduced by 20–30% with that approach, while oil&gas companies try to balance the risk of having a smaller failure list.
In this research, 1037 risk assessments of maintenance notifications are collected within a month. The risk assessments have two dimensions that are likelihood and severity. Severity assessments include four separate branches: Assets, People, Environment and Reputational Consequences, and they have 5 scale levels which are High, Medium, Medium Low, Low and Negligible. The evaluations of assets consequences are made both ordinal and ratio scales. The evaluation of likelihood is also made on both ordinal and ratio scales. In this way, matrix and fuzzy evaluations including proposed models can be performed together and results are able to be compared.
The suggested model’s spherical fuzzification of input and output variables are based on the linguistic scales provided in Tables
1,
2, and
3.
Table 1
Spherical fuzzy linguistic scales for input variables for likelihood.
| Scale $(l=1,2,3,4,5)$
|
Likelihood levels |
Ranges |
$LS=\langle \textit{LSI};m,v,h\rangle $ |
| LSI |
$m,v,h$ |
| $l=1$ |
High (H) |
<2 days |
1 |
$(0.9,0.1,0.1)$ |
| $l=2$ |
Medium High (MH) |
2 days to 2 weeks |
0.75 |
$(0.7,0.3,0.3)$ |
| $l=3$ |
Medium (M) |
2 weeks to 3 months |
0.5 |
$(0.5,0.5,0.5)$ |
| $l=4$ |
Medium Low (ML) |
3 months to 1.5 years |
0.25 |
$(0.3,0.7,0.3)$ |
| $l=5$ |
Low (L) |
>1.5 years |
0 |
$(0.1,0.9,0.1)$ |
Table 2
Spherical fuzzy linguistic scales for input variables for severity.
| Scale $(l=1,2,3,4,5)$
|
Severity levels |
Potential consequences |
$LS=\langle \textit{LSI};m,v,h\rangle $ |
| Assets |
People |
Environment |
Reputation |
LSI |
$m,v,h$ |
| $l=1$ |
Very Low (VL) |
<10k USD |
Slight Health Effect |
Slight Effect |
Slight Impact |
0 |
$(0.1,0.9,0.1)$ |
| $l=2$ |
Low (L) |
10k to 100k USD |
Minor Health Effect |
Minor Effect |
Minor Impact |
0.25 |
$(0.3,0.7,0.3)$ |
| $l=3$ |
Medium (M) |
100k to 1M USD |
Major Heath Effect (PPD) |
Localized Effect |
Considerable Impact |
0.5 |
$(0.5,0.5,0.5)$ |
| $l=4$ |
High (H) |
1M to 10M USD |
Fatalities to Death (FTD) |
Major Effect |
Regional Impact |
0.75 |
$(0.7,0.3,0.3)$ |
| $l=5$ |
Very High (VH) |
>10M USD |
Multiple Fatalities |
Massive Effect |
International Impact |
1 |
$(0.9,0.1,0.1)$ |
Table 3
Spherical fuzzy linguistic scales for output variables for priority.
| Scale $(l=1,2,3,4,6)$
|
Likelihood levels |
Ranges |
$LS=\langle \textit{LSI};m,v,h\rangle $ |
| LSI |
$m,v,h$ |
| $l=1$ |
Extremely Urgent (EU) |
<2 days |
0 |
$(0.1,0.9,0.1)$ |
| $l=2$ |
Very Urgent (VU) |
2 days to 1 week |
0.2 |
$(0.2,0.8,0.2)$ |
| $l=3$ |
Medium Urgent (MU) |
1 week to 2 weeks |
0.4 |
$(0.4,0.6,0.4)$ |
| $l=4$ |
Medium Routine (MR) |
2 weeks to 6 weeks |
0.6 |
$(0.6,0.4,0.4)$ |
| $l=5$ |
Very Routine (VR) |
6 weeks to 8 weeks |
0.8 |
$(0.8,0.2,0.2)$ |
| $l=6$ |
Extremely Routine (ER) |
8 weeks to 3 months |
1 |
$(0.9,0.1,0.1)$ |
The transformed Spherical Fuzzy Linguistic Scales for Input and Output Variables are given in Tables
4 and
5, respectively.
Table 4
Transformed spherical fuzzy linguistic scales for input variables.
| Scale $(l=1,2,3,4,6)$
|
Likelihood levels |
Severity levels |
$LS=\langle \textit{LSI};m,v,h\rangle $ |
$LSo=\langle m,v\rangle $ |
| LSI |
$m,v,h$ |
$mo,vo$ |
| $l=1$ |
Low (L) |
Very Low (VL) |
0 |
$(0.1,0.9,0.1)$ |
$(0.15,0.85)$ |
| $l=2$ |
Medium Low (ML) |
Low (L) |
0.25 |
$(0.3,0.7,0.3)$ |
$(0.33,0.67)$ |
| $l=3$ |
Medium (M) |
Medium (M) |
0.5 |
$(0.5,0.5,0.5)$ |
$(0.5,0.5)$ |
| $l=4$ |
Medium High (MH) |
High (H) |
0.75 |
$(0.7,0.3,0.3)$ |
$(0.73,0.27)$ |
| $l=5$ |
High (H) |
Very High (VH) |
1 |
$(0.9,0.1,0.1)$ |
$(0.96,0.04)$ |
Table 5
Transformed spherical fuzzy linguistic scales for output variables.
| Scale $(l=1,2,3,4,6)$
|
Likelihood levels |
Ranges |
$LS=\langle \textit{LSI};m,v,h\rangle $ |
$LSo=\langle m,v\rangle $ |
| LSI |
$m,v,h$ |
$mo,vo$ |
| $l=1$ |
Extremely Urgent (EU) |
<2 days |
0 |
$(0.1,0.9,0.1)$ |
$(0.15,0.85)$ |
| $l=2$ |
Very Urgent (VU) |
2 days to 1 week |
0.2 |
$(0.2,0.8,0.2)$ |
$(0.25,0.75)$ |
| $l=3$ |
Medium Urgent (MU) |
1 week to 2 weeks |
0.4 |
$(0.4,0.6,0.4)$ |
$(0.41,0.59)$ |
| $l=4$ |
Medium Routine (MR) |
2 weeks to 6 weeks |
0.6 |
$(0.6,0.4,0.4)$ |
$(0.61,0.39)$ |
| $l=5$ |
Very Routine (VR) |
6 weeks to 8 weeks |
0.8 |
$(0.8,0.2,0.2)$ |
$(0.86,0.14)$ |
| $l=6$ |
Extremely Routine (ER) |
8 weeks to 3 months |
1 |
$(0.9,0.1,0.1)$ |
$(0.96,0.04)$ |
The rules of Fuzzy Inference Systems are summarized in Table
6. Triangular membership functions of outputs are created according to rules in Table
7. The inference model operates according to the logic below. IF (Severity = M) AND (Likelihood = ML) THEN (Risk Level = MU).
Table 6
Rules of fuzzy inference system.

Following the construction of rules, the S-FIS procedure will be carried out step by step to obtain the result based on defined IF-THEN rules for our S-FIS model, as shown in Figs.
10 and
11. In the figures, a submodel of severity input, which is the combination of assets, people, environment and reputation, is depicted.
The following Fig.
12 is the S-FIS conclusion result as a Surface View based on input and output variables:

Fig. 11
S-FIS model inputs and output.

Fig. 12
Surface view of the results of S-FIS model.
Table 7
Summary of risk assessment according to matrix, SFIS, PiFIS methods.
| Likelihood scale [days] |
Assets scale [USD] |
Likelihood acc. to the matrix |
Severity acc. to the matrix |
Due date acc. to the matrix |
Due date acc. to the SFIS |
Due date acc. to the PiFIS |
| 540 |
5.000 |
N |
VL |
90 |
(73–86) |
(73–85) |
| 315 |
5.000 |
L |
VL |
90 |
(53–86) |
(55–85) |
| 52 |
5.000 |
ML |
VL |
60 |
(33–83) |
(32–84) |
| 8 |
5.000 |
M |
VL |
45 |
(18–69) |
(19–73) |
| 2 |
5.000 |
H |
VL |
14 |
(13–51) |
(15–55) |
| 540 |
50.000 |
N |
L |
90 |
(53–86) |
(55–85) |
| 315 |
50.000 |
L |
L |
60 |
(31–86) |
(32–85) |
| 52 |
50.000 |
ML |
L |
45 |
(21–74) |
(19–85) |
| 8 |
50.000 |
M |
L |
14 |
(13–67) |
(11–67) |
| 2 |
50.000 |
H |
L |
7 |
(5–49) |
(4–52) |
| 540 |
500.000 |
N |
M |
60 |
(33–83) |
(33–83) |
| 315 |
500.000 |
L |
M |
45 |
(21–82) |
(17–83) |
| 52 |
500.000 |
ML |
M |
14 |
(9–64) |
(5–68) |
| 8 |
500.000 |
M |
M |
7 |
(2–48) |
(3–52) |
| 2 |
500.000 |
H |
M |
2 |
(2–28) |
(3–30) |
| 540 |
5.000.000 |
N |
H |
45 |
(17–70) |
(33–70) |
| 315 |
5.000.000 |
L |
H |
14 |
(4–63) |
(14–66) |
| 52 |
5.000.000 |
ML |
H |
7 |
(3–49) |
(4–53) |
| 8 |
5.000.000 |
M |
H |
2 |
(2–29) |
(2–31) |
| 2 |
5.000.000 |
H |
H |
2 |
(2–12) |
(2–12) |
| 540 |
10.000.000 |
N |
VH |
14 |
(16–51) |
(14–53) |
| 315 |
10.000.000 |
L |
VH |
7 |
(5–51) |
(4–53) |
| 52 |
10.000.000 |
ML |
VH |
2 |
(3–29) |
(2–32) |
| 8 |
10.000.000 |
M |
VH |
2 |
(2–11) |
(2–14) |
| 2 |
10.000.000 |
H |
VH |
2 |
(2–2) |
(2–2) |
Figures
13 to
15 represent the defuzzified outputs, which show the due dates according to SFIS, PiFS, RAM models. Figure
16 gives a comparison of SFIS and RAM in terms of obtained cumulative due dates.
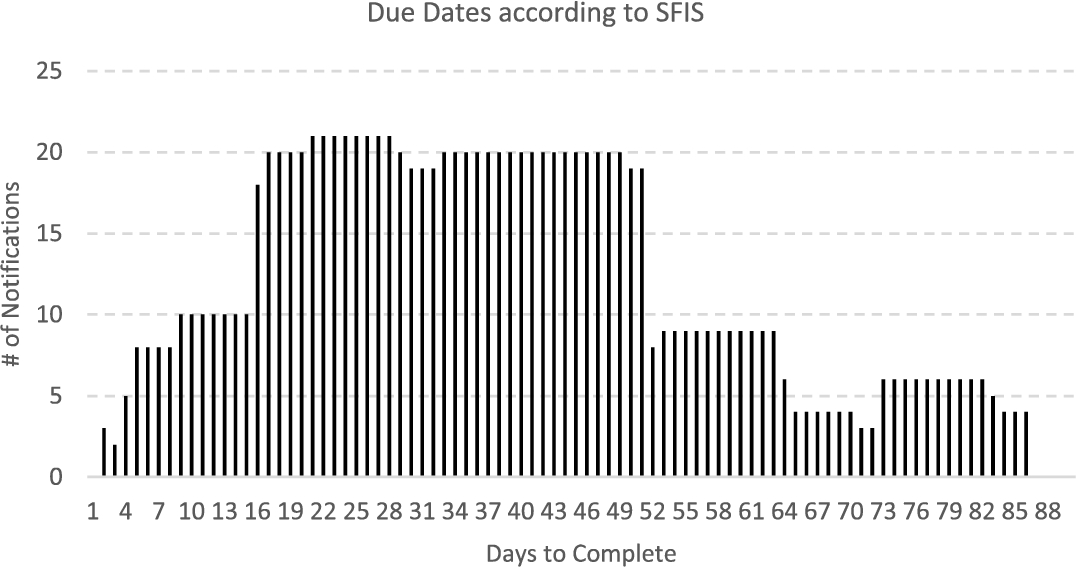
Fig. 13
Due dates of notification according to spherical fuzzy inference systems.
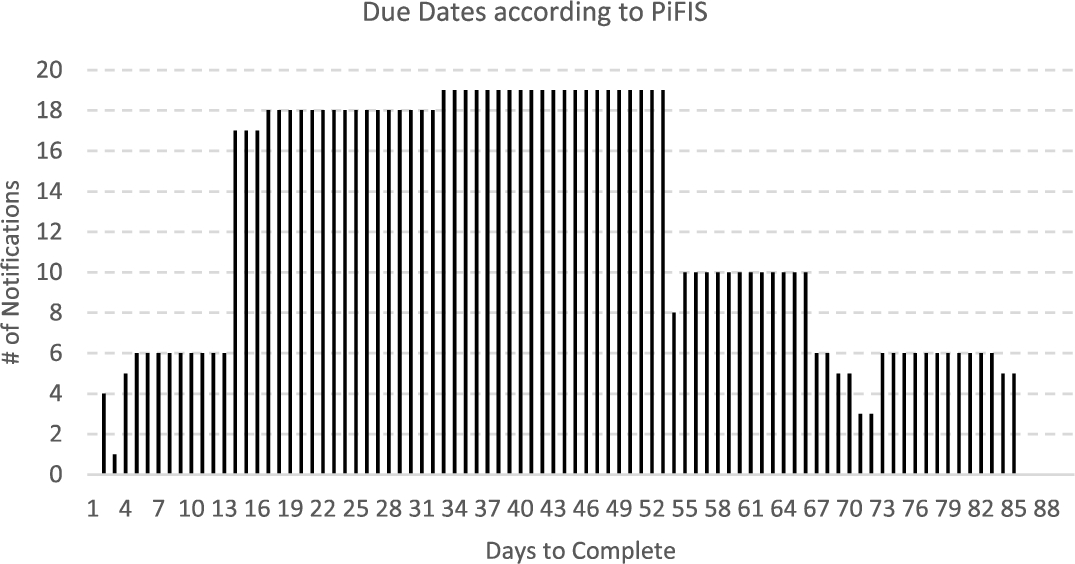
Fig. 14
Due dates of notification according to picture fuzzy inference systems.

Fig. 15
Due dates of notification according to risk assessment matrix (RAM).
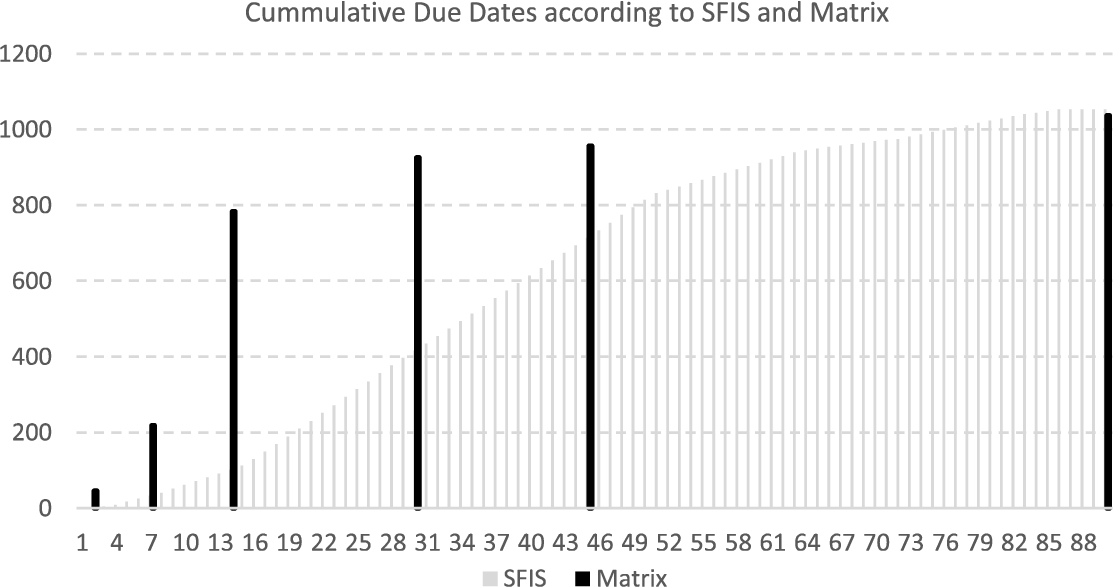
Fig. 16
Comparison between S-FIS and RAM approach by means of due date distribution.
89% of Notifications according to Risk Assessment Matrix, 69% of Notifications according to Spherical Fuzzy Inference Model and 63% of Notifications according to Picture Fuzzy Inference Model should be completed within 45 days, half of due date frame. This means that RAM provides a narrower due date range, restricted with 6 ordinality levels and this causes decision makers to make higher risk assessments to minimize the risk. Unlike RAM approach, fuzzy inference approaches distribute due dates over all time range, resulting in a more effective prioritization over a wide range time frame. Accordingly, resource usage can be optimized more steadily and it results in cost savings from employees. In addition, SFIS transforms hesitancy to membership degree by bringing forward the due dates, resulting in risk degradation.
5 Conclusion
The primary objective of this study is to enhance the decision-making process in maintenance workorder prioritization by utilizing spherical fuzzy inference systems (SFIS). This objective is justified by the need to address the limitations of existing fuzzy inference systems (FIS) that are generally based on ordinary fuzzy sets. These traditional systems do not account for the second and third dimensions of other fuzzy set extensions, which limit their ability to handle hesitations and uncertainties effectively.
The proposed SFIS approach aims to cover hesitancies and uncertainties caused by insufficient assessments of decision-makers more effectively. By incorporating the indecision degree along with membership and non-membership degrees, the SFIS provides a more nuanced representation of uncertainty and hesitancy. This is crucial for industries like oil and gas refining, where the continuous operation and availability of production units are vital for meeting market demands and maintaining profitability.
Furthermore, the application of the proposed approach in a real-world scenario, such as maintenance work order prioritization, demonstrates its practical relevance and effectiveness. The comparison with existing methods like the risk assessment matrix (RAM) technique and Picture Fuzzy Inference Systems (PiFIS) highlights the superior performance of the SFIS approach in handling uncertainties and optimizing maintenance costs.
The proposed approach using spherical fuzzy inference systems (SFIS) for maintenance workorder prioritization has demonstrated significant improvements over traditional methods. The study compared the SFIS approach with the risk assessment matrix (RAM) technique and Picture Fuzzy Inference Systems (PiFIS). The findings indicate that the SFIS method is more efficient in handling hesitations and uncertainties caused by insufficient assessments of decision-makers.
The actual findings from the application of the proposed method in an oil and gas refinery showed that the SFIS approach effectively prioritized maintenance work orders based on risk assessments. The method considered both the likelihood and severity of potential risks, resulting in a more balanced and accurate prioritization process. This approach not only optimized maintenance costs but also ensured that high-risk maintenance tasks were completed within acceptable risk periods, thereby enhancing the overall reliability and availability of the refinery’s production units.
The implications of these findings are substantial for industries that rely heavily on maintenance operations. By adopting the SFIS approach, companies can achieve more accurate and efficient maintenance scheduling, leading to reduced downtime and optimized resource utilization. The ability to handle hesitations and uncertainties more effectively also means that decision-makers can make more informed and confident decisions, ultimately improving the overall performance and reliability of their operations.
This study proposed a decision-making strategy based on spherical fuzzy inference systems (SFIS). Using a particular transformation function, the neutral membership degree is divided between membership and non-membership degrees in balance with reference to hesitation degree during the defuzzification of an inference system based on SFS. The proposed theory on fuzzy inference systems is intended to more effectively cover hesitancies and uncertainties produced by insufficient assessment of decision makers.
The novel contribution of this paper in a methodological manner is defuzzification transfer function which establishes the relationship between the membership function and the other dimensions. In the literature, fuzzy inference based on picture and spherical fuzzy sets have been very rarely studied compared to other fuzzy extensions. The proposed method by operating these extensions allows decision makers not only to employ a membership function with a larger domain, but also fills the gap in the literature by improving their performance with a novel defuzzification transfer function.
According to the literature in terms of application field, it is seen that the studies on maintenance prioritization mainly focus on preventive maintenance, the criticality of the equipment to be maintained, and Failure Modes and Effects Analysis (FMEA). In this study, the prioritization of corrective work orders is studied in a way that does not exceed the acceptable risk level during the deferral period of the equipment after notified as defective, which is one of the issues that the literature does not evaluate in depth.
Based on the results obtained in the case study, it is concluded that fuzzy inference based on spherical fuzzy sets provides a more homogeneous distribution of completion dates over a wider time range and allows for more effective prioritization of large samples compared to risk assessment matrix. On the other hand, picture fuzzy inference also provides a more homogeneous distribution like SFIS, however it transforms the hesitancy to membership by postponing due dates further resulting risk increase.
The proposed method of using spherical fuzzy inference systems (SFIS) for maintenance work order prioritization has some potential limitations. One of the primary concerns is scalability. The effectiveness and performance of SFIS on large datasets have not been thoroughly tested, which raises questions about its applicability in large-scale industrial applications. Additionally, the method’s sensitivity to input data is not fully understood. Small changes in input data could significantly impact the decision-making process, necessitating a more robust approach to handle uncertainties and hesitations. Furthermore, the applicability to different domains beyond maintenance work has not been explored extensively. This limitation suggests that the method may need further validation and adaptation to be effective in other fields.
For future research, several areas could be explored to address these limitations. Conducting scalability tests on large datasets would help evaluate the method’s performance in industrial applications. Additionally, performing sensitivity analyses on input data could provide insights into how the method handles uncertainties and hesitations, leading to more robust decision-making processes. Exploring the method’s applicability in different domains would also be beneficial. By testing the method in various industries and application areas, researchers can determine its generalizability and flexibility.
This discussion provides a balanced view of the proposed method and highlights potential directions for future research.

