1 Introduction
The floating-point (FP) format is extensively employed for data representation across various domains, including computing (Fasi and Mikaitis,
2021; Burgess
et al.,
2019a), neural networks (Zhao
et al.,
2023; Bai-Kui and Shanq-Jang,
2023), and signal processing (Moroz and Samotyy,
2019). The prevalent 32-bit floating-point (FP32) format adheres to standardized specifications (IEEE 754,
2019), boasting exceptional digital representation quality across a very wide range of data variance, ranging from minuscule to substantial values. However, the FP32 format’s computational intensity poses a challenge for implementation on hardware-constrained devices (Yang
et al.,
2022; Syed
et al.,
2021; Cattaneo
et al.,
2018). The 24-bit FP (FP24) (Junaid
et al.,
2022), 16-bit FP (Bfloat16 and DLFloat) (Burgess
et al.,
2019b; Agrawal
et al.,
2019), and 8-bit (FP8) (Wang
et al.,
2018) formats are examples of lower-bit FP formats that reduce computational complexity and energy consumption, making them advantageous for hardware and energy-restricted systems. Conversely, formats such as 64-bit FP (FP64) (IEEE 754,
2019) are utilized in environments necessitating heightened calculation precision (Botta
et al.,
2021).
As evident, there exists a plethora of FP formats, each with varying bit rates, offering distinct qualities in digital representation, dynamic range, computational complexity, and energy usage. Selecting the optimal FP format is a crucial task in both research and practical applications, contingent upon several factors: the required digital representation accuracy for a specific application, the range of data variance, as well as the available hardware and energy resources. Generally, it is preferable to opt for an FP format with fewer bits to minimize hardware demands and energy consumption while ensuring the requisite level of representation accuracy for a specific application across the entire range of data variance. Achieving this necessitates an efficient mechanism for evaluating the performance of FP formats across different bit rates and data variance levels.
It is worth noting that none of the aforementioned papers dealing with the FP formats (Junaid
et al.,
2022; Agrawal
et al.,
2019; Burgess
et al.,
2019a; Wang
et al.,
2018; Botta
et al.,
2021) provide information regarding their actual performance, which is a critical factor for practical applications. A significant stride in this direction was made in Perić
et al. (
2021), Denić
et al. (
2023), where the correlation was established between the FP format and a piecewise uniform quantizer, which was termed
the floating-point quantizer (FPQ). Namely, the piecewise uniform quantizer includes a number of segments, where a unique uniform quantizer is defined in each segment (Dinčić
et al.,
2016; Jayant and Noll,
1984; Gersho and Gray,
1992). This actually allowed assessing the digital representation quality of the FP format using an objective performance measure such as the signal-to-quantization-noise ratio (SQNR) of FPQ. It’s crucial to acknowledge that the performance of the FP format, specifically the SQNR of FPQ, relies heavily on the statistical properties of the data, primarily the probability density function (PDF). This paper considers the Laplacian PDF, given its extensive usage in statistically modelling various data types, e.g., speech (Chu,
2003; Gazor and Zhang,
2003) and neural network weights (Banner
et al.,
2018;
2019).
The primary goal of this paper is to make a significant advancement towards the FP format analysis by providing a performance-evaluating method that is more efficient (in terms of computational complexity) compared to the previously developed method (Perić
et al.,
2021; Denić
et al.,
2023). This is achieved by linking the FP format with the
μ-law companding quantizer (
μCQ), which is actually a novel concept, as research on this topic has not been done before. Namely, the SQNR expression for FPQ in Perić
et al. (
2021), Denić
et al. (
2023) is not provided in a closed form but as the summation of numerous terms (e.g., for the FP32 format, this sum comprises 254 terms, Perić
et al.,
2021), thereby escalating the complexity of FP format performance computation. Hence, the paper aims to eliminate the mentioned drawback of the existing method for assessing the performance of the FP format. A significant contribution is the development of a procedure for designing a
μCQ, tailoring its key parameters (
μ-compression factor and
${x_{\max }}$ – maximal amplitude) to the FP format. The key outcome of this innovative approach is the provision of a simple closed-form approximate expression for closely and efficiently assessing the FP format’s performance. The advantage of this closed-form expression is its broad applicability, as it applies universally to any bit rate and data variance. Aside from the theoretical significance of deriving a closed-form expression for performance evaluation, this paper holds substantial practical value by considerably simplifying the complexity of computing FP format performance.
The paper’s methodology involves designing an appropriate
μCQ, linearizing it, and deriving a piecewise uniform quantizer based on the
μ-law compression function (PUQ
μ). The paper demonstrates that by selecting the appropriate values of the crucial design parameters of the
μCQ, the structure of its linearized version, PUQ
μ, aligns with the FPQ structure. Notably, the paper provides a closed-form expression for the SQNR of
μCQ for the Laplacian PDF, obtained by simplifying the general SQNR expression for
μCQ provided in Perić
et al. (
2010). The accuracy of the derived closed-form SQNR expression for
μCQ is examined considering versions of the FP format with 8-bit exponent, FP24 and FP32, and a very wide dynamic range of input data variances. It is shown that the proposed SQNR expression is highly efficient in estimating FP performance when confronted with the existing approach (Perić
et al.,
2021; Denić
et al.,
2023), with the SQNR calculation error below 1% defining the reasonable accuracy of the SQNR formula (Na,
2011). Thus, utilizing the proposed approach instead of the previously introduced one based on a summation of numerous terms ensures a high level of accuracy and leads to a noteworthy reduction in computational complexity.
The rest of the paper is organized as follows. In Section
2, the description of the
R-bit FP format is provided, and its connection with the piecewise uniform quantization is explained. The main result is exposed in Section
3, which performs the design of the
μCQ along with its linearized version tailored to the FP format and provides the closed-form expression for estimating FP format performance. Section
4 presents simulation results and highlights the benefits of the approach studied in the paper. Section
5 gives concluding remarks.
2 Description of the Floating-Point Format
A real number
x is encoded in the
R-bit FP format as IEEE 754 (
2019):
consisting of one bit
s to indicate the sign,
e bits (
${a_{e-1}}\dots {a_{1}}{a_{0}}$) to represent the exponent
E, and
m bits (
${b_{m-1}}\dots {b_{1}}{b_{0}}$) to represent the significand
M of the number
x, whereas
$R=e+m+1$. The exponent
$E={\textstyle\sum _{i=0}^{e-1}}{a_{i}}{2^{i}}$ can take values from 0 to
${2^{e}}-1$, but the values
$E=0$ and
$E={2^{e}}-1$ are reserved according to IEEE 754 (
2019), leaving
${L^{\textit{FP}}}={2^{e}}-2$ values of
E (from 1 to
${2^{e}}-2$) that can be used to represent numbers. The parameter
$M={\textstyle\sum _{i=1}^{m}}{b_{m-i}}{2^{m-i}}$ can take values from 0 to
${2^{m}}-1$. The number
x, represented with (
1), can be calculated in its decimal form as IEEE 754 (
2019):
where
${E^{\ast }}=E-\textit{bias}$ denotes the biased exponent and
$\textit{bias}={L^{\textit{FP}}}/2$ is a predefined parameter. Therefore, the biased exponent
${E^{\ast }}$ takes values from
${E_{\min }^{\ast }}=1-{L^{\textit{FP}}}/2$ to
${E_{\max }^{\ast }}={L^{\textit{FP}}}/2$. For example, for FP32 we have
$e=8$ and
$m=23$ (IEEE 754,
2019), while for FP24 we have
$e=8$ and
$m=15$. Due to the same
e value, both FP32 and FP24 formats have identical values for the following parameters:
${L^{\textit{FP}}}=254$,
$\textit{bias}=127$,
${E_{\min }^{\ast }}=-126$, and
${E_{\max }^{\ast }}=127$.
The
R-bit FP format exhibits symmetry around 0, as every positive number in the format corresponds to a symmetric negative number. Let’s examine positive numbers within the
R-bit FP format, without losing generality. The maximum positive number representable in this format (for
${E^{\ast }}={E_{\max }^{\ast }}$ and
$M={2^{m}}-1$) is:
For each value of
${E^{\ast }}$ (
${E_{\min }^{\ast }}\leqslant {E^{\ast }}\leqslant {E_{\max }^{\ast }}$) we define a segment
${S_{{E^{\ast }}}}=[{2^{{E^{\ast }}}},{2^{{E^{\ast }}+1}}$) of width
${\delta _{{E^{\ast }}}}={2^{{E^{\ast }}}}$, which includes
${2^{m}}$ equidistant real numbers
${2^{{E^{\ast }}}}(1+\frac{M}{{2^{m}}})$,
$M=0,\dots ,{2^{m}}-1$, placed at a mutual distance
${\Delta _{{E^{\ast }}}}={2^{{E^{\ast }}}}(1+\frac{M+1}{{2^{m}}})-{2^{{E^{\ast }}}}(1+\frac{M}{{2^{m}}})={2^{{E^{\ast }}-m}}$. Hence, in the positive part of the real axis, there are a total of
${L^{\textit{FP}}}$ segments
${S_{{E^{\ast }}}}$, each containing
${2^{m}}$ equidistant numbers with a step size of
${\Delta _{{E^{\ast }}}}$. Due to symmetry, the same structure of
${L^{\textit{FP}}}$ segments with
${2^{m}}$ equidistant numbers also exists in the negative part of the real axis. Since
and
it can be concluded that the width of segment
${S_{{E^{\ast }}+1}}$ is twice as large as the width of segment
${S_{{E^{\ast }}}}$, and the distance between adjacent numbers in
${S_{{E^{\ast }}+1}}$ is twice as high as in
${S_{{E^{\ast }}}}$. Therefore, as the value of
${E^{\ast }}$ increases, the distance between adjacent numbers increases, meaning that the FP format provides a finer representation of smaller numbers.
The described structure of the FP format fully corresponds to the structure of a symmetric piecewise uniform quantizer with a maximum amplitude
${x_{\max }^{\textit{FP}}}$ defined with (
3), which in the positive part has
${L^{\textit{FP}}}$ segments
${S_{{E^{\ast }}}}=[{2^{{E^{\ast }}}},{2^{{E^{\ast }}+1}}$),
${E_{\min }^{\ast }}\leqslant {E^{\ast }}\leqslant {E_{\max }^{\ast }}$, each segment undergoing uniform quantization with
${2^{m}}$ quantization levels and with the step size
${\Delta _{{E^{\ast }}}}={2^{{E^{\ast }}-m}}={2^{{E^{\ast }}-R+e+1}}$. This model of quantizer, whose structure mirrors that of the FP format, is known as
the floating-point quantizer − FPQ (Perić
et al.,
2021; Denić
et al.,
2023). This analogy between the FP format and the FPQ is significant, enabling the FP representation quality to be assessed using an objective measure such as SQNR of the FPQ. SQNR is generally defined as Jayant and Noll (
1984), Chu (
2003), Gersho and Gray (
1992):
where
${\sigma ^{2}}$ represents the variance of data to be quantized and
D (
σ) is distortion that represents an error that occurred during quantization. In the case of FPQ,
${\sigma ^{2}}$ represents the variance of data to be represented in the FP format, while distortion of FPQ represents the error that occurred during FP representation of real numbers and can be expressed in general form as Perić
et al. (
2021), Denić
et al. (
2023):
Multiplication by 2 in the expression (
7) is used to account for the distortion in the negative part of the real axis. The first term in (
7), expressed as a sum, represents the granular distortion
${D_{g}^{\mathrm{FPQ}}}$ in
${L^{\textit{FP}}}$ segments
${S_{{E^{\ast }}}}$ (
${E_{\min }^{\ast }}\leqslant {E^{\ast }}\leqslant {E_{\max }^{\ast }}$), where
${P_{{E^{\ast }}}}(\sigma )={\textstyle\int _{{2^{{E^{\ast }}}}}^{{2^{({E^{\ast }}+1)}}}}\hspace{-0.1667em}\hspace{-0.1667em}p(x,\sigma )dx$ represents the probability that the real number
x belongs to segment
${S_{{E^{\ast }}}}$, with
$p(x,\sigma )$ representing the PDF of the input data. The second term in (
7) represents the overload distortion
${D_{ov}^{\mathrm{FPQ}}}$ that occurs during quantization of numbers outside the support region of the FPQ.
This paper examines the zero-mean Laplacian PDF of variance
${\sigma ^{2}}$, defined as Jayant and Noll (
1984), Gersho and Gray (
1992):
For
$p(x,\sigma )$ defined with (
8), based on (
3), (
6), and (
7), the following SQNR expression for the FPQ quantizer is obtained:
Using (
9), it is possible to compute the performance of the
R-bit FP format for any value of data variance. However, expression (
9) contains the sum of
${L^{\textit{FP}}}$ elements, being computationally demanding since
${L^{\textit{FP}}}$ is typically a large number (Perić
et al.,
2021; Denić
et al.,
2023). This issue will be solved in the next section, where an approximate closed-form expression is supplied for efficiently calculating the performance of the
R-bit FP format.
4 Numerical Results and Discussion
In this Section, we present and discuss numerical results for the derived SQNR formulas (
37) and (
38) obtained in evaluating the performance of the
R-bit FP format with
$e=8$ (8-bit exponent) in a very wide variance range, where
$R=24$ and 32 (i.e. FP24 and FP32 formats). Note that the diversity across bit rate
R is introduced to show the generality of the given formulas, whose effectiveness is measured with respect to formula (
9). To facilitate the observation of variance across a wide range, it is usual to define variance in the logarithmic domain as
${\sigma ^{2}}\hspace{2.5pt}[\mathrm{dB}]=10{\log _{10}}({\sigma ^{2}}/{\sigma _{\textit{ref}}^{2}})$, where
${\sigma _{\textit{ref}}^{2}}$ represents the referent variance. Without loss of generality, we can assume that
${\sigma _{\textit{ref}}^{2}}=1$, obtaining
${\sigma ^{2}}\hspace{2.5pt}[\mathrm{dB}]=10{\log _{10}}{\sigma ^{2}}$. Substituting
$\sigma ={10^{{\sigma ^{2}}\hspace{2.5pt}[\mathrm{dB}]/20}}$ into the previously derived expressions for SQNR yields the dependence of SQNR on
${\sigma ^{2}}\hspace{2.5pt}[\mathrm{dB}]$.
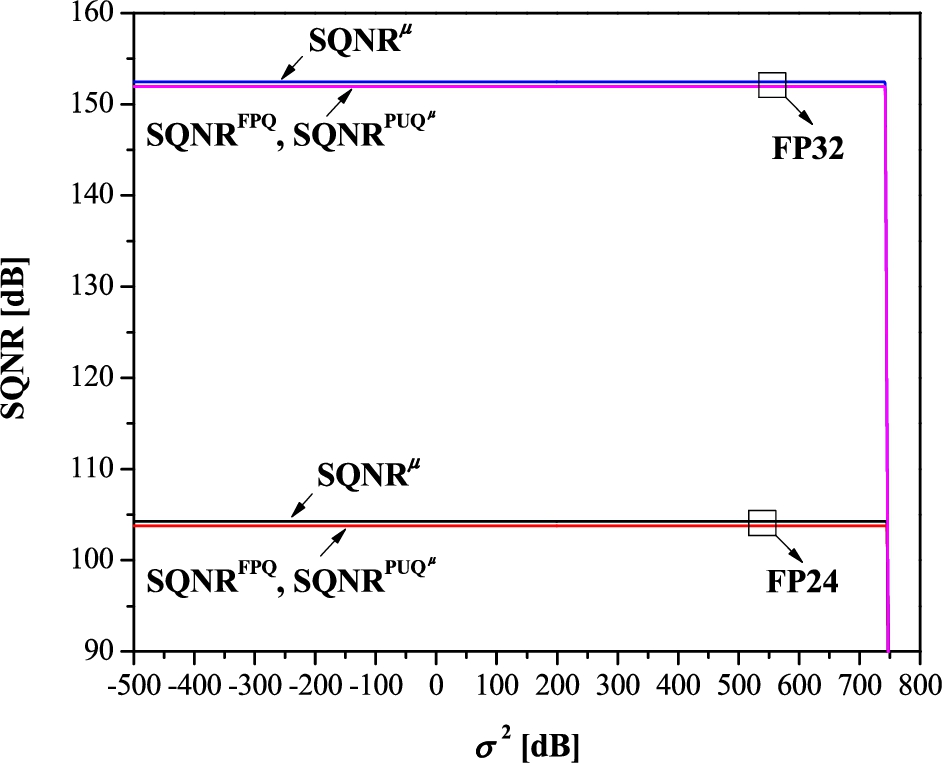
Fig. 1
Performance (SQNR) of FP24 and FP32 formats in a very wide variance range, estimated using different formulas.
Figure
1 shows the performance (SQNR) of the FP24 and FP32 formats over a very wide variance range
${\sigma ^{2}}\hspace{2.5pt}[\mathrm{dB}]\in $ [− 500 dB, 800 dB], calculated using (
9), (
37), and (
38). It’s worth mentioning that the chosen variance range is significantly broader than that commonly used for scalar quantizer analysis (typically
${\sigma ^{2}}\hspace{2.5pt}[\mathrm{dB}]\in $ [− 20 dB, 20 dB] or
${\sigma ^{2}}\hspace{2.5pt}[\mathrm{dB}]\in $ [− 30 dB, 30 dB], as seen in Perić
et al. (
2010), Denić
et al. (
2023)). From the given figure, it can be noted that the results for SQNR formulas (
9) and (
38) are in excellent agreement for each considered
${\sigma ^{2}}\hspace{2.5pt}[\mathrm{dB}]$. Based on this performance matching, we argue that the discussed PUQ
μ and FPQ are compatible, proving the correctness of the applied design process. It can also be observed that the SQNR values achieved by (
37) are very close to those achieved by (
38) (and accordingly by (
9)), which is in agreement with Theorem
2. From Fig.
1, it is clearly evident that there is a threshold variance, denoted by
${\sigma _{t}^{2}}\hspace{2.5pt}[\mathrm{dB}]$, such that for
${\sigma ^{2}}\hspace{2.5pt}[\mathrm{dB}]\leqslant {\sigma _{t}^{2}}\hspace{2.5pt}[\mathrm{dB}]$ the granular distortion
${D_{g}^{\mu }}$ dominates, so
${\mathrm{SQNR}^{\mu }}$ becomes:
i.e. it remains constant and does not depend on the data variance
${\sigma ^{2}}$. This can be interpreted as follows. Since the
${\mathrm{SQNR}^{\mu }}$ is independent of the PDF parameter
${\sigma ^{2}}$, then using any non-parametric Laplacian distribution yields the same SQNR score. On the other hand, for
${\sigma ^{2}}\hspace{2.5pt}[\mathrm{dB}]\gt {\sigma _{t}^{2}}\hspace{2.5pt}[\mathrm{dB}]$ the overload distortion
${D_{ov}^{\mu }}$ prevails, leading to a sharp drop in SQNR. The threshold variance
${\sigma _{t}^{2}}\hspace{2.5pt}[\mathrm{dB}]$ is 745 dB for the FP24 format and 742 dB for the FP32 format.
Let us introduce the relative error
δ SQNR[%] as an accuracy measure of the SQNR formula (
37) with respect to (
9). The values for
δ SQNR [%] are illustrated in Fig
2. Figure
2 indicates that the SQNR calculation error for
${\sigma ^{2}}\hspace{2.5pt}[\mathrm{dB}]\leqslant {\sigma _{t}^{2}}\hspace{2.5pt}[\mathrm{dB}]$ is below 0.5% in the case of FP24 format performance evaluation and below 0.35% in the case of FP32 format performance evaluation; for
${\sigma ^{2}}\hspace{2.5pt}[\mathrm{dB}]\gt {\sigma _{t}^{2}}\hspace{2.5pt}[\mathrm{dB}]$, the SQNR error tends to zero, as predicted. Given that
δ SQNR[%] < 1%, we report that reasonable accuracy of the SQNR formula defined in Na (
2011) is achieved with the proposed approximate formula (
37). Due to this achievement and the fact that (
37) is considerably less computationally intensive than (
9), which includes
${L^{\textit{FP}}}=254$ sum members (since
$e=8$), we confirm that (
37) can indeed be used as an adequate tool for evaluating the performance of the FP format for Laplacian data.
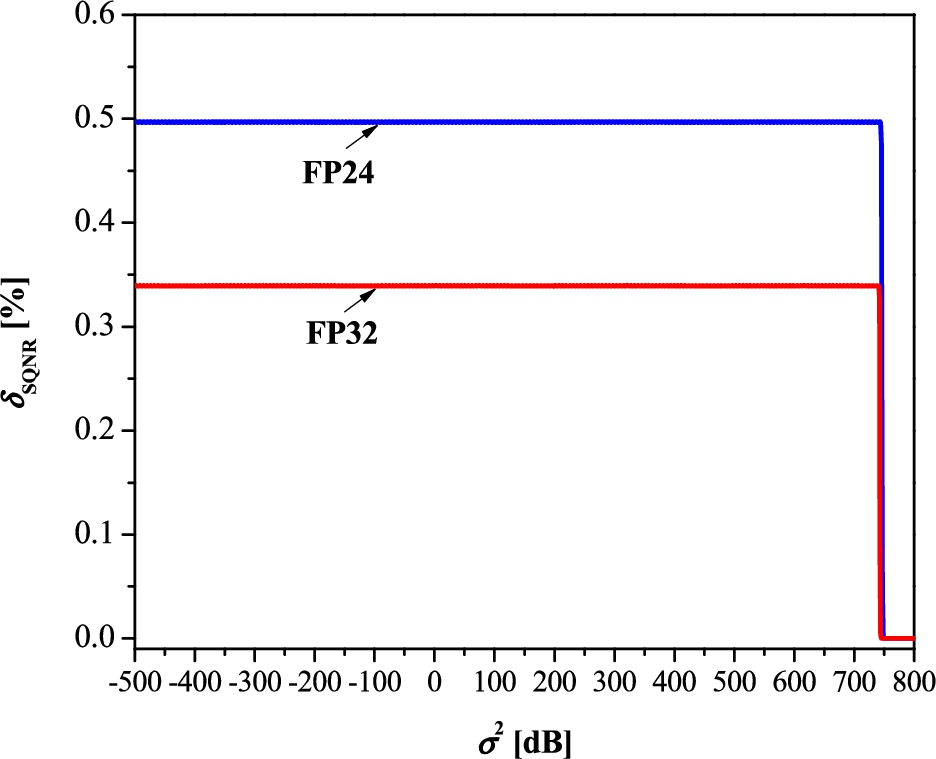
Fig. 2
Accuracy of the SQNR formula (
37) in estimating the performance of FP24 and FP32 formats.
Given SQNR analysis can also be useful in selecting the optimal FP format for the target application. Specifically, from the point of quality of digital representation, FP32 is a better solution than FP24, due to the higher SQNR score; however, from the point of dynamic range, both FP32 and FP24 formats are very efficient as they retain constancy in SQNR across a very wide variance range. Due to these positive features and the fact that its implementation complexity is lower than FP32, FP24 can be seen as an attractive choice for various practical applications.
5 Conclusion
This paper builds upon the analogy between FP digital representation and quantization established in literature, introducing a novel idea regarding the link between the FP format and the μCQ. It presents a method for designing and linearizing the μCQ to achieve a piecewise uniform quantizer PUQμ tailored to the FP format. Given the FP format’s similarity in structure to PUQμ and the close performance of PUQμ to μCQ, a closed-form expression for the SQNR of μCQ has been proposed in this paper to evaluate FP format’s performance, which holds general applicability across various bit rates and data variances. Numerical assessments spanning a very wide variance range, conducted for some commonly used FP formats with an 8-bit exponent, showed the full applicability of the proposed SQNR expression in FP format performance evaluation, as competitive results (SQNR calculation error is below the predefined threshold of 1%) and significantly lower computational intensity have been observed with respect to the existing method reliant on the summation of numerous terms (254 in the situation when $e=8$). As the computational complexity of the existing method increases even more for $e\gt 8$, a significant simplification of the FP format evaluation process is expected by applying the proposed method. Providing an efficient and accurate mechanism for the evaluation of FP format performance, this paper facilitates the selection of the optimal FP bit configuration for a specific application, crucial for digital representation quality, dynamic range, computational overhead, and energy efficiency.

