1 Introduction
Multi-criteria decision-making (MCDM) methods have been refined and enhanced over time to become powerful tools for addressing complex and multidimensional problems. These methods assist decision-makers in selecting the best option in situations where multiple and sometimes conflicting, objectives must be considered. By evaluating various criteria, MCDM ensures a comprehensive and balanced assessment, enhancing both the accuracy and credibility of the decision-making process (Aycin
et al.,
2024; Nagy
et al.,
2024). In real-world applications, decision-making is often challenged by uncertainty and ambiguity, where fuzzy MCDM proves highly effective. By modelling these uncertainties, fuzzy approaches allow decision-makers to integrate qualitative and imprecise information, making the process more adaptable and realistic, especially when precise quantitative data is unavailable or subjective judgements are essential (Bechar
et al.,
2024; Lefranc
et al.,
2025). This flexibility is particularly valuable in domains such as sustainable agriculture, where evaluating diverse solutions requires balancing economic, environmental, and social considerations under uncertain conditions.
Sustainable agriculture is a holistic approach to farming that balances meeting present-day food and fiber needs with conserving the planet’s resources for future generations. By minimizing reliance on nonrenewable inputs and incorporating biological sources, it ensures productivity while protecting the environment (Rao and Rogers,
2006; Thompson,
2007). This system, rooted in an understanding of ecosystem services, aligns with principles from organic farming, regenerative agriculture, permaculture, and agroforestry to promote environmental resilience and long-term sustainability (Hayati
et al.,
2011; Pretty,
2008). Sustainable agriculture encourages multifunctionality by striking a balance between environmental health and productivity, producing food while contributing to public goods such as water conservation and biodiversity, and adapting to local conditions and social dynamics (Arora,
2018; Zhen and Routray,
2003). In order to fulfill the growing demands for food, feed, and biofuels, there is a greater need for agricultural products. Economically speaking, price volatility brought on by the growing demand for agricultural products can affect both the affordability of goods for consumers and the livelihoods of farmers (Bathaei and Štreimikienė,
2023; Martos
et al.,
2021). In terms of society, this demand intensifies competition for limited resources, such as water and land, which can lead to conflicts and uneven allocation of resources. In terms of the environment, the drive for increased production frequently leads to soil deterioration, deforestation, excessive chemical input use, and water resource depletion—all of which exacerbate climate change and biodiversity loss (Janker and Mann,
2020; Janker
et al.,
2019; Montgomery,
2007).
To achieve sustainable agriculture, it is essential to adopt a variety of solutions that are prioritized according to factors such as geographical, economic, social, and political conditions. Deciding which solution should take precedence requires a thorough evaluation from multiple angles, as sustainable agriculture is crucial not only for environmental protection but also for fostering economic growth and social development (Godfray and Garnett,
2014; Rockström
et al.,
2017). Despite the numerous challenges impeding the broader adoption of sustainable agriculture, the variety of solutions emphasizes that assessing the efficacy of solutions to achieve sustainable agriculture can be approached as an MCDM problem (Keshavarz-Ghorabaee,
2023b; Pretty
et al.,
2018). In this structure, experts establish criteria specific to the conditions and challenges of sustainable agriculture, providing a comprehensive framework for evaluation. Decision-makers can then evaluate the effectiveness of different solutions based on these criteria and, through MCDM techniques, identify near-optimal solutions that align with the existing conditions (Cicciù
et al.,
2022; Keshavarz-Ghorabaee,
2023a).
This study introduces a fuzzy multi-criteria group decision-making approach that integrates the Objective Pairwise Adjusted Ratio Analysis (OPARA) method, the Method Based on the Removal Effects of Criteria (MEREC), and the Relative Preference Relation (RPR). OPARA is a new MCDM method, and its efficiency and robustness have been rigorously validated through various analyses (Keshavarz-Ghorabaee
et al.,
2024). MEREC, which has been extensively applied in empirical studies, has been shown to be effective in determining objective weights in MCDM problems (Keshavarz-Ghorabaee
et al.,
2021). The proposed approach is employed to assess sustainable agriculture solutions by integrating subjective weights—representing expert-assigned weights of evaluation criteria—with objective weights derived from MEREC, ensuring a balanced and realistic weighting scheme. The fuzzy OPARA method is utilized for the evaluation process, leveraging comprehensive decision-making data while incorporating parameters that adjust evaluations based on the range and linearity of criteria. To rank fuzzy numbers, the RPR approach is applied, enabling a relative assessment within a set rather than in isolation (Wang,
2015). The proposed approach provides a robust framework for addressing a wide range of decision-making problems in fuzzy environments.
The remainder of the paper is structured as follows. Section
2 provides a review of the literature, focusing on recent research in the field. Section
3 details the methodology employed in this study. Section
4 presents the results and discussion, where the practical application of the proposed approach and the analysis of its results are examined. Finally, the conclusion summarizes the key findings of the study.
2 Literature Review
This section reviews several studies on the application of MCDM methods to agricultural research from recent years. At the end, a table provides a summary of the key features of the reviewed studies.
Zamani
et al. (
2020) investigated farmers’ perceptions and stakeholders’ views on climate change adaptation strategies in the Jarreh agricultural water resources system in southwest Iran. Six adaptation scenarios were developed, and TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) and PROMETHEE II (Preference Ranking Organization METHod for Enrichment of Evaluations) methods were used for evaluation. Results favoured enhancing irrigation efficiency and reducing cultivated area as the most effective strategies to mitigate climate change impacts. Ebad Ardestani
et al. (
2020) addressed the issue of water resource management in Iranian drainage basins. They utilized a framework to evaluate agricultural water supply systems, emphasizing cooperation among all stakeholders. They compared different water supply alternatives across social, economic, bioenvironmental, and technical criteria. Through MCDM techniques, the research showcased the effectiveness of evaluating projects for sustainable development. De Marinis and Sali (
2020) investigated the use of participatory Analytic Hierarchy Process (AHP) in agricultural development projects. The method was utilized for choice criteria elicitation and resource allocation. The methodology facilitated team training and established a shared resource allocation pattern aligned with international guidelines for sustainable agricultural development in the region. Manafi Mollayosefi
et al. (
2020) evaluated agricultural sustainability in East Azerbaijan Province using Entropy and fuzzy AHP techniques. Key indicators included water consumption efficiency, conservation tillage, health, agricultural employment, and greenhouse land. The study emphasized the importance of considering multiple evaluation methods to avoid misleading results.
Rani
et al. (
2021) aimed to address the uncertainty in assessing agricultural residues-to-energy conversion technologies using Pythagorean fuzzy sets (PFSs). Through a combined approach incorporating weighted discrimination-based approximation (WDBA), they improved the assessment process by developing a new ranking method and a score function-based linear programming model to estimate unknown attribute weights. Mishra
et al. (
2021) addressed the uncertainty of season crop assessment as a complex MCDM problem. They proposed a new decision-making framework, combining CRITIC (Criteria Importance Through Intercriteria Correlation) and VIKOR (VlseKriterijumska Optimizacija I Kompromisno Resenje) approaches under PFSs environment. The CRITIC model estimated objective criteria weights, while VIKOR provided simple and accurate results for crop assessment. Yazdani
et al. (
2021) studied the impacts of flooding on agricultural supply chains within a circular economy framework. They utilized the SWARA (Stepwise Weight Assessment Ratio Analysis) and EDAS (Evaluation Based on Distance from Average Solution) methods, to identify and rank flood risk drivers. Tork
et al. (
2021) investigated the modernization of surface water distribution. They employed a combination of structural and non-structural methods alongside automation, evaluating scenarios based on technical, social, economic, and environmental criteria. They applied the AHP and COPRAS (Complex Proportional Assessment) for prioritization.
Kumar
et al. (
2021) employed frequency ratio and AHP methods, integrating remote sensing and geographic information system (GIS) to identify suitable land for agriculture. The results indicated that a significant portion of the area is unsuitable for agriculture, with only a small fraction being highly suitable. Hoose
et al. (
2021) addressed the challenge of optimizing product mixes in the agricultural machinery industry while considering sustainability. Using AHP and data envelopment analysis (DEA), they identified seven alternatives for grain trailer production. The AHP results highlighted one optimal alternative, while the DEA revealed two efficient options, allowing managers to choose between lower environmental impact and higher profitability. Puška
et al. (
2021) focused on the selection of sustainable suppliers for agricultural production, addressing the challenge of asymmetric information in supplier evaluation. They applied MCDM methods, specifically interval fuzzy logic, using PIPRECIA (PIvot Pair-wise RElative Criteria Importance Assessment) to determine criteria weights and MABAC (Multi-Attributive Border Approximation Area Comparison) for supplier ranking. This approach aids agricultural producers in making informed decisions despite information asymmetry. Erdoğan (
2022) addressed the challenge of adopting Agriculture 4.0 technologies for sustainable resource use in agriculture. She proposed a decision-making framework utilizing MCDM that incorporates interval-valued spherical fuzzy numbers to manage uncertainty. The study extended the SWARA and MAIRCA (MultiAtributive Ideal-Real Comparative Analysis) methods, demonstrating their effectiveness in prioritizing farmers’ perceptions of these technologies.
Namiotko
et al. (
2022) examined the agri-environmental situation of selected European Union countries. They utilized SAW (Simple Additive Weighting), TOPSIS, and EDAS to identify strategies for improving agricultural practices and environmental conditions. The study revealed consistent trends across all methods, with Finland, Ireland, and Sweden showing the best agri-environmental performance, while the Netherlands, Denmark, and Germany ranked the lowest. Roy
et al. (
2022) focused on assessing land suitability for rain-fed cultivation in the red and lateritic zones of West Bengal, India. They employed a GIS-based MCDM approach, analysing factors such as slope, soil moisture, and geology. The AHP was used to assign weights and rank the sub-criteria. The study identified four land suitability categories, achieving 85% accuracy in mapping, which supports optimized agricultural practices and drought risk reduction. Çürük and Alptekin (
2022) examined the Turkish floriculture industry to propose sustainable strategies. They conducted a SWOT (strengths, weaknesses, opportunities, and threats) analysis to assess the current state of the industry and utilized an MCDM approach with an ANP (Analytical Network Process) model to evaluate economic, environmental, and socio-political dimensions of sustainability. Puška
et al. (
2022) investigated the selection of green suppliers for agricultural producers. They employed Z-numbers alongside fuzzy LMAW (Logarithm Methodology of Additive Weights) and fuzzy CRADIS (Compromise Ranking of Alternatives from Distance to Ideal Solution) methods to account for uncertainty in expert decision-making. The study confirmed the model’s stability through validation and sensitivity analysis.
Abualkishik
et al. (
2022) addressed the challenge of improving agricultural production efficiency and sustainability through smart agriculture. They developed a fuzzy MARCOS (Measurement Alternatives and Ranking according to Compromise Solution) to evaluate agricultural solutions. The results indicated that specific aspects of agriculture are significantly influenced by the findings, emphasizing the importance of selecting effective smart agriculture solutions. Rouyendegh and Savalan (
2022) developed a hybrid model based on AHP and TOPSIS to aid in selecting sustainable agricultural solutions. The case study highlighted the complexity of agricultural production techniques, emphasizing the need for a holistic assessment approach. The model effectively integrated qualitative and quantitative criteria, demonstrating its validity in evaluating technology suitability. Barbosa Junior
et al. (
2022) investigated the barriers to adopting sustainable agriculture. They identified these barriers through a literature review and analysed their influence using the fuzzy DEMATEL (Decision Making Trial and Evaluation Laboratory) method. The study revealed eleven barriers, with “technical knowledge and qualified workforce” being the most significant. Radmehr
et al. (
2022) focused on sustainable water resources management to enhance water efficiency and food security. They proposed a novel spatial fuzzy strategic planning framework combined with MCDM and a conceptual agricultural water use model, which was applied to an irrigation network in Iran. Using SWOT analysis, AHP and TOPSIS, they identified and ranked barriers to sustainable practices.
Anusha
et al. (
2023) addressed the issue of land suitability for agriculture to enhance sustainable land use strategies. They developed a conceptual process for land suitability analysis using thematic layers derived from satellite images and collateral data. The study applied AHP, providing valuable insights for identifying viable agricultural lands. Abrams
et al. (
2023) employed triangular fuzzy numbers, Monte Carlo simulations and TOPSIS to rank five countermeasures for remediating contaminated agricultural land. Their findings indicated that incorporating uncertainties from linguistic scores, weights, and decision-maker disagreements significantly challenged deterministic rankings, resulting in a fuzzy ranking that encouraged decision-makers to reconsider the perceived superiority of alternatives. Tuan and Canh (
2023) focused on developing priority strategies for agricultural development, amid drought challenges. They utilized the SWOT analysis to identify 15 strategies and employed the fuzzy ANP to rank these factors. The study highlighted effective strategies for agricultural production, emphasizing drought evaluation and market development for key crops. Mokarram
et al. (
2023) investigated the spatial distribution of fig trees infected by the invasive pest to identify areas prone to fig cultivation in Iran. They employed a multi-step approach, which included land suitability mapping through AHP and GIS. The results indicated that central and parts of the east and northwest regions were most suitable for fig cultivation.
Zkik
et al. (
2023) examined the barriers and enablers to adopting blockchain technology for sustainable supply chain performance in e-enabled agricultural supply chains. They utilized a novel hybrid method combining PFS, cumulative prospect theory, and VIKOR. The results provided strategies for blockchain technology implementation. Zhai
et al. (
2023) addressed the challenge of encouraging continued investment in agri-food supply chains. They developed an integrated decision-making framework based on MEREC and PFSs alongside other methods to evaluate and prioritize risks. An empirical case study demonstrated the framework’s effectiveness in assessing risks. Keskes
et al. (
2024) developed an MCDM framework to assist decision-makers in selecting sustainable agricultural practices and waste recovery methods. This framework integrated the 2-Tuple model for uncertainty and VIKOR for ranking sustainability scenarios. A case study on the olive oil life cycle in Sfax, Tunisia, demonstrated the framework’s effectiveness. Nguyen
et al. (
2024) focused on the barriers to digitalization and innovation in the agricultural supply chain. They developed a model combining DEMATEL and ANP with Spherical Fuzzy Sets (SFSs) to identify and quantify these barriers. The SFS-TOPSIS method was then applied to rank potential solutions. The results identified technology and institutional barriers as the most significant.
Prabhjyot
et al. (
2024) employed Agro-Eco-Resource zonation using meteorological, soil, and groundwater data to classify areas based on crop suitability. The AHP assigned weights to various factors, while GIS facilitated the creation of thematic maps. The findings provided a roadmap for sustainable agricultural practices, recommending a reduction in resource-intensive crop cultivation. Yang and Solangi (
2024) focused on promoting sustainable development in China by evaluating natural resource management, environmental protection, and agricultural economics. They utilized fuzzy AHP and fuzzy VIKOR methods to analyse uncertainties in decision-making. The study identified economic viability, policy and governance, and environmental impact as key criteria influencing sustainability. Tao
et al. (
2024) examined the critical success factors necessary for enhancing productivity and performance in Chinese agriculture systems. They identified and prioritized 12 factors from a pool of 18 using the Delphi method, validated by experts’ opinions. Employing SWARA and ARAS (Additive Ratio ASsessment), the study revealed that an entrepreneurial mindset, entrepreneurial awareness among farmers, and technology transfer significantly influence agricultural growth. Atlı (
2024b) focused on the challenges of selecting target markets for agricultural products. He employed fuzzy AHP and fuzzy COPRAS techniques to rank and evaluate market alternatives. The fuzzy AHP method assessed the importance levels of criteria, revealing that economic factors carried the most weight. The fuzzy COPRAS method ranked six importing countries, with the European Union identified as the top target market for processed agricultural products. In another study, Atlı (
2024a) investigated the selection of sustainable fertilizer suppliers within the agricultural supply chain. He utilized AHP and ARAS techniques to evaluate and rank supplier alternatives. The AHP method determined the importance of criteria. Subsequently, the ARAS method ranked the suppliers.
Puška
et al. (
2024) examined the increasing electricity demand in agricultural production and the potential of renewable energy sources. They utilized fuzzy MCDM methods to develop a decision-making model. Their findings highlighted that economic criteria were prioritized, with solar energy identified as the most promising option for sustainable agricultural practices. Ismail
et al. (
2024) addressed the challenge of selecting the best supplier among competitors in agriculture. They developed an MCDM approach based on MEREC and MABAC, incorporating triangular neutrosophic sets to manage uncertainties. Comparison with the WSM (Weighted Sum Model) further validated the results. Bozorgi
et al. (
2024) focused on the risks associated with agricultural water distribution due to various natural and human-caused hazards. They developed a framework using a fuzzy dynamic Bayesian network model for risk assessment. The study defined and implemented several risk management scenarios and ranked them using WASPAS (Weighted Aggregated Sum Product Assessment), TOPSIS, and MOORA (Multi Objective Optimization by Ratio Analysis) methods. Singh
et al. (
2024) examined the disparities in agricultural development across districts in Uttar Pradesh, India. They utilized a combination of factor analysis (FA) and TOPSIS to create a composite index system based on twenty-six agricultural indicators. Biswas
et al. (
2024) investigated the practices for wheat cultivation using conservation agriculture methods. They employed TOPSIS and AHP to evaluate alternative tillage approaches. The performance of these regimes was assessed based on various parameters, including energy use and economics. Tran
et al. (
2024) addressed the issue of post-harvest losses in the agricultural supply chain. They employed a two-stage cause-effect approach using SFSs to manage uncertainty. The Spherical fuzzy Delphi method identified critical criteria, while the Spherical fuzzy DEMATEL method analysed relationships among these factors. The study revealed that transportation was the most significant causal factor.
Table
1 summarizes and examines the studies reviewed above based on their consideration of sustainability, the use of a single or integrated approach, the incorporation of uncertainty, the MCDM methods used, and the research problem addressed.
Table 1
Summary of reviewed studies.
| No. |
Reference |
Sustainability |
Single approach |
Integrated approach |
Uncertainty |
MCDM method |
Problem description |
| 1 |
Zamani et al. (2020) |
✘ |
✘ |
✓ |
✓ |
TOPSIS-PROMETHEE |
Agricultural water allocation |
| 2 |
Ebad Ardestani et al. (2020) |
✓ |
✓ |
✘ |
✘ |
TOPSIS |
Agricultural water supply |
| 3 |
De Marinis and Sali (2020) |
✘ |
✓ |
✘ |
✘ |
AHP |
Resource allocation in agricultural development projects |
| 4 |
Manafi Mollayosefi et al. (2020) |
✓ |
✓ |
✘ |
✓ |
AHP |
Evaluation of agricultural sustainability |
| 5 |
Rani et al. (2021) |
✓ |
✓ |
✘ |
✓ |
WDBA |
Assessment of bioenergy technologies |
| 6 |
Mishra et al. (2021) |
✘ |
✘ |
✓ |
✓ |
CRITIC-VIKOR |
Agriculture crop selection |
| 7 |
Yazdani et al. (2021) |
✘ |
✘ |
✓ |
✘ |
SWARA-EDAS |
Agriculture supply chain risk |
| 8 |
Tork et al. (2021) |
✘ |
✘ |
✓ |
✘ |
AHP-COPRAS |
Agriculture water distribution system |
| 9 |
Kumar et al. (2021) |
✓ |
✓ |
✘ |
✘ |
AHP |
Land evaluation for sustainable development |
| 10 |
Hoose et al. (2021) |
✓ |
✘ |
✓ |
✘ |
AHP-DEA |
Selection of production mix |
| 11 |
Puška et al. (2021) |
✓ |
✘ |
✓ |
✓ |
PIPRECIA-MABAC |
Selecting a sustainable supplier |
| 12 |
Erdoğan (2022) |
✓ |
✘ |
✓ |
✓ |
SWARA-MAIRCA |
Assessing farmers’ perception to Agriculture 4.0 technologies |
| 13 |
Namiotko et al. (2022) |
✓ |
✘ |
✓ |
✘ |
SAW-TOPSIS-EDAS |
Assessment of agri-environmental situation |
| 14 |
Roy et al. (2022) |
✓ |
✓ |
✘ |
✘ |
AHP |
Land suitability analysis |
| 15 |
Çürük and Alptekin (2022) |
✓ |
✓ |
✘ |
✘ |
ANP |
Developing sustainable agriculture strategies |
| 16 |
Puška et al. (2022) |
✘ |
✘ |
✓ |
✓ |
LMAW-CRADIS |
Green supplier selection |
| 17 |
Abualkishik et al. (2022) |
✘ |
✓ |
✘ |
✓ |
MARCOS |
Evaluating smart agricultural production |
| 18 |
Rouyendegh and Savalan (2022) |
✘ |
✘ |
✓ |
✓ |
AHP-TOPSIS |
Analyse agricultural production |
| 19 |
Barbosa Junior et al. (2022) |
✓ |
✓ |
✘ |
✓ |
DEMATEL |
Adoption of sustainable agriculture |
| 20 |
Radmehr et al. (2022) |
✘ |
✘ |
✓ |
✓ |
AHP-TOPSIS |
Agricultural water management |
| 21 |
Anusha et al. (2023) |
✓ |
✓ |
✘ |
✘ |
AHP |
Land suitability analysis |
| 22 |
Abrams et al. (2023) |
✘ |
✓ |
✘ |
✓ |
TOPSIS |
Measures for remediation of agricultural land |
| 23 |
Tuan and Canh (2023) |
✘ |
✘ |
✓ |
✓ |
ANP |
Developing sustainable agriculture |
| 24 |
Mokarram et al. (2023) |
✓ |
✓ |
✘ |
✘ |
AHP |
Sustainable agriculture development |
| 25 |
Zkik et al. (2023) |
✓ |
✓ |
✘ |
✓ |
VIKOR |
Exploration of barriers and enablers of blockchain adoption |
| 26 |
Zhai et al. (2023) |
✘ |
✘ |
✓ |
✓ |
MEREC-GLDS |
Agriculture supply chain risks |
| 27 |
Keskes et al. (2024) |
✓ |
✓ |
✘ |
✓ |
VIKOR |
Agricultural sustainability problem |
| 28 |
Nguyen et al. (2024) |
✘ |
✘ |
✓ |
✓ |
DEMATEL-ANP-TOPSIS |
Digital transformation in agricultural supply chain |
| 29 |
Prabhjyot et al. (2024) |
✓ |
✓ |
✘ |
✘ |
AHP |
Zonation for sustainable agriculture |
| 30 |
Yang and Solangi (2024) |
✓ |
✘ |
✓ |
✘ |
AHP-VIKOR |
Natural resource management |
| 31 |
Tao et al. (2024) |
✘ |
✘ |
✓ |
✘ |
SWARA-ARAS |
Entrepreneurship factors to promote agriculture systems |
| 32 |
Atlı (2024b) |
✘ |
✘ |
✓ |
✓ |
AHP-COPRAS |
Target market selection |
| 33 |
Atlı (2024a) |
✓ |
✘ |
✓ |
✓ |
AHP-ARAS |
Fertilizer supplier selection |
| 34 |
Puška et al. (2024) |
✓ |
✘ |
✓ |
✓ |
DiWeC-RAWEC |
Renewable energy integration |
| 35 |
Ismail et al. (2024) |
✘ |
✘ |
✓ |
✓ |
MEREC-MABAC |
Agricultural machinery supplier selection |
| 36 |
Bozorgi et al. (2024) |
✘ |
✘ |
✓ |
✓ |
WASPAS-TOPSIS-MOORA |
Risk management for water systems |
| 37 |
Singh et al. (2024) |
✘ |
✘ |
✓ |
✘ |
FA-TOPSIS |
Assessment of agricultural development |
| 38 |
Biswas et al. (2024) |
✘ |
✘ |
✓ |
✘ |
AHP-TOPSIS |
Evaluation of cropping system |
| 39 |
Tran et al. (2024) |
✘ |
✘ |
✓ |
✓ |
Delphi-DEMATEL |
Strategic agricultural supply chain |
| 40 |
Current study |
✓ |
✘ |
✓ |
✓ |
MEREC-OPARA |
Assessment of sustainability solutions |
3 Methodology
In this section, the preliminaries of the proposed methodology are provided. Then a novel multi-criteria group decision-making approach in a fuzzy environment is presented.
3.1 Preliminaries
3.1.1 Fuzzy Sets
Definition 1.
A fuzzy subset
$\tilde{A}$ in a universal set
X is described through its membership function
${\mu _{\tilde{A}}}(x)$, which assigns a degree of membership to each element
x. A fuzzy number represents a specific type of fuzzy subset that is both convex and normalized. A fuzzy number
$\tilde{A}$ is classified as a trapezoidal fuzzy number if its membership function takes the following form (Wang and Lee,
2007; Zimmermann,
2010):
Such a fuzzy number can be represented as a quadruplet
$\tilde{A}=(a,b,c,d)$.
Definition 2.
Let
${\tilde{x}_{1}}=({x_{1}^{a}},{x_{1}^{b}},{x_{1}^{c}},{x_{1}^{d}})$ and
${\tilde{x}_{2}}=({x_{2}^{a}},{x_{2}^{b}},{x_{2}^{c}},{x_{2}^{d}})$ represent two positive trapezoidal fuzzy numbers (
${x_{1}^{a}}\gt 0$ and
${x_{2}^{a}}\gt 0$), with
k as a crisp number. The operators applicable to these fuzzy numbers and utilized in this study are defined as follows (Chen and Hwang,
1992; Wang
et al.,
2006):
Definition 3.
Let
$S=\{{\tilde{x}_{1}},{\tilde{x}_{2}},\dots ,{\tilde{x}_{n}}\}$ denotes a set consisting of
n trapezoidal fuzzy numbers, where
${\tilde{x}_{i}}=({x_{i}^{a}},{x_{i}^{b}},{x_{i}^{c}},{x_{i}^{d}})$. Assume
$\tilde{z}=({z^{a}},{z^{b}},{z^{c}},{z^{d}})$ represents the average of the
n fuzzy numbers. Then the RPR degree of
${\tilde{x}_{i}}$ over
$\tilde{z}$ is calculated as follows (Wang,
2015):
where
and,
${t_{s}^{+a}}={\max _{i}}{x_{i}^{a}}$,
${t_{s}^{+b}}={\max _{i}}{x_{i}^{b}}$,
${t_{s}^{+c}}={\max _{i}}{x_{i}^{c}}$,
${t_{s}^{+d}}={\max _{i}}{x_{i}^{d}}$,
${t_{s}^{-a}}={\min _{i}}{x_{i}^{a}}$,
${t_{s}^{-b}}={\min _{i}}{x_{i}^{b}}$,
${t_{s}^{-c}}={\min _{i}}{x_{i}^{c}}$,
${t_{s}^{-d}}={\min _{i}}{x_{i}^{d}}$.
3.1.2 MEREC
MEREC determines criteria weights by evaluating the impact of removing each criterion on the performance of alternatives. Criteria that have a greater influence on performance are assigned higher weights. To apply this method, it is first necessary to define a measure for the performance of alternatives. The objective weights are then calculated using the following steps (Keshavarz-Ghorabaee
et al.,
2021).
Step 1. Create the decision matrix. In this step, a decision matrix is formed, representing the ratings or values of each alternative with respect to each criterion. The matrix elements, denoted as ${x_{ij}}$, must be greater than zero (${x_{ij}}\gt 0$; n alternatives and m criteria). If any negative values are present in the decision matrix, they should be converted into positive values using a suitable transformation method.
Step 2. Normalize the decision matrix (
N). The normalized elements are represented as
${n_{ij}^{x}}$. For criteria, where
B denotes the set of beneficial criteria and
N the set of non-beneficial criteria, the normalization process is carried out using the following equation.
Step 3. Determine the overall performance of the alternatives (
${S_{i}}$). Using the normalized values from the prior step, it is ensured that smaller
${n_{ij}^{x}}$ values result in higher performance scores (
${S_{i}}$). The calculation is performed using the following equation.
Step 4. Evaluate the performance of alternatives by excluding each criterion. The overall performance of the
i-th alternative when the
j-th criterion is removed is denoted as
${S^{\prime }_{ij}}$. The following equation is applied for these calculations.
Step 5. Determine the total absolute deviations. Let
${E_{j}}$ represent the effect of removing the
j-th criterion. This value can be computed using the following equation.
Step 6. Calculate the final criterion weights. Here,
${w_{j}}$ represents the weight assigned to the
j-th criterion. The following formula is employed to compute
${w_{j}}$.
3.2 Proposed Integrated Approach
The proposed approach is based on group decision-making, integrating both subjective and objective decision criteria weights. It utilizes the MEREC weighting method, applies the fuzzy OPARA method, and ranks fuzzy values through the RPR approach. The integration of subjective weights, determined based on decision-makers’ opinions, with objective weights, calculated using the efficient MEREC method and derived from the decision matrix data, enables a more realistic decision-making process. Moreover, the OPARA method, as a novel MCDM approach, facilitates a systemic decision-making process where the evaluation of each alternative requires considering the entirety of the decision matrix data, rather than focusing solely on the information related to that specific alternative. This is achieved by employing pairwise adjusted ratios to determine the dominance or significance degree of each alternative in comparison to the others (Damjanović
et al.,
2024; Keshavarz-Ghorabaee
et al.,
2024).
Notably, two parameters in this method allow decision-makers to adjust the influence of each criterion on the dominance or significance degree of an alternative. One parameter adjusts based on the range of each criterion, while the other modifies it according to the degree of linearity of the criterion. This section outlines the process of implementing the fuzzy OPARA method. At the end of the fuzzy OPARA implementation, the overall fuzzy performance of each alternative is determined. To rank the resulting fuzzy values, an efficient fuzzy ranking method called $\textit{RPR}$ is utilized.
The procedure for applying the proposed approach is illustrated in Fig.
1. The following sections provide a step-by-step explanation of the implementation process with detailed descriptions.
Step 1. Formation of a decision-making group. The first step involves assembling a decision-making group composed of d decision-makers (experts or stakeholders) each with relevant knowledge and experience. This group is responsible for evaluating the decision criteria and alternatives, ensuring a comprehensive and collaborative decision-making process.
Step 2. Identification and definition of evaluation criteria by the decision-making group. In this step, the decision-making group identifies and defines a total of m evaluation criteria, which will serve as the basis for assessing the performance of alternatives. These criteria are collaboratively determined to align with the decision-making objectives.
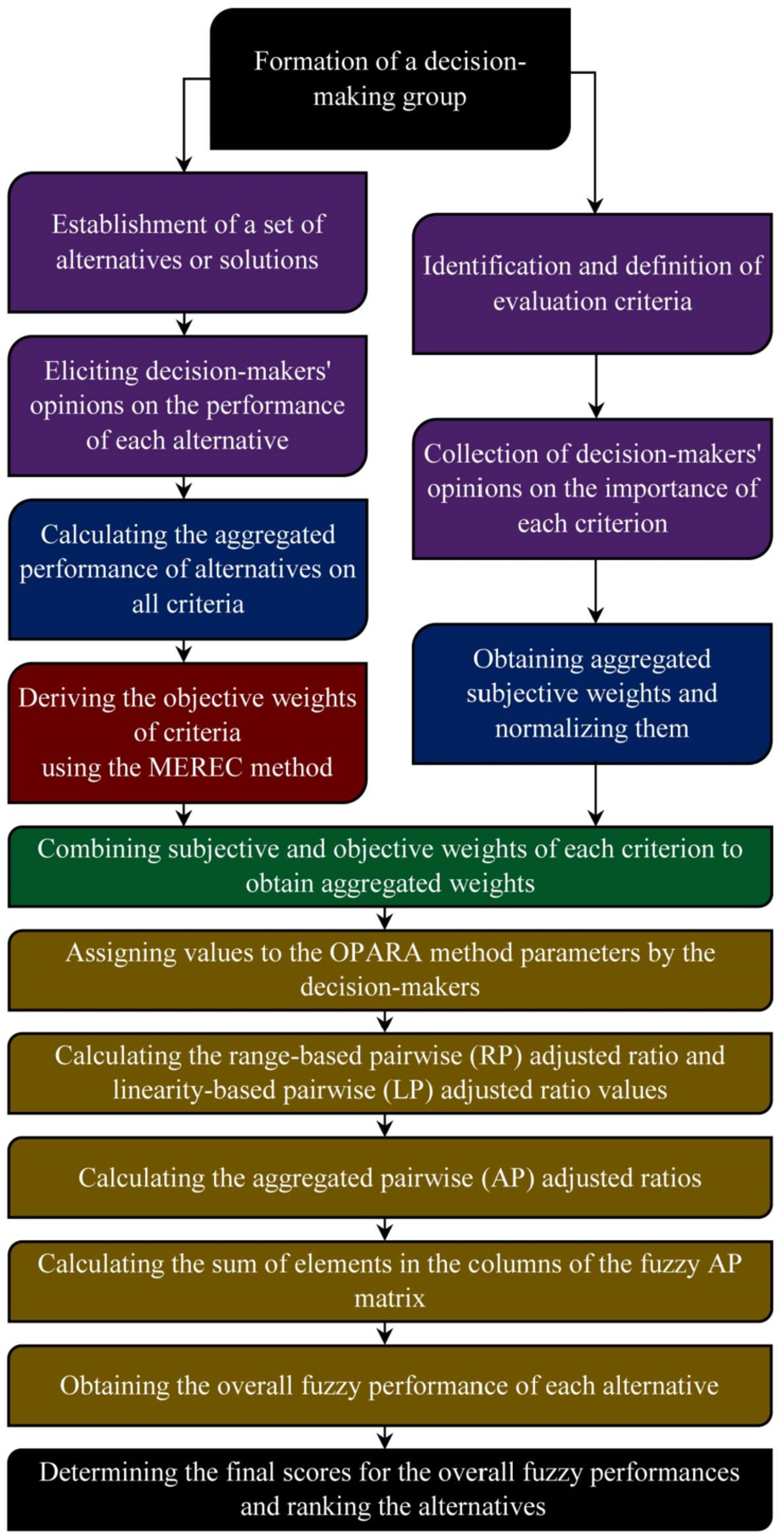
Fig. 1
The procedure of the proposed approach.
Step 3. Establishment of a set of alternatives or solutions by the decision-making group. In this step, the decision-making group establishes a set of potential n alternatives or solutions to be evaluated. These alternatives should represent feasible options that address the objectives of the decision-making process.
Step 4. Collection of decision-makers’ opinions on the importance of each criterion. In this step, the opinions of the decision-makers regarding the importance of each criterion are gathered. These opinions can be expressed using linguistic variables, such that ${\tilde{w}_{jr}^{s}}$ represents the importance of the j-th criterion as expressed by the r-th decision-maker.
Step 5. Obtaining aggregated subjective weights based on the corresponding fuzzy values of the linguistic variables and normalizing them. In this step, the aggregated subjective weights (
${\tilde{w}_{j}^{s}}$) are obtained based on the corresponding fuzzy values, and then normalized (
${\tilde{w}_{j}^{sn}}$) using the following equations, ensuring that the sum of the weights is approximately equal to 1.
Step 6. Eliciting decision-makers’ opinions on the performance of each alternative on each criterion. In this step, the opinions of the decision-makers regarding the performance of each alternative on each criterion are gathered. ${\tilde{x}_{ijr}}$ in this step represents the performance of i-th alternative on j-th criterion as expressed by r-th decision-maker.
Step 7. Calculating the aggregated performance of alternatives on all criteria. In this step, the aggregated performance values of each alternative on each criterion, i.e. the decision matrix elements, are derived. Based on the fuzzy operators and the corresponding fuzzy numbers, the performance values obtained from the decision-makers are aggregated using the following equation:
Step 8. Deriving the objective weights of criteria using the MEREC method. In this step, the objective fuzzy weights of each criterion are calculated using the decision matrix data and the MEREC weighting method. This process involves the following sub-steps to determine the objective weights systematically.
Step 8.1. Decomposing the fuzzy decision matrix elements into their components. If the elements of the decision matrix are defined as trapezoidal fuzzy numbers, represented as ${\tilde{x}_{ij}}=({x_{ij}^{a}},{x_{ij}^{b}},{x_{ij}^{c}},{x_{ij}^{d}}$), then four crisp matrices are derived from the fuzzy decision matrix as follows: ${X_{1}}={[{x_{ij}^{a}}]_{n\times m}}$, ${X_{2}}={[{x_{ij}^{b}}]_{n\times m}}$, ${X_{3}}={[{x_{ij}^{c}}]_{n\times m}}$ and ${X_{4}}={[{x_{ij}^{d}}]_{n\times m}}$.
Step 8.2. Calculating the weights of criteria using the MEREC method for each individual matrix. In this step, the weights of the criteria are calculated for each crisp matrix derived in Step 8.1 using the MEREC method. If the weights obtained for the matrices
${X_{1}}$ to
${X_{4}}$ are denoted as
${w_{j1}^{u}}$,
${w_{j2}^{u}}$,
${w_{j3}^{u}}$, and
${w_{j4}^{u}}$, respectively, then the elements of fuzzy objective weights
${\tilde{w}_{j}^{o}}=({w_{j1}^{o}},{w_{j2}^{o}},{w_{j3}^{o}},{w_{j4}^{o}})$ are determined as follows:
In fact,
${w_{j1}^{o}}$ to
${w_{j4}^{o}}$ represent the sorted values of
${w_{j1}^{u}}$ to
${w_{j4}^{u}}$.
Step 9. Combining subjective and objective weights of each criterion to obtain final weights. In this step, subjective and objective weights calculated in the previous steps are combined using
θ parameter, as shown in the following equation, where
θ is a parameter within the range
$[0,1]$. This process results in more realistic and accurate weights for the evaluation process.
Step 10. Assigning values to the OPARA method parameters by the decision-makers. To implement the OPARA method, its four parameters (α, β, ${\tau _{j}}$ and ω) must be assigned specific values by the decision-makers, based on the characteristics of the decision-making problem and its associated data.
Step 11. Calculating the range-based pairwise (
$\textit{RP}$) adjusted ratio and linearity-based pairwise (
$\textit{LP}$) adjusted ratio values for
k-th alternative over
l-th alternative. These values are derived based on the specified parameters and the aggregated data from the previous steps using the following equations.
where
Eq. (
28) transforms the fuzzy elements equal to zero in the decision matrix into values greater than zero, ensuring the proper execution of fuzzy division in Eqs. (
25) and (
26). In fact, a transformed matrix is used to calculate the
$\widetilde{\textit{RP}}$ and
$\widetilde{\textit{LP}}$ values. If
$k=l$, then it is assumed that
${\widetilde{\textit{RP}}_{kl}}={\widetilde{\textit{LP}}_{kl}}=(1,1,1,1)$.
It should be noted that in Eqs. (
25) and (
26)
B shows the set of beneficial criteria and
N denotes the set of non-beneficial criteria.
Step 12. Calculating the aggregated pairwise (
$\textit{AP}$) adjusted ratios. Using the following equation and the parameter
ω, the
$\widetilde{\textit{RP}}$ and
$\widetilde{\textit{LP}}$ values are aggregated to obtain the
$\widetilde{\textit{AP}}$ values.
Step 13. Calculating the sum of elements in the columns of the fuzzy
$\textit{AP}$ matrix. In this step, the sum of the elements in each column of the fuzzy
$\textit{AP}$ matrix is calculated.
Step 14. Obtaining the overall fuzzy performance of each alternative. In this step, the overall fuzzy performance of each alternative is determined based on the values of aggregated pairwise adjusted ratios calculated in the previous steps.
Step 15. Determining the final scores for the overall fuzzy performances and ranking the alternatives. In this step, the crisp scores corresponding to the fuzzy performances are calculated using the RPR approach described in previous sections. Based on the obtained scores, the final ranking of the alternatives is determined, such that higher scores correspond to higher ranks for the alternatives.
4 Results and Discussion
In this section, the results of applying the proposed approach to evaluate solutions for achieving sustainable agriculture are first presented. Subsequently, a sensitivity analysis and a comparison of the results with other methods are conducted. Finally, a detailed discussion is provided.
4.1 Application of the Proposed Approach
This study explores the assessment of solutions to promote sustainable agricultural practices using a novel integrated multi-criteria group decision-making approach based on fuzzy OPARA. In this section, the proposed approach is demonstrated through its application to a case study involving one of Iran’s most agriculturally significant regions, known for its diverse production of crops and its potential for advancing sustainable agricultural solutions. Golestan’s rich diversity in crop and fruit production has established it as a key agricultural hub, with significant potential for the expansion of agro-industries and food processing sectors. These characteristics make the province an exemplary case for evaluating sustainable agricultural practices tailored to regional needs.
To conduct this research, 30 experts were invited to contribute to the study. Of these, 24 experts agreed to participate, comprising 13 practitioners actively engaged in agriculture and 11 academic specialists in the field. Their expertise played a pivotal role in providing a comprehensive perspective on the problem and validating the criteria and solutions under consideration (Step 1).
The criteria and alternatives were defined through a combination of expert opinions and insights drawn from the literature. Specifically, the study by Cao and Solangi (
2023) served as a foundational reference for the experts in this process. This collaborative process led to the establishment of a decision-making structure that reflects the region’s specific challenges and opportunities (Steps 2 and 3), with 10 criteria (
${C_{1}}$ to
${C_{10}}$) categorized into economic, social, and environmental dimensions, along with 8 solutions (
${\textit{SL}_{1}}$ to
${\textit{SL}_{8}}$) defined by the experts, as detailed in Tables
2 and
3.
Table 2
Assessment criteria for sustainable agriculture solutions.
| Dimension |
Criteria |
Description |
| Economic |
Financial incentives and access to credit (${C_{1}}$) |
The availability of financial incentives and access to credit plays a crucial role in promoting the adoption of sustainable agricultural practices. When farmers are encouraged through financial support, they are more likely to invest in innovative technologies, premium materials, and necessary training to enhance sustainability. |
|
Market dynamics (${C_{2}}$) |
The market dynamics for sustainable agricultural products are influenced by various factors. While sustainable goods may have elevated production costs leading to higher retail prices, this reflects the value of quality and eco-friendly practices. |
|
Technological aspects (${C_{3}}$) |
The role of technology is vital for advancing sustainable agriculture, as innovation plays a key part in enhancing productivity and efficiency. Modern technologies, such as precision farming, smart irrigation systems, and eco-friendly pest control methods, enable farmers to optimize resource use and minimize environmental impact. |
|
Focus on immediate economic returns (${C_{4}}$) |
A focus on immediate economic returns is often seen in farming and agriculture. While prioritizing short-term profits may ensure quick financial stability, it can also lead to hesitation in adopting sustainable techniques that promise long-term benefits. |
| Social |
Awareness and education (${C_{5}}$) |
The presence of awareness and education is crucial for promoting sustainable agriculture. When farmers and community members are informed about the importance of sustainable practices, they are better equipped to understand their role in achieving sustainable development. |
|
Cultural factors (${C_{6}}$) |
Cultural factors play a significant role in shaping attitudes toward sustainable agriculture, influencing how farming practices are accepted and adopted within a community. Traditional farming methods often hold deep roots in cultural identity, which can make the transition to innovative techniques challenging. |
|
Social networks (${C_{7}}$) |
Effective collaboration is essential for promoting sustainable agriculture, as it enables farmers, researchers, and other stakeholders to share knowledge and resources. While social networks can enhance these interactions, their presence may vary significantly across different regions. |
| Environmental |
Health of land and soil (${C_{8}}$) |
The health of land and soil is crucial for sustainable agriculture, as degradation and erosion can significantly impact productivity and ecosystem balance. Unsustainable practices, such as cultivating a single crop type and excessive pesticide application, can lead to the deterioration of soil quality over time. |
|
Availability and quality of water (${C_{9}}$) |
The availability and quality of water are vital components of sustainable agriculture, as challenges such as water scarcity and contamination can hinder agricultural productivity and environmental health. Practices that lead to excessive extraction of groundwater or the introduction of pollutants can compromise water resources over time. |
|
Climate change (${C_{10}}$) |
The effects of climate change present challenges for sustainable agriculture. Shifts in weather patterns, including extreme events such as droughts and floods, can impact crop health and soil integrity. Additionally, changing climatic conditions may influence growing seasons and temperature ranges, which can have implications for crop yield and quality. |
Table 3
Identified solutions for achieving sustainable agriculture.
| Solution |
Description |
| Financial and credit support (${\textit{SL}_{1}}$) |
It provides farmers with the necessary resources to invest in sustainable practices and technologies. By facilitating access to loans, grants, and financial incentives, this support enables agricultural stakeholders to adopt eco-friendly methods, enhance productivity, and improve resource management. |
| Education and enhancement of farmers’ knowledge (${\textit{SL}_{2}}$) |
It equips farmers with the necessary skills and information to implement best practices. By providing training on sustainable farming techniques, soil conservation, water management, and pest control, farmers can make informed decisions that benefit both their productivity and the environment. |
| Improvement of sustainable agricultural policies and regulations (${\textit{SL}_{3}}$) |
By creating policies that promote sustainable land use, water management, and soil health, governments can guide farmers towards adopting practices that reduce environmental impact while enhancing productivity. |
| Enhancement of research and development (${\textit{SL}_{4}}$) |
It fosters innovation and the adoption of new technologies that improve agricultural practices. By investing in R&D, stakeholders can explore alternative farming methods, develop climate-resilient crops, and enhance soil and water conservation techniques. |
| Access to modern technologies (${\textit{SL}_{5}}$) |
It enables farmers to adopt innovative practices that enhance productivity and resource efficiency. By providing access to advanced technologies such as precision agriculture tools, sustainable pest management systems, and efficient irrigation methods, farmers can optimize their operations and reduce environmental impacts. |
| Encouragement of diverse and alternative cropping practices (${\textit{SL}_{6}}$) |
It enhances biodiversity and resilience within farming systems. Promoting the cultivation of a variety of crops can improve soil health, reduce pest and disease pressures, and enhance overall ecosystem stability. |
| Access to and encouragement of the use of organic fertilizers and biological pesticides (${\textit{SL}_{7}}$) |
It reduces reliance on synthetic chemicals and promotes ecological balance. By providing farmers with access to organic fertilizers, such as compost and green manure, soil fertility can be enhanced naturally, improving nutrient availability and supporting healthy crop growth. |
| Improvement of marketing and strengthening local markets (${\textit{SL}_{8}}$) |
It enhances farmers’ economic resilience and supports local economies. By developing efficient marketing strategies and providing farmers with the tools and knowledge to effectively promote their products, access to markets can be significantly improved. |
Experts’ opinions were systematically gathered using linguistic variables defined in Table
4. To evaluate the importance of the criteria, experts rated them using linguistic variables ranging from “very low” to “very high” (Step 4). Similarly, the effectiveness of each proposed solution in relation to each criterion was evaluated using linguistic variables ranging from “very poor” to “very good” (Step 6). Due to space limitations, only the responses of the first expert are presented as an example in Table
5, while the complete dataset is provided as supplementary material in reference (Keshavarz-Ghorabaee,
2025). These assessments are instrumental in quantifying the relative significance and impact of the criteria and solutions within the decision-making framework.
Table 4
Linguistic variables and the corresponding fuzzy numbers.
| Linguistic variables for criteria |
Linguistic variables for solutions |
| Very Low (VL) = $(0,0,0.1,0.2)$
|
Very Poor (VP) = $(0,0,1,2)$
|
| Low (L) = $(0.1,0.2,0.2,0.3)$
|
Poor (P) = $(1,2,2,3)$
|
| Medium Low (ML) = $(0.2,0.3,0.4,0.5)$
|
Medium Poor (MP) = $(2,3,4,5)$
|
| Medium (M) = $(0.4,0.5,0.5,0.6)$
|
Fair (F) = $(4,5,5,6)$
|
| Medium High (MH) = $(0.5,0.6,0.7,0.8)$
|
Medium Good (MG) = $(5,6,7,8)$
|
Table 5
Expert assessments using linguistic variables (sample data).
|
${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
${C_{5}}$ |
${C_{6}}$ |
${C_{7}}$ |
${C_{8}}$ |
${C_{9}}$ |
${C_{10}}$ |
| Weight |
H |
L |
MH |
MH |
MH |
ML |
ML |
ML |
M |
ML |
| ${\textit{SL}_{1}}$ |
VG |
G |
G |
G |
MP |
MP |
F |
MP |
MP |
MP |
| ${\textit{SL}_{2}}$ |
MP |
MP |
F |
F |
MG |
MG |
F |
MG |
MG |
VP |
| ${\textit{SL}_{3}}$ |
F |
P |
P |
F |
P |
MP |
MG |
F |
MP |
MP |
| ${\textit{SL}_{4}}$ |
VP |
P |
F |
P |
MG |
P |
MP |
MG |
G |
F |
| ${\textit{SL}_{5}}$ |
MP |
P |
G |
P |
P |
P |
MP |
F |
F |
MP |
| ${\textit{SL}_{6}}$ |
MP |
MP |
MP |
F |
P |
P |
MP |
G |
F |
MG |
| ${\textit{SL}_{7}}$ |
P |
MP |
P |
MP |
P |
MP |
MP |
F |
MG |
MP |
| ${\textit{SL}_{8}}$ |
F |
VG |
MP |
F |
VP |
MP |
F |
MP |
P |
VP |
As previously mentioned, the aggregated subjective weights of the criteria (Step 5) are obtained based on the opinions gathered from experts and the corresponding fuzzy numbers associated with linguistic variables. Additionally, the aggregated performance and effectiveness of the alternatives or solutions (Step 7) are calculated. Following this, the objective weights of the criteria are determined using the decision matrix and the MEREC method (Step 8). By integrating both subjective and objective weights, the final weights of the criteria for assessing the solutions are determined, where
θ is set to 0.5 (Step 9). A portion of the aggregated decision matrix is illustrated in Table
6, while Table
7 presents the subjective, objective, and combined weights of the criteria. The complete decision matrix is included as supplementary material in reference (Keshavarz-Ghorabaee,
2025). Using the
$\textit{RPR}$ approach, the values of the combined weights are ranked and presented in the last column of Table
7.
According to the results presented in Table
7, the criteria “Availability and quality of water” (
${C_{9}}$), “Focus on immediate economic returns” (
${C_{4}}$), and “Financial incentives and access to credit” (
${C_{1}}$) are the most important criteria based on the
$\textit{RPR}$ values of the combined weights.
Table 6
The aggregated fuzzy decision matrix (partial).
|
${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
$\dots \hspace{0.1667em}$ |
${C_{10}}$ |
| ${\textit{SL}_{1}}$ |
$(7.17,8.17,8.96,9.38)$ |
$(5,6,6.38,7.38)$ |
$(5.38,6.38,6.75,7.75)$ |
$\dots \hspace{0.1667em}$ |
$(2.46,3.46,4.04,5.04)$ |
| ${\textit{SL}_{2}}$ |
$(3.08,4.08,4.92,5.92)$ |
$(2.58,3.58,4.04,5.04)$ |
$(2.13,3.13,3.63,4.63)$ |
$\dots \hspace{0.1667em}$ |
$(1.33,2.25,2.75,3.75)$ |
| ${\textit{SL}_{3}}$ |
$(1.71,2.71,2.92,3.92)$ |
$(1.67,2.67,2.96,3.96)$ |
$(1.33,2.21,2.79,3.79)$ |
$\dots \hspace{0.1667em}$ |
$(3.33,4.33,4.92,5.92)$ |
| ${\textit{SL}_{4}}$ |
$(1.04,1.75,2.38,3.38)$ |
$(1.63,2.63,2.75,3.75)$ |
$(5.75,6.75,7.25,8.25)$ |
$\dots \hspace{0.1667em}$ |
$(4.04,5.04,5.33,6.33)$ |
| ${\textit{SL}_{5}}$ |
$(0.96,1.5,2.38,3.38)$ |
$(0.88,1.42,2.21,3.21)$ |
$(7.29,8.29,9.08,9.46)$ |
$\dots \hspace{0.1667em}$ |
$(2.33,3.33,4.04,5.04)$ |
| ${\textit{SL}_{6}}$ |
$(1.17,1.96,2.54,3.54)$ |
$(2.63,3.63,4.25,5.25)$ |
$(2.04,3.04,3.33,4.33)$ |
$\dots \hspace{0.1667em}$ |
$(3.25,4.25,5,6)$ |
| ${\textit{SL}_{7}}$ |
$(1.25,2.13,2.63,3.63)$ |
$(1.21,2,2.63,3.63)$ |
$(1.04,1.79,2.33,3.33)$ |
$\dots \hspace{0.1667em}$ |
$(1.92,2.92,3.33,4.33)$ |
| ${\textit{SL}_{8}}$ |
$(4.5,5.5,5.75,6.75)$ |
$(7.33,8.33,9.17,9.5)$ |
$(1.17,2,2.5,3.5)$ |
$\dots \hspace{0.1667em}$ |
$(0.75,1.25,2,3)$ |
Table 7
The subjective, objective and combined weights of criteria.
|
Subjective |
Objective |
Combined |
RPR |
Rank |
| ${C_{1}}$ |
$(0.153,0.173,0.187,0.193)$ |
$(0.073,0.073,0.083,0.096)$ |
$(0.113,0.123,0.135,0.145)$ |
0.684 |
3 |
| ${C_{2}}$ |
$(0.024,0.042,0.051,0.071)$ |
$(0.099,0.101,0.111,0.122)$ |
$(0.062,0.071,0.081,0.096)$ |
0.357 |
8 |
| ${C_{3}}$ |
$(0.078,0.098,0.108,0.128)$ |
$(0.1,0.101,0.104,0.105)$ |
$(0.089,0.099,0.106,0.116)$ |
0.516 |
6 |
| ${C_{4}}$ |
$(0.137,0.157,0.171,0.183)$ |
$(0.097,0.102,0.102,0.103)$ |
$(0.117,0.129,0.137,0.143)$ |
0.699 |
2 |
| ${C_{5}}$ |
$(0.109,0.129,0.138,0.158)$ |
$(0.074,0.08,0.085,0.087)$ |
$(0.092,0.105,0.112,0.123)$ |
0.549 |
4 |
| ${C_{6}}$ |
$(0.05,0.07,0.078,0.098)$ |
$(0.086,0.098,0.104,0.106)$ |
$(0.068,0.084,0.091,0.102)$ |
0.412 |
7 |
| ${C_{7}}$ |
$(0.033,0.053,0.062,0.082)$ |
$(0.042,0.047,0.062,0.065)$ |
$(0.038,0.05,0.062,0.073)$ |
0.218 |
10 |
| ${C_{8}}$ |
$(0.015,0.024,0.041,0.061)$ |
$(0.103,0.108,0.109,0.109)$ |
$(0.059,0.066,0.075,0.085)$ |
0.317 |
9 |
| ${C_{9}}$ |
$(0.101,0.121,0.127,0.147)$ |
$(0.142,0.145,0.146,0.147)$ |
$(0.122,0.133,0.136,0.147)$ |
0.718 |
1 |
| ${C_{10}}$ |
$(0.061,0.081,0.097,0.117)$ |
$(0.112,0.115,0.124,0.133)$ |
$(0.086,0.098,0.11,0.125)$ |
0.531 |
5 |
According to the experts’ opinions, the values of
$\alpha =5$,
$\beta =0.8$,
${\tau _{j}}$ = 1, and
$\omega =0.5$ are considered for the OPARA calculations. Based on equations 5 to 9 (Steps 11 and 12) of the proposed approach, the
$\widetilde{\textit{RP}}$,
$\widetilde{\textit{LP}}$, and
$\widetilde{\textit{AP}}$ values are calculated. Some of these values are displayed in Tables
8 to
10, and the detailed calculations are provided as supplementary material in reference (Keshavarz-Ghorabaee,
2025). Considering that the linguistic variables range from ‘very poor’ to ‘very good’, all criteria are treated as beneficial. This is because, when using these linguistic variables, the performance of the alternative is assessed independently of the inherent nature of the criterion.
Table 8
The values of $\widetilde{\textit{RP}}$ (partial).
|
${\textit{SL}_{1}}$ |
${\textit{SL}_{2}}$ |
${\textit{SL}_{3}}$ |
$\dots \hspace{0.1667em}$ |
${\textit{SL}_{8}}$ |
| ${\textit{SL}_{1}}$ |
$(1,1,1,1)$ |
$(0.62,1.02,1.38,2.32)$ |
$(0.74,1.26,1.69,2.99)$ |
$\dots \hspace{0.1667em}$ |
$(0.7,1.25,1.82,3.36)$ |
| ${\textit{SL}_{2}}$ |
$(0.52,0.89,1.2,2.02)$ |
$(1,1,1,1)$ |
$(0.66,1.17,1.62,2.93)$ |
$\dots \hspace{0.1667em}$ |
$(0.66,1.21,1.81,3.38)$ |
| ${\textit{SL}_{3}}$ |
$(0.39,0.71,0.97,1.73)$ |
$(0.41,0.75,1.06,1.94)$ |
$(1,1,1,1)$ |
$\dots \hspace{0.1667em}$ |
$(0.53,1.03,1.62,3.16)$ |
| ${\textit{SL}_{4}}$ |
$(0.51,0.87,1.15,1.98)$ |
$(0.52,0.89,1.21,2.15)$ |
$(0.58,1.05,1.44,2.65)$ |
$\dots \hspace{0.1667em}$ |
$(0.71,1.31,1.96,3.71)$ |
| ${\textit{SL}_{5}}$ |
$(0.43,0.75,1,1.75)$ |
$(0.46,0.79,1.11,1.97)$ |
$(0.5,0.9,1.28,2.36)$ |
$\dots \hspace{0.1667em}$ |
$(0.62,1.16,1.76,3.37)$ |
| ${\textit{SL}_{6}}$ |
$(0.47,0.82,1.08,1.89)$ |
$(0.5,0.87,1.19,2.11)$ |
$(0.53,0.97,1.32,2.45)$ |
$\dots \hspace{0.1667em}$ |
$(0.63,1.19,1.79,3.44)$ |
| ${\textit{SL}_{7}}$ |
$(0.42,0.75,1.02,1.8)$ |
$(0.42,0.75,1.06,1.9)$ |
$(0.48,0.9,1.28,2.4)$ |
$\dots \hspace{0.1667em}$ |
$(0.55,1.07,1.63,3.15)$ |
| ${\textit{SL}_{8}}$ |
$(0.35,0.62,0.87,1.53)$ |
$(0.41,0.71,1.01,1.79)$ |
$(0.51,0.92,1.3,2.43)$ |
$\dots \hspace{0.1667em}$ |
$(1,1,1,1)$ |
Table 9
The values of $\widetilde{\textit{LP}}$ (partial).
|
${\textit{SL}_{1}}$ |
${\textit{SL}_{2}}$ |
${\textit{SL}_{3}}$ |
$\dots \hspace{0.1667em}$ |
${\textit{SL}_{8}}$ |
| ${\textit{SL}_{1}}$ |
$(1,1,1,1)$ |
$(0.62,1.05,1.44,2.51)$ |
$(0.76,1.36,1.86,3.5)$ |
$\dots \hspace{0.1667em}$ |
$(0.7,1.3,1.91,3.65)$ |
| ${\textit{SL}_{2}}$ |
$(0.51,0.9,1.23,2.13)$ |
$(1,1,1,1)$ |
$(0.67,1.25,1.77,3.39)$ |
$\dots \hspace{0.1667em}$ |
$(0.66,1.26,1.91,3.7)$ |
| ${\textit{SL}_{3}}$ |
$(0.37,0.68,0.94,1.72)$ |
$(0.39,0.73,1.05,1.96)$ |
$(1,1,1,1)$ |
$\dots \hspace{0.1667em}$ |
$(0.5,1.01,1.62,3.26)$ |
| ${\textit{SL}_{4}}$ |
$(0.49,0.86,1.15,2.04)$ |
$(0.51,0.89,1.23,2.24)$ |
$(0.58,1.09,1.55,3.02)$ |
$\dots \hspace{0.1667em}$ |
$(0.71,1.35,2.05,4.03)$ |
| ${\textit{SL}_{5}}$ |
$(0.42,0.74,0.99,1.78)$ |
$(0.45,0.79,1.14,2.07)$ |
$(0.5,0.94,1.37,2.68)$ |
$\dots \hspace{0.1667em}$ |
$(0.63,1.21,1.85,3.65)$ |
| ${\textit{SL}_{6}}$ |
$(0.45,0.8,1.06,1.89)$ |
$(0.47,0.85,1.17,2.16)$ |
$(0.51,0.97,1.34,2.64)$ |
$\dots \hspace{0.1667em}$ |
$(0.61,1.18,1.79,3.55)$ |
| ${\textit{SL}_{7}}$ |
$(0.4,0.73,1,1.81)$ |
$(0.39,0.72,1.04,1.92)$ |
$(0.46,0.89,1.29,2.58)$ |
$\dots \hspace{0.1667em}$ |
$(0.53,1.05,1.63,3.26)$ |
| ${\textit{SL}_{8}}$ |
$(0.33,0.6,0.86,1.56)$ |
$(0.4,0.71,1.04,1.9)$ |
$(0.51,0.97,1.39,2.76)$ |
$\dots \hspace{0.1667em}$ |
$(1,1,1,1)$ |
Table 10
The values of $\widetilde{\textit{AP}}$ (partial).
|
${\textit{SL}_{1}}$ |
${\textit{SL}_{2}}$ |
${\textit{SL}_{3}}$ |
$\dots \hspace{0.1667em}$ |
${\textit{SL}_{8}}$ |
| ${\textit{SL}_{1}}$ |
$(1,1,1,1)$ |
$(0.62,1.03,1.41,2.42)$ |
$(0.75,1.31,1.78,3.25)$ |
$\dots \hspace{0.1667em}$ |
$(0.7,1.27,1.87,3.51)$ |
| ${\textit{SL}_{2}}$ |
$(0.52,0.89,1.21,2.08)$ |
$(1,1,1,1)$ |
$(0.66,1.21,1.7,3.16)$ |
$\dots \hspace{0.1667em}$ |
$(0.66,1.24,1.86,3.54)$ |
| ${\textit{SL}_{3}}$ |
$(0.38,0.69,0.95,1.72)$ |
$(0.4,0.74,1.06,1.95)$ |
$(1,1,1,1)$ |
$\dots \hspace{0.1667em}$ |
$(0.51,1.02,1.62,3.21)$ |
| ${\textit{SL}_{4}}$ |
$(0.5,0.86,1.15,2.01)$ |
$(0.51,0.89,1.22,2.19)$ |
$(0.58,1.07,1.49,2.83)$ |
$\dots \hspace{0.1667em}$ |
$(0.71,1.33,2.01,3.87)$ |
| ${\textit{SL}_{5}}$ |
$(0.43,0.74,1,1.77)$ |
$(0.45,0.79,1.12,2.02)$ |
$(0.5,0.92,1.32,2.52)$ |
$\dots \hspace{0.1667em}$ |
$(0.62,1.18,1.8,3.51)$ |
| ${\textit{SL}_{6}}$ |
$(0.46,0.81,1.07,1.89)$ |
$(0.49,0.86,1.18,2.14)$ |
$(0.52,0.97,1.33,2.55)$ |
$\dots \hspace{0.1667em}$ |
$(0.62,1.18,1.79,3.5)$ |
| ${\textit{SL}_{7}}$ |
$(0.41,0.74,1.01,1.8)$ |
$(0.41,0.74,1.05,1.91)$ |
$(0.47,0.9,1.28,2.49)$ |
$\dots \hspace{0.1667em}$ |
$(0.54,1.06,1.63,3.21)$ |
| ${\textit{SL}_{8}}$ |
$(0.34,0.61,0.87,1.55)$ |
$(0.4,0.71,1.02,1.85)$ |
$(0.51,0.95,1.34,2.6)$ |
$\dots \hspace{0.1667em}$ |
$(1,1,1,1)$ |
Based on the computed
$\textit{AP}$ values presented in Table
10, it is possible to calculate the
$\widetilde{\textit{SAP}}$ values, which represent the column sums of the
$\textit{AP}$ matrix, using Eq. (
30) for each column (Step 13). This calculation enables us to derive the overall fuzzy performance of each option, effectively representing the relative effectiveness of each solution (Step 14). The
$\widetilde{\textit{PF}}$ values for each alternative or solution are provided in Table
11. To facilitate a comparison of these fuzzy performances, the
$\textit{RPR}$ approach is employed in this study. This approach allows us to obtain the relative scores for each solution, thus providing a clearer understanding of their performance in relation to one another (Step 15). The final scores and ranking of the solutions are also presented in Table
11, illustrating the comparative effectiveness of each alternative or solution.
Based on the findings displayed in Table
11, “Financial and credit support” (
${\textit{SL}_{1}}$), “Education and enhancement of farmers’ knowledge” (
${\textit{SL}_{2}}$), and “Enhancement of research and development” (
${\textit{SL}_{4}}$) emerge as the top three solutions for achieving sustainable agriculture in the region under investigation, according to the expert opinions.
Table 11
The overall fuzzy performance and the final scores.
| Solutions |
${\widetilde{\textit{PF}}_{i}}$ |
${S_{i}}$ |
Rank |
| ${\textit{SL}_{1}}$ |
$(0.041,0.115,0.212,0.61)$ |
0.5463 |
1 |
| ${\textit{SL}_{2}}$ |
$(0.036,0.104,0.194,0.567)$ |
0.5261 |
2 |
| ${\textit{SL}_{3}}$ |
$(0.026,0.079,0.15,0.452)$ |
0.4757 |
8 |
| ${\textit{SL}_{4}}$ |
$(0.033,0.096,0.177,0.526)$ |
0.5083 |
3 |
| ${\textit{SL}_{5}}$ |
$(0.028,0.083,0.156,0.462)$ |
0.4816 |
7 |
| ${\textit{SL}_{6}}$ |
$(0.031,0.09,0.166,0.496)$ |
0.4955 |
4 |
| ${\textit{SL}_{7}}$ |
$(0.027,0.082,0.155,0.467)$ |
0.4821 |
6 |
| ${\textit{SL}_{8}}$ |
$(0.027,0.082,0.158,0.472)$ |
0.4844 |
5 |
4.2 Sensitivity Analysis and Comparison
In this study, sensitivity analysis is conducted to observe how the effectiveness of the solutions or alternatives varies with changes in the importance or weights of the criteria. This analysis serves to identify the robustness of the decision-making process and ensures that the final recommendations remain valid despite potential fluctuations in the relative importance assigned to each criterion.
To perform the sensitivity analysis, a specific pattern is utilized for adjusting the importance of the criteria. This pattern involves creating sets corresponding to the number of criteria, where each set allocates the highest weight to one criterion and the lowest weight to another. The remaining criteria receive weights that lie between the minimum and maximum assigned values. This structured approach allows decision-makers to understand the impact of increasing or decreasing the weights of the criteria with minimal computational effort, making the analysis more efficient and manageable.
The overall effectiveness or performance of each alternative or solution is computed for each weight set created. By systematically evaluating the performance under varying weights, the analysis provides valuable insights into which criteria significantly influence the outcomes and how robustly each solution performs across different scenarios. This insight is crucial for informed decision-making and helps ensure that the selected solutions are resilient to changes in the criteria weights.
The weighting pattern for each set is illustrated in Fig.
2, while the specific values assigned to each criterion are provided in Table
12. The effectiveness of each solution, or its overall performance obtained using the proposed approach in different sets of criteria weights, can be seen in Fig.
3. Moreover, Fig.
4 presents the changes in rankings of each solution in comparison to the other options, allowing for a clear understanding of how each alternative performs relative to the rest.
Table 12
The weights of the criteria in different sets.
|
${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
${C_{5}}$ |
${C_{6}}$ |
${C_{7}}$ |
${C_{8}}$ |
${C_{9}}$ |
${C_{10}}$ |
| Set 1 |
0.018 |
0.036 |
0.055 |
0.073 |
0.091 |
0.109 |
0.127 |
0.145 |
0.164 |
0.182 |
| Set 2 |
0.036 |
0.055 |
0.073 |
0.091 |
0.109 |
0.127 |
0.145 |
0.164 |
0.182 |
0.018 |
| Set 3 |
0.055 |
0.073 |
0.091 |
0.109 |
0.127 |
0.145 |
0.164 |
0.182 |
0.018 |
0.036 |
| Set 4 |
0.073 |
0.091 |
0.109 |
0.127 |
0.145 |
0.164 |
0.182 |
0.018 |
0.036 |
0.055 |
| Set 5 |
0.091 |
0.109 |
0.127 |
0.145 |
0.164 |
0.182 |
0.018 |
0.036 |
0.055 |
0.073 |
| Set 6 |
0.109 |
0.127 |
0.145 |
0.164 |
0.182 |
0.018 |
0.036 |
0.055 |
0.073 |
0.091 |
| Set 7 |
0.127 |
0.145 |
0.164 |
0.182 |
0.018 |
0.036 |
0.055 |
0.073 |
0.091 |
0.109 |
| Set 8 |
0.145 |
0.164 |
0.182 |
0.018 |
0.036 |
0.055 |
0.073 |
0.091 |
0.109 |
0.127 |
| Set 9 |
0.164 |
0.182 |
0.018 |
0.036 |
0.055 |
0.073 |
0.091 |
0.109 |
0.127 |
0.145 |
| Set 10 |
0.182 |
0.018 |
0.036 |
0.055 |
0.073 |
0.091 |
0.109 |
0.127 |
0.145 |
0.164 |
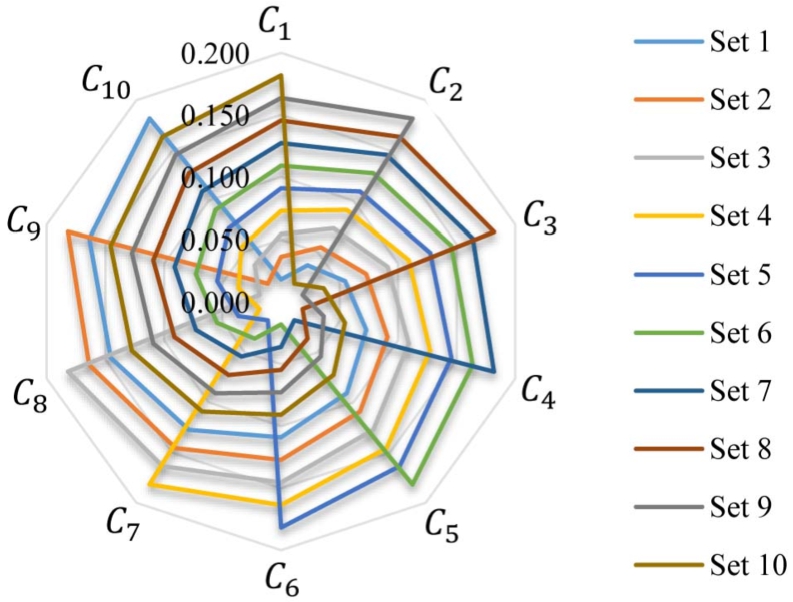
Fig. 2
Weighting pattern for each set.
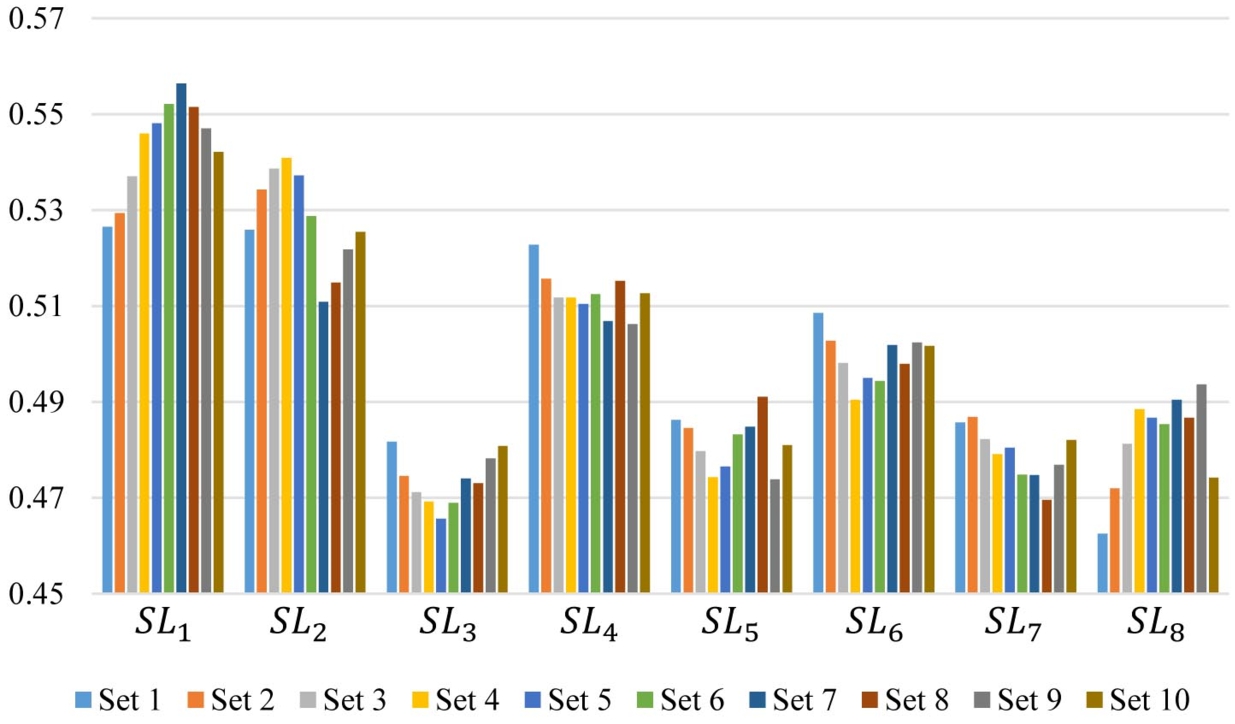
Fig. 3
Overall performance of solutions in different sets.
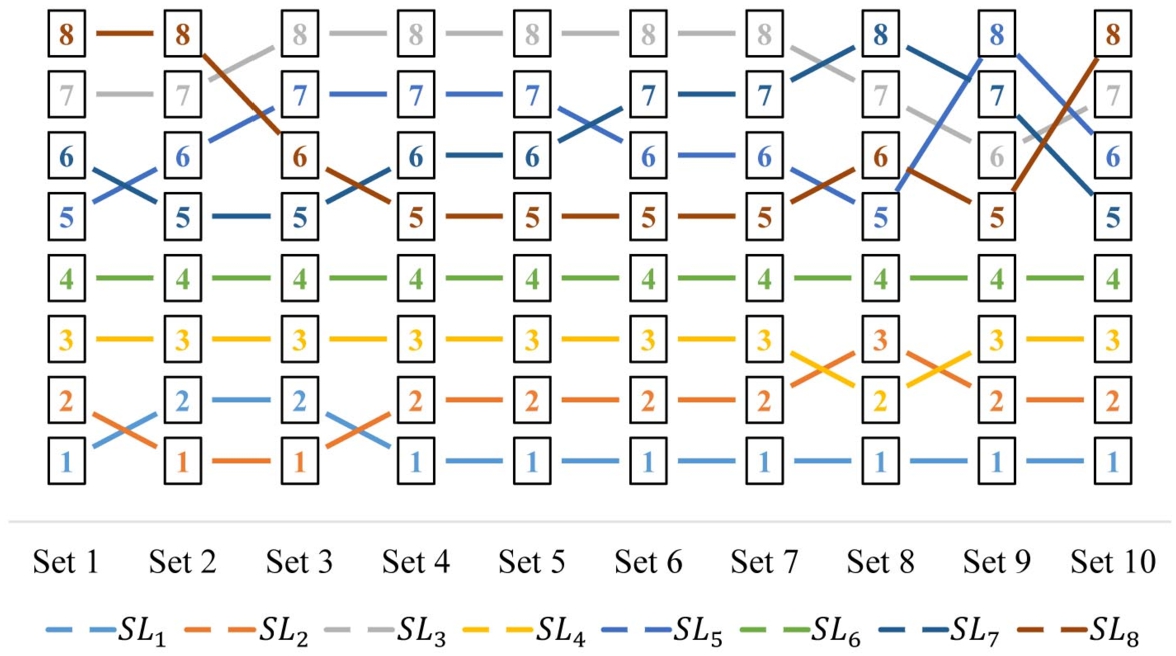
Fig. 4
Ranking variations of solutions across different weight sets.
The results of the sensitivity analysis indicate that there is relative stability in the ranking of the solutions as the weights of the criteria change. Specifically, the rankings for the three solutions “Financial and credit support” (${\textit{SL}_{1}}$), “Education and enhancement of farmers’ knowledge” (${\textit{SL}_{2}}$), and “Enhancement of research and development” (${\textit{SL}_{4}}$), as well as for “Encouragement of diverse and alternative cropping practices” (${\textit{SL}_{6}}$), exhibit the least variation. This suggests that the results obtained are robust and reliable, demonstrating the effectiveness of the proposed approach in evaluating the available solutions. The consistency observed in these rankings reinforces the notion that the selected solutions are resilient to changes in the criteria weights, thereby enhancing confidence in the decision-making process and the overall findings of the study.
To validate the results, the outcomes of the proposed approach were compared with those of six decision-making methods: SAW, WASPAS, COPRAS, TOPSIS, VIKOR, and EDAS. For this purpose, the decision matrix and the combined weights were defuzzified using Eq. (
9), and the defuzzified values were utilized for the analysis. Subsequently, the Spearman correlation coefficient (
${\rho _{s}}$) was calculated between the obtained results. The findings of this comparison are presented in Table
13. As shown, all correlation coefficients exceed 0.6, indicating a strong relationship between the results of the proposed approach and those of other methods (Walters,
2009). This demonstrates the validity of the outcomes achieved using the proposed approach.
Table 13
Comparison of the result with other MCDM methods.
|
SAW |
WASPAS |
COPRAS |
TOPSIS |
VIKOR |
EDAS |
Proposed approach |
| ${\textit{SL}_{1}}$ |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| ${\textit{SL}_{2}}$ |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
| ${\textit{SL}_{3}}$ |
7 |
7 |
8 |
8 |
5 |
8 |
8 |
| ${\textit{SL}_{4}}$ |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
| ${\textit{SL}_{5}}$ |
6 |
6 |
6 |
6 |
7 |
7 |
7 |
| ${\textit{SL}_{6}}$ |
4 |
4 |
4 |
5 |
4 |
4 |
4 |
| ${\textit{SL}_{7}}$ |
5 |
5 |
7 |
7 |
6 |
5 |
6 |
| ${\textit{SL}_{8}}$ |
8 |
8 |
5 |
4 |
8 |
6 |
5 |
| ${\rho _{s}}$ |
0.857 |
0.857 |
0.976 |
0.952 |
0.786 |
0.976 |
– |
4.3 Discussion of Findings
To achieve a more comprehensive and accurate evaluation, OPARA leverages the entire decision matrix, ensuring that no critical information is omitted. This comprehensive inclusion enhances the accuracy and depth of assessments, capturing nuances that might otherwise be overlooked. Furthermore, the method incorporates parameters that adjust evaluations based on the range of variation and the linearity of criteria, providing greater adaptability and precision in the decision-making process. Trapezoidal fuzzy numbers were employed to model uncertainty, offering significant flexibility in representing imprecise or vague data commonly encountered in agricultural evaluations. These fuzzy numbers, while effective, can be replaced with alternative fuzzy sets or similar mathematical tools based on the specific context and requirements of the evaluation. To facilitate the ranking of these fuzzy numbers, the study applied the RPR approach, which enables comparative rankings of fuzzy numbers as a cohesive group rather than in isolation. This relative ranking mechanism enhances the consistency and interpretability of results, making it a robust tool for decision-making.
A key feature of the proposed approach is its integration of subjective and objective weights to determine the relative importance of criteria. Subjective weights were derived from experts’ opinions, reflecting practical knowledge and domain-specific insights, while objective weights were calculated using data-driven methods, particularly the efficient MEREC technique. By combining these perspectives, the approach ensures realistic and balanced weight assignments, capturing both qualitative and quantitative dimensions of the evaluation process. The results of the combined weighting process underscore the critical importance of three key criteria: “Availability and quality of water” (${C_{9}}$), “Focus on immediate economic returns” (${C_{4}}$), and “Financial incentives and access to credit” (${C_{1}}$). The prominence of these criteria was further validated by expert assessments, which highlighted their pivotal role in enabling sustainable agriculture. Access to sufficient and high-quality water (${C_{9}}$) is fundamental for sustainable farming, as water serves as a primary input for crop production. Efficient water management not only enhances productivity but also mitigates resource depletion and environmental degradation. The criterion “Focus on immediate economic returns” (${C_{4}}$) emphasizes the need for tangible financial benefits to encourage farmers to adopt sustainable practices. Demonstrating short-term economic gains can foster wider acceptance of these practices, ensuring their integration into traditional farming systems. Finally, “Financial incentives and access to credit” (${C_{1}}$) provide farmers with the necessary resources to invest in modern technologies, sustainable inputs, and eco-friendly methods, bridging the financial gap that often hinders the transition to sustainable agriculture.
The evaluation of the eight proposed solutions further highlighted the critical role of targeted interventions in achieving sustainable agricultural practices. Among these, “Financial and credit support” (${\textit{SL}_{1}}$), “Education and enhancement of farmers’ knowledge” (${\textit{SL}_{2}}$), and “Enhancement of research and development” (${\textit{SL}_{4}}$) emerged as the top three solutions, with “Encouragement of diverse and alternative cropping practices” (${\textit{SL}_{6}}$) ranking closely behind. Each of these solutions addresses distinct yet interconnected dimensions of sustainable agriculture. Financial and credit support (${\textit{SL}_{1}}$) empowers farmers by enabling investments in advanced technologies, eco-friendly inputs, and modern equipment, all of which are essential for enhancing productivity and sustainability. Education and knowledge enhancement (${\textit{SL}_{2}}$) equip farmers with the skills and awareness needed to adopt innovative practices, bridging the gap between traditional methods and contemporary sustainable solutions. Similarly, research and development (${\textit{SL}_{4}}$) drive the creation of context-specific technologies and strategies, fostering resilience and adaptability in agricultural systems. Lastly, encouraging diverse and alternative cropping practices (${\textit{SL}_{6}}$) promotes biodiversity, improves soil health, and reduces the risks associated with monoculture, contributing to ecological stability and long-term productivity.
Variations in the criteria weights revealed that while changes in the final scores of the solutions were observed, the overall ranking of the solutions remained remarkably stable. This consistency was particularly evident among the top-ranked solutions, which retained their positions despite fluctuations in the weighting parameters. The stability of these results underscores the reliability and validity of the proposed decision-making approach, demonstrating its capacity to deliver dependable insights even under varying conditions.
Conclusion
This study developed a multi-criteria group decision-making approach based on the OPARA method in a fuzzy environment. The proposed method was applied to assess solutions aimed at achieving sustainable agriculture. By integrating subjective expert opinions with objective data, the proposed approach ensured a balanced and comprehensive assessment. The incorporation of fuzzy logic enhanced the robustness of the decision-making process, effectively addressing uncertainties inherent in evaluations. The findings highlighted the critical role of key criteria such as “Availability and quality of water”, “Focus on immediate economic returns”, and “Financial incentives and access to credit” in driving sustainable agricultural practices. Among the proposed solutions, “Financial and credit support”, “Education and enhancement of farmers’ knowledge”, and “Enhancement of research and development” were identified as the most effective interventions. Sensitivity analysis confirmed the stability and reliability of the rankings, demonstrating the robustness of the proposed approach even under varying weight conditions. For future research, further exploration of different fuzzy sets—such as Gaussian, type-2, intuitionistic, or Pythagorean fuzzy sets—could refine the representation of uncertainty. Additionally, integrating OPARA with other MCDM techniques, such as BWM (Best-Worst Method), CRITIC, or FUCOM (Full Consistency Method), may enhance decision-making efficiency. Another promising avenue is the application of the approach to diverse agricultural systems across different socio-economic and environmental contexts. Furthermore, future studies could conduct sensitivity analysis on key OPARA parameters, such as ρ and τ, to better understand their influence on ranking stability and decision outcomes. Extending the method beyond agriculture to domains such as environmental management, energy policy, and urban planning could further validate its versatility and applicability.

