Abstract
Most existing traffic trajectory recommendation methods don’t consider the driver-car-road preferences, resulting in the poor ability to meet the driver-car-road requirements. To address this issue, we propose a traffic Trajectory Recommendation scheme based on Edge-cloud computing Driver-car-road Preferences (named as TREDP). TREDP reduces the computational, storage, and energy burden on the edge through edge-cloud collaborative computing. TREDP enhances the recommended accuracy by considering driver-car-road requirements and the relationship among driver-car-road in different traffic trajectories. Meanwhile, TREDP increases the computational efficiency through edge-cloud computing. Thus, it improves the driver experience of intelligent traffic trajectory recommendation systems.
1 Introduction
The purpose of personalized recommendation is to recommend information and products that users are interested in according to their interests and purchasing behaviours (Guo
et al.,
2024; Kurnianto and Sfenrianto,
2024; bin Zulkiflee
et al.,
2024). Traffic trajectory recommendation is an important part of intelligent transportation (Li
et al.,
2023). It can be applied in many scenarios, including automatic driving (Cao
et al.,
2024), multi-task trajectory (Lei
et al.,
2025), automated parking (Dudakli and Baykasoğlu,
2024), path planning (Jian
et al.,
2024), travel trajectory (Deng
et al.,
2025), etc. The high-quality traffic trajectory recommendation system can provide drivers with fast, safe and personalized travel, which indirectly affects the urban environment (Kalaivani Jayaraman and Malarvizhi,
2024) and economic development (Jin and Choi,
2024) in smart cities. Therefore, more and more researchers pay attention to the research of traffic trajectory recommendation.
At present, the main content of traffic trajectory recommendation research includes how to save energy, reduce driving time (Xing and Hao,
2022), enhance safety, and even improve the profitability of commercial cars (Liu
et al.,
2024). The traffic trajectory recommendation model may be divided into three categories: traffic trajectory recommendation model for connected automated vehicles (Yang
et al.,
2021; Yao
et al.,
2024; Cheng
et al.,
2023; Zhang
et al.,
2023; Zhao
et al.,
2023; Jiang
et al.,
2024), traffic trajectory recommendation model based on multi-objective optimization (Ning
et al.,
2024; Xiao
et al.,
2024; Nishida
et al.,
2024; Li
et al.,
2024; Peng
et al.,
2024) and traffic trajectory recommendation model based on trajectory similarity (Qu
et al.,
2019; Lim
et al.,
2021; Yu
et al.,
2023; Liu
et al.,
2023; Lai
et al.,
2024). These models are proposed to improve various problems in daily traffic and enhance drivers’ satisfaction with the trajectory recommendation system.
However, the existing models cannot personalize traffic trajectory recommendations based on driver-car-road preferences. In fact, the preferences have a crucial impact on their traffic trajectories. Unexpected real-time factors from driver-car-road may make the driver dissatisfied with the current recommended trajectory. For example, a driver may suddenly feel ill and need to go to the nearest hospital, a sudden air leak on the tire may force the driver to go to the nearest repair shop, a road section may collapse suddenly, etc. However, existing recommendation models do not take these sudden driver-car-road situations into account.
Therefore, this paper proposes a traffic Trajectory Recommendation scheme based on Edge-cloud computing Driver-car-road Preferences (named as TREDP). TREDP improves the problems in a practical application of traffic trajectory recommendation systems by considering driver-car-road requirements and the relationship among driver-car-road in different traffic trajectories. Thus, it improves the driver experience of intelligent traffic trajectory recommendation systems. The calculation of TREDP can be divided into the following three categories. (1) TREDP considers the relationship among driver-car-road based on the traffic trajectory analysis on the cloud. (2) TREDP analyses driver-car-road requirements on the edge. (3) TREDP computes driver-car-road preferences based on edge-cloud collaborative computing. Through the above edge-cloud computing driver-car-road preferences, we could enhance recommended accuracy, reduce computational overhead and save traffic consumption (including fuel consumption, electricity consumption, driving time, etc). Meanwhile, via the edge-cloud collaborative computing, TREDP could achieve the real-time recommendation for providing drivers with better trajectory recommendation services.
Our contributions are summarized as follows.
-
• We design an edge-cloud computing traffic trajectory recommendation framework. The framework has two modules to support each other. The two modules provide drivers with timely and continuously updated traffic trajectory recommendation services through iterative analysis.
-
• We propose a lightweight computing method on the edge to reflect the driver-car-road real-time requirements for enhancing the recommended accuracy.
-
• We provide a traffic trajectory analytic method on the cloud for analysing the relationship among driver-car-road based on historical trajectory data.
-
• We construct a traffic trajectory recommendation scheme based on edge-cloud collaborative computing. Extensive experimental results show that our scheme significantly outperforms the existing methods with regard to the recommended accuracy and computational efficiency. The results further verify the validity of our framework.
The rest of this paper is organized as follows. Section
2 discusses related works. Section
3 designs our framework. Section
4 shows our scheme TREDP. Section
5 provides the experimental analysis and Section
6 concludes this paper.
2 Related Work
The current traffic trajectory recommendation models may be divided into the following three categories.
2.1 Traffic Trajectory Recommendation Model for Connected Automated Vehicles
For Connected Automated Vehicles (CAVs), the traffic trajectory recommendation model (Wang
et al.,
2019; Jaurker and Pradhan,
2023) tries to optimize CAV trajectories, while reducing the total travel time and CAV fuel consumption. Secondly, the model is iteratively optimized in order to use real-time data. The model takes traffic sensor data and CAV trajectory information as input based on a large number of traffic data flows. It aims to minimize the total travel time of the trajectory to obtain the expected velocity profile of CAV. Then, with the goal of reducing fuel consumption, the quadratic optimization is carried out to generate the optimal CAV trajectory conforming to the velocity profile.
Meanwhile, Yang
et al. (
2021) take advantage of advances in CAV technology to design an ecological driving and queuing system that could improve fuel efficiency and operational efficiency of cars on highways. Yao
et al. (
2024) present a full-sample trajectory reconstruction method for the mixed traffic flow of common cars and connected cars. Cheng
et al. (
2023) provide a deep reinforcement learning model for hybrid traffic flow control based on Adam optimization to guide the longitudinal trajectory of CAV on a typical urban road with signal-controlled intersections. Zhang
et al. (
2023) introduce CAVSim, which is a micro-traffic simulator that emphasizes feedforward decision-making, planning components and collaborative decision in the CAV environment. Zhao
et al. (
2023) propose a strategy that allows CAV to remain safe with respect to the car in front and behind. Jiang
et al. (
2024) design an optimal control strategy to coordinate the forced lane change of autonomous cars from the common lane to the special lane. Deng
et al. (
2025) constructs a trajectory reconstruction method that makes full use of CAV debris observation data.
2.2 Traffic Trajectory Recommendation Model Based on Multi-Objective Optimization
Traffic trajectory recommendation model based on multi-objective optimization could generally be divided into two modules. The first module is the function optimization module, which uses a multi-objective optimization function to optimize multiple objectives such as minimizing travel time, improving traffic safety and minimizing fuel consumption. It recommends driver trajectory through the ideal value of each target represented in the optimization function. The second module is the traffic track prediction module. This module realizes the prediction of future traffic state by analysing the recent traffic track condition, and timely feedback to the function optimization module to evaluate the future traffic track driving cost.
Ning
et al. (
2024) present a multi-objective optimization model for autonomous car traffic light intersections based on the near-end strategy optimization algorithm. Xiao
et al. (
2024) propose a sustainable and stable trajectory planning scheme for smart city public transportation based on multi-objective optimization. Nishida
et al. (
2024) design an improved version of Pareto Deep Q-Network (PDQN), which is a multi-objective deep reinforcement learning method for optimizing crowd trajectory guidance strategies, etc. Li
et al. (
2024) provide an improved non-dominated sorting genetic algorithm based on considering the travel intentions of drivers and passengers, which is a multi-objective optimization model with the goal of minimizing the loss of time for drivers and passengers. Peng
et al. (
2024) develop an improved constrained multi-objective evolutionary algorithm based on designing an improved genetic operator and repairing constraint processing technique to enhance the overall performance of the algorithm in seeking the Pareto optimal solution. Zhao
et al. (
2025) construct a multi-objective model for system optimization of dynamic traffic guidance.
2.3 Traffic Trajectory Recommendation Model Based on Trajectory Similarity
The core content of the traffic trajectory recommendation model based on trajectory similarity is how to sketch the driven trajectory, so as to recommend the high satisfaction trajectory to the driver. The model can collect massive traffic trajectory data mainly based on the online filtering sampling method and offline filtering sampling method. The online filtering sampling method is primarily aimed at the traffic trajectory data that can be collected in real-time, and these data often require rapid analysis. The online filtering sampling method mainly adopts intermittent sampling, which requires the acquisition device to record the data once every fixed period of time and record the data in the cache area. When the data in the cache area reaches a certain amount, the data would be calculated to get the average value of the trajectory data in the window.
The difficulty of this model lies in how to measure the driver’s satisfaction with a certain trajectory and how to measure the similarity between different trajectories. Measurement of satisfaction with a certain trajectory includes the measurement of a variety of driver concerns, including time cost, economic cost, convenience of driving and road conditions. It is necessary to find a reasonable measurement method to measure it and take them into comprehensive consideration. Similarity measurement between trajectories is also a difficulty in this model. Trajectory states are different in different time and space, and real-time changes in trajectory states may bring difficulties in algorithm complexity and trajectory complexity.
Qu
et al. (
2019) propose an adaptive shortest-range cruising trajectory method ASER for personalized traffic trajectory recommendation. In ASER, a probabilistic network model is established, which uses Kalman filter method to predict the picking probability and picking capacity of each position. It also considers the load balance between passengers and cars, and introduces the shortest expected cruising distance to calculate the potential cruising distance of cars. In addition, it utilizes MapReduce and KDS-Tree to improve recommendation efficiency. Lim
et al. (
2021) provide a hybrid trajectory planning method that combines the advantages of sampling and optimization. The sampling method of transverse motion is used to deal with different trajectories of various maneuvers. This helps generating response trajectories in dynamically changing environments. Yu
et al. (
2023) design a diverse sensory trajectory publication/subscription framework that performs query trajectory matching between continuous location set queries on the trajectory data stream. Liu
et al. (
2023) develop a spatiotemporal dependency and similarity perception method called dependency and similarity perception temporal graph convolutional network. Lai
et al. (
2024) solve the problem of insufficient labels by effectively using the knowledge from several existing measurement methods as the source measurement method.
All kinds of personalized recommendation models mentioned above do solve some problems encountered in real life. However, as ignoring driver-car-road preferences, the above models are difficult to carry out personalized recommendations flexibly and timely for drivers with different driver-car-road needs. Meanwhile, the lack of edge-cloud computing results in insufficient computing efficiency of these models when used in our framework.
3 Framework
Our edge-cloud computing traffic trajectory recommendation framework is shown in Fig.
1. The framework has two modules: the edge module and cloud module. The edge module has three submodules: data collection, driver-car-road requirements, and traffic trajectory recommendation. The cloud module also has three submodules: data preprocessing, analytic method, and traffic trajectory analysis.
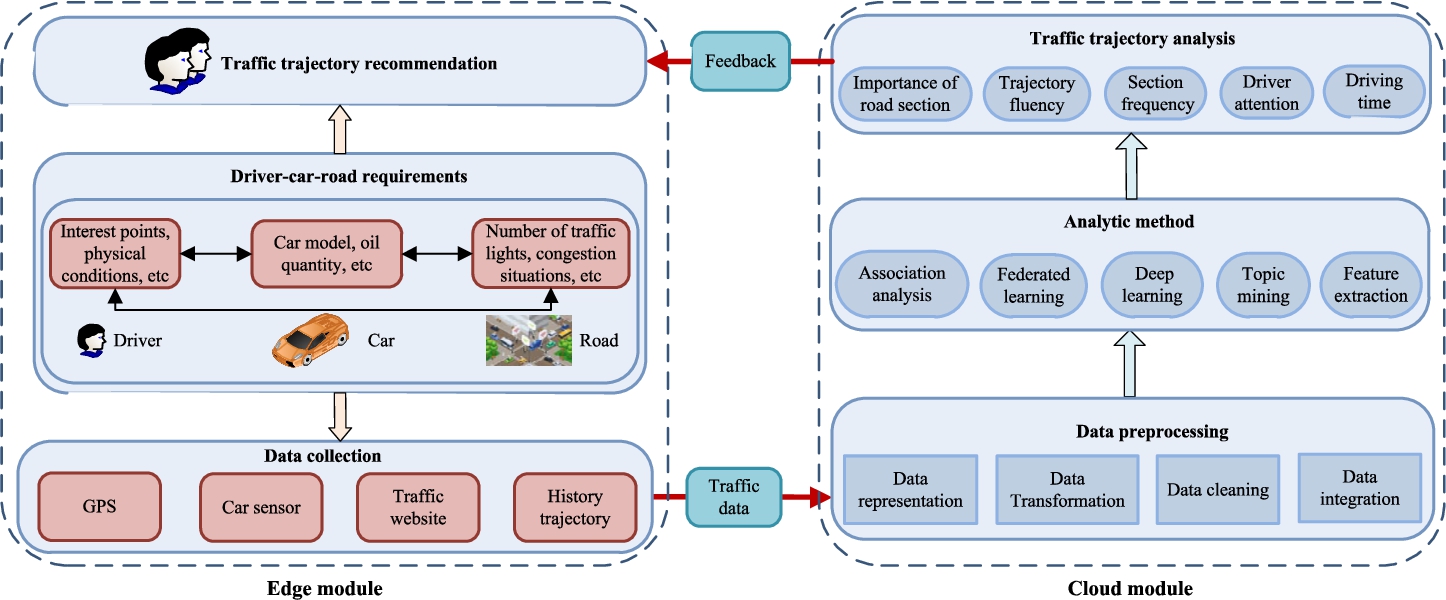
Fig. 1
Edge-cloud computing traffic trajectory recommendation framework.
First, driver-car-road in the driver-car-road requirements submodule generates massive traffic data for the data collection submodule. Meanwhile, the submodule also generates real-time driver-car-road requirements for the traffic trajectory recommendation submodule. Second, the data collection submodule collects the massive traffic data for the data preprocessing submodule based on GPS, car sensors, traffic websites, history trajectories, etc. Third, the traffic data is represented, transformed, cleaned and integrated by the data preprocessing submodule for the analytic method submodule. Fourth, based on suitable analytic methods, the traffic trajectory analysis submodule analyses historical trajectory data to find valuable knowledge such as the relationship among driver-car-road. When the traffic trajectory recommendation submodule receives the feedback analysed results, the submodule combines the edge-cloud analytic results to get the edge-cloud computing driver-car-road preferences. Fifth, the submodule recommends traffic trajectories to drivers based on the driver-car-road preferences. Finally, driver-car-road generates new traffic data based on the recommended results, and the new traffic data can provide the latest services via analysis. Through the above iterations, the framework could continuously improve service quality.
4 TREDP
The main symbols and corresponding explanations used for TREDP are given in Table
1.
Table 1
The main symbols for TREDP.
| Symbol |
Explanation |
| D |
a set of drivers in the system |
| d |
a driver in D
|
| T |
a set of historical trajectory data with the same beginning and ending point |
| S |
a set of road sections in T
|
| $|{T_{{s_{i}}}}|$ |
the total number of trajectories containing road section ${s_{i}}$ in T
|
| $|{t_{j}^{{s_{i}}}}|$ |
the total number of road sections included in trajectory ${t_{j}}$ that contains road section ${s_{i}}$
|
| $|T|$ |
the total number of trajectories in T
|
| ${C_{{s_{i}}}}$ |
the number of cars on road section ${s_{i}}$
|
| $|C|$ |
the total number of cars in T
|
| $|{d_{{s_{i}}}^{j}}|$ |
the number of times driver ${d^{j}}$ has passed through road section ${s_{i}}$
|
| $|{d_{S}^{j}}|$ |
the total number of times driver ${d^{j}}$ has passed through the road sections in S
|
| ${I_{{s_{i}}}^{{d^{j}}}}$ |
the average time for driver ${d^{j}}$’s car to pass through road section ${s_{i}}$
|
| ${r_{d}}$ |
driver d’s requirement |
| ${g_{d}^{{s_{i}}}}$ |
driver d’s requirement for road section ${s_{i}}$
|
| ${g_{{c_{d}}}^{{s_{i}}}}$ |
the requirements of d’s car for road section ${s_{i}}$
|
| ${g_{{s_{i}}}}$ |
the emergency of road section ${s_{i}}$
|
| $\max (f({b_{d}}))$ |
the maximum value of section preferences among all road sections closest to beginning point ${b_{d}}$
|
| $\max (\delta (T))$ |
the maximum value of trajectory references among all trajectories |
4.1 Sectioned Trajectory
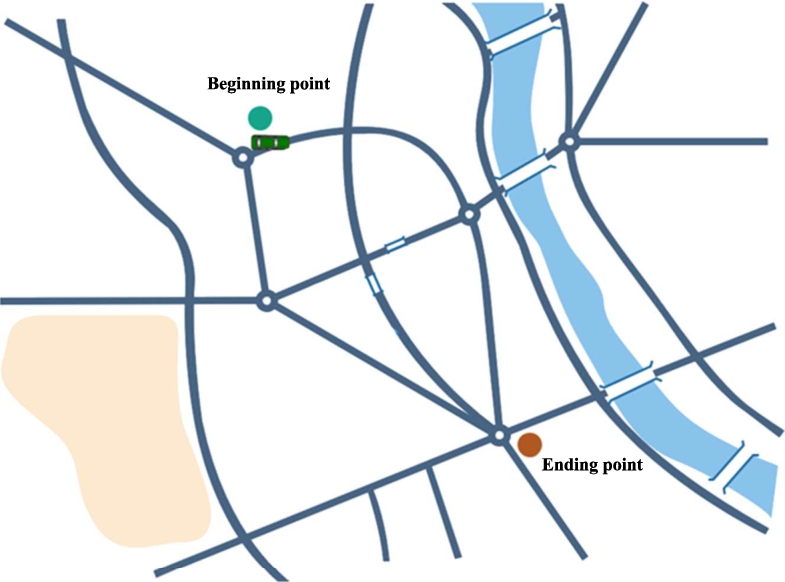
Fig. 2
A running example of traffic trajectories.
Figure
2 shows a running example of traffic trajectory. The definitions and formulas in this paper could be more easily understood by referring to this example.
Definition 1 (Sectioned trajectory).
Let T be a set of historical trajectory data with the same beginning and ending point, i.e. $T=\{{t_{1}},{t_{2}},\dots ,{t_{n}}\}$. Meanwhile, S denotes a set of road sections in T, i.e. $S=\{{s_{1}},{s_{2}},\dots ,{s_{n}}\}$. $\forall {t_{i}}\in T\wedge {s_{j}}\in S\wedge {s_{k}}\in S\wedge {s_{j}}\ne {s_{k}}$, ${t_{i}}=\{{s_{j}},\dots ,{s_{k}}\}$.
Corresponding to Fig.
2, the set of sectioned trajectories is shown in Fig.
3. For example,
${t_{1}}=\{{s_{1}},{s_{2}},{s_{7}}\}$ and
${t_{2}}=\{{s_{1}},{s_{3}},{s_{8}}\}$ denote two different trajectories, respectively.
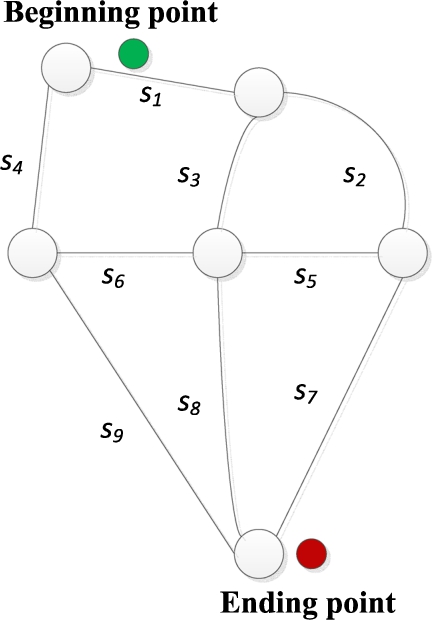
Fig. 3
Sectioned trajectories.
4.2 Traffic Trajectory Analysis on the Cloud
Definition 2 (Importance of road section).
If road section
${s_{i}}$ is included in multiple trajectories, it indicates that the importance of section
${s_{i}}$ for the distance from the beginning point to the ending point is relatively high. The recommended traffic trajectory for drivers may include
${s_{i}}$ as much as possible. We use Mean Specific Gravity (MSG) to record how important
${s_{i}}$ is to the distance. The calculation process of MSG is shown in equation (
1), where
$|{T_{{s_{i}}}}|$ denotes the total number of trajectories that contain road section
${s_{i}}$ in trajectory set
T and
$|{t_{j}^{{s_{i}}}}|$ denotes the total number of road sections included in trajectory
${t_{j}}$ that contains road section
${s_{i}}$.
Larger $|{T_{{s_{i}}}}|$ causes larger ${\textit{MSG}_{{s_{i}}}}$, indicating that road section ${s_{i}}$ is more important.
Definition 3 (Trajectory fluency).
As the traffic on the important road section may often be busy, simply relying on MSG to mine the traffic trajectory may ignore the impact of the trajectory fluency. For this reason, TREDP uses Inverse Document Frequency (IDF) to measure the trajectory fluency. The calculation process of IDF is shown in equation (
2), where
$|T|$ denotes the total number of trajectories in
T.
If there are fewer trajectories containing section ${s_{i}}$ (i.e. smaller $|{T_{{s_{i}}}}|$), then the ${\textit{IDF}_{{s_{i}}}}$ is larger, indicating that section ${s_{i}}$ has a better trajectory fluency. In other words, trajectories containing this section may provide smooth traffic.
Definition 4 (Section frequency).
Calculating the trajectory fluency alone is not enough, and it is also necessary to calculate the usage frequency of the road section itself. Thus, our Section FreQuency (SFQ) is calculated as equation (
3), where
${C_{{s_{i}}}}$ denotes the number of cars on section
${s_{i}}$ and
$|C|$ denotes the total number of cars in
T.
The smaller ${C_{{s_{i}}}}$ brings smaller ${\textit{SFQ}_{{s_{i}}}}$, which indicates that the usage frequency of section ${s_{i}}$ is lower. That is, the road section may be more smooth for a more possible recommendation.
Definition 5 (Driver attention).
Besides the above definitions, TREDP also considers the Driver Attention Degree (DAD) of road section
${s_{i}}$. To a certain extent, DAD measures the driver’s preference for section
${s_{i}}$. The calculation process of DAD is shown in equation (
4), where
$|{d_{{s_{i}}}^{j}}|$ denotes the number of times driver
${d^{j}}$ has passed through section
${s_{i}}$ and
$|{d_{S}^{j}}|$ denotes the total number of times driver
${d^{j}}$ has passed through the road sections in
S.
Larger $|{d_{{s_{i}}}^{j}}|$ indicates driver ${d^{j}}$ prefers road section ${s_{i}}$.
Definition 6 (Driving time).
Driving time is also important in traffic trajectory recommendations. Thus, the calculation process of Average Driving Time (ADT) on road section
${s_{i}}$ is shown in equation (
5), where
${I_{{s_{i}}}^{{d^{j}}}}$ denotes the average time for driver
${d^{j}}$’s car to pass through road section
${s_{i}}$.
Drivers certainly want less driving time. Therefore, the road section with less driving time is more likely to be recommended.
4.3 Driver-Car-Road Requirements on the Edge
The real-time and unexpected driver-car-road requirements are performed on the edge as follows.
Definition 7 (Driver requirement).
Driver d’s requirement ${r_{d}}=\langle {b_{d}},{e_{d}},{g_{d}}\rangle $, where ${b_{d}}$ denotes d’s beginning point, ${e_{d}}$ denotes d’s ending point and ${g_{d}}$ denotes d’s road section requirements, i.e. ${g_{d}}=\{{g_{d}^{{s_{i}}}},\dots ,{g_{d}^{{s_{j}}}}\}$. $\forall {g_{d}^{{s_{i}}}}\in {g_{d}}$, ${g_{d}^{{s_{i}}}}$ denotes driver d’s requirement for road section ${s_{i}}$.
For example, if driver d has already entered fatigued driving, they may need to stay and rest at a hotel on road section ${s_{i}}$. In this case, ${g_{d}^{{s_{i}}}}$ may be a larger value. Larger ${g_{d}^{{s_{i}}}}$ indicates the more urgent need of driver d for road section ${s_{i}}$.
Definition 8 (Car requirement).
${g_{{c_{d}}}}$ denotes the requirements of d’s car for road sections, i.e. ${g_{{c_{d}}}}=\{{g_{{c_{d}}}^{{s_{i}}}},\dots ,{g_{{c_{d}}}^{{s_{j}}}}\}$. $\forall {g_{{c_{d}}}^{{s_{i}}}}\in {g_{{c_{d}}}}$, ${g_{{c_{d}}}^{{s_{i}}}}$ denotes the requirements of d’s car for road section ${s_{i}}$.
For example, driver d’s car needs to be charged or refueled at the gas station on road section ${s_{i}}$. In this case, ${g_{{c_{d}}}^{{s_{i}}}}$ may be a larger value. Larger ${g_{{c_{d}}}^{{s_{i}}}}$ indicates the more urgent need of d’s car for road section ${s_{i}}$.
Definition 9 (Road emergency).
${g_{S}}$ denotes the road emergencies of road section set S, i.e. ${g_{S}}=\{{g_{{s_{i}}}},\dots ,{g_{{s_{j}}}}\}$. $\forall {g_{{s_{i}}}}\in {g_{S}}$, ${g_{{s_{i}}}}$ denotes the emergency of road section ${s_{i}}$.
For example, if an accident occurs on road section ${s_{i}}$, causing certain traffic congestion, ${g_{{s_{i}}}}$ is a relatively large value.
Definition 10 (Real-time unexpected factor).
The calculation on the cloud in Section
4.2 only includes the historical relationships among driver-car-road. However, drivers’ physical conditions, car operating conditions and road conditions are all constantly changing, so the cloud calculations lack the calculation of real-time unexpected factors (such as suddenly discovering that the car is out of battery, unstable vital signs of the owner during safety checks, and accidents on the road ahead). Therefore, our calculation method for Real-time Unexpected Factors (RUF) is shown in equation (
6).
Larger ${\textit{RUF}_{{s_{i}}}}$ indicates a more possible recommendation for road section ${s_{i}}$.
4.4 Edge-Cloud Computing
Definition 11 (Section preference).
Section preference refers to the importance of road section
${s_{i}}$ in trajectory set
T. Its calculation process is shown in equation (
7):
Larger $f({s_{i}})$ indicates that more drivers may prefer road section ${s_{i}}$. However, as more and more cars enter ${s_{i}}$, $f({s_{i}})$ would become smaller, resulting in fewer drivers choosing ${s_{i}}$. This is a game process that continuously updates recommendations through our framework.
Definition 12 (Trajectory preference).
According to driver-car-road preferences for different trajectories, TREDP finds out the trajectories with high driver satisfaction. The computing method of trajectory
${t_{j}}$’s preference is shown in equation (
8):
After getting the section preference and trajectory preference list according to equation (
7) and equation (
8) respectively, TREDP could recommend personalized traffic trajectories to drivers.
4.5 Algorithm
Algorithm
1 takes driver-car-road requirements (
${r_{d}},{g_{{c_{d}}}},{g_{S}}$), a set of historical trajectories
T and a set of drivers
D as input. Meanwhile, it takes a recommended trajectory
${T_{d}}$ for driver
d as output.
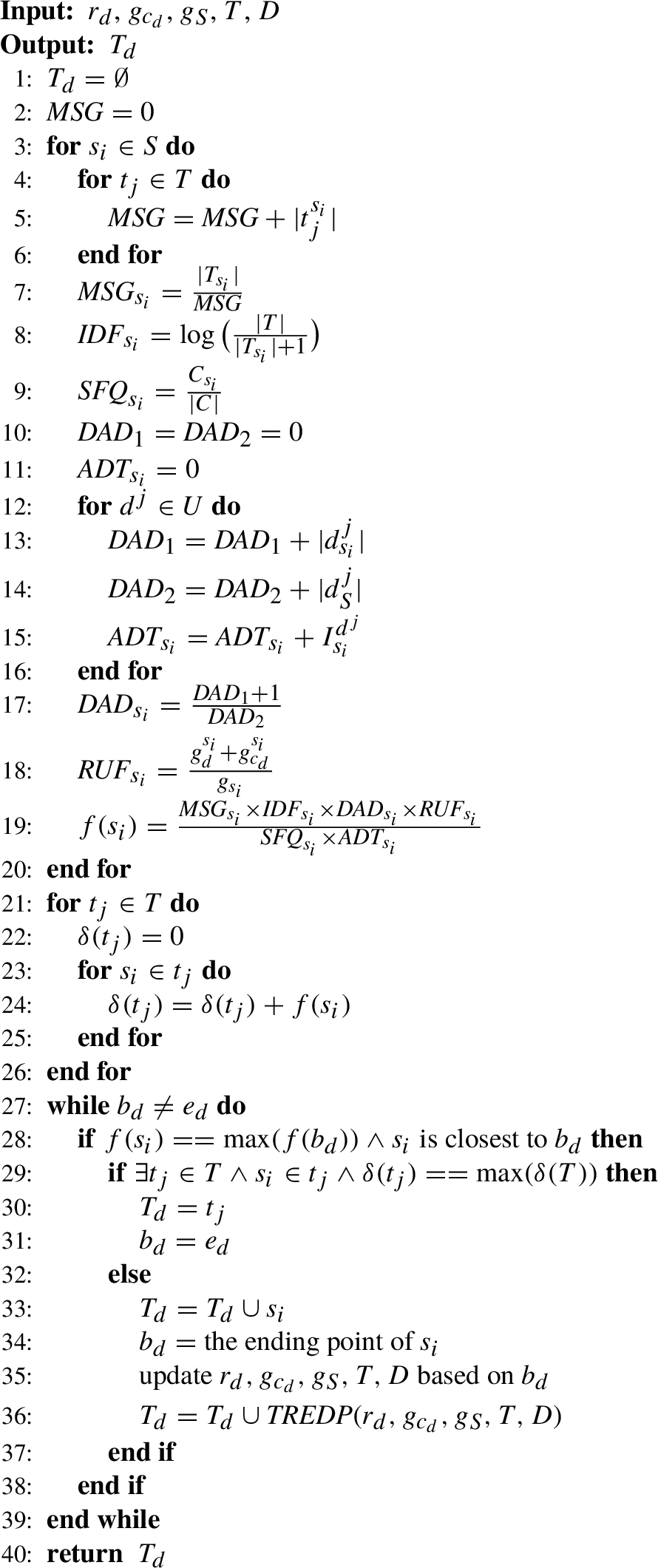
First, Algorithm
1 calculates the importance of road section
${s_{i}}$ as equation (
1) (Steps 2–7). Second, it generates the section preference of
${s_{i}}$ as equation (
7) (Steps 8–19). Third, it computes driver
d’s driver-car-road preferences for traffic trajectory
${t_{j}}$ (i.e.
$\delta ({t_{j}})$) (Steps 22–25). Fourth, if road section
${s_{i}}$ satisfies the following three conditions,
${t_{j}}$ is the best trajectory for driver
d (Steps 28–31). (1)
${s_{i}}$ is closest to beginning point
${b_{d}}$ (Step 28). (2) The section preference of
${s_{i}}$ is the maximum value among all road sections that are closest to
${b_{d}}$ (Step 28). (3) The trajectory preference of
${t_{j}}$ containing
${s_{i}}$ is the maximum value among all trajectories (Step 29). Otherwise, we could only recommend to driver
d one section (i.e.
${s_{i}}$) step by step by iteratively calling Algorithm
1 with new
${r_{d}},{g_{{c_{d}}}},{g_{S}},T$ and
D (Steps 32–37).
Actually, Algorithm
1 can serve a group of drivers with the same beginning/ending point at the same time. And it could be naturally extended for serving various drivers with random beginning/ending points. The scheme proposed in this paper has a high requirement for data updates, and only the preferred trajectories calculated according to the latest data could provide drivers with timely recommendation services. Therefore, our framework and scheme are integrated to provide drivers with intelligent transportation services. The continuous iteration of the framework could bring timely data updates to the scheme and real-time personalized services to the driver.
5 Experimental Analysis
5.1 Experimental Setup
We first establish our experiments from the following three aspects.
Dataset. The experimental dataset used in our experiments is the actual trajectory data of taxis in Shanghai, China during a certain period of time. This dataset uses GPS to record the longitude, dimension, direction, and passenger information of taxis at regular intervals. This dataset contains 4316 taxi drivers, each recording approximately 1800 records, totaling approximately 7.8 million records.
Experimental environment. Table
2 shows the experimental environment.
Compared method. ASER (Qu
et al.,
2019) is a traffic trajectory recommendation model based on trajectory similarity. As ASER is most relevant to our scheme, we compare our scheme TREDP with ASER in recommended accuracy and computational efficiency.
Table 2
Hardware parameters.
| Device |
Cloud |
Edge |
| Core frequency |
3.2 GHz |
2.2 GHz |
| RAM |
32 GB |
4 GB |
| Cores |
8 |
2 |
5.2 Recommended Accuracy
The dataset is divided into two parts in chronological order, with 70% of the older data used for data analysis and the remaining newer data used for verifying recommended accuracy. When the recommended trajectory is consistent with the actual trajectory, the recommendation is accurate. The calculation method is shown in equation (
9), where
T denotes a set of trajectories with the same beginning and ending point,
$\widetilde{T}$ denotes all trajectories with different beginning and ending points in the system,
${t_{{d_{i}}}^{A}}$ denotes the number of actual trajectories (based on the newer data) of driver
${d_{i}}$ in
T,
${t_{{d_{i}}}^{R}}$ denotes the number of the recommended trajectories (based on the older data) that are the same as the actual trajectories for driver
${d_{i}}$ in
T,
$|{D_{T}}|$ denotes the set of drivers in
T, and
$\textit{Average}\big({\textstyle\sum _{i=1}^{|{D_{T}}|}}\frac{{t_{{d_{i}}}^{R}}}{{t_{{d_{i}}}^{A}}}\big)$ represents the average recommended accuracy of trajectory
T.
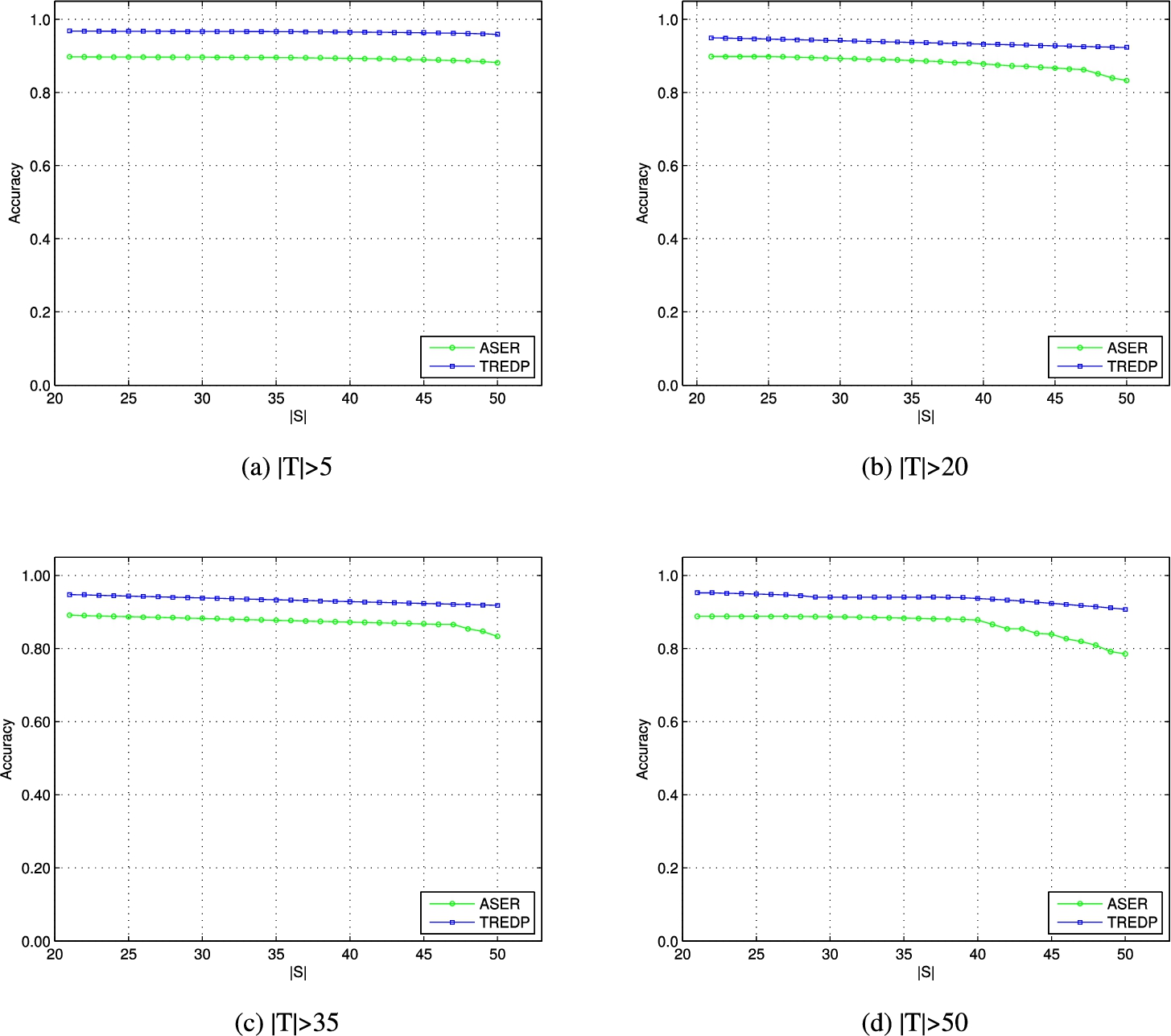
Fig. 4
Comparison of the recommended accuracy with the change of $|S|$ and $|T|$.
Experimental comparison results are shown in Fig.
4, where
$|S|$ denotes the number of road sections that need to be considered in personalized traffic trajectory recommendation.
As shown in Fig.
4, as more road sections
$|S|$ are considered by the personalized trajectory recommendation algorithm, the accuracy rate of trajectory recommendation is slightly decreasing. In addition, the preferred trajectories recommended by TREDP are mainly concentrated in the Top-30 part of the trajectory preference list. At the same time, when the number of
$|S|$ exceeds 25, TREDP has a 95% recommended accuracy. This proves the effectiveness of TREDP in intelligent traffic trajectory recommendation.
The number of road sections included in the trajectories gradually increases with the total number of trajectories
$|T|$ increases. This brings some challenges to TREDP and ASER, but they still maintain a good recommendation effect in Fig.
4. Moreover, TREDP has higher recommended accuracy than ASER method because it takes into account the driver-car-road preferences for numerous practical application requirements and scenarios.
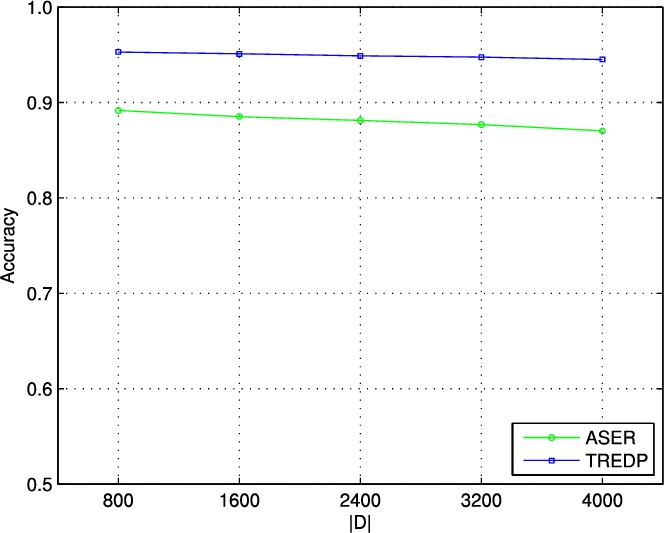
Fig. 5
Comparison of the recommended accuracy with the change of $|D|$.
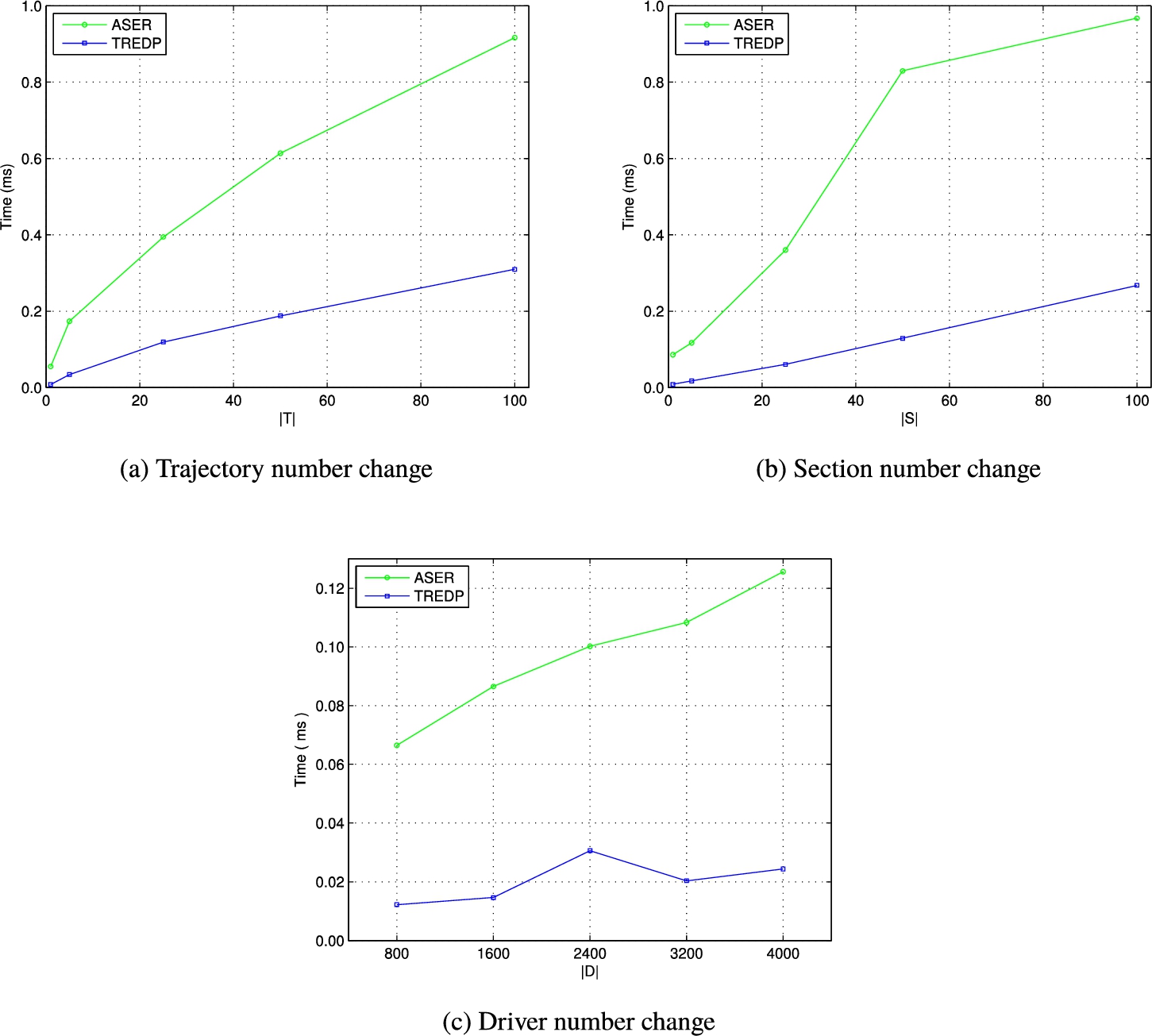
Fig. 6
Comparison of the computational efficiency with the change of $|T|$, $|S|$ and $|D|$.
Figure
5 shows the comparison of the recommended accuracy with the change of driver number
$|D|$. When the number of drivers increases, the recommended accuracy of both TREDP and ASER decreases. This is because as
$|D|$ increases, a large number of drivers may result in game playing and interference among them. For example, a traffic-free road section may become less traffic-free after being recommended to many drivers, and the probability of this road section being recommended may decrease. The interference makes it more difficult for TREDP and ASER to determine the driver’s preferred trajectory. Meanwhile, TREDP considers the real-time relationship among driver-car-road, thus TREDP has better recommended accuracy than ASER.
5.3 Computational Efficiency
Our computational overhead includes all computing and communication time for ASER and TREDP. The experimental results are shown in Fig.
6, where the X-axes denote
$|T|$,
$|S|$ and
$|D|$ respectively, and Y-axes denote running time whose unit is millisecond (ms).
All calculations of ASER are on the edge. TREDP combines the computing resources of both edge and cloud. Even TREDP consumes the communication cost of edge-cloud, it still significantly reduces the computational overhead based on edge-cloud computing. Therefore, our scheme TREDP consumes less time than ASER in Fig.
6. This shows that our scheme is more suitable for large-scale traffic data. Meanwhile, rapid analysis can provide drivers with trajectory recommendation services in a more timely manner.
6 Conclusion
The trajectory recommendation in intelligent transportation systems has broad application value. This paper first proposes an edge-cloud computing traffic trajectory recommendation framework to update data and iterate services. We then propose a traffic trajectory recommendation scheme based on edge-cloud computing driver-car-road preferences for improving driver satisfaction when using the system based on the framework. The data analysed by this scheme is divided into two types. The first type is historical trajectory data analysed by the cloud, and the other type considers driver-car-road real-time requirements analysed by the edge. By edge-cloud collaborative computing of these two types of data, we provide drivers with timely and accurate trajectory recommendation services. Extensive experiments validate the effectiveness of our scheme and framework. Especially when facing a sharp increase in data, our scheme still has stable, accurate and efficient recommendation performance.
In the future, we plan to extend the scheme to more application scenarios and plan to introduce tensor algebra to consider more high-dimensional information, in order to further improve recommended accuracy.

