1 Introduction
Fulfilling the nutritional needs of an expanding global population, projected to reach 10 billion by 2050, stands as a significant global concern (Worldometer:
https://www.worldometers.info/world-population/ “Accessed 5 Feb 2024”). Various factors such as the COVID-19 pandemic, conflicts, and erratic weather patterns due to climate change have hindered progress toward achieving the first Millennium Development Goal of eradicating extreme poverty and hunger (WHO, 2000. Millennium Development Goals (MDGs) [WWW Document]:
https://www.who.int/topics/millennium_development_goals/about/en/. Accessed 29 Nov 2000). The report from the State of Food Security and Nutrition in the World (SOFI) indicates that since 2019, an additional 122 million people have faced hunger, with the global hunger rate stabilizing between 2021 and 2022 but persistent crises in many regions prompting calls for international action to address underlying causes (Ewan Thomson. This is the state of food security in 2023:
https://www.weforum.org/agenda/2023/08/food-security-hunger-global/. Accessed 2 August 2023). Meeting the increased food demands necessitated by a nearly 30% population growth requires a potential 50% rise in global food production (Ivanovich
et al.,
2023). However, various challenges such as natural disasters, climate change, land degradation, rapid urbanization, unfair trade practices, and others have significantly impeded food production rates (Basumatary
et al.,
2023). According to forecasts by Kumar
et al. (
2023), even with endeavours aimed at enhancing crop yields and refining production methodologies, current trajectories indicate that the global food demand might not be satisfied by 2050. Climate change alone is projected to lead to the loss of up to 18% of arable land by the end of the century, exacerbating food insecurity in vulnerable regions (Qiu
et al.,
2023). These challenges underscore the growing need for innovative practices, systems, and methods in the food production industry.
As a practical response to food and environmental challenges, aquaponics farming is gaining increasing recognition as a means to rapidly boost food production without harming the environment. Aquaponics represents an eco-friendly and sustainable approach to food production, leveraging the principles of the circular economy and biological systems to maximize output while minimizing inputs and waste. It integrates two core production methods: aquaculture, focusing on aquatic animal breeding, primarily fish, and hydroponics, which involves growing plants without soil (refer to Fig.
1) (Baganz
et al.,
2022). Within an aquaponic system, waste from aquatic animals is converted into organic fertilizers through microbial processes, while hydroponic plants purify the water by absorbing nutrients, thus facilitating its recycling in the fish tank (Kushwaha
et al.,
2023). In essence, aquaponics functions as an ecosystem where fish, plants, and microbes coexist symbiotically, contributing to sustainable food production. To support crucial bacteria involved in nutrient cycling and maintain system integrity, aquaponic setups prohibit chemical additives and antibiotics, resulting in naturally healthy crops grown essentially organically (David
et al.,
2022). Due to its closed circular nature, aquaponics enhances labour efficiency and offers potential for sustainable output growth, thereby enhancing food security and agricultural profitability (Thakur
et al.,
2023). Compared to conventional farming, aquaponics requires less land and water, making it a viable solution for arid regions and contributing to economic development through its rapid production capabilities. Consequently, aquaponics emerges as an innovative, low-carbon farming technique characterized by its intensity, sustainability, circularity, and high productivity (Okomoda
et al.,
2023).
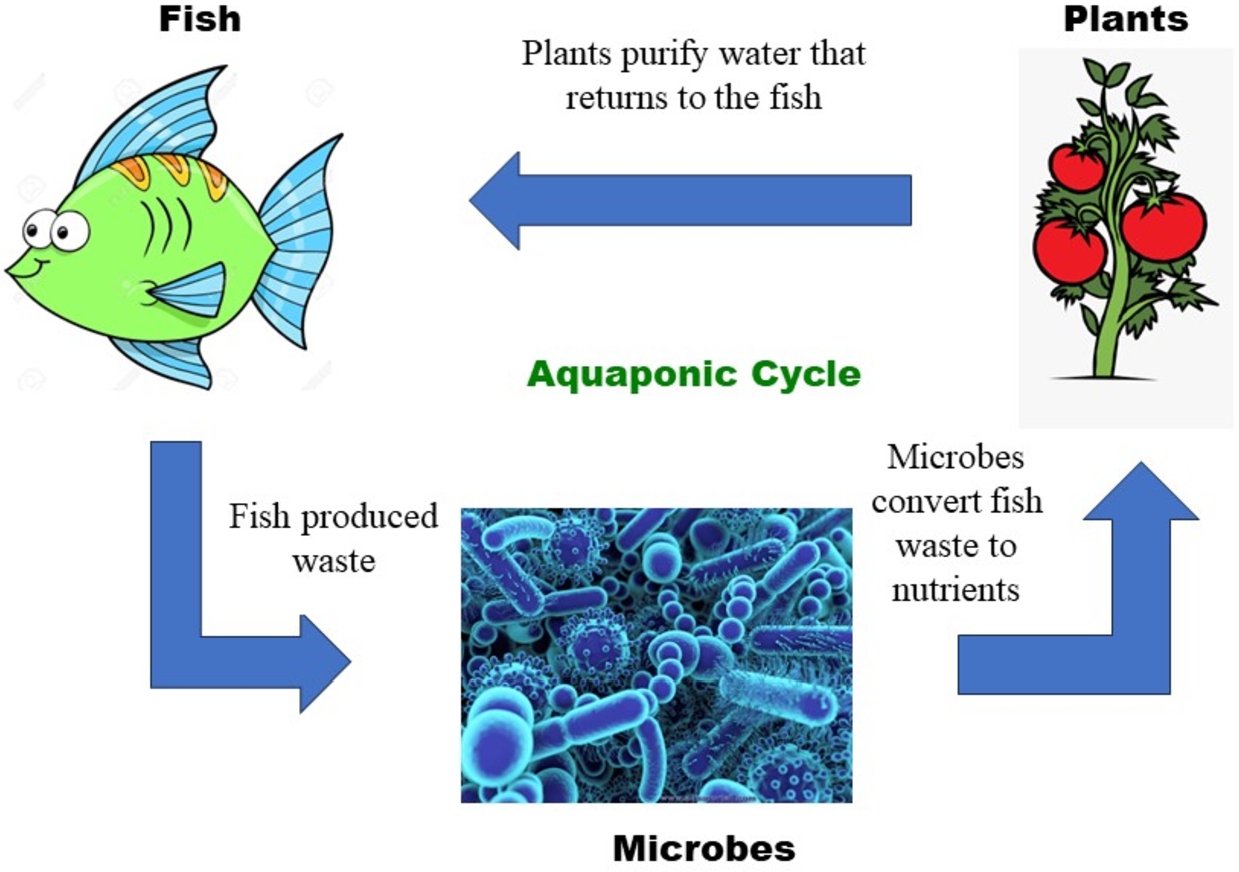
Fig. 1
The aquaponic cycle.
Aquaponic systems operate within a closed-loop water environment, hosting fish, microorganisms, and plants. The physical, chemical, and biological aspects of the circulating water are crucial for the survival of all three components. Hence, it’s imperative to maintain optimal water quality parameters to ensure the independent thriving of each component. Fish growth rate in aquaponics holds significant importance with implications for ecology, evolution, and conservation. Key water quality factors affecting fish growth encompass temperature, dissolved oxygen levels, water pH, ammonium concentration, nitrate levels, and more (Krastanova
et al.,
2022). Temperature directly influences fish metabolism, impacting energy balance, behaviour, appetite, digestion, energy production, and nutrient absorption (Lindmark
et al.,
2022). Inadequate temperatures can lead to fungal infections, affecting both juvenile and adult fish, potentially leading to egg and larvae decay (Cascarano
et al.,
2021). Dissolved oxygen levels are critical for fish respiration, essential for their survival. Water pH also influences fish growth, with slightly acidic environments potentially impacting reproduction rates (Yanes
et al.,
2020). Ammonia is a significant parameter in aquaponic systems, even small amounts can be highly toxic to fish, especially in strongly acidic or alkaline conditions (Levit,
2010). Nitrate levels in water also affect fish growth, particularly detrimental to fry and juvenile fish, impairing their growth (Tilak
et al.,
2007). However, due to system dynamics and environmental factors, these parameters often deviate from ideal values, causing stress, disease, and even death in fish, affecting the productivity and sustainability of the aquaponic systems (Anando
et al.,
2022). Moreover, these water quality parameters are interconnected. Temperature affects oxygen solubility in water, warmer water holding less dissolved oxygen (Butcher and Covington,
1995). pH influences ammonia toxicity, with its proportion of forms influenced by pH levels (Levit,
2010). Understanding these relationships underscores the importance of holistic system management in aquaponics. Maintaining optimal water quality parameters is essential for promoting optimal fish growth, ensuring a stable, well-balanced environment that meets the physiological needs of fish and supports nutrient cycling for both fish and plant health.
The nature of an aquaponic system, which integrates fish, microorganisms, and plants within a closed-loop water environment, requires effective control strategies to maintain optimal water quality parameters. As aquaponics continues to evolve and expand, especially towards industrial-scale operations, various control strategies can be implemented to ensure the success of the system. However, selecting the most appropriate control approach is crucial for achieving the best outcomes, considering some specific criteria of the aquaponic system. One essential aspect to consider when choosing control strategies is the size and scale of the aquaponic system. Smaller-scale systems may require more hands-on, manual control methods, while larger industrial systems can benefit from automated or semi-automated control systems. Automation can help monitor and regulate water quality parameters more efficiently, reducing the need for constant human intervention and ensuring consistent conditions for the aquatic and plant components (Channa
et al.,
2024). Another factor to consider is the complexity of the system and the interrelationships between its components. Aquaponic systems are dynamic and interconnected, with changes in one component affecting others. Control strategies should account for these interactions to maintain balance and harmony within the system (Rossi
et al.,
2024). Additionally, the specific requirements of the fish and plant species being cultivated should inform control strategies. Different species have varying tolerance levels for factors such as temperature, pH, and nutrient concentrations. Tailoring control approaches to meet the needs of the organisms within the system is essential for maximizing growth and productivity while minimizing stress and potential health issues (Lennard and Goddek,
2019). Furthermore, the availability of resources, technology, and expertise will influence the selection of control strategies. Some systems may have access to advanced monitoring equipment, data analysis tools, and specialized knowledge, allowing for more sophisticated control approaches. In contrast, others may rely on simpler, more cost-effective methods that prioritize basic water quality monitoring and manual intervention (Rossi
et al.,
2024). Ultimately, the objective of selecting control strategies in aquaponics is to enhance system performance, productivity, and sustainability while minimizing risks and resource usage. With a plethora of options available, including ON-OFF control, open-loop control, PID control, model predictive control, rule-based control, programmable logic control, and others, determining the most suitable approach can be challenging. Consequently, ensuring long-term success and achieving desired outcomes requires careful consideration and evaluation of these various control methods and selecting the best one.
1.1 Literature Review
A comprehensive review of the existing literature has been conducted to identify and define the problem statement surrounding control strategies in aquaponic systems. Goddek
et al. (
2015) highlight the various challenges involved in implementing effective control strategies within aquaponic systems, emphasizing the unique complexities of these environments. Similarly, Yep and Zheng (
2019) provide a review that addresses the challenges faced when applying control systems in aquaponics, noting the intricate nature of the system and the difficulties in achieving effective regulation. Okomoda
et al. (
2023) offer an in-depth discussion of the challenges associated with the adoption of aquaponics, focusing on the inherent complexities such as nonlinear behaviour, the Multi-Input Multi-Output (MIMO) characteristics of the system, and other system-specific intricacies. Additionally, Ng and Mahkeswaran (
2024) examine the technological barriers in aquaponic systems, which further complicate the implementation of control strategies, thus limiting their potential for optimization. Through this extensive analysis, it became evident that, given the complexities and challenges identified in the literature, there is a pressing need to explore and identify suitable control approaches that can address the unique needs of large-scale aquaponic systems. The ultimate objective of the study is to enhance the production efficiency, profitability, and sustainability of aquaponic systems—goals that cannot be achieved without the effective implementation of control strategies. Therefore, addressing this issue and selecting the most appropriate control strategy for large-scale applications is the central focus of our research.
In recent years, there has been a notable increase in proposals for control mechanisms designed specifically for aquaponic systems. These mechanisms employ a variety of strategies, including ON-OFF control, Rule-based control, Open-loop control, PID (Proportional Integral Derivative), MPC (Model Predictive Control), and PLC (Programmable logic control), each offering unique advantages and applications. However, a significant portion of these proposals focuses on small-scale aquaponic setups, such as kitchen gardens, indoor aquaponic farming, and balcony gardening. In response to the growing interest in small-scale aquaponics, researchers have begun integrating Artificial Intelligence (AI) and Internet of Things (IoT) technologies with traditional ON-OFF control methods. For instance, Vernandhes
et al. (
2017) introduced a smart aquaponics monitoring and control system utilizing a sensor network for water quality parameters, managed through a microcontroller. Similarly, Dutta
et al. (
2018) and Zamora-Izquierdo
et al. (
2019) integrated IoT technology and sensor networks to regulate water quality parameters. Khaoula
et al. (
2021) implemented an IoT-based solution for monitoring and controlling water quality and environmental parameters using sensors for water level, temperature, and CO
2, along with actuators. Additionally, Channa
et al. (
2024) explored the integration of Artificial Intelligence and IoT in a smart aquaponics system to monitor and control essential parameters using Rule-based Control approach. While, much of the focus remains on control mechanisms for small-scale aquaponic systems, there is also emerging interest in applying machine learning techniques for aquaponic setups. Debroy and Seban (
2022a,
2022b) proposed prediction methods for fish weight estimation using Artificial Neural Network (ANN) and its hybrid with fuzzy logic (ANFIS), as well as ANN models for predicting tomato biomass in aquaponic systems, respectively. Eneh
et al. (
2023) presented a yield prediction method for aquaponic systems employing various machine learning algorithms. Furthermore, Rajendiran and Rethnaraj (
2024) discussed a study on IoT-integrated Machine Learning-based Indoor Aquaponics farming.
Recent studies have focused on employing PID (Proportional Integral Derivative) control strategies in aquaponics to efficiently regulate specific water quality parameters. For example, Alipon
et al. (
2021) introduced a design for an automated fertigation system that monitors photoperiod and nutrient consumption, employing a Proportional-Integral-Derivative (PID) system. Li
et al. (
2022) applied PID control to regulate dissolved oxygen concentration in aquaponic recirculating water. Kim
et al. (
2023) presented a Dissolved Oxygen (DO) management system for aquaponic systems using PI and PID controllers. Kannabiran
et al. (
2024) suggested that a PI controller demonstrated robustness in maintaining pH levels within the desired range under varying operating conditions. Wei
et al. (
2019) proposed a laboratory-based aquaponic system utilizing PLC (Programmable Logic Controller) and LabVIEW. Another study by Selvalakshmi
et al. (
2023) developed a PLC-based approach for a small-scale aquaponic system. Chahid
et al. (
2021) conducted a comparative analysis of four Model Predictive Control (MPC) strategies for fish growth reference tracking using a representative bioenergetic growth model in precision aquaculture. Ding
et al. (
2018) explored the opportunities and challenges associated with implementing MPC in aquaponic systems. Lin
et al. (
2020) proposes the use of open-loop control and Model Predictive Control (MPC) for managing greenhouse parameters. Similarly, Debroy
et al. (
2024a) present an MPC-based strategy for controlling aquaponic greenhouse parameters, and they also provide a comparison of this approach with a traditional PI controller. Another publication by Debroy
et al. (
2024c) presents a similar MPC-based strategy, but for controlling water quality parameters in aquaponic systems, and again, they compare this method with a conventional PI controller. In a recent study by Debroy
et al. (
2024b), the authors employed Multi-Criteria Decision Making (MCDM) techniques to identify the most suitable water quality parameter for an aquaponic system. Their research aimed to evaluate and prioritize various water quality indicators by considering multiple criteria, ultimately selecting the one most critical for ensuring the optimal functioning and sustainability of aquaponics. The application of MCDM in this context provides a structured approach to decision-making, helping to balance and assess the different factors that influence water quality in aquaponic environments.
1.2 Research Gap
The existing literature clearly demonstrates the profound impact of integrating aquaculture and hydroponics within aquaponics systems on the reliance of fish growth and yield on water quality parameters. Maintaining these parameters at optimal levels is imperative for the success and productivity of aquaponic systems. However, previous research has predominantly focused on monitoring and controlling small-scale smart aquaponics setups, often employing various control approaches. While some studies have ventured into incorporating IoT-based machine learning methods to predict yields and manage system parameters, the diverse array of control approaches utilized poses a significant challenge in determining the most suitable one for broader application in aquaponic systems. This variability in control strategies further complicates the selection process, particularly when considering implementation in larger-scale aquaponic operations. Moreover, the predominant emphasis on small-scale setups in past research exacerbates the difficulty in identifying the ideal control approach for industrial-scale aquaponics. The lack of specific research tailored to the unique requirements and complexities of large-scale systems underscores a notable gap in the current literature. Consequently, a critical research question arises: Which control strategy is most pertinent for implementation in large-scale aquaponic systems?
Addressing this research gap is paramount for advancing our understanding of optimal control strategies tailored to industrial-scale aquaponics. Such advancements are vital for improving the sustainability, productivity, and viability of large-scale aquaponic operations in real-world applications. Therefore, bridging this gap is essential for driving progress in the field and ensuring the successful integration of aquaponics into broader agricultural practices.
1.3 Objective of the Study
Aquaponics stands as a sustainable farming method, marrying aquaculture with hydroponics to create a harmonious ecosystem. In this system, fish waste provides nutrients for plants, while plants filter and purify the water for the fish. Given the intricate balance required, understanding water quality parameters is paramount, as they directly impact the health and growth of both fish and plants. However, these parameters are susceptible to fluctuations due to external factors and are interrelated, necessitating a careful balance. To tackle these challenges, a robust control strategy is imperative. Moreover, with aquaponics poised for larger-scale adoption, selecting the optimal control approach is crucial, given its promising future prospects. Therefore, the primary objective of this study is to determine the most effective control strategy tailored specifically for industrial-scale aquaponic systems. The overarching goal is to optimize production, enhance system stability, and maximize profitability within these large-scale operations. By identifying the most effective control strategy tailored to the unique requirements of industrial-scale aquaponic systems, this study aims to drive advancements in aquaponic technology and contribute to the sustainable development of agriculture. Ultimately, the findings of this research have the potential to significantly impact the future of food production by enabling the scalable and profitable implementation of aquaponic systems on a large scale. Advancing aquaponic systems through effective control measures holds immense promise in addressing the looming challenges of global food demands and hunger. It can significantly contribute to enhancing food security worldwide by providing a sustainable and efficient method of agricultural production. Thus, the elaboration of this study underscores its potential to revolutionize food production practices and address critical global challenges.
This study aims to introduce a novel hybrid Multiple Criteria Decision Making (MCDM) model tailored to identify the most effective control approach for large-scale aquaponic systems. The proposed approach, named OPA-IF-Neutrosophic-TOPSIS under SVNS Environment, integrates various decision-making techniques into a cohesive framework—a concept not yet explored in existing literature. In this hybrid model, criteria weights are determined using the Intuitionistic Fuzzy ordinal priority Approach (OPA-IF). Subsequently, the ranking of alternatives is refined through the use of TOPSIS within a Neutrosophic fuzzy environment. This comprehensive methodology provides a fresh perspective on optimizing decision-making processes in aquaponic systems by synergistically leveraging diverse analytical tools.
In 2020, Ataei
et al. introduced the MCDM method known as OPA (Ordinal Priority Approach), representing a departure from traditional pairwise comparisons. Building upon this, Mahmoudi
et al. (
2022) developed OPA-F (Fuzzy ordinal priority Approach) in 2022. This approach eliminates the need for pairwise comparisons, automatically estimates attribute weights, and integrates observations without averaging them. However, traditional fuzzy sets face challenges in precisely determining membership mappings, particularly under specific circumstances (Chiao,
2016). To address this limitation, intuitionistic fuzzy sets (IFSs) were introduced. IFSs specify both membership and non-membership degrees of elements within a fuzzy set, thereby accommodating ambiguity levels (Jin
et al.,
2016; Wan
et al.,
2016). In
2024, Majumder and Salomon introduced the Intuitionistic Fuzzy Ordinal Priority Approach (OPA-IF) to better handle uncertainty in decision-making. This method extends the traditional OPA and OPA-F by using triangular intuitionistic fuzzy sets (TIFS) instead of standard fuzzy sets, addressing challenges in determining exact membership values. Unlike OPA-F, OPA-IF relies on ranks rather than weights for criteria, offering a more flexible approach. The study combines OPA-IF with the OPA-F method to improve Multi-Criteria Decision-Making (MCDM) in aquaponic systems, effectively managing ambiguity and optimizing decision outcomes.
In this study, the TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) method, as delineated in the primary reference (Hwang
et al.,
1981), is utilized to ascertain the optimal option. The process of assigning criteria weights is guided by TrF-FOCUM (Majumder,
2023), facilitating this determination. The rationale for opting for Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) stems from its user-friendly interface and its adaptability to meet both qualitative and quantitative requirements. By evaluating each option based on its best and worst outcomes, TOPSIS contributes to a more robust ranking outcome. Furthermore, it can incorporate cost-benefit considerations, rendering it suitable for scenarios where the interaction between performance and cost is significant. While previous research has extensively delved into fuzzy and intuitionistic fuzzy Multiple Criteria Decision Making (MCDM) problems, the growing recognition of ambiguity’s role in MCDM complexities highlights the need to incorporate Neutrosophic sets. Neutrosophic sets are adept at addressing environments characterized by uncertainty, indeterminacy, and inconsistency within the MCDM methodology. Despite the attention dedicated to challenges posed by fuzzy and intuitionistic fuzzy MCDM, integrating indeterminacy into the realm of MCDM complexities is deemed crucial. In 2023, Neutrosophic-TOPSIS was developed by Pramanik
et al. (
2023) to determine alternative rankings, marking a significant advancement in tackling the intricacies of decision-making under uncertainty.
1.4 Advantage and Novelty
The hybrid approach that integrates the Neutrosophic-TOPSIS strategy for assessing alternative levels within a Single Valued Neutrosophic (SVN) framework with the Intuitionistic Fuzzy-Ordinary priority approach (OPA-IF) for evaluating criteria levels offers numerous advantages:
-
I. This method adeptly manages uncertainty within SVN contexts by leveraging both OPA-IF and Neutrosophic logic. Neutrosophic logic addresses uncertainty at the alternative level, while OPA-IF tackles uncertainty at the criteria level, ensuring comprehensive treatment of ambiguity throughout decision-making.
-
II. By eliminating the need for pairwise comparisons among attributes, this paradigm streamlines the decision-making process, making it more straightforward and efficient.
-
III. The Neutrosophic-TOPSIS technique boosts the decision-making process’s resilience to ambiguity by explicitly considering degrees of truth, indeterminacy, and falsehood at the alternative level. This ensures the reliability of decision outcomes, even amidst unclear or ambiguous information.
-
IV. Adopting a multi-criteria approach enhances the generation of logical and dependable conclusions, especially in scenarios with unclear or inconsistent input parameters.
-
V. Beyond providing a novel approach for multi-criteria evaluation, the MCDM tool fosters sound and productive decision-making by promoting logical and evidence-based reasoning.
-
VI. Addressing expert bias poses a significant challenge in decision-making, particularly in subjective scenarios or when experts lack sufficient knowledge or experience. In such cases, traditional pairwise comparison methods may yield unreliable or inconsistent results, undermining the process’s credibility and reliability.
-
VII. The MCDM technique evaluates and ranks control approaches in a Neutrosophic manner. It is noteworthy that employing various fuzzy set extensions, such as hesitant, spherical, and picture, may introduce specific additional constraints or limitations.
5 Conclusion
This research introduces a novel Multi-Criteria Decision-Making (MCDM) approach, termed the OPA-IF-Neutrosophic-TOPSIS hybrid technique under the SVNS Environment. Within this approach, the OPA-IF component evaluates the Priority Value (PV) of different attributes, while the Neutrosophic-TOPSIS strategy establishes rankings among alternative choices. The PV, determined by OPA-IF, plays a crucial role in calculating the Utility Functional Value of alternatives within the Neutrosophic-TOPSIS framework. This hybrid MCDM method aims to aid in selecting the most appropriate control approach for aquaponics systems. Notably, findings from the OPA-IF analysis underscore the importance of the ‘Capability to Handle MIMO Systems’ criterion, leading to the conclusion by the Neutrosophic-TOPSIS strategy that ‘Model Predictive Control (MPC)’ is the optimal choice for large-scale aquaponic systems.
To verify the effectiveness of this proposed MCDM technique, its results are compared with the BWM-Neutrosophic-TOPSIS Strategy under the SVNS Environment. This comparison confirms the alignment of outcomes between the proposed model and existing methods, as demonstrated by a strong positive correlation determined through Pearson correlation analysis. Furthermore, a sensitivity analysis indicates that the MPC strategy is the most sensitive parameter within the proposed method.
Overall, this study makes a significant contribution to the scientific understanding of control strategies in aquaponics by providing a deeper insight into the various methodologies that can be applied to optimize system performance. Beyond advancing theoretical knowledge, it also offers valuable, actionable guidance for farmers, aquaponics practitioners, and stakeholders in the field. By identifying the most effective control approaches and highlighting their practical benefits, the research empowers practitioners to make more informed decisions when managing their aquaponic systems. Through these efforts, the study aims to contribute to the broader goal of promoting sustainable, efficient, and scalable food production systems for the future.
However, despite the numerous advantages of the proposed method, it is essential to recognize its inherent limitations. One of the primary challenges in implementing this technique lies in the substantial amount of data and expertise required to effectively apply the approach. The complexity of integrating various fuzzy logic and decision-making elements demands a high level of technical knowledge, which could pose difficulties for practitioners without specialized training or experience. Furthermore, while the study successfully addresses ranking within the context of a Neutrosophic environment, the method may face constraints when dealing with other extensions of fuzzy set theory, such as hesitant fuzzy sets or spherical fuzzy sets. These alternative frameworks introduce additional layers of complexity and may not be as easily accommodated within the current model, potentially limiting its applicability in certain scenarios. Another limitation stems from the reliance on expert assessments and opinions to establish rankings within the model. While expert judgment is a valuable tool, it is inherently subjective, which means that different experts may interpret the same data in varied ways. This subjectivity can lead to inconsistencies in the rankings and conclusions drawn from the model, as each expert may have differing perspectives or biases, introducing an element of uncertainty into the decision-making process.
Moving forward, this study will expand its scope in several key directions. First, a thorough investigation into the critical decision-making processes that guide the selection of the most appropriate control strategies for large-scale aquaponic systems will be undertaken. Second, the study will leverage a broader range of MCDM methodologies to assess and prioritize various control techniques. These methodologies will be applied to evaluate the performance and suitability of different control strategies based on their ability to manage Multiple Input Multiple Output (MIMO) systems, their capacity to address system non-linearities, and their effectiveness in large-scale, dynamic settings. Third, the research will be enriched by incorporating extensive data collection, analysis, and modelling efforts. This will not only deepen the understanding of aquaponic system dynamics but also result in practical, actionable recommendations for practitioners in the field. By bridging gaps in the existing body of knowledge, the study aims to contribute to improving the efficiency and sustainability of aquaponic food production, providing valuable insights that can be directly applied to real-world settings. Finally, the study will examine the sensitivity and robustness of the MCDM models used in the evaluation process. This will involve testing how well the selected models perform under varying conditions and uncertainties, ensuring their reliability and applicability in real-world aquaponic systems.

