5.1 Experiment Methodology
In this section, we present the experiments’ outcomes to validate the quality of the proposed novel methods. The scope of the study covered both artificial and real-world time series representing different situations. Most of the analysed time series were relatively short, since conventional structural break detection tasks are executed for such cases. We analysed eight synthesized time series, which included instances with different numbers of structural breaks, appearing and disappearing trends, and changing time series mean and variance. There was also an example of a white noise time series with added variation, in which the algorithms should not detect any structural breaks. We have defined “test cases” of synthetic time series. We assumed some underlying time series properties for each test case and then generated each test case multiple times, maintaining the same underlying properties but with some random noise. This entailed that the experiments were repeated multiple times for each test case. Specific differences between particular time series instances within a single “case” arise only because we draw values, but the parameters of distributions we use stay the same.
On top of ten synthetic series, we used two real-world time series representing the power demand of a fridge freezer in a kitchen. They come from the Electrical Load Measurement dataset by Murray
et al. (
2015). Example time series from the synthetic test cases are displayed in Fig.
1. Processed real-world time series are illustrated in Fig.
2.
Let us list and briefly discuss synthetic test cases:
-
1. Time series composed of two segments with the same segment variance but different segment mean (an example is given in Fig.
1(a)).
-
2. Time series composed of two segments with the same mean and different segment variance (an example is given in Fig.
1(b)).
-
3. Time series composed of two segments generated with the use of different AR models (
${y_{t}}=0.9{y_{t-1}}+{\varepsilon _{t}}$ and
${y_{t}}=-0.9{y_{t-1}}+{\varepsilon _{t}}$). In the first three examples, two segments have equal length (like in Fig.
1(c)).
-
4. Test case without structural breaks. It is a white noise series with a small random distortion (example is in Fig.
1(d)).
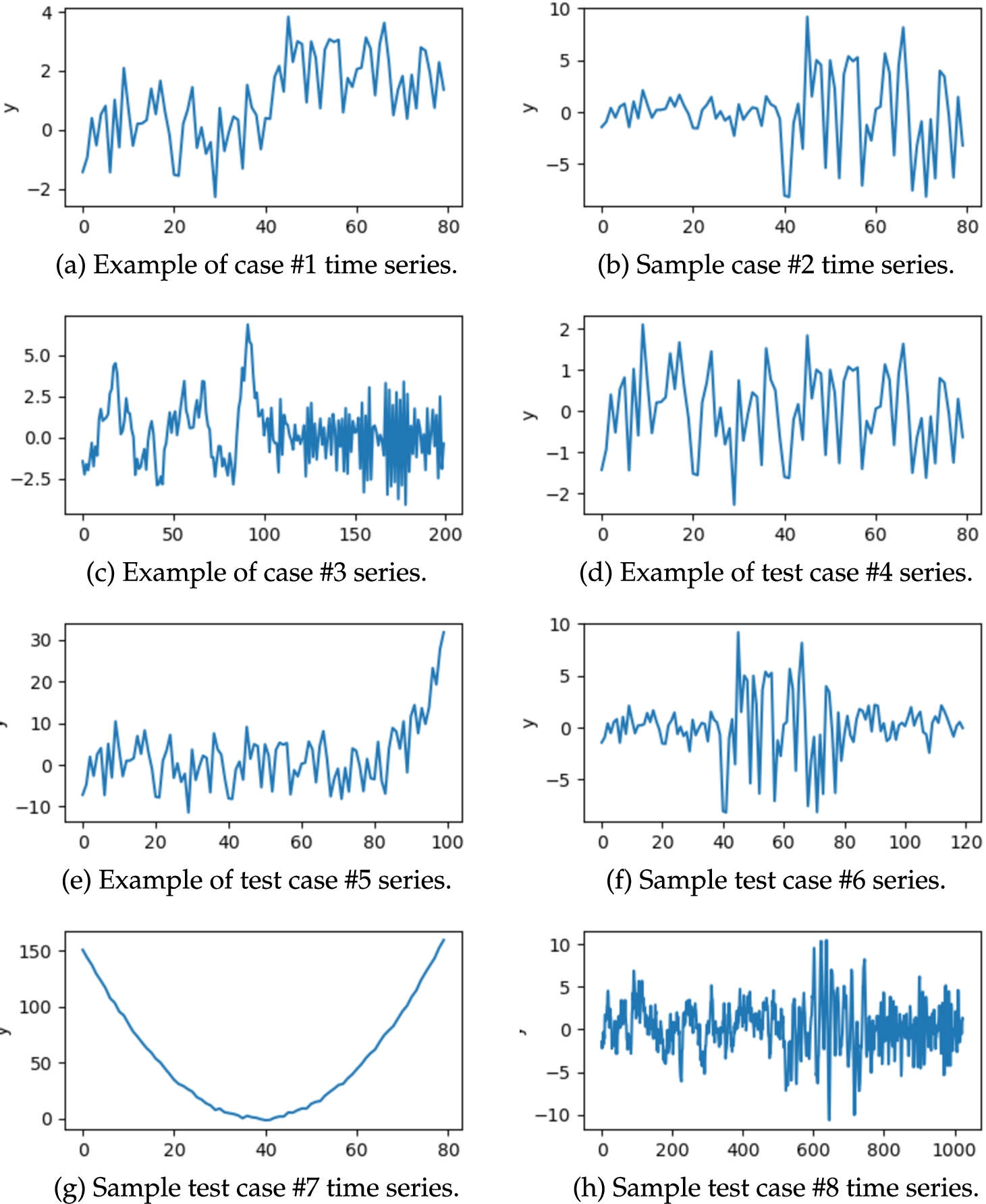
Fig. 1
Example time series coming from artificial test cases analysed in the paper.
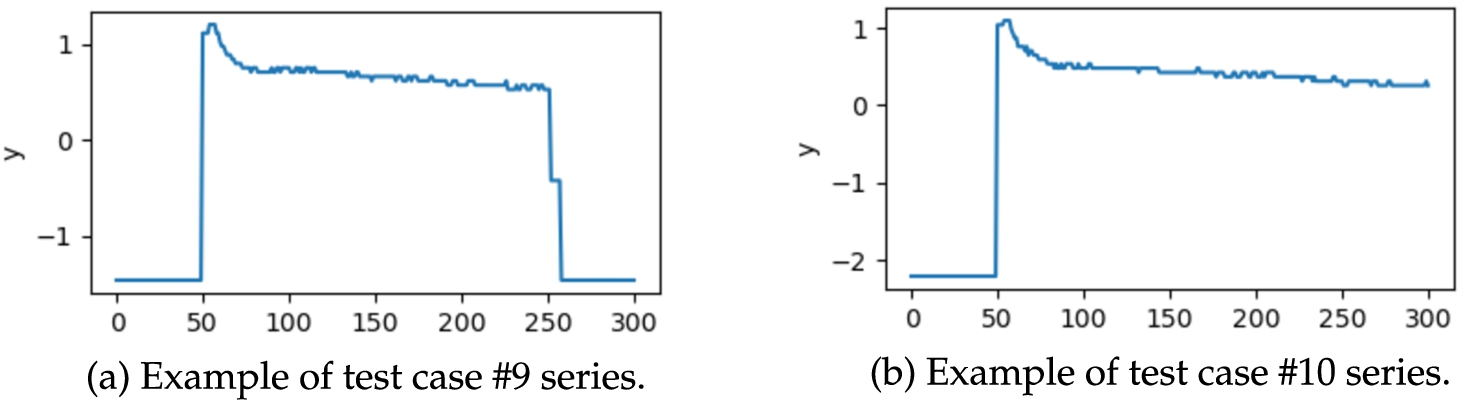
Fig. 2
Two real-world time series describing fridge freezer power demand.
-
5. Test case where time series start with a long and low-variance segment, but at the end there is a short, but intense, rise of values (example is in Fig.
1(e)).
-
6. Time series composed of three segments, where the first and the third segments are identical and have a fixed mean and variance. The segment in the middle has a larger variance than the other two segments (see Fig.
1(f)).
-
7. Test case, which follows a parabolic pattern with low variance of data points. An example is given in Fig.
1(g)).
-
8. Time series generated using the AR model based on the equation:
(example is in Fig.
1(h)).
To eliminate the possible bias arising due to the randomness of the empirical methodology of this study, we have been performing multiple repetitions of the experiments. For each synthesized test case, we generated 10 time series instances with different random number generator seeds. Experiments were executed for each generated time series. As a result, we performed 10 repetitions of each experiment for each test case. Our motivation was to ensure a reasonable variability of the data by maintaining the same data generation process that relies on drawing from distributions. To keep the same level of objectivity in result evaluation, in the case of the real-world time series, we were also repeating the experiments 10 times.
The outcomes of the experiments that were conducted involving different algorithms were compared with each other and with the outcomes obtained by other researchers. We assume three state-of-the-art methods, which we use for such comparisons. The first is the method proposed by Bai and Perron (
1998), Bai and Perron (
2003), and the second is ClaSP by Ermshaus
et al. (
2023). The third is the method by Davis
et al. (
2016), which can be seen as the immediate predecessor of the approach introduced in this paper. In the first two cases, we run the algorithm to produce the results, but in the third case, we compare our results to those presented by Davis
et al. (
2006) using analogous time series examples.
We propose two metrics for the evaluation of the outcomes of structural break detection procedures:
The proposed method of results evaluation is our novel contribution, which is introduced in this paper.
5.2 Experimental Evaluation of Analysed Cost Functions
At first, we compared results obtained with the MDL, SPF1, SPF2, EMDL, DCF, and PDCF cost functions. We used both the AR and ARIMA models and both versions of the cost function: with and without a weight for deviation from a linear trend. The experiments concerned seven synthetic time series and two real-world time series. The only omitted case is Fig.
1(h), which will be discussed in detail in Section
7.
Experiments were performed using PSO with parameters
${C_{11}}$:
$\omega =-0.1832$,
${c_{1}}=0.5287$,
${c_{2}}=3.1913$, population size 47. These parameters come from Hvass Pedersen (
2010). We have tested 188 variants of cost functions: 164 for the AR model and 22 for the ARIMA model. In principle, we have employed a grid search of procedure parameters for SPF1, SPF2, EMDL, DCF, and PDCF functions with the AR model. In the case of ARIMA, we have performed fewer tests due to a more considerable computational complexity – we tested a subset of configurations close to the configurations, for which results for the corresponding functions with the AR model were good.
A detailed discussion on optimization algorithms hyperparameters and their fitting is provided in Section
6.
Our results were evaluated with the use of BPD and SC metrics and conclusions attained with use of both were very similar. The best results (assessed with the use of BPD and SC metrics) were obtained consecutively for configurations: EMDL
${_{\text{AR}}}$ (
$\mu =3$,
$\nu =1$), EMDL
${_{\text{AR}}}$ (
$\mu =3$,
$\nu =1$), MDL
${_{\text{ARIMA}}}$, all without involvement of the MSE modification. There were also other cost functions which led to noteworthy results. The most interesting configurations are presented in Table
1 and Table
2.
Table 1
BPD score for the best-performing cost functions.
| Cost function |
Test case |
|
MSE |
1(a) |
1(b) |
1(c) |
1(d) |
1(e) |
1(f) |
1(g) |
2(a) |
2(b) |
Mean |
| EMDL${_{\text{ARIMA}}}$ ($\mu =3$, $\nu =1$) |
– |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
1.0 |
1.1 |
0.3 |
0.27 |
| EMDL${_{\text{AR}}}$ ($\mu =3$, $\nu =1$) |
– |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.1 |
1.0 |
1.2 |
0.3 |
0.29 |
| MDL${_{\text{ARIMA}}}$
|
– |
0.1 |
0.0 |
0.0 |
0.0 |
0.0 |
0.1 |
1.0 |
1.3 |
0.2 |
0.30 |
| MDL${_{\text{AR}}}$
|
– |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
2.5 |
1.2 |
0.5 |
0.47 |
| DCF${_{\text{ARIMA}}}$ ($\mu =1$, $\nu =0.1$, $\delta =0.5$) |
– |
0.0 |
0.0 |
0.0 |
0.9 |
0.0 |
0.0 |
0.8 |
2.0 |
1.0 |
0.52 |
| PDCF${_{\text{ARIMA}}}$ ($\mu =10$, $\nu =0.1$, $\delta =2$) |
– |
0.0 |
0.0 |
0.0 |
1.0 |
0.0 |
0.0 |
0.7 |
2.0 |
1.0 |
0.52 |
| SPF${_{\text{AR}}}$ ($\mu =0.1$, $\nu =1$) |
– |
0.8 |
1.0 |
0.3 |
0.0 |
1.0 |
2.0 |
0.4 |
0.5 |
0.1 |
0.68 |
| SPF2${_{\text{AR}}}$ ($\mu =0.1$, $\nu =10$) |
– |
0.0 |
1.0 |
0.2 |
0.0 |
0.5 |
2.0 |
2.8 |
0.3 |
0.0 |
0.76 |
| SPF${_{\text{AR}}}$ ($\mu =10$, $\nu =10$) |
+ |
0.2 |
0.7 |
0.8 |
0.1 |
1.4 |
0.4 |
3.7 |
0.0 |
0.0 |
0.81 |
| SPF2${_{\text{AR}}}$ ($\mu =10$, $\nu =1$) |
+ |
0.1 |
0.9 |
0.8 |
0.1 |
1.0 |
0.8 |
3.9 |
0.0 |
0.1 |
0.86 |
Table 2
SC score for the best-performing cost functions.
| Cost function |
Test case |
| Type |
MSE |
1(a) |
1(b) |
1(c) |
1(d) |
1(e) |
1(f) |
1(g) |
2(a) |
2(b) |
Mean |
| EMDL${_{\text{ARIMA}}}$ ($\mu =3$, $\nu =1$) |
– |
0.019 |
0.001 |
0.007 |
0.000 |
0.013 |
0.004 |
2.062 |
2.265 |
1.203 |
0.619 |
| EMDL${_{\text{AR}}}$ ($\mu =3$, $\nu =1$) |
– |
0.006 |
0.001 |
0.009 |
0.000 |
0.011 |
0.224 |
2.036 |
2.465 |
1.181 |
0.659 |
| MDL${_{\text{ARIMA}}}$
|
– |
0.225 |
0.001 |
0.007 |
0.000 |
0.028 |
0.218 |
2.062 |
2.673 |
1.051 |
0.659 |
| MDL${_{\text{AR}}}$
|
– |
0.019 |
0.001 |
0.009 |
0.000 |
0.006 |
0.013 |
5.023 |
2.465 |
1.432 |
0.996 |
| DCF${_{\text{ARIMA}}}$ ($\mu =1$, $\nu =0.1$ $\delta =0.5$) |
– |
0.050 |
0.008 |
0.009 |
1.800 |
0.060 |
0.010 |
1.679 |
4.062 |
2.062 |
1.082 |
| PDCF${_{\text{ARIMA}}}$ ($\mu =10$, $\nu =0.1$, $\delta =2$) |
– |
0.050 |
0.008 |
0.008 |
2.000 |
0.081 |
0.018 |
1.473 |
4.062 |
2.062 |
1.085 |
| SPF${_{\text{AR}}}$ ($\mu =0.1$, $\nu =1$) |
– |
1.652 |
2.062 |
0.624 |
0.000 |
2.062 |
4.062 |
1.087 |
1.042 |
0.293 |
1.431 |
| SPF2${_{\text{AR}}}$ ($\mu =0.1$, $\nu =10$) |
– |
0.006 |
2.062 |
0.505 |
0.000 |
1.045 |
4.062 |
5.659 |
0.630 |
0.000 |
1.552 |
| SPF${_{\text{AR}}}$ ($\mu =10$, $\nu =10$) |
+ |
0.421 |
1.517 |
1.639 |
0.200 |
2.866 |
0.891 |
7.418 |
0.010 |
0.000 |
1.662 |
| SPF2${_{\text{AR}}}$ ($\mu =10$, $\nu =1$) |
+ |
0.215 |
1.902 |
1.640 |
0.200 |
2.015 |
1.699 |
7.844 |
0.009 |
0.217 |
1.749 |
Let us discuss the behaviour of various cost functions in more detail. For the simplest cases, analysed functions perform very well. For test case
1(a) most of the cost functions in almost each run correctly detect places where the average value of time series changes. The exception was SPF
${_{\text{AR}}}$ (
$\mu =0.1$,
$\nu =1$) with no MSE modification, which did not find any structural break.
Most of analysed methods correctly find the place where the variance changes (test case
1(b)). Problems have only SPF and SPF2 methods. They generally did not detect a break in such a case. The SPF
${_{\text{AR}}}$ (
$\mu =10$,
$\nu =10$) with MSE is an exception, because it finds structural breaks but locates them in incorrect places.
Most of presented cost functions detect change between two different AR models very well (case
1(c)). The exception are methods involving MSE modification. They detect usually two structural breaks and only small part of them is close to correct structural break location.
Most of presented cost functions correctly solved the task of processing white noise time series (case
1(d)). The expected outcome in this scenario is not to return any structural breaks. The only cost functions which almost always failed the test are the PDCF and DCF cost functions.
Test case
1(e) contained series composed of two segments: white noise and a segment with a trend. In this scenario, the classical MDL and the elastic MDL rule produced excellent outcomes. PDCF and DCF cost functions were less precise, but they detected one structural break near the expected location (slightly too early). Methods based on penalty cost function in most cases returned more than one structural break. Usually one of them was in the expected location (with the exception of configuration SPF
${_{\text{AR}}}$ (
$\mu =0.1$,
$\nu =1$) without MSE where no structural breaks were found.
Result obtained for the test cases composed of three segments of the same length (case
1(f)) were generally good. Only SPF and SPF2 cost functions had problems. The configurations did not detect any structural break or detected (often more than one) in incorrect places.
The next test case concentrated on a rather theoretical example, where time series was the shape of a parabola (see Fig.
1(g)). The parabola case is very difficult as there are many viable locations of structural breaks. In this test case, the introduced BPD and SC scores are not very informative and a valid evaluation must be manual. The experiments have shown, that the methods including the MSE modification and SPF2
${_{\text{AR}}}$ (
$\mu =0.1$,
$\nu =10$) detected too many structural breaks and were not very practical. Conversely, cost functions employing the ARIMA model had a strong tendency not to detect any structural change. Results generated by SPF
${_{\text{AR}}}$ (
$\mu =0.1$,
$\nu =1$) also were very impractical (one structural break detected closely to start or end of time series). Other cost functions usually allowed for detecting a few structural changes near the
$\frac{1}{4}$th and the
$\frac{3}{4}$th of the time series length. The best results were obtained with the EMDL
${_{\text{AR}}}$ (
$\mu =3$,
$\nu =1$) model.
The last two examples were the real-world time series describing fridge freezer power demand. We analysed two examples. First, where the freezer was turned on and turned off after some time (case
2(a)). Second, where the freezer was turned on and was working until the end of the time series (case
2(b)). The best results were obtained for chosen configurations of SPF and SPF2 methods. For case
2(a) they allowed for a correct detection of both structural breaks and for case
2(b) the same methods returned one structural break in the correct location. It is worth to say that cost function variants using MSE modification give more reliable results for case
2(a). All other cost functions listed in the tables did not find any structural break or found one near to the end of the time series. The latter behaviour is a result of a phenomenon which will be discussed in the next subsection.
We have observed that the proposed cost functions enhance time series processing capabilities for structural break detection algorithms. Noteworthy, for all of the proposed cost functions, we can find a set of parameters that works very well for various test cases. Furthermore, we will demonstrate in Section
7 that the proposed cost functions are generally better performing than the state-of-the-art MDL
${_{\text{AR}}}$ cost function. Promising results have been achieved with the use of the SPF and SPF2 cost functions. Their superiority was the clearest when we processed real-world time series. Their only weakness is that they may tend to output incorrect structural break count – too many or too few, more often too many, especially when the methods are used with MSE modification.
The empirical experiments have shown that the cost functions using the ARIMA model are very good, and in many cases, they are better than the ones using the AR model. Their weak point is computational complexity, which is higher, and this difference grows as the time series length increases. For example, it took only 0.3s for the AR model to calculate MDL cost function partial values for all possible time series segments for the test case with 50 data points and 190.0s for ARIMA. In contrast, for a case with 100 data points, it took 1.4s and 937.7s, respectively. This shows that cost functions using the ARIMA model are helpful for short time series. In practice, it is not a severe limitation for many real-world domains applying break detection methods (such as economics), in which relatively short time series are of interest.
The proposed objective functions punish for deviations from theoretical models constructed on developed segments. Therefore, if these models cannot reflect the underlying data well, there is no reasonable justification to apply this model. If the data contains a clearly visible and changing trend, the recommended choice is an objective function that punishes deviations from theoretical models. The component that punishes for short intervals should we weighted as less important. Punishing for deviations from a theoretical model is a lousy strategy for high-variance time series or if variance is the crucial distinction for subsequent segments. In this case, punishing for short segments and diminishing the punishment for deviations from theoretical models is much better.

