3.1 Dataset Definition, Preprocessing and Partitioning
In order to create the initial dataset, different types of factors are extracted. They can be divided into four main categories: internal factors, technical indicators, external factors, and attractiveness measures. The considered factors are given in Table
2.
Table 2
Factors considered in analysis.
| Category |
Variables |
Source |
| Internal factors |
Close price, volume, market capitalization, average block size, average block time, average hash rate, average transaction fee |
https://bitinfocharts.com |
| Technical indicators |
Moving average of close price, lag return |
Calculated |
| External factors |
S&P500, VIX, Gold |
https://fred.stlouisfed.org |
| Attractiveness measure |
Google Trends, Tweets |
https://bitinfocharts.com |
Market and blockchain variables are differentiated among internal factors. Market data usually include OHLC Bitcoin prices, volume, and market capitalization. Since Bitcoin prices are not affected by seasonality like stock prices, the open, high, and low Bitcoin prices are excluded from our analysis. In that manner, the dimensionality problem is avoided. Average block size, average block time, average hash rate, and average transaction fee are selected from a set of available blockchain metrics. Namely, Poyser (
2017) define supply and demand (transaction cost, reward system, mining difficulty, coins circulation, rule changes), i.e. blockchain measures, as the main internal factors that have a direct impact on their market price. Since previous research involving different technical indicators yielded good results (Pabuccu
et al.,
2020; Li and Dai,
2020; Cavalli and Amoretti,
2021), the moving average of the close price, as well as the lag return are selected as inputs as well. Although researchers disagree on the impact of external factors on Bitcoin prices and returns, the following external factors: S&P500, Chicago Board Options Exchange volatility index (VIX), and Gold prices are considered in this paper. Finally, widely utilized indicators of attractiveness such as Google Trends are used. Google Trends provides insights into the fluctuation of interest in Bitcoin as a search term over a certain timeframe, while Tweets indicate the daily count of tweets using the word “Bitcoin”. Bitcoin closing prices are used to calculate the return for the following day, which is the dependent variable in the model (Šestanović and Kalinić Milićević,
2023).
More formally, the next-day return
${R_{t}}$, is calculated as follows:
where
${P_{t}}$ are Bitcoin closing prices. Moreover, prices
${P_{t}}$ are used to calculate lag returns as well as moving average values, for different window lengths
w with equations (
2) and (
3):
Using the aforementioned variables, i.e. different internal factors, technical indicators, external factors, and based on two attractiveness measures, i.e. Google Trends and Tweets, two initial (
$\textit{IN}$) datasets are created:
${D_{\textit{IN}}^{1}}$ containing all the variables and the variable Google Trend and
${D_{\textit{IN}}^{2}}$ containing all the variables and the variable Tweets. Those sets were used to compare the predictive performance of the models depending on the selected measures of attractiveness.
More formally, initial datasets can be defined in the form of supervised data as ${D_{\textit{IN}}^{1}}={\{({x_{t,i}},{y_{t}})\}_{t\in {T^{\prime }}}}$ and ${D_{\textit{IN}}^{2}}={\{({z_{t,i}},{y_{t}})\}_{t\in {T^{\prime }}}}$, where ${T^{\prime }}$ is the total initial sample size, ${x_{t}}\in {\mathbf{R}^{p}}$ and ${z_{t}}\in {\mathbf{R}^{p}}$ are vectors of $p=14$ ($i=1,\dots ,p$) independent variables differing only by the attractiveness measure, and ${y_{t}}={R_{t}}\in \mathbf{R}$ is a dependent variable, i.e. next-day return.
The data-preprocessing phase of analysis consists of dealing with missing data, calculating the percentage changes, and scaling the data. The selected period does not include an abundance of data gaps that would reflect negatively on the quality of the chosen data collection. Missing values were found at some points in time, and were mostly related to external factors. Linear interpolation was used to fill in the gaps.
In order to improve training efficacy and NN convergence, the actual values for the majority of independent variables were replaced with percentage changes. For all the observed variables except lag returns $(i=1)$, existing values are replaced with corresponding percentage changes, i.e. ${x_{t,i}}\gets \frac{({x_{t,i}}-{x_{t-1,i}})}{{x_{t,i}}}$, $t\in {T^{\prime }}$, $i=2,\dots ,p$ and ${z_{t,i}}\gets \frac{({z_{t,i}}-{z_{t-1,i}})}{{z_{t,i}}}$, $t\in {T^{\prime }}$, $i=2,\dots ,p$.
Following the preparation of the initial datasets ${D_{\textit{IN}}^{1}}$ and ${D_{\textit{IN}}^{2}}$, each of final dataset ${D^{1}}={\{({x_{t,i}},{y_{t}})\}_{t\in T}}$ and ${D^{2}}={\{({z_{t,i}},{y_{t}})\}_{t\in T}}$ for $T=0,1,\dots ,2337$ included in our analysis contains a total of 2338 points. Indices $t=0$ and $t=2337$ correspond to the dates 2016-01-06 and 2022-05-31, respectively. To conclude this step of preprocessing, given that machine learning algorithms perform better with scaled data, the min-max scaler, which rescales variables into the $[0,1]$ range, is used.
In the majority of research papers examining Bitcoin price and return forecasting, the dataset is split into a training set and a testing set in a predetermined proportion. On the contrary, in this paper, the breakpoints in the Bitcoin price trend are detected. The model is then trained on the period preceding the trend break and tested on the part of period following the breakpoint for each breakpoint. In this way, the ability of a NN model to make predictions in a new environment which is set up in an objective and unbiased manner can be tested. The Bai-Perron structural break change test is used to detect structural breaks. Bai and Perron (
1998) considered issues associated with multiple structural changes in the linear regression model derived by minimizing the sum of squared residuals. Throughout, the dates of the
m breaks were treated as unknown variables that needed to be estimated. The primary considerations are the features of the estimators, particularly the break date estimates, and the design of tests that provide inferences about the presence of structural change and the number of breaks. This test is employed to identify breakpoints, resulting in the identification of indices of five dates
${T_{1}},{T_{2}},\dots ,{T_{5}}\in T$ at which the test recognized a structural change. For each
${T_{k}},k=1,\dots ,5$ two sets are defined:
-
1. Train set ${D_{\textit{train}}^{k}}\{({x_{t,i}},{y_{t}})|t\in \{0,1,\dots ,{T_{k}}\}\}\subset {D^{1}}$ and
-
2. Test set ${D_{\textit{test}}^{k}}\{({x_{t,i}},{y_{t}})|t\in \{{T_{k}}+1,\dots ,{T_{k}}+n\}\}\subset {D^{1}}$, where $n=\frac{{T_{k}}\cdot 5}{100}$.
Namely, each subset, or training set, is followed by a test set. The size of each test set corresponds to five percent of the size of the associated train set.
Table
3 displays the time interval and number of observations for each partition. Four out of five partitions (subsets) are used to build models with different NN architecture. Due to the low quantity of data points, the first partition is excluded from the study.
Table 3
Dataset partitions obtained with Bai-Perron multiple structural break test.
|
Subset 1 |
Subset 2 |
Subset 3 |
Subset 4 |
Subset 5 |
| Start date |
2016-01-06 |
2016-01-06 |
2016-01-06 |
2016-01-06 |
2016-01-06 |
| Close date |
2016-12-27 |
2017-12-15 |
2019-03-25 |
2020-03-11 |
2021-03-12 |
| Number of data points |
357 |
710 |
1175 |
1527 |
1893 |
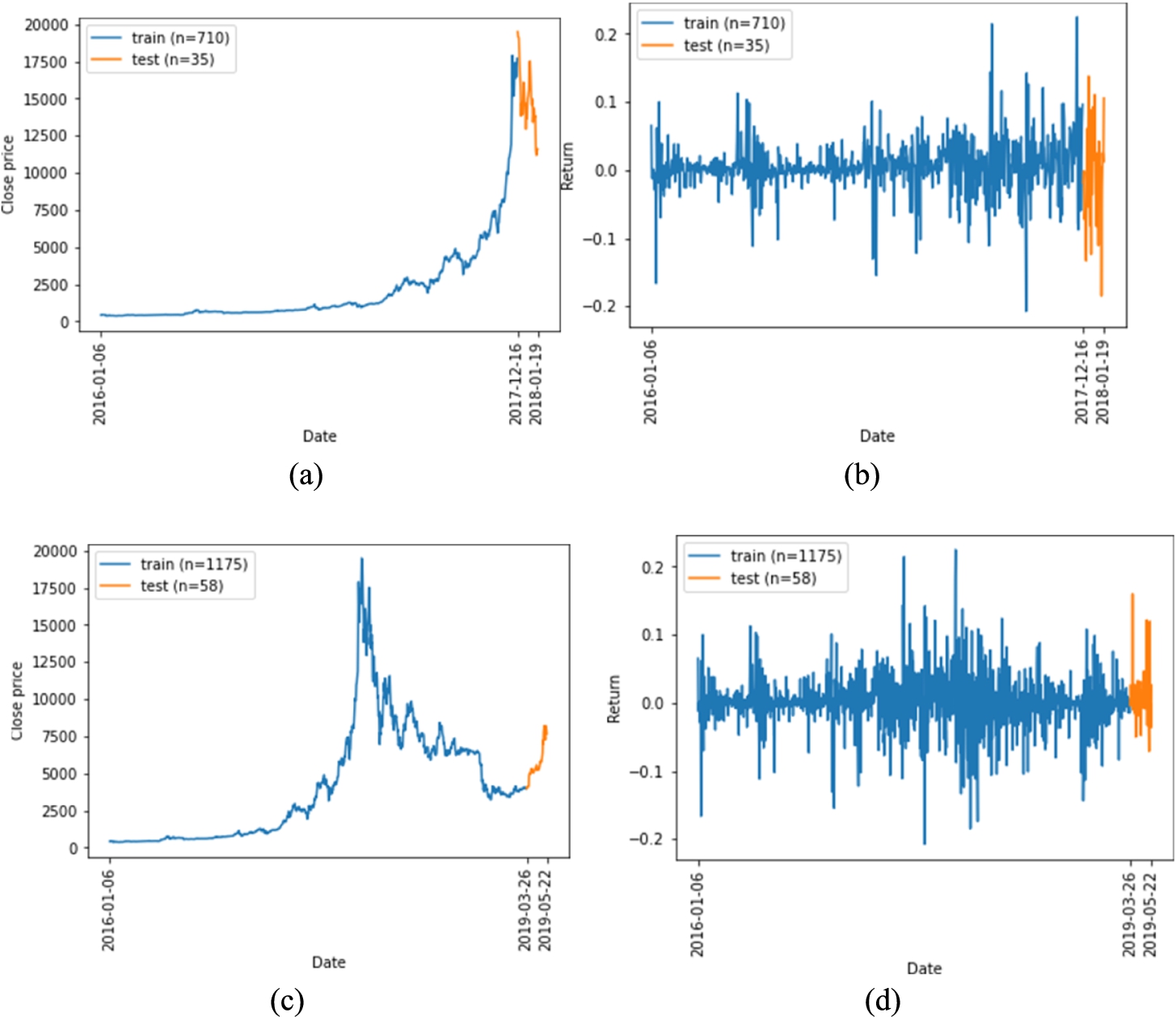
Fig. 1
Flow chart of close price and return within train and test sets for observed partitions.
A graphical representation of price movements and next-day returns within the training and testing set for each observed partition are shown in Fig.
1.

