1 Introduction
In the healthcare industry, cloud computing has revolutionized data management and has been efficiently implemented across various healthcare units. It provides an attractive solution to the vast problem of handling massive volumes of data in this sector. Healthcare organizations can improve their work culture and address data management challenges by incorporating cloud computing into their systems. Cloud computing in healthcare includes data analysis, sharing, access, and storage capabilities, which become more effective and scalable as data volumes grow (Satoskar
et al.,
2023). Furthermore, cloud computing aids in increasing customer engagement and commercial outcomes for large enterprises and healthcare organizations. Given that research has demonstrated a beneficial relationship between cloud computing and data management in the healthcare industry, it is clear that this novel technology has the potential to play a significant role in this industry and others in the future. Despite various issues confronting the healthcare business, the demand for advanced technology is increasing, making cloud computing an increasingly important component in overcoming these obstacles and driving advancement in the field (Agapito and Cannataro,
2023).
The usage of cloud computing by healthcare organizations is subtle in India compared to other countries like the USA and China. As of 2022, it was determined that only 400 out of 62,000 hospitals in India actively utilized cloud computing to collect, organize, and manage data (Krishankumar
et al.,
2022b). Although India has become well-advanced in using cloud services in the healthcare industry, there must be a gap in how the data are effectively organized, stored, and managed. After surveying the Indian healthcare industry, Dash
et al. (
2019) inferred that implementing cloud computing in healthcare industry sectors is crucial for handling massive amounts of medical data and promoting healthcare quality. Due to the high demand for cloud computing services, there has been a sharp increase in CVs (“cloud vendors”) globally. The fast growth of CVs has complicated the selection of the appropriate vendor for the healthcare industry.
From the user’s point-of-view, different CVs have different preferences based on different QoS (“quality of service”) parameters, making the selection of CVs even more challenging. Mardani
et al. (
2019) reviewed various decision models available in the healthcare industry. They inferred that fuzzy sets are crucial for handling uncertainty, and MCDM (“multi-criteria decision-making”) can be adopted for solving decision problems. MCDM is a promising concept that can effectively consider multiple competing/conflicting criteria for rating different alternatives (CVs) based on pre-defined preference scales from a group of experts. Since then, researchers, including Sharma and Sehrawat (
2020) and Krishankumar
et al. (
2022b), have developed interesting MCDM solutions for selecting CVs in the healthcare industry. According to this research, it can be inferred that existing CV selection approaches (i) may inadequately handle uncertainty, (ii) may overlook expert hesitation and uncertainty, (iii) struggle with extreme value hesitancy in criteria, and (iv) may neglect the importance of compromise solutions in balancing conflicting criteria. These inferences have motivated the following research points:
-
• A decision framework must be adopted to handle the uncertainty of the experts’ and users’ views. This structure has to reduce the uncertainty present in the data.
-
• The data from the experts must be preprocessed to acquire preference and non-preference degree values, which would greatly help in handling the uncertainty.
-
• The importance of the experts must be effectively captured in an uncertain environment to handle extreme values.
-
• The hesitation in the criteria must be effectively captured in an uncertain environment using a model that also considers the experts’ importance.
-
• An effective and compromised ranking model considering the importance of both experts and criteria must be modelled in an uncertain environment.
Driven by these motivations, the key contributions achieved in the presented study include:
-
• Uncertainty has been handled effectively by adopting FFS (“Fermatean fuzzy sets”) since it represents the choices as degree values of preference and non-preference using a broader window than the earlier orthopair versions.
-
• The importance of the experts has been effectively captured using the variance approach since it captures the hesitation present in the criteria.
-
• The importance of the criteria has been effectively captured using the LOPCOW (“logarithmic percentage change-driven objective weighting”), which captures the extreme values effectively using a logarithmic operator.
-
• Finally, a compromise ranking of CVs is obtained using the CoCoSo (“combined compromise solution”) algorithm, which provides a ranking index as a cumulative aggregate of three measures: sum, minimum, and maximum compromise solutions.
The contributions presented above are backed by some rationale that is presented here. FFS (Senapati and Yager,
2020) was introduced as an extension of the IFS (“intuitionistic fuzzy sets”) (Atanassov,
1986) and PFS (“Pythagorean fuzzy sets”) (Yager,
2016). FFS has properties similar to an orthopair fuzzy set with value
$q=3$, offering higher flexibility by preference-sharing for experts. To calculate the expert importance, the variance approach has been used since it captures experts’ hesitation and considers all data points before determining the preference distribution. Further, the LOPCOW method (Ecer and Pamucar,
2022) captures the importance of criteria intending to generate more reasonable weights. Finally, to rank the CVs, the CoCoSo method (Yazdani
et al.,
2019) has been utilized since it provides an overview of all possible compromise solutions by aggregating the weights of the compared sequences of the alternatives using the multiplication rule and weighted power of distances and provides a ranking index as a cumulative aggregate of three measures for every given alternative. The research problem addressed by the authors in this study is to select a suitable cloud vendor for managing data and analytics within healthcare centres by considering FFS as the rating information and an integrated LOPCOW-CoCoSo method as the decision approach. The study aims to reduce human intervention and model uncertainty better by presenting a methodical approach for determining the values for the decision parameters. A group of experts rates different vendors based on quality of service parameters or criteria fed to the system for determining criteria weights and ranks for cloud vendors in the cumulative and personalized fashion. The former way of ranking vendors is the traditional decision-making style where the group opinion is considered holistically to arrive at a decision. At the same time, in a personalized fashion, authors provide a ranking of vendors for each expert’s data. This provides a sense of personalization and aids in better tracking the reasons for a specific selection, which is lacking in the earlier models.
The rest of the article is presented as follows. Section
2 reviews the recent work done on CV selection, FFS, variance method, LOPCOW, and CoCoSo. Section
3 describes the methodology of the proposed framework. Section
4 presents a case study to demonstrate the usefulness of the proposed framework. Section
5 compares the proposed framework with existing frameworks to reveal its strengths and limitations. Section
6 provides the concluding remarks and directs attention to future work.
3 Methodology
This section describes the methodology used in the present study. A pictorial representation of the methodology is shown in Fig.
1.
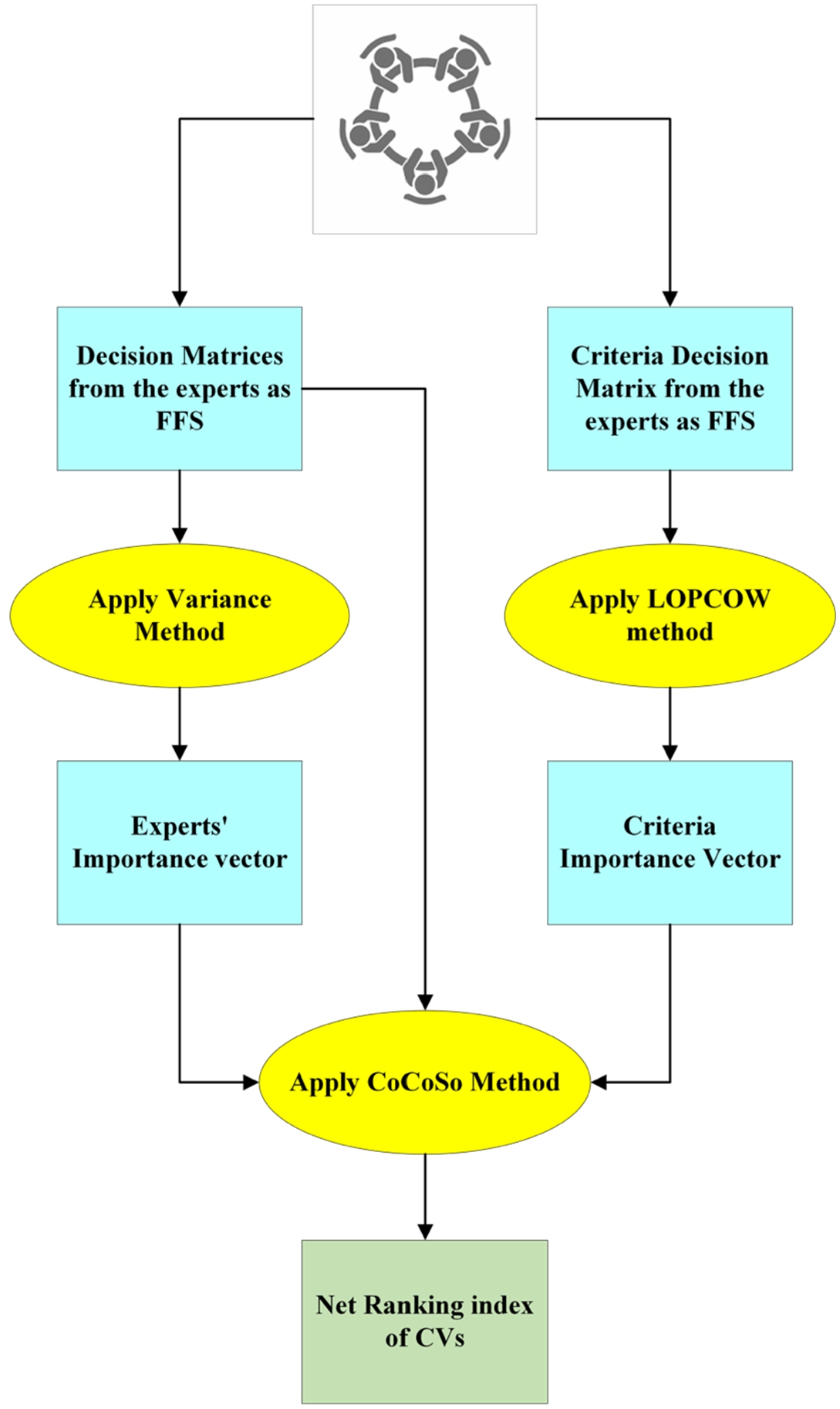
Fig. 1
Methodology of the proposed framework.
Fig.
1 depicts the research model and methodology used in this research to solve the MCDP of CV selection for healthcare centres in uncertain environments. The methodology described in Fig.
1 is presented below in the following manner: (i) Section
3.1 presents some basic concepts related to FFS; (ii) Section
3.2 describes the steps involved in calculating the expert’s importance vector using the variance method; (iii) Section
3.3 explains the steps involved in calculating the criteria importance vector using the LOPCOW method; and (iv) Section
3.4 discusses the steps involved in calculating the net ranking index of CVs using the CoCoSo method.
3.1 Preliminaries
Some basic concepts related to IFS and FFS are presented below:
Definition 1 (Atanassov, 1986).
Let
H be a fixed set and let
N be another fixed set such that
$N\subset H$.
$\bar{N}$ is an IFS in
H and is defined in Eq. (
1):
It is to be noted that in Eq. (
1),
${\mu _{\bar{N}}}(h)$,
${v_{\bar{N}}}(h)$, and
${\pi _{\bar{N}}}(h)=1-({\mu _{\bar{N}}}(h)+{v_{\bar{N}}}(h))$ are the degrees of truth, false, and hesitancy such that they belong to
$[0,1]$, and
${\mu _{\bar{N}}}(h)+{v_{\bar{N}}}(h)\leqslant 1$.
Definition 2 (Senapati and Yager, 2020).
Let
H be a fixed set.
$\bar{V}$ is an FFS in
H and is given by Eq. (
2):
It is to be noted that in Eq. (
2),
${\mu _{\bar{V}}}(h)$ and
${v_{\bar{V}}}(h)$ are the degrees of preference and non-preference such that they belong to
$[0,1]$, and
${\mu _{\bar{V}}}{(h)^{3}}+{v_{\bar{V}}}{(h)^{3}}\leqslant 1$.
Definition 3 (Senapati and Yager, 2020).
Let
${V_{p}}$ be a FFN given by Eq. (
3). FFS
V is defined as a collection of FFN
${V_{p}}$ given by Eq. (
4). Eqs. (
5)–(
8) define the unary operations, i.e. scalar product, power, accuracy, score of
${V_{p}}$, respectively:
Definition 4 (Senapati and Yager, 2020).
Let
${V_{1}}$ and
${V_{2}}$ be two FFNs. Eqs. (
9)–(
10) define the binary operations, i.e. sum and product of
${V_{1}}$ and
${V_{2}}$, respectively:
3.2 Expert Weight Estimation
This section discusses the calculation of experts’ weights, which were calculated using the variance method. The advantage of the variance method inferred from Section
2.3 is as follows: (i) The variance method effectively captures the hesitation and uncertainty exhibited by experts when assigning weights to different criteria. A higher variance in weight values signifies greater uncertainty, allowing the model to reflect real-world complexities that experts may grapple with; and (ii) This method allows for a nuanced understanding of how experts view the importance of various criteria. From a pessimistic perspective, these criteria are vital as they significantly influence the ranking. This behavioural depiction is made possible through the use of variance, providing a more comprehensive understanding of the decision-making process. The steps followed for the calculation of expert weights using the variance method are given below:
Step 1: Let d experts give ratings on x CVs based on c competing criteria. Likert scales are used for converting the ratings into FFNs. The following points are to be noted:
-
• l refers to the expert number, where $l=1,2,\dots ,d$.
-
• i refers to the alternative, i.e. CV number, where $i=1,2,\dots ,x$.
-
• j refers to the criteria number, where $j=1,2,\dots ,c$.
The dimension of the decision matrices for every expert l is $x\times c$.
Step 2: Calculate the accuracy
$A({V_{ij}^{l}})$ of each FFN using Eq. (
7). Please note that the dimensions of the matrices remain intact for every expert
l after calculating the accuracy.
Step 3: Determine the normalized accuracy
$\textit{AN}({V_{ij}^{l}})$ using Eq. (
11). Please note that the dimensions of the matrices remain intact for every expert
l after calculating the normalized accuracy.
Step 4: Determine the variance vector for every expert
d by applying Eq. (
12). Please note that Eq. (
12) yields a
$1\times c$ vector.
It is to be noted that
$\overline{\textit{AN}({V_{j}^{l}})}$ is the mean of the normalized accuracy for every criteria
c calculated in Step 3.
Step 5: Determine the experts’ net confidence using Eq. (
13), which is considered the importance of the experts. Please note that Eq. (
13) yields a
$1\times c$ vector.
It is to be noted that in Eq. (
13),
${w_{l}}$ represents the net confidence value of every expert
l, where
${w_{l}}\in [0,1]$ and
3.3 Criteria Weight Estimation
This section gives an overview of the steps involved in calculating the weight of the criteria, which was calculated via the LOPCOW method. A few advantages of the LOPCOW method can be inferred from Section
2.3 as follows: (i) LOPCOW method is designed to handle significant differences in the criteria weights, making it more adaptable for real-time problems; (ii) This method can also handle negative values present in the criteria, making it more versatile to different decision-making scenarios; (iii) This method also provides a more balanced and reasonable criteria importance, since it achieves relatively smaller ration between most important and least important criteria; (iv) LOPCOW can also manage data size discrepancies, make it more adaptable to varying size of datasets; and (v) LOPCOW provides a more acceptable and a comprehensive criteria importance in decision-making processes. The steps involved in the calculation of criteria weights using the LOPCOW method are presented below:
Step 1: Let d experts give ratings on c competing criteria. Likert scales are used for converting the ratings into FFNs. The following points are to be noted:
-
• l refers to the expert number, where $l=1,2,\dots ,d$.
-
• j refers to the criteria number, where $j=1,2,\dots ,c$.
The dimension of the criteria decision matrix is $d\times c$.
Step 2: Calculate the accuracy
$A({V_{lj}})$ of each FFN using Eq. (
7). Please note that the dimension of the matrix remains intact after calculating the accuracy.
Step 3: Determine the normalized accuracy
$\textit{AN}({V_{lj}})$ using Eq. (
14). The
linear min-max normalization is used in this step. Please note that the dimension of the matrix remains intact after calculating the normalized accuracy.
Step 4: Calculate the percentage values
$p{v_{j}}$ using Eq. (
15). Please note that Eq. (
15) yields a
$1\times c$ vector.
It is to be noted that in Eq. (
15),
${\sigma _{j}}$ represents the standard deviation of the criterion
j.
Step 5: Compute the criteria weights using Eq. (
16). Please note that Eq. (
16) yields a
$1\times c$ vector.
It is to be noted that in Eq. (
16),
${w_{j}}$ represents the net confidence value of every criterion
j, where
${w_{j}}\in [0,1]$ and
3.4 Ranking Algorithm
This section elucidates the steps involved in ranking the CVs, which were performed using the CoCoSo method. The advantages of the CoCoSo method can be inferred from Section
2.3 as follows: (i) CoCoSo method provides a comprehensive approach to ranking alternatives by considering three levels of compromise space: sum, minimum, and maximum allowing for a more nuanced and balanced decision-making process; (ii) This method employs multiple techniques for aggregating weights, such as the multiplication rule and weighted power of distance methods enhancing the flexibility of its applicability in various scenarios; (iii) This method captures the behavioural aspects of decision-making, allowing for a more human-centric evaluation that can be more aligned with real-world decision-making processes; (iv) The method’s ability to aggregate weights using various methods makes it well-suited for scenarios where simple weighting schemes may not capture the complexity of the decision-making environment; and (v) The method’s flexibility in aggregating weights allows it to adapt to problems with different scales or units, making it easier to combine disparate types of information into a unified decision-making framework. The steps involved in ranking the CVs using the CoCoSo method are presented below:
Step 1: Let d experts give ratings on x CVs based on c competing criteria. Likert scales are used for converting the ratings into FFNs. The following points are to be noted:
-
• l refers to the expert number, where $l=1,2,\dots ,d$.
-
• i refers to the alternative, i.e. CV number, where $i=1,2,\dots ,x$.
-
• j refers to the criteria number, where $j=1,2,\dots ,c$.
The dimension of the decision matrices for every expert l is $x\times c$.
Step 2: Calculate the accuracy
$A({V_{ij}^{l}})$ of each FFN using Eq. (
7). Please note that the dimensions of the matrices remain intact for every expert
l after calculating the accuracy.
Step 3: Determine the normalized accuracy
$\textit{AN}({V_{ij}^{l}})$ using Eq. (
11). Please note that the dimensions of the matrices remain intact for every expert
l after calculating the normalized accuracy.
Step 4: Determine the weighted normalized accuracy
$\textit{W AN}({V_{ij}^{l}})$ using Eq. (
17). Please note that the dimensions of the matrices remain intact for every expert
l after calculating the weighted normalized accuracy.
It is to be noted that in Eq. (
17),
${w_{j}}$ refers to the weight of the criteria
j.
Step 5: Determine the multi-stage compromise solutions
${X_{1}^{l}}$,
${X_{2}^{l}}$, and
${X_{3}^{l}}$ using Eqs. (
18)–(
20). Please note that Eqs. (
20)–(
22) yield a
$1\times x$ vector for every expert
l.
It is to be noted that in Eq. (
19) and Eq. (
20),
$\min (.)$ and
$\max (.)$ are the minimum and maximum operators, respectively.
Step 6: Combine the compromise solutions using Eq. (
21) to obtain the net ranking vector for every expert
l. Please note that Eq. (
21) yields a
$1\times x$ vector for every expert
l.
Step 7: Aggregate the rank values for every expert
l using Eq. (
22). Please note that Eq. (
22) yields a
$1\times x$ vector.
It is to be noted that in Eq. (
22),
${w_{l}}$ is the weight of the expert
l, and
${X_{i}}$ is the net ranking index of the
ith CV. Ordering of the net ranking index of the CVs is done by arranging them in the descending order of values based on the vector obtained from Eq. (
22), i.e. if the net ranking index of a CV is high, it is more preferred compared to the other CVs.
The flowchart of the proposed model has been presented in Fig.
2.
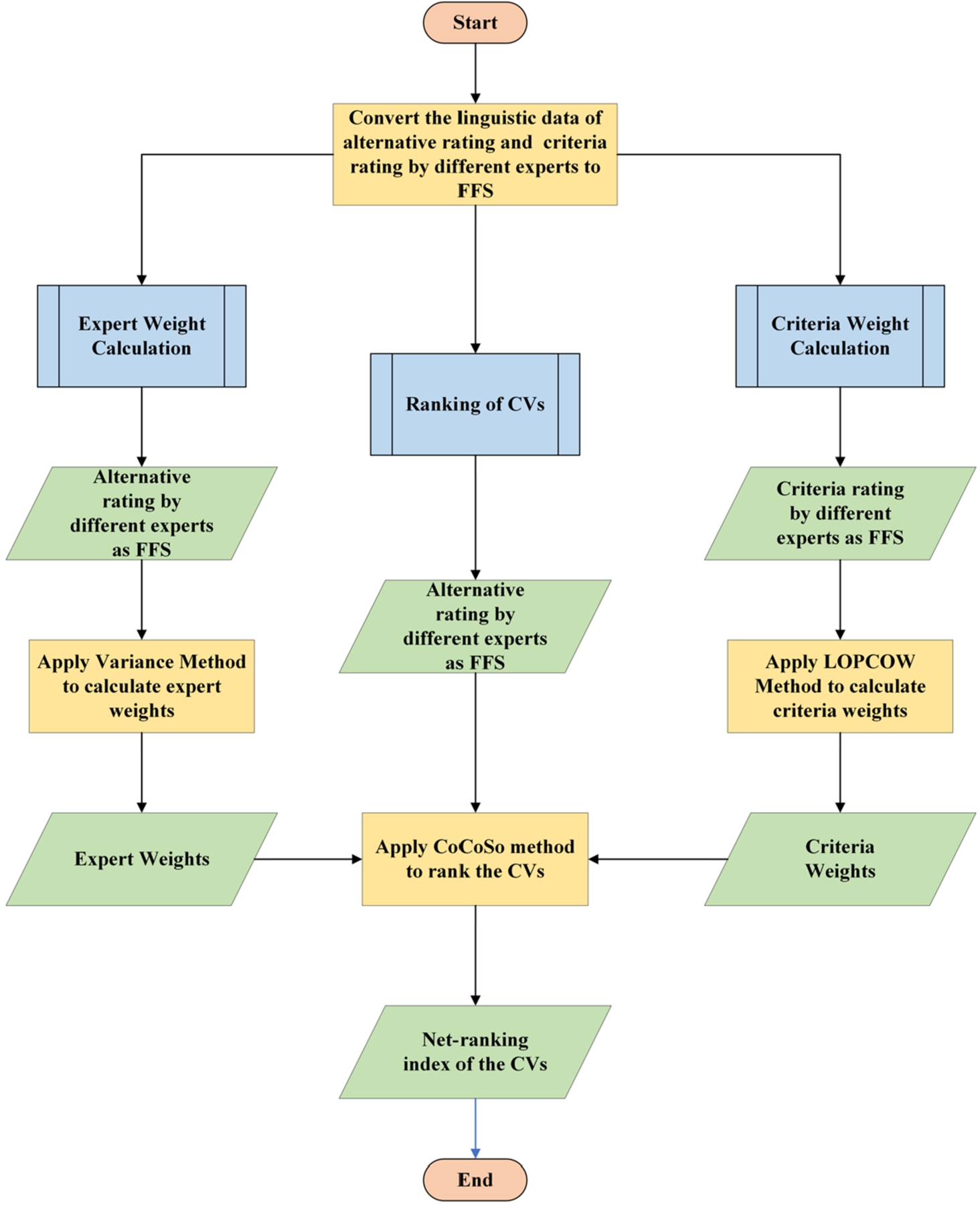
Fig. 2
Flowchart of the proposed model.
In Fig.
2, the flowchart delineates a systematic process for evaluating and ranking CVs. The process commences by converting the linguistic data of both alternative ratings and criteria ratings from various experts into FFS. Subsequently, the evaluation splits into two parallel paths: the left focuses on the calculation of expert weights by first obtaining alternative ratings as FS from different experts and then applying the Variance Method, culminating in a derived set of expert weights. The right path is dedicated to calculating criteria weights, which involves obtaining criteria ratings as FS from different experts and employing the LOPCOW Method. Once both weights are ascertained, the CoCoSo method ranks the CVs, resulting in a net-ranking index. The procedure concludes once the final rankings of the CVs are established.
4 Case Study
This section presents a case example of CV selection for a health centre, concentrating effectively on the centre’s core activities without compromising utility activities. Such utility activities include data storage for patients’ data, employee data, inventory data, and official records, appointment maintenance, and analytics operations for planning the next five-year target and focusing on the mechanism for improving profitability. As a result, there was an urge for rational selection of CVs to support the health centre.
During the annual audit meeting, the centre’s officials decided to invest in cloud technology to stay competitive and balance core and utility activities. The advent of the pandemic emphasized the urgent need for effective data storage and maintenance to serve patients and employees better. Learning from the pandemic, the officials framed a panel of three experts with six to eight years of experience in their respective fields, such as technology, finance and audit, and legal/ethical aspects. The experts include a senior professor from the cloud computing division, legal/audit personnel, and a senior cloud admin from a company. These experts selected ten CVs from a cloud armor repository. Based on a peer discussion through emails and phone calls, seven CVs were chosen for the study and were rated by experts based on ten QoS attributes, considered from CSMIC (Siegel and Perdue,
2012) that offers benchmarking factors for cloud services. The ten QoS criteria are agility, assurance, scalability, availability, security, user-friendliness, customer relationship, privacy breach, total cost, and integrity risk. For ease of representation,
${C_{1}},{C_{2}},\dots ,{C_{10}}$ denotes the criteria considered,
${A_{1}},{A_{2}},\dots ,{A_{7}}$ represents the CVs considered, and
${D_{1}},{D_{2}},{D_{3}}$ represents the experts. Criteria
${C_{1}},{C_{2}},\dots ,{C_{7}}$ are the benefit criteria, and
${C_{8}},{C_{9}}$, and
${C_{10}}$ are the cost criteria.
The steps involved in ranking the seven CVs against the ten criteria with the collected data by three experts using the proposed framework are presented below:
Step 1: Construct a
$7\times 10$ matrix for every expert by considering their ratings from Table
3. Convert the data into an FFN defined in Section
3.1 with Eq. (
7) using the Likert scale in Table
2.
Table 2
Likert scale to convert data to FFN.
| CV rating |
Criteria rating |
| Linguistic term |
FFN |
Linguistic term |
FFN |
| Extremely Low (EL) |
$(0.6,0.9)$ |
Extremely Less Preferred (ELP) |
$(0.6,0.9)$ |
| Very Low (VL) |
$(0.7,0.8)$ |
Very Less Preferred (VLP) |
$(0.7,0.8)$ |
| Moderately Low (ML) |
$(0.6,0.8)$ |
Moderately Less Preferred (MLP) |
$(0.6,0.8)$ |
| Low (L) |
$(0.6,0.7)$ |
Less Preferred (LP) |
$(0.6,0.7)$ |
| Moderate (M) |
$(0.5,0.5)$ |
Neutral (N) |
$(0.5,0.5)$ |
| High (H) |
$(0.7,0.6)$ |
Highly Preferred (HP) |
$(0.7,0.6)$ |
| Moderately High (MH) |
$(0.8,0.6)$ |
Moderately Highly Preferred (MHP) |
$(0.8,0.6)$ |
| Very High (VH) |
$(0.8,0.7)$ |
Very Highly Preferred (VHP) |
$(0.8,0.7)$ |
| Extremely High (EH) |
$(0.9,0.6)$ |
Extremely Highly Preferred (EHP) |
$(0.9,0.6)$ |
Table
2 presents the Likert scale for converting linguistic data to FFN. Values from Table
2 were used in Table
3 and Table
4 for performing the decision-making process.
Table 3
Dataset consisting of ratings of seven CVs by three experts using ten criteria.
| CVs |
Experts |
Criteria |
| ${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
${C_{5}}$ |
${C_{6}}$ |
${C_{7}}$ |
${C_{8}}$ |
${C_{9}}$ |
${C_{10}}$ |
| ${A_{1}}$ |
${D_{1}}$ |
ML |
VH |
EH |
VL |
H |
VH |
L |
M |
L |
H |
|
${D_{2}}$ |
L |
VL |
MH |
ML |
VL |
H |
EH |
L |
EH |
M |
|
${D_{3}}$ |
EH |
VH |
L |
EH |
ML |
VL |
L |
M |
ML |
ML |
| ${A_{2}}$ |
${D_{1}}$ |
VH |
H |
MH |
MH |
M |
L |
MH |
L |
M |
M |
|
${D_{2}}$ |
VH |
VH |
ML |
MH |
H |
ML |
VH |
VH |
M |
VH |
|
${D_{3}}$ |
L |
H |
VH |
M |
ML |
L |
MH |
VH |
ML |
MH |
| ${A_{3}}$ |
${D_{1}}$ |
MH |
H |
VH |
ML |
VL |
ML |
M |
L |
L |
MH |
|
${D_{2}}$ |
H |
M |
H |
ML |
ML |
EH |
VL |
M |
VH |
L |
|
${D_{3}}$ |
M |
H |
ML |
M |
M |
EH |
ML |
M |
M |
L |
| ${A_{4}}$ |
${D_{1}}$ |
VH |
ML |
ML |
VL |
H |
M |
H |
EH |
MH |
MH |
|
${D_{2}}$ |
EH |
EH |
VL |
VH |
H |
M |
L |
ML |
MH |
M |
|
${D_{3}}$ |
VH |
H |
VL |
ML |
L |
M |
VL |
VL |
VH |
VH |
| ${A_{5}}$ |
${D_{1}}$ |
M |
H |
H |
M |
MH |
L |
VH |
M |
EH |
M |
|
${D_{2}}$ |
M |
VH |
ML |
L |
M |
MH |
ML |
VL |
ML |
H |
|
${D_{3}}$ |
M |
ML |
L |
VL |
ML |
M |
MH |
M |
L |
L |
| ${A_{6}}$ |
${D_{1}}$ |
VH |
VL |
M |
ML |
EH |
MH |
VL |
VH |
VH |
L |
|
${D_{2}}$ |
H |
M |
H |
MH |
VH |
L |
ML |
ML |
M |
ML |
|
${D_{3}}$ |
H |
ML |
H |
L |
ML |
VL |
M |
H |
MH |
VH |
| ${A_{7}}$ |
${D_{1}}$ |
M |
MH |
M |
MH |
L |
L |
VH |
VL |
H |
EH |
|
${D_{2}}$ |
EH |
VH |
VL |
L |
M |
ML |
EH |
ML |
M |
L |
|
${D_{3}}$ |
H |
M |
M |
H |
EH |
MH |
ML |
ML |
EH |
M |
Table
3 presents the dataset containing ratings for seven CVs based on the ten criteria by three experts. This data was converted into an FFN by finding the accuracy using Eq. (
7) after converting it to
$(u,v)$ structure using the Likert scale presented in Table
2.
Step 2: Calculate the experts’ importance with the matrices from Step 1 using the variance method presented in Section
3.2 using Eqs. (
11)–(
13).
The accuracy computed using Eq. (
7) was normalized based on cost and benefit criteria using Eq. (
11). Variance values were then determined by considering Eq. (
12), and later, the experts’ importance was computed using Eq. (
13). The importance of experts
${D_{1}}$,
${D_{2}}$, and
${D_{3}}$ was computed to be 0.339, 0.310, and 0.351, respectively, which were further used for rational decision-making.
Step 3: Construct a
$3\times 10$ matrix by considering the criteria ratings by the experts from Table
4. Convert the data into an FFN defined in Section
3.1 using the Likert scale in Table
2.
Table 4
Dataset consisting of ratings of ten criteria by three experts.
| Experts |
Criteria |
| ${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
${C_{5}}$ |
${C_{6}}$ |
${C_{7}}$ |
${C_{8}}$ |
${C_{9}}$ |
${C_{10}}$ |
| ${D_{1}}$ |
N |
MHP |
LP |
VHP |
MHP |
N |
EHP |
VLP |
N |
HP |
| ${D_{2}}$ |
VHP |
VHP |
LP |
N |
MLP |
EHP |
VHP |
MHP |
HP |
HP |
| ${D_{3}}$ |
MLP |
LP |
MHP |
MLP |
N |
N |
EHP |
HP |
HP |
VHP |
Table
4 contains the ratings of the ten criteria by the three experts. This data was converted into an FFN by finding the accuracy using Eq. (
7) after converting it to
$(u,v)$ structure using the Likert scale presented in Table
2.
Step 4: Calculate the criteria importance with the matrices from Step 3 using the LOPCOW method presented in Section
3.3 using Eqs. (
14)–(
16).
The accuracy computed using Eq. (
7) was normalized based on cost and benefit criteria using Eq. (
14). The criteria importance was computed to be 0.068, 0.102, 0.153, 0.068, 0.057, 0.153, 0.057, 0.131, 0.153, and 0.057 for criteria
${C_{1}},{C_{2}},\dots ,{C_{10}}$, respectively, by applying Eq. (
15) to determine the log vector of the estimates that were further normalized with Eq. (
16) to determine weights of criteria shown above.
Step 5: Calculate the net ranking index of CVs with the matrices from Step 1, experts’ importance from Step 2, and criteria importance from Step 4 using the CoCoSo method presented in Section
3.4 using Eqs. (
17)–(
22).
Table 5
Net ranking index of CVs.
| Cloud vendors |
Net ranking index |
| Experts |
Cumulative |
| ${D_{1}}$ |
${D_{2}}$ |
${D_{3}}$ |
| ${A_{1}}$ |
17.876 |
16.966 |
19.901 |
18.263 |
| ${A_{2}}$ |
14.675 |
17.874 |
18.302 |
16.856 |
| ${A_{3}}$ |
17.652 |
15.343 |
13.318 |
15.312 |
| ${A_{4}}$ |
18.543 |
16.238 |
20.202 |
18.338 |
| ${A_{5}}$ |
13.903 |
15.299 |
15.232 |
14.787 |
| ${A_{6}}$ |
19.973 |
14.568 |
17.776 |
17.387 |
| ${A_{7}}$ |
16.769 |
16.104 |
16.510 |
16.470 |
After finding the accuracy with Eq. (
7) and normalizing them with Eq. (
11), the weighted normalized accuracy was computed using Eq. (
17). The multi-stage compromise solutions, i.e. sum, minimum, and maximum, were computed using Eqs. (
18)–(
20), respectively. Eq. (
21) was then used to aggregate the compromise solutions as the sum of the arithmetic and geometric mean of these solutions. Finally, the net-ranking index was computed using Eq. (
22), multiplying all the compromise solutions raised to its corresponding expert weights.
Table
5 presents the net-ranking index of each expert,
${D_{1}}$,
${D_{2}}$, and
${D_{3}}$, and the cumulative net-ranking index for all the CVs,
${A_{1}},{A_{2}},\dots ,{A_{7}}$. From Table
5, it can be concluded that the ranking order of the CVs is
${A_{4}}\gt {A_{1}}\gt {A_{6}}\gt {A_{2}}\gt {A_{7}}\gt {A_{3}}\gt {A_{5}}$ with ${A_{4}}$ being the viable candidate for the process followed by ${A_{1}}$, ${A_{6}}$, and so on.
6 Conclusion
The framework developed in this article is valuable for the rational selection of CVs to manage utility activities in the health industry effectively. Primarily, the framework focuses on better modelling uncertainty and reducing human intervention to tackle the issues of bias and subjectivity. Weights of experts and criteria are methodically determined with better capturing of hesitation of experts during preference articulation along with personalized rank orders of CVs, which aids in mitigating subjectivity and biases. The model provides both cumulative and personalized ordering of CVs that offers better planning and rationale toward a specific selection. Utilization of FFN for data models uncertainty effectively from three dimensions, i.e. membership, hesitancy, and non-membership, gives a broader window for preference expressions. Variance and LOPCOW methods are presented for determining the weights of entities, and later, a ranking algorithm with CoCoSo and rank fusion is put forward for determining the rank values of CVs at both the individualistic and cumulative levels.
From Table
6, Fig.
3, and Fig.
4, the efficacy of the framework is clarified from both the application and method perspectives. Some notable aspects of the proposed framework include consistency, broad rank values, and methodical parameter calculations. Further, some implications of the framework include: (i) is a ready-to-use module that can supplement decisions from stakeholders; (ii) reduces human intervention and provides a methodical approach for calculating decision parameters that reduce inaccuracies and subjectivity; (iii) can be used both by users and CVs for their respective purposes, such as aiding selection and planning strategies to improve market growth, respectively; (iv) offers both sense of personalization and cumulative rank estimation that adds value to stakeholders at the decision-making process; (v) uncertainty is handled from three dimensions – preference, non-preference, and hesitancy; (vi) subjective randomness issue and bias from the system is handled via methodical calculation of entities; and (vii) can be used by policymakers and other stakeholders after training which can be facilitated via seminars, hands-on sessions, and workshop.
Some limitations of the work are: (i) data are assumed to be complete, and if, due to hesitation, some instances are not available, the system cannot handle the issue; (ii) partial information about entities cannot be considered in the present formulation; (iii) customized ranking; (iii) pre-defined terms are being used, which in some sense restricts the experts from flexibly providing her/his rating; and (iv) functional criteria are considered for rating CVs, but social and environmental factors are not included in the present study. In terms of future research scope, we plan to address the limitations and extend the framework to different MCDM applications from supply chains, energy, sustainability, environment sectors, and so on. Further, we also anticipate extending different fuzzy versions, such as interval and probabilistic variants of orthopair fuzzy sets, hesitant fuzzy sets, neutrosophic fuzzy sets, and alike, to better understand uncertainty modelling for CV selection. Also, the data-preprocessing module is planned to enhance the rating information with consistent preference information from experts either via feedback mechanism or methodical data entry. Finally, concepts of machine learning and recommender systems can be integrated with the proposed framework to perform large-scale decision-making better.
Author contributions
S. Dhruva – Conceptualization, Data curation, Prototyping, Implementation, Writing and Editing.
R. Krishankumar – Conceptualization, Data curation, Implementation, Writing and Editing.
E.K. Zavadskas – Implementation, Supervision, Review, Writing and Editing.
K.S. Ravichandran – Prototyping, Supervision, Review Writing and Editing.
A.H. Gandomi – Language Editing, Implementation, Supervision, Writing and Editing.

