1 Introduction
In our world which is becoming a more global marketplace, the global environment is forcing companies to take almost everything into consideration at the same time, remain competitive and respond to rapidly changing markets. In this aspect, supply chain management and strategic sourcing have been one of the fastest-growing and most important areas of management in companies. Since technological complexity has affected the logistics and supply chains directly, the supply chain management has to adapt to these complex and dynamic factors. So, in this trading world, the search for new and strategic suppliers is a continuous priority for companies in order to upgrade the variety and typology of their product range. Hence, supplier selection represents one of the most important functions to be performed by the purchasing department that determines the long-term viability of a company. Strategic supplier selection is a multi-criteria problem that includes both qualitative and quantitative criteria. In order to select the best suppliers, it is necessary to make a tradeoff between tangible and intangible criteria, some of which may conflict. In this case, we are required to handle a decision-making problem.
Decision-making is the process of identifying different and possible alternatives that can solve a problem and choosing the one that will best meet the expectations among these alternatives. Since complexity prolongs the decision-making process, as it requires the evaluation of many alternatives according to many criteria in the process, many studies and decision-making methods have been developed in the literature to work with complex data and make an appropriate choice (Chen,
1988; Maji
et al.,
2001). Multi-criteria decision-making (MCDM) is one of the decision-making methods based on an expert’s opinion. If more than one expert is attending, this method is called MCGDM. In literature, there are many techniques that have been developed to solve MCDM and MCGDM problems such as the Analytic Hierarchy Process (AHP) (Saaty,
1980), Technique for Order Performance by Similarity to Ideal Solution (TOPSIS) (Hwang and Yoon,
1981), COPRAS (Zavadskas
et al.,
1994), VIsekriterijumsko optimizacija Kompromisno Rangiranje (VIKOR) (Opricovic,
1998), Multi-Objective Optimization by Ratio Analysis (MOORA) (Brauers and Zavadskas,
2006) and so on.
Fuzzy set (FS) theory (Zadeh,
1965) is an effective tool for solving decision-making problems in this increasingly complex world, as FS is a way of thinking used to describe the imprecise. However, since the evaluation is only made on the degree of membership in FS theory, this is also insufficient to solve complex problems. For this reason, many generalizations of FS theory have been made in the literature. The intuitionistic fuzzy set (IFS) (Atanassov,
2003) which is one of these generalizations, refers to a set whose sum of positive-membership degree and negative-membership degree is less than or equal to 1. After, the IFS theory was extended to Pythagorean fuzzy set (PyFS) (Yager,
2013) theory by considering the sum of the squares of its positive-membership degree and negative-membership degree is less than or equal to 1. The other extension of IFS is Picture Fuzzy Set (PFS) (Cuong,
2013) which has positive-membership, neutral-membership and negative-membership degrees and the sum of these degrees is less than or equal to 1. PFS is able to deal with problems that have more answers. Then the theory of SFS has been developed by Mahmood
et al. (
2018) to encounter situations that PFS cannot meet. In the SFS, the sum of the squares of positive-membership, neutral-membership and negative-membership degrees is less than or equal to 1. Many authors have studied on these sets (Aydoğdu and Gül,
2020; Güner and Aygün,
2020,
2022). Geometric representations of the theories IFS, PyFS, PFS and SFS are shown in Fig.
1. The mentioned set theories are highly proficient and skilled to carry ambiguous information but their capabilities are limited to handle one-dimensional data. Many MCDM problems comprise two-dimensional data but the existing MCDM strategies are incompetent to handle the two-dimensional information. To handle such phenomena, complex generalizations of FSs mentioned above have been studied by Ramot
et al. (
2002,
2003), Alkouri and Salleh (
2013), Ullah
et al. (
2020), Akram
et al. (
2021c) and these sets have been applied to many decision-making problems. Azam
et al. (
2022) gave an example of evaluating the enterprise’s information security management issue in a particular organization on complex intuitionistic fuzzy sets (CIFSs). Akram
et al. (
2020) made an example of selecting the best capable ERP systems as candidates after collecting information about ERP vendors and systems from all aspects of the complex picture fuzzy set (CPFS) environment. Recently, Akram
et al. (
2021c) introduced the theory of CSFSs to handle the two-dimensional data where we consider the degrees of positive-membership, neutral-membership, negative-membership and refusal that lie inside a complex unit circle. According to this theory, the sum of squares of their amplitude (and phase terms) can not exceed 1. In this way, lots of decision-making problems, consisting of the mentioned data, became solvable by using the developed MCGDM methods.
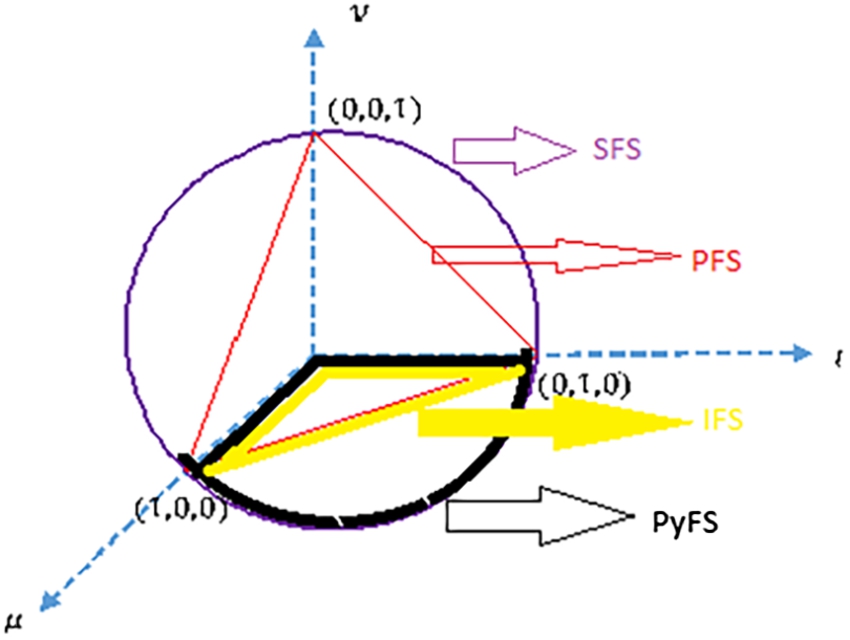
Fig. 1
Geometric representations of IFS, PyFS, PFS and SFS.
One of the most critical steps in MCDM/MCGDM techniques is to determine the weights of the criteria because the weights directly affect the ranking of the alternatives. For this reason, many methods have been developed to calculate criterion weights. Some of these are subjective and some are weighting methods based on an objective point of view. Methods such as AHP (Saaty,
1980), Analytic Network Process (ANP) (Saaty,
1996), Step-Wise Weight Assessment Ratio Analysis (SWARA) (Keršuliene
et al.,
2010), Full Consistency Method (FUCOM) (Pamucar
et al.,
2018) and Level Based Weight Assessment (LBWA) (Žižović and Pamucar,
2019) are among the subjective weighting methods in which the preferences of DMs are taken into account. In some objective weighting methods such as Entropy (De Luca and Termini,
1972), CRiteria Importance Through Intercriteria Correlation (CRITIC) by Diakoulaki
et al. (
1995), Best Worst Method (BWM) (Rezaei,
2015) and Method based on the Removal Effects of Criteria (MEREC) by Keshavarz-Ghorabaee
et al. (
2021), the mathematical model is solved without considering the ideas of the DMs.
Entropy is the random measurement of the uncertainty in a process or the amount of information produced. It is also relevant to questions about how to measure the uncertainty of the entropy fuzzy environment. Many authors (De Luca and Termini,
1972,
1977; Xuecheng,
1992; Fan and Xie,
1999) introduced the axiom construction of FS entropy. Hung and Yang (
2006) extended these ideas to construct the concept of the fuzzy entropy of IFSs. Thaoa and Smarandache (
2019) extended the fuzzy entropy of Hung and Yang (
2006) to PFSs. Many authors (Thaoa and Smarandache,
2019; Rani
et al.,
2020b; Alipour
et al.,
2021; Gül and Aydoğdu,
2021; Chaurasiya and Jain,
2022) gave the entropy measure on PFS to solve many decision-making problems. Aydoğdu and Gül (
2020) proposed a novel entropy measure for SFSs and applied this entropy to solve the MCGDM problems. Also, Naeem
et al. (
2022) and Aydoğdu
et al. (
2023) defined the new entropy measure functions to calculate the weights of criteria objectively. In Table
1, one can find some remarkable studies that are combined with the traditional methods and the mentioned objective and subjective weighting approaches.
1.1 Literature Review
The COPRAS method, introduced by Zavadskas
et al. (
1994), is used to assess the maximizing and minimizing index values where the effect of maximizing and minimizing indexes of attributes on the assessment of the results is considered separately. The effectiveness and usefulness of this method are based on the fact that this method is a compensatory method, attributes are independent and the qualitative attributes are converted into the quantitative attributes. Since this method was presented by Zavadskas
et al. (
1994), many authors established this approach on the different set theories with the objective/subjective weighting of both weights of DMs and criteria by giving several applications in the different real-life problems as seen in Table
2.
Table 1
Some combinations with traditional methods via objective and subjective weighting.
| Obj. w. |
Some combined versions |
Given by |
Subj. w. |
Some combined versions |
Given by |
| MEREC |
MEREC-ARAS |
Rani et al. (2022) |
ANP |
ANP-TOPSIS |
Sakthivel et al. (2015) |
| MEREC |
MEREC-MULTIMOORA |
Mishra et al. (2022) |
ANP |
ANP-DEMATEL |
Yang et al. (2008) |
| MEREC |
MEREC-WASPAS |
Keshavarz-Ghorabaee (2021) |
ANP |
ANP-COPRAS |
Balali et al. (2021) |
| CRITIC |
CRITIC-CoCoSo |
Peng et al. (2020) |
AHP |
AHP-COPRAS |
Ecer (2014) |
| CRITIC |
CRITIC-WASPAS |
Keshavarz-Ghorabaee et al. (2017) |
AHP |
AHP-TOPSIS |
Anser et al. (2020) |
| BWM |
BWM-LBWA-CoCoSo |
Torkayesh et al. (2021) |
LBWA |
BWM-LBWA-CoCoSo |
Torkayesh et al. (2021) |
| BWM |
BWM-TOPSIS |
Gupta and Barua (2017) |
LBWA |
LBWA-WASPAS |
Pamucar et al. (2020) |
| Entropy |
Entropy-COPRAS-MULTIMOORA |
Alkan and Albayrak (2020) |
FUCOM |
FUCOM-MABAC |
Bozanic et al. (2020) |
| Entropy |
Entropy-WASPAS |
Aydoğdu and Gül (2020) |
FUCOM |
FUCOM-MARCOS |
Pamucar et al. (2021) |
| Entropy |
Entropy-ARAS |
Aydoğdu and Gül (2022) |
SWARA |
SWARA-COPRAS |
Rani et al. (2020a) |
| Entropy |
Entropy-TOPSIS |
Aydoğdu et al. (2023) |
SWARA |
SWARA-VIKOR |
Alimardani et al. (2013) |
Table 2
Literature review for COPRAS method.
| Given by |
Model |
Method |
Group |
Criteria weights |
Application area |
| Kumari and Mishra (2020) |
IFS |
COPRAS |
X |
Obj. (Entropy) |
Green supplier selection |
| Mishra et al. (2020) |
IFS |
SWARA-COPRAS |
X |
Subj. (SWARA) |
Select. of an optimal bioenergy production tech. |
| Schitea et al. (2019) |
IFS |
WASPAS-COPRAS-EDAS |
X |
Subj. |
Hydrogen mobility roll-up site selection |
| Buyukozkan and Gocer (2019) |
PyFS |
AHP-COPRAS |
X |
Subj. (AHP) |
Digital supply chain partner selection |
| Rani et al. (2020b) |
PyFS |
COPRAS |
X |
Obj. (Entropy) |
Pharmacological therapy select. for type-2 diabetes |
| Dorfeshan and Mousavi (2019) |
PyFS |
COPRAS-TOPSIS |
√ |
|
Marble processing plants project |
| Chaurasiya and Jain (2022) |
PyFS |
COPRAS |
X |
Obj. (Entropy) |
Multi-criteria healthcare waste treatment problem |
| Thaoa and Smarandache (2019) |
PyFS |
COPRAS |
X |
Obj. (Entropy) |
Select. of teaching management system |
| Alipour et al. (2021) |
PyFS |
SWARA-COPRAS |
X |
Obj. (Entropy) |
Fuel cell and hydrogen components supplier select |
|
|
|
X |
Subj. (SWARA) |
|
| Lu et al. (2021) |
PFS |
COPRAS |
√ |
Obj. (CRITIC) |
Green supplier selection |
| Kahraman et al. (2020) |
PFS |
COPRAS-VIKOR-TOPSIS |
X |
Subj. (AHP) |
A state of the art survey |
| Omerali and Kaya (2022) |
SFS |
COPRAS |
√ |
Subj. |
Selection of the augmented reality solution |
| Güner et al. (2022) |
SFS |
AHP-COPRAS |
√ |
Subj. (AHP) |
Renewable energy selection |
Nowadays, researchers are handling MCDM/MCGDM problems including uncertain two-dimensional data. Especially, the CSFSs have drawn attention to their broader structure when comparing other set theories. Different approaches with several applications in the CSF environment have been presented: Ali
et al. (
2020) introduced the complex spherical fuzzy Bonferroni mean (CSFBM) and complex spherical fuzzy weighted Bonferroni mean (CSFWBM) operators and presented the TOPSIS method on CSFSs based on these operators. Then, Akram
et al. (
2021c) presented the complex spherical fuzzy VIKOR (CSF-VIKOR) method by merging the grounds of VIKOR method and CSFSs and applied this approach in the field of business related to an advertisement on Facebook. As a continuation, Akram
et al. (
2021a) presented the complex spherical fuzzy TOPSIS (CSF-TOPSIS) method that cumulates the novel features of CSFSs with the potential of the TOPSIS method. Then they ranked the alternatives in an ascending order of revised closeness index, evaluated by deploying normalized Euclidean distance. They also explicated the adequacy of the CSF-TOPSIS method and conducted a comparative study with CSF-TOPSIS and CSF-VIKOR. Akram
et al. (
2021b) and Zahid
et al. (
2022) presented the CSF-ELECTRE I and CSF-ELECTRE II in the CSF environment and solved the problems of “selection of network monitoring software” and “selection of the most efficient technology to treat cadmium-contaminated water”, respectively. Moreover, Naeem
et al. (
2022) established an MCGDM method based on some aggregation operators and entropy measure function which is used to calculate the weights of criteria objectively, and applied this method to the green supplier selection problem consisting of two-dimensional information. Recently, Aydoğdu
et al. (
2023) established a novel CSF-TOPSIS based on entropy method under the complex spherical fuzzy environment by calculating the weights of both the DMs and criteria objectively with a novel entropy measure function. All mentioned studies in the CSF environment are listed categorically in Table
3.
Table 3
Literature review for the MCDM-MCGDM methods in the CSFSs.
| Given by |
Model |
Method |
Group |
Criteria weights |
Application area |
| Ali et al. (2020) |
CSFS |
TOPSIS |
X |
Subj. |
Select. of organization to extend the income |
| Akram et al. (2021b) |
CSFS |
ELECTRE-I |
X |
Subj. |
Select. of location for new branch of a company |
| Akram et al. (2021a) |
CSFS |
TOPSIS |
√ |
Subj. |
Select. of best water supply strategy |
| Akram et al. (2021c) |
CSFS |
VIKOR |
√ |
Subj. |
Select. of the advertisement on Facebook |
| Aldemir et al. (2021) |
CSFS |
TOPSIS based on aggregation op. |
√ |
Subj. |
|
| Zahid et al. (2022) |
CSFS |
ELECTRE-II |
√ |
Subj. |
Selection of the tech. to treat cad.-contam. water |
| Naeem et al. (2022) |
CSFS |
Aggregation operators |
√ |
Obj. |
Green supplier selection |
| Aydoğdu et al. (2023) |
CSFS |
TOPSIS based on entropy |
√ |
Obj. |
Select. of the advertisement on Facebook |
1.2 Motivation and Main Contribution
COPRAS method is used for the evaluation of the multi-criteria system of variables for maximizing and minimizing the values. Since this method allows us to compare and also check the final results of measuring easily, it is preferred more over the other existing methods. Also, this method allows being used to implement the comparison and evaluation of variables described hierarchically without requiring such transformation as minimizing the variables. On the other hand, CSFS theory is more powerful with its superior structure to those modern extensions of FS theory which can elaborate the two-dimensional ambiguous information. By considering all positive sides, in this study, we establish a novel method by considering respect to the advantages of CSFSs in describing uncertain information, the useful structure of the COPRAS method in MCGDM problems and the entropy measure which allows for determining the objective weights of the criteria. While the proposed method determines the unknown criteria weights by using the entropy measure, it satisfies that the smaller entropy measure of a criterion among alternatives should be imposed as the bigger weight to that criterion, and otherwise, the smaller weight to that criterion. We can enlist the main objectives of the article as follows:
-
1) We establish a novel improved COPRAS method in CSFS. In this method, a new formula is developed to evaluate unknown weight information of both DMs and criteria weights. These weights are calculated by using the entropy measure method to obtain objective weights. For this reason, we propose a new entropy measure function and explain why we need this entropy measure function and what kind of superiority it has over the existing functions.
-
2) We solve the problem of “selection of the strategic supplier” by the proposed method as an objective weight of DMs and criteria.
-
3) To explicate the adequacy of the proposed strategy and consistency of the result, a comparison analysis and method analysis with the existing method are presented.
-
4) The versatility and decision-making skills of our proposed COPRAS method is not only limited to two-dimensional data but also this method exhibits the same accuracy when applied to one-dimensional data inclusive of spherical fuzzy data and picture fuzzy data by taking their phase term equal to zero. Thus, the proposed methodology is a flexible approach that competently manages both traditional and two-dimensional uncertain information with precision.
-
5) The proposed COPRAS technique not only deals excellently with CSF information but also can be successfully applied to the complex Pythagorean model and complex intuitionistic model by taking their neutral-membership equal to zero.
-
6) The objective weight data of our proposed method is not limited to the COPRAS methodology. Proposed objective criteria weighting schema and objective DMs’ weighting schema can be applied to different CSF-MCGDM methods with the same example if their methods include subjective weighting data.
-
7) We compare this method with the CSF-TOPSIS based on entropy method given by Aydoğdu
et al. (
2023), CSF-ELECTRE II method by Zahid
et al. (
2022) and based on aggregation operators method by Naeem
et al. (
2022) in the CSF environment to show the consistency of the proposed method. We also analyse the results obtained by using the F-TOPSIS and SF-COPRAS methods in fuzzy and SF environments.
The rest of the paper is organized as follows. In Section
2, we recall some basic definitions of CSFSs and necessary operators. We introduce a novel entropy measure for CSFS in Section
3. Section
4 presents the improved COPRAS method with calculated objective weights of both DMs and criteria. In Section
5, we give an application of the proposed COPRAS method in a real-life problem related to the strategic supplier selection. The results are compared with other methods such as F-TOPSIS, SF-COPRAS, CSF-TOPSIS based on entropy, CSF-ELECTRE II and based on aggregation operators methods in CSF environment in Section
6. The effectiveness of the proposed method is clarified with the comparisons.
4 COPRAS Method Based on Entropy
In this section, we establish the COPRAS method to solve MCGDM problems in the complex spherical fuzzy environment when the information of both weights of DMs and criteria are completely unknown. With this aim, we calculate the weights of DMs based on Euclidean distance and the weights of criteria based on the proposed new entropy measure.
Let
$A=\{{A_{1}},{A_{2}},\dots ,{A_{k}}\}$ be the set of
k alternatives,
$C=\{{C_{1}},{C_{2}},\dots ,{C_{m}}\}$ be the set of
m criteria and
$E=\{{E_{1}},{E_{2}},\dots ,{E_{n}}\}$ be the set of
n experts (DMs) hired for decision-making. Each expert
${E_{r}}$ evaluates the alternatives
${A_{p}}$ with respect to
${C_{q}}$ by considering the influence of
${C_{q}}$ on the alternatives
${A_{p}}$ and by using the linguistic table given in Table
4.
Table 4
Linguistic terms to evaluate the alternatives via criteria (Zahid
et al.,
2022).
| Lingusitic terms |
CSFNs |
| Very good (VG)/Very important (VI) |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
| Good (G)/Important (I) |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
| Medium good (MG)/Medium important (MI) |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
| Medium (M) |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
| Medium poor (MP)/Medium unimportant (MUI) |
$\big(0.54{e^{i2\pi (0.53)}},0.31{e^{i2\pi (0.33)}},0.62{e^{i2\pi (0.65)}}\big)$ |
| Poor (P)/Unimportant(UI) |
$\big(0.47{e^{i2\pi (0.46)}},0.23{e^{i2\pi (0.26)}},0.73{e^{i2\pi (0.76)}}\big)$ |
| Very poor (VP)/Very unimportant (VUI) |
$\big(0.33{e^{i2\pi (0.31)}},0.17{e^{i2\pi (0.19)}},0.82{e^{i2\pi (0.83)}}\big)$ |
Then these values establish the complex spherical fuzzy decision matrix (CSFDM)
${D^{(r)}}={({d_{pq}^{(r)}})_{k\times m}}$ for all
$r\in \{1,2,\dots ,n\}$, where
${{d_{pq}}^{(r)}}=\big({f_{{D_{pq}}}^{(r)}}{e^{i{\alpha _{{D_{pq}}}^{(r)}}}},{{g_{{D_{pq}}}}^{(r)}}{e^{i{\beta _{{D_{pq}}}^{(r)}}}},{{h_{{D_{pq}}}}^{(r)}}{e^{{i{\gamma _{{D_{pq}}}}^{(r)}}}}\big)$. The CSFDM built by expert
${E_{r}}$ is represented as follows:
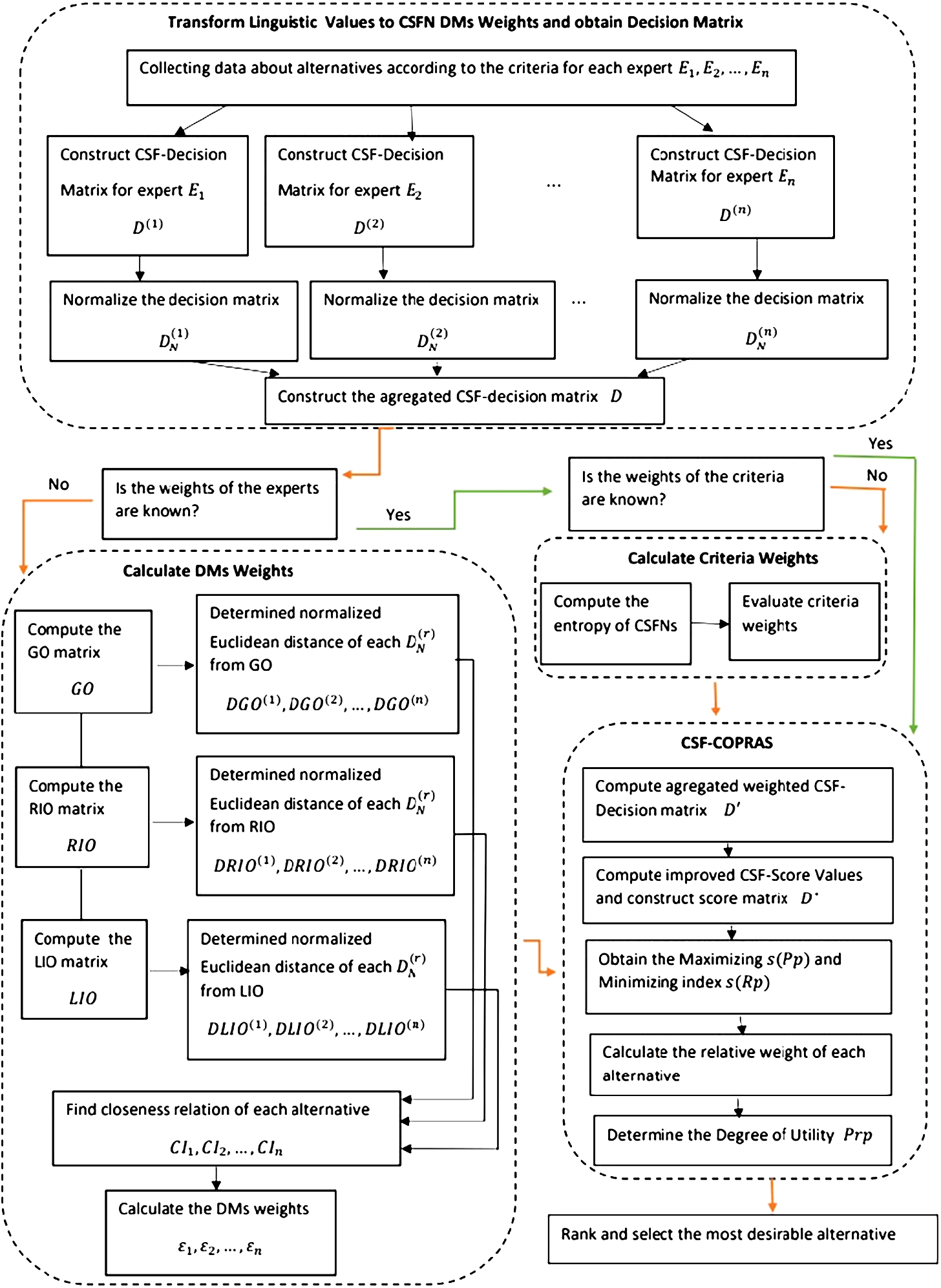
Fig. 2
Flow chart of the CSF-COPRAS technique based on entropy.
The procedure of the new COPRAS method based on entropy consists of the following steps:
Step I: Since the CSFDM may have some benefit and cost types criteria, as a first step, the information given by experts is normalized in the following way:
for all
$p=1,2,\dots ,k$,
$q=1,2,\dots ,m$ and
$r=1,2,\dots ,n$, where
${({d_{pq}^{(r)}})^{c}}$ is the complement of
${d_{pq}^{(r)}}$. Hence, the normalized complex spherical fuzzy decision matrix (NCSFDM)
${D_{N}^{(r)}}={({s_{pq}^{(r)}})_{k\times m}}$, where
${s_{pq}^{(r)}}=\big({f_{pq}^{(r)}}{e^{i{\alpha _{pq}^{(r)}}}},{g_{pq}^{(r)}}{e^{i{\beta _{pq}^{(r)}}}},{h_{pq}^{(r)}}{e^{i{\gamma _{pq}^{(r)}}}}\big)$ for all
$r\in \{1,2,\dots ,n\}$, is written as follows:
Step II: Consider the weights of the experts. There are two cases:
Case I: If the weights of experts are known, these values can be used. So this step is skipped.
Case II: If the weights of the experts are completely unknown, it is not possible to establish the final NCSFDM. So, the weights of the experts need to be determined. The weights of the experts are calculated in the following way:
I: As a first substep, the group opinion (GO) matrix is obtained by using the CSFWA operator of decision values in the NCSFDMs and the GO matrix is represented as follows:
where
II: Determine the right ideal opinion (RIO) matrix and left ideal opinion (LIO) matrix as follows:
where
${\textit{RIO}_{pq}}=\big\{{s_{pq}^{(r)}}:{\max _{r}}(SF({s_{pq}^{(r)}}))\big\}$ and
${\textit{LIO}_{pq}}=\big\{{s_{pq}^{(r)}}:{\min _{r}}(SF({s_{pq}^{(r)}}))\big\}$ for all
$p=1,2,\dots ,k$ and
$q=1,2,\dots ,m$.
III: By using the normalized Euclidean distance function, calculate the distances of each NCSFDMs
${D_{N}^{(r)}}$ from
$\textit{GO}$,
$\textit{RIO}$ and
$\textit{LIO}$, denoted by
${\textit{DGO}^{(r)}}$,
${\textit{DRIO}^{(r)}}$ and
${\textit{DLIO}^{(r)}}$, respectively. The values
${\textit{DGO}^{(r)}}$,
${\textit{DRIO}^{(r)}}$ and
${\textit{DLIO}^{(r)}}$ are obtained as follows:
for all
$p=1,2,\dots ,k$ and
$r=1,2,\dots ,n$.
IV: The closeness indices (CI) (given by Yue,
2013) are calculated as follows:
for all
$r=1,2,\dots ,n$.
V: The weights of experts are computed as follows:
Step III: The collective decision of all experts is obtained by merging the independent decision of each expert with their weights via CSFWA operator and the aggregated complex spherical fuzzy decision matrix (ACSFDM)
$D={({s_{pq}})_{k\times m}}$ is constructed as follows:
Let us denote
${s_{pq}}=\big({f_{{A_{p}}}}({c_{q}}){e^{i{\alpha _{{A_{p}}}}({c_{q}})}},{g_{{A_{p}}}}({c_{q}}){e^{i{\beta _{{A_{p}}}}({c_{q}})}},{h_{{A_{p}}}}({c_{q}}){e^{i{\gamma _{{A_{p}}}}({c_{q}})}}\big)$ for all
$p=1,2,\dots ,k$ and
$q=1,2,\dots ,m$.
Step IV: Since the weight matrix of criteria shows the importance of each criterion, this matrix should be constructed. There are two cases:
Case I: If the weights of criteria are known, these values can be used. So this step is skipped.
Case II: If the weights of criteria are completely unknown, construct the weight matrix of the criteria from ACSFDM by using the entropy measure function. Let
${\omega _{q}^{(r)}}=\big({f_{q}^{(r)}}{e^{i{\alpha _{q}^{(r)}}}},{g_{q}^{(r)}}{e^{i{\beta _{q}^{(r)}}}},{h_{q}^{(r)}}{e^{i{\gamma _{q}^{(r)}}}}\big)$ be the CSF weight assigned to the criteria by expert
${E_{r}}$. Then the weights of the criteria
${\omega _{q}}=\big({f_{\omega }}({c_{q}}){e^{i{\alpha _{\omega }}({c_{q}})}},{g_{\omega }}({c_{q}}){e^{i{\beta _{\omega }}({c_{q}})}},{h_{\omega }}({c_{q}}){e^{i{\gamma _{\omega }}({c_{q}})}}\big)$ are found using the following equation:
where
Step V: Find the aggregated weighted complex spherical fuzzy decision matrix (AWCSFDM) ${D^{\prime }}={({s^{\prime }_{pq}})_{k\times m}}={({\omega _{q}}{s_{pq}})_{k\times m}}$ by considering the ACSFDM and the weight matrix Ω for criteria.
The
${s^{\prime }_{pq}}=\big({f^{\prime }_{{A_{p}}}}({c_{q}}){e^{i{\alpha ^{\prime }_{{A_{p}}}}({c_{q}})}},{g^{\prime }_{{A_{p}}}}({c_{q}}){e^{i{\beta ^{\prime }_{{A_{p}}}}({c_{q}})}},{h^{\prime }_{{A_{p}}}}({c_{q}}){e^{i{\gamma ^{\prime }_{{A_{p}}}}({c_{q}})}}\big)$ is calculated as follows:
Step VI: Since the elements of the AWCSFDM
${D^{\prime }}$ are CSFN, the score matrix
${D^{\ast }}$ has to be constructed using the score function. The score matrix
${D^{\ast }}={({s_{pq}^{\ast }})_{k\times m}}$ is constructed as follows:
where
for all
$p=1,2,\dots ,k$ and
$q=1,2,\dots ,m$.
Step VII: Let
${\mathfrak{C}_{B}}$ and
${\mathfrak{C}_{C}}$ denote the set of benefit type and cost type criteria, respectively. Maximizing index
$s({P_{p}})$ and minimizing index
$s({R_{p}})$ are obtained as follows:
and
for all
$q=1,2,\dots ,m$.
Step VIII: Calculate the relative weight of each alternative
${Q_{p}}$ as:
for all
$p=1,2,\dots ,k$.
Step IX: Determine the priority order
$P{r_{p}}$ by using the formula
for all
$p=1,2,\dots ,k$.
Step X: If $P{r_{p}}\geqslant P{r_{t}}$, then the ranking alternatives ${A_{p}}\geqslant {A_{t}}$ for all $p,t=1,2,\dots ,k$. Hence the alternative with the highest rank is the best solution for the problem.
5 An Illustrative Example
Suppliers have always been an integral component of a company’s management policy; however, the relationship between companies and their suppliers has traditionally been distant. In today’s global economy of just-in-time (JIT) manufacturing and value-added focus, there is a heightened need to change this adversarial relationship to one of cooperation and seamless integration. JIT requires the vendor to manufacture and deliver to the company the precise quantity and quality of material at the required time. Thus the performance of the supplier becomes a key element in a company’s success or failure. In order to attain the goals of low cost, consistently high quality, flexibility, and quick response, companies have increasingly considered better supplier selection approaches. These approaches require cooperation in sharing costs, benefits, and expertise in attempting to understand one another’s strengths and weaknesses, which in turn leads to single sourcing, supplier, and long-term partnerships. Since the supplier selection process encompasses different functions (such as purchasing, quality, production, etc.) within a company, it is a multi-objective problem, encompassing many tangible and intangible factors in a hierarchical manner. The evaluation of intangible factors requires the assessment of expert judgment, and the hierarchical structure requires decomposition and synthesis of these factors (Bhutta and Huq,
2002).
Now, we consider the problem “selection of the strategic supplier selection” given by Igoulalene
et al. (
2015) and solve this problem to demonstrate the applicability and effectiveness of the proposed method. In this problem, the stakeholders (DMs) evaluate the five suppliers given as
${A_{1}}$,
${A_{2}}$,
${A_{3}}$,
${A_{4}}$ and
${A_{5}}$ according to the criteria “performance strategy”, “quality of service”, “innovation” and “risk”. Therefore, we have the set of DMs
$D=\{{E_{1}},{E_{2}},{E_{3}}\}$, the set of alternatives
$A=\{{A_{1}},{A_{2}},{A_{3}},{A_{4}},{A_{5}}\}$ and the set of criteria
$C=\{{c_{1}},{c_{2}},{c_{3}},{c_{4}}\}$, where
${c_{1}}$ = performance strategy,
${c_{2}}$ = quality of service,
${c_{3}}$ = innovation and
${c_{4}}$ = risk. Also, the only cost type criteria is
${c_{4}}$. Each expert
${E_{r}}$ $(r=1,2,3)$ evaluates the alternatives
${A_{p}}\hspace{2.5pt}(p=1,2,\dots ,5)$ with respect to
${c_{q}}$ $(q=1,2,3,4)$. The relationship between alternatives and criteria according to each expert (
${E_{1}}$,
${E_{2}}$,
${E_{3}}$) are shown in Table
5 and the corresponding CSFN values are presented in Tables
6,
7 and
8.
Table 5
Illustrative example (stakeholder preferences given in Igoulalene
et al.,
2015).
| ${A_{i}}$ |
${c_{j}}$ |
${E_{1}}$ |
${E_{2}}$ |
${E_{3}}$ |
| ${A_{1}}$ |
${c_{1}}$ |
G |
VG |
G |
|
${c_{2}}$ |
MG |
G |
MG |
|
${c_{3}}$ |
VG |
G |
VG |
|
${c_{4}}$ |
G |
G |
G |
| ${A_{2}}$ |
${c_{1}}$ |
MG |
G |
M |
|
${c_{2}}$ |
M |
MG |
G |
|
${c_{3}}$ |
G |
MG |
MG |
|
${c_{4}}$ |
MG |
M |
MG |
| ${A_{3}}$ |
${c_{1}}$ |
VG |
VG |
VG |
|
${c_{2}}$ |
VG |
G |
VG |
|
${c_{3}}$ |
VG |
VG |
G |
|
${c_{4}}$ |
VG |
VG |
G |
| ${A_{4}}$ |
${c_{1}}$ |
MG |
G |
G |
|
${c_{2}}$ |
M |
M |
MG |
|
${c_{3}}$ |
VG |
G |
G |
|
${c_{4}}$ |
G |
MG |
MG |
| ${A_{5}}$ |
${c_{1}}$ |
M |
MG |
MG |
|
${c_{2}}$ |
MP |
M |
M |
|
${c_{3}}$ |
G |
G |
MG |
|
${c_{4}}$ |
M |
MG |
M |
Table 6
CSFDMsestablished by expert ${E_{1}}$.
| ${D^{(1)}}$ |
${c_{1}}$ |
${c_{2}}$ |
| ${A_{1}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
| ${A_{2}}$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
| ${A_{3}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
| ${A_{4}}$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
| ${A_{5}}$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
$\big(0.54{e^{i2\pi (0.53)}},0.31{e^{i2\pi (0.33)}},0.62{e^{i2\pi (0.65)}}\big)$ |
|
${c_{3}}$ |
${c_{4}}$ |
| ${A_{1}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
| ${A_{2}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
| ${A_{3}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
| ${A_{4}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
| ${A_{5}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
Table 7
CSFDMsestablished by expert ${E_{2}}$.
| ${D^{(2)}}$ |
${c_{1}}$ |
${c_{2}}$ |
| ${A_{1}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
| ${A_{2}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
| ${A_{3}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
| ${A_{4}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
| ${A_{5}}$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
|
${c_{3}}$ |
${c_{4}}$ |
| ${A_{1}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
| ${A_{2}}$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
| ${A_{3}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
| ${A_{4}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
| ${A_{5}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
Table 8
CSFDMsestablished by expert ${E_{3}}$.
| ${D^{(3)}}$ |
${c_{1}}$ |
${c_{2}}$ |
| ${A_{1}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
| ${A_{2}}$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
| ${A_{3}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
| ${A_{4}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
| ${A_{5}}$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
|
${c_{3}}$ |
${c_{4}}$ |
| ${A_{1}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
| ${A_{2}}$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
| ${A_{3}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
| ${A_{4}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
| ${A_{5}}$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
Table 9
NCSFDM of the expert ${E_{1}}$.
| ${D_{N}^{(1)}}$ |
${c_{1}}$ |
${c_{2}}$ |
| ${A_{1}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
| ${A_{2}}$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
| ${A_{3}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
| ${A_{4}}$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
| ${A_{5}}$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
$\big(0.54{e^{i2\pi (0.53)}},0.31{e^{i2\pi (0.33)}},0.62{e^{i2\pi (0.65)}}\big)$ |
|
${c_{3}}$ |
${c_{4}}$ |
| ${A_{1}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.34{e^{i2\pi (0.37)}},0.23{e^{i2\pi (0.22)}},0.83{e^{i2\pi (0.82)}}\big)$ |
| ${A_{2}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.45{e^{i2\pi (0.48)}},0.30{e^{i2\pi (0.31)}},0.73{e^{i2\pi (0.71)}}\big)$ |
| ${A_{3}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.21{e^{i2\pi (0.23)}},0.17{e^{i2\pi (0.15)}},0.91{e^{i2\pi (0.89)}}\big)$ |
| ${A_{4}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.34{e^{i2\pi (0.37)}},0.23{e^{i2\pi (0.22)}},0.83{e^{i2\pi (0.82)}}\big)$ |
| ${A_{5}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.53{e^{i2\pi (0.54)}},0.45{e^{i2\pi (0.47)}},0.67{e^{i2\pi (0.65)}}\big)$ |
Table 10
NCSFDM of the expert ${E_{2}}$.
| ${D_{N}^{(2)}}$ |
${c_{1}}$ |
${c_{2}}$ |
| ${A_{1}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
| ${A_{2}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
| ${A_{3}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
| ${A_{4}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
| ${A_{5}}$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
|
${c_{3}}$ |
${c_{4}}$ |
| ${A_{1}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.34{e^{i2\pi (0.37)}},0.23{e^{i2\pi (0.22)}},0.83{e^{i2\pi (0.82)}}\big)$ |
| ${A_{2}}$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
$\big(0.53{e^{i2\pi (0.54)}},0.45{e^{i2\pi (0.47)}},0.67{e^{i2\pi (0.65)}}\big)$ |
| ${A_{3}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.21{e^{i2\pi (0.23)}},0.17{e^{i2\pi (0.15)}},0.91{e^{i2\pi (0.89)}}\big)$ |
| ${A_{4}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.45{e^{i2\pi (0.48)}},0.30{e^{i2\pi (0.31)}},0.73{e^{i2\pi (0.71)}}\big)$ |
| ${A_{5}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.45{e^{i2\pi (0.48)}},0.30{e^{i2\pi (0.31)}},0.73{e^{i2\pi (0.71)}}\big)$ |
Table 11
NCSFDM of the expert ${E_{3}}$.
| ${D_{N}^{(3)}}$ |
${c_{1}}$ |
${c_{2}}$ |
| ${A_{1}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
| ${A_{2}}$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
| ${A_{3}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
| ${A_{4}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
| ${A_{5}}$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
|
${c_{3}}$ |
${c_{4}}$ |
| ${A_{1}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.34{e^{i2\pi (0.37)}},0.23{e^{i2\pi (0.22)}},0.83{e^{i2\pi (0.82)}}\big)$ |
| ${A_{2}}$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
$\big(0.45{e^{i2\pi (0.48)}},0.30{e^{i2\pi (0.31)}},0.73{e^{i2\pi (0.71)}}\big)$ |
| ${A_{3}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.34{e^{i2\pi (0.37)}},0.23{e^{i2\pi (0.22)}},0.83{e^{i2\pi (0.82)}}\big)$ |
| ${A_{4}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.45{e^{i2\pi (0.48)}},0.30{e^{i2\pi (0.31)}},0.73{e^{i2\pi (0.71)}}\big)$ |
| ${A_{5}}$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
$\big(0.53{e^{i2\pi (0.54)}},0.45{e^{i2\pi (0.47)}},0.67{e^{i2\pi (0.65)}}\big)$ |
| GO |
${c_{1}}$ |
${c_{2}}$ |
| ${A_{1}}$ |
$\big(0.86{e^{i2\pi (0.85)}},0.21{e^{i2\pi (0.19)}},0.29{e^{i2\pi (0.32)}}\big)$ |
$\big(0.77{e^{i2\pi (0.75)}},0.27{e^{i2\pi (0.28)}},0.41{e^{i2\pi (0.44)}}\big)$ |
| ${A_{2}}$ |
$\big(0.75{e^{i2\pi (0.74)}},0.31{e^{i2\pi (0.32)}},0.43{e^{i2\pi (0.46)}}\big)$ |
$\big(0.75{e^{i2\pi (0.74)}},0.31{e^{i2\pi (0.32)}},0.43{e^{i2\pi (0.46)}}\big)$ |
| ${A_{3}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.89{e^{i2\pi (0.87)}},0.19{e^{i2\pi (0.17)}},0.25{e^{i2\pi (0.27)}}\big)$ |
| ${A_{4}}$ |
$\big(0.80{e^{i2\pi (0.79)}},0.25{e^{i2\pi (0.25)}},0.37{e^{i2\pi (0.40)}}\big)$ |
$\big(0.69{e^{i2\pi (0.67)}},0.39{e^{i2\pi (0.41)}},0.50{e^{i2\pi (0.52)}}\big)$ |
| ${A_{5}}$ |
$\big(0.71{e^{i2\pi (0.69)}},0.34{e^{i2\pi (0.36)}},0.48{e^{i2\pi (0.50)}}\big)$ |
$\big(0.63{e^{i2\pi (0.62)}},0.40{e^{i2\pi (0.42)}},0.56{e^{i2\pi (0.57)}}\big)$ |
|
${c_{3}}$ |
${c_{4}}$ |
| ${A_{1}}$ |
$\big(0.89{e^{i2\pi (0.87)}},0.19{e^{i2\pi (0.17)}},0.25{e^{i2\pi (0.27)}}\big)$ |
$\big(0.34{e^{i2\pi (0.37)}},0.23{e^{i2\pi (0.22)}},0.83{e^{i2\pi (0.82)}}\big)$ |
| ${A_{2}}$ |
$\big(0.77{e^{i2\pi (0.76)}},0.27{e^{i2\pi (0.28)}},0.41{e^{i2\pi (0.44)}}\big)$ |
$\big(0.48{e^{i2\pi (0.50)}},0.34{e^{i2\pi (0.36)}},0.71{e^{i2\pi (0.69)}}\big)$ |
| ${A_{3}}$ |
$\big(0.89{e^{i2\pi (0.87)}},0.19{e^{i2\pi (0.17)}},0.25{e^{i2\pi (0.27)}}\big)$ |
$\big(0.26{e^{i2\pi (0.29)}},0.19{e^{i2\pi (0.17)}},0.88{e^{i2\pi (0.87)}}\big)$ |
| ${A_{4}}$ |
$\big(0.86{e^{i2\pi (0.85)}},0.21{e^{i2\pi (0.19)}},0.29{e^{i2\pi (0.32)}}\big)$ |
$\big(0.42{e^{i2\pi (0.45)}},0.27{e^{i2\pi (0.28)}},0.76{e^{i2\pi (0.74)}}\big)$ |
| ${A_{5}}$ |
$\big(0.80{e^{i2\pi (0.79)}},0.25{e^{i2\pi (0.25)}},0.37{e^{i2\pi (0.40)}}\big)$ |
$\big(0.51{e^{i2\pi (0.52)}},0.39{e^{i2\pi (0.41)}},0.69{e^{i2\pi (0.67)}}\big)$ |
| RIO |
${c_{1}}$ |
${c_{2}}$ |
| ${A_{1}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
| ${A_{2}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
| ${A_{3}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
| ${A_{4}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
| ${A_{5}}$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
|
${c_{3}}$ |
${c_{4}}$ |
| ${A_{1}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.34{e^{i2\pi (0.37)}},0.23{e^{i2\pi (0.22)}},0.83{e^{i2\pi (0.82)}}\big)$ |
| ${A_{2}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.45{e^{i2\pi (0.48)}},0.30{e^{i2\pi (0.31)}},0.73{e^{i2\pi (0.71)}}\big)$ |
| ${A_{3}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.34{e^{i2\pi (0.37)}},0.23{e^{i2\pi (0.22)}},0.83{e^{i2\pi (0.82)}}\big)$ |
| ${A_{4}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.45{e^{i2\pi (0.48)}},0.30{e^{i2\pi (0.31)}},0.73{e^{i2\pi (0.71)}}\big)$ |
| ${A_{5}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.53{e^{i2\pi (0.54)}},0.45{e^{i2\pi (0.47)}},0.67{e^{i2\pi (0.65)}}\big)$ |
Step I: In this example,
${c_{4}}$ is the only cost type criteria. The NCSFDMs are constructed by using Eq. (
2) and NCSFDMs (
${D_{N}^{(1)}}$,
${D_{N}^{(2)}}$,
${D_{N}^{(3)}}$ ) are given in Tables
9,
10 and
11.
| LIO |
${c_{1}}$ |
${c_{2}}$ |
| ${A_{1}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
| ${A_{2}}$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
| ${A_{3}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
| ${A_{4}}$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
| ${A_{5}}$ |
$\big(0.67{e^{i2\pi (0.65)}},0.45{e^{i2\pi (0.47)}},0.53{e^{i2\pi (0.54)}}\big)$ |
$\big(0.54{e^{i2\pi (0.53)}},0.31{e^{i2\pi (0.33)}},0.62{e^{i2\pi (0.65)}}\big)$ |
|
${c_{3}}$ |
${c_{4}}$ |
| ${A_{1}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.34{e^{i2\pi (0.37)}},0.23{e^{i2\pi (0.22)}},0.83{e^{i2\pi (0.82)}}\big)$ |
| ${A_{2}}$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
$\big(0.45{e^{i2\pi (0.48)}},0.30{e^{i2\pi (0.31)}},0.73{e^{i2\pi (0.71)}}\big)$ |
| ${A_{3}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.21{e^{i2\pi (0.23)}},0.17{e^{i2\pi (0.15)}},0.91{e^{i2\pi (0.89)}}\big)$ |
| ${A_{4}}$ |
$\big(0.83{e^{i2\pi (0.82)}},0.23{e^{i2\pi (0.22)}},0.34{e^{i2\pi (0.37)}}\big)$ |
$\big(0.34{e^{i2\pi (0.37)}},0.23{e^{i2\pi (0.22)}},0.83{e^{i2\pi (0.82)}}\big)$ |
| ${A_{5}}$ |
$\big(0.73{e^{i2\pi (0.71)}},0.30{e^{i2\pi (0.31)}},0.45{e^{i2\pi (0.48)}}\big)$ |
$\big(0.53{e^{i2\pi (0.54)}},0.45{e^{i2\pi (0.47)}},0.67{e^{i2\pi (0.65)}}\big)$ |
Step II: The objective weighs of experts are calculated using the following steps:
I: GO matrix is obtained using the CSFWA operator (Eq. (
3)) and is shown in Table
12.
II: RIO and LIO matrices are shown in Tables
13 and
14.
III: DGO, DRIO and DLIO matrices are calculated using normalized Euclidean distance function and shown in Table
15.
IV: By using equation (
3), we obtain the closeness indices as
$C{I_{1}}=0.7376$,
$C{I_{2}}=0.7610$,
$C{I_{3}}=0.7430$.
Table 15
DGO, DRIO and DLIO matrices.
| DGO |
${A_{1}}$ |
${A_{2}}$ |
${A_{3}}$ |
${A_{4}}$ |
${A_{5}}$ |
| ${E_{1}}$ |
0.1213 |
0.3204 |
0.1112 |
0.2494 |
0.2432 |
| ${E_{2}}$ |
0.2332 |
0.2106 |
0.1858 |
0.1538 |
0.1930 |
| ${E_{3}}$ |
0.1213 |
0.2587 |
0.2210 |
0.1856 |
0.2363 |
| DRIO |
${A_{1}}$ |
${A_{2}}$ |
${A_{3}}$ |
${A_{4}}$ |
${A_{5}}$ |
| ${E_{1}}$ |
0.2766 |
0.4791 |
0.2171 |
0.3612 |
0.3175 |
| ${E_{2}}$ |
0.2171 |
0.4439 |
0.3070 |
0.3146 |
0.2277 |
| ${E_{3}}$ |
0.2766 |
0.3020 |
0.2171 |
0.2171 |
0.2695 |
| DLIO |
${A_{1}}$ |
${A_{2}}$ |
${A_{3}}$ |
${A_{4}}$ |
${A_{5}}$ |
| ${E_{1}}$ |
0.2171 |
0.2774 |
0.3070 |
0.2171 |
0.2695 |
| ${E_{2}}$ |
0.2766 |
0.3497 |
0.2171 |
0.2805 |
0.4746 |
| ${E_{3}}$ |
0.2171 |
0.4727 |
0.3070 |
0.3612 |
0.3175 |
V: The weights of experts are found using equation (
4) as
${\varepsilon _{1}}=0.3291$,
${\varepsilon _{2}}=0.3395$,
${\varepsilon _{3}}=0.3315$.
Step III: The ACSFDM is calculated by considering the CSFDMs, which are given in Table
9 and the ACSFDM is given in Table
16.
Step IV: The objective weights of the criteria are calculated by using the proposed entropy-based approach. First, the entropy value of each criterion is calculated by applying Eq. (
2). Then entropy is used in Eq. (
5) for obtaining objective weights of the criteria and these weights are given in Table
17.
| D |
${c_{1}}$ |
${c_{2}}$ |
| ${A_{1}}$ |
$\big(0.86{e^{i2\pi (0.85)}},0.21{e^{i2\pi (0.19)}},0.29{e^{i2\pi (0.31)}}\big)$ |
$\big(0.77{e^{i2\pi (0.75)}},0.27{e^{i2\pi (0.28)}},0.41{e^{i2\pi (0.44)}}\big)$ |
| ${A_{2}}$ |
$\big(0.76{e^{i2\pi (0.74)}},0.31{e^{i2\pi (0.32)}},0.43{e^{i2\pi (0.46)}}\big)$ |
$\big(0.75{e^{i2\pi (0.74)}},0.31{e^{i2\pi (0.32)}},0.43{e^{i2\pi (0.46)}}\big)$ |
| ${A_{3}}$ |
$\big(0.91{e^{i2\pi (0.89)}},0.17{e^{i2\pi (0.15)}},0.21{e^{i2\pi (0.23)}}\big)$ |
$\big(0.89{e^{i2\pi (0.87)}},0.19{e^{i2\pi (0.17)}},0.25{e^{i2\pi (0.27)}}\big)$ |
| ${A_{4}}$ |
$\big(0.80{e^{i2\pi (0.79)}},0.25{e^{i2\pi (0.25)}},0.37{e^{i2\pi (0.40)}}\big)$ |
$\big(0.69{e^{i2\pi (0.67)}},0.39{e^{i2\pi (0.41)}},0.50{e^{i2\pi (0.52)}}\big)$ |
| ${A_{5}}$ |
$\big(0.71{e^{i2\pi (0.69)}},0.34{e^{i2\pi (0.36)}},0.47{e^{i2\pi (0.50)}}\big)$ |
$\big(0.63{e^{i2\pi (0.62)}},0.40{e^{i2\pi (0.42)}},0.56{e^{i2\pi (0.57)}}\big)$ |
|
${c_{3}}$ |
${c_{4}}$ |
| ${A_{1}}$ |
$\big(0.89{e^{i2\pi (0.87)}},0.19{e^{i2\pi (0.17)}},0.25{e^{i2\pi (0.27)}}\big)$ |
$\big(0.34{e^{i2\pi (0.37)}},0.23{e^{i2\pi (0.22)}},0.83{e^{i2\pi (0.82)}}\big)$ |
| ${A_{2}}$ |
$\big(0.77{e^{i2\pi (0.75)}},0.27{e^{i2\pi (0.28)}},0.41{e^{i2\pi (0.44)}}\big)$ |
$\big(0.48{e^{i2\pi (0.50)}},0.34{e^{i2\pi (0.36)}},0.71{e^{i2\pi (0.69)}}\big)$ |
| ${A_{3}}$ |
$\big(0.89{e^{i2\pi (0.87)}},0.19{e^{i2\pi (0.17)}},0.25{e^{i2\pi (0.27)}}\big)$ |
$\big(0.26{e^{i2\pi (0.29)}},0.19{e^{i2\pi (0.17)}},0.88{e^{i2\pi (0.87)}}\big)$ |
| ${A_{4}}$ |
$\big(0.86{e^{i2\pi (0.85)}},0.21{e^{i2\pi (0.19)}},0.29{e^{i2\pi (0.31)}}\big)$ |
$\big(0.42{e^{i2\pi (0.45)}},0.27{e^{i2\pi (0.28)}},0.76{e^{i2\pi (0.74)}}\big)$ |
| ${A_{5}}$ |
$\big(0.80{e^{i2\pi (0.79)}},0.25{e^{i2\pi (0.25)}},0.37{e^{i2\pi (0.40)}}\big)$ |
$\big(0.51{e^{i2\pi (0.52)}},0.39{e^{i2\pi (0.41)}},0.69{e^{i2\pi (0.67)}}\big)$ |
Step V: After determining the weights of the criteria, the AWCSFDM
${D^{\prime }}$ is calculated using Eq. (
6) and shown in Table
18.
Table 17
Weights of criteria.
| ω |
${c_{1}}$ |
${c_{2}}$ |
${c_{3}}$ |
${c_{4}}$ |
| ${E_{q}}$ |
0.2802 |
0.4421 |
0.1876 |
0.3697 |
| $1-{E_{q}}$ |
0.7198 |
0.5578 |
0.8124 |
0.6303 |
| ${\omega _{q}}$ |
0.2646 |
0.2051 |
0.2986 |
0.2317 |
Step VI: Table
18 gives the aggregated scores of each alternative which are represented as CSFNs in the column. To calculate the real values, we defuzzify these CSFNs by using Eq. (
6) and so, we obtain the score matrix as given in Table
19.
| ${D^{\prime }}$ |
${c_{1}}$ |
${c_{2}}$ |
| ${A_{1}}$ |
$\big(0.55{e^{i2\pi (0.53)}},0.66{e^{i2\pi (0.66)}},0.71{e^{i2\pi (0.75)}}\big)$ |
$\big(0.41{e^{i2\pi (0.39)}},0.77{e^{i2\pi (0.78)}},0.83{e^{i2\pi (0.85)}}\big)$ |
| ${A_{2}}$ |
$\big(0.44{e^{i2\pi (0.43)}},0.73{e^{i2\pi (0.75)}},0.80{e^{i2\pi (0.82)}}\big)$ |
$\big(0.39{e^{i2\pi (0.38)}},0.79{e^{i2\pi (0.80)}},0.84{e^{i2\pi (0.86)}}\big)$ |
| ${A_{3}}$ |
$\big(0.61{e^{i2\pi (0.57)}},0.62{e^{i2\pi (0.62)}},0.66{e^{i2\pi (0.69)}}\big)$ |
$\big(0.52{e^{i2\pi (0.49)}},0.71{e^{i2\pi (0.71)}},0.75{e^{i2\pi (0.78)}}\big)$ |
| ${A_{4}}$ |
$\big(0.48{e^{i2\pi (0.47)}},0.69{e^{i2\pi (0.70)}},0.77{e^{i2\pi (0.79)}}\big)$ |
$\big(0.35{e^{i2\pi (0.33)}},0.83{e^{i2\pi (0.84)}},0.87{e^{i2\pi (0.88)}}\big)$ |
| ${A_{5}}$ |
$\big(0.41{e^{i2\pi (0.39)}},0.75{e^{i2\pi (0.77)}},0.82{e^{i2\pi (0.84)}}\big)$ |
$\big(0.31{e^{i2\pi (0.30)}},0.83{e^{i2\pi (0.85)}},0.89{e^{i2\pi (0.90)}}\big)$ |
|
${c_{3}}$ |
${c_{4}}$ |
| ${A_{1}}$ |
$\big(0.61{e^{i2\pi (0.58)}},0.61{e^{i2\pi (0.60)}},0.66{e^{i2\pi (0.68)}}\big)$ |
$\big(0.17{e^{i2\pi (0.20)}},0.71{e^{i2\pi (0.67)}},0.96{e^{i2\pi (0.95)}}\big)$ |
| ${A_{2}}$ |
$\big(0.48{e^{i2\pi (0.46)}},0.68{e^{i2\pi (0.69)}},0.76{e^{i2\pi (0.79)}}\big)$ |
$\big(0.24{e^{i2\pi (0.27)}},0.78{e^{i2\pi (0.76)}},0.93{e^{i2\pi (0.91)}}\big)$ |
| ${A_{3}}$ |
$\big(0.61{e^{i2\pi (0.58)}},0.61{e^{i2\pi (0.60)}},0.66{e^{i2\pi (0.68)}}\big)$ |
$\big(0.13{e^{i2\pi (0.15)}},0.68{e^{i2\pi (0.63)}},0.97{e^{i2\pi (0.96)}}\big)$ |
| ${A_{4}}$ |
$\big(0.58{e^{i2\pi (0.55)}},0.62{e^{i2\pi (0.62)}},0.69{e^{i2\pi (0.72)}}\big)$ |
$\big(0.21{e^{i2\pi (0.24)}},0.74{e^{i2\pi (0.71)}},0.94{e^{i2\pi (0.92)}}\big)$ |
| ${A_{5}}$ |
$\big(0.52{e^{i2\pi (0.50)}},0.66{e^{i2\pi (0.67)}},0.74{e^{i2\pi (0.77)}}\big)$ |
$\big(0.26{e^{i2\pi (0.28)}},0.81{e^{i2\pi (0.79)}},0.92{e^{i2\pi (0.90)}}\big)$ |
Table 19
Score matrix ${D^{\ast }}$.
| ${D^{\ast }}$ |
${c_{1}}$ |
${c_{2}}$ |
${c_{3}}$ |
${c_{4}}$ |
| ${A_{1}}$ |
0.8919 |
0.5810 |
1.0357 |
0.4101 |
| ${A_{2}}$ |
0.6699 |
0.5376 |
0.7791 |
0.3996 |
| ${A_{3}}$ |
1.0191 |
0.7958 |
1.0412 |
0.4185 |
| ${A_{4}}$ |
0.7636 |
0.4468 |
0.9705 |
0.4131 |
| ${A_{5}}$ |
0.6032 |
0.4082 |
0.8401 |
0.3855 |
Step VII, VIII, IX, X: Using Eq. (
7) and Eq. (
8), calculate
$s({P_{p}})$ and
$s({R_{p}})$. Finally,
${Q_{p}}$ and
$P{r_{p}}$ are obtained by using Eq. (
9), Eq. (
10) and shown in Table
20.
Table 20
$s({P_{p}})$, $s({R_{p}})$, $s({Q_{p}})$ and Ranking of alternatives.
| ${D^{\ast }}$ |
${P_{p}}$ |
${R_{p}}$ |
${Q_{p}}$ |
$P{r_{p}}$ |
Rank |
| ${A_{1}}$ |
0.8362 |
0.4101 |
1.2366 |
91.98 |
2 |
| ${A_{2}}$ |
0.6622 |
0.3996 |
1.0732 |
79.82 |
4 |
| ${A_{3}}$ |
0.9520 |
0.4185 |
1.3443 |
100 |
1 |
| ${A_{4}}$ |
0.7270 |
0.4131 |
1.1244 |
83.64 |
3 |
| ${A_{5}}$ |
0.6172 |
0.3855 |
1.0431 |
77.60 |
5 |
As a result, we can see that the order of ranking among seven alternatives is ${A_{3}}\gt {A_{1}}\gt {A_{4}}\gt {A_{2}}\gt {A_{5}}$, where “>” indicates the relation “preferred to”. Therefore, the best choice would be ${A_{3}}$ with the objective weights of DMs and criteria.
7 Conclusion
CSF is a broader and more dominant model than the existing set theories since this theory does not only competently deal with two-dimensional information but also takes into account the doubtless and refusal part of the judgment as well as positive-membership and negative-membership. The main contribution of the study is the introduction of a novel improved COPRAS method under the CSF environment with unknown information about the DMs and criteria weights. In this study, the data of the weights of criteria and DMs are objectively determined. To obtain objective criteria weights, a new entropy measure is given on CSFs and the entropy weight model is developed. In order to eliminate the subjective collective information during the implementation of the method, the CSF-COPRAS method aggregates with the computed weights of the criteria weights of DMs to acquire the final alternative rank. Then, to explain and show the validity of the proposed method, a numerical example and comparative analyses are given. Moreover, the applied methods’ preference ranking of alternatives is compared with different MCDM and MCGDM approaches under different environments. The fact that the best alternative is the same in all compared methods showed that the entropy-based CSF-COPRAS method is quite robust. So, we have presented the proposed study as a more general model than all the compared studies and have explained its advantages with method analysis. For future work, we aim to investigate different types of entropy measure functions and apply these functions to the different types of traditional MCGDM methods such as WASPAS, AHP, SWAM, etc. Also, we plan to obtain some new kind of similarity measure for CSFs environment and further, we will research to find the applications areas of these approaches to real-life problems such as medical diagnosis, image detection and pattern recognition.

