1 Introduction
The MCDM is a procedure of choosing the best solution from a collection of alternatives based on the multi-criteria appraisal data given by the decision-makers. As the social and economic environment becomes more and more complex, the characteristics of human cognition and thinking are the major internal causes of vague and inaccurate judgments on decision-making problems. To accurately and effectively express evaluation information is a challenging job. After the classical fuzzy set (Zadeh,
1965), its extensions have been proposed and applied successively. For instance, the ideas of intuitionistic fuzzy set (IFS) were introduced by Atanassov (
1986), some notions of Pythagorean fuzzy set (PFS) were advanced by Yager (
2014) and the generalized concepts of
q-ROFS were extended by Yager (
2017). Among these extensions,
q-ROFS is considered as a viable tool which is capable of dealing with complexity, indeterminacy and ambiguity (Yager,
2017). There are membership degree (MD)
$(0\leqslant \mu \leqslant 1)$ and non-membership degree (ND)
$(0\leqslant \nu \leqslant 1)$ in
q-ROFS, which respectively represent the degree of support and opposition of the objective belonging to this set, the MD and ND meet
${\mu ^{q}}+{\nu ^{q}}\leqslant $1 (Yager,
2017). Obviously, when
q values are one and two, the
q-ROFS is reduced to the IFS and PFS, respectively. The relationships of IFS, PFS, and
q-ROFS are revealed in Fig.
1 (Wang,
et al.,
2020a). In addition, the parameter
q value can be changed dynamically to achieve a suitable scope of information expression according to the requirements of specific decision scenarios, thus the
q-ROFS can be employed to portray more uncertain and vague evaluation information.
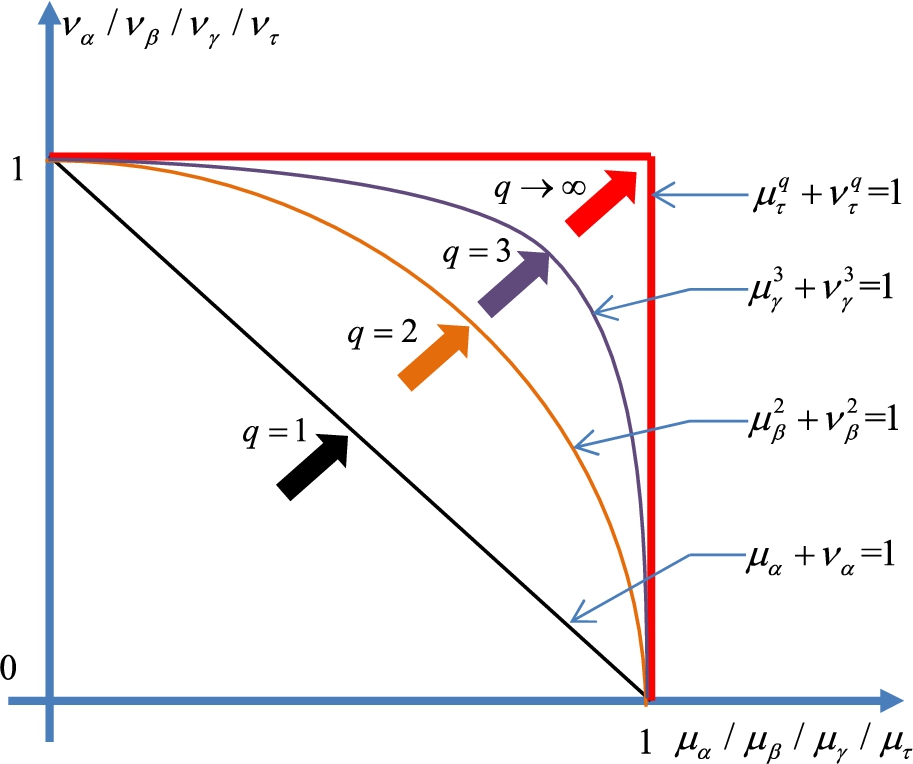
Fig. 1
The relationships of IFS, PFS and
q-ROFS (Wang
et al.,
2020a).
In the
q-ROF context, apart from the development of various aggregation operators (Peng and Luo,
2021; Saha
et al.,
2022a), the alternative ranking techniques have become one of the focuses of many scholars. So far, various types of decision-making techniques have been extended and utilized in the
q-ROF environment, and these methods can be classified according to their characteristics as: (1) the distance-based methods, such as TOPSIS (Dincer
et al.,
2022; Pinar
et al.,
2021; Ye
et al.,
2021; Alkan and Kahraman,
2021; Pinar and Boran,
2020; Khan
et al.,
2021b), TODIM (Krishankumar
et al.,
2021; Chen
et al.,
2021; Arya and Kumar,
2021; Liu
et al.,
2021; Wang and Li,
2018), VIKOR (Khan
et al.,
2021a; Sun
et al.,
2021), CODAS (Deveci
et al.,
2022a), EDAS (Darko and Liang,
2020; Liang
et al.,
2023), and MABAC (Gong
et al.,
2020; Wang
et al.,
2020a); (2) the utility-based approaches, such as WASPAS (Deveci
et al.,
2022b; Xiao
et al.,
2022), ARAS (Mishra and Rani,
2021), COPRAS (Krishankumar
et al.,
2019) and MARCOS (Ali,
2022); (3) the distance- and utility-based hybrid approaches, such as MULTIMOORA (Mishra
et al.,
2022; Riaz
et al.,
2022; Aydemir and Gunduz,
2020), PROMETHEE (Liu L.
et al.,
2020; Akram and Shumaiza,
2021; Zhang
et al.,
2021b), DNMA (Saha
et al.,
2022b), CoCoSo (Deveci
et al.,
2022c), and GLDS (Liu
et al.,
2020; Liao
et al.,
2020); (4) other methods, such as ORESTE (Long and Liao,
2021) and Thermodynamic (Li
et al.,
2021; Zhang
et al.,
2021a). These aforementioned decision-making approaches have been widely applied to handle complex decision issues in real-life, such as solid waste management (Ali,
2022; Mishra
et al.,
2022), renewable energy management (Krishankumar
et al.,
2019; Deveci
et al.,
2022c), COVID-19 epidemic management (Khan
et al.,
2021a; Alkan and Kahraman,
2021) and supply chain management (Liu
et al.,
2020; Long and Liao,
2021; Wang and Li,
2018), etc.
In 2014, Pamucar
et al. (
2014) proposed the MAIRCA method for the first time, which has received massive attention from lots of scholars. This approach determines the best solution in view of the deviation between the defined theoretical and the real results. The merits of the MAIRCA method are described as below: (1) it can be employed to settle decision-making issues which have multitudinous criteria and alternatives; (2) it can also solve decision problems with mixed quantitative and qualitative evaluation criteria; (3) the decision process of MAIRCA is easily understood and can be flexibly applied in combination with other methods; and (4) the method has a distinctive linear normalization algorithm which can obtain highly reliable discrepancies and produce consistent results. Due to the above merits, many scholars have employed the MAIRCA to settle real-world decision issues in a great number of fields, such as flood susceptibility assessment (Hadian
et al.,
2022), ammunition depot site selection problems (Gigovic
et al.,
2016), biological inspiration evaluation (Zhu
et al.,
2021), supplier performance evaluation (Chatterjee
et al.,
2018), failure risk evaluation (Boral
et al.,
2020), business partner selection (Trung
et al.,
2022), and energy storage technology selection (Pamucar
et al.,
2020). To indicate the ambiguous and indetermined evaluation information, some scholars have extended the traditional MAIRCA method by combining it into various decision environments, such as classical fuzzy sets (Gul and Ak,
2020; Boral
et al.,
2020; Mestanza and Bakhat,
2021), fuzzy rough sets (Zhu
et al.,
2021), spherical fuzzy sets (Trung
et al.,
2022; Erdogan,
2022), rough sets (Chatterjee
et al.,
2018; Pamucar
et al.,
2017a; Bozanic
et al.,
2020; Pamucar
et al.,
2017b) and intuitionistic fuzzy sets (Ecer,
2022). For example, the MAIRCA method was combined with the AHP (Analytic Hierarchy Process) (Boral
et al.,
2020; Mestanza and Bakhat,
2021) and BWM (Best-Worst Methods) (Gul and Ak,
2020) approaches for obtaining criteria weights to solve the MCDM problem in classical fuzzy sets, respectively. Pamucar
et al. (
2017a) proposed the rough BWM-MAIRCA method to deal with the wind farm site selection problems based on the geographic information system MCDM model. Similarly, in the rough set environment, Chatterjee
et al. (
2018) designed the R’DAMETEL (Rough Decision-Making Trial and Evaluation Laboratory) technique to structure the relationship between different criteria and utilized the R’ANP (Rough Analytic Network Process) method to calculate the weights; the R’MAIRCA (Rough MAIRCA) method was proposed to evaluate supplier performance; Bozanic
et al. (
2020) constructed a hybrid LBWA-IR-MAIRCA (Level Based Weight Assessment-Interval Rough-MAIRCA) MCDM model to determine the weapon structure elements in an interval-valued rough set environment. Zhu
et al. (
2021) integrated DEMATEL-MAIRCA with rough fuzzy information to evaluate biological inspiration for biologically inspired design; Ecer (
2022) proposed a MAIRCA approach extended from intuitionistic fuzzy to evaluate and select COVID-19 vaccines; Trung
et al. (
2022) advanced a hybrid MCDM model integrating AHP and MAIRCA approaches in the spherical fuzzy context; Erdogan (
2022) extended the SWARA (Stepwise Weight Assessment Ratio Analysis) and MAIRCA techniques under interval-valued spherical fuzzy setting. This method has been applied to various fields by many scholars (Hashemkhani Zolfani
et al.,
2020; Ecer,
2021; Ecer
et al.,
2022).
From the above investigation, the comments on this technique can be summarized as below:
-
(1) The MAIRCA technique integrated and applied with methods (e.g. AHP, ANP, DEMATEL, BWM, LBWA, and SWARA) for determining subjective criterion weights. At present, there is no integration of MAIRCA and objective criteria weighting approaches.
-
(2) Except for MAIRCA methods extended in rough set and interval rough set, the total gap matrix is often determined by using Euclidean distance measures (Boral
et al.,
2020; Mestanza and Bakhat,
2021; Gul and Ak,
2020), and some scholars have also used relative closeness degree (Ecer,
2022) for defuzzification, first based on Euclidean distance, and then on traditional MAIRCA methods for alternative ranking. If we adopt the
q-ROF Hamming or Euclidean distance proposed by Du (
2018) (see Definition
4 below for details), the fuzzy information will be partially lost because the influence of the refusal degree in
q-ROFN is neglected in these distance measures. So, we need a new distance measure to apply in MAIRCA.
-
(3) Some existing studies have also demonstrated that the MAIRCA method can effectively work combined with various decision environments, and it can provide a better technique to solve MCDM problems in other environments. So far this method has not been extended in q-ROFS environment. Meanwhile, it is necessary to consider the interactive operational relationship between the membership functions in q-ROFN in the MAIRCA method to avoid the counter intuitive situation.
Based on the existing researches on decision-making methods in the
q-ROFS environment, we have not found that the MAIRCA approach is utilized to solve
q-ROF MCDM problems. Therefore, the purpose of our article is to integrate the MAIRCA and
q-ROFSs to settle the MCDM issue, this is the dominant motivation of this article. Moreover, the Hamming or Euclidean distance measures are often used in existing MAIRCA method, and some
q-ROF distance measures are more sensitive to large biased data, such as Minkowski-type distance (the special cases include Euclidean, Hamming and Chebyshev), cosine distance, multi-parametric distance and projection-based distance, etc. (Peng and Luo,
2021) However, Lance distance measure can overcome this limitation and make it for biased data, and it has greater applicability. So, we will newly define Lance distance in the
q-ROF environment, which is the second motivation for this paper. In addition, the some extended MAIRCA method in IFSs, spherical fuzzy sets and its extended environments did not consider the special case when the MD or ND is zero, which may have an impact on the results of alternative ranking. In order to avoid the counterintuitive phenomena during the decision process, it is necessary for us to take the interaction operations between MD and ND of
q-ROFNs into account in the extended
q-ROF MAIRCA method, which is the third motivation. And some contributions of this article are presented as below:
-
(1) A novel Lance distance is defined by extending the Lance distance measure under the q-ROF environment;
-
(2) The MDM model is constructed in view of the q-ROF Lance distance to obtain the optimal objective weight vector;
-
(3) The new MAIRCA (MAIRCA-L) approach is advanced in q-ROF setting and improved by q-ROF Lance distance and q-ROFNs interaction operations;
-
(4) By numerical examples, we validate the availability and advantage of the developed methodology.
The rest of the article is arranged as below: Section
2 briefly reviews the
q-ROFSs and traditional MAIRCA approach. The new
q-ROF Lance distance measures are defined in Section
3. Section
4 uses the new MAIRCA-L to solve the
q-ROF MCDM problems. Two numerical examples are provided to prove the validity of the developed method, and the superiorities are shown by comparative analysis and parameter analysis in Section
5. Conclusions and future plans are shown in Section
6.
3 Lance Distance Measure for q-ROFNs
Lance and Williams (
1966) proposed the Lance distance, which is less sensitive to biased data because it is independent of the units (magnitudes) of the variables and judges the distance between data in the form of a ratio, which is less affected by extravagant values. For data with large bias of criterion evaluation values, the Lance distance is better than other distances. Hence, it is a general approach for measuring distance in data analysis (Fan
et al.,
2022).
Definition 6 (Lance and Williams, 1966).
Suppose there are arbitrary two non-negative real number sets
A and
B, then the Lance distance between
A and
B is described as below:
where
${u_{A}}({y_{i}})$ and
${u_{B}}({y_{i}})$ are presented the elements of
A and
B, respectively. And the astriction is satisfied, i.e.
${u_{A}}({y_{i}})+{u_{B}}({y_{i}})\ne 0$,
${y_{i}}\in Y$,
$i=1,2,\dots ,n$.
However, we cannot directly apply Eq. (
13) in the
q-ROF environment, and there are two reasons: (1) The definition of Lance distance in Eq. (
13) is based on real numbers, but it is not quite appropriate for
q-ROFNs which consist of MD and ND. Therefore, a suitable approach is needed to achieve defining Lance distance in the
q-ROF environment. (2) If different MD and ND in
q-ROFNs are equal to zero at the same time, it will make the denominator in the Lance distance zero, which causes the Lance distance calculation of
q-ROFNs to have no theoretical and practical meaning. Due to these reasons, we need to define a new Lance distance measure in the
q-ROF context.
Definition 7.
Let
M and
N on any set
$X=\{{x_{1}},{x_{2}},\dots ,{x_{n}}\}$ be two any
q-ROFSs, where the corresponding
q-ROFN is
${\delta _{M}}({x_{i}})=({\mu _{M}}({x_{i}}),{\nu _{M}}({x_{i}}))$ and
${\delta _{Ni}}({x_{i}})=({\mu _{N}}({x_{i}}),{\nu _{N}}({x_{i}}))$. Then the normalized
q-ROFS Lance distance between
M and
N can be described as:
Theorem 1.
For any set $X=\{{x_{1}},{x_{2}},\dots ,{x_{n}}\}$ on q-ROFS M and N, there are several properties of the Lance distance ${D_{\mathit{Lance}}}(M,N)$ between M and N as follows:
-
(1) ${D_{\mathit{Lance}}}(M,N)\in [0,1]$;
-
(2) ${D_{\mathit{Lance}}}(M,N)=0$, iff $M=N$;
-
(3) ${D_{\mathit{Lance}}}(M,N)={D_{\mathit{Lance}}}(N,M)$.
Proof.
(1) ${D_{\mathit{Lance}}}(M,N)\geqslant 0$ is obvious, and it is only necessary to prove that ${D_{\mathit{Lance}}}(M,N)\leqslant 1$ is hold.
For any
$i=1,2,\dots ,n$, there are
$|{\mu _{M}^{q}}({x_{i}})-{\mu _{N}^{q}}({x_{i}})|\leqslant {\mu _{M}^{q}}({x_{i}})+{\mu _{N}^{q}}({x_{i}})$,
$|{\nu _{M}^{q}}({x_{i}})-{\nu _{N}^{q}}({x_{i}})|\leqslant {\nu _{M}^{q}}({x_{i}})+{\nu _{N}^{q}}({x_{i}})$ and
$|{\pi _{M}^{q}}({x_{i}})-{\pi _{N}^{q}}({x_{i}})|\leqslant {\pi _{M}^{q}}({x_{i}})+{\pi _{N}^{q}}({x_{i}})$, thus:
so,
Therefore,
${D_{\mathit{Lance}}}(M,N)\leqslant 1$, and
$0\leqslant {D_{\mathit{Lance}}}(M,N)\leqslant 1$.
(2) If
${D_{\mathit{Lance}}}(M,N)=0$, it is obvious that:
Then,
$|{\mu _{M}^{q}}({x_{i}})-{\mu _{N}^{q}}({x_{i}})|=0$,
$|{\nu _{M}^{q}}({x_{i}})-{\nu _{N}^{q}}({x_{i}})|=0$,
$|{\pi _{M}^{q}}({x_{i}})-{\pi _{N}^{q}}({x_{i}})|=0$ i.e.
${\mu _{M}}({x_{i}})={\mu _{N}}({x_{i}})$,
${\nu _{M}}({x_{i}})={\nu _{N}}({x_{i}})$,
${\pi _{M}}({x_{i}})={\pi _{N}}({x_{i}})$
Obviously, $M=N$.
When
$M=N$, for any
$i=1,2,\dots ,n$, there are
$|{\mu _{M}^{q}}({x_{i}})-{\mu _{N}^{q}}({x_{i}})|=0$,
$|{\nu _{M}^{q}}({x_{i}})-{\nu _{N}^{q}}({x_{i}})|=0$,
$|{\pi _{M}^{q}}({x_{i}})-{\pi _{N}^{q}}({x_{i}})|=0$, then:
Then, ${D_{\mathit{Lance}}}(M,N)=0$.
Therefore, the law (2) holds.
Therefore, ${D_{\mathit{Lance}}}(M,N)={D_{\mathit{Lance}}}(N,M)$. □
According to Definition
7, suppose there are two arbitrary two
q-ROFNs
${\delta _{1}}=({\mu _{1}},{\nu _{1}})$,
${\delta _{2}}=({\mu _{2}},{\nu _{2}})$. The
q-ROF Lance distance measure between them is defined as
Compared with various distance measures in Definition
4, the proposed
q-ROF Lance distance measure has the following two merits: (i) The MD, ND and abstention degree containing
q-ROFN in Eq. (
15) can more comprehensively reflect the evaluation information expressed by
q-RON. (ii) In Eq. (
15), the influence of biased data on the measurement result is overcome in the form of ratio, and it is more stable.
6 Conclusion
As for the MCDM problem with the weights completely unknown in the q-ROF environment, the MAIRCA method considering the interaction between membership functions and Lance distance measure was extended in this paper. Firstly, we briefly sorted out some relative basics; secondly, we advanced the q-ROF Lance distance measure; and then, the q-ROF MCDM model was constructed, including, using the q-ROF Lance distance measure to determine the criterion weight vector, and utilizing the extended q-ROF MAIRCA-L method for the alternative ranking. Lastly, the developed methodology was employed in two numerical examples, the effectiveness and advantage of the method were illustrated by comparing it with some existing methods.
However, there are three weaknesses in the developed methodology: (1) The proposed method is not concerned with the subjective evaluation of experts in the process of calculating the criterion weight; (2) The interrelationship between criteria cannot be captured when the MAIRCA-L method is applied to solve practical decision-making problems; (3) In determining the total gap matrix, we applied the Lance distance, which only emphasizes reducing the impact of biased data on decision results, but this is still not sufficient and comprehensive in practical decision-making problems. To remedy above shortcomings, we will explore more scientific group decision-making model considering subjective-objective combined weight information. Then, we will introduce the Bonferroni mean, Heronian mean and Hamy mean operators that can concern the interrelationship between two or multiple input arguments to integrate in MAIRCA-L method. And we will comprehensively utilize the advantages of multiple distance measures such Lance, Hamming and Euclidean in determining the total gap matrix, and the threshold parameters will be introduced to reflect decision behaviour in this process, thereby further improving the MAIRCA method.
In the future, the defined
q-ROF Lance distance will be further combined with existing ranking techniques, such as MABAC (Wang
et al.,
2020a), CODAS (Deveci
et al.,
2022a), CoCoSo (Deveci
et al.,
2022c) and DNMA (Saha
et al.,
2022b), etc. And the proposed model will be extended to various decision-making environments, i.e. picture fuzzy sets (Cuong,
2014), probabilistic linguistic sets (Guo and Xu,
2016), T-spherical uncertain linguistic sets (Wang and Ullah,
2022), etc. Moreover, we will utilize the MAIRCA-L to settle practical multi-attribute group decision-making issues expressed in
q-ROFNs, and we also need to use key technologies like determining the weights of experts and attributes when the information is completely unknown or partially known, and achieving group consensus to solve practical decision-making problems, such as investment decisions (Bashir
et al.,
2021), supplier management (Liu
et al.,
2022), technology selection (Manupati
et al.,
2021), etc.
Conflicts of Interest
The authors declare that they have no conflicts of interest to report regarding the present study.

