Abstract
In this paper, at first, we define the notion of general fuzzy automaton over a field; we call this automaton vector general fuzzy automaton (VGFA). Moreover, we present the concept of max-min vector general fuzzy automaton. We show that if two max-min VGFA are similar, they constitute an isomorphism. After that, we prove that if two VGFA constitute an isomorphism with threshold α, they are equivalent with threshold α, where $\alpha \in [0,1]$. Also, some examples are given to clarify these new notions.
1 Introduction
Theoretical computer science is the mathematical study of models of computation. As such, it originated in the 1930s, well before the existence of modern computers, in the work of the logicians Church, Godel, Kleene, Post, and Turing. This early work has had a profound influence on the practical and theoretical development of computer science. Not only has the Turing machine model proved essential for theory, but the work of these pioneers presaged many aspects of computational practice that are now commonplace and whose intellectual antecedents are typically unknown to users. Control theory is a branch of mathematics that deals with the behaviour of dynamical systems studied in terms of inputs and outputs.
Automata theory is one of the longest-established areas in computer science. Standard applications of automata theory include pattern matching, syntax analysis, and formal verification. In recent years, novel applications of automata-theoretic concepts have emerged from numerous sciences, like biology, physics, cognitive sciences, control, linguistics, and biology. For more information, see Aceto
et al. (
2007), Cassandras and Lafortune (
2009), Shamsizadeh
et al. (
2020), Dovier
et al. (
2004), Even (
1965), Roggenbach and Majster-Cederbaum (
2000), Shamsizadeh
et al. (
2016), Shamsizadeh and Zahedi (
2019). Directable automata were introduced in Starke (
1969), and also definite automata by Kleene (
1956). Wee (
1967) and Santos (
1968) have introduced the idea of fuzzy automata. Accordingly, fuzzy finite automata have been applied in many areas, such as learning systems, the model of computing with words, pattern recognition, lattice-valued fuzzy finite automata, and clinical monitoring, and also used as models of machine learning systems (Ying,
2002; Li and Shi,
2000). In general, fuzzy automata have provided an attractive systematic way of generalizing discrete applications (Cattaneo
et al.,
1997; Doostfatemeh and Kremer,
2003; Reiter,
2002; Srivastava and Tiwari,
2002). Moreover, fuzzy automata developed capabilities that are hardly achievable by other tools (Ying,
2002).
Several researchers have contributed to the growth of the fuzzy automata theory. Among these works, the work of Jin and his coworkers (Jin
et al.,
2013) is directed towards the algebraic study of fuzzy automata based on Po-monoids; the work of Abolpour and Zahedi (Abolpour
et al.,
2020; Abolpour and Zahedi,
2017) is directed towards the use of categorical concepts in the study of general fuzzy automata with membership values in different lattice structures; the work of Qiu (
2001,
2002) is directed towards the algebraic, topological and categorical study of fuzzy automata theory based on residuated lattices; the work of Peeva (
1988,
1991) relates to the study of minimizing the states of fuzzy automata and its application to study pattern recognition; the work of Pal and their coworkers (Pal
et al.,
2019) is directed towards the study of fuzzy automaton based on the residuated and co-residuated lattice, the work of Shamsizadeh and coworkers (Shamsizadeh
et al.,
2021; Raisi Sarbizhan
et al.,
2022; Shamsizadeh and Zahedi,
2022; Shamsizadeh,
2022) is directed towards the study of fuzzy automaton based on graph theory and multiset theory and neutrosophic sets; Ghorani, Moghari and coworkers (Ghorani and Moghari,
2022; Ghorani
et al.,
2022) study fuzzy tree automata based on lattice-valued.
In this paper, we define the notion of general fuzzy automaton over a field. We call this automaton vector general fuzzy automaton (VGFA). Moreover, we present the concept of max-min vector general L-fuzzy automaton. VGFA are used for generation of linear codes, detection and correction of errors, construction of testing sequence, and generation of pseudo-random sequences of numbers. They are also used in experiments that require Monte Carlo methods, in the protection of data stored in computer systems and radio location. We show that if two max-min VGFA are similar, then they constitute an isomorphism. After that, we prove that if two VGFA constitute an isomorphism with threshold α, they are equivalent with threshold α, where $\alpha \in [0,1]$. Also, some examples are given to clarify these new notions.
2 Preliminaries
In this section, we review some notions which are needed in the next section.
Definition 1 (Mordeson and Malik, 2002).
A fuzzy finite state machine (ffsm) is a triple $M=(Q,X,\upsilon )$, where Q is a finite set of states, X is a set of input symbols and $\upsilon :Q\times X\times Q\to [0,1]$ is a fuzzy transition function.
As usual,
${X^{\ast }}$ denotes the set of all words of elements of
X of finite length, including the empty word Λ in
${X^{\ast }}$ and
$|x|$ denotes the length of
x, for any
$x\in {X^{\ast }}$.
Definition 2 (Zahedi et al., 2008).
A fuzzy finite state automaton (FFA) is a six-tuple denoted by
$\tilde{F}=(Q,X,R,Z,\delta ,\omega )$, where:
-
• $Q=\{{q_{1}},{q_{2}},\dots ,{q_{n}}\}$ is a finite set of states,
-
• $X=\{{a_{1}},{a_{2}},\dots ,{a_{m}}\}$ is a finite set of input symbols,
-
• R is the start state of $\tilde{F}$,
-
• $Z=\{{b_{1}},{b_{2}},\dots ,{b_{k}}\}$ is a finite set of output symbols,
-
• $\delta :Q\times X\times Q\to [0,1]$ is the fuzzy transition function which is used to map a state (current state) into another state (next state) upon an input symbol, attributing a value in the interval $[0,1]$,
-
• $\omega :Q\to Z$ is the output function.
In an FFA, as can be seen, associated with each fuzzy transition a membership value in
$[0,1]$. We call this membership value, the value of the transition.
Definition 3 (Doostfatemeh and Kremer, 2005).
A general fuzzy automaton (GFA)
$\tilde{F}$ is an eight-tuple machine denoted by
$\tilde{F}=(Q,X,\tilde{R},Z,\tilde{\delta },\omega ,{F_{1}},{F_{2}})$, where:
-
• $Q=\{{q_{1}},{q_{2}},\dots ,{q_{n}}\}$ is a finite set of states,
-
• $X=\{{a_{1}},{a_{2}},\dots ,{a_{m}}\}$ is a finite set of input symbols,
-
• $\tilde{R}\subseteq \tilde{P}(Q)$ is the set of fuzzy start states,
-
• $Z=\{{b_{1}},{b_{2}},\dots ,{b_{k}}\}$ is a finite set of output symbols,
-
• $\tilde{\delta }:(Q\times [0,1])\times X\times Q\to [0,1]$ is the augmented transition function,
-
• $\omega :Q\to Z$ is the output function,
-
• ${F_{1}}:[0,1]\times [0,1]\to [0,1]$ is called the membership assignment function. The function
${F_{1}}(\mu ,\delta )$, as is seen, is motivated by two parameters
μ and
δ, where
μ is the membership value of a predecessor and
δ is the value of a transition. In this definition, the process that takes place upon the transition from state
${q_{i}}$ to
${q_{j}}$ on an input
${a_{k}}$ is represented as
Which means that membership value (MV) of the state
${q_{j}}$ at time
$t+1$ is computed by function
${F_{1}}$ using both the membership value of
${q_{i}}$ at time
t and the membership value of the transition. There are many options which can be used for the function
${F_{1}}(\mu ,\delta )$. It can be, for example,
$\max \{\mu ,\delta \},\min \{\mu ,\delta \},\frac{\mu +\delta }{2}$ or any other applicable mathematical function.
-
• ${F_{2}}:{[0,1]^{\ast }}\to [0,1]$ is called the multi-membership resolution function. The multi-membership resolution function resolves the multi-membership active states and assigns a single non-membership value to them.
${[0,1]^{\ast }}$ is the set of elements in [0, 1]. The multi-membership resolution function ${F_{2}}$ is a function which specifies the strategy that resolves the multi-membership active states and assigns a single mv to them.
Definition 4 (Bag and Samanta, 2003).
Let
U be a linear space over a field
F. A fuzzy subset
N of
$U\times R$ is called a fuzzy norm on
U if and only if for every
$x,u\in U$ and
$c\in F$,
-
1. For every $t\in R$ with $t\leqslant 0$, $N(x,t)=0$,
-
2. For every $t\in R$, $t\gt 0$, $N(x,t)=1$ if and only if $x=0$,
-
3. For every $t\in R$, $t\gt 0$, $N(cx,t)=N(x,\frac{t}{|c|})$ if $c\ne 0$,
-
4. For every $s,t\in R$, $x,u\in U$, $N(x+u,s+t)\geqslant \min \{N(x,s),N(u,t)\}$,
-
5. $N(x,.)$ is a non-decreasing function of R and ${\lim \nolimits_{t\to \infty }}N(x,t)=1$.
The pair
$(U,N)$ will be referred to as a fuzzy normed linear space.
Example 1 (Bag and Samanta, 2003).
Let
$(U,\| \| )$ be a normed linear space. Define
Then
$(U,N)$ is a fuzzy normed linear space.
Example 2 (Bag and Samanta, 2003).
Let
$(U,\| \| )$ be a normed linear space. Define
Then
$(U,N)$ is a fuzzy normed linear space.
3 Vector General Fuzzy Automaton
Definition 5.
Let
F be a field and
$n\in {N_{0}}$. By
${F_{n}}$ we denote the vector space of column vectors of dimension
n over
F. A vector general fuzzy automaton (VGFA) is an automaton
${\tilde{F}_{v}}=(Q,X,\tilde{R},Z,\tilde{\delta },\tilde{\omega },{F_{1}},{F_{2}},{F_{3}},{F_{4}})$ with the following properties:
-
(i) There exists a field F and integers $k,m,r\in {N_{0}}$, such that
-
1. $Q={F_{k}}$ is a nonempty finite set of states, $Q=\{{u_{1}},{u_{2}},{u_{3}},\dots \}$, where ${u_{1}}=({u_{1}^{(1)}},{u_{1}^{(2)}},\dots ,{u_{1}^{(k)}})\in {F_{k}}$,
-
2. $X={F_{m}}$ is a finite set of input symbols, $X=\{{a_{1}},{a_{2}},{a_{3}},\dots \}$, where ${a_{1}}=({a_{1}^{(1)}},{a_{1}^{(2)}},\dots ,{a_{1}^{(m)}})\in {F_{m}}$,
-
3. $\tilde{R}\subseteq P(\tilde{Q})$ is the set of L-fuzzy start symbols,
-
4. $Z={F_{r}}$ is a finite set of output symbols, $Z=\{{z_{1}},{z_{2}},{z_{3}},\dots \}$, where ${z_{1}}=({z_{1}^{(1)}},{z_{1}^{(2)}},\dots ,{z_{1}^{(r)}})\in {F_{r}}$;
-
(ii) There exist a $k\times k$ matrix A, a $k\times m$ matrix B, and a $r\times k$ matrix C, all over F, such that
-
1. $\tilde{\delta }:(Q\times [0,1])\times X\times Q\to [0,1]$ is the augmented transition function, where $\delta (u,a,Au+Ba)\in \Delta $.
-
2. $\tilde{\omega }:(Q\times [0,1])\times Z\to [0,1]$ is the augmented output function.
-
3. ${F_{1}}:[0,1]\times [0,1]\to [0,1]$ is called the membership assignment function. The function
${F_{1}}(\mu ,\delta )$, as is seen, is motivated by two parameters
μ and
δ, where
μ is the membership value of a predecessor and
δ is the value of a transition. In this definition, the process that takes place upon the transition from state
${u_{i}}$ to
${u_{j}}$ on an input
${a_{k}}$ is represented as
Which means that membership value (MV) of the state
${u_{j}}$ at time
$t+1$ is computed by function
${F_{1}}$ using both the membership value of
${u_{i}}$ at time
t and the membership value of the transition. There are many options which can be used for the function
${F_{1}}(\mu ,\delta )$. For example, it can be
$\max \{\mu ,\delta \}$,
$\min \{\mu ,\delta \}$,
$\frac{\mu +\delta }{2}$ or any other applicable mathematical function.
-
4. ${F_{2}}:[0,1]\times [0,1]\to [0,1]$ is called the membership assignment output function.
${F_{2}}(\mu ,\omega )$ as is seen, is motivated by two parameters
μ and
ω, where
μ is the membership value of present state and
ω is the membership value of an output function. Then
Notice that
$\omega (u,z)\gt 0$ if and only if
$z=Cu$.
-
5. ${F_{3}}:{[0,1]^{\ast }}\to [0,1]$ is called the multi-membership resolution function. The multi-membership resolution function resolves the multi-membership active states and assigns a single membership value to them.
-
6. ${F_{4}}:{[0,1]^{\ast }}\to [0,1]$ is called the multi-membership resolution output function. The multi-membership resolution output function resolves the output multi-membership active state and assigns a single output membership value to it.
We let the set of all transitions of
${\tilde{F}_{v}}$ is denoted by Δ. Now, suppose that
${Q_{act}}({t_{i}})$ be the set of all active states at time
${t_{i}}$, for all
$i\geqslant 0$. We have
${Q_{act}}({t_{0}})=\tilde{R}$ and
where
$\Delta =\{\delta (u,a,Au+Ba)\hspace{0.1667em}|\hspace{0.1667em}u\in Q,a\in X\}$ for every
$i\geqslant 1$. Since
${Q_{act}}({t_{i}})$ is a fuzzy set, to show that a state
u belongs to
${Q_{act}}({t_{i}})$ and
T is a subset of
${Q_{act}}({t_{i}})$, we write
$u\in \textit{Domain}({Q_{act}}({t_{i}}))$. Hereafter, we denote these notations by
The combination of the operations of functions
${F_{1}}$ and
${F_{3}}$ on a multi-membership state
${u_{j}}$ leads to the multi-membership resolution algorithm. By using (Doostfatemeh and Kremer,
2005; Shamsizadeh and Zahedi,
2015) we have the following algorithms.
Algorithm: Multi-membership resolution for transition function:
If there are several simultaneous transitions to the active state
${u_{j}}$ at time
$t+1$, then the following algorithm will assign a unified membership value to that.
-
Step 1. Input: ${\delta _{1}}({u_{i}},{a_{k}},{u_{j}})$, ${\mu ^{t}}({u_{i}})$, $i,j=1,2,\dots ,m$, and $k=1,2,\dots ,l$,
-
Step 2. For $i,j=1,2,\dots ,m$, and $k=1,2,\dots ,l$, compute ${\tilde{\delta }_{1}}(({u_{i}},{\mu ^{t}}({u_{i}})),{a_{k}},{u_{j}})={F_{1}}({\mu ^{t}}({u_{i}}),{\delta _{1}}({u_{i}},{a_{k}},{u_{j}}))$,
-
Step 3. For $j=1,2,\dots ,m$, ${\mu ^{t+1}}({u_{j}})={({F_{3}})^{n-1}}({x_{1}},{x_{2}},\dots ,{x_{n}})$, where n is the number of simultaneous transitions to the active state ${u_{j}}$ at time $t+1$ and ${x_{r}}={F_{1}}({\mu ^{t}}({u_{i}}),{\delta _{1}}({u_{i}},{a_{k}},{u_{j}}))$, $1\leqslant r\leqslant n$,
-
Step 4. Output: for $j=1,2,\dots ,m$, print: ${\mu ^{t+1}}({u_{j}})$.
Algorithm: Multi-membership resolution for output function:
If there are several simultaneous outputs to the active state
${u_{i}}$ at time
t, the following algorithm will assign a unified membership value to it.
-
Step 1. Input: ${\omega _{1}}({u_{i}},{z_{k}})$, ${\mu ^{t}}({u_{i}})$, $i=1,2,\dots ,m$, $k=1,2,\dots ,l$,
-
Step 2. For
$i=1,2,\dots ,m$,
$k=1,2,\dots ,l$, compute:
-
Step 3. For $i=1,2,\dots ,m$, ${\omega _{1}^{t}}({u_{i}})={F_{4}^{n-1}}({x_{1}},{x_{2}},\dots ,{x_{n}})$, where n is the number of simultaneous outputs to the active state ${u_{i}}$ at time t, ${x_{r}}={F_{2}}({\mu ^{t}}({u_{i}}),{\omega _{1}}({u_{i}},{z_{j}}))$, $1\leqslant r\leqslant n$,
-
Step 4. Output: for $i=1,2,\dots ,m$, print: ${\omega _{1}^{t}}({u_{i}})$.
Remark 1.
For every $u\in Q$, such that $u\notin \tilde{R}$, we have ${\mu ^{{t_{0}}}}(u)=0$ and $q\in \tilde{R}$ implies that ${\mu ^{{t_{0}}}}(q)\gt 0$.
Definition 6.
We shall often want to refer to a finite non-empty set
${F_{m}}$ as a vector alphabet. If
${F_{m}}$ is a vector alphabet, let
${F_{m}^{+}}$ consist of all finite sequences
where
$({a_{i}^{(1)}},{a_{i}^{(2)}},\dots ,{a_{i}^{(m)}})\in {F_{m}}$ and
$1\leqslant i\leqslant k$.
The multiplication given by (
3) then corresponds to just a simple position:
Definition 7.
Let
${\tilde{F}_{v}}=(Q,X,\tilde{R},Z,\tilde{\delta },\tilde{\omega },{F_{1}},{F_{2}},{F_{3}},{F_{4}})$ be a VGFA. We define the max-min vector general fuzzy automaton
${\tilde{F}_{v}^{\ast }}=(Q,X,\tilde{R},Z,{\tilde{\delta }^{\ast }},\tilde{\omega },{F_{1}},{F_{2}},{F_{3}},{F_{4}})$, such that
${\tilde{\delta }^{\ast }}:{Q_{act}}\times {X^{\ast }}\times Q\to [0,1]\times [0,1]$, where
${Q_{act}}=\{{Q_{act}}({t_{0}}),{Q_{act}}({t_{1}}),{Q_{act}}({t_{2}}),\dots \}$ and for every
$i\geqslant 0$,
Also, for every
$i\geqslant 0$,
${\tilde{\delta }^{\ast }}(({u_{1}},{\mu ^{{t_{i}}}}({u_{1}})),{a_{i+1}},{u_{2}})=\tilde{\delta }(({u_{1}},{\mu ^{{t_{i}}}}({u_{1}})),{a_{i+1}},{u_{2}})$ and recursively,
in which
${a_{i}}\in X$ for every
$1\leqslant i\leqslant n-1$, and assume that
${a_{i+1}}$ is the entered input at time
${t_{i}}$, for every
$0\leqslant i\leqslant n-2$.
Actually, the fact that the VGFA acts in discrete time we will also use the notation
where
${u_{t}}\in {Q_{act}}(t)$,
${a_{t}}\in X$,
${\omega _{{q_{t}}}}\in Z$ for
$t\in {N_{0}}$.
Notice that when we want to consider a word, we can write it as enumeration. If we have
for use of equation (
6), we consider
w as follows:
Since field
F and matrices
A,
B and
C entirely characterize the vector general fuzzy automaton (VGFA), we shall also denote automaton by 13-tuple machine
$(F,Q,X,A,B,C,\tilde{R},Z,\tilde{\delta },\tilde{\omega },{F_{1}},{F_{2}},{F_{3}},{F_{4}})$.
Example 3.
Let
L be a bounded lattice as in Fig.
1. Let
${\tilde{F}_{v}}=(F,Q,X,A,B,C,\tilde{R},Z,\tilde{\delta },\tilde{\omega },{F_{1}},{F_{2}},{F_{3}},{F_{4}})$ be a VGFA defined over field
$F={Q_{2}}$ of integers modulo 2, such that
$A=\bigg[\begin{array}{c@{\hskip4.0pt}c}0\hspace{1em}& 1\\ {} 1\hspace{1em}& 0\end{array}\bigg]$,
$B=\bigg[\begin{array}{c}1\\ {} 1\end{array}\bigg]$,
$C=[\begin{array}{c@{\hskip4.0pt}c}0\hspace{2.5pt}\hspace{0.1667em}& 1\end{array}]$,
$Q=\Big\{\bigg[\begin{array}{c}0\\ {} 0\end{array}\bigg],\bigg[\begin{array}{c}1\\ {} 1\end{array}\bigg],\bigg[\begin{array}{c}0\\ {} 1\end{array}\bigg],\bigg[\begin{array}{c}1\\ {} 0\end{array}\bigg]\Big\}$,
$X=\{[0],[1]\}$,
$\tilde{R}=\Big(\bigg[\begin{array}{c}0\\ {} 0\end{array}\bigg],1\Big)$,
$Z=\{[0],\hspace{2.5pt}[1]\}$ and
δ,
ω are defined as follows:
If we choose
${F_{1}}=\wedge $ and
${F_{2}}=\vee $ and
${\mu ^{{t_{0}}}}\Big(\bigg[\begin{array}{c}0\\ {} 0\end{array}\bigg]\Big)=1$, we have
Notice that there exists no
${\mu ^{{t_{1}}}}\Big(\bigg[\begin{array}{c}1\\ {} 0\end{array}\bigg]\Big)$, since
$\delta \Big(\bigg[\begin{array}{c}0\\ {} 0\end{array}\bigg],\left[0\right],\bigg[\begin{array}{c}1\\ {} 0\end{array}\bigg]\Big)$ does not belong to Δ. By choosing a different Matrices
A and
B, it is possible to obtain
${\mu ^{{t_{1}}}}\Big(\bigg[\begin{array}{c}1\\ {} 0\end{array}\bigg]\Big)$ and
${\mu ^{{t_{1}}}}\Big(\bigg[\begin{array}{c}0\\ {} 1\end{array}\bigg]\Big)$. Now, we have
The diagram of VGFA is presented on Fig.
2.
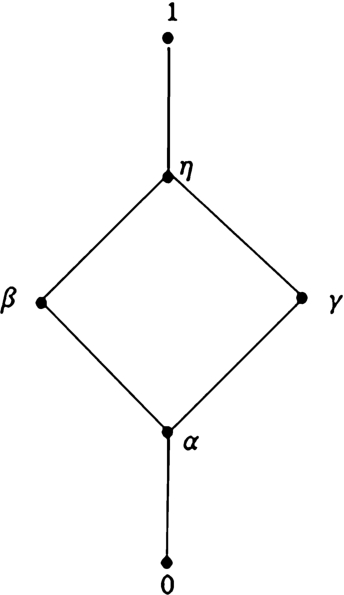
Fig. 1
The bounded lattice
L of Example
3.
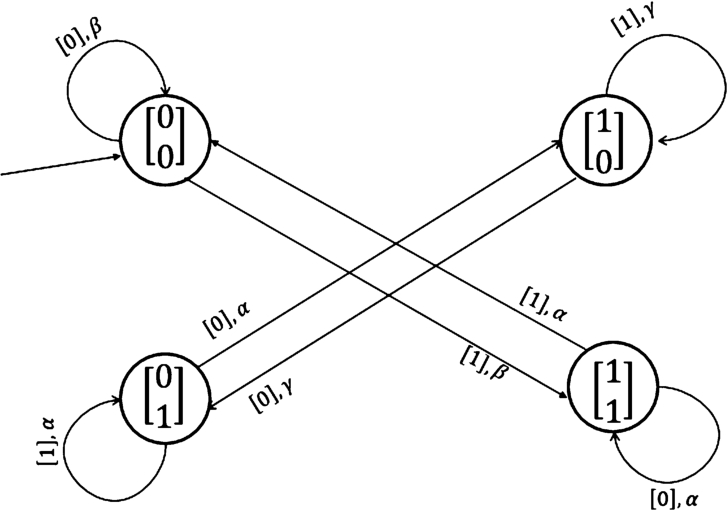
Fig. 2
The vector general fuzzy automaton
${\tilde{F}_{v}}$ of Example
3.
4 Equivalence and Isomorphism for Vector General Fuzzy Automata
Theorem 1.
Let a VGFA ${\tilde{F}_{v}}=(F,Q,X,A,B,C,\tilde{R},Z,\tilde{\delta },\tilde{\omega },{F_{1}},{F_{2}},{F_{3}},{F_{4}})$ be given. Then the following properties hold:
-
1. ${u_{t}}={A^{t}}{u_{0}}+{\textstyle\sum _{i=0}^{t-1}}{A^{t-i-1}}B{a_{i}}$, for every $t\in N$,
-
2. ${\omega _{t}}=C{A^{t}}{u_{0}}$, for every $t\in {N_{0}}$.
Proof.
1. We prove the claim by induction on
t. If
$t=1$, then we have
Now, suppose the claim holds for
$t=n$, so we have
${u_{n}}={A^{n}}{u_{0}}+{\textstyle\sum _{i=0}^{n-1}}{A^{n-i-1}}B{a_{i}}$. Let
$t=n+1$. Then
2. By induction on
t, it is omitted. □
Definition 8.
Let
${\tilde{F}_{vi}}=(F,{Q_{i}},X,{A_{i}},{B_{i}},{C_{i}},{\tilde{R}_{i}},Z,{\tilde{\delta }_{i}},{\tilde{\omega }_{i}},{F_{1}},{F_{2}},{F_{3}},{F_{4}})$ where
$i=1,2$, be two VGFAs. We say that
${\tilde{F}_{v1}}$ is similar to
${\tilde{F}_{v2}}$ if there exists a nonsingular matrix
P, such that
-
i. $u\in {\tilde{R}_{1}}$ if and only if $Pu\in {\tilde{R}_{2}}$,
-
ii. ${A_{2}}=P{A_{1}}{P^{-1}}$,
-
iii. ${B_{2}}=P{B_{1}}$,
-
iv. ${C_{2}}={C_{1}}{P^{-1}}$.
Definition 9.
Let
F be a field. Let
${\tilde{F}_{vi}}=({Q_{i}},X,{A_{i}},{B_{i}},{C_{i}},{\tilde{R}_{i}},Z,{\tilde{\delta }_{i}},{\tilde{\omega }_{i}},{F_{1}},{F_{2}},{F_{3}},{F_{4}})$ where
$i=1,2$, be two VGFAs. A homomorphism from
${\tilde{F}_{v1}}$ onto
${\tilde{F}_{v2}}$ with threshold
α, is a function
φ from
${Q_{1}}$ onto
${Q_{2}}$ such that for every
$u,{u^{\prime }}\in {Q_{1}}$ and
$a\in X$ and
$z\in Z$ the following conditions hold:
-
I. ${\mu ^{{t_{0}}}}(u)\gt \alpha $ if and only if ${\mu ^{{t_{0}}}}(\varphi (u))\gt \alpha $,
-
II. ${\delta _{1}}(u,a,{u^{\prime }})\gt \alpha $ if and only if ${\delta _{2}}(\varphi (u),a,\varphi ({u^{\prime }}))\gt \alpha $.
Actually, I and II show that
${\tilde{\delta }_{1}}((u,{\mu ^{t}}(u)),a,{u^{\prime }})\gt \alpha $ if and only if
-
III. ${\tilde{\omega }_{1}}((u,{\mu ^{{t_{i}}}}(u)),z)\gt \alpha $ implies that ${\tilde{\omega }_{2}}((\varphi (u),{\mu ^{{t_{i}}}}(\varphi (u))),z)\gt \alpha $.
We say that φ constitutes an isomorphism with threshold α if φ constitutes an a homomorphism with threshold α that is one-to-one and ${\tilde{\omega }_{1}}((u,{\mu ^{{t_{i}}}}(u)),z)\gt \alpha $ if and only if ${\tilde{\omega }_{2}}((\varphi (u),{\mu ^{{t_{i}}}}(\varphi (u))),z)\gt \alpha $.
If
φ constitutes an isomorphism with threshold 0, then we say that
φ constitutes an isomorphism.
Theorem 2.
Let ${\tilde{F}_{vi}}=(F,{Q_{i}},X,{A_{i}},{B_{i}},{C_{i}},{\tilde{R}_{i}},Z,{\tilde{\delta }_{i}},{\tilde{\omega }_{i}},{F_{1}},{F_{2}},{F_{3}},{F_{4}})$ where $i=1,2$, be two VGFAs. If ${\tilde{F}_{v1}}$ is similar to ${\tilde{F}_{v2}}$, then ${\tilde{F}_{v1}}$ and ${\tilde{F}_{v2}}$ constitute an isomorphism.
Proof.
Let
P be a nonsingular matrix such that
${A_{2}}=P{A_{1}}{P^{-1}}$,
$B=P{B_{1}}$,
${C_{2}}={C_{1}}{P^{-1}}$. Let
$\varphi :{Q_{1}}\to {Q_{2}}$ be a map such that
$\varphi (u)=Pu$, for every
$u\in {F_{k}}$. It is clear that
φ is well defined. Now, let
$\varphi ({u_{1}})=\varphi ({u_{2}})$, for every
${u_{1}},{u_{2}}\in {Q_{1}}$. Then
$P{u_{1}}=P{u_{2}}$. Since
P is a nonsingular matrix, then
${u_{1}}={u_{2}}$. Therefore,
φ is one-one. Hence,
φ is bijection. Now, let
${\mu ^{{t_{0}}}}(u)\gt 0$, where
$u\in {F_{k}}$. Then
$u\in {\tilde{R}_{1}}$. Since
$\varphi (u)=Pu$ and by considering Definition
8 we have
$Pu\in {\tilde{R}_{2}}$, so
$\varphi (Pu)\gt 0$. Suppose that
${\mu ^{{t_{0}}}}(\varphi (u))\gt 0$ thus,
$\varphi (u)\in {\tilde{R}_{2}}$. By using Definition
8, we have
${\mu ^{{t_{0}}}}(u)\gt 0$ and
$u\in {\tilde{R}_{1}}$. Let
${\delta _{1}}(u,a,{u^{\prime }})\gt 0$. Then by Definition
5, we have
${\delta _{1}}(u,a,{u^{\prime }})\in \Delta $. It implies that
${u^{\prime }}={A_{1}}u+{B_{1}}a$. Therefore,
By Definition
5,
${\delta _{2}}(\varphi (u),a,{A_{2}}\varphi (u)+{B_{2}}a)={\delta _{2}}(\varphi (u),a,\varphi ({u^{\prime }}))\in \Delta $, hence,
${\delta _{2}}(\varphi (u),a,\varphi ({u^{\prime }}))\gt 0$. Now, let
${\delta _{2}}(v,a,{v^{\prime }})\gt 0$, where
$v,{v^{\prime }}\in {Q_{2}}$. Then there exists
$u,{u^{\prime }}\in {Q_{1}}$, such that
$\varphi (u)=v$ and
$\varphi ({u^{\prime }})={v^{\prime }}$. So,
We show that
${\delta _{1}}((u,{\mu ^{{t_{0}}}}(u)),a,{u^{\prime }})\gt 0$ if and only if
${\delta _{2}}((\varphi (u),{\mu ^{{t_{0}}}}(\varphi (u))),a,\varphi ({u^{\prime }}))\gt 0$. Let
${\tilde{\omega }_{1}}((u,{\mu ^{{t_{i}}}}(u)),z)\gt 0$. Then
${\mu ^{{t_{i}}}}(u)\gt 0$ and
${\omega _{1}}(u,z)\gt 0$. By Definition
5, we have
$z={C_{1}}u$. By considering Definition
8, we have
$z={C_{1}}u={C_{2}}Pu={C_{2}}\varphi (u)$. Thus,
${\omega _{2}}(\varphi (u),z)\gt 0$. Also, we have
${\mu ^{{t_{i}}}}(u)\gt 0$ if and only if
${\mu ^{{t_{i}}}}(\varphi (u))\gt 0$. Therefore,
${\tilde{\omega }_{2}}((\varphi (u),{\mu ^{{t_{i}}}}(\varphi (u))),z)\gt 0$. The opposite can be proved in a similar way. □
The opposite of Theorem
2 is not true because there exist isomorphic VGFA which are not similar. As an illustration, let us give the following example.
Example 4.
Let
L be a bounded lattice as in Fig.
1,
${Q_{7}}$ be a field and
and
where
$\alpha \in [0,1]$. Also, let
$\varphi :{Q_{1}}\to {Q_{2}}$ be a map such that
$\varphi ([m])=[m]$ and
${\delta _{1}}([u],[0],[3][u])=\alpha $, for every
$[u]\in {Q_{1}}$ and
${\delta _{2}}([u],[0],[5][u])=\alpha $, for every
$[u]\in {Q_{2}}$, and suppose that
${\omega _{i}}([u],[2][u])=\alpha $, for every
$[u]\in {Q_{1}}={Q_{2}}$ and
$i=1,2$. It is clear that
${\tilde{F}_{v1}}$ and
${\tilde{F}_{v2}}$ are isomorphic but not similar because the matrix
$[3]$ is not similar to matrix
$[5]$ over the field
${Q_{7}}$ of integers modulo 7.
Definition 10.
Let
$\tilde{F}=(F,Q,X,A,B,C,\tilde{R},Z,\tilde{\delta },\tilde{\omega },{F_{1}},{F_{2}},{F_{3}},{F_{4}})$ be a max-min VGFA. The language with threshold
α,
$\alpha \in [0,1]$, recognized by
$\tilde{F}$, is a subset of
${F_{m}^{\ast }}$ defined by
Definition 11.
Two max-min VGFAs ${\tilde{F}_{v1}}$ and ${\tilde{F}_{v2}}$ are called equivalent with threshold α if ${\mathcal{L}^{\alpha }}({F_{1}})={\mathcal{L}^{\alpha }}({F_{2}})$, where $\alpha \in [0,1]$.
Theorem 3.
Let ${\tilde{F}_{v1}}$ and ${\tilde{F}_{v2}}$ be two max-min VGFAs. Let ${\tilde{F}_{v1}}$ and ${\tilde{F}_{v2}}$ be isomorphic with threshold α, where $\alpha \in [0,1]$. Then they are equivalent with threshold α.
Proof.
Let
${\tilde{F}_{vi}}=(F,{Q_{i}},X,{A_{i}},{B_{i}},{C_{i}},{\tilde{R}_{i}},Z,{\tilde{\delta }_{i}},{\tilde{\omega }_{i}},{F_{1}},{F_{2}},{F_{3}},{F_{4}})$,
$i=1,2$, be two max-min VGFAs and
$\varphi :{Q_{1}}\to {Q_{2}}$ be a homomorphism. Now, let
${a_{1}}{a_{2}}\dots {a_{k}}=x\in \mathcal{L}({\tilde{F}_{v1}})$. Then there exist
$u,v\in {F_{k}}$ and
$z\in {F_{r}}$, such that
${\tilde{\delta }_{1}^{\ast }}((u,{\mu ^{{t_{0}}}}(u)),x,v)\wedge {\tilde{\omega }_{1}}((v,{\mu ^{{t_{0}}+|x|}}(v)),z)\gt \alpha $, where
$\alpha \in [0,1]$. So,
${\tilde{\delta }_{1}^{\ast }}((u,{\mu ^{{t_{0}}}}(u)),x,v)\gt \alpha $ and
${\tilde{\omega }_{1}}((v,{\mu ^{{t_{0}}+|x|}}(v)),z)\gt \alpha $. Then there exists
${u_{1}},{u_{2}},\dots ,{u_{k-1}}\in {Q_{1}}$, such that
By Definition
9, we have
It is implied that
$x\in \mathcal{L}({\tilde{F}_{v2}})$. Therefore,
$\mathcal{L}({\tilde{F}_{v1}})\subseteq \mathcal{L}({\tilde{F}_{v2}})$. In a similar way
$\mathcal{L}({\tilde{F}_{v2}})\subseteq \mathcal{L}({\tilde{F}_{v1}})$. Hence,
$\mathcal{L}({\tilde{F}_{v1}})=\mathcal{L}({\tilde{F}_{v2}})$. □
5 General Fuzzy Automaton on Fuzzy Normed Linear Space
Definition 12.
Let
F be a field and
$n\in {N_{0}}$. By
${F_{n}}$ we denote the vector space of column vectors of dimension
n over
F. A general automaton on fuzzy normed linear space (or simply fuzzy norm general automata (FNGA)) is an automaton
${\tilde{F}_{n}}=(Q,X,I,Z,\tilde{\delta },\tilde{\omega },{N_{1}},{N_{2}},\vee ,\vee )$ with the following properties:
-
(i) There exist a field F and integers $k,m,r\in {N_{0}}$, such that
-
1. $Q={F_{k}}$ is a nonempty finite set of states, $Q=\{{u_{1}},{u_{2}},{u_{3}},\dots \}$, where ${u_{1}}=({u_{1}^{(1)}},{u_{1}^{(2)}},\dots ,{u_{1}^{(k)}})\in {F_{k}}$,
-
2. $X={F_{m}}$ is a finite set of input symbols, $X=\{{a_{1}},{a_{2}},{a_{3}},\dots \}$, where ${a_{1}}=({a_{1}^{(1)}},{a_{1}^{(2)}},\dots ,{a_{1}^{(m)}})\in {F_{m}}$,
-
3. $I\subseteq Q$ is the set of start symbols,
-
4. $Z={F_{r}}$ is a finite set of output symbols, $Z=\{{z_{1}},{z_{2}},{z_{3}},\dots \}$, where ${z_{1}}=({z_{1}^{(1)}},{z_{1}^{(2)}},\dots ,{z_{1}^{(r)}})\in {F_{r}}$;
-
(ii) There exist a $k\times k$ matrix A, a $k\times m$ matrix B, and a $r\times k$ matrix C, all over F such that
-
1. $\tilde{\delta }:(Q\times R)\times X\times Q\to [0,1]$ is the augmented transition function, where $\delta (u,a,Au+Ba)\in R$, $\delta (u,\Lambda ,Au+B\Lambda )=0$, and R is set of real number,
-
2. $\tilde{\omega }:(Q\times R)\times Z\to [0,1]$ is the augmented output function,
-
3. ${N_{1}}:U\times R\to [0,1]$ is called the membership assignment function. In this definition, the process that takes place upon the transition from state
${u_{i}}$ to
${u_{j}}$ on an input
$a\in X$ is represented as follows:
where
${N_{1}}$ is a fuzzy normed linear space and
U is a linear space over a fileld
F,
-
4. ${N_{2}}:U\times R\to [0,1]$ is called the membership assignment output function.
${N_{2}}(\mu ,\omega )$, as it seems, is motivated by two parameters
μ and
ω, where
μ is the membership value of present state and
ω is the membership value of an output function. Then
We let the set of all transitions of
${\tilde{F}_{v}}$ be denoted by Δ. Now, suppose that
${Q_{act}}({t_{i}})$ is the set of all active states at time
${t_{i}}$, for all
$i\geqslant 0$. We have
${Q_{act}}({t_{0}})=I$ and
where
$\Delta =\{\delta (u,a,Au+Ba)\hspace{0.1667em}|\hspace{0.1667em}u\in Q,a\in X\}$ for every
$i\geqslant 1$.
${Q_{act}}({t_{i}}),i\gt 0$ is a fuzzy set.
Remark 2.
For every $u\in Q$, such that $u\notin I$, we have ${\mu ^{{t_{0}}}}(u)=0$ and $q\in I$ implies that ${\mu ^{{t_{0}}}}(q)\gt 0$.
Definition 13.
Let
${\tilde{F}_{n}}=(Q,X,I,Z,\tilde{\delta },\tilde{\omega },{N_{1}},{N_{2}},\vee ,\vee )$ be a FNGA. We define the max-min fuzzy norm general automaton
${\tilde{F}_{n}^{\ast }}=(Q,X,I,Z,{\tilde{\delta }^{\ast }},\tilde{\omega },{N_{1}},{N_{2}},\vee ,\vee )$, such that
${\tilde{\delta }^{\ast }}:{Q_{act}}\times {X^{\ast }}\times Q\to [0,1]$, where
${Q_{act}}=\{{Q_{act}}({t_{0}}),{Q_{act}}({t_{1}}),{Q_{act}}({t_{2}}),\dots \}$ and for every
$i\geqslant 0$,
Also, for every
$i\geqslant 0$,
${\tilde{\delta }^{\ast }}(({u_{1}},{\mu ^{{t_{i}}}}({u_{1}})),{a_{i+1}},{u_{2}})=\tilde{\delta }(({u_{1}},{\mu ^{{t_{i}}}}({u_{1}})),{a_{i+1}},{u_{2}})$ and recursively,
in which
${a_{i}}\in X$, for every
$1\leqslant i\leqslant n-1$, and assume that
${a_{i+1}}$ is the entered input at time
${t_{i}}$, for every
$0\leqslant i\leqslant n-2$.
Example 5.
Let
${\tilde{F}_{v}}=(F,Q,X,A,B,C,\tilde{R},Z,\tilde{\delta },\tilde{\omega },{N_{1}},{N_{2}},\vee ,\vee )$ be an FNGA defined over field
$F={Q_{2}}$ of integers modulo 2 such that
$A=\bigg[\begin{array}{c@{\hskip4.0pt}c}0\hspace{1em}& 1\\ {} 1\hspace{1em}& 0\end{array}\bigg]$,
$B=\bigg[\begin{array}{c}1\\ {} 1\end{array}\bigg]$,
$C=\left[\begin{array}{c@{\hskip4.0pt}c}0& 1\end{array}\right]$,
$Q=\Big\{\bigg[\begin{array}{c}0\\ {} 0\end{array}\bigg],\bigg[\begin{array}{c}1\\ {} 1\end{array}\bigg],\bigg[\begin{array}{c}0\\ {} 1\end{array}\bigg],\bigg[\begin{array}{c}1\\ {} 0\end{array}\bigg]\Big\}$,
$X=\{[0],[1]\},\tilde{R}=\Big(\bigg[\begin{array}{c}0\\ {} 0\end{array}\bigg],1\Big)$, and
$Z=\{[0],[1]\}$. Let
${\mu ^{{t_{0}}}}\Big(\bigg[\begin{array}{c}0\\ {} 0\end{array}\bigg]\Big)=9$. If we consider
${N_{1}^{a}}$ as Example
1, and
${N_{2}}$ as Example
1, then we have:
Now, we have
6 Conclusion
General fuzzy automaton over a field are used for generation of linear codes, detection and correction of errors, construction of testing sequence, and generation of pseudo-random sequences of numbers. They are also used in experiments that require Mote Carlo methods, in the protection of data stored in computer systems and radio-location.
In the recent study, we defined the notion of general fuzzy automaton and max-min general fuzzy automaton over a field; we call this automaton vector general fuzzy automaton. Moreover, we presented the concept of max-min vector general fuzzy automaton. We proved that if two max-min VGFA are similar, they constitute an isomorphism. Moreover, we showed that if two VGFA constitute an isomorphism with threshold α, they are equivalent with threshold α, where $\alpha \in [0,1]$. Also, we presented a general automaton on fuzzy normed linear space.
Further, we try to present a connection between VGFA and similar automata. Also, we try to present fuzzy finite tree automaton over a fuzzy normed linear space.

