1 Introduction
Every day we receive an enormous amount of data, information, and knowledge. Data becomes information when it is contextualised and related to a specific problem or solution. Data mining is an important part of knowledge discovery processes in various fields and sectors, such as medicine, economics, finance, telecommunications. Data mining helps uncover hidden information from vast amounts of data, which is valuable for recognising important facts, relationships, trends, and patterns. As data sets become increasingly large, more efficient ways of visualizing, analysing and interpreting the information they contain are needed. Comprehension of data is challenging, especially when the data relates to a complex object, a phenomenon that is described by many parameters, attributes, or features. Such data are called multidimensional, and the main goal is to make some visual insight into the data set being analysed. Visual information can be perceived much faster than textual information. For human perception, the multidimensional data must be represented in a low-dimensional space, usually two or three dimensions.
The main task in dimensionality reduction is to represent objects with a smaller set of more “compressed” features. Another reason for reducing the dimensionality or visualization of the data is to reduce the computational load for further data processing. Dimensionality reduction techniques enable the extraction of meaningful information hidden in the data. In addition, one of the most important purposes of data visualization is to get an idea of how close or far away certain points of the analysed multidimensional data are from each other.
Consider the multidimensional data set as an array $X=\{{X_{i}}=({x_{i1}},\dots ,{x_{in}})$, $i=1,\dots ,m\}$ of n-dimensional data points ${X_{i}}\in {\mathbb{R}^{n}},\hspace{2.5pt}n\geqslant 3$. A data point ${X_{i}}$ is the result of an observation of some object or phenomenon that depends on n features. Dimensionality reduction means finding a set of coordinates (locations) of points ${Y_{i}}=({y_{i1}},\dots ,{y_{id}})$, $i=1,\dots ,m$, in a lower-dimensional space $(d<n)$, where the particular point ${X_{i}}\in {\mathbb{R}^{n}}$ is represented by ${Y_{i}}\in {\mathbb{R}^{d}}$. If $d\leqslant 3$, then dimensionality reduction results can be presented visually for more convenient human decision-making.
Dimensionality reduction or data visualization techniques play an important role in machine learning (Murphy,
2022; Zhou,
2021; Ray
et al.,
2021; Dzemyda
et al.,
2013; Dos Santos and Brodlie,
2004; Buja
et al.,
2008). Such visualization is useful, especially in exploratory analysis: they provide insights into similarity relationships in high-dimensional data that would be unlikely to be obtained without visualization (Lee and Verleysen,
2007; Van Der Maaten
et al.,
2009; Markeviciute
et al.,
2022; Xu
et al.,
2019; Bernatavičienė
et al.,
2007; Kurasova and Molyte,
2011; Borg and Groenen,
2005; Dzemyda and Kurasova,
2006; Dzemyda
et al.,
2013; Jolliffe,
2002; Karbauskaitė and Dzemyda,
2015,
2016; Groenen
et al.,
1995). The classical dimensionality reduction methods for data visualization include linear principal component analysis (PCA) (Jolliffe,
2002; Jackson,
1991) and multidimensional scaling (MDS) (Torgerson,
1958; Borg and Groenen,
2005; Borg
et al.,
2018). PCA seeks to reduce the dimensionality of the data by finding orthogonal linear combinations (principal components) of the original variables with the highest variance (Jackson,
1991; Medvedev
et al.,
2011). The interpretation of principal components can sometimes be complex. PCA cannot cover non-linear structures consisting of arbitrarily shaped clusters or manifolds because it describes the data in terms of a linear subspace. Since global methods such as PCA and MDS cannot represent the local non-linear structure, there have been developed methods that preserve the raw local distances, i.e. the values of distances between nearest neighbours. Isomap, Local Linear Embedding (LLE), Hessian Local Linear Embedding and Laplacian Eigenmaps are traditional methods that attempt to preserve local Euclidean distances from the original space (Wang
et al.,
2021; Espadoto
et al.,
2021). More recent methods that focus on local structure preservation are t-Distributed Stochastic Neighbour Embedding (t-SNE) (Van der Maaten and Hinton,
2008) and UMAP (McInnes
et al.,
2018). A comprehensive review of dimensionality reduction methods is presented in Murphy (
2022), Espadoto
et al. (
2021), Wang
et al. (
2021), Vachharajani and Pandya (
2022), Dzemyda
et al. (
2013), Lee and Verleysen (
2007), Van Der Maaten
et al. (
2009), Xu
et al. (
2019).
Artificial neural networks can also be applied to reduce dimensionality and visualize data (Dzemyda
et al.,
2007). A feedforward neural network is used for a topographic, structure-preserving, dimension-reducing transformation of data, with the additional ability to incorporate various degrees of related subjective information. There is also a neural network architecture developed specifically for topographic mapping, known as a Self-Organizing Map (SOM) (Kohonen,
2001; Stefanovic and Kurasova,
2011), which uses implicit lateral connections in the output layer of neurons. SOM is a technique used for both clustering and data dimensionality reduction (Dzemyda
et al.,
2007,
2013). In addition, there is a special learning rule, similar to backpropagation, which allows an ordinary feedforward artificial neural network to learn the Sammon mapping, which is a special case of metric MDS, in an unsupervised way. The learning rule for this type of neural network is known as SAMANN (Mao and Jain,
1995; Ivanikovas
et al.,
2007; Medvedev
et al.,
2011; Dzemyda
et al.,
2007).
An alternative view of dimensionality reduction is offered by multidimensional scaling (Borg and Groenen,
2005). Multidimensional scaling (MDS) is a classical non-linear approach that maps an original high-dimensional data set onto a lower-dimensional data set, but does so in an attempt to preserve the proximities between the corresponding data points. It is one of the most popular methods for multidimensional data visualization (Murphy,
2022; Borg
et al.,
2018; Dzemyda
et al.,
2013). Despite the fact that MDS demonstrates great versatility, it is computationally demanding. This can be challenging when the data amount increases. Traditional MDS approaches are limited when analysing very large data sets, as they require long computational time and large amounts of memory. Until now, there have been various studies aimed at creating a new solution or modifying the MDS to analyse large amounts of data and speed up the visualization process (Orts
et al.,
2019; Qiu and Bae,
2012; Pawliczek
et al.,
2014; Ingram
et al.,
2008; Medvedev
et al.,
2011; Ivanikovas
et al.,
2007).
The input data for MDS is a symmetric
$m\times m$ matrix
$\mathbf{D}=\{{d_{ij}},i,j=1,\dots ,m\}$ of proximities (similarities or dissimilarities) between the pairs of objects. More often, the dissimilarities are used to represent the proximities, however, the formulation of the multidimensional scaling problem and its solving methods remain the same in both cases. A lower dissimilarity value means that the objects are more similar. As dissimilarity,
${d_{ij}}$ can be a distance between points
${X_{i}}$ and
${X_{j}},$ $i,j=1,\dots ,m$ (Dzemyda
et al.,
2013). The smaller the distance, the closer the points are.
One of the most popular algorithms for MDS is SMACOF (De Leeuw,
1977; De Leeuw and Mair,
2009). The algorithm is based on the majorization approach (Groenen
et al.,
1995), which iteratively replaces the original objective function with an auxiliary majorization function that is much easier to optimize. Majorization is not just an algorithm, it is more of a prescription for constructing optimization algorithms. The principle of majorization consists in constructing a auxiliary function that majorizes a certain objective function (De Leeuw and Mair,
2009). Experimental studies have shown that SMACOF is the most accurate algorithm compared to others (Orts
et al.,
2019; Ingram
et al.,
2008). There are a number of popular software implementations of SMACOF (De Leeuw and Mair,
2009; Pedregosa
et al.,
2011; Orts
et al.,
2019; MATLAB,
2012).
An alternative to SMACOF the Geometric MDS proposed in Dzemyda and Sabaliauskas (
2020) and Dzemyda and Sabaliauskas (
2021a), and developed in Sabaliauskas and Dzemyda (
2021), Dzemyda and Sabaliauskas (
2021b,
2021c), Dzemyda
et al. (
2022), Dzemyda and Sabaliauskas (
2022). This will be discussed in more detail further in the paper. Figure
1 illustrates the visualization using Geometric MDS of 10, 50, and 100-dimensional datasets generated with Gaussian and Ellipsoidal cluster generators (Handl and Knowles,
2005). The dimensionality of the multidimensional data has been reduced to 2 (
$d=2$). The Gaussian cluster generator is based on a standard cluster model using multivariate normal distributions, and the ellipsoidal cluster generator creates ellipsoidal clusters with the major axis at an arbitrary orientation. For each cluster, data points are generated at a Gaussian distributed distance from a uniformly random point on the major axis, in a uniformly random direction, and are rejected if they lie outside the boundary (Handl and Knowles,
2005). As the datasets are generated using cluster generators for large high-dimensional data sets with large numbers of clusters, some noisy data may be included. The example in Fig.
1 illustrates the use of visualization techniques to identify outliers, patterns in data in the form of clusters, relationships, and trends. The figure clearly shows clusters of analysed data and the location of individual multidimensional data among the rest.
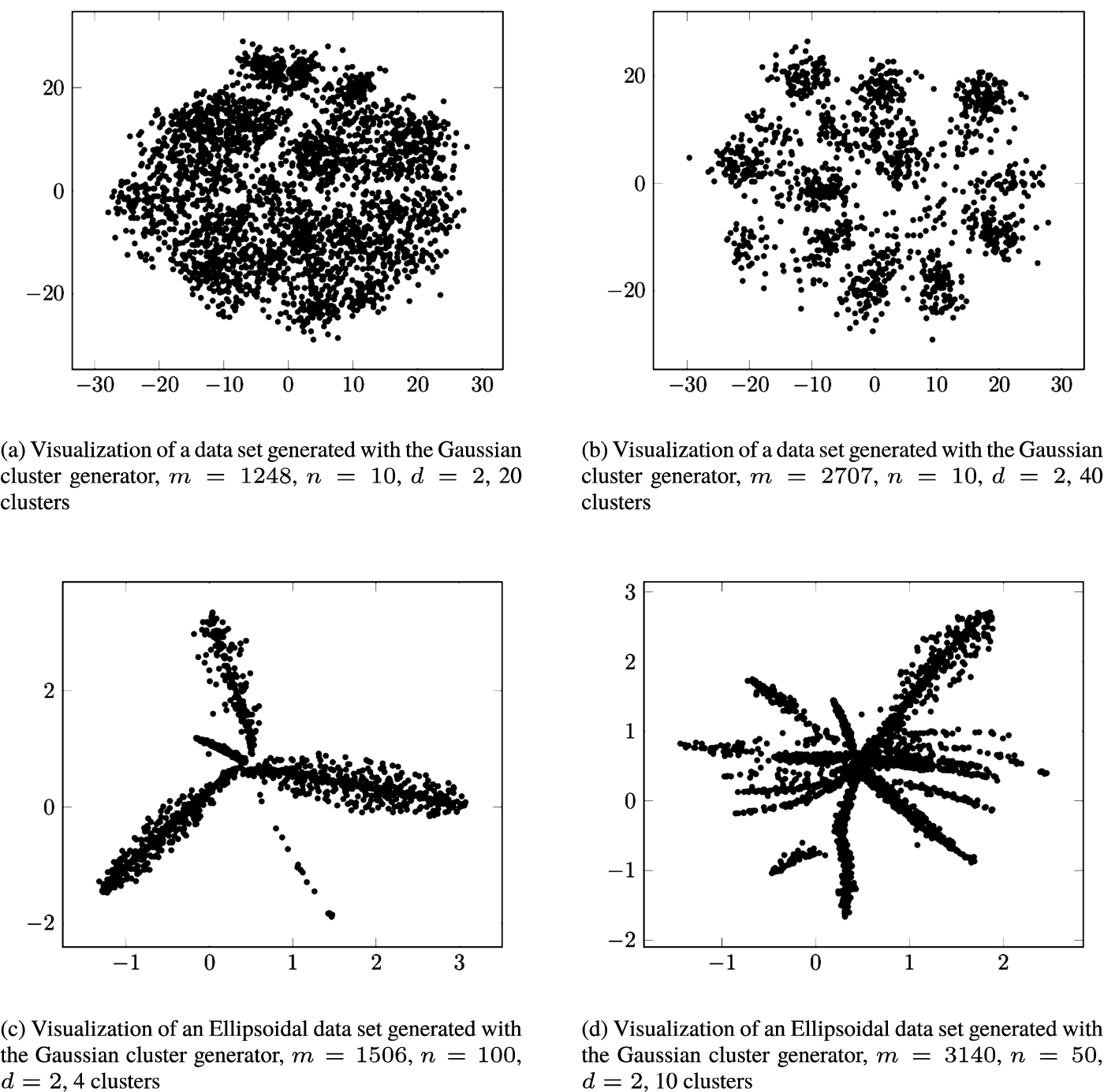
Fig. 1
Examples of dimensionality reduction results obtained using Geometric MDS.
The novelty of this paper consists in the experimental investigation of parallelization of recently developed Geometric Multidimensional Scaling. The process of parallelization can lead to faster dimensionality reduction and data visualization process and to the possibility to process a large-scale multidimensional data. Theoretically proved properties of Geometric MDS are applied in parallelization. In addition, Geometric MDS is also experimentally compared with SMACOF, which is one of the most popular implementations of MDS. It was found that Geometric MDS is superior to the SMACOF in most cases.
2 Geometric MDS: Multidimensional Scaling From a Geometric Point of View
MDS looks for coordinates of points
${Y_{i}}$ representing
${X_{i}}$ in the lower-dimensional Euclidean space
${\mathbb{R}^{d}}$ by minimizing the stress function (Dzemyda
et al.,
2013). There are several MDS implementations with different stress functions (see review in Dzemyda
et al.,
2013). However, their minimization is rather complicated. In Dzemyda and Sabaliauskas (
2020), Sabaliauskas and Dzemyda (
2021), Dzemyda and Sabaliauskas (
2021a,
2021c) a new approach, called Geometric MDS, with low computational complexity is proposed, making metric MDS applicable to large-scale data. This method is valuable and advantageous because the stress function and the multidimensional scaling have been considered from a geometrical point of view. The new interpretation of the stress function allows us to find the proper step size and direction of descent forward to the minimum of the stress function analytically, if we consider and move a single point of the projected space. A special property of the new approach is that there is no need for an analytical expression of the stress function. Even more, no linear search, which is used for local descent in optimization, is needed. Theoretical investigation showed that the step direction determined by Geometric MDS coincides with the direction of the steepest descent method (Dzemyda and Sabaliauskas,
2021a). The step size found analytically is such that it guarantees stress reduction in that direction.
A Geometric MDS has the advantage that it can use the simplest stress function, and there is no need to normalize it based on the number of data points and the scale of proximities. In Dzemyda and Sabaliauskas (
2021a) it is shown that Geometric MDS does not depend on the scale of proximities and can therefore use a simple stress function, such as a raw stress function:
where
${d_{ij}^{\ast }}$ is the Euclidean distance between points
${Y_{i}}$ and
${Y_{j}}$ in a lower-dimensional space:
The optimization problem is to find the minimum of the function
$S(\cdot )$ (
1), and the optimal coordinates of the points
${Y_{i}}=({y_{i1}},\dots ,{y_{id}})$,
$i=1,\dots ,m$:
Let there be some initial configuration of points
${Y_{1}},\dots ,{Y_{m}}$. The simplest way to minimize the stress
$S(\cdot )$ by Geometric MDS is a consecutive changing of positions of separate points
${Y_{1}},\dots ,{Y_{m}}$ many times (iterations). This realization is denoted by GMDS1. One iteration of GMDS1 changes all points
${Y_{i}}=({y_{i1}},\dots ,{y_{id}})$ in consecutive order when
i runs from 1 to
m once. Here we compute a new position
${Y_{i}^{\ast }}=({y_{i1}^{\ast }},\dots ,{y_{id}^{\ast }})$ of
${Y_{i}}=({y_{i1}},\dots ,{y_{id}})$ when the positions of remaining points
${Y_{1}},\dots ,{Y_{j-1}},{Y_{j+1}},\dots ,{Y_{m}}$ are fixed, and update
${Y_{j}}$ by
${Y_{j}^{\ast }}$ then. So, Geometric MDS recalculates the coordinates of a single
d-dimensional point
${Y_{j}}$ at each step, and one of its iterations consists of
m steps. The result is a new point
${Y_{j}^{\ast }}$. The stopping condition may be the number of iterations or the value of decrease of the stress function (
1). Convergence of this algorithm to the local minimum of the stress is proved.
The core formula of Geometric MDS, when defining the transition from
${Y_{j}}$ to the new position
${Y_{j}^{\ast }}$, is as follows:
where the point
${A_{ij}}$ lies on the line between
${Y_{i}}$ and
${Y_{j}}$,
$i\ne j$, at a distance
${d_{ij}}$ from
${Y_{i}}$ (see Dzemyda and Sabaliauskas,
2020; Dzemyda and Sabaliauskas,
2021a; Sabaliauskas and Dzemyda,
2021):
Let’s consider a generalized way to update the entire set of points
$Y=\{{Y_{1}},\dots ,{Y_{m}}\}$ to
${Y^{\ast }}=\{{Y_{1}^{\ast }},\dots ,{Y_{m}^{\ast }}\}$. The main equation of Geometric MDS (
4) is used for defining the transition from
${Y_{j}}$ to the new position
${Y_{j}^{\ast }}$. The raw stress function (
1) decreases after
${Y_{j}}$ goes to
${Y_{j}^{\ast }}$, that is, moving any of the projected points by the Geometric MDS method reduces the stress (Dzemyda and Sabaliauskas,
2021a). But in the generalized scenario, all points
${Y_{1}},\dots ,{Y_{m}}$ change their coordinates to
${Y_{1}^{\ast }},\dots ,{Y_{m}^{\ast }}$ simultaneously and independently of each other during a single iteration of stress minimization. Therefore, we perform a simultaneous repositioning of all points
${Y_{1}},\dots ,{Y_{m}}$ of the projected space in the directions determined by the Geometric MDS strategy for individual points. We update
${Y_{1}},\dots ,{Y_{m}}$ by
${Y_{1}^{\ast }},\dots ,{Y_{m}^{\ast }}$ after all the points
${Y_{1}^{\ast }},\dots ,{Y_{m}^{\ast }}$ are computed, only. This realization is denoted by GMDS
m. One iteration of GMDS
m changes all points
${Y_{i}}=({y_{i1}},\dots ,{y_{id}})$ simultaneously once. The convergence is proved theoretically in Dzemyda and Sabaliauskas (
2022).
3 Multi-Core Implementation of Geometric MDS
The GMDS
m version of the Geometric MDS updates all points
${Y_{1}},\dots ,{Y_{m}}$ in a lower dimension simultaneously and independently of each other. This enables the use of parallel computing for updating each
${Y_{i}}$ independently, i.e. in parallel (see Algorithm
1). Such possibility of parallelization has been investigated further in this paper utilising multi-core processing. The computational resources of a single personal computer were used in this work. Experiments using different number of CPU threads were performed to obtain preliminary estimates of the efficiency of multi-core implementation of GMDS
m.

Algorithm 1
A parallel Geometric MDS algorithm for simultaneous calculation of new points ${Y_{j}^{\ast }}$ in the projected space
The purpose of the experiment is to compare the time required to compute new points
${Y_{1}^{\ast }},\dots ,{Y_{m}^{\ast }}$ in the projected space from
${Y_{1}},\dots ,{Y_{m}}$, when using a sequential programming implementation of GMDS
m with the computing power of one CPU core (single thread), and respectively when using a parallel algorithm using 2, 4, 6, 8, 10, 12 CPU threads. Here each point
${Y_{j}^{\ast }}$ is computed using Eq. (
4), and all points
${Y_{1}},\dots ,{Y_{m}}$ change their coordinates to
${Y_{1}^{\ast }},\dots ,{Y_{m}^{\ast }}$ at once simultaneously and independently of each other during a single iteration. One iteration is a recalculation (optimal updating) of all points
${Y_{i}}=({y_{i1}},\dots ,{y_{id}})$,
$i=1,\dots ,m$ once. The pseudo-code of the algorithm used for experiments is provided in Algorithm
1 (Dzemyda
et al.,
2022). Note that only the time taken to compute the new coordinates was measured during the experiments (see the part of Algorithm
1 that is marked as running in parallel). The California Housing dataset (Pace and Barry,
1997) was used for the experiments. The dataset consists of data collected in the 1990 California Census, it has 20640 examples of block groups, each containing an average of 1425.5 people living in a geographically compact area. There are 10 different features per example: 8 numeric attributes, one predictive attribute and the target. For preliminary experiments and due to limited computing resources, only part of the data was used (see Table
1), i.e. data of 500, 1000, 1500, 2000, 2500, 3000, 3500, 4000, 4500 and 5000 observations were analysed, and the dimensionality of the multidimensional data was reduced to 2. This increase in data size reveals a trend which demonstrates that with further increases in data size, the use of parallel computing becomes more efficient. The experiments resulted in an average dependence of the time to calculate new point coordinates (without taking into account the full visualization process) on the size of the data when using different numbers of CPU threads for parallel processing. Each experiment was repeated 10 times to obtain more reliable data, so Table
1 presents the average value of the generalized data. For the experiments we used an AMD Ryzen 5 2600 processor, 4000 MHz (6 cores, 12 threads) with high multiprocessor performance, with 16GB of DDR4-2666 1333 MHz RAM, and the Python-Anaconda (Anaconda,
2022) environment was used as the software.
Table 1
Average dependence of the computation time of new coordinates (not considering the complete visualization process) on the data size when using different numbers of CPU threads for parallel processing, $n=8$; the dimensionality of multidimensional data was reduced to 2 ($d=2$).
| Number of points, m
|
Sequential algorithm |
Number of CPU threads (parallel processing) |
| 2 |
4 |
6 |
8 |
10 |
12 |
| 100 |
0.0445 |
0.6492 |
0.7018 |
0.8365 |
1.0246 |
1.2450 |
1.3315 |
| 500 |
1.1770 |
1.1783 |
0.9902 |
1.0372 |
1.2384 |
1.4430 |
1.5087 |
| 1000 |
4.8455 |
2.9246 |
1.9148 |
1.7087 |
1.9091 |
2.0435 |
2.0459 |
| 1500 |
10.8324 |
5.8416 |
3.4209 |
2.8879 |
2.9647 |
3.0228 |
3.0353 |
| 2000 |
19.1812 |
9.8804 |
5.5490 |
4.3496 |
4.3921 |
4.4029 |
4.3415 |
| 2500 |
30.3274 |
15.3864 |
8.2581 |
6.2743 |
6.3550 |
6.2527 |
6.2111 |
| 3000 |
43.6203 |
21.5616 |
11.6450 |
8.7684 |
8.7479 |
8.6064 |
8.2878 |
| 3500 |
59.4401 |
28.9800 |
15.8067 |
11.5609 |
11.2593 |
11.0542 |
10.6939 |
| 4000 |
79.0386 |
37.7887 |
20.7712 |
15.1054 |
14.3880 |
14.3113 |
13.4704 |
| 4500 |
99.2351 |
47.8711 |
25.8535 |
18.8063 |
18.0433 |
17.4048 |
16.8381 |
| 5000 |
124.6468 |
59.0778 |
31.7166 |
23.1730 |
22.3510 |
21.3549 |
20.6990 |
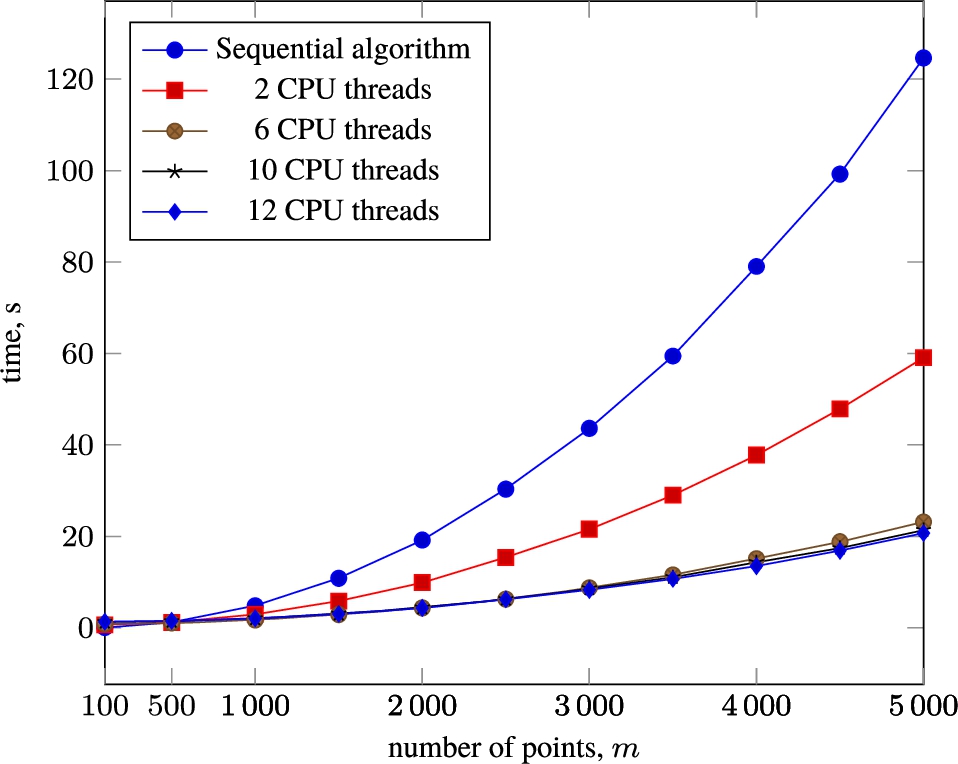
Fig. 2
Average dependence of the computation time of new coordinates (not taking into account the complete visualization process) on the size of the data, when using different numbers of CPU threads for parallel processing, $n=8$.
The results obtained (see Table
1 and Fig.
2) demonstrate that even using two CPU threads for parallel processing, it is possible to achieve significant process speedup (on average up to 2 times) compared to sequential computing. The results obtained conclude that when using more than two processor threads for parallel computing, it is possible to increase the speed of the process of calculating new coordinates in the projected space on average up to 6 times. It is also worth noting that the difference in time increases with increasing the size of the analysed data, that is, the larger the size of the data used for visualization, the more efficient the process of parallel computing (see Fig.
2). It should be noted that these data were obtained as a result of initial experiments, using the computational power of a personal computer. Consider also that the CPU used for the experiments had 6 cores and 12 threads, so, as can be seen from the results, the efficiency of calculations using more than 6 threads is not high. The results are promising, which indicates the feasibility of using Geometric MDS to visualize large-scale multidimensional data using the computing power of a supercomputer or cluster for parallel computing.
4 Sequential Implementation of Geometric MDS
Although MDS demonstrates great versatility, it is computationally expensive and not scalable, and requires handling the entire data distance or other proximity matrix. This can be challenging when we deal with large-scale data. In this section, we propose the optimized Python implementation of GMDSm for sequential computations.
MDS-type algorithms require to update a matrix of
$m\times m$ of all pairwise Euclidean distances
${d_{ij}^{\ast }}$ between points
${Y_{i}}$ and
${Y_{j}}$, i.e. for
m points a
$m\times m$ matrix is required, each entry of which defines a non-negative distance between the pair of points. Calculations of Euclidean distance occur frequently in machine learning and computer vision (Albanie,
2019; Song
et al.,
2016). The element of the distance matrix is defined by (
2).
However, as noted in Albanie (
2019), the Euclidean distance matrix can be computed in another way, which is equivalent to (
2):
where the first and last terms are the norms of vectors and can be calculated separately.
This method defined by (
6) of calculating the Euclidean distance matrix has been implemented and used in Geometric MDS Python programming implementation. Applying (
6) allows to speed up the visualization significantly because of much simpler calculations, and also allows to extend the dimensionality reduction for relatively large-scale data. Python function code for calculating distance matrix from a given
$m\times d$ matrix
$Y=({Y_{i}}=({y_{i1}},\dots ,{y_{id}}),i=1,\dots ,m)$ is presented in Listing
1. This code can be used to compute a
$m\times m$ distance matrix from
$m\times n$ matrix
$X=({X_{i}}=({x_{i1}},\dots ,{x_{in}}))$,
$i=1,\dots ,m$, too.

Listing 1
Python function code for calculating distance matrix.

Listing 2
Python function code for calculating new points ${Y^{\ast }}=\{{Y_{1}^{\ast }},\dots ,{Y_{m}^{\ast }}\}$ in a low-dimensional space using Geometric MDS.

Listing 3
Python function code for calculating new points ${\hat{Y}^{\ast }}=\{{\hat{Y}_{1}^{\ast }},\dots ,{\hat{Y}_{m}^{\ast }}\}$ in a low-dimensional space using SMACOF (optimized version of SMACOF, referred to as SMACOF-Fast).
The algorithm in Listing
1 returns
${10^{-5}}$ values on the diagonal of the proximity matrix and in other situations when points among
${X_{i}}$ and
${X_{j}}$ coincide (the coincidence is only possible before Geometric MDS starts). This avoids dividing by zero for further calculations.
The Geometric MDS and SMACOF programming implementation code for Python has been optimized for computational speed. The Geometric MDS stress minimization method as well as the SMACOF implementation are featured by the fact that all points in low-dimensional space change their coordinates simultaneously and independently of each other during one iteration of stress minimization. We provide a function code implemented to calculate new coordinates of points in
d-dimensional space in one iteration using Geometric MDS and SMACOF (see Listings
2 and
3), as well as the code of a fully working Python program that implements the sequential Geometric MDS algorithm (see Listing
4), where the stopping condition for stress (
1) minimization is either the iteration number or the accuracy. In one iteration (see Listings
2 and
3), the coordinates of all points in the projected space are recalculated once. Listing
3 presents the function code for calculating new coordinates using SMACOF, adapted from the scikit-learn library (Pedregosa
et al.,
2011) and updated to improve computation speed (this implementation is denoted as SMACOF-Fast). In this implementation, the stress majorization, which is also known as the Guttman transform, guarantees monotonic stress convergence and is more powerful than traditional methods such as gradient descent.

Listing 4
Main program of Geometric MDS.
Geometric MDS becomes the main competitor of SMACOF. We would like to highlight the main differences between the two algorithms. More detailed theoretical comparison of them is provided in Dzemyda and Sabaliauskas (
2022).
At first, we define a Geometric MDS step from point
${Y_{j}}$ to
${Y_{j}^{\ast }}$,
$j=1,\dots ,m$ that calculates new coordinates of point
${Y_{j}^{\ast }}$:
SMACOF is an iterative procedure that calculates the Guttman transform (Guttman,
1968) at each iteration and updates simultaneously the coordinates of
m points
${Y_{j}}=({y_{j1}},\dots ,{y_{jd}})$,
$j=1,\dots ,m$:
where
${\hat{Y}_{j}^{\ast }}=({\hat{y}_{j1}^{\ast }},\dots ,{\hat{y}_{jd}^{\ast }}),\hspace{2.5pt}j=1,\dots ,m$ are new points,
Y and
${\hat{Y}^{\ast }}$ are
$m\times d$ matrices of coordinates of points
${Y_{j}}$ and
${\hat{Y}_{j}^{\ast }}$, respectively,
$B=B(Y)$ is
$m\times m$ matrix with elements
It is easy to check that SMACOF works very similarly to Geometric MDS. By calculating coordinates of point
${\hat{Y}_{j}^{\ast }}$,
$j=1,\dots ,m$, (
8) and (
9) can be expressed as
It is proved in Dzemyda and Sabaliauskas (
2022) that both Geometric MDS and SMACOF make a step from the point
${Y_{j}}$ to its new position
${Y_{j}^{\ast }}$ or
${\hat{Y}_{j}^{\ast }}$, respectively in the same direction with different step size. The step size by Geometric MDS is longer by
$\frac{m}{m-1}$ times.
Geometric MDS can be expressed in matrix form as well:
where
${Y_{j}^{\ast }}=({y_{j1}^{\ast }},\dots ,{y_{jd}^{\ast }}),\hspace{2.5pt}j=1,\dots ,m$ are new points,
Y and
${Y^{\ast }}$ are
$m\times d$ matrices of coordinates of points
${Y_{j}}$ and
${Y_{j}^{\ast }}$, respectively,
$\hat{B}=\hat{B}(Y)$ is
$m\times m$ matrix with elements
4.1 Computation Time Cost by Geometric MDS and SMACOF
The dimensionality reduction performance was compared using SMACOF (from the scikit-learn library, Pedregosa
et al.,
2011), SMACOF-Fast (Listing
3) and Geometric MDS algorithms (Listing
2). Experiments were carried out using:
-
• randomly generated sets of 10-dimensional data points ${X_{i}}=({x_{i1}},\dots ,{x_{id}})$, $i=1,\dots ,m$, with coordinates uniformly distributed in the interval $(0,1)$;
-
• random proximity matrices with elements uniformly distributed in the interval $(0,1)$.
Table 2
Average dependency of time required to compute new coordinates and Stress function values per iteration on data size when $n=10$, using SMACOF-Fast, SMACOF and Geometric MDS.
|
|
|
|
|
|
|
Ratio |
| Number of points, m
|
SMACOF |
SMACOF-Fast |
Geometric MDS |
SMACOF/SMACOF-Fast |
Geometric MDS/SMACOF-Fast |
|
|
|
|
|
| Stress |
Time, s |
Stress |
Time, s |
Stress |
Time, s |
Stress ratio |
Time ratio |
Stress ratio |
Time ratio |
| 10 |
11.6 |
0.00019 |
11.6 |
0.00003 |
11.7 |
0.00003 |
1.0000000 |
7.3152985 |
1.0095220 |
1.2097938 |
| 20 |
66.7 |
0.00036 |
66.7 |
0.00005 |
66.7 |
0.00006 |
1.0000000 |
6.9684499 |
1.0011044 |
1.1193416 |
| 50 |
479.1 |
0.00056 |
479.1 |
0.00009 |
478.8 |
0.00009 |
1.0000000 |
6.3983110 |
0.9992541 |
1.0824801 |
| 100 |
2128.1 |
0.00093 |
2128.1 |
0.00016 |
2127.0 |
0.00017 |
1.0000000 |
5.9893883 |
0.9995029 |
1.0680442 |
| 200 |
8946.6 |
0.00194 |
8946.6 |
0.00035 |
8944.1 |
0.00037 |
1.0000000 |
5.5188379 |
0.9997245 |
1.0489429 |
| 500 |
51188.6 |
0.00885 |
51188.6 |
0.00246 |
51183.4 |
0.00267 |
1.0000000 |
3.5984986 |
0.9998969 |
1.0861585 |
| 1000 |
218604.8 |
0.03845 |
218604.8 |
0.01419 |
218594.0 |
0.01452 |
1.0000000 |
2.7084907 |
0.9999505 |
1.0227548 |
| 2000 |
894694.9 |
0.18151 |
894694.9 |
0.06169 |
894672.8 |
0.06175 |
1.0000000 |
2.9422145 |
0.9999753 |
1.0009971 |
| 5000 |
5106657.3 |
1.15621 |
5106657.3 |
0.32358 |
5106605.3 |
0.32322 |
1.0000000 |
3.5731957 |
0.9999898 |
0.9988961 |
| 10000 |
21892993.0 |
5.06069 |
21892993.0 |
1.27452 |
21892881.6 |
1.26265 |
1.0000000 |
3.9706513 |
0.9999949 |
0.9906829 |
| 15000 |
59857709.1 |
14.66615 |
59857709.1 |
3.51422 |
59857507.2 |
3.46431 |
1.0000000 |
4.1733769 |
0.9999966 |
0.9857980 |
| 20000 |
127201601.7 |
32.07792 |
127201601.7 |
7.49513 |
127201281.2 |
7.45024 |
1.0000000 |
4.2798321 |
0.9999975 |
0.9940104 |
Table 3
Average dependence of the time required to compute new coordinates and Stress function values per iteration on the data size on random proximity matrices whose element takes uniformly distributed values in the interval (0, 1), using SMACOF-Fast, SMACOF and Geometric MDS.
|
|
|
|
|
|
|
Ratio |
| Number of points, m
|
SMACOF |
SMACOF-Fast |
Geometric MDS |
SMACOF/SMACOF-Fast |
Geometric MDS/SMACOF-Fast |
|
|
|
|
|
| Stress |
Time, s |
Stress |
Time, s |
Stress |
Time, s |
Stress ratio |
Time ratio |
Stress ratio |
Time ratio |
| 10 |
3.812807 |
0.00018 |
3.812807 |
0.00003 |
3.738581 |
0.00003 |
1.00000000 |
6.20922293 |
0.98053234 |
1.01140901 |
| 20 |
22.02273 |
0.00036 |
22.02273 |
0.00006 |
21.81476 |
0.00006 |
1.00000000 |
6.34562798 |
0.99055667 |
1.02805624 |
| 50 |
164.0261 |
0.00057 |
164.0261 |
0.00010 |
163.6571 |
0.00010 |
1.00000000 |
6.00706317 |
0.99774989 |
1.02165017 |
| 100 |
788.3272 |
0.00112 |
788.3272 |
0.00017 |
787.7029 |
0.00017 |
1.00000000 |
6.75047562 |
0.99920800 |
1.02180998 |
| 200 |
3295.794 |
0.00230 |
3295.794 |
0.00035 |
3294.927 |
0.00035 |
1.00000000 |
6.49822251 |
0.99973703 |
0.99185505 |
| 500 |
19294.97 |
0.00888 |
19294.97 |
0.00272 |
19293.7 |
0.00286 |
1.00000000 |
3.26174940 |
0.99993376 |
1.04896365 |
| 1000 |
83109.29 |
0.03834 |
83109.29 |
0.01447 |
83107.34 |
0.01415 |
1.00000000 |
2.65000273 |
0.99997652 |
0.97795314 |
| 2000 |
339234.9 |
0.17323 |
339234.9 |
0.05924 |
339231.9 |
0.05665 |
1.00000000 |
2.92438158 |
0.99999104 |
0.95639967 |
| 5000 |
1940633 |
1.15612 |
1940633 |
0.30542 |
1940628 |
0.29682 |
1.00000000 |
3.78540252 |
0.99999716 |
0.97186003 |
| 10000 |
8348942 |
5.42154 |
8348942 |
1.22316 |
8348932 |
1.23237 |
1.00000000 |
4.43240329 |
0.99999878 |
1.00752752 |
| 15000 |
22765379 |
15.06911 |
22765379 |
3.37158 |
22765362 |
3.44193 |
1.00000000 |
4.46944395 |
0.99999926 |
1.02086564 |
| 20000 |
48401588 |
32.37652 |
48401588 |
7.35390 |
48401562 |
7.41715 |
1.00000000 |
4.40263131 |
0.99999946 |
1.00860033 |
The dimensionality was reduced to
$d=2$. After one iteration, the time taken to calculate the new coordinates of the point positions in the projected space was measured and the stress value
$S(\cdot )$ defined by (
1) was obtained. Data with different number of points
m were used: 10, 20, 50, 100, 200, 500, 1000, 2000, 5000, 10000, 15000, and 20000. In order to obtain more accurate and reliable results, each experiment was repeated 100 times. The results of these experiments are shown in Tables
2 and
3. Since the number of computational operations using Geometric MDS and SMACOF-Fast is approximately the same (it can be concluded from Listing
2 and Listing
3), the time required to compute new coordinates using Geometric MDS and SMACOF-Fast is about the same.
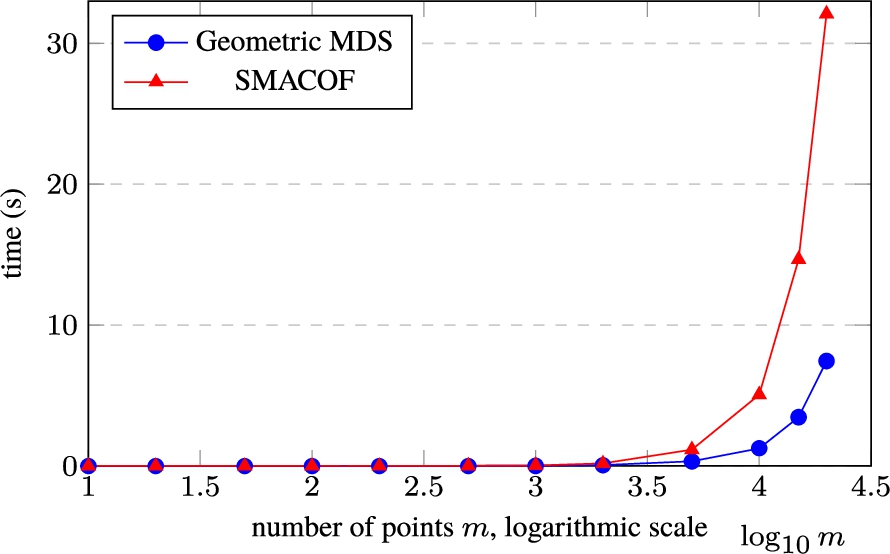
Fig. 3
Dependence of computation time on the number of points when reducing the dimensionality of 10-dimensional data $(n=10)$ to $d=2$. The number of points ($m=10$, 20, 50, 100, 200, 500, 1000, 2000, 5000, 10000, 15000, and 20000) is given in a logarithmic scale. All results are averaged, as a result of each experiment being repeated 100 times to calculate one iteration.
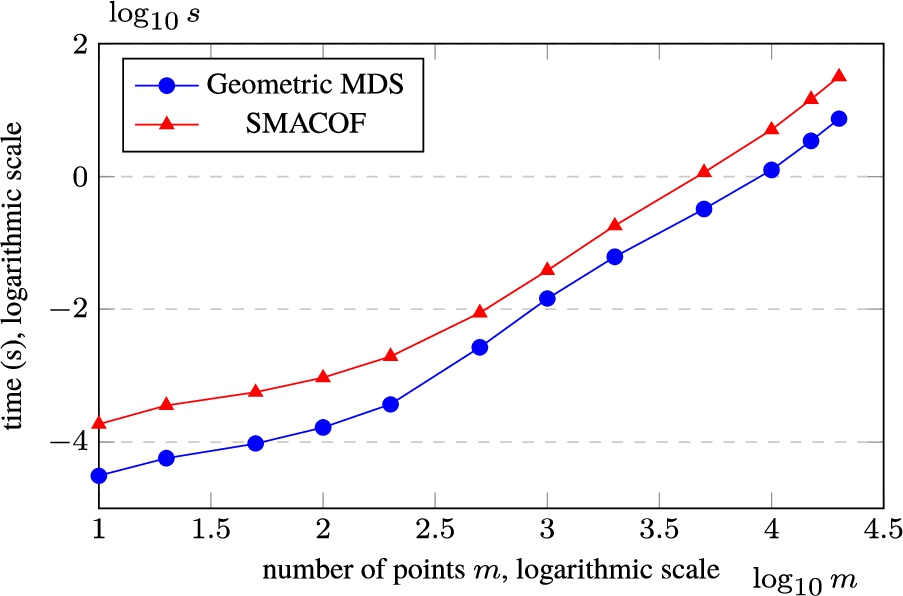
Fig. 4
Dependence of computation time on the number of points when reducing the dimensionality of 10-dimensional data $(n=10)$ to $d=2$. The time of calculation and the number of points ($m=10$, 20, 50, 100, 200, 500, 1000, 2000, 5000, 10000, 15000, and 20000) are given in a logarithmic scale. All results are averaged, as a result of each experiment being repeated 100 times to calculate one iteration.
The dependency of the calculation time on a number of points using Geometric MDS (see Listing
2) and SMACOF (Pedregosa
et al.,
2011) is shown in Fig.
3. The number
m of points (
$m=10$, 20, 50, 100, 200, 500, 1000, 2000, 5000, 10000, 15000, and 20000) is given in a logarithmic scale. Each experiment was repeated 100 times, so the figures summarise the results with the average time and the value of the Stress function for each case of
m. In order to provide the results in a more informative form, and to emphasize the differences in the time required to calculate new coordinates using Geometric MDS (see Listing
2) and SMACOF (Pedregosa
et al.,
2011), the time of calculation and the number of points are additionally given in a logarithmic scale in Fig.
4. The results demonstrate that Geometric MDS (Listing
2) outperforms the SMACOF (from the scikit-learn library, Pedregosa
et al.,
2011) in all cases in terms of the computation time required to recalculate the coordinates of new points
${Y_{1}},\dots ,{Y_{m}}$ in the projected space. Comparing the results obtained using SMACOF, SMACOF-Fast and Geometric MDS, it can be observed that with increasing data size Geometric MDS requires less computing time and the resulting stress is smaller than that by SMACOF under the same conditions (see Fig.
4, Tables
2 and
3). Meanwhile, the time required to recalculate new coordinates using Geometric MDS and SMACOF-Fast is approximately the same.
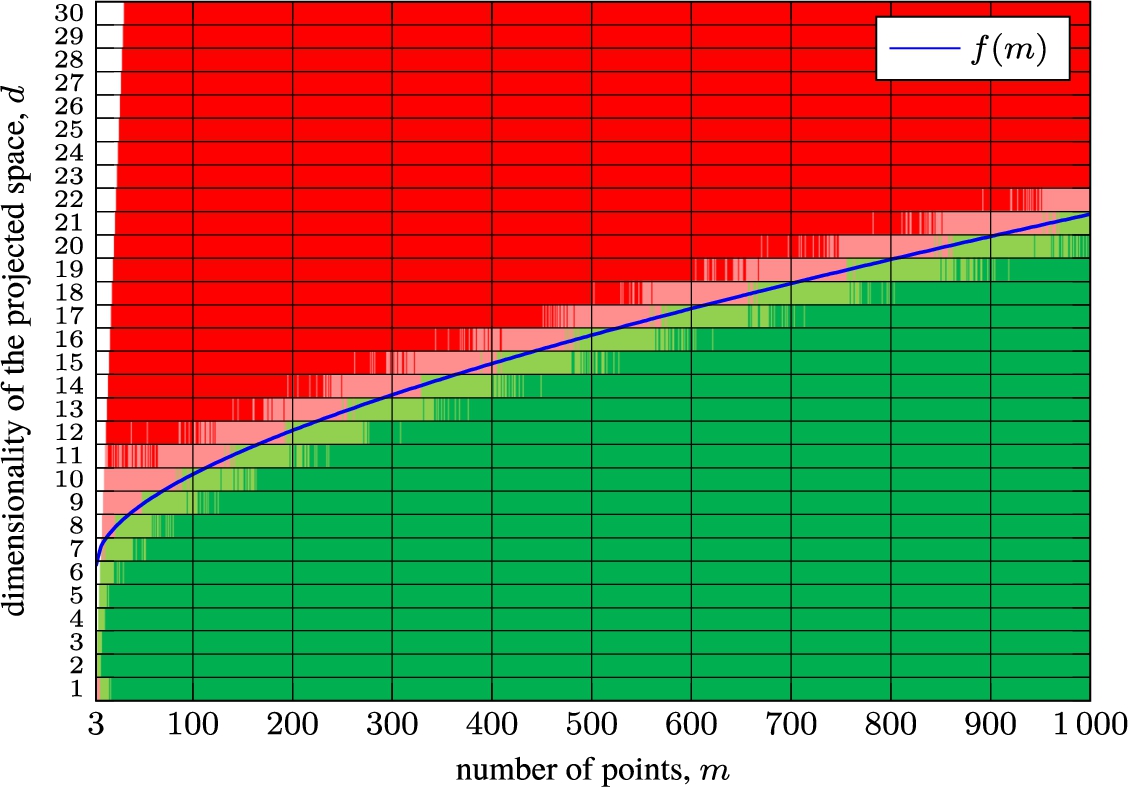
Fig. 5
Stress comparison between Geometric MDS and SMACOF depending on the number of points m and and the dimensionality of the projected space d.
4.2 Comparative Efficiency of Geometric MDS and SMACOF
To compare which method, Geometric MDS or SMACOF, better reduces the MDS stress
$S(\cdot )$ defined by (
1), we tested these methods on random proximity matrices whose elements take uniformly distributed values in the interval
$(0,1)$. 101 tests were performed with different
$m=3,\dots ,1000$ and
$d=1,\dots ,30$. The experiments were carried out using the programming implementations provided earlier in this section: SMACOF-Fast based on Listing
3 and Geometric MDS based on Listing
2. The results of the experiments are given in Fig.
5, which visually shows which algorithm, SMACOF or Geometric MDS, get a smaller value of the stress function
$S(\cdot )$ after updating the points
${Y_{1}},\dots ,{Y_{m}}$ only once, i.e. after one iteration, depending on the number
m of points and the dimensionality
d of the projected space. The red colour indicates cases in which SMACOF stress was superior to Geometric MDS in all cases, the light red indicates cases in which SMACOF stress was superior to Geometric MDS in more cases, the light green indicates cases in which Geometric MDS stress was superior to SMACOF in more cases, and the green indicates cases in which Geometric MDS stress was superior to SMACOF in all cases.
Figure
5 discloses a very interesting and essential difference between the performance of Geometric MDS and SMACOF. Geometric MDS finds smaller stress when the dimensionality of projected space is lower. This is particularly important for the multidimensional data visualization task.
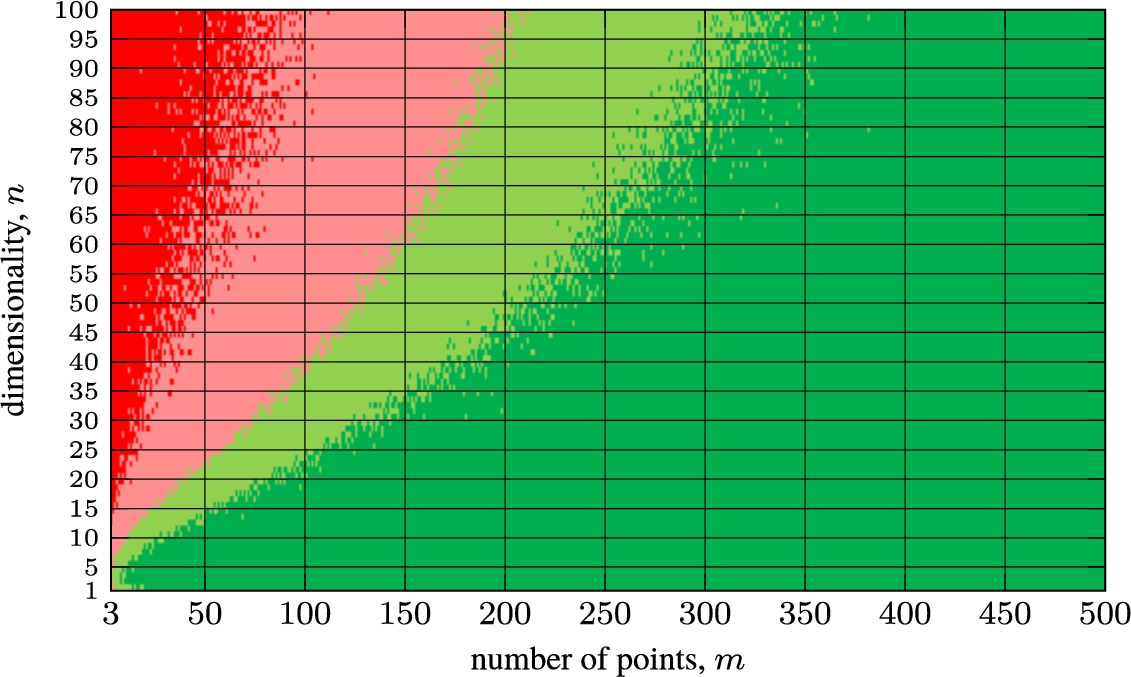
Fig. 6
Stress comparison between Geometric MDS and SMACOF depending on the number of points m and the dimensionality n, when reducing the dimensionality to $d=2$.
In Fig.
5, we present a curve that would allow us to choose either Geometric MDS or SMACOF in order to get a better stress after their first step and assuming that the values of the elements of the symmetric distance matrix are uniformly distributed in the interval
$(0,1)$. The upper part of the parabola was used to determine the distinguishing curve. The optimization package of the MAPLE software (Bernardin
et al.,
2021) was used to define the coefficients in the equation that is as follows in this particular case:
Particular case is
$d=2$, because it is the most used in multidimensional data visualization. Figure
6 illustrates the values of the stress function
$S(\cdot )$ depending on the number of points
m and the dimensionality
n of the analysed multidimensional data. By random generating a set of
m n-dimensional points
${X_{1}},\dots ,{X_{m}}$, the distance matrix
$m\times m$ was calculated. Then a random set of 2-dimensional (
$d=2$) points
${Y_{1}},\dots ,{Y_{m}}$ was selected as a starting position for optimization of the stress. The coordinates of these points were recalculated in one iteration using Geometric MDS and SMACOF (see Listings
2 and
3). The colours in Fig.
6 were labelled using the same rules as in Fig.
5: red means that in 101 such independent trials, SMACOF gave better stress in all cases, light red means that SMACOF gave better stress in more cases than Geometric MDS, light green means that Geometric MDS gave better stress in more cases than Geometric MDS but not in all cases, and light green means that Geometric MDS gave better stress in all cases. Figure
6 shows visually whether Geometric MDS or SMACOF gives lower stress depending on the number of points
m and on the dimensionality
n after one iteration of 101 tries. The results in Fig.
6 can be useful for choosing an appropriate method when the dimensionality
n of the data to be analysed and the number of points
n are known.
5 Conclusions
A new Geometric MDS method with the low computational complexity has been proposed in Dzemyda and Sabaliauskas (
2021a,
2022). Geometric MDS provides an iterative procedure to minimize MDS stress where coordinates of a particular point of the projected space are moved to a new position defined analytically. Such a change in position is easily interpreted geometrically. Moreover, the coordinates of points of the projected space may be recalculated simultaneously, i.e. in parallel, independently of each other during one iteration of stress minimization. Two implementations of Geometric MDS are suggested and analysed experimentally: parallel and sequential.
A parallel implementation of Geometric MDS is developed for dimensionality reduction using multithreaded multi-core processors. Based on the results obtained, we can claim that Geometric MDS allows to implement parallel computing using multithreaded multi-core processors, as a result, the time to calculate new coordinates of points in the low-dimensional space may be reduced by 6 times on average, depending on the data size.
The sequential implementation given in this paper is optimized for computational speed, enabling it to solve large data problems. It is compared with the SMACOF version of MDS. Python codes for both Geometric MDS and SMACOF are presented to highlight the differences between the two implementations. These codes were optimized for computational speed. The comparison was carried out on several aspects: the comparative performance of Geometric MDS and SMACOF depending on the projection dimension, data size and computation time. Geometric MDS usually finds lower stress when the dimensionality of the projected space is smaller.
SMACOF is an iterative procedure that calculates the Guttman transform. We discovered that the procedure of updating lower-dimensional points by Geometric MDS is a generalization of the Guttman transform. If we apply
$\frac{1}{m}$ instead of
$\frac{1}{m-1}$ in Eq. (
7) to all the lower-dimensional points
${Y_{1}},\dots ,{Y_{m}}$ simultaneously and independently of each other during a single iteration of stress minimization, we get the same result as with the Guttman transform. However, it is proved in Dzemyda and Sabaliauskas (
2022) that both Geometric MDS (GMDS
m) and SMACOF make a step from the point
${Y_{j}}$ to its new position in the same direction with different step size. The step size by Geometric MDS is
$\frac{m}{m-1}$ times longer. In both cases, the stress (
1) decreases. Moreover, Geometric MDS allows to update coordinates of a single point
${Y_{j}}$, and it guarantees the decrease of the stress, too. These are the reasons for further exploring the potential of Geometric MDS and applying the advantages discovered.

