1 Introduction
Multiple attribute decision making (MADM) or multiple attribute group decision making (MAGDM) is an effective approach to solve complex decision-making issues (Huang
et al.,
2021; Lei
et al.,
2021; Liu
et al.,
2018; Zhang D.
et al.,
2021; Zhang
et al.,
2018). In the decision-making process, decision makers are usually experts in their fields. Therefore, decision makers (DMs) would like to use linguistic terms rather than utilize the exact real numbers due to the complication of the socioeconomic setting and fuzziness of human beings’ thinking (Lei
et al.,
2021; Wei
et al.,
2021a). It means that the linguistic terms given by experts contain uncertainty and preference. To solve the uncertainty of decision-making problems, a lot of effective work has been done. Wang and Garg (
2021) proposed new interaction Pythagorean operators and designed an algorithm to solve the MADM issues with Pythagorean fuzzy uncertainties. Yazdi
et al. (
2020) proposed an integrated method which combined BWM with Weighted Aggregated Sum-Product Assessment (WASPAS) on uncertain decision-making environments with Z-numbers. Xiao
et al. (
2021) built Taxonomy method for MAGDM based on interval-valued intuitionistic fuzzy information. Zhang H.
et al. (
2021) defined the CPT-MABAC method for spherical fuzzy MAGDM. Zhang S.
et al. (
2021) defined the grey relational analysis method based on cumulative prospect theory for intuitionistic fuzzy MAGDM.
The decision makers are more likely to choose ‘good’, ‘medium’, ‘a little good’ and ‘excellent’ to evaluate alternatives. Therefore, Rodriguez
et al. (
2012) defined hesitant fuzzy linguistic term set (HFLTS) to use the hesitancy degree in the linguistic context. Zeng
et al. (
2019) introduced several weighted operators to aggregate weighted hesitant fuzzy linguistic information. Liu
et al. (
2019) improved incomplete hesitant fuzzy linguistic preference relations (IHFLPRs). These concepts can describe ambiguity and preference in linguistic term sets, but ignored differences in the importance of evaluation information. Thus, Pang
et al. (
2016) used probabilistic linguistic term sets (PLTSs) to depict fuzziness and uncertainty with certain probabilities. They proposed some rules of operation and aggregation operators for PLTSs. We can find that PLTSs can more comprehensively and precisely represent the attitude of decision makers. Furthermore, many improvements have been made in decision-making issues on PLTSs. Yue
et al. (
2020b) put forward the group utility measure, the individual regret measure and the compromise measure under PLTSs. Some studies discussed decision making methods under PLTSs. Wei
et al. (
2021b) built the DAS method for probabilistic linguistic MAGDM. Chen
et al. (
2020) combined distillation algorithm with ELECTRE III method on PLTSs. He
et al. (
2021) modified the FMEA (the failure mode and effect analysis) model on the PLTSs. You
et al. (
2020) designed PL-VIKOR method and modified the distance measure. Some studies have introduced and defined some new distance formulas. Chang
et al. (
2021) introduced Hellinger distance measure. Jiang and Liao (
2021) defined Kolmogorov-Smirnov distance measure on the PLTSs. Some studies have proposed effective tools to solve decision-making issues under PLTSs. Du and Liu (
2021) researched quality function deployment tool under PLTSs. Lin
et al. (
2021) proposed score C-PLTSs and probability splitting algorithm. And a novel PLTS correlation coefficient was put forward by Luo
et al. (
2020). Peng and Wang (
2020) introduced linguistic scale functions. Shen
et al. (
2021) came up with a model to reduce limitations of evaluation on the PLTSs. Teng
et al. (
2021) designed the Choquet integral operator under PLTSs. Wang and Liang (
2020) put away a preference degree for g-granularity PLTS. Wang
et al. (
2021) extended the operational laws of PLTSs. Wang
et al. (
2020) proposed probabilistic linguistic Z-numbers to describe related information. Xie
et al. (
2020) defined the dual probabilistic linguistic correlation coefficient. Xu
et al. (
2020) proposed a method to make probabilistic linguistic more complete in describing evaluation information. Yu
et al. (
2020) combined stochastic dominance degrees with PLTSs. Yue
et al. (
2020a) introduced the projection formulas and Qu
et al. (
2020) introduced new utility functions on the PLTSs. Su
et al. (
2021a) built PT-TODIM method for probabilistic linguistic MAGDM.
Applying PLTSs and related methods to some practical cases can reflect advantages and the applicability of PLTSs. Liang
et al. (
2020) improved customer satisfaction evaluation system on PLTSs. Mo (
2020) proposed the D-PLTS method to settle emergency decision-making issues. Pan
et al. (
2021) designed a probabilistic linguistic data envelopment analysis model. Xu C.
et al. (
2020) applied probabilistic linguistic preference relations to handle the healthcare insurance audits in China. Gao
et al. (
2021) proposed the PLTSs to describe information and built the MCGDM framework for the risk assessment. Luo
et al. (
2021) designed the IDOCRIW-COCOSO model to evaluate tourism attractions on the PLTSs. Ming
et al. (
2020) structured a medical service evaluation criteria system under PLTSs.
The MABAC method is an effective method to address some difficult decision making issues. Xu
et al. (
2019) used the MABAC algorithm to select the optimal green supplier. To select the optimal university, Gong
et al. (
2020) designed a new UTAE (undergraduate teaching audit and evaluation) approach combined with the MABAC method. Biswas (
2020) selected the MABAC method to prepare a comparative analysis of supply chain performances. In order to make better use of the MABAC method, experts put it in different linguistic environments. Verma (
2021) applied IFS (intuitionistic fuzzy set) with the MABAC algorithm. Liang
et al. (
2019) came up with the MABAC approach based on TFN to evaluate the risk of rock-burst. Hu
et al. (
2019) combined the MABAC method with the similarity of interval type-2 fuzzy numbers (IT2FNs). Sun
et al. (
2018) extended the MABAC method to HFLTSs (hesitant fuzzy linguistic term sets) for patients’ prioritization. Aydin (
2021) applied the MABAC method with Fermantean fuzzy sets into decision-making process. Liu and Zhang (
2021) integrated the MABAC model with prospect theory (PT) on a normal wiggly hesitant fuzzy set (NWHFS). Additionally, many studies combined MABAC with another algorithm to solve MADM or MAGDM problems. Pamucar
et al. (
2018) defined the IR-AHP-MABAC (interval rough analytic hierarchy process-MABAC) model to assess the quality of websites. Jiang
et al. (
2022) built the picture fuzzy MABAC method based on prospect theory for MAGDM.
The above investigations described a particular assumption that DMs are perfectly rational. However, many studies show that people’s behaviour is affected by their emotions. For example, people are inclined to be more sensitive to losses than to gains. That’s to say, the perception of equal gains and losses are not the same for DMs. In general, people are inclined to be risk-averse. Based on these assumptions of bounded rationality, the cumulative prospect theory (CPT) (Tversky and Kahneman,
1992) broke through the classical utility theory and defined the weight function and value function. Gong
et al. (
2018) built a new model based on CPT to tackle portfolio selection. Zhao
et al. (
2021b) combined CPT with TODIM method under several linguistic environments, such as pythagorean fuzzy sets (2021), the 2-tuple linguistic pythagorean fuzzy sets (Zhao
et al.,
2021c). Additionally, Zhao
et al. (
2021a) introduced the intuitionistic fuzzy MABAC method based on CPT. Furthermore, picture fuzzy sets (Jiang
et al.,
2021a,
2021b) were dealt with CPT. Su
et al. (
2021b) built the probabilistic uncertain linguistic EDAS method based on prospect theory for MAGDM.
In the originalMABAC method, the psychological factor such as the DMs’ preference towards risk will affect the distance between the border approximation area. Furthermore, there are relatively few researches on constructing the MABAC method for MAGDM depending on the CPT under PLTSs. The main research significance of this paper is the modified MABAC method with CPT which can reduce the affection. Therefore, the PL-MABAC based on cumulative prospect theory (CPT-PL-MABAC) method in this paper is defined to solve the location selection of express distribution centre, which is a classical MAGDM issue. This article makes contributions as follows: (1) the concept of CPT is integrated into the PL-MABAC method for MAGDM. This method not only has unambiguous logic and relatively simple calculation, but also expresses the DM’s psychological state, which is closer to reality; (2) we improved the entropy method, which is characterized by the mean value of attributes as the reference point; (3) the combined attribute weights are obtained through objective weight by the entropy method and by getting the subjective weight given by decision makers; (4) the effectiveness and stability of this new method is fully testified by taking advantage of a case about location selection of express distribution centre and comparisons with the existing methods.
To sum up, the structure of this paper is built as follows. The second part mainly introduces and reviews the basic knowledge, including the PLTSs and CPT. In Section
3, the PL-MABAC based on cumulative prospect theory (CPT-PL-MABAC) method is defined to solve the MAGDM. In Section
4, a case for location selection of express distribution centre is given as the justification of the usefulness of the designed method. Also, we compared our method with existing methods and demonstrated the stability and availability of this method. Finally, the main contributions of this paper, the limitations of the new method and future research directions are included.
3 CPT-PL-MABAC Model for MAGDM Issues
We will introduce the MABAC method based on CPT and on the PLTS. We will also give the following mathematical symbols which are used to express the relevant information. We suppose that there is a collection of alternatives $\mathrm{\Re }=\{{\mathrm{\Re }_{1}},{\mathrm{\Re }_{2}},\dots ,{\mathrm{\Re }_{m}}\}$ and n qualitative attributes $\mathrm{\Im }=\{{\mathrm{\Im }_{1}},{\mathrm{\Im }_{2}},\dots ,{\mathrm{\Im }_{n}}\}$. Experts will evaluate every attribute and use linguistics ${\zeta _{ij}^{k}}$ $(i=1,2,\dots ,m,j=1,2,\dots ,n,k=1,2,\dots ,q)$ to express the value of evaluation. $\varpi =({\varpi _{1}},{\varpi _{2}},\dots ,{\varpi _{n}})$ represents the attribute weight vector, where ${\varpi _{j}}\in [0,1]$, ${\textstyle\sum _{j=1}^{n}}{\varpi _{j}}=1$ and $\mathrm{\aleph }=\{{\mathrm{\aleph }_{1}},{\mathrm{\aleph }_{2}},\dots ,{\mathrm{\aleph }_{q}}\}$ is a collection of q experts.
We designed the new PL-MABAC method in which the CPT is introduced to address MAGDM problems. A laconic frame diagram and the specific calculating procedure as follows:
3.1 The CPT-PL-MABAC Frame Diagram
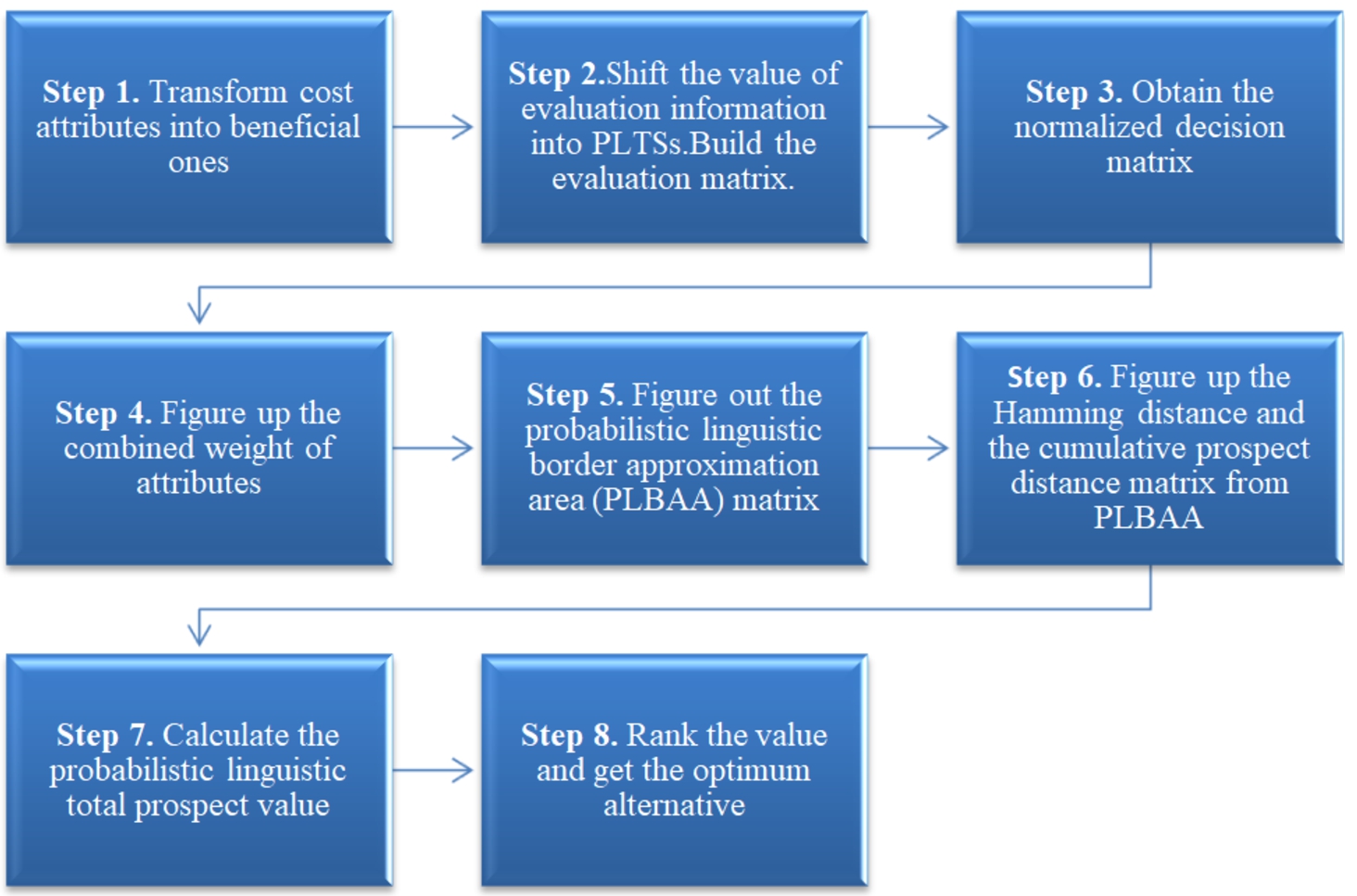
Fig. 1
CPT-PL-MABAC frame diagram.
3.2 The CPT-PL-MABAC Calculating Procedure
Step 1. Transform cost attributes into beneficial ones.
Given an LTS $L=\{{\zeta _{ƛ}}|ƛ=-\partial ,\dots ,-1,0,1,\dots \partial \}$, and transform the cost attribute ${\zeta _{ƛ}}$ into the beneficial attribute ${\zeta _{-ƛ}}$.
Step 2. Shift the value of evaluation information $L=\{{\zeta _{ij}^{k}}\big|k=1,2,\dots ,q,i=1,2,\dots ,m,j=1,2,\dots ,n\}$ into PLTSs $\textit{PL}=\{{\zeta _{ij}^{(\gamma )}}({p_{ij}^{(\gamma )}})\big|\gamma =1,2,\dots ,\mathrm{\# }{L_{ij}}(p)\}$. Build the evaluation matrix $M={({\textit{PL}_{ij}}(p))_{m\times n}}$, ${\textit{PL}_{ij}}(p)=\big\{{\zeta _{ij}^{(\gamma )}}({p_{ij}^{(\gamma )}})\big|\gamma =1,2,\dots ,\mathrm{\# }{L_{ij}}(p)\big\}$ $(i=1,2,\dots ,m,j=1,2,\dots ,n)$.
Step 3. Obtain the normalized decision matrix $\textit{NM}={({\textit{NPL}_{ij}}(\tilde{p}))_{m\times n}}$ with PLTSs, ${\textit{NPL}_{ij}}(\tilde{p})=\{{\zeta _{ij}^{(\gamma )}}({\tilde{p}_{ij}^{(\gamma )}})\big|\gamma =1,2,\dots ,\mathrm{\# }{L_{ij}}(\tilde{p}),{\textstyle\sum _{\gamma =1}^{\mathrm{\# }{L_{ij}}(\tilde{p})}}{\tilde{p}_{ij}^{(\gamma )}}=1\}$ $(i=1,2,\dots ,m,j=1,2,\dots ,n)$.
Step 4. Figure up the combined weight of attributes.
We acquire the objective weight by the entropy method and get the subjective weight given by decision makers.
First, we introduce the specific procedure of the entropy method. It should be noted that when calculating entropy, we use the mean value of the attribute as the reference point to calculate its distance from the normalized attribute value.
-
1. Calculate the mean value of
jth attribute, the formula is expressed below:
-
2. Let
${\mathrm{\wp }_{j}}$ be the entropy of the
jth attribute, and calculate it by using Eq. (
11):
-
3. Compute the objective weights of the
jth attribute by using Eq. (
12):
where
${w_{oj}}\in [0,1]$ and
${\textstyle\sum _{j=1}^{n}}{w_{oj}}=1$.
Then, we calculate the combined weights by using the following equation. The advantage of using combined weight is that the influence of subjective weight and objective weight can be considered comprehensively.
Decision makers gave the subjective weights
${w_{sj}}=({w_{s1}},{w_{s2}},\dots ,{w_{sn}})$, where
${w_{sj}}\in [0,1]$,
$j=1,2,\dots ,n$,
${\textstyle\sum _{j=1}^{n}}{w_{sj}}=1$. The objective weight
${w_{oj}}=({w_{o1}},{w_{o2}},\dots ,{w_{on}})$ is calculated by using Eq. (
12) directly, where
${w_{oj}}\in [0,1]$,
$j=1,2,\dots ,n$,
${\textstyle\sum _{j=1}^{n}}{w_{oj}}=1$. Therefore, the combined weights of attributes
${w_{cj}}=({w_{c1}},{w_{c2}},\dots ,{w_{cn}})$ could be defined:
where
${w_{cj}}\in [0,1]$,
$j=1,2,\dots ,n$,
${\textstyle\sum _{j=1}^{n}}{w_{cj}}=1$.
Step 5. Figure out the probabilistic linguistic border approximation area (PLBAA) matrix
$\mathrm{PLBAA}={({\textit{PLBAA}_{j}})_{1\times n}}$. The PLBAA could be obtained according to Eqs. (
14)–(
16).
Step 6. Figure up the Hamming distance from PLBAA by Eq. (
17) and the cumulative prospect distance matrix by using Eq. (
18).
We take ${\textit{PLBAA}_{j}}$ as reference point and the parameters in value function are $\tau =\varsigma =0.88$, $\theta =2.25$.
Step 7. Calculate the probabilistic linguistic total prospect value.
Step 8. Rank the value of ${\Lambda _{i}^{\ast }}$ $(i=1,2,\dots ,m)$ to obtain the best alternative.
5 Conclusion
The location selection of the express distribution centre is of great significance in the development of the express delivery industry. Therefore, a new PL-MAGDM method (CPT-PL-MABAC) is established to be applied to this issue. The main contributions of this article can be summarized as follows. Firstly, we introduce the CPT into the original MABAC method under PLTSs. The psychological factors of experts are introduced in the evaluation. Secondly, we improved the entropy method under PLTSs, which is characterized by the mean value of attributes as the reference point. Thirdly, we improved the distance formula between the evaluation values of the alternative and PLBBA. Finally, the new method enriches the decision-making method based on PLTS and enriches the model of location selection.
The CPT-PL-MABAC model is a stable decision-making tool with direct computation algorithms. Also, it can get comprehensive final sorting results because it considers the potential values of gains and losses. However, the method proposed is ineffective in the face of some problems when attribute weights and evaluation information are not completely known. Moreover, we only refer to reference points and value functions in CPT.
In future studies, we plan to deal with the situation where the weights are not completely known. Additionally, this method can be applied to other specific decision-making problems and many other unpredictable and fuzzy environments, for example, green energy supplier issues and other location selection issues.

