1 Introduction
With the increasing complexity of the socio-economic environment, it is difficult for single Decision Maker (DM) to consider all relevant aspects of a problem, because of the limitation of individual’s knowledge or experience. Multi-Criteria Group Decision-Making (MCGDM) is a widely used efficient method for the complex decision-making problems. DMs or experts express their opinions or preferences about alternatives with respect to different criteria to obtain the best alternative (Wu
et al.,
2019). For traditional MCGDM, the decision information is represented by crisp numerical values. However, due to the complexity and vagueness of decision-making problems, it is usually challenging for experts to evaluate an object with crisp numerical values. Therefore, various types of fuzzy sets have been applied to MCGDM problems, such as Fuzzy Set (FS) (Zadeh,
1965; Choua and Shen,
2008; Chiclana
et al.,
2007), Intuitionistic Fuzzy Set (IFS) (Atanassov,
1986; Jiang and Hu,
2021), Pythagorean Fuzzy Set (PFS) (Yager,
2014; Mohagheghi
et al.,
2017; Zhou and Chen,
2020), etc. Although IFS and PFS are extensively scrutinized by scholars, their applications are relatively limited due to many limitations over the selection of the membership and non-membership grades.
Since Fermatean Fuzzy Set (FFS) proposed by Senapati and Yager (
2019c) is able to model the uncertainty in real-life decision-making problems better than IFS and PFS, FFS has received increasing attention. The advantage of FFS is illustrated by an example that an expert may express his/her preference for an alternative over criterion with membership degree 0.8 and non-membership degree 0.9, then it is clearly
$0.8+0.9\nleqq 1$ and
$0.{8^{2}}+0.{9^{2}}\nleqq 1$, but
$0.{8^{3}}+0.{9^{3}}\leqslant 1$. From this point of view, the FFS provides a larger preference domain for experts to express fuzzy information than PFS and IFS. Hence, the space of Fermatean Fuzzy Membership Grades (FFMGs) is greater than the space of Intuitionistic Fuzzy Membership Grades (IFMGs) and Pythagorean Fuzzy Membership Grades (PFMGs), which is shown in Fig.
1. Figure
1 indicates that IFMGs are all points below the line
$x+y\leqslant 1$, PFMGs are all points with
${x^{2}}+{y^{2}}\leqslant 1$, and FFMGs are all points with
${x^{3}}+{y^{3}}\leqslant 1$. The analysis above suggests that FFS can be used more extensively in MCGDM problems. Therefore, it is necessary to research the theory of FFS.
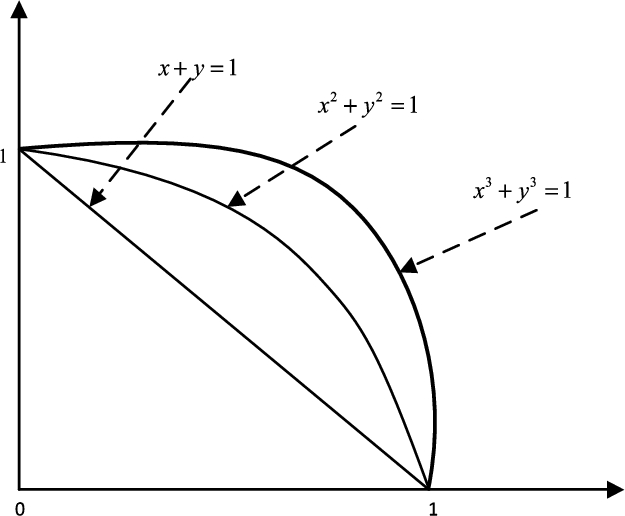
Fig. 1
Comparison of spaces of FMGS, PMGs and IMGs.
Since the seminal work of Senapati and Yager (
2019c), FFS has been investigated by many scholars. Senapati and Yager (
2019c) combined the technique for order preference by similarity to ideal solution (TOPSIS) approach with FFS to handle the multi-criteria decision-making (MCDM) problem. Senapati and Yager (
2019b) defined four new weighted aggregated operators including Fermatean fuzzy weighted average operator, Fermatean fuzzy weighted geometric operator, Fermatean fuzzy weighted power average operator, Fermatean fuzzy weighted power geometric operator. Senapati and Yager (
2019a) introduced some operations over FFS, then developed a weighted product model based on Fermatean fuzzy information to solve the MCDM problem. Based on Dombi operations, Aydemir and Gunduz (
2020) presented a series of aggregation operators for FFS. They then extended TOPSIS with the proposed Fermatean fuzzy Dombi operators. Although some researches are conducted on MCDM methods in the FFS context, there still remain some drawbacks to be handled. The weights of criteria are given by experts in advance. Besides, most of existing decision-making methods for FFSs are aggregation operator-based methods and compromising methods rather than outranking methods. The outranking methods may lead to compensation effect.
Outranking methods are treated as the suitable means for making a successful assessment on the competing criteria. The most widely used outranking method is ELECTRE (elimination and choice translating reality) method, which was proposed by Roy (
1991). Since then, numerous studies have been conducted to extend ELECTRE method under fuzzy decision environments, such as triangular fuzzy numbers (Zandi and Roghanian,
2013; Kabak
et al.,
2012), trapezoidal fuzzy numbers (Hatami and Tavana,
2011), FS (Ferreira
et al.,
2016), IFS (Shen
et al.,
2016; Wu and Chen,
2011; Çalı and Balaman,
2019; Mishra
et al.,
2020; Kilic
et al.,
2020), interval-valued intuitionistic fuzzy set (Chen,
2014a; Hashemi
et al.,
2016; Xu and Shen,
2014), hesitant fuzzy set (Chen and Xu,
2015; Mousavi
et al.,
2017), PFS (Akram
et al.,
2019,
2021, Chen,
2020) neutrosophic set (Peng
et al.,
2014; Karasan and Kahraman,
2020; Zhang
et al.,
2015), etc. However, to the best of our knowledge, no research on ELECTRE method within the context of FFS has yet been conducted.
Recently, many researchers have focused on the construction of outranking relation by using different indices, e.g. the value of score function (Wu and Chen,
2011; Xu and Shen,
2014; Liao
et al.,
2018), distance measure (Zhang and Yao,
2017; Chen,
2014b), possibility measure (Chen,
2014b,
2015). In general, outranking relation can be sorted as strong dominance and weak dominance. In essence, these two dominance relations are insufficient to describe the degree of superiority and demonstrate superior relation among alternatives. Furthermore, the weights of concordance and discordance sets play an important role in the solution of a MCDM problem with ELECTRE method, which may eventually affect the ranking or selection of alternatives. However, most current ELECTRE methods (Wu and Chen,
2011; Kilic
et al.,
2020; Chen and Xu,
2015; Akram
et al.,
2019; Razi,
2015) directly give the weights of concordance and discordance sets on the basis of the subjective judgments of DMs, which lacks the basis of scientific theory and may be unreasonable.
Previous studies on FFS and ELECTRE methods have achieved fruitful research results, some challenging gaps can be identified as follows: Firstly, some methods (Senapati and Yager,
2019a,
2019b,
2019c) under FFSs environment were developed to solve the single expert MCDM problems, which is not suitable for solving group decision-making problems. Literature (Senapati and Yager,
2019a,
2019b,
2019c; Aydemir and Gunduz,
2020) failed to consider the determination of criteria weights, which may lead to unreasonable and unreliable decision-making results. Secondly, distance measure of FFSs in (Senapati and Yager,
2019c) might generate the counter-intuitive results in some cases (see Example
2 in Section
3). Thirdly, there is no research on ELECTRE method with FFS. In addition, due to the computational complexity, many ELECTRE methods (Wu and Chen,
2011; Kilic
et al.,
2020; Chen and Xu,
2015; Akram
et al.,
2019; Razi,
2015) provide a priori weights of concordance and discordance sets, which can be easily influenced by DMs’ subjective randomness.
To achieve the aforementioned main objective and fill outlined research gaps, this paper proposes a Fermatean fuzzy ELECTRE method for MCGDM problems. The main contributions and innovations of this paper are outlined below. Firstly, a new distance measure between FFSs is designed by making use of the Jensen–Shannon divergence. The objective weights of concordance and discordance sets are generated by applying the weighted distance measure based on the proposed new distance measure, which is subjectively given by experts in a majority of the studies related to ELECTRE literature (Wu and Chen,
2011; Kilic
et al.,
2020; Chen and Xu,
2015). Secondly, the weights of DMs are dynamic with respect to each alternative over different criteria, which are generated using the credibility degrees of each DM. As for the DMs’ weights, previous studies usually give them in advance (Wang
et al.,
2020) or views them as unchangeable for different criteria over different alternatives. Thirdly, the grey relational coefficient and grey relational degree of the FFSs are defined and applied to compute the weights of criteria. Fourthly, in order to show the dominance degree between the pairwise FFNs more exactly, this paper uses membership degree, non-membership degree and indeterminacy degree to compare the outranking relationship for each pair of FFNs. Based on this, the outranking relationship for FFNs can be extended into three situations: strong dominance, medium dominance and weak dominance.
The remainder of this paper is organized as follows: Section
2 introduces some basic concepts associated with FFSs. In Section
3, some information measures for FFSs, including distance measure, cross entropy measure, and grey relational degree, are defined. Outranking relationships for FFSs are introduced in this section, where the related properties of outranking relationships are discussed. An ELECTRE method for MCGDM problems with FFNs is proposed in Section
5. Section
6 illustrates the concrete implementation of the proposed ELECTRE method using a case study on site selection of fangcang shelter hospitals (FSHs), and demonstrates the superiority and effectiveness of the proposed ELECTRE method by comparative analyses. Section
7 gives some conclusions and future research directions
3 Some New Fermatean Fuzzy Information Measures
In this section, we put forward some new information measures for FFSs, including distance measure, cross entropy measure, and grey relational degree. They will be used later.
3.1 A New Distance Measure for FFSs
In this section, we recall Jensen–Shannon divergence measure. Secondly, a distance measure between FFSs is defined based on Jensen–Shannon divergence. Then, some desirable properties of the proposed new distance measure are inferred.
(1) Jensen–Shannon divergence measure
Definition 8 (Kullback and Leibler, 1951).
Let
X be a discrete random variable, and
${p_{1}}$ and
${p_{2}}$ be two probability distributions in
X. The
I directed divergence is defined as
It is worthy to note that
$I({p_{1}},{p_{2}})$ is non-negative, additive, but not symmetric. Hence, the symmetric measure is defined as
which is known as
J divergence (Jeffreys,
1946). Obviously,
$J({p_{1}},{p_{2}})$ is undefined if
${P_{2}}(x)=0$ and
${P_{1}}(x)\ne 0$ for
$x\in X$.
To solve this problem, Lin (
1991) proposed a new directed divergence measure as
An obvious relation between
$K({p_{1}},{p_{2}})$ and
$I({p_{1}},{p_{2}})$ is that
$K({p_{1}},{p_{2}})=I({p_{1}},\frac{{p_{1}}+{p_{2}}}{2})$. It can be observed that
$K({p_{1}},{p_{2}})$ is not a symmetric measure. Accordingly, a symmetric measure is defined as
Jensen–Shannon divergence measure can be derived from Eq. (
8) as follows:
where
$\Phi (p)=-p\log p$ is the Shannon entropy function.
In this paper, we define Fermatean fuzzy distance based on Jensen–Shannon divergence.
(2) A new distance measure for FFSs
Definition 9.
Let
$X=({x_{1}},{x_{2}},\dots ,{x_{n}})$ be a universe of discourse, and
G and
H be two FFSs in
X, where
$G=\{\langle {x_{i}},{G_{\alpha }}({x_{i}}),{G_{\beta }}({x_{i}})\rangle \mid {x_{i}}\in X\}$ and
$H=\{\langle {x_{i}},{H_{\alpha }}({x_{i}}),{H_{\beta }}({x_{i}})\rangle \mid {x_{i}}\in X\}$. The Fermatean fuzzy divergence between
G and
H is defined as
where
$\Phi (G)=-{G_{\eta }^{3}}(x)\log {G_{\eta }^{3}}(x)$,
$\eta \in (\alpha ,\beta ,\pi )$, is the Shannon entropy,
${G_{\pi }^{3}}(x)=1-{G_{\alpha }^{3}}(x)-{G_{\beta }^{3}}(x)$.
In the line with Definition
9, a new distance measure for FFSs is given below.
Definition 10.
Let
X be a universe of discourse, and
G and
H be two FFSs. A new distance measure for FFSs, denoted as
$\bar{d}(G,H)$, is defined as
where,
$\eta \in (\alpha ,\beta ,\pi )$, the base of log is 10.
Some desirable properties of
$\bar{d}(G,H)$ can be inferred as follows:
Theorem 1.
Let G, H and M be three arbitrary FFSs in a universe of discourse X, then some properties hold:
-
(P1) $\bar{d}(G,H)=0$ iff $G=H$, for $G,H\in X$;
-
(P2) $\bar{d}(G,H)=\bar{d}(H,G)$, for $G,H\in X$;
-
(P3) $\bar{d}(G,H)+\bar{d}(H,M)\geqslant \bar{d}(G,M)$, for $G,H,M\in X$;
-
(P4) $0\leqslant \bar{d}(G,H)\leqslant 1$, for $G,H\in X$.
Proof.
(P1) Let
G and
H be two FFSs in a universe of discourse
X. For the necessity, If
$G=H$, which means
${G_{\eta }^{3}}(x)={H_{\eta }^{3}}(x)$, then
$\bar{d}(G,H)=0$ can be obtained based on Definition
9. For the sufficiency, if
$\bar{d}(G,H)=0$, then
$\sqrt{\frac{1}{2}\big\{{\textstyle\sum _{\eta }}{G_{\eta }^{3}}(x)\log \frac{2{G_{\eta }^{3}}(x)}{{G_{\eta }^{3}}(x)+{H_{\eta }^{3}}(x)}+{\textstyle\sum _{\eta }}{H_{\eta }^{3}}(x)\log \frac{2{H_{\eta }^{3}}(x)}{{G_{\eta }^{3}}(x)+{H_{\eta }^{3}}(x)}\big\}}=0$. It is evident that
${G_{\eta }^{3}}(x)={H_{\eta }^{3}}(x)$. Thus,
$G=H$. As a result,
$\bar{d}(G,H)=0$ iff $G=H$.
(P2) Since
one has
$\bar{d}(G,H)=\bar{d}(H,G)$.
(P3) Four hypotheses are formulated as follows:
-
Hypothesis 1: ${G_{\alpha }^{3}}(x)\leqslant {H_{\alpha }^{3}}(x)\leqslant {M_{\alpha }^{3}}(x)$,
-
Hypothesis 2: ${M_{\alpha }^{3}}(x)\leqslant {H_{\alpha }^{3}}(x)\leqslant {G_{\alpha }^{3}}(x)$,
-
Hypothesis 3: ${H_{\alpha }^{3}}(x)\leqslant \min \{{G_{\alpha }^{3}}(x),{M_{\alpha }^{3}}(x)\}$,
-
Hypothesis 4: ${H_{\alpha }^{3}}(x)\geqslant \max \{{G_{\alpha }^{3}}(x),{M_{\alpha }^{3}}(x)\}$.
According to Hypothesis 1 and Hypothesis 2, it holds that
$|{G_{\alpha }^{3}}(x)-{M_{\alpha }^{3}}(x)|\leqslant |{G_{\alpha }^{3}}(x)-{H_{\alpha }^{3}}(x)|+|{H_{\alpha }^{3}}(x)-{M_{\alpha }^{3}}(x)|$. Due to Hypothesis 3, it has
${G_{\alpha }^{3}}(x)-{H_{\alpha }^{3}}(x)\geqslant 0$ and
${M_{\alpha }^{3}}(x)-{H_{\alpha }^{3}}(x)\geqslant 0$. Then, we can obtain
In the same way, according to Hypothesis 4, we can get
${H_{\alpha }^{3}}(x)-{G_{\alpha }^{3}}(x)\geqslant 0$ and
${H_{\alpha }^{3}}(x)-{M_{\alpha }^{3}}(x)\geqslant 0$. Therefore, it holds that
As a result, $|{G_{\alpha }^{3}}(x)-{M_{\alpha }^{3}}(x)|\leqslant |{G_{\alpha }^{3}}(x)-{H_{\alpha }^{3}}(x)|+|{H_{\alpha }^{3}}(x)-{M_{\alpha }^{3}}(x)|$ holds in the contexts of Hypothesis 3 and Hypothesis 4.
Analogously, it follows that $|{G_{\beta }^{3}}(x)-{M_{\beta }^{3}}(x)|\leqslant |{G_{\beta }^{3}}(x)-{H_{\beta }^{3}}(x)|+|{H_{\alpha }^{3}}(x)-{M_{\beta }^{3}}(x)|$ and $|{G_{\pi }^{3}}(x)-{M_{\pi }^{3}}(x)|\leqslant |{G_{\pi }^{3}}(x)-{H_{\pi }^{3}}(x)|+|{H_{\pi }^{3}}(x)-{M_{\pi }^{3}}(x)|$.
Hence, this completes the proof of $\bar{d}(G,H)+\bar{d}(H,M)\geqslant \bar{d}(G,M)$.
(P4) Consider two FFSs
G and
H in a universe of discourse
X, one has
It has been proven in Gallager (
1968) that, for and
$0\leqslant \theta \leqslant 1$,
$H(\theta ,1-\theta )\geqslant 2\min (\theta ,1-\theta )$. For
$\min (\theta ,1-\theta )=\frac{1}{2}(1-|(\theta -(1-\theta )|)$, it can be obtained that
$1-H(\theta ,1-\theta )\leqslant |\theta -(1-\theta )|$. Then, we can get
where
$V(G,H)$ is the variational divergence measure (Vajda,
1970). Since the value of
$V(G,H)$ ranges from
$[0,2]$, which is testified in Toussaint (
1975). Therefore, we have
$0\leqslant \bar{d}(G,H)\leqslant 1$.
This completes the proof of Theorem
1. □
Example 1.
Let G and H be two FFSs in the universe of discourse X. These FFSs over X are defined as $G=\langle x,\eta ,\gamma \rangle $, $H=\langle x,\gamma ,\eta \rangle $.
The parameters η and γ are the membership and non-membership degrees, respectively, which range from 0 to 1, meeting the condition ${\eta ^{3}}+{\gamma ^{3}}\leqslant 1$.
Using Eq. (
11), the distance for FFSs can be measured, as shown in Fig.
2.
In consideration of the distance measure results of Example
1, we can verify the non-negativity, symmetry and boundedness properties of distance measure for FFSs.
It can be seen from Fig.
2 that the distance measure for FFSs is always greater than or equal to zero when the parameters
η and
γ take different values within
$[0,1]$. The non-negativity of distance measure for FFSs is verified.
As shown in Fig.
2, it is obvious that the distance measure for FFSs satisfies symmetry property. Let us cite a concrete instance that
$\eta =0.9$ and
$\gamma =0.3$. Based on Eq. (
11), the values of
$\bar{d}(G,H)$ and
$\bar{d}(H,G)$ are 0.4207, thus
$\bar{d}(G,H)=\bar{d}(H,G)$.
From Fig.
2, we clearly know the values of distance measure are
$[0,1]$. Specifically, when the parameters
$\eta =1$ and
$\gamma =0$, or when
$\eta =0$ and
$\gamma =1$,
$\bar{d}(G,H)=\bar{d}(H,G)=\hspace{2.5pt}1$. The boundedness of distance measure for FFSs is proved.
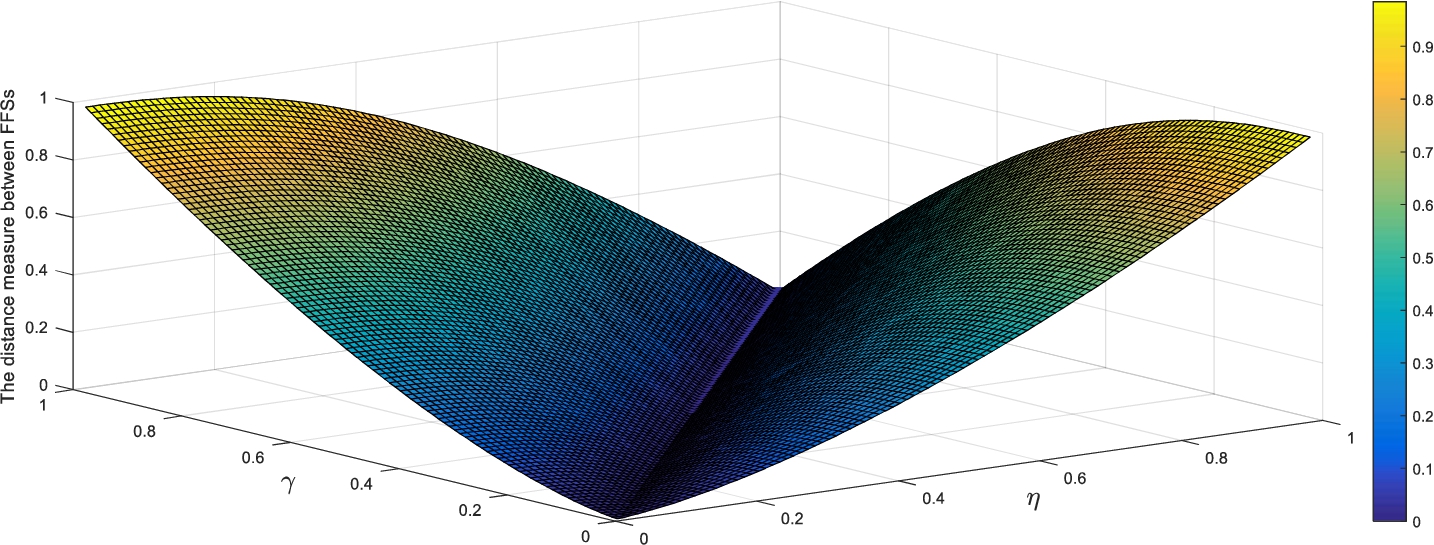
Fig. 2
The FFSs distance measure in Example
1.
(3) Comparisons of distance measures for FFNs
In this section, in order to testify the superiority and reasonability of the proposed distance measure, we compare the proposed distance measure with the existing Euclidean distance measure (Senapati and Yager,
2019c) in Example
2.
Example 2.
Let
${A_{i}}=\{{A_{1}},{A_{2}},\dots ,{A_{18}}\}$ and
${B_{i}}=\{{B_{1}},{B_{2}},\dots ,{B_{18}}\}$ be two sets of FFNs under Case
i $(i=1,2,\dots ,18)$, which are shown in Table
1.
Table 1
Two FFNs
${A_{i}}$ and
${B_{i}}$ under different cases in Example
2.
| FFNs |
Case 1 |
Case 2 |
Case 3 |
Case 4 |
Case 5 |
Case 6 |
| ${A_{i}}$ |
$\langle [0.595,0.690]\rangle $ |
$\langle [0.840,0.660]\rangle $ |
$\langle [0.629,0.834]\rangle $ |
$\langle 0.810,0.673\rangle $ |
$\langle [0.849,0.609]\rangle $ |
$\langle [0.827,0.665]\rangle $ |
| ${B_{i}}$ |
$\langle [0.650,0.779]\rangle $ |
$\langle [0.726,0.749]\rangle $ |
$\langle [0.731,0.755]\rangle $ |
$\langle 0.888,0.601\rangle $ |
$\langle [0.912,0.510]\rangle $ |
$\langle [0.894,0.600]\rangle $ |
| FFNs |
Case 7 |
Case 8 |
Case 9 |
Case 10 |
Case 11 |
Case 12 |
| ${A_{i}}$ |
$\langle [0.888,0.601]\rangle $ |
$\langle [0.679,0.788]\rangle $ |
$\langle [0.804,0.606]\rangle $ |
$\langle [0.637,0.833]\rangle $ |
$\langle [0.818,0.622]\rangle $ |
$\langle [0.755,0.679]\rangle $ |
| ${B_{i}}$ |
$\langle [0.788,0.678]\rangle $ |
$\langle [0.606,0.888]\rangle $ |
$\langle [0.871,0.607]\rangle $ |
$\langle [0.731,0.755]\rangle $ |
$\langle [0.894,0.600]\rangle $ |
$\langle [0.650,0.779]\rangle $ |
| FFNs |
Case 13 |
Case 14 |
Case 15 |
Case 16 |
Case 17 |
Case 18 |
| ${A_{i}}$ |
$\langle [0.629,0.834]\rangle $ |
$\langle [0.637,0.833]\rangle $ |
$\langle [0.881,0.606]\rangle $ |
$\langle [0.815,0.628]\rangle $ |
$\langle [0.827,0.665]\rangle $ |
$\langle [0.818,0.622]\rangle $ |
| ${B_{i}}$ |
$\langle [0.606,0.888]\rangle $ |
$\langle [0.606,0.888]\rangle $ |
$\langle [0.788,0.678]\rangle $ |
$\langle [0.726,0.749]\rangle $ |
$\langle 0.728,0.732\rangle $ |
$\langle 0.728,0.732\rangle $ |
Table 2
Comparisons of Euclidean distance measure and the proposed distance measure.
| Methods |
Case1 |
Case 2 |
Case 3 |
Case 4 |
Case 5 |
Case 6 |
| ${d_{E}}(A,B)$ |
0.184 |
0.184 |
0.146 |
0.146 |
0.129 |
0.129 |
| $\bar{d}(A,B)$ |
0.1022 |
0.0987 |
0.0767 |
0.0841 |
0.0743 |
0.0764 |
| Methods |
Case 7 |
Case 8 |
Case 9 |
Case 10 |
Case 11 |
Case 12 |
| ${d_{E}}(A,B)$ |
0.183 |
0.183 |
0.141 |
0.141 |
0.158 |
0.158 |
| $\bar{d}(A,B)$ |
0.1063 |
0.1081 |
0.0887 |
0.0733 |
0.1038 |
0.0855 |
| Methods |
Case 13 |
Case 14 |
Case 15 |
Case 16 |
Case 17 |
Case 18 |
| ${d_{E}}(A,B)$ |
0.109 |
0.109 |
0.167 |
0.166 |
0.156 |
0.157 |
| $\bar{d}(A,B)$ |
0.0730 |
0.0707 |
0.0967 |
0.0890 |
0.0868 |
0.0808 |
The distance measure results obtained by two methods are shown in Table
2. Carefully observing Table
2, the main conclusions are described as follows.
(1) Compared with the Euclidean distance measure (Senapati and Yager,
2019c), the proposed distance measure has satisfactory performances under Case 1–Case 14. The values of the Euclidean distance measure are equal under Case 1–Case 14. These results seem counter-intuitive, which are highlighted in bold in Table
2. The proposed distance can measure the difference under Case 1–Case 14, which demonstrates the feasibility of the proposed distance.
(2) The discrimination degrees of the proposed distance measure are significantly higher than those of the Euclidean distance measure under Case 15 and Case 16 or Case 17 and Case 18. It can be seen from Table
2 that the discrimination degrees of Euclidean distance measure under Case 15 and Case 16 or Case 17 and Case 18 are only 0.01, while the discrimination degrees of the proposed distance measure under the corresponding cases are over 0.06.
3.2 Cross Entropy Measure for FFSs
As one of the most popular information measure, cross entropy is used to measure the divergence information and extensively applied in current literature. However, cross entropy measure for FFSs is rare. Inspired by Song
et al. (
2019), this paper gives a definition of Fermatean fuzzy cross entropy.
Definition 11.
Let
X be a universe of discourse such that
$X=({x_{1}},{x_{2}},\dots ,{x_{n}})$, and
G and
H be two FFSs in
X, in which
$G=\{\langle {x_{i}},{G_{\alpha }}({x_{i}}),{G_{\beta }}({x_{i}}),{G_{\pi }}({x_{i}})\rangle \mid {x_{i}}\in X\}$ and
$H=\{\langle {x_{i}},{H_{\alpha }}({x_{i}}),{H_{\beta }}({x_{i}}),{H_{\pi }}({x_{i}})\rangle \mid {x_{i}}\in X\}$. The Fermatean fuzzy cross entropy measure of
G against
H, denoted as
$\textit{CE}(G,H)$, is defined as:
where
$\Delta G({x_{i}})=|{G_{\alpha }^{3}}({x_{i}})-{G_{\beta }^{3}}({x_{i}})|$ indicates the difference between membership cube and non-membership cube.
Since
$\textit{CE}(G,H)$ is not symmetric, a symmetric cross entropy measure can be given as:
Definition 12.
Let
X be a universe of discourse such that
$X=({x_{1}},{x_{2}},\dots ,{x_{n}})$, and
G and
H be two FFSs in
X, in which
$G=\{\langle {x_{i}},{G_{\alpha }}({x_{i}}),{G_{\beta }}({x_{i}}),{G_{\pi }}({x_{i}})\rangle \mid {x_{i}}\in X\}$ and
$H=\{\langle {x_{i}},{H_{\alpha }}({x_{i}}),{H_{\beta }}({x_{i}}),{H_{\pi }}({x_{i}})\rangle \mid {x_{i}}\in X\}$. The normalized Fermatean fuzzy cross entropy measure between
G and
H, denoted as
$\textit{NCE}(G,H)$, is defined as:
Theorem 2.
Let G, H and M be three arbitrary FFSs in a universe of discourse X, then $\textit{NCE}(G,H)$ satisfies the following properties:
-
(P1) $\textit{NCE}(G,H)=\textit{NCE}\big({G^{C}},H\big)=\textit{NCE}\big(G,{H^{C}}\big)=\textit{NCE}\big({G^{C}},{H^{C}}\big)$;
-
(P2) $0\leqslant \textit{NCE}(G,H)\leqslant 1$;
-
(P3) $\textit{NCE}(G,H)=0$ iff $G=H$ or $G={H^{C}}$, for $G,H\in X$.
Proof.
(P1) For two FFSs in X defined as $G=\{\langle x,{G_{\alpha }}(x),{G_{\beta }}(x)\rangle \mid x\in X\}$ and $H=\{\langle x,{H_{\alpha }}(x),{H_{\beta }}(x)\rangle \mid x\in X\}$, we have ${G^{C}}=\{\langle x,{G_{\beta }}(x),{G_{\alpha }}(x)\rangle \mid x\in X\}$, ${H^{C}}=\{\langle x,{H_{\beta }}(x),{H_{\alpha }}(x)\rangle \mid x\in X\}$.
Then, we can get that ${G_{\pi }^{3}}(x)={G_{{\pi ^{C}}}^{3}}(x)=1-{G_{\alpha }^{3}}(x)-{G_{\beta }^{3}}(x)$, ${H_{\pi }^{3}}(x)={H_{{\pi ^{C}}}^{3}}(x)=1-{H_{\alpha }^{3}}(x)-{H_{\beta }^{3}}(x)$, $\Delta G(x)=\Delta {G^{C}}(x)$, $\Delta H(x)=\Delta {H^{C}}(x)$, $\forall x\in X$.
Therefore, $\textit{NCE}(G,H)=\textit{NCE}({G^{C}},H)=\textit{NCE}(G,{H^{C}})=\textit{NCE}({G^{C}},{H^{C}})$.
(P2) If ${G_{\pi }^{3}}(x)\leqslant {H_{\pi }^{3}}(x)$, then it has ${G_{\pi }^{3}}(x)-{H_{\pi }^{3}}(x)\leqslant 0$, $\frac{1+{G_{\pi }^{3}}(x)}{1+{H_{\pi }^{3}}(x)}\leqslant 1$, $({G_{\pi }^{3}}(x)-{H_{\pi }^{3}}(x))\ln \frac{1+{G_{\pi }^{3}}(x)}{1+{H_{\pi }^{3}}(x)}\geqslant 0$. If ${G_{\pi }^{3}}(x)>{H_{\pi }^{3}}(x)$, one gets that ${G_{\pi }^{3}}(x)-{H_{\pi }^{3}}(x)>0$, $\frac{1+{G_{\pi }^{3}}(x)}{1+{H_{\pi }^{3}}(x)}>1$, $({G_{\pi }^{3}}(x)-{H_{\pi }^{3}}(x))\ln \frac{1+{G_{\pi }^{3}}(x)}{1+{H_{\pi }^{3}}(x)}>0$. Hence, $({G_{\pi }^{3}}(x)-{H_{\pi }^{3}}(x))\ln \frac{1+{G_{\pi }^{3}}(x)}{1+{H_{\pi }^{3}}(x)}\geqslant 0$ always holds for $x\in X$. Analogously, we can get $(\Delta G({x_{i}})-\Delta H({x_{i}}))\ln \frac{1+\Delta G({x_{i}})}{1+\Delta H({x_{i}})}\geqslant 0$, $\forall x\in X$.
Since $0\leqslant {G_{\pi }^{3}}(x)\leqslant 1$, $0\leqslant {H_{\pi }^{3}}(x)\leqslant 1$, $0\leqslant \Delta G(x)\leqslant 1$, $0\leqslant \Delta H(x)\leqslant 1$, $\textit{NCE}(G,H)$ gets its maximum when ${G_{\pi }^{3}}(x)=1$, ${H_{\pi }^{3}}(x)=0$, $\Delta G(x)=0$, $\Delta H(x)=1$ or ${G_{\pi }^{3}}(x)=0$, ${H_{\pi }^{3}}(x)=1$, $\Delta G(x)=1$, $\Delta H(x)=0$, $\forall x\in X$. Hence, it holds that $0\leqslant \textit{NCE}(G,H)\leqslant 1$.
(P3) In this case of $G=H$ or $G={H^{C}}$, obviously, $\textit{NCE}(G,H)=0$. For the sufficiency, if $\textit{NCE}(G,H)=0$, we have $G=H$ or $G={H^{C}}$, due to $({G_{\pi }^{3}}(x)-{H_{\pi }^{3}}(x))\ln \frac{1+{G_{\pi }^{3}}(x)}{1+{H_{\pi }^{3}}(x)}\geqslant 0$ and $(\Delta G({x_{i}})-\Delta H({x_{i}}))\ln \frac{1+\Delta G({x_{i}})}{1+\Delta H({x_{i}})}\geqslant 0$. So, $\textit{NCE}(G,H)=0$ iff $G=H$ or $G={H^{C}}$, for $G,H\in X$.
Therefore, Theorem
2 is proved. □
3.3 Grey Relation Analysis Between FFSs
In this section, grey relational theory is extended to FFSs environment, and the FFSs grey relational coefficient and grey relational degree are defined for the first time.
(1) Grey relation analysis
The grey system theory first created by Deng (
1982) is a useful method to study the problems with insufficient, poor and uncertain information. As an indispensable part of grey system theory, the basic idea of grey relational analysis (GRA) is to judge whether the geometric shapes of sequence curves are closely related according to their similarity degrees. The closer the curve is, the greater the correlation between the corresponding sequences is, and vice versa. GRA has been widely applied in addressing different kinds of MCMD problems (Li
et al.,
2020; Wu,
2009; Hamzaçebi and Pekkaya,
2011), due to being computationally simple, robust and practical. In the following, GRA is introduced.
Definition 13 (Deng, 1989).
Let
${X_{0}}=({x_{0}}(1),{x_{0}}(2),\dots ,{x_{0}}(j))$ and
${X_{i}}=({x_{i}}(1),{x_{i}}(2),\dots ,{x_{i}}(j))$ (
$i=1,2,\dots ,m$;
$j=1,2,\dots ,k$) be sets of the sequences. The grey relational coefficient is defined by
where
$\rho \in (0,1)$ is the distinguished coefficient.
The grey relational degree is defined as:
(2) Grey relational analysis between FFSs
Definition 14.
Let
X be a universe of discourse such that
$X=({x_{1}},{x_{2}},\dots ,{x_{n}})$, and
G and
H be two FFSs in
X, in which
$G=\{\langle {x_{i}},{G_{\alpha }}({x_{i}}),{G_{\beta }}({x_{i}})\rangle \mid {x_{i}}\in X\}$ and
${H_{j}}=\{\langle {x_{i}},{H_{{\alpha _{j}}}}({x_{i}}),{H_{{\beta _{j}}}}({x_{i}})\rangle \mid {x_{i}}\in X\}$,
$i=1,2,\dots ,n$,
$j=1,2,\dots ,m$. The grey relational coefficient between
G and
H is defined as:
where
$\bar{d}(G,{H_{j}})$ is the distance between FFSs
G and
${H_{j}}$, which is calculated by Eq. (
11).
In view of grey relational coefficient between FFSs, the grey relational degree between FFSs
G and
${H_{j}}$ is defined as:
5 A FermateanFuzzy ELECTRE Method for MCGDM
This section develops a Fermatean fuzzy ELECTRE method for MCGDM.
5.1 Problem Description of MCGDM Using FFNs
Assuming there are m non-inferior alternatives ${A_{i}}$ $(i=1,2,\dots ,m)$, each alternative is evaluated on n criteria ${C_{j}}$ $(j=1,2,\dots ,n)$ by t experts ${E_{l}}$ $(l=1,2,\dots ,t)$. To be specific, the set ${C_{j}}$ is classified into two different types of sets, namely, ${C_{\mathrm{I}}}$ and ${C_{\mathrm{II}}}$. Here, ${C_{\mathrm{I}}}$ and ${C_{\mathrm{II}}}$ show a collection of benefit criteria and a collection of cost criteria, respectively. Let $\boldsymbol{\lambda }={({\lambda _{1}},{\lambda _{2}},\dots ,{\lambda _{t}})^{T}}$ be the weight vector of DMs, in which ${\lambda _{l}}\in [0,1]$ and ${\textstyle\sum _{l=1}^{t}}{\lambda _{t}}=1$; $\boldsymbol{w}={({w_{1}},{w_{2}},\dots ,{w_{n}})^{T}}$ be the weight vector of criteria where ${w_{j}}\in [0,1]$ and ${\textstyle\sum _{j=1}^{n}}{w_{j}}=1$. $\boldsymbol{\lambda }={({\lambda _{1}},{\lambda _{2}},\dots ,{\lambda _{t}})^{T}}$, $\boldsymbol{w}={({w_{1}},{w_{2}},\dots ,{w_{n}})^{T}}$ are completely unknown and incomplete, respectively. The evaluation information for ${A_{i}}$ $(i=1,2,\dots ,m)$ with respect of ${C_{j}}$ $(j=1,2,\dots ,n)$ is given by t experts in terms of linguistic assessment. These linguistic assessments can be transformed into FFNs. Let ${R^{l}}={({a_{ij}^{l}})_{m\times n}}$ be the Fermatean fuzzy decision matrix, where ${a_{ij}^{l}}$ is the performance of alternative ${A_{i}}$ with respect to criterion ${C_{j}}$ provided by DM ${E_{l}}$, and ${a_{ij}^{l}}=({\alpha _{ij}^{l}},{\beta _{ij}^{l}},{\pi _{ij}^{l}})$ is an FFN, where ${\alpha _{ij}^{l}}$, ${\beta _{ij}^{l}}$, ${\pi _{ij}^{l}}$ are membership degree, non-membership degree and indeterminacy degree, respectively. The MCGDM considered in this paper is how to select the best alternative according to Fermatean fuzzy decision matrices ${R^{l}}={({a_{ij}^{l}})_{m\times n}}$ $(l=1,2,\dots ,t)$.
5.2 Determine Dynamic Weights of DMs with Respect to Each Criterion over Different Alternatives
Aggregating all individual decisions into a collective decision is regarded as a key part of MCGDM process. Therefore, how to determine the weights of DMs is one of the main activities for MCGDM problems, because different weights of DMs may generate different collective decision matrices and then can have significant impact on the final result. Hence, methods for determining the weights of DMs have received much attention by researchers, however, most of existing methods usually assume that DMs’ weights for all alternatives and criteria are changeless (Yue,
2012; Lin and Chen,
2020; Wan
et al.,
2013; Ju,
2014; Wan
et al.,
2015). In the actual decision-making process, it is unlikely that each DM is expected to be good at commenting on all alternatives and criteria due to differences in educational background, knowledge, experience, preference, and title, the weights of each DM may change with different criteria and different alternatives. Hence, distributing different weights to each DM with respect to different alternatives under different criteria is more reasonable and in line with the actual decision-making situation. Therefore, the study of dynamic DM weights is of some practical significance. According to Geng
et al. (
2017), dynamic weights refer to assigning different weights to each DM with respect to different criteria over different alternatives. DM’s weights will vary with different criteria and different alternatives. However, to the best of our knowledge, there are only several scholars (Geng
et al.,
2017; Wu
et al.,
2019) involving this issue up to now. In particular, determining the objectively dynamic weights of DMs in the context of Fermatean fuzzy information remains an unexplored area. To fill the research gap, this paper proposes a new method for determining dynamic weights of DMs. Inspired by Geng
et al. (
2017), based on the proposed the cross entropy, dynamic weights of DMs are determined as follows:
(1) Determine the positive ideal decision matrix (PIDM) and the negative ideal decision matrix (NIDM)
Let
${R^{+}}={({a_{ij}^{+}})_{m\times n}}$ and
${R^{-}}={({a_{ij}^{-}})_{m\times n}}$ be PIDM and NIDM for all individual decision matrices given by DMs, in which
$\{{a_{ij}^{+}}=({\alpha _{ij}^{+}},{\beta _{ij}^{+}}),\hspace{2.5pt}1\leqslant i\leqslant m,\hspace{2.5pt}1\leqslant j\leqslant n\}$ and
$\{{a_{ij}^{-}}=({\alpha _{ij}^{-}},{\beta _{ij}^{-}}),\hspace{2.5pt}1\leqslant i\leqslant m,\hspace{2.5pt}1\leqslant j\leqslant n\}$ are positive ideal decision-making information (PIDMI) and negative ideal decision-making information (NIDMI) with respect to
i-th alternative over
j-th criterion. We construct the following optimization model to determine
$({\alpha _{ij}^{+}},{\beta _{ij}^{+}})$ and
$({\alpha _{ij}^{-}},{\beta _{ij}^{-}})$, respectively.
(2) Determine the credibility degree
The credibility degree is determined in line with cross entropy. If
${\alpha _{ij}^{l}}$ has a larger difference from
${\alpha _{ij}^{+}}$ or
${a_{ij}^{-}}$, it has more credibility. So, the credibility of
${\alpha _{ij}^{l}}$, denoted by
${\tau _{ij}^{l}}$, is defined as
(3) Determine the dynamic weights of DMs
It is obvious that the DM
${E_{l}}$ who gives decision-making information with respect to different criteria with larger credibility should be allocated a bigger weight. Accordingly, objective and dynamic weights of DMs, denoted by
${\lambda _{ij}^{l}}$, are determined as follows:
Using Eq. (
3),
${R^{l}}$ $(l=1,2,\dots ,t)$ can be integrated into a collective matrix
$R={({a_{ij}})_{m\times n}}$, in which
${a_{ij}}$ can be derived by
5.3 Obtain Criteria Weights Based on the Proposed GRA
Criteria weights play a pivotal role in MCDM problems, because they have an important and direct influence on ranking results. Due to the increasing complexity, time pressure or lack of data in practical situations, the weights of criteria are usually unknown. Therefore, it is an interesting research topic to deduce plausible weights for criteria by selecting suitable methods in the real-life MCDM process, since plausible weights can ensure scientific and plausible decision-making results. In the current literature, methods for deriving criteria weights can be divided into two categories: the subjective weight-determining methods, the objective weight-determining methods.
The subjective weight-determining methods, such as the Delphi method (Dalkey and Helmer,
1963), the AHP method (Saaty,
1987; Kaya and Kahraman,
2011) and SRF method (Figueira and Roy,
2002), determine the weights of criteria based on experiences and subjective judgments. The subjective weight-determining methods are impacted by subjective randomness of the DM’s preference. In addition, when there are a great number of assessment criteria, the subjective weight-determining methods are not suitable for identification of weights of these criteria (Çalı and Balaman,
2019). Different from the subjective methods, the objective methods are capable of eliminating man-made instabilities and obtaining more realistic weights according to mathematical model. A majority of them have focused on calculation of entropy value so as to derive the criteria weights. Entropy weight method, which is a straightforward method for weight determination, has been extensively applied to diverse decision-making fields (Zhang and Yao,
2017; Xu and Shen,
2014; Ye,
2010; Liu and Zhang,
2011), however, it can deduce irrational weight values in some cases (Das
et al.,
2015).
Since its inception in Deng (Wang,
1997), GRA method has been widely employed for obtaining objective weights of criteria (Wei,
2011a,
2010; Luo
et al.,
2019; Meng
et al.,
2015), because its greatest strength is that it is computationally simple, robust and practical (Wei,
2011b). This is a discerning evidence that the GRA method is deemed to be a more feasible method to obtain criteria weights in this study.
In the following, we utilize GRA method to determine the criteria weights with incomplete information.
Firstly, the Fermatean Fuzzy Positive Ideal Point (FF-PIP)
${a_{j+}}$ and the Fermatean Fuzzy Negative Ideal Point (FF-NIP)
${a_{j-}}$ can be defined as:
Then, based on the proposed distance measure for FFSs in Section
3.2, the distances of the rating values
${a_{ij}}$ to the FF-PIP
${a_{j+}}$ and FF-NIP
${a_{j-}}$ can be computed respectively by:
where
$\eta \in (\alpha ,\beta ,\pi )$ in Eqs. (
26) and (
27).
Next, the grey relational coefficients of the rating values
${a_{ij}}$ from PIP and NIP are computed using the following equations, respectively:
where
$\bar{d}({\alpha _{ij}},{\alpha _{j+}})$ and
$\bar{d}({\alpha _{ij}},{\alpha _{j-}})$ are the distance of the rating values
${a_{ij}}$ to the FF-PIP
${a_{j+}}$ and FF-NIP
${a_{j-}}$, respectively,
$i=1,2\dots ,m$,
$j=1,2,\dots ,n$;
δ is considered as an identification coefficient to mitigate the effect of the
${\max _{j}}\bar{d}({\alpha _{ij}},{\alpha _{j+}})$ or
${\max _{j}}\bar{d}({\alpha _{ij}},{\alpha _{j-}})$ on the relational coefficient, with a value ranging from 0 to 1. In this paper,
δ is equal to 0.5.
Subsequently, the degrees of grey relational coefficient of the alternative
${A_{i}}$ from PIP and NIP are computed using the following equations, respectively:
where
${w_{j}}$ (
$j=1,2,\dots ,n$) are the criteria weights.
According to the GRA method, the optimal alternative should have the “largest degree of grey relation” from the positive-ideal solution and the “smallest degree of grey relation” from the negative-ideal solution. Based on this idea, a multiple objective optimization model (
M-1) is established to get criteria weights with incomplete weight information with respect to alternative
${A_{i}}$.
where Λ is set of incomplete information about weight criteria given by DMs. Incomplete information structures of criteria weights are constructed in the following five forms (Wan
et al.,
2015; Xu,
2007; Xu and Da,
2008), for
$h\ne j$:
-
Form 1. A weak ranking: ${w_{h}}\geqslant {w_{j}}$;
-
Form 2. A strict ranking: ${w_{h}}-{w_{j}}\geqslant {\varepsilon _{j}},{\varepsilon _{j}}>0$;
-
Form 3. A ranking with multiples: ${w_{h}}\geqslant {\varepsilon _{j}}{w_{j}}$, $0\leqslant {\varepsilon _{j}}\leqslant 1$;
-
Form 4. An interval form: ${\kappa _{h}}\leqslant {w_{h}}\leqslant {\kappa _{h}}+{\iota _{h}}$, $0\leqslant {\kappa _{h}}w\leqslant {\kappa _{h}}+{\iota _{h}}$;
-
Form 5. A ranking of differences: ${w_{h}}-{w_{j}}\geqslant {w_{k}}-{w_{l}}\geqslant {\varepsilon _{j}}$, $j\ne k\ne l$.
Since each alternative is non-inferior, there exists no preference relation on all alternatives. We may aggregate the above multiple objective optimization model with equal weights into the following single-objective optimization model (
M-2):
By solving the model (
M-2), we obtain the optimal weight vector of criteria
${\boldsymbol{w}^{i}}=({w_{1}^{i}},{w_{2}^{i}},\dots ,{w_{n}^{i}})$ with respect to alternative
${A_{i}}$.
Then, we will substitute
${\boldsymbol{w}^{k}}=({w_{1}^{k}},{w_{2}^{k}},\dots ,{w_{n}^{k}})$ $(k=1,2,\dots ,m)$ into the objective function
${\Theta _{i}}$ in model (
M-2). The value of objective function
${\Theta _{i}}$ can be calculated as
Then, let
${\Theta _{i}^{+}}=\max \{{\Theta _{i}^{k}}\mid k=1,2,\dots ,m\}$ and
${\Theta _{i}^{-}}=\min \{{\Theta _{i}^{k}}\mid k=1,2,\dots ,m\}$ be maximum and minimum values of
${\Theta _{i}}$, respectively. It is easy to know from model (
M-2) that
${\Theta _{i}^{+}}={\Theta _{i}^{i}}$.
The weight vector ${\boldsymbol{w}^{t}}$ $(t=1,2,\dots ,m)$ corresponding to the value ${\Theta _{i}^{-}}$ is defined as the worst weight vector for ${A_{i}}$ and denoted by ${\boldsymbol{w}^{i-}}$. The weight vector ${\boldsymbol{w}^{s}}$ $(s=1,2,\dots ,m)$ corresponding to the value ${\Theta _{i}^{+}}$ is defined as the optimal weight vector for ${A_{i}}$ and denoted by ${\boldsymbol{w}^{i+}}$.
In the following, an optimization model motivated by the ideal of TOPSIS method is constructed to determine the weight of each criterion in incomplete weight information context. The main steps are described as follows:
(1) Determine the Positive Ideal Weight Vector (PIWV) and Negative Ideal Weight Vector (NIWV) of the criterion weight for each alternative.
According to the above analysis, PIWV and NIWV are defined as
(2) Calculate the distance of each criterion weight from the PIWV and NIWV respectively.
where
${w_{j}}$ is the
j-th criterion weight.
${w_{j}^{i}}$ and
${w_{j}^{t}}$ are
$ij$-th element of
j-th criteria for
i-th alternative in PIWV and NIWV, respectively.
According to the ideal of TOPSIS method, a multiple objective optimization model (
M-3) is constructed to derive criteria weights with incomplete weight information,
The above multiple objective optimization model is equal to the following single objective optimization model (
M-4) by using equal weight linear weighting method:
The optimal solution
$\boldsymbol{w}=({w_{1}},{w_{2}},\dots ,{w_{n}})$ can be obtained by the model (
M-4).
5.4 Construct the Concordance and Discordance Sets
For each Fermatern fuzzy pair of
${A_{f}}$ and
${A_{g}}$, the set of criteria is classified into two distinct subsets: concordance set and discordance set. The concordance set consists of all criteria for which
${A_{f}}$ is preferred to alternative
${A_{g}}$. The discordance set, the complement set of concordance set, contains all criteria for which
${A_{f}}$ is worse than
${A_{g}}$. On account of Definition
15, the concordance set for any two alternatives
${A_{f}}$ and
${A_{g}}$ can be partitioned into three categories.
-
(1) Strong concordance set is portrayed as:
-
(2) Medium concordance set is portrayed as:
-
(3) Weak concordance set is portrayed as:
The discordance set
${J_{{D_{fg}}}}$ of
${A_{f}}$ and
${A_{g}}$ consists of all criteria for which
${A_{f}}$ is not superior to
${A_{g}}$. The discordance set
${J_{{D_{fg}}}}$ can also divided into three categories in the same way.
-
(1) Strong discordance set is portrayed as:
-
(2) Medium discordance set is portrayed as:
-
(3) Weak discordance set is portrayed as:
5.5 Identify the Weights of Concordance and Discordane Sets
This paper applies objective weighting method based on the proposed distance measure to identify the weights of concordance and discordance sets. The weights of strong, medium, and weak concordance sets are computed by Eqs. (
43), (
44) and (
45), respectively.
The weight of strong concordance set
${w_{C}}$ is computed with Eq. (
43) as follows:
The weight of medium concordance set
${w_{{C^{\prime }}}}$ is computed with Eq. (
44) as follows:
The weight of weak concordance set
${w_{{C^{\prime\prime }}}}$ is computed with Eq. (
45) as follows:
The weights of strong, medium, and weak discordance sets are computed by Eqs. (
46), (
47) and (
48), respectively.
The weight of strong discordance set
${w_{D}}$ is computed with Eq. (
46) as follows:
The weight of strong discordance set
${w_{{D^{\prime }}}}$ is computed with Eq. (
47) as follows:
The weight of strong discordance set
${w_{{D^{\prime\prime }}}}$ is computed with Eq. (
48) as follows:
In Eqs. (
43)–(
48),
$\bar{d}({A_{fj}},{A_{gj}})$ is the distance between
${\alpha _{f}}$ and
${\alpha _{g}}$ under
${C_{j}}$,
${w_{j}}$ is the weight of
${C_{j}}$.
5.6 Construction of Fermatern Fuzzy Concordance Matrix and Discordance Matrix
The concordance matrix and discordance matrix are constructed based on the concordance and discordance index, respectively. In order to specify an outranking relationship between
${A_{f}}$ and
${A_{g}}$, it is essential to compute two main indices called concordance index and discordance index. The concordance index for a pair of alternative
${A_{f}}$ and
${A_{g}}$, which shows the degree of superiority of alternative
${A_{f}}$ to alternative
${A_{g}}$, is related to the weights of the concordance sets and the corresponding criteria weights. Therefore, the concordance index
${V_{fg}}$ between two alternatives
${A_{f}}$ and
${A_{g}}$ is defined as
where
${w_{C}}$,
${w_{{C^{\prime }}}}$ and
${w_{{C^{\prime\prime }}}}$ are the weights of strong concordance set, medium concordance set and weak discordance set, respectively;
${w_{j}}$ is the weight of the corresponding criterion.
After determination of all concordance indices, the concordance matrix
V is generated as follows:
The discordance index for a pair of alternative
${A_{f}}$ and
${A_{g}}$ shows the degree of inferiority of alternative
${A_{f}}$ to alternative
${A_{g}}$ according to criteria in the discordance sets. The discordance index
${D_{fg}}$ between
${A_{f}}$ and
${A_{g}}$ is represented as
where
${w_{D}}$,
${w_{{D^{\prime }}}}$ and
${w_{{D^{\prime\prime }}}}$ are the weights of three kinds of Fermatern fuzzy discordance sets, and
$\bar{d}({A_{fj}},{A_{gj}})$ stands for the distance measure between alternative
${A_{f}}$ and
${A_{g}}$ with reference to criterion
${C_{j}}$.
Based on the discordance index, the discordance matrix
D is defined as follows:
5.7 Computation of the Net Superiority Index and the Net Inferiority Index
As mentioned above, the concordance index
${V_{fg}}$ reveals the degree of superiority of alternative
${A_{f}}$ to alternative
${A_{g}}$, the bigger the value of
${V_{fg}}$, the more superior
${A_{f}}$ is to
${A_{g}}$. Likewise, the discordance index
${D_{fg}}$ shows the degree to which alternative
${A_{f}}$ is inferior to alternative
${A_{g}}$, the bigger the value of
${D_{fg}}$, the more inferior
${A_{f}}$ is to
${A_{g}}$. That is to say,
${V_{fg}}$, to some degree, represents the inferiority degree of alternative
${A_{g}}$ to alternative
${A_{f}}$, and
${D_{fg}}$, shows superiority degree of alternative
${A_{g}}$ to alternative
${A_{f}}$. Hence, both
${V_{fg}}$ and
${D_{gf}}$ display the superiority degree of
${A_{f}}$ to
${A_{g}}$, and both
${V_{gf}}$ and
${D_{fg}}$ display the inferiority degree of
${A_{f}}$ to
${A_{g}}$. Therefore, the net superiority index of alternative
${A_{f}}$ can be computed as
Thus, it may be known that the net superiority index $N{S_{f}}$ shows the relative superiority degree of alternative ${A_{f}}$ over all the other alternatives.
Furthermore, the net inferiority index of alternative
${A_{f}}$ can be computed as
The net inferiority index ${\textit{NI}_{f}}$ shows the relative inferiority degree of alternative ${A_{f}}$ to all the other alternatives.
To rank alternatives an overall evaluation index is defined as
The overall evaluation index ${Z_{f}}$ stands for the overall superiority degree of alternative ${A_{f}}$ over all the other alternatives. If an alternative has the biggest value of the net superiority index and the smallest value of the net inferiority index, it is the optimal alternative.
On the basis of the overall evaluation index, the optimal alternative can be selected as follows:
5.8 A Fermatean Fuzzy ELECTRE Method
On the basis of the above analyses, the steps of the proposed Fermatean fuzzy ELECTRE method are summarized as follows:
-
Step 1. Form the group decision matrices. DMs give their evaluations of all alternatives regarding to each criterion with linguistic terms. Then, these linguistic assessments can be transformed into FFNs, and thus build up the group decision matrices.
-
Step 2. Determine dynamic weights of DMs using Eqs. (
19)–(
22).
-
Step 3. Aggregate all individual decision matrices into a collective one using Eq. (
23).
-
Step 4. Obtain criteria weights using Eqs. (
24)–(
36) and models (
M-1)–(
M-4).
-
Step 5. Construct strong, medium and weak concordance sets and discordance sets based on Eqs. (
37)–(
39) and Eqs. (
40)–(
42), respectively.
-
Step 6. Identify the weights of strong, medium and weak concordance and discordance sets by using Eqs. (
43)–(
45) and Eqs. (
46)–(
48), respectively.
-
Step 7. Construct concordance matrix and discordance matrix using Eq. (
49) and Eq. (
50), respectively.
-
Step 8. Compute the net superiority index and the net inferiority index using Eq. (
51) and Eq. (
52), respectively.
-
Step 9. Compute the overall evaluation indices for all alternatives by Eq. (
53).
-
Step 10. Choose the optimal alternative based on Eq. (
54).
6 Case Study Concerning Site Selection of FSHs for COVID-19 Patients in Wuhan
In this section, a practical case concerning site selection of FSHs for COVID-19 in Wuhan is provided to show the implementation process of the proposed ELECTRE method. Then, some comparisons are carried out to verify the superiority and effectiveness of the proposed ELECTRE method.
6.1 Description of Site Selection of FSHs
Nevertheless the spread of the COVID-19 around the world, it was unfortunately detected at the end of 2019 in Wuhan, the capital city of Hubei Province, China. By February 26, 2020, there have been 47824 confirmed cases in Wuhan, accounting for 60.9% of the total confirmed cases in China. Owing to the lack of medical resources, especially the number of beds for patients with confirmed COVID-19 is seriously insufficient, a large number of confirmed patients failed to be isolated and treated in time, causing cross infection in the community and accelerating the spread of the epidemic. In order to collect and treat patients with mild COVID-19, the Chinese government launched an emergency construction of FSHs. The rapid establishment and operation of FSHs have played an irreplaceable role in COVID-19 prevention and control.
Site selection is the first and most critical step in the construction of FSHs. Without loss of generality, this paper only considers the site selection for the first FSHs in Wuhan. Site selection takes three aspects into consideration: first, it should be far away from residential areas and densely populated places, and be in the downwind position of this area; second, it should be convenient for transportation of patients and medical staff; third, the internal structure of the site is convenient for rapid transformation and has certain functionality.
There exist five candidate buildings (alternatives) suitable for being reconstructed to FSHs in Wuhan. They are Wuhan Sports Center (${A_{1}}$), Hongshan Gymnasium (${A_{2}}$), Wuhan International Conference and Exhibition Center (${A_{3}}$), Wuhan Gymnasium (${A_{4}}$), and China (Wuhan) Cultural Exhibition Center (${A_{5}}$). ${A_{1}}$ is located in the southwest of Wuhan and situated in Wuhan economic and technological development zone. ${A_{2}}$ is located in Hongshan Square, the centre of Wuchang District. ${A_{3}}$ is located in Jianghan District, which is the most prosperous business center in Wuhan. ${A_{4}}$ is located at No. 612, Jiefang Avenue in downtown Hankou. ${A_{5}}$ is located in Jinyintan, Dongxihu District.
The experts (or DMs) panel consists of five experts. They were selected from the areas of disease control and prevention, scientific research institution, public health education, architectural design and research institute, etc. They had more than ten-year working experience and high-level academic titles.
In light of technical requirements for design and reconstruction of FSHs issued by Department of Housing and Urban-Rural Development of Hubei Province (see
http://zjt.hubei.gov.cn/), eight main technical requirements (i.e., criteria) for candidate buildings (alternatives) are extracted as follows: traffic convenience (
${C_{1}}$), environmental protection (
${C_{2}}$), geographical position (
${C_{3}}$), infrastructure (
${C_{4}}$), regional communication convenience (
${C_{5}}$), capacity (
${C_{6}}$), reconstruction difficulty (
${C_{7}}$) and reconstruction cost (
${C_{8}}$). Here,
${C_{1}}$,
${C_{2}}$,
${C_{3}}$,
${C_{4}}$,
${C_{5}}$ and
${C_{6}}$ are benefit criteria, but
${C_{7}}$ and
${C_{8}}$ are cost criteria. After further discussion and negotiation, the information regarding to criteria weights given by the group of DMs is incomplete as follows:
The hierarchical structure of this group decision-making problem is shown in Fig.
3.
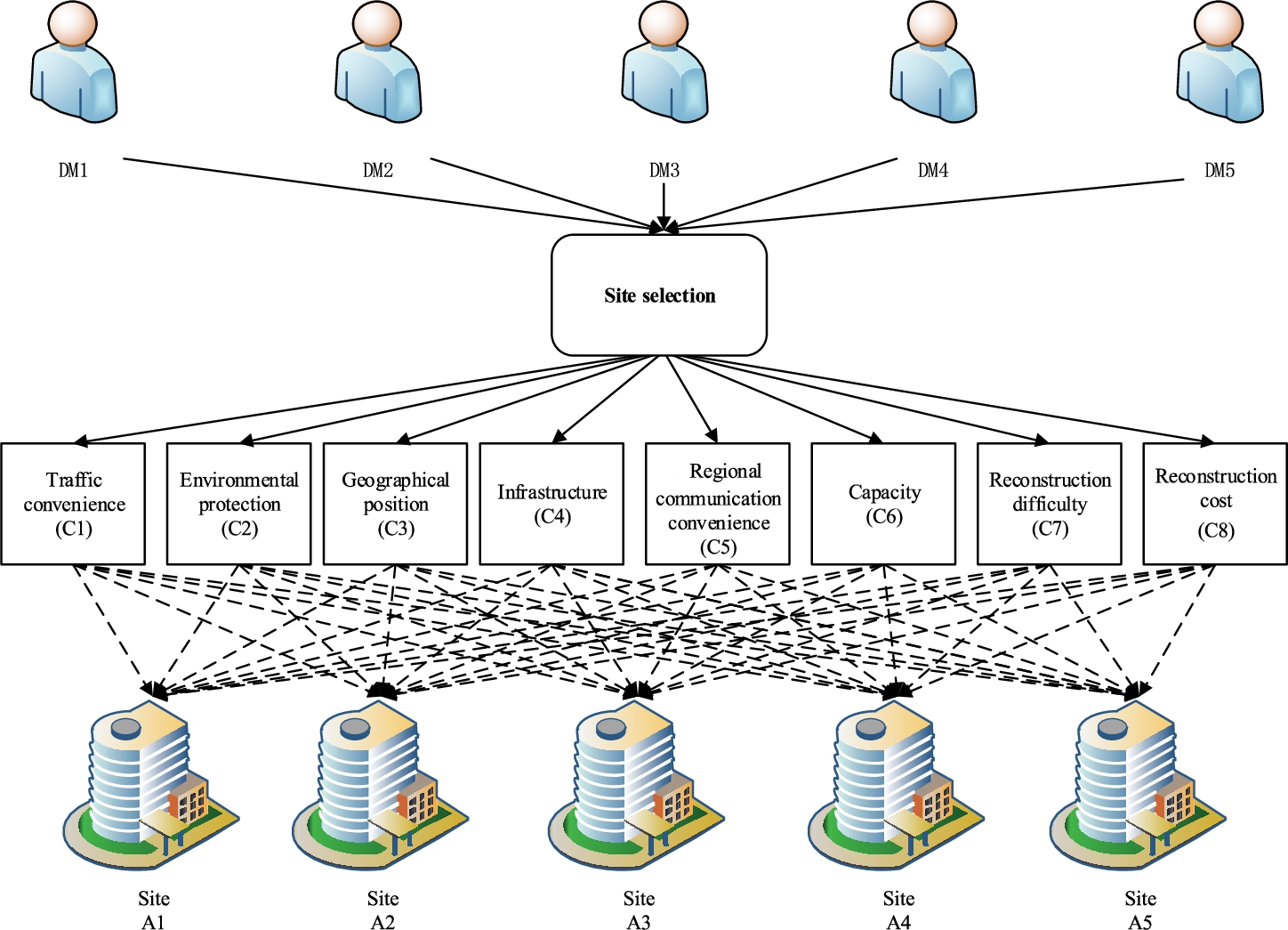
Fig. 3
Hierarchical structure of case study.
6.2 Application of the Proposed Fermatean Fuzzy ELECTRE Method
The main steps of the proposed ELECTRE method can be described as follows:
Step 1: Form Fermatean fuzzy group decision matrices.
Each DM is required to present his/her evaluations of alternative
${A_{i}}$ (
$i=1,2,3,4,5$) with respect to criterion
${C_{j}}$ (
$j=1,2,\dots ,8$). Five DMs evaluate five alternatives under the given criteria using the linguistic variables defined in Table
3. Table
4 describes the linguistic values for alternatives over different criteria given by five DMs. The linguistic evaluations shown in Table
4 are transformed into FFNs by using the mapping relations given by in Table
3. Consequently, Fermatean fuzzy group decision matrices
${R^{l}}={({a_{ij}^{l}})_{m\times n}}$ are constructed and shown in Table
5.
Table 3
Performance ratings of alternatives as linguistic values.
| Linguistic variables |
FFNs |
IFNs |
PFNs |
| Absolutely Good (AG) |
F(0.98, 0.02) |
I(1.0, 0.0) |
P(0.98, 0.1) |
| Very Good (VG) |
F(0.9, 0.6) |
I(0.90, 0.05) |
P(0.87, 0.35) |
| Good (G) |
F(0.8, 0.65) |
I(0.75, 0.2) |
P(0.7, 0.4) |
| Medium Good (MG) |
F(0.75, 0.6) |
I(0.65, 0.3) |
P(0.65, 0.45) |
| Average (A) |
F(0.5, 0.5) |
I(0.55, 0.4) |
P(0.5, 0.55) |
| Medium Bad (MB) |
F(0.6, 0.7) |
I(0.4, 0.5) |
P(0.4, 0.7) |
| Bad (B) |
F(0.7, 0.8) |
I(0.36, 0.6) |
P(0.36, 0.8) |
| Very Bad (VB) |
F(0.6, 0.9) |
I(0.2, 0.7) |
P(0.25, 0.87) |
| Absolutely Bad (AB) |
F(0.02, 0.98) |
I(0.1, 0.8) |
P(0.1, 0.98) |
Table 4
Evaluation values described as linguistic variables by five DMs.
| DM |
Alternative |
${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
${C_{5}}$ |
${C_{6}}$ |
${C_{7}}$ |
${C_{8}}$ |
| ${E_{1}}$ |
${A_{1}}$ |
MG |
VB |
A |
VG |
G |
A |
MG |
G |
|
${A_{2}}$ |
MB |
VG |
A |
MG |
A |
MG |
VG |
MG |
|
${A_{3}}$ |
VG |
VG |
MB |
MG |
VG |
VG |
VB |
G |
|
${A_{4}}$ |
MB |
VG |
MG |
A |
MG |
MB |
MG |
MB |
|
${A_{5}}$ |
VG |
VG |
MB |
MG |
AG |
G |
G |
MG |
| E2
|
${A_{1}}$ |
VG |
MG |
MB |
MG |
MB |
MG |
A |
G |
|
${A_{2}}$ |
MG |
G |
MB |
VB |
MB |
G |
MG |
A |
|
${A_{3}}$ |
G |
MG |
VG |
VB |
VB |
VG |
VG |
B |
|
${A_{4}}$ |
MG |
VG |
VG |
B |
MG |
MG |
A |
VB |
|
${A_{5}}$ |
AG |
B |
MG |
MB |
VB |
G |
VB |
A |
| ${E_{3}}$ |
${A_{1}}$ |
MG |
VG |
A |
B |
MB |
MG |
A |
B |
|
${A_{2}}$ |
VG |
VG |
MB |
VB |
VB |
VG |
MB |
MB |
|
${A_{3}}$ |
VG |
MB |
G |
B |
B |
VG |
VB |
VB |
|
${A_{4}}$ |
VB |
MG |
B |
VB |
VB |
VG |
VB |
VB |
|
${A_{5}}$ |
VG |
VG |
MB |
VB |
B |
MB |
MG |
MB |
| ${E_{4}}$ |
${A_{1}}$ |
G |
VG |
A |
VB |
MB |
G |
B |
MB |
|
${A_{2}}$ |
VG |
G |
MB |
VB |
B |
VG |
VB |
VB |
|
${A_{3}}$ |
VG |
VG |
B |
MG |
VB |
B |
VB |
VB |
|
${A_{4}}$ |
MG |
G |
MB |
VB |
VB |
VG |
B |
VB |
|
${A_{5}}$ |
VG |
B |
B |
B |
VG |
B |
VG |
B |
| ${E_{5}}$ |
${A_{1}}$ |
VG |
MG |
MB |
B |
B |
VG |
VB |
B |
|
${A_{2}}$ |
VG |
VG |
MB |
VB |
MB |
VG |
B |
VB |
|
${A_{3}}$ |
MG |
VG |
VB |
B |
VB |
VG |
VB |
B |
|
${A_{4}}$ |
G |
VG |
MB |
B |
B |
B |
VB |
MB |
|
${A_{5}}$ |
VG |
MG |
VB |
VB |
B |
VG |
B |
VB |
Step 2: Normalize the decision matrix.
Table 5
Evaluation values described as FFNs by five DMs.
| DM |
Alternative |
C1
|
C2
|
C3
|
C4
|
C5
|
C6
|
C7
|
C8
|
| ${E_{1}}$ |
${A_{1}}$ |
$(0.75,0.6)$ |
$(0.6,0.9)$ |
$(0.5,0.5)$ |
$(0.9,0.6)$ |
$(0.8,0.65)$ |
$(0.5,0.5)$ |
$(0.75,0.6)$ |
$(0.8,0.65)$ |
|
${A_{2}}$ |
$(0.6,0.7)$ |
$(0.9,0.6)$ |
$(0.5,0.5)$ |
$(0.75,0.6)$ |
$(0.5,0.5)$ |
$(0.75,0.6)$ |
$(0.9,0.6)$ |
$(0.75,0.6)$ |
|
${A_{3}}$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.6,0.7)$ |
$(0.75,0.6)$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.6,0.9)$ |
$(0.8,0.65)$ |
|
${A_{4}}$ |
$(0.6,0.7)$ |
$(0.9,0.6)$ |
$(0.75,0.6)$ |
$(0.5,0.5)$ |
$(0.75,0.6)$ |
$(0.6,0.7)$ |
$(0.75,0.6)$ |
$(0.6,0.7)$ |
|
${A_{5}}$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.6,0.7)$ |
$(0.75,0.6)$ |
$(0.98,0.02)$ |
$(0.8,0.65)$ |
$(0.8,0.65)$ |
$(0.75,0.6)$ |
| ${E_{2}}$ |
${A_{1}}$ |
$(0.9,0.6)$ |
$(0.75,0.6)$ |
$(0.6,0.7)$ |
$(0.75,0.6)$ |
$(0.6,0.7)$ |
$(0.75,0.6)$ |
$(0.5,0.5)$ |
$(0.8,0.65)$ |
|
${A_{2}}$ |
$(0.75,0.6)$ |
$(0.8,0.65)$ |
$(0.6,0.7)$ |
$(0.6,0.9)$ |
$(0.6,0.7)$ |
$(0.8,0.65)$ |
$(0.75,0.6)$ |
$(0.5,0.5)$ |
|
${A_{3}}$ |
$(0.8,0.65)$ |
$(0.75,0.6)$ |
$(0.9,0.6)$ |
$(0.6,0.9)$ |
$(0.6,0.9)$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.7,0.8)$ |
|
${A_{4}}$ |
$(0.75,0.6)$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.7,0.8)$ |
$(0.75,0.6)$ |
$(0.75,0.6)$ |
$(0.5,0.5)$ |
$(0.6,0.9)$ |
|
${A_{5}}$ |
$(0.98,0.02)$ |
$(0.7,0.8)$ |
$(0.75,0.6)$ |
$(0.6,0.7)$ |
$(0.6,0.9)$ |
$(0.8,0.65)$ |
$(0.6,0.9)$ |
$(0.5,0.5)$ |
| ${E_{3}}$ |
${A_{1}}$ |
$(0.75,0.6)$ |
$(0.9,0.6)$ |
$(0.5,0.5)$ |
$(0.7,0.8)$ |
$(0.6,0.7)$ |
$(0.75,0.6)$ |
$(0.5,0.5)$ |
$(0.7,0.8)$ |
|
${A_{2}}$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.6,0.7)$ |
$(0.6,0.9)$ |
$(0.6,0.9)$ |
$(0.9,0.6)$ |
$(0.6,0.7)$ |
$(0.6,0.7)$ |
|
${A_{3}}$ |
$(0.9,0.6)$ |
$(0.6,0.7)$ |
$(0.8,0.65)$ |
$(0.7,0.8)$ |
$(0.7,0.8)$ |
$(0.9,0.6)$ |
$(0.6,0.9)$ |
$(0.6,0.9)$ |
|
${A_{4}}$ |
$(0.6,0.9)$ |
$(0.75,0.6)$ |
$(0.7,0.8)$ |
$(0.6,0.9)$ |
$(0.6,0.9)$ |
$(0.9,0.6)$ |
$(0.6,0.9)$ |
$(0.6,0.9)$ |
|
${A_{5}}$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.6,0.7)$ |
$(0.6,0.9)$ |
$(0.7,0.8)$ |
$(0.6,0.7)$ |
$(0.75,0.6)$ |
$(0.6,0.7)$ |
| ${E_{4}}$ |
${A_{1}}$ |
$(0.8,0.65)$ |
$(0.9,0.6)$ |
$(0.5,0.5)$ |
$(0.6,0.9)$ |
$(0.6,0.7)$ |
$(0.8,0.65)$ |
$(0.7,0.8)$ |
$(0.6,0.7)$ |
|
${A_{2}}$ |
$(0.9,0.6)$ |
$(0.8,0.65)$ |
$(0.6,0.7)$ |
$(0.6,0.9)$ |
$(0.7,0.8)$ |
$(0.9,0.6)$ |
$(0.6,0.9)$ |
$(0.6,0.9)$ |
|
${A_{3}}$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.7,0.8)$ |
$(0.75,0.6)$ |
$(0.6,0.9)$ |
$(0.7,0.8)$ |
$(0.6,0.9)$ |
$(0.6,0.9)$ |
|
${A_{4}}$ |
$(0.75,0.6)$ |
$(0.8,0.65)$ |
$(0.6,0.7)$ |
$(0.6,0.9)$ |
$(0.6,0.9)$ |
$(0.9,0.6)$ |
$(0.7,0.8)$ |
$(0.6,0.9)$ |
|
${A_{5}}$ |
$(0.9,0.6)$ |
$(0.7,0.8)$ |
$(0.7,0.8)$ |
$(0.7,0.8)$ |
$(0.9,0.6)$ |
$(0.7,0.8)$ |
$(0.9,0.6)$ |
$(0.7,0.8)$ |
| ${E_{5}}$ |
${A_{1}}$ |
$(0.9,0.6)$ |
$(0.75,0.6)$ |
$(0.6,0.7)$ |
$(0.7,0.8)$ |
$(0.7,0.8)$ |
$(0.9,0.6)$ |
$(0.6,0.9)$ |
$(0.7,0.8)$ |
|
${A_{2}}$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.6,0.7)$ |
$(0.6,0.9)$ |
$(0.6,0.7)$ |
$(0.9,0.6)$ |
$(0.7,0.8)$ |
$(0.6,0.9)$ |
|
${A_{3}}$ |
$(0.75,0.6)$ |
$(0.9,0.6)$ |
$(0.6,0.9)$ |
$(0.7,0.8)$ |
$(0.6,0.9)$ |
$(0.9,0.6)$ |
$(0.6,0.9)$ |
$(0.7,0.8)$ |
|
${A_{4}}$ |
$(0.8,0.65)$ |
$(0.9,0.6)$ |
$(0.6,0.7)$ |
$(0.7,0.8)$ |
$(0.7,0.8)$ |
$(0.7,0.8)$ |
$(0.6,0.9)$ |
$(0.6,0.7)$ |
|
${A_{5}}$ |
$(0.9,0.6)$ |
$(0.75,0.6)$ |
$(0.6,0.9)$ |
$(0.6,0.9)$ |
$(0.7,0.8)$ |
$(0.9,0.6)$ |
$(0.7,0.8)$ |
$(0.6,0.9)$ |
Since criteria are classified into cost criteria and benefit criteria in this paper, it is necessary to convert raw data into comparable value by a normalization procedure. During the normalization, cost criteria must be converted into benefit criteria. The mathematical expression of the decision matrix
${R^{l}}={({a_{ij}^{l}})_{m\times n}}$ normalized into
${\tilde{R}^{l}}={({\tilde{a}_{ij}^{l}})_{m\times n}}$ is given below:
The normalized decision matrix is presented in Tables
6.
Step 3: Compute the dynamic DMs’ weights for different alternatives and different criteria.
Table 6
Normalized evaluation values described as FFNs from five DMs.
| DM |
Alternative |
${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
${C_{5}}$ |
${C_{6}}$ |
${C_{7}}$ |
${C_{8}}$ |
| ${E_{1}}$ |
${A_{1}}$ |
$(0.75,0.6)$ |
$(0.6,0.9)$ |
$(0.5,0.5)$ |
$(0.9,0.6)$ |
$(0.8,0.65)$ |
$(0.5,0.5)$ |
$(0.6,0.75)$ |
$(0.65,0.8)$ |
|
${A_{2}}$ |
$(0.6,0.7)$ |
$(0.9,0.6)$ |
$(0.5,0.5)$ |
$(0.75,0.6)$ |
$(0.5,0.5)$ |
$(0.75,0.6)$ |
$(0.6,0.9)$ |
$(0.6,0.75)$ |
|
${A_{3}}$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.6,0.7)$ |
$(0.75,0.6)$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.65,0.8)$ |
|
${A_{4}}$ |
$(0.6,0.7)$ |
$(0.9,0.6)$ |
$(0.75,0.6)$ |
$(0.5,0.5)$ |
$(0.75,0.6)$ |
$(0.6,0.7)$ |
$(0.6,0.75)$ |
$(0.7,0.6)$ |
|
${A_{5}}$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.6,0.7)$ |
$(0.75,0.6)$ |
$(0.98,0.02)$ |
$(0.8,0.65)$ |
$(0.65,0.8)$ |
$(0.6,0.75)$ |
| ${E_{2}}$ |
${A_{1}}$ |
$(0.9,0.6)$ |
$(0.75,0.6)$ |
$(0.6,0.7)$ |
$(0.75,0.6)$ |
$(0.6,0.7)$ |
$(0.75,0.6)$ |
$(0.5,0.5)$ |
$(0.65,0.8)$ |
|
${A_{2}}$ |
$(0.75,0.6)$ |
$(0.8,0.65)$ |
$(0.6,0.7)$ |
$(0.6,0.9)$ |
$(0.6,0.7)$ |
$(0.8,0.65)$ |
$(0.6,0.75)$ |
$(0.5,0.5)$ |
|
${A_{3}}$ |
$(0.8,0.65)$ |
$(0.75,0.6)$ |
$(0.9,0.6)$ |
$(0.6,0.9)$ |
$(0.6,0.9)$ |
$(0.9,0.6)$ |
$(0.6,0.9)$ |
$(0.8,0.7)$ |
|
${A_{4}}$ |
$(0.75,0.6)$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.7,0.8)$ |
$(0.75,0.6)$ |
$(0.75,0.6)$ |
$(0.5,0.5)$ |
$(0.9,0.6)$ |
|
${A_{5}}$ |
$(0.98,0.02)$ |
$(0.7,0.8)$ |
$(0.75,0.6)$ |
$(0.6,0.7)$ |
$(0.6,0.9)$ |
$(0.8,0.65)$ |
$(0.9,0.6)$ |
$(0.5,0.5)$ |
| ${E_{3}}$ |
${A_{1}}$ |
$(0.75,0.6)$ |
$(0.9,0.6)$ |
$(0.5,0.5)$ |
$(0.7,0.8)$ |
$(0.6,0.7)$ |
$(0.75,0.6)$ |
$(0.5,0.5)$ |
$(0.8,0.7)$ |
|
${A_{2}}$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.6,0.7)$ |
$(0.6,0.9)$ |
$(0.6,0.9)$ |
$(0.9,0.6)$ |
$(0.7,0.6)$ |
$(0.7,0.6)$ |
|
${A_{3}}$ |
$(0.9,0.6)$ |
$(0.6,0.7)$ |
$(0.8,0.65)$ |
$(0.7,0.8)$ |
$(0.7,0.8)$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
|
${A_{4}}$ |
$(0.6,0.9)$ |
$(0.75,0.6)$ |
$(0.7,0.8)$ |
$(0.6,0.9)$ |
$(0.6,0.9)$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
|
${A_{5}}$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.6,0.7)$ |
$(0.6,0.9)$ |
$(0.7,0.8)$ |
$(0.6,0.7)$ |
$(0.6,0.75)$ |
$(0.7,0.6)$ |
| ${E_{4}}$ |
${A_{1}}$ |
$(0.8,0.65)$ |
$(0.9,0.6)$ |
$(0.5,0.5)$ |
$(0.6,0.9)$ |
$(0.6,0.7)$ |
$(0.8,0.65)$ |
$(0.8,0.7)$ |
$(0.7,0.6)$ |
|
${A_{2}}$ |
$(0.9,0.6)$ |
$(0.8,0.65)$ |
$(0.6,0.7)$ |
$(0.6,0.9)$ |
$(0.7,0.8)$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
|
${A_{3}}$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.7,0.8)$ |
$(0.75,0.6)$ |
$(0.6,0.9)$ |
$(0.7,0.8)$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
|
${A_{4}}$ |
$(0.75,0.6)$ |
$(0.8,0.65)$ |
$(0.6,0.7)$ |
$(0.6,0.9)$ |
$(0.6,0.9)$ |
$(0.9,0.6)$ |
$(0.8,0.7)$ |
$(0.9,0.6)$ |
|
${A_{5}}$ |
$(0.9,0.6)$ |
$(0.7,0.8)$ |
$(0.7,0.8)$ |
$(0.7,0.8)$ |
$(0.9,0.6)$ |
$(0.7,0.8)$ |
$(0.6,0.9)$ |
$(0.8,0.7)$ |
| ${E_{5}}$ |
${A_{1}}$ |
$(0.9,0.6)$ |
$(0.75,0.6)$ |
$(0.6,0.7)$ |
$(0.7,0.8)$ |
$(0.7,0.8)$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.8,0.7)$ |
|
${A_{2}}$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.6,0.7)$ |
$(0.6,0.9)$ |
$(0.6,0.7)$ |
$(0.9,0.6)$ |
$(0.8,0.7)$ |
$(0.9,0.6)$ |
|
${A_{3}}$ |
$(0.75,0.6)$ |
$(0.9,0.6)$ |
$(0.6,0.9)$ |
$(0.7,0.8)$ |
$(0.6,0.9)$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.8,0.7)$ |
|
${A_{4}}$ |
$(0.8,0.65)$ |
$(0.9,0.6)$ |
$(0.6,0.7)$ |
$(0.7,0.8)$ |
$(0.7,0.8)$ |
$(0.7,0.8)$ |
$(0.9,0.6)$ |
$(0.7,0.6)$ |
|
${A_{5}}$ |
$(0.9,0.6)$ |
$(0.75,0.6)$ |
$(0.6,0.9)$ |
$(0.6,0.9)$ |
$(0.7,0.8)$ |
$(0.9,0.6)$ |
$(0.8,0.7)$ |
$(0.9,0.6)$ |
(i) Determine PIDM and NIDM by using Models (
19)–(
20), respectively. For example, PIDM is presented in Table
7.
| Alternative |
${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
${C_{5}}$ |
${C_{6}}$ |
${C_{7}}$ |
${C_{8}}$ |
| ${A_{1}}$ |
$(0.8,0.6)$ |
$(0.75,0.6)$ |
$(0.5,0.5)$ |
$(0.7,0.8)$ |
$(0.6,0.7)$ |
$(0.75,0.6)$ |
$(0.6,0.6)$ |
$(0.7,0.7)$ |
| ${A_{2}}$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.6,0.7)$ |
$(0.6,0.9)$ |
$(0.6,0.7)$ |
$(0.8,0.6)$ |
$(0.7,0.7)$ |
$(0.7,0.6)$ |
| ${A_{3}}$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.7,0.7)$ |
$(0.7,0.8)$ |
$(0.6,0.9)$ |
$(0.9,0.6)$ |
$(0.9,0.6)$ |
$(0.8,0.7)$ |
| ${A_{4}}$ |
$(0.75.0.65)$ |
$(0.9,0.6)$ |
$(0.7,0.7)$ |
$(0.6,0.8)$ |
$(0.7,0.8)$ |
$(0.75,0.6)$ |
$(0.8,0.6)$ |
$(0.9,0.6)$ |
| ${A_{5}}$ |
$(0.9,0.6)$ |
$(0.75,0.6)$ |
$(0.6,0.7)$ |
$(0.6,0.8)$ |
$(0.7,0.8)$ |
$(0.8,0.65)$ |
$(0.65,0.75)$ |
$(0.7,0.6)$ |
(ii) Calculate credibility degree for DM
${E_{l}}$ based on Eq. (
21), which are shown in Table
8.
Table 8
Credibility degree for ${E_{l}}$.
| DM |
Alternative |
${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
${C_{5}}$ |
${C_{6}}$ |
${C_{7}}$ |
${C_{8}}$ |
| ${E_{1}}$ |
${A_{1}}$ |
0.1954 |
0.4824 |
0.0241 |
0.5199 |
0.3817 |
0.0738 |
0.1558 |
0.2778 |
|
${A_{2}}$ |
0.0257 |
0.5892 |
0.0302 |
0.0977 |
0.0302 |
0.1954 |
0.3950 |
0.1975 |
|
${A_{3}}$ |
0.5892 |
0.5892 |
0.1237 |
0.1765 |
0.5892 |
0.5892 |
0.5892 |
0.3144 |
|
${A_{4}}$ |
0.1329 |
0.5892 |
0.1755 |
0.1413 |
0.1765 |
0.1361 |
0.1954 |
0.0257 |
|
${A_{5}}$ |
0.1002 |
0.4824 |
0.1431 |
0.1954 |
0.5948 |
0.3200 |
0.3105 |
0.1975 |
| ${E_{2}}$ |
${A_{1}}$ |
0.5357 |
0.2045 |
0.0889 |
0.1765 |
0.1431 |
0.2045 |
0.0097 |
0.2778 |
|
${A_{2}}$ |
0.0977 |
0.2641 |
0.1431 |
0.5892 |
0.1431 |
0.3161 |
0.1755 |
0.0302 |
|
${A_{3}}$ |
0.2641 |
0.0977 |
0.3950 |
0.5199 |
0.5892 |
0.5892 |
0.5892 |
0.3630 |
|
${A_{4}}$ |
0.2006 |
0.5892 |
0.3950 |
0.3439 |
0.1765 |
0.2045 |
0.1413 |
0.5892 |
|
${A_{5}}$ |
0.0733 |
0.3350 |
0.1975 |
0.1109 |
0.5199 |
0.3200 |
0.4783 |
0.0302 |
| ${E_{3}}$ |
${A_{1}}$ |
0.1954 |
0.4824 |
0.0241 |
0.3630 |
0.1431 |
0.2045 |
0.0097 |
0.3272 |
|
${A_{2}}$ |
0.5892 |
0.5892 |
0.1431 |
0.5892 |
0.4204 |
0.5357 |
0.1237 |
0.1431 |
|
${A_{3}}$ |
0.5892 |
0.0257 |
0.2778 |
0.3630 |
0.2937 |
0.5892 |
0.5892 |
0.5199 |
|
${A_{4}}$ |
0.4783 |
0.0977 |
0.3272 |
0.5357 |
0.5199 |
0.4824 |
0.5357 |
0.5892 |
|
${A_{5}}$ |
0.1002 |
0.4824 |
0.1431 |
0.5357 |
0.3630 |
0.1075 |
0.2006 |
0.1431 |
| ${E_{4}}$ |
${A_{1}}$ |
0.3161 |
0.4732 |
0.0241 |
0.5199 |
0.1431 |
0.3070 |
0.2481 |
0.1237 |
|
${A_{2}}$ |
0.5892 |
0.2641 |
0.1431 |
0.5892 |
0.3128 |
0.5357 |
0.3950 |
0.4204 |
|
${A_{3}}$ |
0.5892 |
0.5892 |
0.3272 |
0.1765 |
0.5892 |
0.2937 |
0.5892 |
0.5199 |
|
${A_{4}}$ |
0.2006 |
0.2641 |
0.1237 |
0.5357 |
0.5199 |
0.4824 |
0.3439 |
0.5892 |
|
${A_{5}}$ |
0.1002 |
0.3350 |
0.3128 |
0.3439 |
0.5199 |
0.3574 |
0.4783 |
0.3128 |
| ${E_{5}}$ |
${A_{1}}$ |
0.5357 |
0.2045 |
0.0889 |
0.3630 |
0.3128 |
0.4824 |
0.2894 |
0.3272 |
|
${A_{2}}$ |
0.5892 |
0.5892 |
0.1431 |
0.5892 |
0.1431 |
0.5357 |
0.3272 |
0.4204 |
|
${A_{3}}$ |
0.0977 |
0.5892 |
0.3950 |
0.3630 |
0.5892 |
0.5892 |
0.5892 |
0.3630 |
|
${A_{4}}$ |
0.3105 |
0.5892 |
0.1237 |
0.3439 |
0.3630 |
0.3350 |
0.5357 |
0.0257 |
|
${A_{5}}$ |
0.1002 |
0.2045 |
0.4204 |
0.5357 |
0.3630 |
0.5333 |
0.3479 |
0.4204 |
(iii) Calculate the dynamic weights of DMs using Eq. (
22). The obtained dynamic DMs’ weights for different alternatives and criteria are shown in Table
9.
Step 4: Aggregate all individual normalized Fermatean Fuzzy decision matrices
${\tilde{R}^{l}}={({\tilde{a}_{ij}^{l}})_{5\times 8}}$ (
$l=1,2,3,4,5$) into a collective one
${\hat{R}^{l}}={({\hat{a}_{ij}^{l}})_{5\times 8}}$ by Eq. (
23), which is shown in Table
10.
Table 9
Dynamic weights for ${E_{l}}$.
| DM |
Alternative |
${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
${C_{5}}$ |
${C_{6}}$ |
${C_{7}}$ |
${C_{8}}$ |
| ${E_{1}}$ |
${A_{1}}$ |
0.1099 |
0.2612 |
0.0963 |
0.2677 |
0.3396 |
0.0580 |
0.2187 |
0.2083 |
|
${A_{2}}$ |
0.0136 |
0.2567 |
0.0501 |
0.0398 |
0.0287 |
0.0922 |
0.2789 |
0.1630 |
|
${A_{3}}$ |
0.2767 |
0.3116 |
0.0815 |
0.1104 |
0.2223 |
0.2223 |
0.2000 |
0.1511 |
|
${A_{4}}$ |
0.1005 |
0.2767 |
0.1532 |
0.0743 |
0.1005 |
0.0830 |
0.1115 |
0.0141 |
|
${A_{5}}$ |
0.2113 |
0.2623 |
0.1176 |
0.1135 |
0.2520 |
0.1954 |
0.1710 |
0.1789 |
| ${E_{2}}$ |
${A_{1}}$ |
0.3013 |
0.1107 |
0.3555 |
0.0909 |
0.1274 |
0.1608 |
0.0136 |
0.2083 |
|
${A_{2}}$ |
0.0516 |
0.1150 |
0.2375 |
0.2401 |
0.1364 |
0.1492 |
0.1239 |
0.0249 |
|
${A_{3}}$ |
0.1240 |
0.0516 |
0.2601 |
0.3252 |
0.2223 |
0.2223 |
0.2000 |
0.1745 |
|
${A_{4}}$ |
0.1516 |
0.2767 |
0.3449 |
0.1810 |
0.1005 |
0.1247 |
0.0806 |
0.3239 |
|
${A_{5}}$ |
0.1547 |
0.1821 |
0.1623 |
0.0644 |
0.2202 |
0.1954 |
0.2635 |
0.0273 |
| ${E_{3}}$ |
${A_{1}}$ |
0.1099 |
0.2612 |
0.0963 |
0.1869 |
0.1274 |
0.1608 |
0.0136 |
0.2453 |
|
${A_{2}}$ |
0.3116 |
0.2567 |
0.2375 |
0.2401 |
0.4005 |
0.2529 |
0.0874 |
0.1181 |
|
${A_{3}}$ |
0.2767 |
0.0136 |
0.1829 |
0.2270 |
0.1108 |
0.2223 |
0.2000 |
0.2499 |
|
${A_{4}}$ |
0.3616 |
0.0459 |
0.2857 |
0.2819 |
0.2961 |
0.2941 |
0.3058 |
0.3239 |
|
${A_{5}}$ |
0.2113 |
0.2623 |
0.1176 |
0.3112 |
0.1538 |
0.0656 |
0.1105 |
0.1296 |
| ${E_{4}}$ |
${A_{1}}$ |
0.1777 |
0.2562 |
0.0963 |
0.2677 |
0.1274 |
0.2413 |
0.3481 |
0.0928 |
|
${A_{2}}$ |
0.3116 |
0.1150 |
0.2375 |
0.2401 |
0.2980 |
0.2529 |
0.2789 |
0.3470 |
|
${A_{3}}$ |
0.2767 |
0.3116 |
0.2155 |
0.1104 |
0.2223 |
0.1108 |
0.2000 |
0.2499 |
|
${A_{4}}$ |
0.1516 |
0.1240 |
0.1080 |
0.2819 |
0.2961 |
0.2941 |
0.1963 |
0.3239 |
|
${A_{5}}$ |
0.2113 |
0.1821 |
0.2570 |
0.1998 |
0.2202 |
0.2181 |
0.2635 |
0.2833 |
| ${E_{5}}$ |
${A_{1}}$ |
0.3013 |
0.1107 |
0.3555 |
0.1869 |
0.2783 |
0.3791 |
0.4061 |
0.2453 |
|
${A_{2}}$ |
0.3116 |
0.2567 |
0.2375 |
0.2401 |
0.1364 |
0.2529 |
0.2310 |
0.3470 |
|
${A_{3}}$ |
0.0459 |
0.3116 |
0.2601 |
0.2270 |
0.2223 |
0.2223 |
0.2000 |
0.1745 |
|
${A_{4}}$ |
0.2347 |
0.2767 |
0.1080 |
0.1810 |
0.2067 |
0.2042 |
0.3058 |
0.0141 |
|
${A_{5}}$ |
0.2113 |
0.1112 |
0.3455 |
0.3112 |
0.1538 |
0.3255 |
0.1916 |
0.3808 |
Step 5: Compute the optimal weights of criteria.
Table 10
Collective Fermatean Fuzzy decision matrix.
| Criteria |
${A_{1}}$ |
${A_{2}}$ |
${A_{3}}$ |
${A_{4}}$ |
${A_{5}}$ |
| ${C_{1}}$ |
$(0.8493,0.6089)$ |
$(0.8882,0.6014)$ |
$(0.8807,0.6062)$ |
$(0.6924,0.7303)$ |
$(0.9124,0.5103)$ |
| ${C_{2}}$ |
$(0.7884,0.6784)$ |
$(0.8770,0.6115)$ |
$(0.8882,0.6014)$ |
$(0.8807,0.6062)$ |
$(0.8105,0.6729)$ |
| ${C_{3}}$ |
$(0.5711,0.6422)$ |
$(0.5950,0.6900)$ |
$(0.7362,0.7384)$ |
$(0.7550,0.6788)$ |
$(0.6500,0.7786)$ |
| ${C_{4}}$ |
$(0.7313,0.7551)$ |
$(0.6060,0.8881)$ |
$(0.6785,0.7884)$ |
$(0.6288,0.8341)$ |
$(0.6370,0.8831)$ |
| ${C_{5}}$ |
$(0.6958,0.6981)$ |
$(0.6269,0.8042)$ |
$(0.6778,0.8222)$ |
$(0.6508,0.8190)$ |
$(0.7926,0.5815)$ |
| ${C_{6}}$ |
$(0.8044,0.6063)$ |
$(0.8712,0.6075)$ |
$(0.8778,0.6222)$ |
$(0.8156,0.6491)$ |
$(0.7976,0.6697)$ |
| ${C_{7}}$ |
$(0.7887,0.6649)$ |
$(0.7386,0.7253)$ |
$(0.8400,0.6600)$ |
$(0.8147,0.6283)$ |
$(0.7259,0.7490)$ |
| ${C_{8}}$ |
$(0.7282,0.7324)$ |
$(0.8175,0.6220)$ |
$(0.8273,0.6651)$ |
$(0.8944,0.6000)$ |
$(0.7811,0.6524)$ |
(1) Determine the FF-PIP
${\hat{a}_{j+}}$ and the FF-NIP
${\hat{a}_{j-}}$ using Eqs. (
24) and (
25), where
$j=1,2,\dots ,8$. We have
(2) Compute the distances between
${\hat{a}_{ij}}$ and FF-PIP
${\hat{a}_{j+}}$ as well as FF-NIP
${\hat{a}_{j-}}$ by Eqs. (
26) and (
27), respectively. The computation results are represented in Tables
11–
12.
Table 11
Distance between ${\hat{a}_{ij}}$ and ${\hat{a}_{j+}}$.
| Alternatives |
${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
${C_{5}}$ |
${C_{6}}$ |
${C_{7}}$ |
${C_{8}}$ |
| ${A_{1}}$ |
0.0609 |
0.1063 |
0.1359 |
0.0000 |
0.0876 |
0.0992 |
0.0637 |
0.1603 |
| ${A_{2}}$ |
0.0537 |
0.0149 |
0.1121 |
0.1290 |
0.1640 |
0.0107 |
0.0917 |
0.1052 |
| ${A_{3}}$ |
0.0550 |
0.0000 |
0.0755 |
0.0385 |
0.1780 |
0.0164 |
0.0000 |
0.0767 |
| ${A_{4}}$ |
0.2037 |
0.0112 |
0.0296 |
0.0769 |
0.1726 |
0.0696 |
0.0579 |
0.0000 |
| ${A_{5}}$ |
0.0000 |
0.0840 |
0.1034 |
0.0734 |
0.0000 |
0.0839 |
0.0988 |
0.1326 |
Table 12
Distance between ${\hat{a}_{ij}}$ and ${\hat{a}_{j-}}$.
| Alternatives |
${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
${C_{5}}$ |
${C_{6}}$ |
${C_{7}}$ |
${C_{8}}$ |
| ${A_{1}}$ |
0.1319 |
0.0000 |
0.1081 |
0.1290 |
0.1025 |
0.0477 |
0.0537 |
0.0000 |
| ${A_{2}}$ |
0.1797 |
0.0918 |
0.0700 |
0.0000 |
0.0212 |
0.0746 |
0.0110 |
0.0838 |
| ${A_{3}}$ |
0.1698 |
0.1063 |
0.1156 |
0.1080 |
0.0471 |
0.0906 |
0.1022 |
0.0853 |
| ${A_{4}}$ |
0.0000 |
0.0958 |
0.1250 |
0.0732 |
0.0183 |
0.0169 |
0.0797 |
0.1603 |
| ${A_{5}}$ |
0.2037 |
0.0238 |
0.0573 |
0.0707 |
0.1770 |
0.0000 |
0.0212 |
0.0577 |
(3) The grey relation coefficients with reference to
${\hat{a}_{j+}}$ and
${\hat{a}_{j-}}$ can be computed using Eqs. (
28) and (
29), respectively. The computation results are represented in Tables
13–
14.
Table 13
Grey relation coefficients with reference to ${\hat{a}_{j+}}$.
| Alternative |
${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
${C_{5}}$ |
${C_{6}}$ |
${C_{7}}$ |
${C_{8}}$ |
| ${A_{1}}$ |
0.6258 |
0.4893 |
0.4284 |
1.0000 |
0.5376 |
0.5376 |
0.6152 |
0.3885 |
| ${A_{2}}$ |
0.6548 |
0.8724 |
0.4760 |
0.4412 |
0.3831 |
0.5066 |
0.5262 |
0.4919 |
| ${A_{3}}$ |
0.6493 |
1.0000 |
0.5743 |
0.7257 |
0.3639 |
0.9049 |
1.0000 |
0.5704 |
| ${A_{4}}$ |
0.3333 |
0.9009 |
0.7748 |
0.5698 |
0.3711 |
0.8613 |
0.6376 |
1.0000 |
| ${A_{5}}$ |
1.0000 |
0.5480 |
0.4962 |
0.5812 |
1.0000 |
0.5941 |
0.5076 |
0.4344 |
Table 14
Grey relation coefficients with reference to ${\hat{a}_{j-}}$.
| Alternative |
${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
${C_{5}}$ |
${C_{6}}$ |
${C_{7}}$ |
${C_{8}}$ |
| ${A_{1}}$ |
0.4357 |
1.0000 |
0.4851 |
0.4412 |
0.4984 |
0.6810 |
0.6548 |
1.0000 |
| ${A_{2}}$ |
0.3617 |
0.5259 |
0.5927 |
1.0000 |
0.8277 |
0.5772 |
0.9025 |
0.5486 |
| ${A_{3}}$ |
0.3749 |
0.4893 |
0.4684 |
0.4853 |
0.6838 |
0.5292 |
0.4991 |
0.5442 |
| ${A_{4}}$ |
1.0000 |
0.5153 |
0.4490 |
0.5818 |
0.8477 |
0.8577 |
0.5610 |
0.3885 |
| ${A_{5}}$ |
0.3333 |
0.8106 |
0.6400 |
0.5903 |
0.3653 |
1.0000 |
0.8277 |
0.6384 |
(3) Calculate PIWV and NIWV by model (
M-2) and Eq. (
32). Alternative
${A_{1}}$ is provided as a presentative example, and the results are shown as
${\boldsymbol{w}^{1+}}={(0.20,0.13,0.10,0.12,0.15,0.16,0.06,0.08)^{T}}$,
${\boldsymbol{w}^{1-}}={(0.20,0.13,0.10,0.12,0.15,0.16,0.04,0.10)^{T}}$.
(4) Obtain optimal criteria weights by model (
M-4). We get the following optimal criteria weights:
Step 6: Construct the concordance and discordance sets.
The outranking relationships of all binary alternatives with respect to different criteria can be obtained based on Definition
15. Combining the outranking relationships and Eqs. (
37)–(
42), the concordance and discordance sets can be determined. The strong, medium and weak concordance sets are determined using Eqs. (
37), (
38) and (
39), respectively. The strong, medium and weak discordance sets are determined using Eqs. (
40), (
41) and (
42), respectively. The results are shown as follows:
here,
ϕ is an empty set.
Step 7: Compute the weights of the concordance sets and the discordance sets.
The weights of the strong, medium, and weak concordance sets are computed using Eqs. (
43), (
44), and (
45), respectively. The results are
${w_{C}}=0.5377$,
${w_{{C^{\prime }}}}=0.3228$, and
${w_{{C^{\prime\prime }}}}=0.1395$. The weights of the strong, medium, and weak discordance sets are computed by Eqs. (
46), (
47), and (
48), respectively. The results are
${w_{D}}=0.5187$,
${w_{{D^{\prime }}}}=0.3114$, and
${w_{{D^{\prime\prime }}}}=0.1699$.
Step 8: Establish the concordance and discordance matrices.
The concordance indices and the discordance indices can be computed based on Eqs. (
49) and (
50), respectively. Afterwards, the concordance matrix and the discordance matrix are generated as follows, respectively.
Step 9: Compute the net superiority index and the net inferiority index.
Using Eqs. (
51) and (
52), the net superiority index and the net inferiority index are obtained as follows:
${\textit{NS}_{1}}=1.7810$,
${\textit{NS}_{2}}=1.9319$,
${\textit{NS}_{3}}=2.8204$,
${\textit{NS}_{4}}=2.2293$,
${\textit{NS}_{5}}=2.2213$;
${\textit{NI}_{1}}=2.5699$,
${\textit{NI}_{2}}=2.0925$,
${\textit{NI}_{3}}=1.1801$,
${\textit{NI}_{4}}=2.9030$,
${\textit{NI}_{5}}=2.2383$.
Step 10: Compute the overall evaluation indices for all alternatives.
The overall evaluation indices for all alternatives can be computed based on Eq. (
53). The results are
${Z_{1}}=-0.7889$,
${Z_{2}}=-0.1606$,
${Z_{3}}=1.6403$,
${Z_{4}}=-0.6738$,
${Z_{5}}=-0.0170$.
Step 11: Get the ranking order of all alternatives and choose the optimal one.
The ranking order of the five alternatives is
${A_{3}}\succ {A_{5}}\succ {A_{2}}\succ {A_{4}}\succ {A_{1}}$. Thus, the optimal alternative is
${A_{3}}$ in accordance with Eq. (
54).
6.3 Comparative Analysis and Discussion
In this section, comparisons are conducted to further demonstrate the superiority and effectiveness of the proposed ELECTRE method.
6.3.1 Comparison with IFS and PFS Environments Using the Proposed ELECTRE Method
The decision-making results of the proposed FFS ELECTRE method are compared with those obtained by the IFS ELECTRE method and PFS ELECTRE method with the identical original assessment data of the criteria in Table
4. The performance ratings of each alternative on each criterion given by DMs in terms of linguistic variables under IFS and PFS environments and mapping relations transformed linguistic terms into IFNs and PFNs are shown in Table
3. The decision-making results derived by the proposed ELECTRE method under different decision environments are shown in Table
15, in which the numbers in brackets are comprehensive evaluation indices for alternatives. Moreover, Fig.
4 presents the ranking orders of alternatives under different decision context.
Table 15
Rankingorder of alternatives under different decision environments.
| Decision information |
Ranking order of alternatives |
Dominance |
| IFS |
${A_{5}}(1.8780)\succ {A_{1}}(0.7190)\succ {A_{3}}(-0.1380)\succ {A_{2}}(-0.5066)\succ {A_{4}}(-1.9524)$ |
0.3026 |
| PFS |
${A_{5}}(1.5627)\succ {A_{3}}(0.6484)\succ {A_{2}}(-0.3323)\succ {A_{1}}(-0.6740)\succ {A_{4}}(-1.2048)$ |
0.3304 |
| FFS |
${A_{3}}(1.6403)\succ {A_{5}}(-0.0170)\succ {A_{2}}(-0.1606)\succ {A_{4}}(-0.6738)\succ {A_{1}}(-0.7889)$ |
0.6822 |
Fig. 4
Alternatives ranking orders under different ELECTRE methods.
As shown in Table
15 and Fig.
4, the final ranking orders of alternatives have distinct differences between the three methods. For example,
${A_{5}}$ ranks first under the IFS ELECTRE method and PFS ELECTRE method, while
${A_{3}}$ ranking first with the proposed FFS ELECTRE method. This is in line with the actual situation. In addition,
${A_{3}}$,
${A_{5}}$ and
${A_{2}}$ rank in the top three among all of site selections using the proposed FFS ELECTRE method, and are the site of the first three FSHs (see
http://www.xinhuanet.com/local/2020-02/05/c_1125536024.htm?baike), indicating the effectiveness of the proposed ELECTRE method. Compared with IFS ELECTRE method and PFS ELECTRE method, the prominent characteristics of the proposed FFS ELECTRE method are as follows.
(1) The proposed method can obtain decision-making result according with the actual situation. The optimal alternative obtained by the proposed ELECTRE method is
${A_{3}}$. Jianghan FSH, which is the first FSH in Wuhan to use and treat patients, is exactly located in Wuhan International Conference and Exhibition Center
${A_{3}}$ (see
http://www.xinhuanet.com/local/2020-02/05/c_1125536024.htm?baike).
(2) The proposed method can easily discriminate the best alternative. The dominance of the ranking first alternative is the difference between the normalized comprehensive evaluation scores of ranking first and ranking second alternatives. In order to get the dominance of the ranking first alternative, the comprehensive evaluation score of each alternative is standardized by
${\bar{Z}_{i}}=({Z_{i}}-{\min _{i}}{Z_{i}})/({\max _{i}}{Z_{i}}-{\min _{i}}{Z_{i}})$. Take the proposed ELECTRE method as an example, the comprehensive evaluation scores of
${A_{3}}$ and
${A_{5}}$ are standardized as
${\bar{Z}_{3}}=(1.6403-(-0.7889))/(1.6403-(-0.7889))=1$ and
${\bar{Z}_{5}}=((-0.0170)-(-0.7889))/(1.6403-(-0.7889))=0.3178$. The dominance degree of the ranking first alternative over second alternative is computed as
$|{\bar{Z}_{3}}-{\bar{Z}_{5}}|=0.6822$. Analogously, the dominance degrees of the ranking first alternative under other fuzzy environments are computed and shown in the third column of Table
15. As shown in Table
15, the dominance degree of the ranking first alternative using the FFS ELECTRE method is significantly higher than those obtained by IFS ELECTRE method and PFS ELECTRE method. Thus, the FFS ELECTRE method outperforms the IFS ELECTRE method and PFS method in discriminating the best alternative.
(3) The proposed method allows the DMs to express their opinions more freely. Compared with IFS and PFS, FFS provides a broader scope for preference elicitation.
6.3.2 Comparison with Other Existing Methods
To certificate the superiority and effectiveness of the proposed ELECTRE method, a comparative analysis is conducted with some existing methods, including the Fermatean fuzzy TOPSIS method (Senapati and Yager,
2019c) and Fermatean fuzzy MABAC method (Wang
et al.,
2020). The ranking orders obtained by two comparative methods and the proposed ELECTRE method are revealed in Fig.
5.
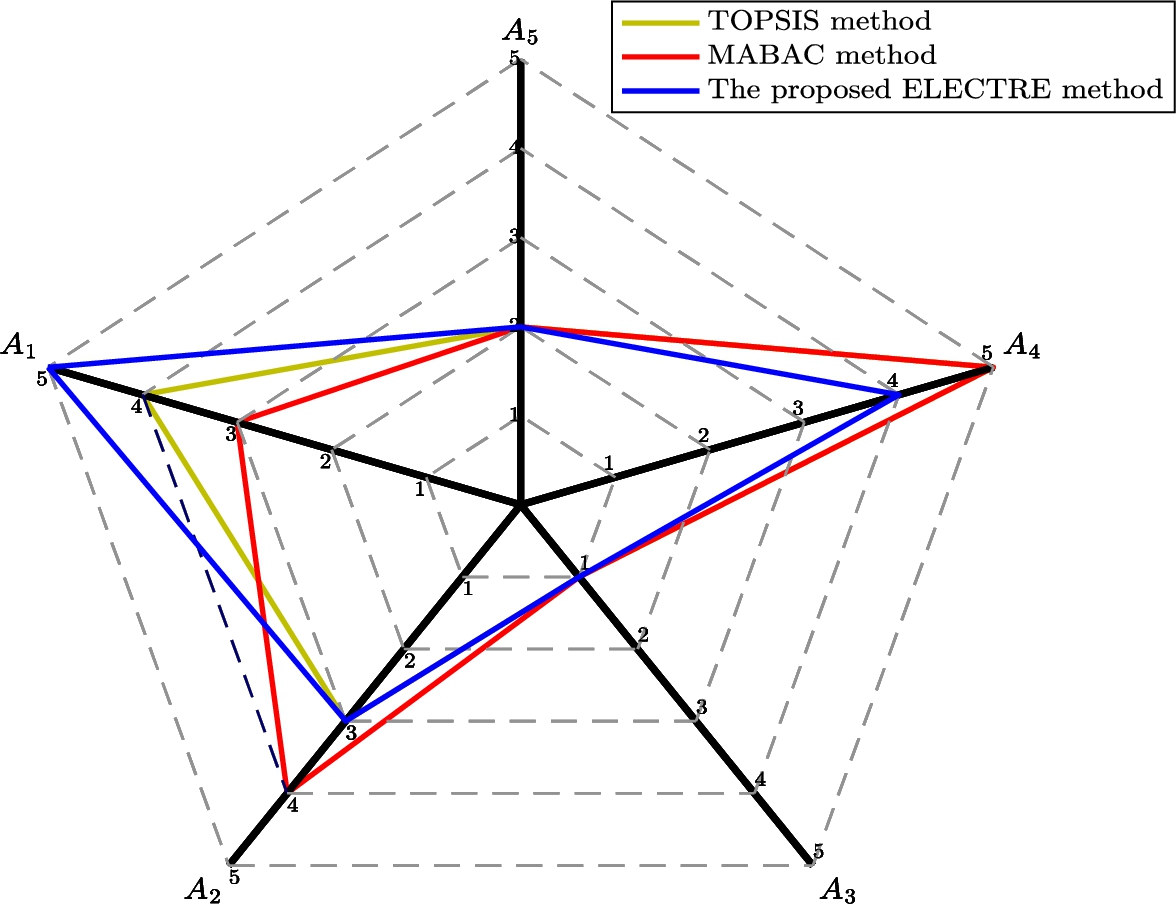
Fig. 5
Ranking orders of alternatives obtained by using different ELECTRE methods.
The proposed method is superior to other two comparative methods in the following aspects:
(1) Superiority in obtaining more convincing and reasonable ranking orders of alternatives. As can been seen from Fig.
5,
${A_{3}}$ is the optimal site selection based on the proposed ELECTRE method and the two comparative methods. Therefore, it justifies the effectiveness of the proposed ELECTRE method for FSHs site selection. As shown in Fig.
5, the primary difference in the ranking sequences is between
${A_{1}}$ and
${A_{4}}$. In the proposed ELECTRE method,
${A_{4}}$ is better than
${A_{1}}$, while
${A_{1}}$ is better than
${A_{4}}$ based on the TOPSIS method and the MABAC method. These different rank results can illustrate the superiority of the proposed method in this paper. The TOPSIS method and the MABAC method assume that the final ranking will be completely compensated among different criteria, that is, a very good value on a criterion can be balanced by bad values on other criteria. Therefore, this unavoidably brings about information loss. But the proposed ELECTRE method based on non-compensation principle among criteria can overcome the aforementioned drawbacks, because it determines the ranking order of alternatives by comparing the advantages of each two criteria values, which offsets the compensate effect among different criteria, thus obtaining a reasonable ranking result. It can be seen from Table
10,
${A_{4}}$ is much better than
${A_{1}}$ on the criteria
${C_{2}}$,
${C_{3}}$,
${C_{6}}$,
${C_{7}}$ and
${C_{8}}$, but these advantages are balanced by other criteria such that the final ranking is
${A_{1}}\succ {A_{4}}$ in the TOPSIS method and the MABAC method due to compensation problem. In fact, criteria may be non-compensatory in site selection of FSHs. For example, low reconstruction cost cannot compensate for traffic inconvenience, poor environmental protection, poor geographical position, imperfect infrastructure, regional communication inconvenience, limited capacity, reconstruction difficulty. Obviously,
${A_{4}}\succ {A_{1}}$ obtained by the proposed ELECTRE method is more reasonable than that given by the TOPSIS method and the MABAC method. Therefore, the ranking order obtained by the proposed method is more convincing and reasonable.
Table 16
Number of times an alternative is assigned to different ranks (${P_{ik}}$).
| Alternatives |
Rank |
| 1 |
2 |
3 |
4 |
5 |
| ${A_{1}}$ |
0 |
0 |
1 |
1 |
1 |
| ${A_{2}}$ |
0 |
0 |
2 |
1 |
0 |
| ${A_{3}}$ |
3 |
0 |
0 |
0 |
0 |
| ${A_{4}}$ |
0 |
0 |
0 |
1 |
2 |
| ${A_{5}}$ |
0 |
3 |
0 |
0 |
0 |
(2) Superiority in obtaining the optimal ranking order. To validate the superiority of the proposed ELECTRE method, we adopt an aggregation technique (Jahan
et al.,
2011) to find out the optimal ranking order from the TOPSIS method, the MABAC method and the proposed ELECTRE method. First,
${P_{ik}}$ is computed, which represents the number of times alternative
${A_{i}}$ is assigned to the
kth ranking, shown in Table
16. For example,
${A_{2}}$ has twice a ranking of 3 and once a ranking of 4. Then, the values of
${T_{ik}}$ are computed.
${T_{ik}}$ is
${P_{ik}}+{T_{i,k-1}}i$,
$k=1,2,\dots ,m$ and
${T_{i,0}}=0$, shown in Table
17. Finally, to find the optimal ranking order, a linear programming model is constructed as follows:
where
${N_{ik}}=1$ if the
$k\mathrm{th}$ rank assign to alternative
${A_{i}}$ and
${N_{ik}}=0$ otherwise. MATLAB software is used to solve this linear programming problem. By solving this linear programming model, the optimal ranking order is derived as
${A_{3}}\succ {A_{5}}\succ {A_{2}}\succ {A_{4}}\succ {A_{1}}$. For illustration, all ranking orders obtained by the aggregation technique, TOPSIS method, MABAC method and the proposed ELECTRE method are shown in Fig.
6. It is easy to see that the optimal ranking order is identical with the ranking order of the proposed ELECTRE method. This means the proposed ELECTRE method is better than other two methods in dealing with the FSHs site selection problem.
Table 17
Values of ${T_{ik}}$.
| Alternative |
Rank |
| 1 |
2 |
3 |
4 |
5 |
| ${A_{1}}$ |
0 |
0 |
1 |
2 |
3 |
| ${A_{2}}$ |
0 |
0 |
2 |
3 |
3 |
| ${A_{3}}$ |
3 |
3 |
3 |
3 |
3 |
| ${A_{4}}$ |
0 |
0 |
0 |
1 |
3 |
| ${A_{5}}$ |
0 |
3 |
3 |
3 |
3 |
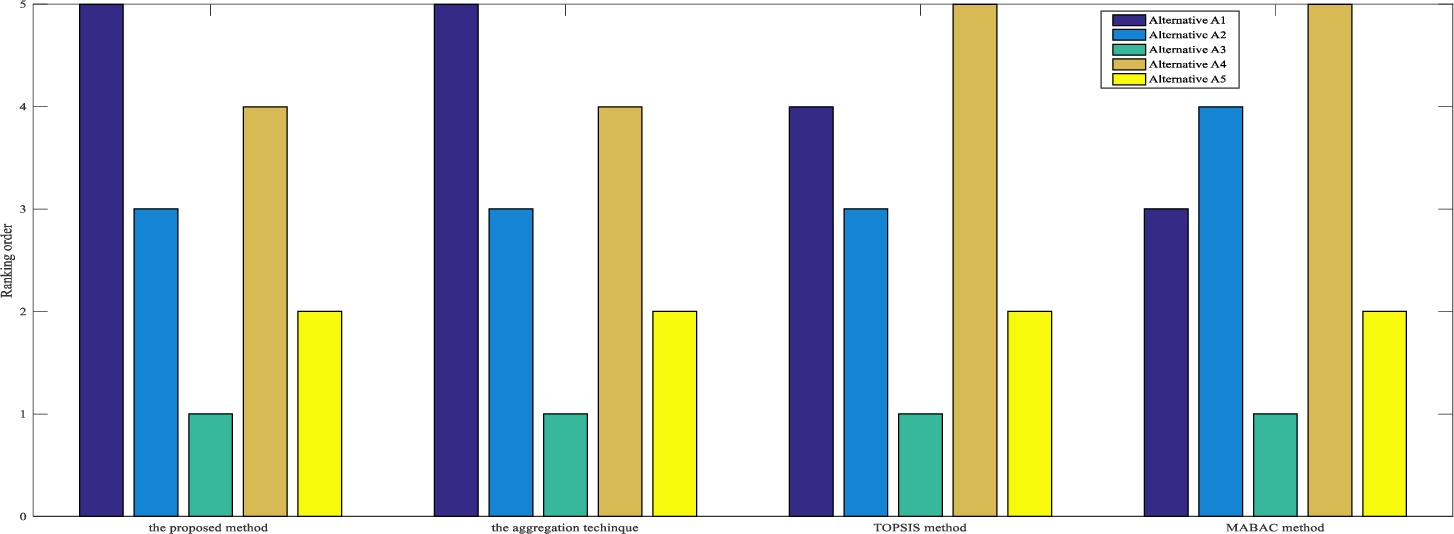
Fig. 6
Ranking results of different methods.
7 Conclusion
This paper proposed an ELECTRE method aimed to solve MCGDM problems with completely unknown DMs’ weights and incomplete criteria weights under Fermatean fuzzy environment. These are advantages of the proposed method. First, the proposed method can determine dynamic and objective DMs’ weights based on the credibility degrees of each DM, which is measured by the proposed cross entropy. Second, the proposed method not only determines the weights of the criteria, but also obtains the weights of the concordance set and discordance set. As a result, the proposed ELECTRE method can make the decision-making result more accurate compared with the existing ELECTRE methods which only give the weight of criteria and concordance set and discordance set in advance. Third, the proposed method is suitable for complex MCGDM problem with non-compensatory criteria.
Although the proposed method can effectively deal with Fermatean fuzzy MCGDM problems, there still exist some limitations. Firstly, the main limitation of the proposed method is inability to capture a discrete decision-making problem with non-commensurable and conflicting criteria. Secondly, it determines the objective weights of criteria, but it hardly obtains the weights when the interactions among the criteria exist. Thirdly, only two information measures for FFSs are taken into consideration in this study. The future work can be extended as follows. The VIKOR method is to be extended into Fermatean fuzzy MCGDM problems, due to its advantage of treating decision-making with non-commensurable and conflicting criteria. A new MCGDM method will be proposed by integrating ELECTRE and Fermatean fuzzy DEMATEL technique which considers the impacts of interactions among the criteria. Some information measures for FFSs including similarity measure, entropy measure and correlation measure will be defined.

