In this paper, the Best-Worst method is applied for determining the criteria weights using the mean of the expert opinions via taking advantage of pairwise comparison from best to worst. This method has been preferred for reasons such as making less and more consistent comparisons, being able to be used with other methods to be used for sorting, and not having to deal with fractional numbers. On the other hand, the choice of CNC machine tool is one of the decision problems that require a very high investment. For this reason, alternatives and decisions can be compared by using more than one method rather than a single method for ranking the alternatives. As for the choice of alternatives, GRA is selected with reference series, COPRAS is also selected to evaluate the performance of each alternative, taking into account the contradictory situations, and MULTIMOORA is preferred to apply dominance solution in terms of the subordinate ranking methods for this study. These alternative selection methods are used with the determined criteria weights from the Best-Worst method. Consequently, the whole solution procedure is designed for the proper decision-making process on the CNC selection research problem.
3.2.1 Best-Worst Method
The method proposed by Rezaei (
2015) is a multi-criteria decision-making method based on pairwise comparison. In areas such as supplier selection (Rezaei
et al.,
2016), assessment of the social sustainability of supply chains (Ahmadi
et al.,
2017), evaluation of service quality in the aviation industry (Gupta,
2018), and evaluation of companies’ RandD performance (Salimi and Rezaei,
2018) applications have been made. The steps of the method are presented below (Kheybari
et al.,
2019).
Step 1: Evaluation criteria $[{c_{1}},{c_{2}},\dots ,{c_{n}}]$ are determined.
Step 2: The best (most important) and the worst (least important) criteria are determined.
Step 3: A pairwise comparison is made between the best criterion and other criteria using a scale of 1-9 and the BO vector ${A_{B}}=({a_{B1}},{a_{B2}},\dots ,{a_{Bj}},\dots ,{a_{Bn}})$ is obtained. (Here 1 means equally important, 9 means much more important.)
Step 4: A binary comparison is made between the other criteria and the worst criterion, again using the scale 1–9, and the OW vector (${A_{w}}=({a_{1w}},{a_{2w}},\dots ,{a_{jw}},\dots ,{a_{nw}})$) is obtained.
Step 5: Optimal weights (${w_{1}^{\ast }},{w_{2}^{\ast }},\dots ,{w_{n}^{\ast }}$) are calculated for each criterion.
Here, the status
$\frac{{w_{B}}}{{w_{j}}}={a_{Bj}}$ and
$\frac{{w_{j}}}{{w_{w}}}={a_{jw}}$ must be provided for each pair of
${w_{B}}/{w_{j}}$ and
${w_{j}}/{w_{jw}}$. The following mathematical model has been created to minimize the maximum differences (
$|\frac{{w_{B}}}{{w_{j}}}-{a_{Bj}}|$ and
$|\frac{{w_{j}}}{{w_{w}}}-{a_{jw}}|$) for all
j’s.
Then the expressions here are converted into the mathematical model shown below:
With the solving of the model, the value of the optimal weights is obtained that is the criterion that shows how consistent the evaluations are. If this value is close to zero, it means that a consistent evaluation has been made.
3.2.2 Grey Relational Analysis (GRA)
An essential approach of the grey system theory (GST) used in the decision-making process and measuring the changes of similarities and differences between its factors over time is called Grey Relational Analysis (GRA) (Feng and Wang,
2000; Aydemir
et al.,
2013). This method is used in the elimination and analysis of ambiguous relationships between criteria and options, examination of integrated circuit marking process (Jiang
et al.,
2002), restoration planning of power distribution systems (Chen
et al.,
2005), recruitment decisions (Olson and Wu,
2006), damage assessment (He and Hwang,
2007), a causal decision-making model (Tseng,
2009), determination of critical path through a network (Zhongmin and Xizu,
2009), supplier selection (Yang and Chen,
2006; Özdemir and Deste,
2009; Zavadskas
et al.,
2010; Hashemi
et al.,
2015; Cakir and Akel,
2017), stock market forecasts and portfolio selection (Huang and Jane,
2009), optimization of turning parameters (Yilmaz and Gungor,
2010; Ramesh
et al.,
2016; Prakash
et al.,
2020; Lakshmanan
et al.,
2021), evaluation of e-commerce system security (Liu,
2011), ergonomics (Akay,
2011), evaluation of the performance of enterprises (Tayyar
et al.,
2014; Aydemir and Sahin,
2019), risk and quality analysis (Baynal
et al.,
2018; Yazdani
et al.,
2019), product analysis (Chan and Tong,
2007; Sahin and Aydemir,
2019), and social networks (Weng
et al.,
2021).
In the method, when the decision-maker has no information, that is, when the information is black, the greyness of a process is done. In most decision problems with insufficient and/or incomplete information, the GRA method is used to select, rank, and evaluate (Chan and Tong,
2007; Yildirim,
2014; Aydemir,
2020). In the solution process, logical and numerical measurements between two decision series are called grey relational degrees, and values are assigned between 0–1. The method consists of three steps: normalization, grey relational coefficient calculation, and grey relational degree calculation. In the first step, the data of the alternatives are transformed into comparison sequences by the normalization process. In the GRA method, the normalization process is performed using Eqs. (
7)–(
9), respectively, according to benefit, cost, and optimality (Feng and Wang,
2000; Yildirim,
2014; Sahin and Aydemir,
2019):
here:
${x_{i}}(j)$: The value of criteria j for alternative i;
${\min _{j}}{x_{i}}(j)$: the smallest value for criteria j;
${\max _{j}}{x_{i}}(j)$: the greatest value for criteria j;
${x_{ob}}(j)$: the reference series (ideal sequence) value for criteria j.
After the normalization process, all values take values between 0–1. A decision alternative (
i) getting a value close to 1, and 1 for a criterion (
j) means that the alternative is one of the best alternatives for that criteria. It is uncommon in practice that any decision alternative provides the best value for all criteria. Therefore, the closest alternative to a reference series should be determined (Kuo
et al.,
2008). For this process, the absolute differences between the reference series values and the normalized benchmark value are calculated using Eq. (
10) and thus the absolute difference matrix is created (Yildirim,
2014).
here:
${x_{o}^{\ast }}(j)$: the normalized value of reference value for criteria j;
${x_{i}^{\ast }}(j)$: the normalized value alternative i for criteria j.
In the following step, the relationship between the desired and actual experimental data is determined by calculating the grey relational coefficient from the absolute difference matrix. Grey coefficients (
${\gamma _{01}}(j)$) are calculated with the help of Eq. (
11).
${\Delta _{\min }}$ and
${\Delta _{\max }}$ in the equation are the smallest and largest values in the absolute difference matrix,
${\Delta _{0i}}$ is the reference series value and expresses the absolute difference between the value of the alternative
j. The discriminant coefficient (
ζ) is the discriminant coefficient that can take values between 0 and 1 and generally takes 0.5 (Ho and Lin,
2003).
In the last step, the grey relational degree is calculated by taking the average of the grey relational coefficients and the ranking is performed according to this value. Grey relational degrees (
${\gamma _{i}}$) are determined by Eq. (
12) by dividing the sum of the grey relational coefficients calculated by Eq. (
11) by the number of criteria (
n), that is, for the case where the criteria are equally weighted (Lin
et al.,
2002). Also, if the criteria have weights in terms of the decision-maker (
${w_{j}}$), grey relational degrees (
${\gamma _{i}}$) are determined by Eq. (
13). The order of suitability and/or preference of the alternatives is obtained with the order of the calculated grey relational degrees in descending order.
3.2.3 COPRAS Method
The COPRAS method developed by Zavadskas
et al. (
1994) applies a stepwise ranking procedure to evaluate the performance of each alternative, taking into account the contradictory situations. It is a frequently preferred method especially for ranking processes in subjects such as evaluation of road design solutions (Zavadskas
et al.,
2007), supplier selection (Keshavarz Ghorabaee
et al.,
2014; Yildirim and Timor,
2019), investment project selection (Popović
et al.,
2012), and analysis of the basic factors of sustainable architecture (Amoozad Mahdiraji
et al.,
2018).
The COPRAS method assumes a direct and proportional dependence of the degree of importance and utility of decision options on a system of criteria that adequately defines the alternatives and the values and weights of the criteria. Determining the importance, priority order, and degree of use of alternatives is carried out in five stages (Kaklauskas
et al.,
2005,
2006):
Step 1: The weighted normalized decision matrix
$(D)$ is created. The aim is to take non-dimensional weighted values from comparative indices. For this, the following equation is used:
The sum of the dimensionless weighted index values is equal to “
${q_{ij}}$”, which is the weight value of each criteria
Step 2: The sum of the weighted normalized indices defining the alternative
j is calculated. The index of the criteria trying to be minimized is shown as “
${S_{-j}}$” and the index of the criteria trying to be maximized is shown as “
${S_{+j}}$”. The lower the value of indices such as total cost and implementation time (
${S_{-j}}$) is, the larger the value of indices calculated for criteria such as utility and strategy fit (
${S_{+j}}$), the better the goals are achieved. Based on this, the total value of the indices is calculated with the following equation:
Step 3: The degree of importance of comparative alternatives (
${Q_{j}}$) is determined by the following equation:
The larger the value of ${Q_{j}}$, the higher the priority of the alternative. The alternative with the highest ${Q_{j}}$ value will be the one that meets the demands and targets the most.
Step 4: The utility degree of the alternative
j (
${N_{j}}$) is calculated using equation (
18):
Step 5: The order of the alternatives is determined according to the degree of use (${N_{j}}$). The alternative with this value of 100 is the best.
3.2.4 MULTIMOORA Method
The Multi-Objective Optimization Based on Ratio Analysis (MOORA) method proposed by Brauers and Zavadskas (
2006) was later developed as MULTIMOORA by Brauers and Zavadskas (
2010) with the addition of the “Full Multiplicative Form of Multiple Objectives” method. MOORA plus the full Multiplicative form, which consists of three subordinate methods: full multiplicative, reference point, and full multiplicative.
MULTIMOORA is mostly used as a multi-criteria decision-making technique in fields such as industry, economy, environment, health services, and information technologies as practical applications. In this section, we first explain the MULTIMOORA method in terms of the subordinate ranking methods. The first step also involves generating a decision matrix and weight vector, as seen below, with ${x_{ij}}$ ratings for m alternatives and n criteria.

Also, on the MCDM problems, the ratings of alternatives may have different dimensions generally, so, the normalized ratings should be required and for this, Van Delft and Nijkamp normalization approach is used in MULTIMOORA application considering the most robust choice and proving by Brauers
et al. (
2008) for the denominator in the ratio system:
In certain cases, the triple subordinate methods are also known as the ratio, complete multiplicative, and reference point forms, and they are used to solve the exits problem. The ratio method should be used as a completely compensatory model if the problem has any independent criteria. The ratio system is computed by Eq. (
21), where g is the number of useful criteria and
${y_{i}}$ is the utility value. The best alternative solution by using the ratio system is applied to select the maximum utility
${y_{i}}$ in descending order with Eq. (
22) (Hafezalkotob
et al.,
2019):
The reference point approach, on the other hand, is a conservative method for measuring and comparing the ratio system and complete multiplicative form with Eqs. (
23)–(
25). Initially, the maximal objective reference point (MORP) vector is defined as Eq. (
23), where
${r_{j}}$ represents the utility value (Hafezalkotob
et al.,
2019):
Eq. (
24) defines the distance between the weighted value of the vector members and the weighted alternative rating, and the efficiency of the Reference Point Approach is obtained by maximizing the distance introduced in Eq. (
25):
The best alternative found by the Reference Point Approach has the least benefit (
${z_{i}}$), and the approach’s order is provided by Eq. (
26):
Although Brauers and Zavadskas (
2012) demonstrated that using weights as multipliers in the full multiplicative form is meaningless, it is mentioned that the weights determined in the developed MULTIMOORA method proposed by Hafezalkotob and Hafezalkotob (
2016) can be calculated as shown in Eq. (
27):
The maximum utility alternative is the best alternative based on the Full Multiplicative Form, and the sequence of this technique is obtained by equation (
28) in descending order:
Using these subordinate ranks, we also should decide the final ranking of the alternatives in the final phase. The aggregating multiple subordinate rankings are presented by Brauers and Zavadskas (
2012) to obtain a final ranking list that is more robust than each ranking list of the subordinate methods. Dominance-based principles, mathematical operators, MCDM methods, and programming approaches are examples of these approaches. Using the principle of dominance, the original MULTIMOORA incorporates MOORA with the exact multiplicative form. At this point, it is obvious that Dominance Theory (Brauers and Zavadskas,
2011) is the most widely applied method; but, in recent years, other tools with potential success have been used instead of this theory (Brauers and Zavadskas,
2006; Hafezalkotob
et al.,
2019). As a result, the dominance theory is used in this analysis to produce a unified final ranking list.
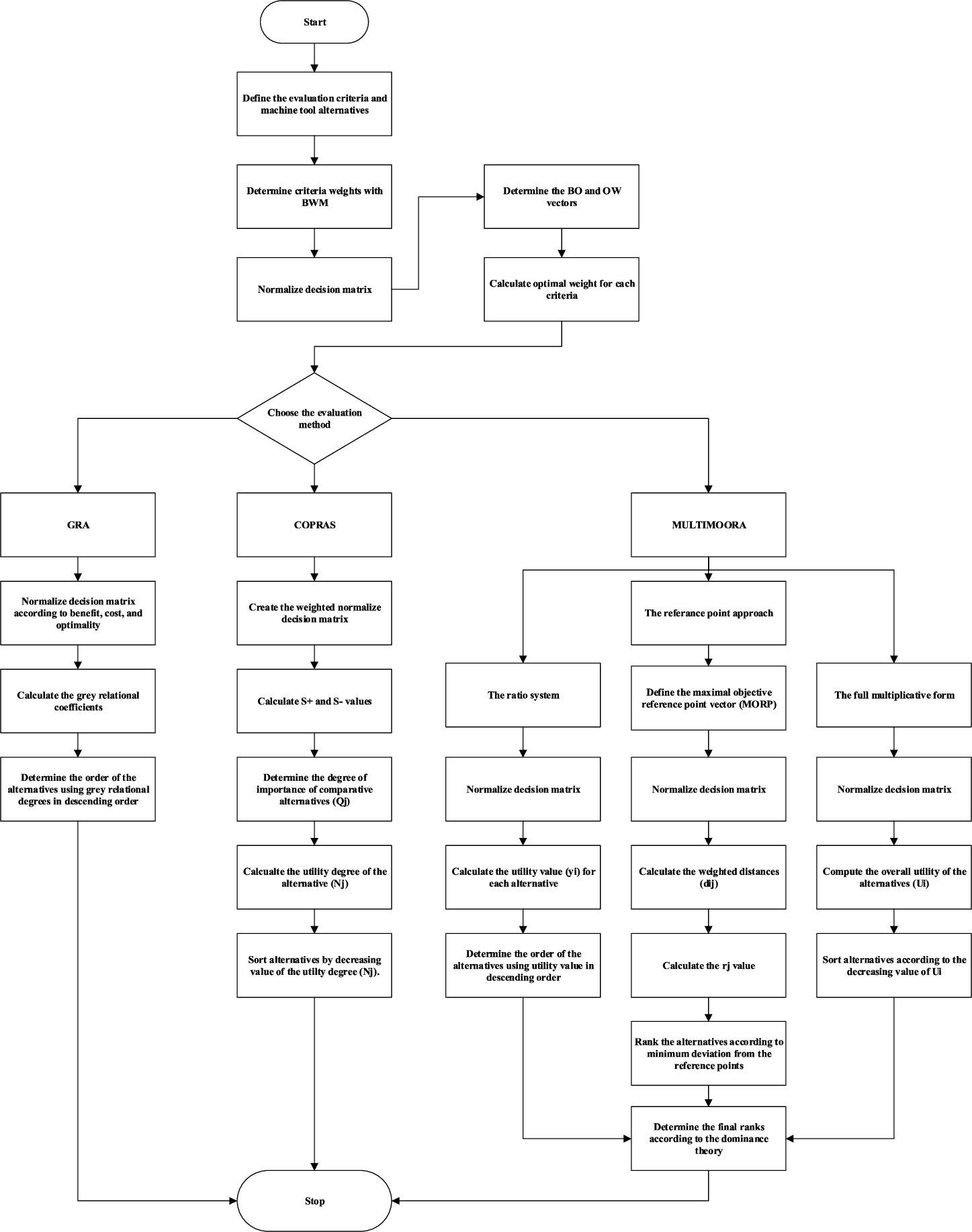
Fig. 1
The basic framework of the proposed method.

