1 Introduction
Many Multiple Attribute Decision Making (MADM) problems do not involve appropriate data which are directly measurable such as cost, net profit, any financial ratio, volume or weight of an item, etc. To deal with the quantification problems, the decision-makers can benefit from linguistic terms in stating their thoughts and preferences regarding the problem. Linguistic terms are often defined in different fuzzy environments. Zadeh (
1965) launched the domain of fuzzy sets for symbolizing human judgments. In conventional fuzzy set definition, the opinions can be represented by a single membership degree (
μ) which ranges between 0 and 1. This membership degree measures the optimism or agreement level and possesses a positive perspective.
To smooth the representation challenge of the uncertainty in human judgments, fuzzy set domain has been extended by researchers from different fields. Atanassov (
1986) introduced the intuitionistic fuzzy sets (IFS) by defining a negative membership (or non-membership) degree (
v). This new element in the fuzzy set definition brings resilience to the uncertainty representation issue because the experts are able to specify their pessimistic views or disagreements in this way. Hence, non-membership degree points out a negative perspective. Atanassov (
1986) also defined a new element regarding the indeterminacy (or hesitancy) which shows the experts’ neutral preference:
$\pi =1-\mu -v$. Thus, IFS was the first fuzzy concept that can cope with three dimensions of judgments (positive membership, negative membership, and indeterminacy). In real life, these degrees are the equivalents of yes, no, and abstain, respectively, in a voting environment. Nonetheless, the drawback in IFS is that the indeterminacy degree cannot be independently assigned by the experts.
After the introduction of the horizon widening features of fuzzy sets and IFSs, new fuzzy concepts have been proposed in the literature. Pythagorean fuzzy sets (Yager,
2013), q-Rung orthopair fuzzy sets (Yager,
2017), and Fermatean fuzzy sets (Senapati and Yager,
2020) have extended the representation domain of the expert by just considering the independently assignable positive and negative membership degrees. The independently assignable hesitancy degree is considered in neutrosophic sets (Smarandache,
1999) and spherical fuzzy sets (Kutlu Gündoğdu and Kahraman,
2019a). Many researchers work on developing aggregation operators, information measures such as entropy, distance, inclusion (subsethood), and knowledge measures for easing the uncertainty handling issue in decision-making problems.
The most recent fuzzy set concept considering all the three independently assignable membership degrees was presented by Cuong and Kreinovich (
2013). This novel concept is called picture fuzzy sets (PFS) as a logical reasoning of fuzzy sets and IFSs. A PFS is characterized by three independently assignable degrees expressing the positive (
μ), the neutral (
η – which means hesitancy), and the negative (
v – which is an equivalent to non-membership) membership degrees. The sole constraint defined in PFS enforces that their sum must not exceed 1. The gap between their sum and 1 is called refusal degree. The expert’s choice of refusing the idea sharing is quantified in PFS by this novel element. The refusal degree is here defined as
$\pi =1-\mu -\eta -v$.
PFS exhibits its importance in voting environments. Cuong (
2014) clarifies the items in PFS for the voting case. The voters can be divided into four groups: vote for the candidate, abstain, vote against the candidate, and refusal of the voting, i.e. casting a veto. It is obvious that PFS has a broader representation power than previous extensions of fuzzy sets since it involves a fourth component called refusal degree. PFS is the only fuzzy set definition handling this issue. Son (
2016) introduced an example showing the importance of PFS for MADM. The personnel selection activity needs information about the candidates for understanding whether they are eligible for the job or not. The result of this selection could be one of the 4 classes: true positive, true negative, false negative, and false positive which can be accepted as the equivalents to the membership degrees of PFS. Each candidate is evaluated by considering 4 classes. The selection is based on these evaluations. Assume that two candidates are evaluated:
A took (50%, 20%, 20%, 10%) and
B took (40%, 10%, 30%, 20%). The most appropriate candidate can be selected by applying the score function defined for PFS. As given in Definition
3, score value of
A is
$50\% -20\% =30\% $ and score value of
B is
$40\% -30\% =10\% $. Thus, candidate
A will be selected as a result.
Most of the business and management issues are MADM problems because the companies, institutions, even societies, and governments are enforced to take a lot of features of the decisions they should take into account. The problem definition of any MADM problem involves the determination of three basic elements: the attributes which can possess a potential impact on the results, the decision-makers who will be consulted due to their expertise, and the alternatives that are the potential solutions.
In MADM understanding, each alternative is evaluated by the decision-makers with respect to attributes, and the very first issue that should be addressed in decision analysis emerges after this data collection activity: how will we process these data to obtain the overall performance of each alternative? The motivation behind this question is that the decision analyst has many methodologies that can be used in reflecting the importance of the attributes to the decision. Each attribute has its own mean with discrete and changing significance for the problem at hand.
The requirement explained above is also called attribute weighting and it can be handled via applying one of two basic methods or a mixture of them: (1) subjective methods such as AHP-Analytic Hierarchy Process, SWARA-Stepwise Weight Assessment Ratio Analysis and Simos’ procedure are based on the experts’ evaluations; (2) objective methods do not demand these individualistic preferences and thoughts. In calculating the attribute weights, they just examine the performances of the alternatives with the aim of removing or at least limiting the risk of manipulative preferential actions of decision-makers or too long data collection periods. Particularly, in auditing the companies in terms of the quality assurance performance of their business processes, occupational health issues, and their financial strength, the subjectivity in attribute weighting may be misleading. Therefore, objective attribute weighting tools can be used to handle these issues.
Entropy measure which is based on the performance scores can support the objective attribute weighting effort. In this study, two new entropy measures are developed for PFSs and their applicability in MADM is manifested in integration to a novel extension of CODAS (COmbinative Distance-based ASsessment) method under picture fuzzy environment. The main contributions of the study are listed as follows:
There are 7 sections in the study. After this first section regarding the introduction, Section
2 covers the preliminaries of PFS and the results of an extensive literature review on the recent fuzzy extension of CODAS. Novel entropy measures for PFS are demonstrated and proved in Section
3. Section
4 presents the novel picture fuzzy extension of CODAS (PF-CODAS) and the integration of entropy measures into the model. In section
5, the newly proposed PF-CODAS version with entropy-based objective weighting is implemented in an example that was previously studied by Meksavang
et al. (
2019). The results of various implementations are compared in order to show the validity of the novel entropy-based PF-CODAS approach in Section
6. Section
7 concludes the study with some remarks and the future research possibilities are also mentioned.
4 CODAS Extension Under Picture Fuzzy Environment (PF-CODAS)
The study has extended CODAS method into the picture fuzzy environment as a contribution to the literature. In this novel proposition, PFNs provide a better opportunity of independency to the decision-makers since it is allowed to express independent degrees for positive, negative, and hesitant preferences. The refusal degrees can also be calculated as the fourth element in PFS. Especially, the consideration of the refusal degree in decision analysis is scarce in the literature of MADM. Moreover, entropy-based objective weighting process is joint to the method in case that the initial problem definition does not have the attribute weights. The algorithm is given as follows:
Step 1. Decision-makers
$(e=1,\dots ,k)$ express their judgments about alternatives’
$(i=1,\dots ,m)$ performances with respect to attributes
$(j=1,\dots ,n)$ via linguistic evaluations. The linguistic term set (Table
1) having PFN correspondences can be used for this purpose.
Table 1
Linguistic terms for expert evaluations (Meksavang
et al.,
2019).
| Linguistic term |
PFN correspondence |
| Very Poor (VP) |
(0.10, 0.00, 0.85) |
| Poor (P) |
(0.25, 0.05, 0.60) |
| Moderately Poor (MP) |
(0.30, 0.00, 0.60) |
| Fair (F) |
(0.50, 0.10, 0.40) |
| Moderately Good (MG) |
(0.60, 0.00, 0.30) |
| Good (G) |
(0.75, 0.05, 0.10) |
| Very Good (VG) |
(0.90, 0.00, 0.05) |
After gathering evaluations from decision-makers, there will be
k decision matrices
$({\tilde{X}^{1}},{\tilde{X}^{2}},\dots ,{\tilde{X}^{k}})$. The judgments are combined through an aggregation operator defined in PFS. In this aggregation, we consider the decision-makers’ weights representing their expertise (
${\omega _{e}}$).
${\tilde{X}^{e}}=[{\tilde{x}_{ij}^{e}}]$ is the
${e^{th}}$ decision-maker’s evaluation matrix where
${\tilde{x}_{ij}^{e}}=\langle {\mu _{ij}^{e}},{\eta _{ij}^{e}},{v_{ij}^{e}}\rangle $ depicts the PFN correspondence of the linguistic evaluation and
$\tilde{X}=[{\tilde{x}_{ij}}]$ is the aggregated decision matrix where
${\tilde{x}_{ij}}=\langle {\mu _{ij}},{\eta _{ij}},{v_{ij}}\rangle $. For obtaining
${\tilde{X}^{e}}$ given in Eq. (
55), the picture fuzzy weighted averaging (PFWA) operator (Eq. (
56)) is performed (Wei,
2017a).
Step 2. The attribute considered in any decision problem can be a cost or a benefit type attribute. To convert cost attributes to benefit ones, the positive (${\mu _{ij}}$) and negative (${v_{ij}}$) membership degrees should be replaced while the neutral membership degrees (${\eta _{ij}}$) keep their values. This is called normalization.
Step 3. After normalization, the weights of attributes representing their importance and significance should be considered. 4 possibilities might be thought of in weighting:
-
(I) If the weights are already known as prior information, we can directly use them;
-
(II) If the decision-makers’ preferences are important for the analyst, their expertise can be gathered, and the subjective weights are computed via various MADM tools such as AHP, Analytic Network Process (ANP), SWARA, Simos’ procedure, etc.;
-
(III) When the subjectivity is not desired with the purpose of eliminating manipulation risk or when there is not enough time for data collection or when the analyst does not have the weights of any kind, the weights can be objectively calculated from the current data by referring to the methods such as entropy-based approaches or maximizing standard deviation method;
-
(IV) When required, a mixture of objective and subjective methods can be exploited (Kabak and Ruan,
2011; Çalışkan
et al.,
2013; Li
et al.,
2014; Freeman and Chen,
2015).
This proposition aims at showing the applicability of entropy-based objective weighting with the integration of CODAS under PF environment. Therefore, the method requires first the calculation of the entropies of each attribute via Eq. (
57) or Eq. (
58). Then, the weights are obtained as formulated in Eq. (
59) (Aydoğdu and Gül,
2020)
The attribute weights obtained in Eq. (
59) are used in constructing the weighted normalized decision matrix
$\tilde{R}=[{\tilde{r}_{ij}}]$ via Eq. (
60). This equation is a reorganization of the multiplication operation defined in Eq. (
5)
Step 4. The distinctive feature of CODAS is the consideration of the distance of each alternative from the negative-ideal solution which can be obtained via Eq. (
60)
Step 5. Euclidean and Hamming distances of each alternative
i to
$\tilde{ns}=[{\tilde{ns}_{j}}]$ are computed
The distance values are crisp numbers now. So, the remaining three steps are the same as the original CODAS method.
Step 6. Identical to Step 6 of CODAS given in Section
2.2.
Step 7. Identical to Step 7 of CODAS given in Section
2.2.
Step 8. Identical to Step 8 of CODAS given in Section
2.2.
5 An Application of Green Supplier Selection in the Beef Industry
In the study, we have developed a novel PFS version of CODAS with the integration of entropy-based objective attribute weighting. We have also tried to keep the computations picture fuzzy until the very end of the method. The proposed PF-CODAS is here applied in a supplier selection problem for the beef industry previously defined and analysed by Meksavang
et al. (
2019).
Büyüközkan and Çifçi (
2012) stated that even if material, funds, and information flows establish a supply chain system, due to governmental rules and growing consciousness in the society about keeping the environment safe, organizations must be more sensitive to environmental issues, particularly if they want to keep their existence in global markets. Supplier selection issue has gained greater attraction today because organizations focus on improving their core competence and they need to outsource less profitable activities to supply chain partners for this reason (Govindan
et al.,
2015). In this selection process, environmental issues have been emphasized from a perspective of green supply chain management. In the literature, green supplier selection problem is very fruitful. Govindan
et al. (
2015) presented a very extensive literature review on MADM applications on green supplier selection problem. Liou
et al. (
2021) integrated support vector machines, fuzzy best-worst method, and fuzzy TOPSIS method and presented the model’s applicability in a real case of a Taiwanese electronics company. Wei
et al. (
2021) developed a probabilistic uncertain linguistic version of CODAS and applied it to a green supplier selection problem. Kumar and Barman (
2021) applied and compared the results of fuzzy VIKOR and fuzzy TOPSIS methods in the green supplier selection issue of India’s small-scale iron and steel industry. Çalık (
2021) proposed a Pythagorean fuzzy extension of AHP and TOPSIS integration for green supply chain management in the Industry 4.0 era and made a trial for agricultural tool manufacturers in Turkey.
After a brief explanation about MADM in green supply chain management field, we can return to the application of the proposed method in a case that was previously defined by Meksavang
et al. (
2019). The authors stated that carbon footprint reduction received great attention throughout the world, and the agriculture sector is one of the main contributors to global carbon emission. They also mentioned the increasing pressure on the beef industry from the government and clients to reduce carbon emissions in its supply chain. For mitigating carbon emission, the proposed entropy-based PF-CODAS approach is here applied to the selection of a supplier for a beef abattoir company.
Step 1. Ten potential beef farmers are considered as supplier alternatives and denoted as
${A_{i}}$ $(i=1,\dots ,10)$. Their green supply performance is assessed following seven attributes
$(j=1,\dots ,7)$: quality of meat (
${C_{1}}$), age of cattle (
${C_{2}}$), diet fed to cattle (
${C_{3}}$), average weight (
${C_{4}}$), traceability (
${C_{5}}$), carbon footprint (
${C_{6}}$), and price (
${C_{7}}$). Three decision-makers (
$D{M_{1}}$,
$D{M_{2}}$,
$D{M_{3}}$) make the evaluations of the performance ratings of suppliers. The weight set for the decision-makers’ is assumed as (0.3, 0.4, 0.3) due to the differences in their technical knowledge and expertise levels. The linguistic evaluations given in Table
1 are used for this purpose and the corresponding PFNs are found in the same table. Table
A2 and Table
A3 in Appendix
A show the linguistic evaluations of decision-makers and the corresponding PFNs (
${\tilde{X}^{e}}=[{\tilde{x}_{ij}^{e}}]$), respectively. In order to build the aggregated picture fuzzy decision matrix, Eq. (
56) is performed.
Table 2
The aggregated picture fuzzy decision matrix.
|
${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
${C_{5}}$ |
${C_{6}}$ |
${C_{7}}$ |
| ${A_{1}}$ |
0.900 |
0.000 |
0.050 |
0.300 |
0.000 |
0.600 |
0.900 |
0.000 |
0.050 |
0.750 |
0.050 |
0.100 |
0.868 |
0.000 |
0.062 |
0.483 |
0.000 |
0.414 |
0.500 |
0.100 |
0.400 |
| ${A_{2}}$ |
0.543 |
0.000 |
0.357 |
0.750 |
0.050 |
0.100 |
0.500 |
0.100 |
0.400 |
0.781 |
0.000 |
0.113 |
0.900 |
0.000 |
0.050 |
0.629 |
0.000 |
0.235 |
0.447 |
0.000 |
0.452 |
| ${A_{3}}$ |
0.581 |
0.000 |
0.266 |
0.354 |
0.000 |
0.531 |
0.781 |
0.000 |
0.113 |
0.600 |
0.000 |
0.300 |
0.629 |
0.000 |
0.235 |
0.600 |
0.000 |
0.300 |
0.354 |
0.000 |
0.531 |
| ${A_{4}}$ |
0.600 |
0.000 |
0.300 |
0.500 |
0.100 |
0.400 |
0.781 |
0.000 |
0.113 |
0.250 |
0.050 |
0.600 |
0.856 |
0.000 |
0.066 |
0.856 |
0.000 |
0.066 |
0.388 |
0.000 |
0.510 |
| ${A_{5}}$ |
0.718 |
0.000 |
0.191 |
0.900 |
0.000 |
0.050 |
0.810 |
0.000 |
0.081 |
0.265 |
0.000 |
0.600 |
0.224 |
0.000 |
0.666 |
0.750 |
0.050 |
0.100 |
0.435 |
0.081 |
0.452 |
| ${A_{6}}$ |
0.750 |
0.050 |
0.100 |
0.354 |
0.000 |
0.531 |
0.750 |
0.050 |
0.100 |
0.750 |
0.050 |
0.100 |
0.900 |
0.000 |
0.050 |
0.629 |
0.000 |
0.235 |
0.428 |
0.000 |
0.470 |
| ${A_{7}}$ |
0.551 |
0.000 |
0.298 |
0.300 |
0.000 |
0.600 |
0.483 |
0.000 |
0.414 |
0.354 |
0.000 |
0.531 |
0.265 |
0.000 |
0.600 |
0.483 |
0.000 |
0.414 |
0.428 |
0.000 |
0.470 |
| ${A_{8}}$ |
0.817 |
0.000 |
0.105 |
0.629 |
0.000 |
0.235 |
0.629 |
0.000 |
0.235 |
0.354 |
0.000 |
0.531 |
0.250 |
0.050 |
0.600 |
0.781 |
0.000 |
0.113 |
0.428 |
0.000 |
0.470 |
| ${A_{9}}$ |
0.484 |
0.000 |
0.403 |
0.354 |
0.000 |
0.531 |
0.483 |
0.000 |
0.414 |
0.781 |
0.000 |
0.113 |
0.600 |
0.000 |
0.300 |
0.500 |
0.100 |
0.400 |
0.500 |
0.100 |
0.400 |
| ${A_{10}}$ |
0.653 |
0.000 |
0.216 |
0.483 |
0.000 |
0.414 |
0.600 |
0.000 |
0.300 |
0.900 |
0.000 |
0.050 |
0.900 |
0.000 |
0.050 |
0.900 |
0.000 |
0.050 |
0.435 |
0.081 |
0.452 |
Table
2 shows the aggregated decision matrix (Eq. (
55)). As an illustration, the aggregated performance value (
${\tilde{x}_{31}}$) of
${A_{3}}$ with respect to
${C_{1}}$ is computed as follows where the evaluations are P
$(0.25,0.05,0.60)$, MG
$(0.60,0.00,0.30)$, G
$(0.75,0.05,0.10)$:
Step 2. In normalization step, the normalized decision matrix is constructed as given in Table
3. There is only one cost attribute in this problem: price (
${C_{7}}$). Hence, this last attribute’s positive (
${\mu _{i7}}$) and negative membership (
${v_{i7}}$) degrees are replaced.
Step 3. Entropy-based objective weights of the attributes are calculated in this step. For each attribute
j, Eq. (
57) or Eq. (
58) is performed for computing entropies and the weights are gathered after making a normalization which is formulated in Eq. (
59). The related entropies and weights of the attributes are given in Table
4. Generating from the definitions of the entropy measures, there are few differences between the importance rankings of the attributes as well as the weights. Therefore, in further steps, we will see the impact of this difference on the solution of the problem.
Table 3
The normalized picture fuzzy decision matrix.
|
${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
${C_{5}}$ |
${C_{6}}$ |
${C_{7}}$ |
| ${A_{1}}$ |
0.900 |
0.000 |
0.050 |
0.300 |
0.000 |
0.600 |
0.900 |
0.000 |
0.050 |
0.750 |
0.050 |
0.100 |
0.868 |
0.000 |
0.062 |
0.483 |
0.000 |
0.414 |
0.400 |
0.100 |
0.500 |
| ${A_{2}}$ |
0.543 |
0.000 |
0.357 |
0.750 |
0.050 |
0.100 |
0.500 |
0.100 |
0.400 |
0.781 |
0.000 |
0.113 |
0.900 |
0.000 |
0.050 |
0.629 |
0.000 |
0.235 |
0.452 |
0.000 |
0.447 |
| ${A_{3}}$ |
0.581 |
0.000 |
0.266 |
0.354 |
0.000 |
0.531 |
0.781 |
0.000 |
0.113 |
0.600 |
0.000 |
0.300 |
0.629 |
0.000 |
0.235 |
0.600 |
0.000 |
0.300 |
0.531 |
0.000 |
0.354 |
| ${A_{4}}$ |
0.600 |
0.000 |
0.300 |
0.500 |
0.100 |
0.400 |
0.781 |
0.000 |
0.113 |
0.250 |
0.050 |
0.600 |
0.856 |
0.000 |
0.066 |
0.856 |
0.000 |
0.066 |
0.510 |
0.000 |
0.388 |
| ${A_{5}}$ |
0.718 |
0.000 |
0.191 |
0.900 |
0.000 |
0.050 |
0.810 |
0.000 |
0.081 |
0.265 |
0.000 |
0.600 |
0.224 |
0.000 |
0.666 |
0.750 |
0.050 |
0.100 |
0.452 |
0.081 |
0.435 |
| ${A_{6}}$ |
0.750 |
0.050 |
0.100 |
0.354 |
0.000 |
0.531 |
0.750 |
0.050 |
0.100 |
0.750 |
0.050 |
0.100 |
0.900 |
0.000 |
0.050 |
0.629 |
0.000 |
0.235 |
0.470 |
0.000 |
0.428 |
| ${A_{7}}$ |
0.551 |
0.000 |
0.298 |
0.300 |
0.000 |
0.600 |
0.483 |
0.000 |
0.414 |
0.354 |
0.000 |
0.531 |
0.265 |
0.000 |
0.600 |
0.483 |
0.000 |
0.414 |
0.470 |
0.000 |
0.428 |
| ${A_{8}}$ |
0.817 |
0.000 |
0.105 |
0.629 |
0.000 |
0.235 |
0.629 |
0.000 |
0.235 |
0.354 |
0.000 |
0.531 |
0.250 |
0.050 |
0.600 |
0.781 |
0.000 |
0.113 |
0.470 |
0.000 |
0.428 |
| ${A_{9}}$ |
0.484 |
0.000 |
0.403 |
0.354 |
0.000 |
0.531 |
0.483 |
0.000 |
0.414 |
0.781 |
0.000 |
0.113 |
0.600 |
0.000 |
0.300 |
0.500 |
0.100 |
0.400 |
0.400 |
0.100 |
0.500 |
| ${A_{10}}$ |
0.653 |
0.000 |
0.216 |
0.483 |
0.000 |
0.414 |
0.600 |
0.000 |
0.300 |
0.900 |
0.000 |
0.050 |
0.900 |
0.000 |
0.050 |
0.900 |
0.000 |
0.050 |
0.452 |
0.081 |
0.435 |
Table 4
The weights of the attributes which are based on two novel entropy measures.
|
${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
${C_{5}}$ |
${C_{6}}$ |
${C_{7}}$ |
|
$E{n_{j}}$ (Eq. 51) |
0.330 |
0.441 |
0.339 |
0.297 |
0.211 |
0.355 |
0.732 |
| 1- Enj
|
0.670 |
0.559 |
0.661 |
0.703 |
0.789 |
0.645 |
0.268 |
| ${w_{j}}$ |
0.156 |
0.130 |
0.154 |
0.164 |
0.184 |
0.150 |
0.062 |
| Importance ranking |
3 |
6 |
4 |
2 |
1 |
5 |
7 |
|
$E{n_{j}}$ (Eq. 52) |
0.391 |
0.436 |
0.365 |
0.374 |
0.291 |
0.375 |
0.532 |
| 1- Enj
|
0.609 |
0.564 |
0.635 |
0.626 |
0.709 |
0.625 |
0.468 |
| ${w_{j}}$ |
0.144 |
0.133 |
0.150 |
0.148 |
0.167 |
0.147 |
0.111 |
| Importance ranking |
5 |
6 |
2 |
3 |
1 |
4 |
7 |
| Difference between weights |
0.012 |
−0.003 |
0.004 |
0.016 |
0.016 |
0.003 |
−0.048 |
By considering the weights of the attributes, the normalized matrix is weighted by using the formula in Eq. (
60). For simplicity, the application of the further steps will be explained for the weight set which is found by Eq. (
57): [0.156, 0.130, 0.154, 0.164, 0.184, 0.150, 0.062]. Table
5 shows the weighted normalized picture fuzzy decision matrix.
Step 4. In CODAS, the origin point for the comparison of alternatives is the negative-ideal solution. By performing Eq. (
60),
$\tilde{ns}=[{\tilde{ns}_{j}}]$ is found as a row vector and shown in the last row of Table
5.
Step 5. The ranking of the alternatives is based on the distances between the alternatives and the negative-ideal solution. Euclidean and Hamming distances are found via Eq. (
62) and Eq. (
63), respectively, and shown in Table
6. These distances are now crisp numbers.
Table 5
The weighted normalized picture fuzzy decision matrix.
|
${C_{1}}$ |
${C_{2}}$ |
${C_{3}}$ |
${C_{4}}$ |
${C_{5}}$ |
${C_{6}}$ |
${C_{7}}$ |
| ${A_{1}}$ |
0.302 |
0.000 |
0.627 |
0.045 |
0.000 |
0.936 |
0.298 |
0.000 |
0.631 |
0.203 |
0.613 |
0.121 |
0.311 |
0.000 |
0.599 |
0.094 |
0.000 |
0.876 |
0.031 |
0.866 |
0.102 |
| ${A_{2}}$ |
0.115 |
0.000 |
0.851 |
0.165 |
0.677 |
0.104 |
0.101 |
0.702 |
0.197 |
0.220 |
0.000 |
0.700 |
0.345 |
0.000 |
0.577 |
0.138 |
0.000 |
0.805 |
0.037 |
0.000 |
0.951 |
| ${A_{3}}$ |
0.127 |
0.000 |
0.813 |
0.055 |
0.000 |
0.921 |
0.209 |
0.000 |
0.715 |
0.139 |
0.000 |
0.821 |
0.166 |
0.000 |
0.766 |
0.129 |
0.000 |
0.835 |
0.046 |
0.000 |
0.937 |
| ${A_{4}}$ |
0.133 |
0.000 |
0.829 |
0.086 |
0.741 |
0.173 |
0.209 |
0.000 |
0.715 |
0.046 |
0.613 |
0.319 |
0.299 |
0.000 |
0.607 |
0.252 |
0.000 |
0.665 |
0.044 |
0.000 |
0.943 |
| ${A_{5}}$ |
0.179 |
0.000 |
0.772 |
0.259 |
0.000 |
0.677 |
0.226 |
0.000 |
0.679 |
0.049 |
0.000 |
0.920 |
0.046 |
0.000 |
0.928 |
0.188 |
0.638 |
0.114 |
0.037 |
0.855 |
0.105 |
| ${A_{6}}$ |
0.194 |
0.627 |
0.117 |
0.055 |
0.000 |
0.921 |
0.192 |
0.631 |
0.116 |
0.203 |
0.613 |
0.121 |
0.345 |
0.000 |
0.577 |
0.138 |
0.000 |
0.805 |
0.039 |
0.000 |
0.948 |
| ${A_{7}}$ |
0.117 |
0.000 |
0.828 |
0.045 |
0.000 |
0.936 |
0.096 |
0.000 |
0.873 |
0.069 |
0.000 |
0.902 |
0.055 |
0.000 |
0.910 |
0.094 |
0.000 |
0.876 |
0.039 |
0.000 |
0.948 |
| ${A_{8}}$ |
0.233 |
0.000 |
0.704 |
0.121 |
0.000 |
0.828 |
0.141 |
0.000 |
0.800 |
0.069 |
0.000 |
0.902 |
0.051 |
0.577 |
0.347 |
0.204 |
0.000 |
0.721 |
0.039 |
0.000 |
0.948 |
| ${A_{9}}$ |
0.098 |
0.000 |
0.868 |
0.055 |
0.000 |
0.921 |
0.096 |
0.000 |
0.873 |
0.220 |
0.000 |
0.700 |
0.155 |
0.000 |
0.802 |
0.099 |
0.708 |
0.193 |
0.031 |
0.866 |
0.102 |
| ${A_{10}}$ |
0.152 |
0.000 |
0.787 |
0.082 |
0.000 |
0.892 |
0.132 |
0.000 |
0.831 |
0.314 |
0.000 |
0.613 |
0.345 |
0.000 |
0.577 |
0.292 |
0.000 |
0.638 |
0.037 |
0.855 |
0.105 |
| $\tilde{ns}$ |
0.098 |
0.000 |
0.868 |
0.045 |
0.000 |
0.936 |
0.096 |
0.000 |
0.873 |
0.046 |
0.000 |
0.920 |
0.046 |
0.000 |
0.928 |
0.094 |
0.000 |
0.876 |
0.031 |
0.000 |
0.951 |
Step 6. The pairwise comparison matrix including the combinative distances is built by performing the procedure explained by the algorithm in Section
2.2. Table
7 gives the comparison matrix. The required parameter of Θ is set to 0.05.
Table 6
Euclidean and Hamming distances to the negative-ideal solution.
|
${E_{i}}$ |
${T_{i}}$ |
| ${A_{1}}$ |
0.642 |
0.681 |
| ${A_{2}}$ |
0.587 |
0.601 |
| ${A_{3}}$ |
0.122 |
0.137 |
| ${A_{4}}$ |
0.554 |
0.581 |
| ${A_{5}}$ |
0.612 |
0.596 |
| ${A_{6}}$ |
0.677 |
0.761 |
| ${A_{7}}$ |
0.022 |
0.020 |
| ${A_{8}}$ |
0.333 |
0.297 |
| ${A_{9}}$ |
0.603 |
0.538 |
| ${A_{10}}$ |
0.526 |
0.523 |
Step 7. The assessment score generated by summing the row values of the comparison matrix is computed for each alternative. These
${H_{i}}$ assessment values are represented in Table
7.
Step 8. The highest separation measure refers to the best alternative. So, the alternatives are ranked in descending order of
${H_{i}}$ values as given in the last column of Table
7. Hence, the best alternative is the 6th supplier while the worst one is the 7th supplier of beef in terms of green supply performance. The full rank is
${A_{6}}\succ {A_{1}}\succ {A_{5}}\succ {A_{2}}\succ {A_{9}}\succ {A_{4}}\succ {A_{10}}\succ {A_{8}}\succ {A_{3}}\succ {A_{7}}$.
In Step 3, there are two sets of attribute weights and we have shown the calculations for the first weight set until now for simplicity. The application of PF-CODAS with the second weight set determined via Eq. (
58) is not shown in detail but the tables constituted are given in Appendix
A. While Table
A4 shows the weighted normalized picture fuzzy decision matrix, Table
A5 depicts the distances obtained. Table
A6 summarizes the comparison results, assessment scores, and the rankings of the alternatives which is
${A_{6}}\succ {A_{1}}\succ {A_{2}}\succ {A_{5}}\succ {A_{4}}\succ {A_{9}}\succ {A_{10}}\succ {A_{8}}\succ {A_{3}}\succ {A_{7}}$. A comparison of the rankings will be made in Section
6.
Table 7
Comparison of distances and the ranking of alternatives.
|
${A_{1}}$ |
${A_{2}}$ |
${A_{3}}$ |
${A_{4}}$ |
${A_{5}}$ |
${A_{6}}$ |
${A_{7}}$ |
${A_{8}}$ |
${A_{9}}$ |
${A_{10}}$ |
${H_{i}}$ |
Rank |
| ${A_{1}}$ |
0.000 |
0.135 |
1.064 |
0.188 |
0.030 |
−0.034 |
1.282 |
0.693 |
0.039 |
0.274 |
3.671 |
2 |
| ${A_{2}}$ |
−0.055 |
0.000 |
0.930 |
0.033 |
−0.025 |
−0.089 |
1.147 |
0.558 |
−0.016 |
0.139 |
2.622 |
4 |
| ${A_{3}}$ |
−0.520 |
−0.465 |
0.000 |
−0.432 |
−0.490 |
−0.555 |
0.217 |
−0.211 |
−0.481 |
−0.404 |
−3.341 |
9 |
| ${A_{4}}$ |
−0.088 |
−0.033 |
0.876 |
0.000 |
−0.059 |
−0.123 |
1.094 |
0.505 |
−0.049 |
0.028 |
2.150 |
6 |
| ${A_{5}}$ |
−0.030 |
0.025 |
0.950 |
0.074 |
0.000 |
−0.064 |
1.167 |
0.579 |
0.010 |
0.159 |
2.871 |
3 |
| ${A_{6}}$ |
0.034 |
0.249 |
1.179 |
0.303 |
0.229 |
0.000 |
1.396 |
0.807 |
0.297 |
0.388 |
4.882 |
1 |
| ${A_{7}}$ |
−0.621 |
−0.565 |
−0.100 |
−0.532 |
−0.591 |
−0.655 |
0.000 |
−0.311 |
−0.581 |
−0.505 |
−4.461 |
10 |
| ${A_{8}}$ |
−0.309 |
−0.254 |
0.371 |
−0.221 |
−0.279 |
−0.344 |
0.589 |
0.000 |
−0.270 |
−0.193 |
−0.910 |
8 |
| ${A_{9}}$ |
−0.039 |
0.016 |
0.882 |
0.049 |
−0.010 |
−0.074 |
1.099 |
0.511 |
0.000 |
0.091 |
2.525 |
5 |
| ${A_{10}}$ |
−0.116 |
−0.061 |
0.791 |
−0.028 |
−0.086 |
−0.150 |
1.008 |
0.419 |
−0.077 |
0.000 |
1.701 |
7 |
6 Comparison of Results
In order to check the validity of the proposed entropy-based PF-CODAS method, we have analysed two cases. In the first analysis, the rankings of the alternatives which are found by different entropy measures are compared. In the second one, a similar comparison is done for the applications with various versions of CODAS and TOPSIS methods.
Table 8
The weights of the attributes which are based on several measures.
|
$E{n_{j}}$ with Eq. (44) |
${w_{j}}$ with Eq. (44) |
Rank |
$E{n_{j}}$ with Eq. (48) |
${w_{j}}$ with Eq. (48) |
Rank |
${w_{j}}$ with Eq. (66) |
Rank |
$E{n_{j}}$ with Eq. (57) |
${w_{j}}$ with Eq. (57) |
Rank |
$E{n_{j}}$ with Eq. (58) |
${w_{j}}$ with Eq. (58) |
Rank |
| ${C_{1}}$ |
0.346 |
0.143 |
5 |
0.472 |
0.149 |
4 |
0.147 |
4 |
0.330 |
0.156 |
3 |
0.391 |
0.144 |
5 |
| ${C_{2}}$ |
0.409 |
0.132 |
6 |
0.511 |
0.134 |
6 |
0.136 |
6 |
0.441 |
0.130 |
6 |
0.436 |
0.133 |
6 |
| ${C_{3}}$ |
0.343 |
0.149 |
2 |
0.448 |
0.149 |
3 |
0.148 |
3 |
0.339 |
0.154 |
4 |
0.365 |
0.150 |
2 |
| ${C_{4}}$ |
0.332 |
0.147 |
3 |
0.456 |
0.151 |
2 |
0.152 |
2 |
0.297 |
0.164 |
2 |
0.374 |
0.148 |
3 |
| ${C_{5}}$ |
0.253 |
0.170 |
1 |
0.373 |
0.169 |
1 |
0.165 |
1 |
0.211 |
0.184 |
1 |
0.291 |
0.167 |
1 |
| ${C_{6}}$ |
0.354 |
0.147 |
4 |
0.457 |
0.147 |
5 |
0.146 |
5 |
0.355 |
0.150 |
5 |
0.375 |
0.147 |
4 |
| ${C_{7}}$ |
0.555 |
0.112 |
7 |
0.586 |
0.101 |
7 |
0.106 |
7 |
0.732 |
0.062 |
7 |
0.532 |
0.111 |
7 |
Table 9
The comparison of assessment scores and alternative rankings.
|
${H_{i}}$ |
Ranks with Eq. (44) |
${H_{i}}$ |
Ranks with Eq. (48) |
${H_{i}}$ |
Ranks with Eq. (66) |
${H_{i}}$ |
Ranks with Eq. (57) |
${H_{i}}$ |
Ranks with Eq. (58) |
| ${A_{1}}$ |
3.327 |
2 |
3.203 |
2 |
3.274 |
2 |
3.671 |
2 |
3.271 |
2 |
| ${A_{2}}$ |
2.712 |
3 |
2.751 |
3 |
2.713 |
3 |
2.622 |
4 |
2.731 |
3 |
| ${A_{3}}$ |
−3.279 |
9 |
−3.255 |
9 |
−3.273 |
9 |
−3.341 |
9 |
−3.260 |
9 |
| ${A_{4}}$ |
2.377 |
5 |
2.469 |
5 |
2.360 |
5 |
2.150 |
6 |
2.447 |
5 |
| ${A_{5}}$ |
2.627 |
4 |
2.547 |
4 |
2.606 |
4 |
2.871 |
3 |
2.558 |
4 |
| ${A_{6}}$ |
5.305 |
1 |
5.436 |
1 |
5.330 |
1 |
4.882 |
1 |
5.406 |
1 |
| ${A_{7}}$ |
−4.349 |
10 |
−4.324 |
10 |
−4.331 |
10 |
−4.461 |
10 |
−4.326 |
10 |
| ${A_{8}}$ |
−0.658 |
8 |
−0.639 |
8 |
−0.591 |
8 |
−0.910 |
8 |
−0.615 |
8 |
| ${A_{9}}$ |
2.266 |
6 |
2.186 |
6 |
2.240 |
6 |
2.525 |
5 |
2.192 |
6 |
| ${A_{10}}$ |
1.277 |
7 |
1.170 |
7 |
1.224 |
7 |
1.701 |
7 |
1.180 |
7 |
In terms of entropy-based comparison, the weight sets are determined. Table
8 gives the results of the comparison of weights and Table
9 shows the rankings of the alternatives. The entropy measures used are represented on the columns. The last two are the novel entropy measures proposed in the study and the first three are the existing ones in the literature: Eq. (
44) defined by Wang
et al. (
2018), Eq. (
48) defined by Joshi (
2020a), and the knowledge measure in Eq. (
52) defined by Lin
et al. (
2020). The third one provides a knowledge measure which is based on entropy measure and hesitancy degrees. The stepwise methodology is summarized as follows:
-
(a) The entropy matrix showing the entropies for each pair of alternative and attribute is derived as follows:
where
$En({\tilde{x}_{ij}})=\frac{\min ({d_{H}}({\tilde{x}_{ij}},{C_{\min }}),{d_{H}}({\tilde{x}_{ij}},{C_{\max }}))}{\max ({d_{H}}({\tilde{x}_{ij}},{C_{\min }}),{d_{H}}({\tilde{x}_{ij}},{C_{\max }}))}$ and
${C_{\min }}=\langle 0,0,1\rangle $ and
${C_{\max }}=\langle 1,0,0\rangle $.
-
(b) The knowledge matrix is derived as follows:
where
$K({\tilde{x}_{ij}})=1-0.5(En({\tilde{x}_{ij}})+{\pi _{ij}})$ and
${\pi _{ij}}=1-{\mu _{ij}}-{\eta _{ij}}-{\nu _{ij}}$.
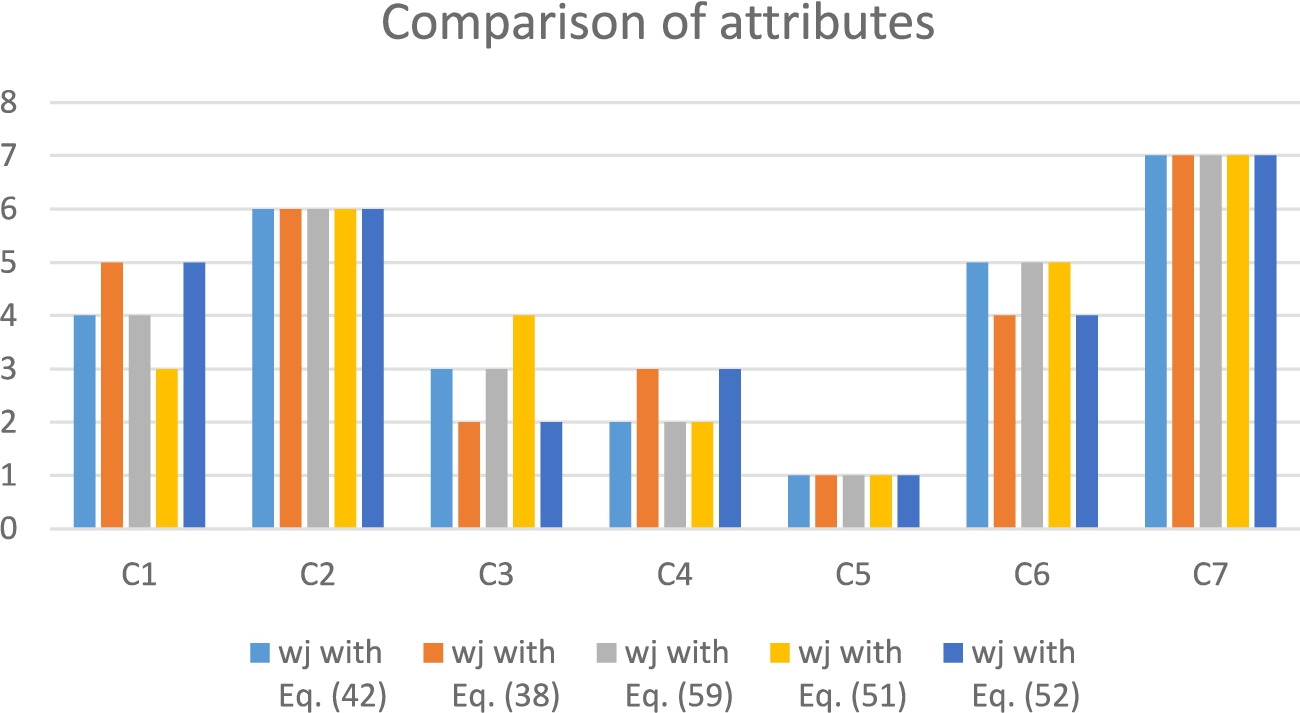
Fig. 1
Comparison of the ranks of the attributes.
-
(c) If the knowledge measure of a criterion is larger across the alternative, it means that the value of this criterion has a smaller variation. Hence, this one shows a greater impact on the overall ratings of the alternatives. From this understanding, Eq. (
66) is used for attribute weighting:
The importance ranking of the attributes is presented in Fig.
1. It is seen that there are few differences among the weight sets. Throughout the five sets, while
${C_{5}}$,
${C_{2}}$, and
${C_{7}}$ keep their ranks, the most changing attributes are
${C_{1}}$ and
${C_{3}}$. Table
9 and Fig.
2 show the comparisons of the alternative rankings gathered by applying the entropy-based weightings determined in Table
8. As seen in Fig.
2, the rankings are slightly different for the alternative pairs (
${A_{2}}$,
${A_{5}}$) and (
${A_{4}}$,
${A_{9}}$), while the other six alternatives keep their rankings in all 5 applications. Another important finding is that the three applications which are based on the existing entropy measures in the literature give the same ranking as the proposed second entropy (Eq. (
58)). The slightly different rankings are generated by the application based on the first novel entropy proposition given in Eq. (
57). In conclusion, it is seen that although there are differences in entropy measures and attribute weights associated, the rankings of the alternatives are stable throughout the process.
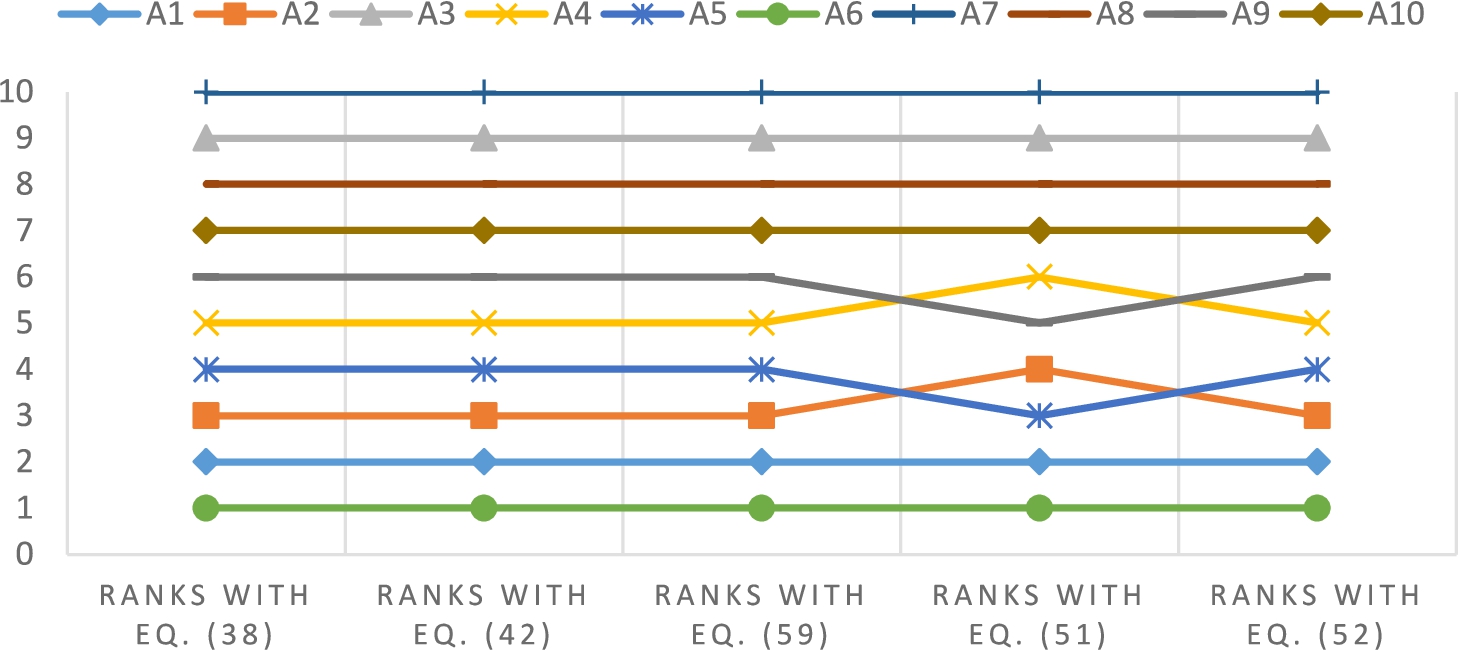
Fig. 2
Comparison of the ranks of alternatives for different weight sets.
The second analysis aims to compare the rankings of the alternatives of various approaches. Traditional CODAS developed by Keshavraz Ghorabaee
et al. (2016), spherical fuzzy version of CODAS developed by Kutlu Gündoğdu and Kahraman (
2019b), and spherical fuzzy extension of TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution) developed by Kutlu Gündoğdu (
2020) are utilized for this purpose. Each method is performed by considering two entropy measure propositions of the study, separately. To keep the flow of the study, the details of the methods are not given. The interested readers can look at the referred studies.
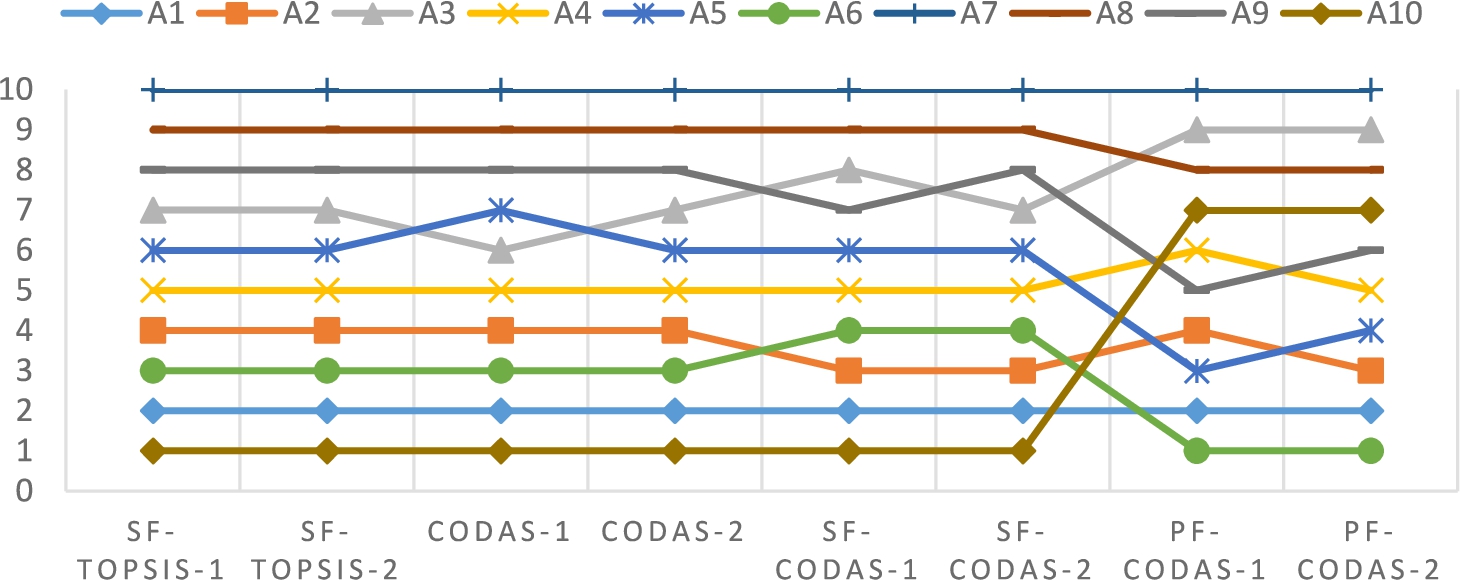
Fig. 3
Comparison of the ranks of alternatives for CODAS and TOPSIS versions.
Fig.
3 shows the results of the comparisons. SF-TOPSIS, CODAS, and SF-CODAS give slightly different results while the proposed PF-CODAS generates different rankings of the alternatives. In terms of
${A_{2}}$ which is the best alternative obtained by PF-CODAS, CODAS and SF-TOPSIS rank it as the 3rd best while SF-CODAS sees it as the 4th best.
${A_{10}}$ is found as the best alternative by the mentioned methods but PF-CODAS ranks it as the 7th best.
${A_{1}}$ and
${A_{7}}$ keep their 2nd and 10th positions, respectively, but it is obvious that there are significant differences for the other 8 alternatives. For a more comprehensive view, Fig.
2 and Fig.
3 are aggregated and the result is depicted in Fig.
4.
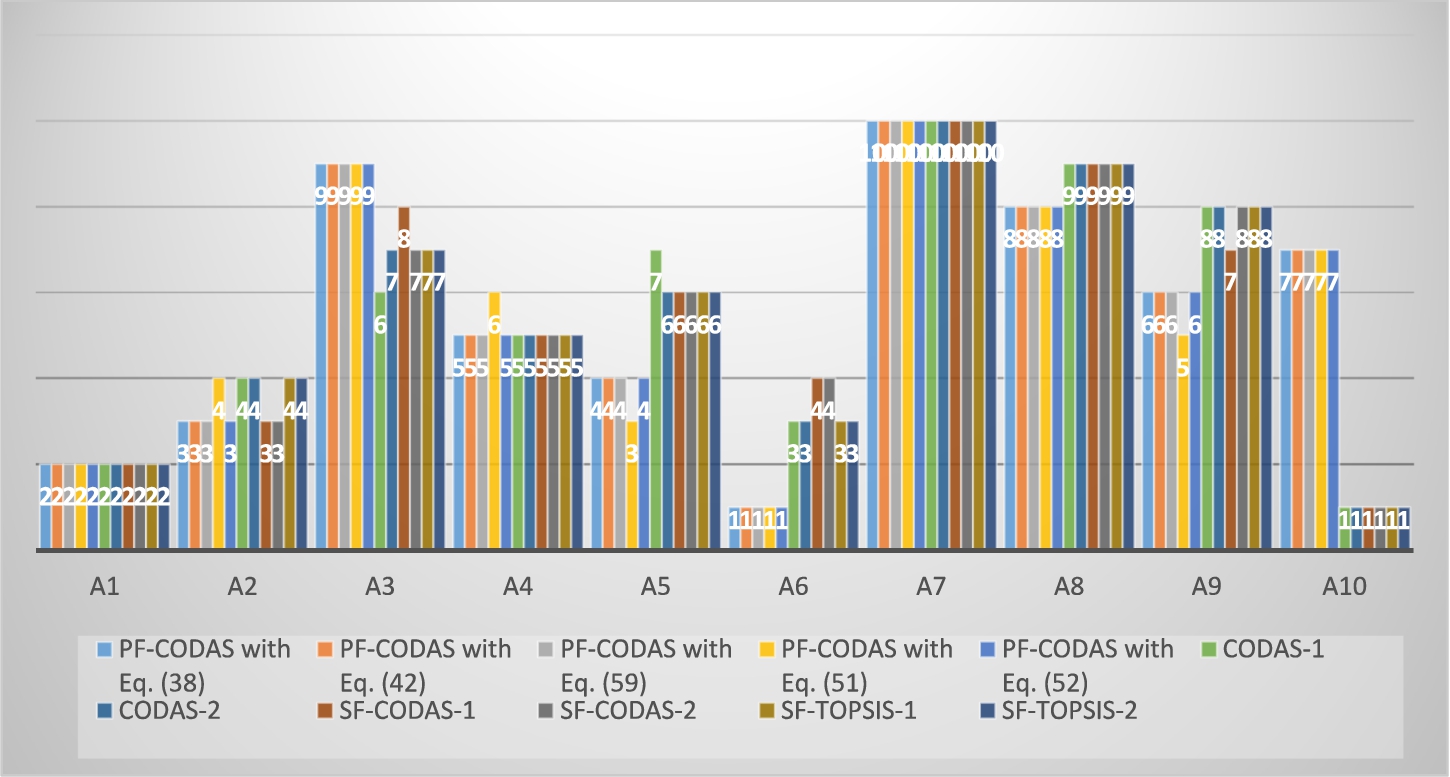
Fig. 4
A comprehensive comparison.
As Fig.
4 indicates, the most rank fluctuating alternatives are
${A_{10}}$ and
${A_{6}}$ while the rankings of the other alternatives stay in an interval. For example,
${A_{8}}$ is ranked as either 8th or 9th best while the ranking interval of
${A_{3}}$ is [6–9]. The reason for these significantly different findings can be that the PFSs allow the decision analysts to take the refusal degree into account while aiding a MADM process. Spherical fuzzy versions of CODAS and TOPSIS are selected for this comparison due to their hesitancy consideration power but they do not cope with the refusal degree of the decision-makers. In short, it seems that the fourth element considered by PF-CODAS may generate different rankings from the existing CODAS and TOPSIS versions.
For a deeper understanding of the differences generated by the proposed entropy-based SF-CODAS, Spearman’s rank correlation coefficients are also computed. Kahraman
et al. (
2009) proposed the usage of this statistical tool for revealing the differences between the rankings of various methods under group environment. Eq. (
67) shows Spearman’s rank correlation coefficient. A larger coefficient indicates a larger level of consensus among the results of the compared approaches.
where
d is the difference between the rank of the alternatives determined by each pair of approaches applied.
Table
10 shows the sum of the squared differences among the ranking results of CODAS and TOPSIS versions and PF-CODAS method while Table
11 shows the correlation coefficients of
ρ. Except for 2 comparisons [CODAS-1 & PF-CODAS with Eq. (
57) and SF-CODAS-2 & PF-CODAS with Eq. (
57)],
ρ coefficients are higher than 0.60. For this case, it is concluded that there are medium to high level positive correlations among the rankings of the methods used.
Table 10
Sum of the squared differences between methods.
|
PF-CODAS with Eq. (44) |
PF-CODAS with Eq. (48) |
PF-CODAS with Eq. (66) |
PF-CODAS with Eq. (57) |
PF-CODAS with Eq. (58) |
| CODAS-1 |
64 |
64 |
64 |
76 |
64 |
| CODAS-2 |
54 |
54 |
54 |
64 |
54 |
| SF-CODAS-1 |
52 |
52 |
52 |
62 |
52 |
| SF-CODAS-2 |
58 |
58 |
58 |
70 |
58 |
| SF-TOPSIS-1 |
54 |
54 |
54 |
64 |
54 |
| SF-TOPSIS-2 |
54 |
54 |
54 |
64 |
54 |
Table 11
Spearman rank correlation coefficients between methods.
|
PF-CODAS with Eq. (44) |
PF-CODAS with Eq. (48) |
PF-CODAS with Eq. (66) |
PF-CODAS with Eq. (57) |
PF-CODAS with Eq. (58) |
| CODAS-1 |
0.612 |
0.612 |
0.612 |
0.539 |
0.612 |
| CODAS-2 |
0.673 |
0.673 |
0.673 |
0.612 |
0.673 |
| SF-CODAS-1 |
0.685 |
0.685 |
0.685 |
0.624 |
0.685 |
| SF-CODAS-2 |
0.648 |
0.648 |
0.648 |
0.576 |
0.648 |
| SF-TOPSIS-1 |
0.673 |
0.673 |
0.673 |
0.612 |
0.673 |
| SF-TOPSIS-2 |
0.673 |
0.673 |
0.673 |
0.612 |
0.673 |
7 Concluding Remarks
PFS has been recently accepted by the MADM domain as one of the useful fuzzy environments because of its extensive representation power of the preferences and opinions of decision-makers. PFS is defined by four elements, namely positive, negative, neutral, and refusal membership degrees and the first three elements can be independently assignable. The only rule that must be satisfied is that the sum of these four elements should be equal to 1.
Entropy is a very important information measure of fuzzy sets such as distance, inclusion, or similarity. In the literature, there are few entropy measures developed for PFSs. Entropy measures are exploited for determining the objective weights of attributes or the importance of decision-makers. These objective weights are found beneficial in case the subjective evaluation of weights is not desired or needed. The contributions of the study may be listed as follows:
-
• Two novel entropy measures for PFSs are developed and their proofs are given.
-
• CODAS, which is based on two different distance measures from the negative-ideal solution such as Euclidean and Hamming distance, is extended into PFS for the first time in the literature. Although spherical fuzzy and neutrosophic versions of CODAS can handle the hesitancy degree of the decision-makers, none of the current versions of CODAS are capable of handling their refusal degrees. The most powerful aspect of the novel extension is the simultaneous consideration of both the hesitancy and refusal degrees of the decision-makers.
-
• To validate the novel PF-CODAS, a real green supplier selection application for the beef industry is conducted. The rankings are compared with different applications’ rankings such as SF-TOPSIS, CODAS, and SF-CODAS. It is found that the proposed method generates different rankings of the alternatives due to the consideration of refusal degree.
-
• To understand the meaning of the differences in alternative rankings better, Spearman’s rank correlation coefficient is used, and it is seen that there are medium to high correlations among the alternative ranking results of the methods compared in the study. In future applications, this situation should be investigated deeply.
In the proposed method, there are some limitations that should be handled. To cope with the disadvantageous parts of the study, the possible improvements are listed as follows:
-
• Rather than enforcing the decision-makers to use a fixed and not-flexible linguistic term set that has PFN correspondences, a future study may work on allowing the decision-makers to directly allocate positive, neutral, and negative membership degrees so that the data collection process becomes more realistic.
-
• Further studies should investigate the reason behind the finding of generating different rankings of alternatives by PF-based MADM methods. In order to make more comprehensive comparisons, novel fuzzy set definitions such as Fermatean fuzzy sets (Senapati and Yager,
2020), diophantine fuzzy sets (Riaz and Hashmi,
2019), and bipolar soft sets (Mahmood,
2020) may be utilized.
-
• The entropy-based attribute weighting technique has some drawbacks. In some cases requiring expert opinions about the importance of attributes, subjective and objective methods can be incorporated. In this manner, the subjectivity can be kept in control while respecting the expertise of the decision-makers.
-
• In the literature, a few studies (Wang,
2009; Han and Xiao,
2009) criticized the entropy definitions from a probability perspective and claimed that entropy measure is not enough to measure information in a data set. To deal with these sorts of problems, future works can focus on studying newer objective attribute weighting methods, such as MEREC, SECA, CRITIC, maximizing standard deviation, etc. under picture fuzzy environment.
Table A1
The literature on fuzzy extensions of CODAS and their applications.
| Paper |
CODAS Version |
Hybrid Method(s) |
Application |
| Keshavarz-Ghorabaee et al. (2017) |
Fuzzy sets |
F-EDAS and F-TOPSIS for comparison |
Numerical example on market segment evaluation |
| Panchal et al. (2017) |
Fuzzy sets |
F-AHP for attribute weighting |
Selection of an optimal maintenance strategy for an Ammonia Synthesis Unit of a urea fertilizer industry located in North India |
| Peng and Garg (2018) |
Interval-valued fuzzy soft sets |
IVFS-MABAC and IVFS-WDBA for comparison |
A numerical example of emergency decision-making issue of mine accidents |
| Karaşan et al. (2019c) |
Interval-valued hesitant fuzzy sets |
F-CODAS and HF-TOPSIS for comparison |
Residential construction site selection |
| Büyüközkan and Göçer (2019) |
Intuitionistic fuzzy sets |
IF-TOPSIS and IF-VIKOR for comparison |
Prioritization of the strategies for smart city logistics |
| Karagöz et al. (2020) |
Intuitionistic fuzzy sets |
IF-WASPAS and IF-TOPSIS for comparison |
Locating an authorized dismantling centre in Turkey |
| Dahooei et al. (2018) |
Interval-valued intuitionistic fuzzy sets |
IVIF-TODIM, IVIF-COPRAS, IVIF-MABAC for comparison |
Evaluation of business intelligence for enterprise systems |
| Bolturk and Kahraman (2018) |
Interval-valued intuitionistic fuzzy sets |
CODAS for comparison |
Evaluation of wave energy technology investments in Turkey |
| Roy et al. (2019) |
Interval-valued intuitionistic fuzzy sets |
The linear programming model for attribute weighting CODAS, F-CODAS, IVIF-VIKOR, IVIF-TOPSIS for comparison |
Numerical example on an automotive parts factory in India searching for the best material for the automotive instrument panel |
| Yeni and Özçelik (2019) |
Interval-valued intuitionistic fuzzy sets |
IVIF-TOPSIS, IVIF-VIKOR, IVIF-SAW for comparison |
Personnel selection for an engineering position in a company |
| Dahooei et al. (2020) |
Interval-valued intuitionistic fuzzy sets |
– |
Choosing the appropriate system for cloud computing implementation in Iran |
| Deveci et al. (2020) |
Interval-valued intuitionistic fuzzy sets |
– |
Evaluation of renewable energy alternatives in Turkey |
| Ouhibi and Frikha (2020) |
Interval-valued intuitionistic fuzzy sets |
– |
Sorting of natural resources in Tunisia |
| Remadi and Frikha (2020) |
Triangular interval-valued intuitionistic fuzzy sets |
TOPSIS, VIKOR, GRA, and CODAS for comparison |
Green supplier selection problem for olive oil |
| Seker and Aydin (2020) |
Interval-valued intuitionistic fuzzy sets |
IVIF-AHP for attribute weighting AHP&CODAS, F-AHP&F-CODAS for comparison |
Determination of the most appropriate public transportation system to transfer people along the campus |
| Yalçın and Yapıcı Pehlivan (2019) |
Hesitant fuzzy linguistic term sets |
F-EDAS, F-TOPSIS, F-WASPAS, F-ARAS, F-COPRAS for comparison |
Blue-collar personnel selection problem for a manufacturing firm in Turkey |
| Sansabas-Villalpando et al. (2019) |
Hesitant fuzzy linguistic term sets |
AHP for attribute weighting |
Appraisal of the organizational culture of innovation and complex technological changing environments |
| Mukul et al. (2020) |
Hesitant fuzzy linguistic term sets |
HFL-AHP for attribute weighting |
Evaluation of smart health technologies |
| Büyüközkan and Mukul (2020) |
Hesitant fuzzy linguistic term sets |
HFL-AHP for attribute weighting HFL-TOPSIS for comparison |
Evaluation of smart health technologies |
| Bolturk (2018) |
Pythagorean fuzzy sets |
CODAS for comparison |
Supplier selection in a manufacturing firm |
| Peng and Ma (2020) |
Pythagorean fuzzy sets |
TOPSIS and TODIM for comparison |
Several hypothetical examples |
| Büyüközkan and Göçer (2020) |
Pythagorean fuzzy sets |
– |
Selection of additive manufacturing technologies for the needs of the supply chain in Turkey |
| Bolturk and Kahraman (2019) |
Interval-valued Pythagorean fuzzy sets |
– |
Selection of the best AS/RS technology |
| Peng and Li (2019) |
Hesitant fuzzy soft sets |
HFS-WDBA |
A numerical example of an emergency decision-making issue of mine accidents |
| Wang et al. (2020) |
2-tuple linguistic neutrosophic sets |
– |
A numerical example for the safety assessment of a construction project |
| He et al. (2020) |
2-tuple linguistic Pythagorean fuzzy sets |
2TLPF-TODIM for comparison |
Numerical example on the assessment of financial management performance |
| Karaşan et al. (2019a) |
Neutrosophic sets |
IVIF-TOPSIS for comparison |
Wind energy plant location selection problem |
| Karaşan et al. (2019b) |
Neutrosophic sets |
– |
Assessment of livability index of urban districts in Turkey |
| Karaşan et al. (2020) |
Neutrosophic sets |
– |
Evaluation of defense strategies for Turkey |
| Kutlu Gündoğdu and Kahraman (2019b) |
Spherical fuzzy sets |
IF-TOPSIS and IF-CODAS for comparison |
A hypothetical example |
| Kutlu Gündoğdu and Kahraman (2020) |
Spherical fuzzy sets |
IF-TOPSIS for comparison |
Warehouse site selection problem |
| Karaşan et al. (2021) |
Spherical fuzzy sets |
– |
Assessment of livability index of suburban districts in Turkey |

