We have developed the Windkessel model of the arterial system and an agent-based blood vessel model of the CVS in order to observe changes in the pressure of the vascular system when the $LV$ pumps blood to the aorta. We explain these models and our approaches in the following subsections.
4.1 Windkessel Model
The Windkessel is a lumped parameter model of the arterial system. The Windkessel model describes the hemodynamics of the arterial system such as compliance and resistance (see Fig.
1) and is analogous to the electric circuit model (Frank,
1899; Mei
et al.,
2018).
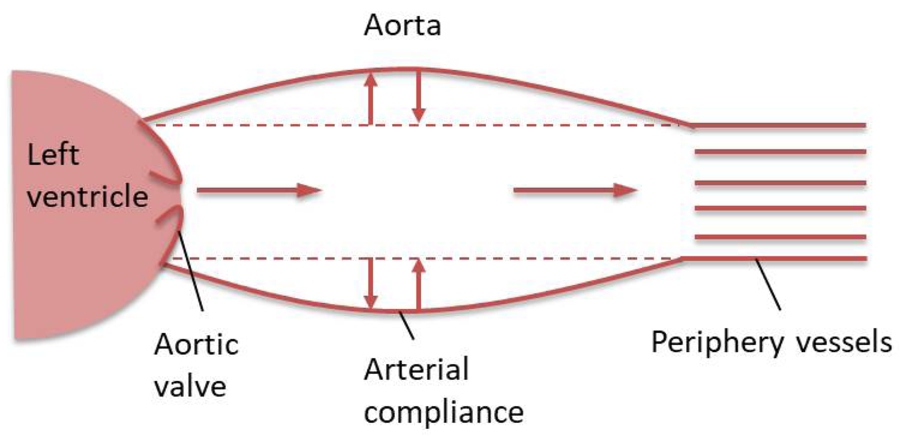
Fig. 1
Concept of the Windkessel model.
The Windkessel model takes into consideration the following parameters as shown in Fig.
1 and characterizes peripheral resistance of the aortic valve, arterial compliance and peripheral resistance of the vessels:
-
• Resistance of the aortic valve (r) refers to the flow resistance encountered by the blood as it is pumped from the heart to the arterial system.
-
• Arterial compliance (${C_{\mathrm{a}}}$) stands for the elasticity and extensibility of the aorta.
-
• Peripheral resistance (${R_{1}},{R_{2}},\dots ,{R_{n}}$) represents blood vessels’ resistance to the flow resistance encountered by the blood depending on the blood viscosity and the vessel diameter.
The original version of the Windkessel is the 2-element model, which consists of a capacitor (
C) to account for arterial compliance (
${C_{\mathrm{a}}}$) of the arterial system and a resistor (
R) to account for peripheral resistance
$({R_{1}},{R_{2}},\dots ,{R_{n}})$. The 3-element model is described by the Swiss physiologists Ph. Broemser and Otto Frank in an article published in 1930 (Broemser and Ranke,
1930). Added to the 2-element circuit is an extra resistor (
r) to represent resistance (
r) to blood flow due to the aortic valve. And, the 4-element model includes an inductor
$(L)$, which represents the inertia of the blood flow (Ortiz-Leon
et al.,
2014; Hlavac and Holcik,
2020).
The Windkessel model takes into account the effects of arterial compliance and total peripheral resistance determined by the systolic and diastolic phases of the cardiac cycle. As shown in Table
1,
$u(t)$ and
$i(t)$ represent blood pressure and blood flow and both are functions of the time,
t. Using Kirchoff’s law for currents, the differential equation of the 2-element Windkessel model is given as:
During the diastole phase, the
$LV$ expands and
$i(t)=0$. Then,
$u(t)$ is calculated by:
${t_{d}}$ is the starting time of the diastole.
The differential equation of the 3-element Windkessel model is given as:
In the 2- or 3-element Windkessel model, no defined time-varying potential
$u(t)$ is applied to the circuit. Therefore, the output of the Windkessel circuit does not reflect the real behaviour of the arterial system from the timing perspective. In order to realize the systole and diastole phases of the cardiac cycle, we designed an astable multivibrator (Craig,
1994) circuit that provides a clock signal with unequal low and high intervals of 0.3 s and 0.5 s, respectively.
Given that it does not have a stable operating state, an astable multivibrator oscillates back and forth between reset and set states. Also referred to as clock circuits, astable multivibrators are used to provide a clock signal to digital circuits so that these can operate. Figure
3a shows a circuit diagram of an astable multivibrator. A characteristic of an astable multivibrator is the availability of two outputs (0 and 1) that are logically inverse. The action of the transistors in a multivibrator can be considered an ideal switch. If a transistor is off, it does not draw a current through the collector-emitter and is an open-circuit. Thus, the power supply voltage
$+{V_{\mathrm{CC}}}$ drops at the collector-emitter terminals. If the transistor is on, the voltage across the base-emitter,
${({V_{\mathrm{BE}}})_{\mathrm{on}}}$ is 0.7 V for silicon transistors. Thus, the collector-emitter voltage is near 0 V. In Fig.
3a, the cross-coupling components are capacitors
${C_{2}}$ and
${C_{1}}$ such that the circuit does not have a stable operating state so that the output of the astable multivibrator switches constantly between two states. Figure
2 shows the collector-emitter and base-emitter waveforms of the astable multivibrator.
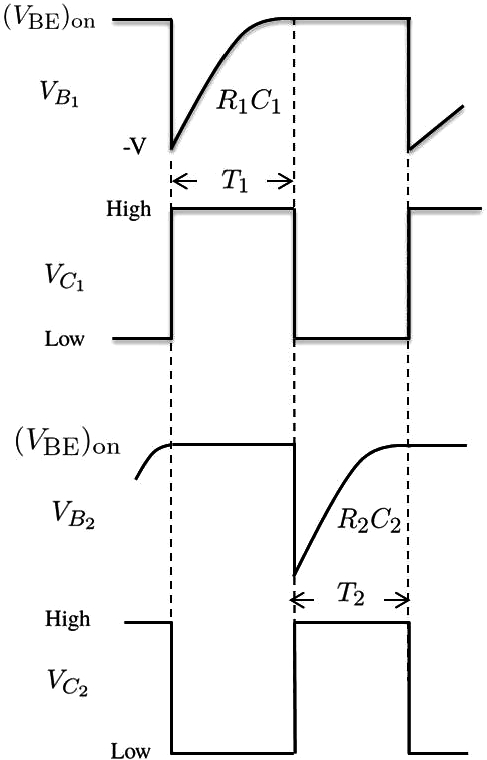
Fig. 2
Waveforms of an astable multivibrator.
The period of the wavefoms
$(T)$ is composed by pulse interval
${T_{1}}$ and pulse interval
${T_{2}}$ of the output waveforms. In order to calculate the period of the waveform, a general solution for step response of an
$RC$ circuit is given by the following formula:
By using equation (
4), the voltage across the capacitor
${C_{1}}$ or
${C_{2}}$ can be derived. However, we use (
4) to find the lengths of
${T_{1}}$ and
${T_{2}}$ pulse intervals. In (
4), the initial voltages on capacitors are denoted by
${V_{\mathrm{initial}}}$ at
$t=0$, whereas the expected final voltages on capacitors are denoted by
${V_{\mathrm{final}}}$ for
$t={T_{1}}$ or
$t={T_{2}}$. Therefore, (
1) requires that
${V_{\mathrm{initial}}}$ replace
$-({V_{\mathrm{CC}}}-{({V_{\mathrm{BE}}})_{\mathrm{on}}})$,
${V_{\mathrm{final}}}$ replace
${V_{\mathrm{CC}}}$. In order to calculate
${T_{1}}$ or
${T_{2}}$,
${V_{C}}(t)$ replace
${({V_{\mathrm{BE}}})_{\mathrm{on}}}$ since
${V_{C}}(t)$ reaches
${({V_{\mathrm{BE}}})_{\mathrm{on}}}$ at the end of the
${T_{1}}$ or
${T_{2}}$ time intervals while the base voltage of transistor increases exponentially from
$-({V_{\mathrm{CC}}}-{({V_{\mathrm{BE}}})_{\mathrm{on}}})$ to
$+{V_{\mathrm{CC}}}$. Then, we yield
For this circuit to work,
${V_{\mathrm{CC}}}\gg {V_{\mathrm{BE}}}$ (for example:
${V_{\mathrm{CC}}}=12$ V,
${V_{\mathrm{BE}}}=0.7$ V), therefore the equation can be simplified to:
In our design, the astable multivibrator has the component values of
${R_{1}}=33\hspace{2.5pt}\text{K}\Omega $,
${R_{2}}=22\hspace{2.5pt}\text{K}\Omega $,
$\textit{RC}=270\hspace{2.5pt}\text{Ω}$, and
${C_{1}}={C_{2}}=22\hspace{2.5pt}\text{μ}\text{F}$. When power is turned on,
${V_{\mathrm{CC}}}$ supplies 12 V to the circuit. Transistors
${Q_{1}}$ and
${Q_{2}}$ are chosen as BC238 NPN Epitaxial Silicon Transistor. We expect to yield the period of circuit output waveforms using equations as follows:
According to the calculations, ${T_{1}}$ is expected to exhibit the diastole phase and ${T_{2}}$ to exhibit the systole phase of the cardiac cycle. The astable multivibrator arranges the systole and diastole phases in a timely way by using the ${R_{1}}$, ${R_{2}}$, ${C_{1}}$ and ${C_{2}}$ components. These components are defined to adjust time intervals for the diastole and systole phases.
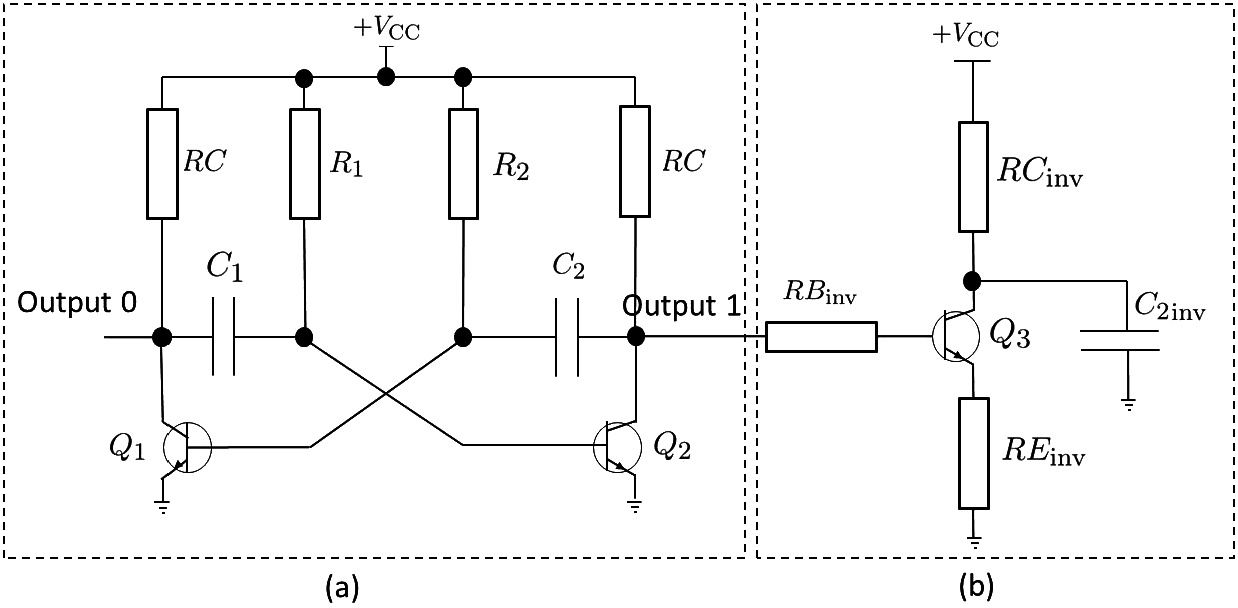
Fig. 3
Proposed Windkessel model: (a) astable multivibrator circuit; (b) inverter circuit.
The astable multivibrator followed by an inverter (see Fig.
3b) is sufficient to obtain cardiac events during the cardiac cycle. The inverter circuit operates in the following way: If the input to the inverter is logical 0, the transistor of that circuit is held in cutoff such that there is no base current and the base-emitter appears as an open circuit. If there is no base current, there is no collector current and the output voltage is the supply voltage value. If the input to the inverter is logical 1 (12 V), the transistor becomes saturated and the transistor begins to turn on. When the output waveform of the collector of the transistor
${Q_{2}}$ of the astable multivibrator is inputted to an inverter circuit (see Fig.
3), the inverter becomes saturated or is held in cutoff. When the input voltage of the inverter is near 0 V, then the transistor of the inverter is turned off and the capacitor
${C_{2}}$${_{\mathrm{inv}}}$ charges through the resistor
$R{C_{\mathrm{inv}}}$. When the input voltage is fixed at
$+{V_{\mathrm{CC}}}$, the transistor becomes saturated and the capacitor
${C_{2}}$${_{\mathrm{inv}}}$ discharges through the collector-emitter of the inverter. The operation repeats indefinitely.
The inverter circuit represents the aortic valve of the heart. A resistor
$R{B_{\mathrm{inv}}}$ at the base terminal is added in series to account for this resistance to blood flow due to the aortic valve. From the perspective of physiology, the transistor of the inverter circuit behaves like a switch representing a valve that allows blood flow. Capacitor
${C_{2}}$${_{\mathrm{inv}}}$ models the compliance of the arterial system: When blood is pumped through the aortic valve into the aortic arch, the walls of the aorta expand. The capacitor charges to near the supply voltage at the beginning of the systole phase. Resistor
$R{E_{\mathrm{inv}}}$, which is connected to the emitter of the inverter, represents the peripheral resistance of the systemic arterial system in order to dissipate the energy stored in
${C_{2}}$${_{\mathrm{inv}}}$ (arterial compliance). When the elapsed time exceeds five time constants, the capacitor releases its stored energy to the resistor and the capacitor voltage approaches zero. The time constant
τ for the RC circuit (Craig,
1994) equals the product of the resistance and capacitance. The value of
$R{E_{\mathrm{inv}}}$ is selected such that the capacitor
${C_{2}}$${_{\mathrm{inv}}}$ cannot be discharged entirely as the switching time of the inverter is less than 5
τ and the voltage across the capacitor during the diastole phase decreases to 7 V or lower.
The astable multivibrator represents the left heart from the perspective of physiology. The transistor ${Q_{2}}$, capacitor ${C_{2}}$, and resistor ${R_{2}}$ together represent the LV, and the transistor ${Q_{1}}$, capacitor ${C_{1}}$, and resistor ${R_{1}}$ together represent the LA. The voltage drops at the collectors of ${Q_{2}}$ and ${Q_{1}}$, representing a change in the pressure at the ventricle and the atrium, respectively.
In the diastole phase, the LV is relaxed. In this case, the collector voltage of transistor ${Q_{2}}$ is 0 V, which represents the pressure of the LV. The sinoatrial (SA) node triggers the LA to contract (i.e. the pressure increases at the LA), and in the astable multivibrator, the voltage across the collector of ${Q_{1}}$ increases to $+{V_{\mathrm{CC}}}$, which represents the pressure of the LA. At the other side, capacitor ${C_{1}}$ discharges through resistor ${R_{1}}$ (i.e. the LA empties its contents), as the collector voltage of ${Q_{2}}$ is 0 V. The voltage drop at capacitor ${C_{1}}$ increases from – $({V_{\mathrm{CC}}}-{({V_{\mathrm{BE}}})_{\mathrm{on}}})$ to 0 V and then reaches 0.7 V, thereby causing transistor ${Q_{1}}$ to turn on after the time interval determined by the product of ${R_{1}}$ and ${C_{1}}$. At the same time, ${Q_{2}}$ starts to turn off.
Moreover, when the inverter circuit is connected to the collector of the ${Q_{2}}$, the current will not flow from the collector of ${C_{2}}$ through the inverter (i.e. blood will not flow from the ventricle through the aorta) during the diastole phase, since the collector voltage of transistor ${Q_{2}}$ is 0 V. Therefore, the transistor of the inverter is held in cutoff. The capacitor at the output is charged through the resistor connected to the power supply, and it represents the pressure inside the aorta.
In the systole phase, the LV contracts and pumps the blood out of the arteries. At the same time, when the LA is relaxed, the voltage drop on the collector of ${Q_{1}}$ is near 0 V in the circuit. The voltage drop on the collector of the ${Q_{2}}$ transistor is $+{V_{\mathrm{CC}}}$, which means that the maximum pressure occurs at the LV at this time. On the right-hand side, the emitter of the inverter circuit is connected to the ground. Because of the potential difference between the emitter of ${Q_{3}}$ and the collector of the ${Q_{2}}$, a current flows from the collector of ${Q_{2}}$ through the emitter of the inverter. Thus, transistor ${Q_{3}}$ is turned on and the capacitor at the output discharges through the emitter of ${Q_{3}}$. The voltage drop across the capacitor decreases to 7 V because of the $R{E_{\mathrm{inv}}}$ connected to the emitter of ${Q_{3}}$. This means that the pressure in the aorta decreases. The transistor ${Q_{3}}$ as a switch represents the aorta valve from the physiology perspective.
4.2 Agent-Based Blood Vessel Model
Agent-based modelling and simulation (ABMS) is a rule-based computational modelling approach that focuses on rules and interactions among the individuals or components of a real system. ABMS is useful for representing, creating, analysing, and experimenting with artificial worlds populated by agents that behave autonomously and interact with other agents or collective entities (Di Marzo Serugendo
et al.,
2011). In ABMS, each agent has its own characteristics and behaviour, and each act as a component of the system. The behaviour of any given agent may affect other agents in a simulated environment. During the simulation, the agents’ interactions with each other and/or with their environment may reveal behaviour patterns not defined in the system (emergence phenomena). Time in the simulation environment is typically represented as a time step or tick count. In each time step, each agent performs actions, interacts with other agents, and/or interacts with other components in the environment.
In a previous study (Bora
et al.,
2019), we have developed an agent-based blood vessel model of the CVS. However, in the present study, we observed changes in the pressure of the arterial system through the aorta when the LV pumps blood to the aorta. Thus, we have implemented an agent-based blood vessel approach to model the behaviour of the aorta.
In agent-based blood vessel model, the aorta is divided into segments referred to as aorta agents (see Fig.
4), each of which mimics the aorta’s functionality.
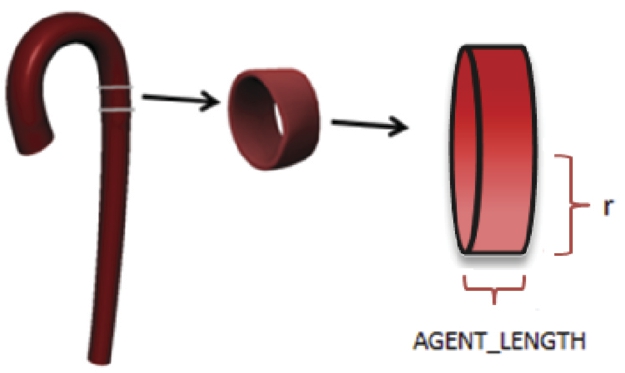
Fig. 4
Agent-based aorta model.
Information is transferred between consecutive agents. When the LV contracts, the pressure on the first aorta agent reaches its maximum value in the cardiac cycle. This pressure value is transferred to the second aorta agent. In the next cardiac simulation cycle, the aortic pressure on the second aorta agent reaches its maximum value and is transferred to the next aorta agent, and so on. We implement the well-known pattern of publish-subscribe in order to provide interaction between the agents. Each agent subscribes itself to the corresponding agent and publishes messages in order to propagate messages to its listeners. On receiving a message, an agent updates itself (adapts itself if required) and regulates its behaviour according to the current environment situation. Each aorta agent evaluates its current situation according to its local knowledge and behaves accordingly (Bora
et al.,
2019).
In Fig.
5, the aortic pressure waveform is represented in respect to time. The aorta can be in one of the following states in a cardiac cycle: systolic uptake, systolic decline, dicrotic notch, diastolic runoff, and end-diastolic pressure. When the LV pumps blood into the aorta, the pressure in the aorta is at its maximum value. Before the LV ejects the blood to the aorta, the pressure in the aorta is at its minimum value.
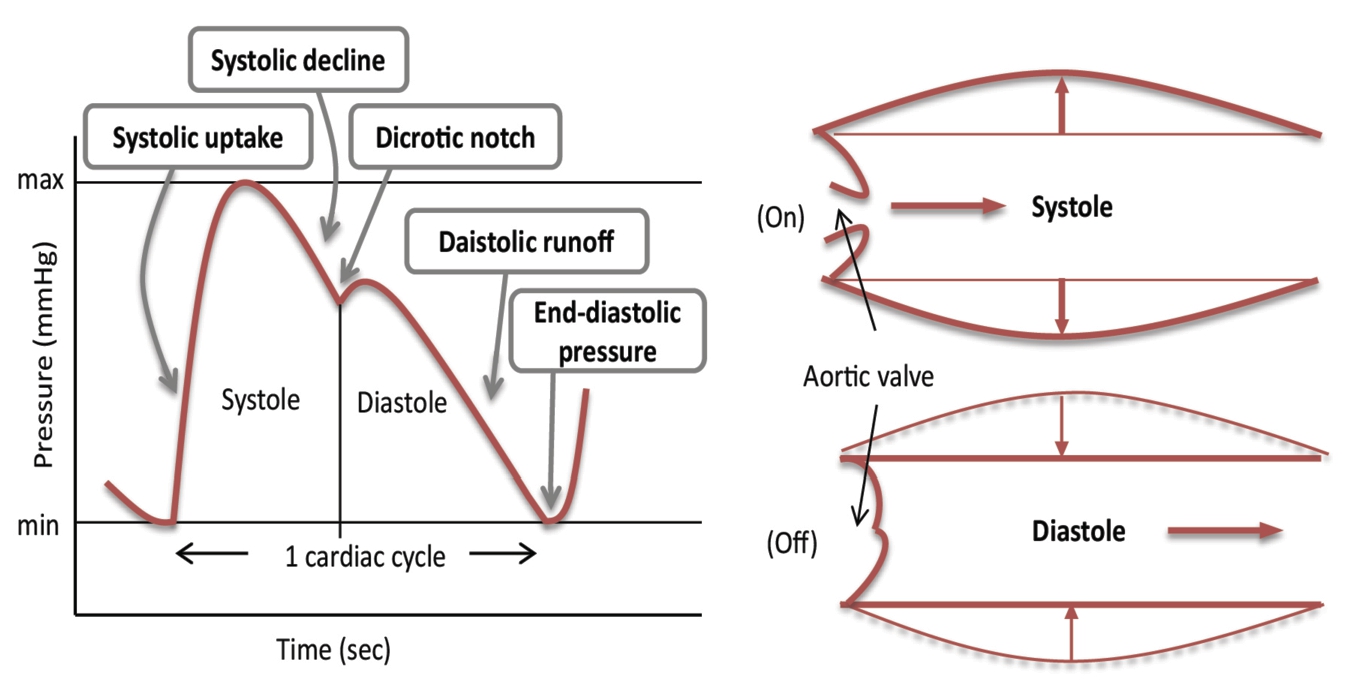
Fig. 5
Aortic pressure waveform.
We show the cardiac cycle in the state machine in Fig.
6. We use the state machine to represent the agent’s states. The state machine is an abstract concept used to design algorithms or/and describe program interactions. It is defined as an initial state, a set of input and output events, a set of new states that result from the input events, a set of possible actions that result from a new state. During a cardiac cycle, each agent is being at an agent state which is defined in the state machine at a time (Cakırlar,
2015).

Fig. 6
State machine of the aorta during a cardiac cycle.
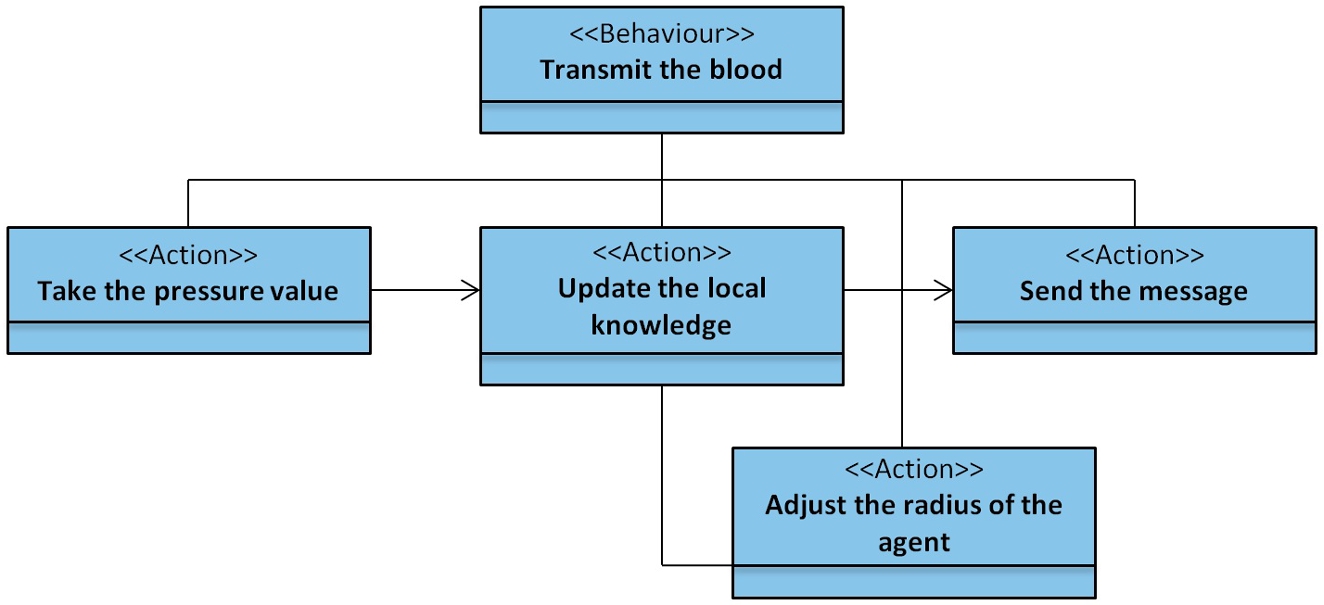
Fig. 7
Aorta agents’ behaviour.
Figure
7 shows the behaviour of the aorta agents that transmit oxygen-rich blood. Aorta agents represent a specific aortic cross-section. The message transmitted through the aorta agents is that the blood pressure value is to be pumped from the LV of the heart. Each aorta agent updates the value of its pressure according to its radius and other vessel parameter values (length, resistance, volume, compliance, etc.) and sends these values to neighbour agents. If the incoming pressure value indicates that dilation is necessary, the radius of the aorta is adjusted.
At any given time, the aorta agents can be in various states: whereas some are in systolic uptake, others can be in systolic decline, dicrotic notch, diastolic runoff, or end-diastolic pressure. In order to represent a wave of pressure, a cardiac cycle is represented in 100 simulation cycles (see Fig.
5). The aorta agents’ states in a cardiac cycle that we observed and the corresponding simulation cycles (
n) and formula for obtaining the value of the pressure at the
nth cycle are given in Table
2.
Table 2
Aorta agent states during a cardiac cycle and associated pressure values.
| Aorta agent state |
Cardiac cycle phase |
Simulation cycle (n) |
Pressure (n) |
| Systolic uptake |
Systole |
1–20 |
Pressure($n-1$) + U(2.0, 3.0) |
| Systolic decline |
Systole |
21–30 |
Pressure($n-1$) + U(2.0, 3.0) |
| Dicrotic notch |
Diastole |
31–40 |
Pressure($n-1$) + U(0.5, 1.0) |
| Diastolic runoff |
Diastole |
41–90 |
Pressure($n-1$) + U(0.5, 1.0) |
| End-diastolic pressure |
|
91–100 |
Pressure($n-1$) + U(8.0, 8.5) |
In Table
2, the pressure values for each state of agents are calculated uniformly.
$U(a,b)$ is represented by the value uniformly distributed in
$[a,b]$.

