1 Introduction
Until now, users’ attentiveness in mobile communication is increasing and is analogous to this concern; Smartphone developers have manufactured various latest models. As per the survey report of the International Telecommunication Union (ITU) (ITU, 2017), the utilization of communication technologies is increased, while communication costs are reduced. Due to quick evolution in Smartphone models, the subscribers have faced decision making complexity when acquiring the most desirable Smartphone. Moreover, the young generations are using Smartphones not only for phone calls, but also for numerous functions, viz., internet access, camera, music, and video players, and so on. For that reason, the customers desire to select the Smartphone by considering different qualitative and quantitative criteria. Quantitative criteria contain camera quality, RAM size, battery capacity, built-in memory, screen dimension, processor type, and cost, while qualitative criteria contain durability, user-friendliness, and brand.
Nowadays, MCDM approaches are extensively applied to elucidate the problems, namely Smartphone selection problem. However, MCDM problems differ according to the solution status and the approaches’ implementation. Up until now various MCDM approaches have been proposed in the literature, like the TOPSIS (Akyene,
2012; Mishra,
2016; Mishra
et al.,
2017a; Büyüközkan and Güleryüz,
2016), VIKOR (Vls Kriteriju miska Optimizacija I Kompromisno Resenje) (Hu
et al.,
2014; Mishra and Rani,
2019; Rani and Mishra,
2020a; Rani
et al.,
2019b), ELECTRE (ELimination and Choice Expressing REality) (Chen
et al.,
2018; Mishra
et al.,
2020a), WASPAS (Weighted Aggregates Sum Product Assessment) (Mishra
et al.,
2019a; Rani and Mishra,
2020b), PROMETHEE (Rani and Jain,
2017; Liao
et al.,
2018), MULTIMOORA (Wu
et al.,
2018) and GLDS (Wu and Liao,
2019) methods. From the literature, various MCDM approaches have been applied to identify the most desirable Smartphone (Hu
et al.,
2014; Akyene,
2012; Büyüközkan and Güleryüz,
2016; Wu
et al.,
2018). Hu
et al. (
2018) proposed a procedure that can promote mobile-commerce improvement towards attaining the aspiration level in a fuzzy setting. They developed fusion model to conduct the feedback-effect and dependency among criteria, and it combined the DEMATEL, DANP, and GRA methods.
The MABAC is an original MCDM approach pioneered by Pamučar and Ćirović (
2015). MABAC has an easy computational process, organized procedure, and an innovative direction that determines the foundation of real-world decision-making problems. Peng and Yang (
2016) utilized MABAC method to solve R&D project assessment with Pythagorean fuzzy sets (PFSs). Under IVIFSs (interval-valued intuitionistic fuzzy sets) environment, the MABAC approach is implemented for material evaluation (Xue
et al.,
2016) and programming language selection (Mishra
et al.,
2020d). Therefore, it is an attractive explorative way to implement the MABAC in the Smartphone selection. Atanassov (
1986) developed the notion of IFSs which extends the fuzzy sets doctrine by accumulating the non-membership degree. As IFSs doctrine has widely been implemented by the researchers in various disciplines for handling uncertainties in the MCDM (Liu and Liao,
2017; Mishra and Rani,
2019), their analogous analysis is significant.
Discrimination and entropy and measures are prominent tools for tackling the ambiguous information in the various fields. Entropy measures, measurement of the degree of fuzziness for FSs and IFSs have gained huge concentration from scholars in various disciplines (Liao
et al.,
2014; Tang and Liao,
2019). To evaluate the discrimination information between IFSs, first, Vlachos and Sergiadis (
2007) proposed IF-discrimination measure, established relation between them and implemented it in various disciplines. Consequently, various prominent discrimination measures have been introduced for FSs and IFSs (Mishra
et al.,
2017b; Ansari
et al.,
2018; Rani
et al.,
2019a; Jiang
et al.,
2019; Liang
et al.,
2019b; Rani
et al.,
2020; Mishra
et al.,
2020b,
2020c; Kumari and Mishra,
2020).
Nevertheless, from the literature, it is examined that all the measures do not incorporate the decision expert opinion of the preferences into the measure. In addition, the existing measure is in linear order and does not show the accurate behaviour of alternatives. As a result, by concentrating the standards of flexibility and proficiency of IFSs, this study proposes novel parametric discrimination measures. It has been observed from the literature that the existing discrimination measures are the special cases of the developed one. Next, to estimate the weights criteria, the developed IF-discrimination measures have been applied. Using this procedure for weighting criteria, an intuitionistic fuzzy MABAC (IF-MABAC) approach is developed to deal with MCDM problems. Now, we implement only subjective considerations of options; however, developed method is appropriate for ordinary MCDM circumstances with objective and/or subjective evaluations. Further, a Smartphone selection problem is considered to elucidate the procedure and interpret the performance of IF-MABAC approach in real case decision-making issues. To illustrate the reliability of the results, a comparative discussion between our developed approach and the other current approaches is performed to determine the validity of the results.
However, according to the above motivations, the main contributions of the paper are pointed out as
-
i. New IF-discrimination measures using the characteristics of IFSs are proposed and compared with other current discrimination measures under IFSs.
-
ii. Considering the discrimination between alternatives, a procedure to assess the criteria weights is carried out.
-
iii. After defining the border approximation area (BAA) matrix using the proposed discrimination measure, an integrated MCDM method, IF-MABAC, is developed for MCDM problems under intuitionistic fuzzy environment.
-
iv. Considering a real-life smartphone selection problem, the IF-MABAC approach is implemented to choose the desirable smartphone. The usefulness of the introduced approach is examined by comparing it with existing approaches.
The organization of this paper is as follows. In Section
2, we discuss the review of the MABAC method and existing discriminations measures for IFSs. Section
3 illustrates the research method based on the basic information of IFSs, and the recent related works about IF-discrimination measures. In Section
4, the novel IF-discrimination measures are presented, and some attractive properties of proposed measures are conferred. Section
5 presents the IF-MABAC approach for MCDM problem. In Section
6, we discuss the application of smartphone selection of IF-MABAC approach and compare it with currents works. In the last section, the conclusion of this paper is provided.
6 Application of Smartphone Selection of IF-MABAC Method
In the present section, the developed IF-MABAC approach is implemented to solve SPS problem. Seven Smartphones as alternatives are considered as follows: Apple
$({M_{1}})$, Xiaomi
$({M_{2}})$, Nokia
$({M_{3}})$, HTC
$({M_{4}})$, OPPO
$({M_{5}})$, VIVO
$({M_{6}})$ and Samsung
$({M_{7}})$, by a user who needs to purchase a smartphone and three DEs who have thorough knowledge on Smartphones (to construct DEs committee), consequently, a study of the relevant websites and the technology markets is conducted. To select a desirable Smartphone, the following 8 criteria are characterized into three main groups according to the DEs opinions, namely, technical specifications (e.g. storage capacity & RAM, camera, battery power, processor type, operating system), physical specifications (viz., screen size), and user-oriented features (viz., ease of use, price). The operational parameters are given as follows: Price
$({F_{1}})$, Battery Power
$({F_{2}})$, Camera
$({F_{3}})$, Storage Capacity and RAM
$({F_{4}})$, Processor Type
$({F_{5}})$, Screen Size
$({F_{6}})$, Ease of Use
$({F_{7}})$ and Operating System
$({F_{8}})$ (see Fig.
2).
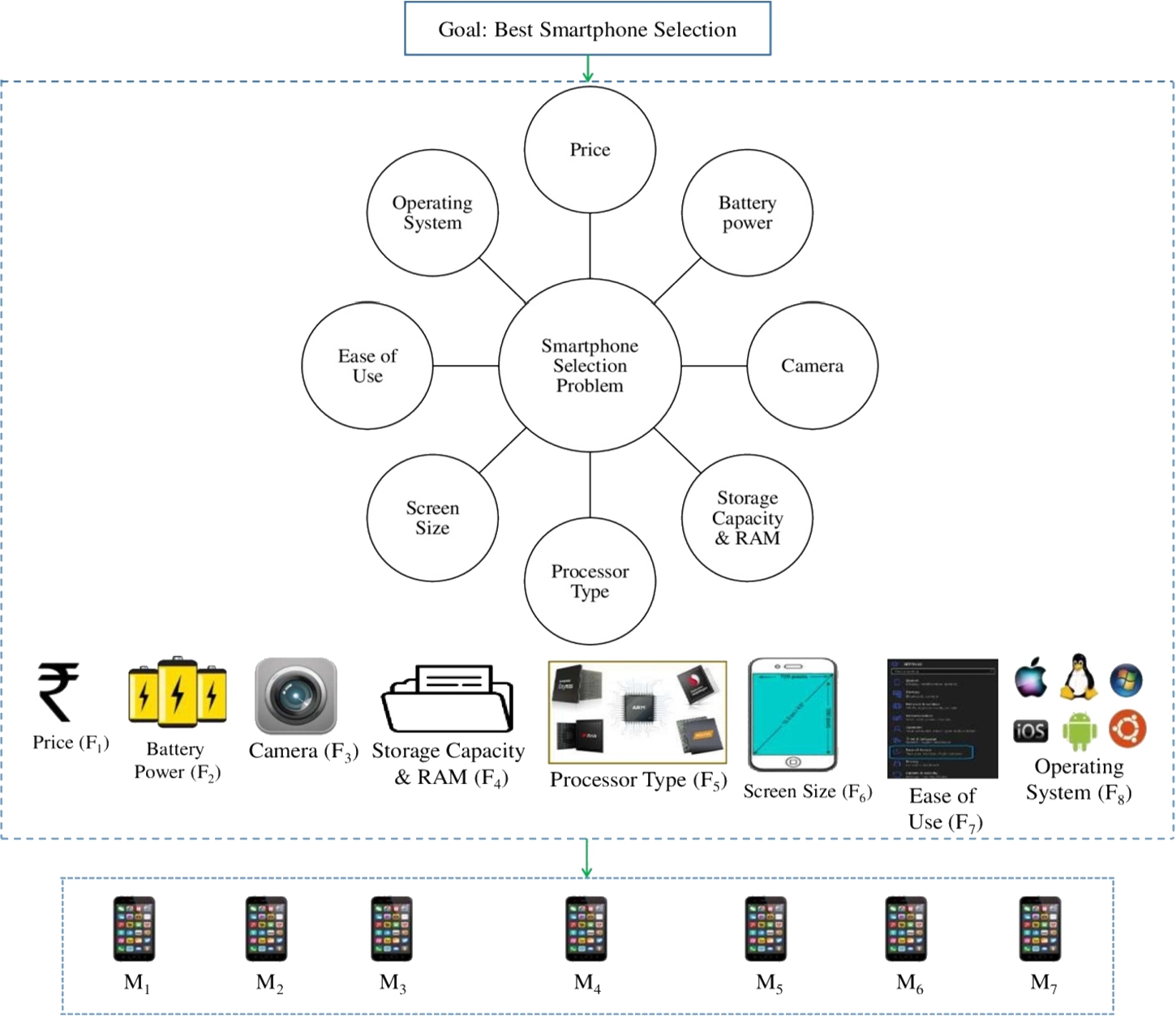
Fig. 2
Hierarchical configuration of Smartphone selection problem.
Here, Table
3 and Table
4 describe the linguistic terms (LTs) in the forms of IFNs for the criteria and DEs importance. According to these two tables and Eq. (
9), the DEs’ weights are calculated and presented in Table
5. The linguistic values illustrated in Table
6 by three DEs under the criteria parameters of specified SPSs.
Table 3
The LTs to rate the significant criteria and DEs.
| LTs |
IFNs |
| Very Significant (VS) |
(0.90, 0.10) |
| Significant (S) |
(0.80, 0.15) |
| Moderate (M) |
(0.65, 0.30) |
| Insignificant (IS) |
(0.45, 0.50) |
| Very Insignificant (VI) |
(0.20, 0.70) |
Table 4
The LTs to rate the Smartphones selection.
| LTs |
IFNs |
| Extremely High (EH) |
$(1.00,0.00)$ |
| Very High (VH) |
$(0.90,0.10)$ |
| High (H) |
$(0.70,0.20)$ |
| Average (A) |
$(0.60,0.30)$ |
| Low (L) |
$(0.40,0.50)$ |
| Very Low (VL) |
$(0.20,0.70)$ |
| Extremely Low (EL) |
$(0.10,0.80)$ |
Table 5
The significance of the weights by experts.
|
${E_{1}}$ |
${E_{2}}$ |
${E_{3}}$ |
| LTs |
Very significant |
Significant |
Moderate |
| IFNs |
$(0.90,0.10)$ |
$(0.80,0.15)$ |
$(0.65,0.30)$ |
| Weight |
0.3709 |
0.3470 |
0.2821 |
Table 6
The linguistic variable for Smartphones rating.
| Parameters |
Smartphone |
Experts |
| ${E_{1}}$ |
${E_{2}}$ |
${E_{3}}$ |
| Price $({F_{1}})$
|
${M_{1}}$ |
H |
H |
H |
|
${M_{2}}$ |
L |
L |
A |
|
${M_{3}}$ |
H |
H |
H |
|
${M_{4}}$ |
H |
VH |
H |
|
${M_{5}}$ |
VL |
H |
H |
|
${M_{6}}$ |
VL |
A |
VH |
|
${M_{7}}$ |
H |
VH |
H |
| Battery power $({F_{2}})$
|
${M_{1}}$ |
H |
VH |
VH |
|
${M_{2}}$ |
A |
VH |
H |
|
${M_{3}}$ |
VH |
VH |
A |
|
${M_{4}}$ |
VH |
H |
H |
|
${M_{5}}$ |
A |
VH |
H |
|
${M_{6}}$ |
H |
A |
VH |
|
${M_{7}}$ |
H |
VH |
VH |
| Camera $({F_{3}})$
|
${M_{1}}$ |
A |
VH |
VH |
|
${M_{2}}$ |
H |
A |
A |
|
${M_{3}}$ |
A |
A |
H |
|
${M_{4}}$ |
A |
VH |
VH |
|
${M_{5}}$ |
L |
VH |
H |
|
${M_{6}}$ |
L |
VH |
H |
|
${M_{7}}$ |
A |
VH |
VH |
| Storage capacity and RAM $({F_{4}})$
|
${M_{1}}$ |
L |
A |
VH |
|
${M_{2}}$ |
VH |
A |
VH |
|
${M_{3}}$ |
L |
H |
VH |
|
${M_{4}}$ |
L |
H |
H |
|
${M_{5}}$ |
L |
H |
VH |
|
${M_{6}}$ |
H |
L |
H |
|
${M_{7}}$ |
VH |
A |
VH |
| Processor type $({F_{5}})$
|
${M_{1}}$ |
A |
H |
H |
|
${M_{2}}$ |
A |
H |
H |
|
${M_{3}}$ |
H |
H |
A |
|
${M_{4}}$ |
H |
H |
A |
|
${M_{5}}$ |
A |
H |
A |
|
${M_{6}}$ |
H |
H |
A |
|
${M_{7}}$ |
VH |
VH |
VH |
| Screen size $({F_{6}})$
|
${M_{1}}$ |
VH |
VH |
H |
|
${M_{2}}$ |
H |
VH |
A |
|
${M_{3}}$ |
H |
H |
VH |
|
${M_{4}}$ |
H |
H |
VH |
|
${M_{5}}$ |
H |
VH |
A |
|
${M_{6}}$ |
VH |
VH |
H |
|
${M_{7}}$ |
VH |
VH |
H |
| Ease of use $({F_{7}})$
|
${M_{1}}$ |
A |
H |
VH |
|
${M_{2}}$ |
A |
H |
VH |
|
${M_{3}}$ |
H |
L |
A |
|
${M_{4}}$ |
H |
L |
A |
|
${M_{5}}$ |
L |
H |
H |
|
${M_{6}}$ |
L |
VH |
H |
|
${M_{7}}$ |
VH |
H |
VH |
| Operating system $({F_{8}})$
|
${M_{1}}$ |
A |
A |
H |
|
${M_{2}}$ |
H |
A |
H |
|
${M_{3}}$ |
A |
A |
H |
|
${M_{4}}$ |
A |
VH |
A |
|
${M_{5}}$ |
A |
VH |
A |
|
${M_{6}}$ |
H |
A |
H |
|
${M_{7}}$ |
A |
A |
VH |
According to DEs weights obtained by Eq. (
9), and Eq. (
5), IF-ADM regarding SPSs is constructed and shown in Table
7. Since one criterion is non-benefit type and the remaining are benefit type, by Eq. (
11), Table
8 depicts the normalized decision matrix for SPSs.
Table 7
The IF-ADM for Smartphones.
|
${M_{1}}$ |
${M_{2}}$ |
${M_{3}}$ |
${M_{4}}$ |
${M_{5}}$ |
${M_{6}}$ |
${M_{7}}$ |
| ${F_{1}}$ |
(0.7000, 0.2000) |
(0.4648, 0.4329) |
(0.7000, 0.2000) |
(0.7951, 0.1572) |
(0.5684, 0.3183) |
(0.6502, 0.3013) |
(0.7951, 0.1572) |
| ${F_{2}}$ |
(0.8493, 0.1293) |
(0.7720, 0.1828) |
(0.8521, 0.1363) |
(0.8004, 0.1547) |
(0.7720, 0.1828) |
(0.7568, 0.1893) |
(0.8493, 0.1293) |
| ${F_{3}}$ |
(0.8328, 0.1503) |
(0.6405, 0.2581) |
(0.6312, 0.2676) |
(0.8328, 0.1503) |
(0.7350, 0.2209) |
(0.7350, 0.2209) |
(0.8328, 0.1503) |
| ${F_{4}}$ |
(0.6856, 0.2660) |
(0.8382, 0.1464) |
(0.7154, 0.2310) |
(0.6121, 0.2809) |
(0.7154, 0.2310) |
(0.6184, 0.2749) |
(0.8382, 0.1464) |
| ${F_{5}}$ |
(0.6662, 0.2325) |
(0.6662, 0.2325) |
(0.6746, 0.2242) |
(0.6746, 0.2242) |
(0.6380, 0.2606) |
(0.6746, 0.2242) |
(0.9000, 0.1000) |
| ${F_{6}}$ |
(0.8637, 0.1216) |
(0.7778, 0.1763) |
(0.7799, 0.1645) |
(0.7799, 0.1645) |
(0.7778, 0.1763) |
(0.8637, 0.1216) |
(0.8637, 0.1216) |
| ${F_{7}}$ |
(0.7552, 0.1912) |
(0.7552, 0.1912) |
(0.5862, 0.3082) |
(0.5862, 0.3082) |
(0.6121, 0.2000) |
(0.7350, 0.2209) |
(0.8536, 0.1272) |
| ${F_{8}}$ |
(0.6312, 0.2676) |
(0.6685, 0.2302) |
(0.6312, 0.2676) |
(0.7527, 0.2049) |
(0.7527, 0.2049) |
(0.6685, 0.2302) |
(0.7295, 0.2201) |
Table 8
The normalized IF-ADM for Smartphones.
|
${M_{1}}$ |
${M_{2}}$ |
${M_{3}}$ |
${M_{4}}$ |
${M_{5}}$ |
${M_{6}}$ |
${M_{7}}$ |
| ${F_{1}}$ |
(0.2000, 0.7000) |
(0.4329, 0.4648) |
(0.2000, 0.7000) |
(0.1572, 0.7951) |
(0.3183, 0.5684) |
(0.3103, 0.6502) |
(0.1572, 0.7951) |
| ${F_{2}}$ |
(0.8493, 0.1293) |
(0.7720, 0.1828) |
(0.8521, 0.1363) |
(0.8004, 0.1547) |
(0.7720, 0.1828) |
(0.7568, 0.1893) |
(0.8493, 0.1293) |
| ${F_{3}}$ |
(0.8328, 0.1503) |
(0.6405, 0.2581) |
(0.6312, 0.2676) |
(0.8328, 0.1503) |
(0.7350, 0.2209) |
(0.7350, 0.2209) |
(0.8328, 0.1503) |
| ${F_{4}}$ |
(0.6856, 0.2660) |
(0.8382, 0.1464) |
(0.7154, 0.2310) |
(0.6121, 0.2809) |
(0.7154, 0.2310) |
(0.6184, 0.2749) |
(0.8382, 0.1464) |
| ${F_{5}}$ |
(0.6662, 0.2325) |
(0.6662, 0.2325) |
(0.6746, 0.2242) |
(0.6746, 0.2242) |
(0.6380, 0.2606) |
(0.6746, 0.2242) |
(0.9000, 0.1000) |
| ${F_{6}}$ |
(0.8637, 0.1216) |
(0.7778, 0.1763) |
(0.7799, 0.1645) |
(0.7799, 0.1645) |
(0.7778, 0.1763) |
(0.8637, 0.1216) |
(0.8637, 0.1216) |
| ${F_{7}}$ |
(0.7552, 0.1912) |
(0.7552, 0.1912) |
(0.5862, 0.3082) |
(0.5862, 0.3082) |
(0.6121, 0.2000) |
(0.7350, 0.2209) |
(0.8536, 0.1272) |
| ${F_{8}}$ |
(0.6312, 0.2676) |
(0.6685, 0.2302) |
(0.6312, 0.2676) |
(0.7527, 0.2049) |
(0.7527, 0.2049) |
(0.6685, 0.2302) |
(0.7295, 0.2201) |
Using Eqs. (
7) and (
10), the objective weights of the criteria is computed as:
${w_{j}}={(0.2726,0.0388,0.1222,0.1479,0.1638,0.0446,0.1718,0.0383)^{T}}$. In the following, the weighted IF-ADM is made and provided in Table
9.
Table 9
The weighted IF-ADM for Smartphone selection.
|
${M_{1}}$ |
${M_{2}}$ |
${M_{3}}$ |
${M_{4}}$ |
${M_{5}}$ |
${M_{6}}$ |
${M_{7}}$ |
| ${F_{1}}$ |
(0.0590, 0.9073) |
(0.1433, 0.8115) |
(0.0590, 0.9073) |
(0.0456, 0.9394) |
(0.0992, 0.8573) |
(0.0963, 0.8893) |
(0.0456, 0.9394) |
| ${F_{2}}$ |
(0.0708, 0.9237) |
(0.0557, 0.9362) |
(0.0715, 0.9256) |
(0.0606, 0.9301) |
(0.0557, 0.9362) |
(0.0534, 0.9375) |
(0.0709, 0.9237) |
| ${F_{3}}$ |
(0.1963, 0.7933) |
(0.1175, 0.8475) |
(0.1148, 0.8512) |
(0.1963, 0.7933) |
(0.1498, 0.8315) |
(0.1498, 0.8315) |
(0.1963, 0.7933) |
| ${F_{4}}$ |
(0.1573, 0.8221) |
(0.2362, 0.7526) |
(0.1696, 0.8052) |
(0.1307, 0.8288) |
(0.1696, 0.8052) |
(0.1328, 0.8261) |
(0.2362, 0.7526) |
| ${F_{5}}$ |
(0.1645, 0.7874) |
(0.1645, 0.7874) |
(0.1680, 0.7828) |
(0.1680, 0.7828) |
(0.1533, 0.8023) |
(0.1680, 0.7828) |
(0.3142, 0.6858) |
| ${F_{6}}$ |
(0.0850, 0.9103) |
(0.0649, 0.9255) |
(0.0653, 0.9227) |
(0.0653, 0.9227) |
(0.0649, 0.9255) |
(0.0850, 0.9103) |
(0.0850, 0.9103) |
| ${F_{7}}$ |
(0.2148, 0.7526) |
(0.2148, 0.7526) |
(0.1407, 0.8169) |
(0.1407, 0.8169) |
(0.1502, 0.7584) |
(0.2040, 0.7715) |
(0.2811, 0.7017) |
| ${F_{8}}$ |
(0.0375, 0.9508) |
(0.0414, 0.9453) |
(0.0375, 0.9508) |
(0.0521, 0.9411) |
(0.0521, 0.9411) |
(0.0414, 0.9453) |
(0.0488, 0.9437) |
The BAA
$(\stackrel{\frown }{G})$ is obtained based on Table
10 and Eq. (
14), which is
$\stackrel{\frown }{G}=\{(0.0719,0.9009),(0.0622,0.9307),(0.1564,0.8219),(0.1716,0.8011),(0.1802,0.7755),(0.0730,0.9185),(0.1899,0.7702),(0.0440,0.9181)\}$.
Next, the discrimination matrix of SPSs option from BAA is evaluated by Eq. (
7) and Eq. (
15). The corresponding discrimination matrix is established and revealed in Table
10. The closeness degree of the BAA for each Smartphone is computed by Eq. (
15) and shown in Table
10. Finally, all Smartphones ranks are shown based on the values which are depicted in Table
10. As a result, Smartphone
${M_{7}}$ (Samsung) is preferred as the most desirable Smartphone among the seven SPSs.
Table 10
The discrimination matrix of all alternatives from the BAA for Smartphones.
|
${F_{1}}$ |
${F_{2}}$ |
${F_{3}}$ |
${F_{4}}$ |
${F_{5}}$ |
${F_{6}}$ |
${F_{7}}$ |
${F_{8}}$ |
${\mathbb{C}_{i}}$ |
Rank |
| ${M_{1}}$ |
−0.0001 |
0.00004 |
0.00033 |
−0.00009 |
−0.00005 |
0.0039 |
0.0004 |
−0.0003 |
0.00413 |
2 |
| ${M_{2}}$ |
0.0026 |
0.00002 |
0.0003 |
0.0008 |
0.00005 |
0.00003 |
0.0001 |
0.0001 |
0.00400 |
3 |
| ${M_{3}}$ |
0.00005 |
0.00003 |
0.0004 |
0.000003 |
0.00002 |
0.00002 |
0.0006 |
0.0003 |
0.001423 |
5 |
| ${M_{4}}$ |
0.0007 |
0.0000 |
0.0003 |
0.0003 |
0.00002 |
0.00002 |
0.0006 |
0.00004 |
0.00198 |
4 |
| ${M_{5}}$ |
0.0005 |
0.00002 |
0.00002 |
0.00002 |
0.0002 |
0.00003 |
0.00005 |
0.00004 |
0.00088 |
6 |
| ${M_{6}}$ |
0.0001 |
0.00004 |
0.00002 |
0.0003 |
0.00002 |
0.00005 |
0.00001 |
0.0001 |
0.00064 |
7 |
| ${M_{7}}$ |
0.0007 |
0.00004 |
0.0003 |
0.0008 |
0.0028 |
0.00005 |
0.0014 |
0.00008 |
0.00617 |
1 |
6.1 Comparison with Other Works
Here, we illustrate a comparative evaluation with the existing method to show the validity and usefulness of the IF-MABAC approach based on IF-discrimination measures. We have implemented the same numerical example applying the developed approach for comparing with the existing approaches.
The above Smartphone selection problem is also solved by the ANP-Generalized Choquet integral method (Yildiz and Ergul,
2015), the fuzzy ELECTRE method (Belbag
et al.,
2016) and the Shapley discrimination measure VIKOR method (Mishra and Rani,
2019). Outcomes of the different approaches were obtained to certify the outcomes of the developed IF-MABAC method. Moreover, we implement the given case study to investigate the above methods and to show the effectiveness of the proposed approach. Figure
3 and Table
11 demonstrate the preference orders of the SPSs alternatives as achieved by applying the existing methods.
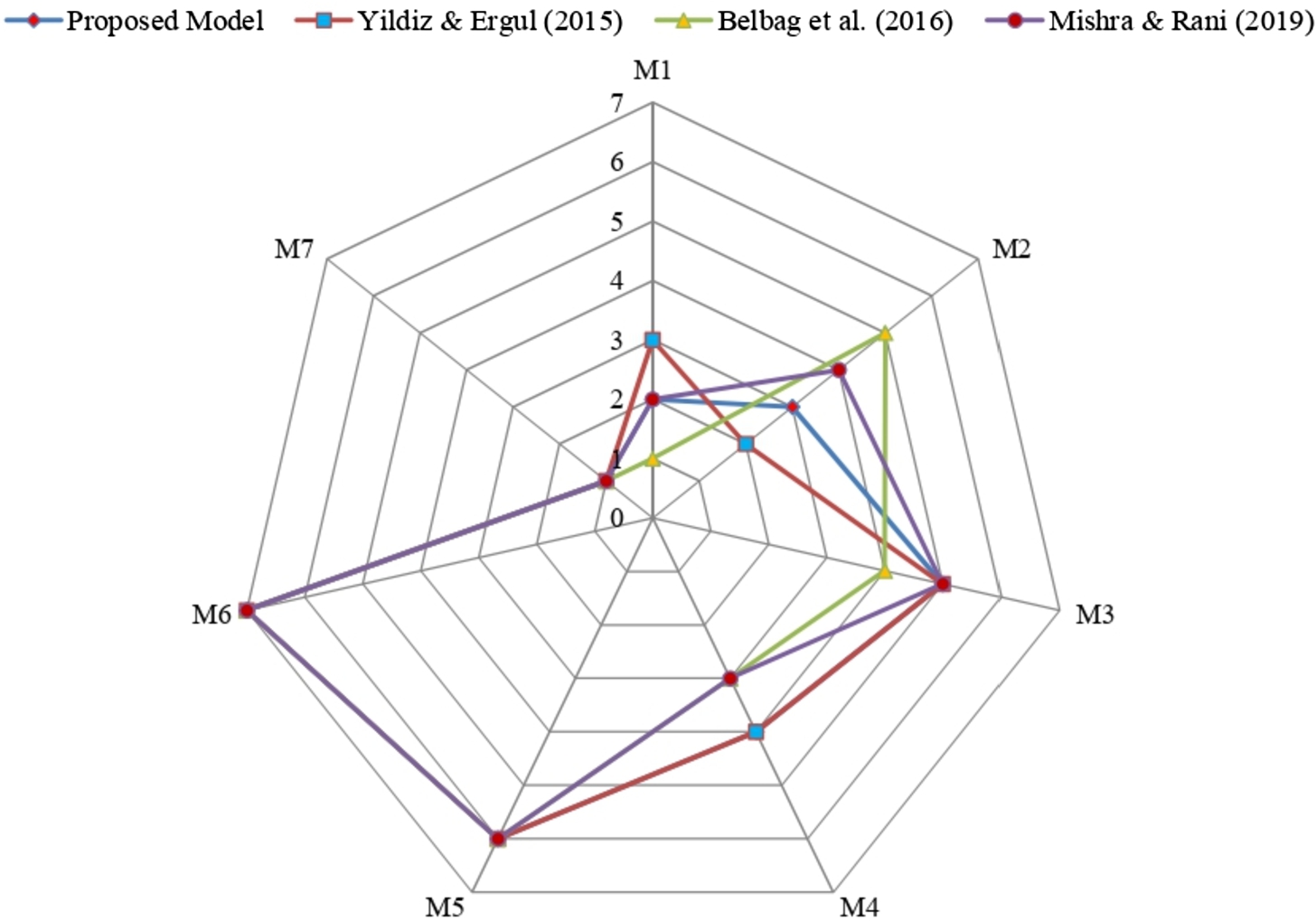
Fig. 3
Rankings order comparison of Smartphones with different methods.
Table 11
Discussion of the developed method with current methods.
| Methods |
Discipline |
Benchmark |
Criterion weights |
Expert weights |
Ranking order |
Best Smartphone |
| Yildiz and Ergul (2015) |
FSs |
ANP – Generalized choquet integral |
ANP |
Assumed |
${M_{7}}\succ {M_{2}}\succ {M_{1}}\succ {M_{4}}\succ {M_{3}}\succ {M_{5}}\succ {M_{6}}$ |
${M_{7}}$ |
| Belbag et al. (2016) |
FSs |
Fuzzy ELECTRE |
TFNs |
Assumed |
${M_{7}}\approx {M_{1}}\succ {M_{4}}\succ {M_{3}}\succ {M_{2}}\succ {M_{5}}\succ {M_{6}}$ |
${M_{7}}$, ${M_{1}}$
|
| Mishra and Rani (2019) |
IFSs |
IF-VIKOR |
Shapley function with entropy method |
Not considered |
${M_{7}}\succ {M_{1}}\succ {M_{4}}\succ {M_{2}}\succ {M_{3}}\succ {M_{5}}\succ {M_{6}}$ |
${M_{7}}$ |
| Proposed method |
IFSs |
IF-MABAC |
Discrimination measure |
Computed |
${M_{7}}\succ {M_{1}}\succ {M_{2}}\succ {M_{4}}\succ {M_{3}}\succ {M_{5}}\succ {M_{6}}$ |
${M_{7}}$ |
The outcomes show that the optimal preference of SPSs is the same, i.e. ${M_{7}}$ (Samsung), based on the introduced framework and the existing models. Further, the correlation values among the preference orders evaluated by the developed and other methods are 0.964, 0.884, and 0.964, respectively. The analyses express the strength of the introduced IF-MABAC framework.
The key distinctive outcomes of the developed IF-MABAC framework are as follows:
-
i. To tackle with uncertainty in MCDM problems, all the facets, namely, the alternative on the assessments criteria by various DEs, the DEs weights, and the criteria weights are taken in the form of IFNs.
-
ii. The developed approach utilizes IFSs to develop the procedure, different from the methods in Yildiz and Ergul (
2015) and Belbag
et al. (
2016), wherein the FSs are implemented.
-
iii. The criteria weights of proposed IF-MABAC approach are obtained through the proposed IF-discrimination measure, which gives more precise weights, different from the randomly assumed criteria weights in Belbag
et al. (
2016).
-
iv. Multiple DEs have been selected in the developed method whose weights are given in terms of IFNs, while the methodology proposed in Yildiz and Ergul (
2015), Belbag
et al. (
2016) and Mishra and Rani (
2019) did not incorporate the group decision making (GDM) procedure.
-
v. Criteria weights in the developed IF-MABAC method are provided as IFNs, whereas in Belbag
et al. (
2016) and Mishra and Rani (
2019), the crisp weights are assumed, leaving no space to handle the uncertainty.
7 Conclusions
With the use of technology, human life becomes more comfortable, and therefore it becomes a requisite for users. Several brands or products materialize on the business world with fast-growing technology and Smartphones are one of these products. A desirable Smartphone selection from the available options is a complex problem since it has different types of processors, RAM in GB, screens with HD resolution, O/S, etc. Several interesting criteria affect the SPS, as similar to various products. Hence, MCDM approaches can facilitate to evaluate SPS problem. Here, an integrated approach based on MABAC under IFSs was developed to assess the SPS problem. To compute the weight of the vector, new IF-discrimination measures were developed, and some useful properties were presented. The novel developed discrimination measure based on IFSs is verified, it would solve the problem of some current distance measures. The assessment of each SPSs alternative over different criteria was assessed on IFSs, and a new IF-MABAC framework was applied to prefer the most desirable Smartphone. To investigate the usefulness of the IF-MABAC method, comparative analyses with existing approaches were presented. The computational findings found that the ranking outcomes achieved based on the IF-MABAC method were reliable with existing ones; and hence, the developed method was sound to the SPSs under uncertainty. By employing the integrated IF-MABAC approach, a more consistent and best ranking findings of SPS case would be obtained, which help to make the accurate decision for selection of smartphone.
Further, we will integrate the MABAC framework with various other procedures, viz., CRITIC, AHP and SWARA, in the MCDM process. Also, the introduced approach would be employed for deciphering the several real-world problems, namely, supplier or material selection, and electric vehicles charging station selection to elucidate its strength and usefulness.

