1 Introduction
The data hiding technique is a kind of multimedia security technique. It hides secret information into another unimportant original data, and the original data is still meaningful. Because the original data is not gibberish, the technique could defraud the adversary and send the secret information. Data hiding technology can be grouped into non-reversible and reversible data hiding schemes (Chen
et al.,
2020; Chen and Guo,
2020; Chen Y.
et al.,
2020). The image of the former will be completely damaged and cannot be restored after hiding the secret information. However, the image of the latter, after retrieving the secret information, can still be recovered to the original image. The data hiding technique has been applied to many domains, such as videos, images for medicine (Lu
et al.,
2015a), digital sounds, etc. An interesting application of this technique is applied in the relational database.
IBM’s first relational database product for business purposes was released in 1981, and the relational database has become an important tool for enterprises and the government agencies to save data today. Enterprises use it to save employee data, customer data, product data, etc. The government uses it to save financial data, tax data, judicature data, etc. Original relational databases only save data; afterwards, Data Warehouse and Data Mining techniques make us analyse the relational database and find out the relationships among data, and then provide analytical results to enterprises for decision-making (Ke and Wang,
2006). Therefore, data has become an important resource for enterprises. Because of the importance of data, Taiwan has implemented Personal Data Protection Act in 2012; and thus the question is how to protect data from being stolen by someone else. We discuss security issues in the relational databases in the next section.
The data saved in relational databases is digital data, and it is the same as videos and images, which can all be copied easily. After the Internet has appeared, digital data can be delivered easily to others, resulting that the problem of data theft is becoming more and more serious. Relational databases have an authority control mechanism; only legitimate users can access the data in the database, and thereby it can prevent data from being stolen by unauthorized users. However, if legitimate users steal data and sell it to B, and then B asserts the data belongs to him, how can we prove who owns the data? The ownership information in the relational database can prove to whom these data belong.
Furthermore, let us consider another case; a data owner needs data mining service, so he transmits the relational database to a data mining company (Kamran
et al.,
2013). When he transmits, the attacker may steal and tamper the relational database, so the recipient will receive the tampered relational database. When it happens, how can we prove the relational database is original, and the data is not tampered? Tamper proofing can help us.
A kind of technique, called watermarking relational databases, can achieve above-mentioned purposes. Its concept comes from the data hiding technique. Its purpose is to hide invisible digital watermark into relational databases for ownership protection and tamper proofing (Agrawal and Kiernan,
2002; Iftikhar
et al.,
2015; Ke and Wang,
2006).
This paper is organized as follows: Section
2 will briefly describe the development history of watermark relational databases. We carefully explain our proposed method in Section
3. The experimental results are given in Section
4. Finally, the conclusion summarizes the results obtained and proposes future work for this article.
2 Related Works
Using a digital watermark to prove copyright of digital media has been a well-known technique. The first ones who proposed a new idea of using a digital watermark to secure a database is Khanna and Zane in 2000 (Khanna and Zane,
2000), and then Rakesh Agrawal and Jerry Kiernan proposed the first scheme for Watermarking relational databases in 2002 (Agrawal and Kiernan,
2002). Their scheme uses a hash function to pick out the LSB (Least-Significant-Bit) of some tuples they want to mark, and then they embed the watermark by setting the selected LSB. If the hash function value of the concatenation of the private key and the primary key is even, the selected LSB will be set to 0; otherwise the selected LSB will be set to 1.
According to the scientific studies of Bhesaniya
et al. (
2014) Dwivedi
et al. (
2014) Mohanpurkar and Joshi (
2011), the Watermarking relational databases can include two kinds of databases: data distortion watermarking relational databases and data distortion-free watermarking relational databases. Agrawal’s and Kiernan’s scheme is improved by embedding fingerprints instead of meaningless bits in Li
et al. (
2003). Mehta and Rao proposed to embed the digital watermark in two attributes, namely the LSB of the digital attribute and the SS of the date attribute (Mehta and Rao,
2011). Hanyurwimfura
et al. proposed a digital watermark could be expressed by the horizontal shifting position of a non-numeric attribute of selected tuples (Hanyurwimfura
et al.,
2010). Melkundi
et al. proposed embedding a digital watermark into a textual attribute and a numeric attribute, and finally used Levenshtein Distance to verify the extracted watermark and the original watermark (Melkundi and Chandankhede,
2015). In Kamran
et al. (
2013), a high robustness and distortion minimization scheme for data distortion watermarking relational databases was proposed. This scheme first divides the data set into several data partitions, and then uses thresholds and hash functions to select tuples for embedding the watermark. If the embedded watermark bit is 1, the selected tuple value is added to the percentage value; if the embedded watermark bit is 0, the selected tuple value is subtracted from the percentage value. Experimental results show that this scheme can not only resist six attacks, but also minimize data distortion.
In the data distortion watermarking relational database, Zhang
et al. proposed a subdomain in 2006, called the reversible watermarking relational database (Zhang
et al.,
2006). They use histogram extension techniques to implement a reversible watermarking scheme. The idea of reversible watermarking relational databases was derived from the image because the data in the database will be distorted after embedding a digital watermark. However, for some data, for example, categorical data, it cannot tolerate any distortion; otherwise, it will become useless (Li
et al.,
2004); therefore, we need this technique to restore raw data in the database. Gupta and Pieprzyk proposed a reversible blind watermarking scheme that can resist secondary watermarking attacks (Gupta and Pieprzyk,
2009). This scheme will analyse the features and select the appropriate watermark features, then use the genetic algorithm (GA) to generate the watermark. Therefore, the watermark will evolve from a random binary string to the best watermark information string, and obtain the best fitness value
$(\beta )$. The best fitness value is used to embed the watermark bit and ensure that the data quality is not affected. Experimental results show that RRW can retrieve the original data and watermark after malicious attacks.
The next domain we want to introduce is data distortion-free watermarking relational databases. Its main concept is to use the function of the database to generate a watermark, and the watermark will not be directly embedded in the database. Therefore, this technology can maintain the integrity of the original data without causing data distortion. Li
et al. proposed the first scheme in 2004 (Li
et al.,
2004). Their scheme generates a fragile watermark based on the group’s data order (ascending order means watermark bit = 0; descending order means watermark bit = 1). The fragile watermark is used to detect any modification in a relational database. In 2014, Camara
et al. proposed a fragile watermarking technology that generates watermarks based on data partitions in a relational database (Camara
et al.,
2014). Encrypt the watermark and record it in a certificate authority. A certification authority (CA) is a trusted party that can detect suspicious databases. When we want to validate the database, we first generate a watermark from the data partition and then compare the watermark with the original watermark retrieved from the CA.
Our proposed scheme is inspired from Lu
et al.’s data hiding technology (Lu
et al.,
2015a,
2015b). They are based on the LSB matching method to devise a dual imaging-based reversible hiding technique. First, it copies the original image into the same images. By LSB matching method, it embeds confidential messages into two image pixel values, respectively. Lastly, through the LSB and LSB matching methods, it will get the confidential messages. Through the averaging method, it will restore the original image.
3 The Proposed Reversible Data Hiding Scheme for Relational Databases
3.1 Basic Concept
In this section, we propose a new reversible data hiding technique using LSB matching method for relational databases. The main difference between the proposed method and Lu
et al.’s method is that a confidential message is hidden in the digital attributes of a relational database, not a pixel in an image. After hiding confidential messages (for example, the digital watermark of the database owner) into a relational database, the data in the database will be distorted, but the proposed method can restore the original data. Because the research is not robust enough to resist malicious attacks, it is a reversible data hiding technique for relational databases. Moreover, Section
4 also proves the proposed technique is a linear time algorithm (the running time linearly increases as the size of a data set); therefore, our technique is suitable for relational databases with a large amount of data.
Database relation D is the original data set with primary key attributes
P and
n attributes, whose scheme is
$(P,{A_{0}},\dots ,{A_{n-1}})$. Table
1 gives an overview of D. Therefore, this method can hide all numeric attributes in D. However, to simplify the description, only one numerical attribute
${A_{i}}$ is selected to explain the method.
Table 1
The overview of D.
| Tuple index |
P |
${A_{0}}$ |
${A_{i}}$ |
${A_{i2}}$ |
${A_{n-1}}$ |
| j |
|
|
${\mathit{tuple}_{j}}({A_{i}})$ |
${\mathit{tuple}_{j}}({A_{i2}})$ |
|
| $j+1$ |
|
|
${\mathit{tuple}_{j+1}}({A_{i}})$ |
${\mathit{tuple}_{j+1}}({A_{i2}})$ |
|
Figure
1 is the LSB matching method of relational database inspired by Mielikainen (
2006). This steganography is designed to hide binary messages into tuple values in a relational database.
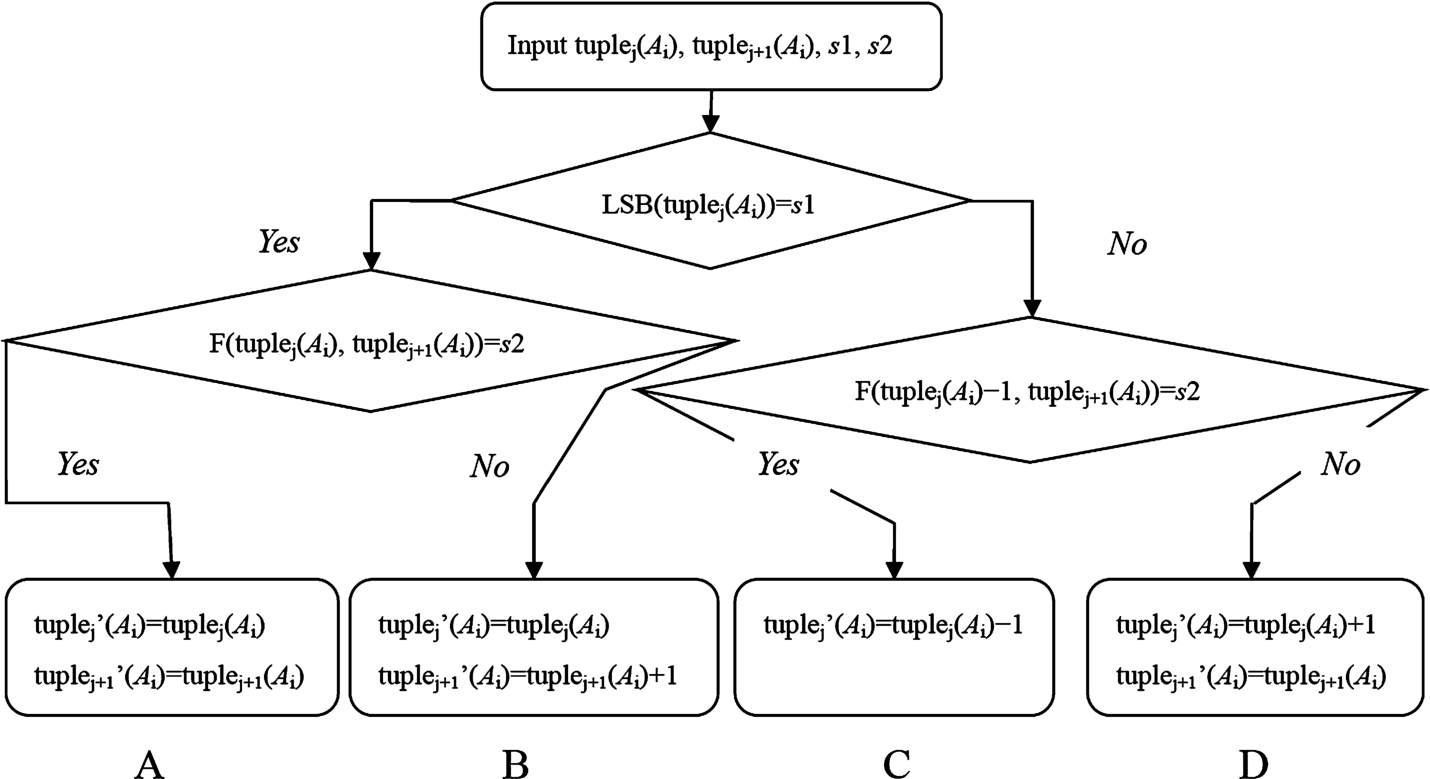
Fig. 1
LSB matching method for relational databases.
Assume that the encrypted confidential message (CM) is a binary number, $s1$ is the first bit of the CM, $s2$ is the second bit of the CM, $s3$ is the third bit of the CM, and $s4$ is the fourth bit of the CM; i is the attribute index; j is the tuple index. First, calculate the LSB of the ${\mathit{tuple}_{j}}({A_{i}})$. If the LSB of the ${\mathit{tuple}_{j}}({A_{i}})$ is equal to $s1$, go to the second layer $F({\mathit{tuple}_{j}}({A_{i}}),{\mathit{tuple}_{j+1}}({A_{i}}))=s2$. Otherwise, go to the second layer $F({\mathit{tuple}_{j}}({A_{i}})-1,{\mathit{tuple}_{j+1}}({A_{i}}))=s2$. In the second layer, $F(\cdot )$ is used to check whether the value of $F(\cdot )$ is the same as $s2$. In layer 3, pretend tuple values are generated. Here, ${\mathit{tuple}_{j}}({A_{i}})$ and ${\mathit{tuple}_{j+1}}({A_{i}})$ are the original tuple values; ${\mathit{tuple}_{j}}‘({A_{i}})$ and ${\mathit{tuple}_{j+1}}‘({A_{i}})$ pretend to be tuple values after hiding $s1$ and $s2$. The situations are explained as follows:
When $\mathit{LSB}({\mathit{tuple}_{j}}({A_{i}}))=s1$ and $F(\cdot )=s2$, ${\mathit{tuple}_{j}}({A_{i}})$ and ${\mathit{tuple}_{j+1}}({A_{i}})$ are unchanged.
When $\mathit{LSB}({\mathit{tuple}_{j}}({A_{i}}))=s1$ and $F(\cdot )\ne s2$, ${\mathit{tuple}_{j}}({A_{i}})$ is unchanged and ${\mathit{tuple}^{\prime }_{j+1}}({A_{i}})={\mathit{tuple}_{j+1}}({A_{i}})+1$.
When $\mathit{LSB}({\mathit{tuple}_{j}}({A_{i}}))\ne s1$ and $F(\cdot )=s2$, ${\mathit{tuple}^{\prime }_{j}}({A_{i}})={\mathit{tuple}_{j}}({A_{i}})-1$ and ${\mathit{tuple}^{\prime }_{j+1}}({A_{i}})$ is unchanged.
When $\mathit{LSB}({\mathit{tuple}_{j}}({A_{i}}))\ne s1$ and $F(\cdot )\ne s2$, ${\mathit{tuple}^{\prime }_{j}}({A_{i}})={\mathit{tuple}_{j}}({A_{i}})+1$ and ${\mathit{tuple}^{\prime }_{j+1}}({A_{i}})$ is unchanged.
Through the LSB matching method of the relational database,
${\mathit{tuple}_{j}}‘({A_{i}})$ and
${\mathit{tuple}_{j+1}}‘({A_{i}})$ are embedded in the secret messages
$s1$ and
$s2$, and
${\mathit{tuple}_{j}}‘({A_{i2}})$ and
${\mathit{tuple}_{j+1}}‘({A_{i2}})$ are embedded in the secret messages
$s3$ and
$s4$. Table
2 shows when the secret messages are hidden in two pairs of tuple values at the same time through the LSB matching method of a relational database, and under what circumstances can the two pairs of tuple values be restored to the original tuple values. 0 means that the tuple value does not need to be modified; +1 means that the tuple value is increased by 1; −1 means that the tuple value is subtracted by 1. We use the symbol
x to indicate that the recovered tuple value calculated by the averaging method is different from the original tuple value. To handle the case where the tuple value cannot be restored, we modify Table
2 and describe the new modification rules for relational databases in Table
3.
Table 2
The rule table for relational databases.
| Cases |
The tuple value modification statuses |
Original tuple values restoration statuses |
| ${\mathit{tuple}_{j}}({A_{i}})$ |
${\mathit{tuple}_{j+1}}({A_{i}})$ |
${\mathit{tuple}_{j}}({A_{i2}})$ |
${\mathit{tuple}_{j+1}}({A_{i2}})$ |
${\mathit{tuple}_{j}}({A_{i}})$ |
${\mathit{tuple}_{j+1}}({A_{i}})$ |
| 1 |
0 |
0 |
0 |
0 |
|
|
| 2 |
0 |
0 |
0 |
+1 |
|
|
| 3 |
0 |
0 |
−1 |
0 |
x |
|
| 4 |
0 |
0 |
+1 |
0 |
|
|
| 5 |
0 |
+1 |
0 |
0 |
|
|
| 6 |
0 |
+1 |
0 |
+1 |
|
x |
| 7 |
0 |
+1 |
−1 |
0 |
x |
|
| 8 |
0 |
+1 |
+1 |
0 |
|
|
| 9 |
−1 |
0 |
0 |
0 |
x |
|
| 10 |
−1 |
0 |
0 |
+1 |
x |
|
| 11 |
−1 |
0 |
−1 |
0 |
x |
|
| 12 |
−1 |
0 |
+1 |
0 |
|
|
| 13 |
+1 |
0 |
0 |
0 |
|
|
| 14 |
+1 |
0 |
0 |
+1 |
|
|
| 15 |
+1 |
0 |
−1 |
0 |
|
|
| 16 |
+1 |
0 |
+1 |
0 |
x |
|
Table 3
The extraordinary process of modification rule table.
| Rules |
Cases |
The final modified pretend tuple values |
| ${\mathit{tuple}^{\prime }_{j}}({A_{i}})$ |
${\mathit{tuple}^{\prime }_{j+1}}({A_{i}})$ |
${\mathit{tuple}^{\prime }_{j}}({A_{i2}})$ |
${\mathit{tuple}^{\prime }_{j+1}}({A_{i2}})$ |
| 1 |
3 |
${\mathit{tuple}_{j}}({A_{i}})+2$ |
${\mathit{tuple}_{j+1}}({A_{i}})+1$ |
${\mathit{tuple}_{j}}({A_{i2}})-1$ |
${\mathit{tuple}_{j+1}}({A_{i2}})+1$ |
| 2 |
6 |
${\mathit{tuple}_{j}}({A_{i}})$ |
${\mathit{tuple}_{j+1}}({A_{i}})+1$ |
${\mathit{tuple}_{j}}({A_{i2}})$ |
${\mathit{tuple}_{j+1}}({A_{i2}})-1$ |
| 3 |
7 |
${\mathit{tuple}_{j}}({A_{i}})+2$ |
${\mathit{tuple}_{j+1}}({A_{i}})$ |
${\mathit{tuple}_{j}}({A_{i2}})-1$ |
${\mathit{tuple}_{j+1}}({A_{i2}})$ |
| 4 |
9 |
${\mathit{tuple}_{j}}({A_{i}})-1$ |
${\mathit{tuple}_{j+1}}({A_{i}})$ |
${\mathit{tuple}_{j}}({A_{i2}})+2$ |
${\mathit{tuple}_{j+1}}({A_{i2}})+1$ |
| 5 |
10 |
${\mathit{tuple}_{j}}({A_{i}})-1$ |
${\mathit{tuple}_{j+1}}({A_{i}})$ |
${\mathit{tuple}_{j}}({A_{i2}})+2$ |
${\mathit{tuple}_{j+1}}({A_{i2}})$ |
| 6 |
11 |
${\mathit{tuple}_{j}}({A_{i}})-1$ |
${\mathit{tuple}_{j+1}}({A_{i}})+2$ |
${\mathit{tuple}_{j}}({A_{i2}})+1$ |
${\mathit{tuple}_{j+1}}({A_{i2}})-1$ |
| 7 |
16 |
${\mathit{tuple}_{j}}({A_{i}})-1$ |
${\mathit{tuple}_{j+1}}({A_{i}})-1$ |
${\mathit{tuple}_{j}}({A_{i2}})+1$ |
${\mathit{tuple}_{j+1}}({A_{i2}})+2$ |
Taking Case 6 as an example, the first pair of
${\mathit{tuple}_{j}}({A_{i}})$ is 0 and
${\mathit{tuple}_{j+1}}({A_{i}})$ is +1. The second pair of
${\mathit{tuple}_{j}}({A_{i2}})$ is 0 and
${\mathit{tuple}_{j+1}}({A_{i2}})$ is +1 of the tuple value modification statuses; In this case, the recovered tuple value calculated by the averaging method is different from the original tuple value, so we need to use Rule 2 in Table
3. Therefore, the new tuple value modification state is that the first pair of
${\mathit{tuple}_{j}}({A_{i}})$ is 0, the
${\mathit{tuple}_{j+1}}({A_{i}})$ is +1, and the second pair of
${\mathit{tuple}_{j}}({A_{i2}})$ is 0, the
${\mathit{tuple}_{j+1}}({A_{i2}})$ is −1. Therefore, the final modified pretend tuple values are:
${\mathit{tuple}_{j}}‘({A_{i}})$ does not need to be changed,
${\mathit{tuple}_{j+1}}‘({A_{i}})={\mathit{tuple}_{j+1}}({A_{i}})+1$,
${\mathit{tuple}_{j}}‘({A_{i2}})$ is unchanged,
${\mathit{tuple}_{j}}‘({A_{i2}})={\mathit{tuple}_{j+1}}({A_{i2}})-1$.
3.2 Hiding Phase
The private key was originally used to encrypt secret messages. It is assumed that the length of the encrypted confidential message is
m bits, and the attribute to be hidden is located in
${A_{i}}$. First, copy
${A_{i}}$ into the same two attributes
${A_{i}}$ and
${A_{i2}}$. In Fig.
1, two tuple values are used:
${\mathit{tuple}_{j}}({A_{i}},{A_{i2}})$ and
${\mathit{tuple}_{j+1}}({A_{i}},{A_{i2}})$ as sets to hide all sets to obtain D’ (hidden data set after CM) =
$\{{\mathit{tuple}^{\prime }_{1}}({A_{i}},{A_{i2}})$,
${\mathit{tuple}^{\prime }_{2}}({A_{i}},{A_{i2}}),\dots ,{\mathit{tuple}^{\prime }_{(m/2-1)}}({A_{i}},{A_{i2}})$,
${\mathit{tuple}^{\prime }_{(m/2)}}({A_{i}},{A_{i2}})\}$. The overall steps are as follows: First, use Table
2 to hide CM into D. If something happens during the hiding process, use Table
3 to modify the pretend tuple value. By the averaging method, the pretend tuple values can be restored:
${\mathit{tuple}^{\prime }_{j}}({A_{i}})$,
${\mathit{tuple}^{\prime }_{j}}({A_{i2}})$,
${\mathit{tuple}^{\prime }_{j+1}}({A_{i}})$, and
${\mathit{tuple}^{\prime }_{j+1}}({A_{i2}})$ can be recovered to the original
${\mathit{tuple}_{j}}({A_{i}})$ and
${\mathit{tuple}_{j+1}}({A_{i}})$, respectively.
The complete explanation for hiding phases is as follows:

Algorithm 1
Hiding function.
Algorithm
1 is a hiding function that implements the concepts of Fig.
1, Table
2 and Table
3, and Fig.
2 is Algorithm
1 flow chart. Algorithm
2 is a function that retrieves an assigned bit of CM. As shown in Table
1,
${\mathit{tuple}_{j}}({A_{i}})$ and
${\mathit{tuple}_{j}}({A_{i2}})$, and
${\mathit{tuple}_{j+1}}({A_{i}})$ and
${\mathit{tuple}_{j+1}}({A_{i2}})$ are two pairs of tuple values in D. In lines 5–11, Algorithm
1 first retrieves tuples from D, and temporarily saves them into tempDBValue array (a two-dimensional array); hence lines 12–60 can hide confidential message into tempDBValue array, and then tempDBValue array is updated to D in line 61. Line 12 is that when a tuple number is even, lines 13–60 begin to hide CM through the LSB matching method for relational databases and Modification rule table. Every time, lines 13–19 get 4 continuous bits from CM by Get_CMbit function (Algorithm
2), and they are stored in
$s1$,
$s2$,
$s3$, and
$s4$, respectively. Lines 20–45 determine which situation
${\mathit{tuple}_{j}}({A_{i}},{A_{i2}})$ and
${\mathit{tuple}_{j+1}}({A_{i}},{A_{i2}})$ belong to. Afterwards, if some cases happen, Table
3 is further used to adjust tempDBValue array in lines 46–60. Therefore, CM is hidden into tempDBValue array.
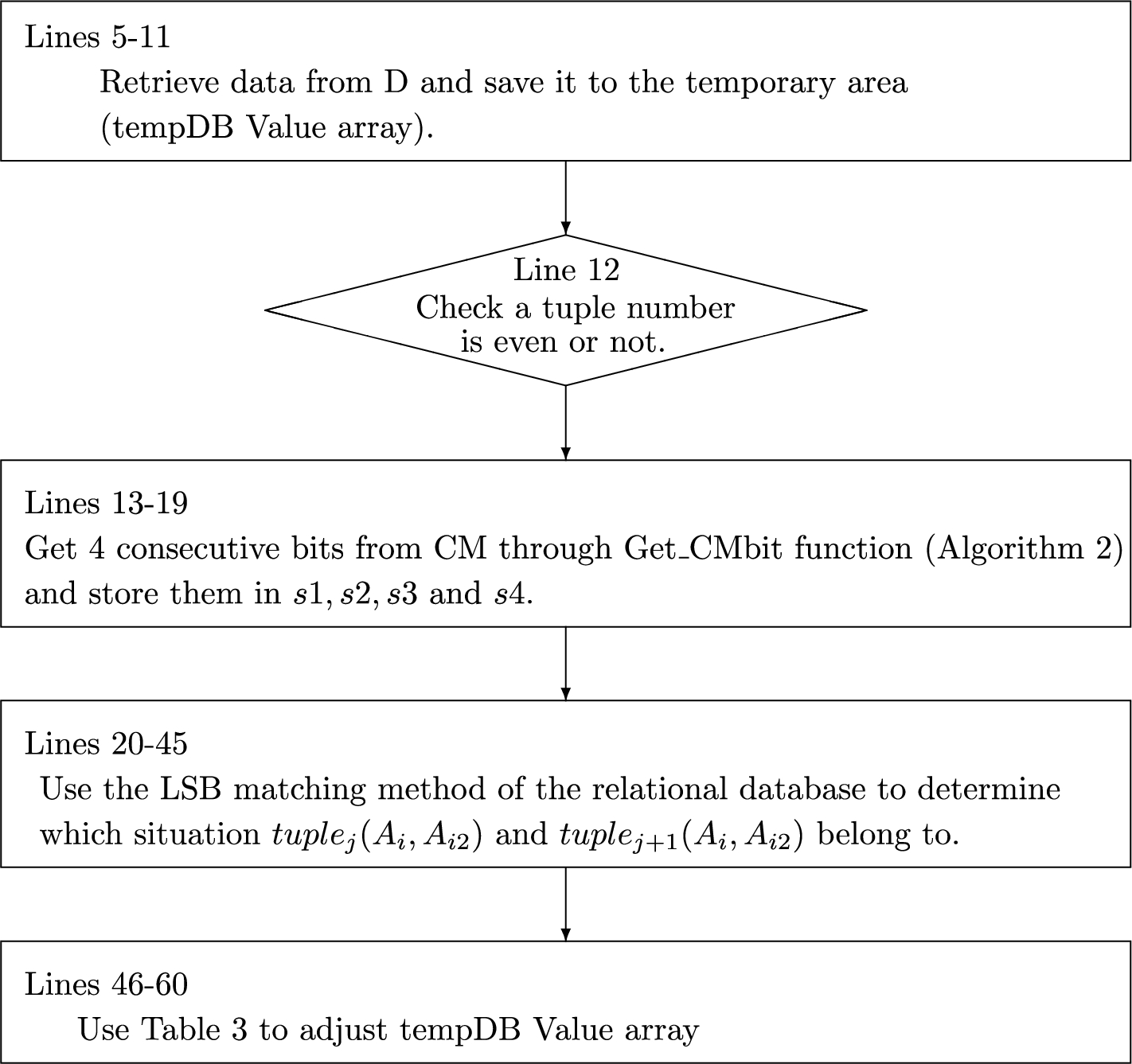
Fig. 2
Algorithm 1 flow chart.

Algorithm 2
Get_CMbit function.
3.3 Extraction and Restoration Phases
CM and recovery raw data are extracted separately in this phase. Firstly, we extract CM from the first pair tuple values:
${\mathit{tuple}_{j}}({A_{i}})$,
${\mathit{tuple}_{j+1}}({A_{i}})$, and the second pair tuple values:
${\mathit{tuple}_{j}}({A_{i2}})$,
${\mathit{tuple}_{j+1}}({A_{i2}})$ through the LSB and LSB matching method for relational databases.
$s1$ is obtained from
${\mathit{tuple}_{j}}({A_{i}})$ by the LSB equation. After that,
$s2$ is gained by equation (
1). Substitute
$x={\mathit{tuple}_{j}}({A_{i}})$ and
$y={\mathit{tuple}_{j+1}}({A_{i}})$ into
$F(\cdot )$, and the value for
$F(\cdot )$ represents
$s2$. In the same way,
$s3$ and
$s4$ are obtained from the second pair tuple values:
${\mathit{tuple}_{j}}({A_{i2}})$,
${\mathit{tuple}_{j+1}}({A_{i2}})$. Lastly, CM is decrypted by the same private key.
During restoration phases, the average value of the two tuple values can be calculated through the averaging method to recover the raw data, namely, using equation (
2) to compute
$\lfloor ({\mathit{tuple}_{{j^{\prime }}}}({A_{i}})+{\mathit{tuple}_{{j^{\prime }}}}({A_{i2}}))/2\rfloor $ we can restore the original
${\mathit{tuple}_{j}}({A_{i}})$; by computing
$\lfloor ({\mathit{tuple}_{j+{1^{\prime }}}}({A_{i}})+{\mathit{tuple}_{j+{1^{\prime }}}}({A_{i2}}))/2\rfloor $ we can restore the original
${\mathit{tuple}_{j+1}}({A_{i}})$. The following formula is equation (
1) (Lu
et al.,
2015a):
The following formula for the averaging method is equation (
2):

Algorithm 3
Extract Restore function.
Algorithm
3 is an extract restore function that extracts CM from D’ and restores the raw data, and Fig.
3 is Algorithm
3 flow chart. In lines 5–12, Algorithm
3 first retrieves tuples from D’, and temporarily saves them into tempDBValue array (a two-dimensional array); hence, lines 14–18 can get CM, and then lines 19–20 restore raw data into tempDBValue array, and, finally, tempDBValue array is updated to D in line 21. Line 13 is that when tuple number is even, it calculates the CM through LSB and LSB matching method for relational databases in lines 14–18, and restores the raw data through averaging method in lines 19–20. Lastly, this function returns CM and D.
3.4 Example
We have already proved our algorithms are feasible on a computer with Intel(R) Core(TM)2 Quad CPU, 4 GB of RAM, and MySQL 5.6 is our database. In this section, we illustrate our experimental examples to let readers understand the proposed scheme.

Fig. 4
An example for hiding phase.
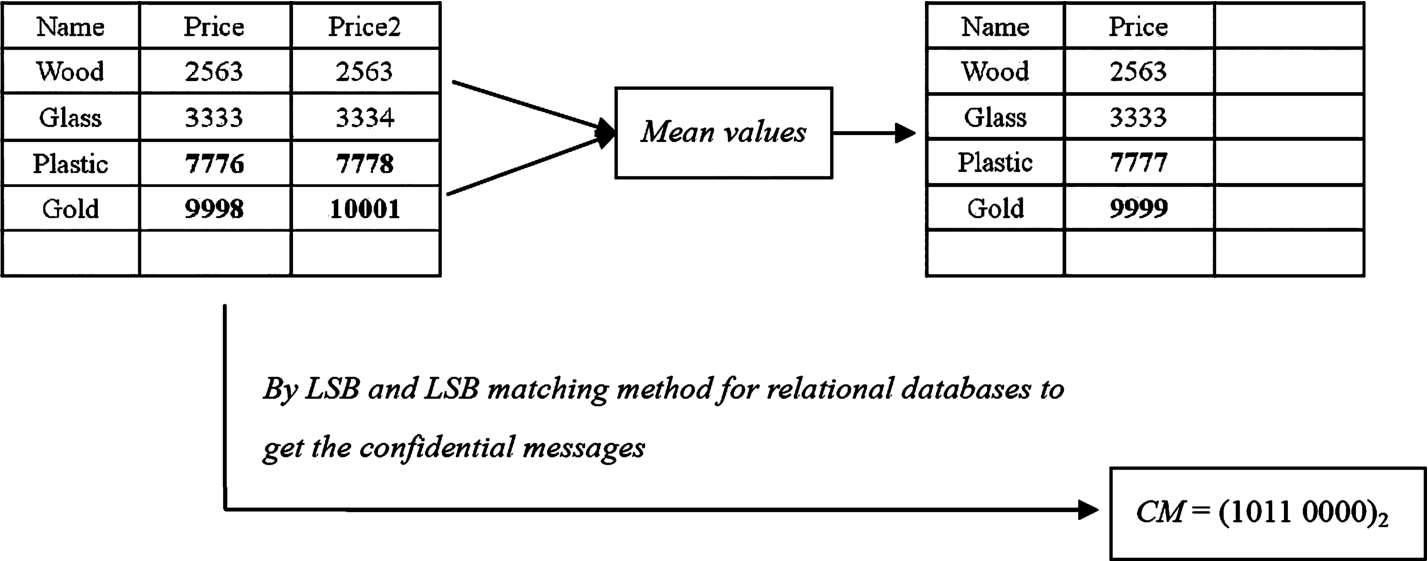
Fig. 5
An example for extraction and restoration phase.
The format of Figs.
4 and
5 in (Lu
et al.,
2015a) are taken as a reference to design our own experimental examples. Take Fig.
4 for example, we explain hiding phases as follows: firstly, Price is copied into two same attributes Price and Price2, and then use (2563, 2563) and (3333, 3333) as the first set. Suppose that the CM = 1011, through Fig.
1,
$s1$,
$s2$ are hidden into
$({\mathit{tuple}_{j}}({A_{i}})$,
${\mathit{tuple}_{j+1}}({A_{i}}))=(2563,3333)$ in Price separately, and then
$s3$,
$s4$ are hidden into
$({\mathit{tuple}_{j}}({A_{i2}})$,
${\mathit{tuple}_{j+1}}({A_{i2}}))=(2563,3333)$ in Price2 separately. When hiding
$s1$,
$s2$, because
$\mathit{LSB}(2563)=1=s1=1$, substituting 2563, 3333 into equation (
1), it gains
$F(2563,3333)=\mathit{LSB}(4614)=0=s2=0$. Because of
F value =
$s2$, therefore, this is Situation A in Fig.
1. Afterwards,
$s3$,
$s4$ are hidden into
$({\mathit{tuple}_{j}}({A_{i2}})$,
${\mathit{tuple}_{j+1}}({A_{i2}}))=(2563,3333)$. Because
$\mathit{LSB}(2563)=1=s3=1$, substituting 2563, 3333 into equation (
1), it obtains
$F(2563,3333)=\mathit{LSB}(4614)=0\ne s4(=1)$. Due to
F value
$\ne s4$, therefore, this is Situation B in Fig.
1. As just mentioned,
$({\mathit{tuple}_{j}}({A_{i}})$,
${\mathit{tuple}_{j+1}}({A_{i}}))$ is Situation A = (2563, 3333), and
$({\mathit{tuple}_{j}}({A_{i2}})$,
${\mathit{tuple}_{j+1}}({A_{i2}}))$ is Situation B = (2563, 3333+1). This is Case-2 in Table
2, and thus the original tuple values can be recovered. Therefore, Table
3 is not needed, and we get
${\mathit{tuple}^{\prime }_{j}}({A_{i}})=2563$,
${\mathit{tuple}^{\prime }_{j+1}}({A_{i}})=3333$ and
${\mathit{tuple}^{\prime }_{j}}({A_{i2}})=2563$,
${\mathit{tuple}^{\prime }_{j+1}}({A_{i2}})=3334$.
Next, assume that the CM = 0000, and then (7777, 7777) and (9999, 9999) are used as the second set.
$s1$,
$s2$ are hidden into
$({\mathit{tuple}_{j}}({A_{i}})$,
${\mathit{tuple}_{j+1}}({A_{i}}))=(7777,9999)$ in Price, respectively, and then hide
$s3$,
$s4$ into
$({\mathit{tuple}_{j}}({A_{i2}})$,
${\mathit{tuple}_{j+1}}({A_{i2}}))=(7777,9999)$ in Price, respectively. By Fig.
1, it knows
$({\mathit{tuple}_{j}}({A_{i}})$,
${\mathit{tuple}_{j+1}}({A_{i}}))$ is Situation
$D=(7777+1,9999)$, and
$({\mathit{tuple}_{j}}({A_{i2}})$,
${\mathit{tuple}_{j+1}}({A_{i2}}))$ is Situation D = (7777+1, 9999). This is Case-16 in Table
2, so the original tuple values cannot be restored. Therefore, Table
3 (Modification rule table) is further used to modify the pretend tuple values. Case-16 follows Rule-7 in Table
3, so it gains
${\mathit{tuple}^{\prime }_{j}}({A_{i}})=7777-1=7776$,
${\mathit{tuple}^{\prime }_{j+1}}({A_{i}})=9999-1=9998$ and
${\mathit{tuple}^{\prime }_{j}}({A_{i2}})=7777+1=7778$,
${\mathit{tuple}^{\prime }_{j+1}}({A_{i2}})=9999+2=10001$.
Take Fig.
5 as an example, we illustrate extraction and restoration phases as follows: Extract CM and recovery raw data separately. In the first set,
$s1=1$ is gotten from
${\mathit{tuple}^{\prime }_{j}}({A_{i}})=2563$ by the LSB equation. After that, substitute
$x={\mathit{tuple}^{\prime }_{j}}({A_{i}})=2563$ and
$y={\mathit{tuple}^{\prime }_{j+1}}({A_{i}})=3333$ into equation (
1), and then get
$s2=F(2563,3333)=0$. In the same way,
$s3=1$ and
$s4=1$ are obtained from the second pair tuple values:
${\mathit{tuple}^{\prime }_{j}}({A_{i2}})=2563$,
${\mathit{tuple}^{\prime }_{j+1}}({A_{i2}})=3334$. By the above-mentioned way, CM is also extracted from the second set, i.e.
$s1=\mathit{LSB}(7776)=0$,
$s2=F(7776,9998)=0$,
$s3=\mathit{LSB}(7778)=0$, and
$s4=F(7778,10001)=0$.
During restoration phase, equation (
2) is used to compute
$\lfloor ({\mathit{tuple}_{{j^{\prime }}}}({A_{i}})=2563+{\mathit{tuple}_{{j^{\prime }}}}({A_{i2}})=2563)/2\rfloor $, and then the original
${\mathit{tuple}_{j}}({A_{i}})=2563$ is restored.
$\lfloor ({\mathit{tuple}_{j+{1^{\prime }}}}({A_{i}})=3333+{\mathit{tuple}_{j+{1^{\prime }}}}({A_{i2}})=3334)/2\rfloor $ is computed, and then the original
${\mathit{tuple}_{j+1}}({A_{i}})=3333$ is restored. Similarly, the original tuple value 7777, 9999 are restored.
4 Capacity and Complexity Analysis of Our Method
We all know that the data-hiding technique has two important requirements, the integrity of raw data and data hiding capacity. With respect to the integrity of raw data, since our proposed technique is reversible, it can recover the raw data. Therefore, the following paragraphs analyse data hiding capacity and the complexity of our algorithms:
4.1 Data Hiding Capacity
The data hiding capacity of our technique depends on the database. The more tuples in D, the more hiding capacity of our technique. Assume there are n tuples in D, and then the maximum hiding capacity = 2n bits.
Our technique uses each 2 tuple values: ${\mathit{tuple}_{j}}({A_{i}},{A_{i2}})$ and ${\mathit{tuple}_{j+1}}({A_{i}},{A_{i2}})$ as a set, and then hides a bit into each tuple value, i.e. hiding four bits into ${\mathit{tuple}_{j}}({A_{i}})$, ${\mathit{tuple}_{j}}({A_{i2}})$, ${\mathit{tuple}_{j+1}}({A_{i}})$, ${\mathit{tuple}_{j+1}}({A_{i2}})$, respectively. Therefore, the watermark bits we intend to hide must be multiple of four. Furthermore, if n is odd, the last tuple cannot be used to hide confidential messages.
4.2 The Complexity of Our Algorithms
According to Franco-Contreras
et al. (
2014), Xie
et al. (
2016), computation time is an important issue we should consider. Thus, we analyse the complexity of Algorithm
1 and Algorithm
3, and try to prove whether they are efficient or not. We assume there are
n tuples in D, and the time of updating the value in the database is TDB (it is determined by the database and the amount of data, so we ignore it); moreover, assume situations A–D in Fig.
1 will happen averagely, and furthermore assume the probability of occurrence of the cases in Table
3 is very small, so we can ignore them. Therefore, the number of executions of every instruction is shown in comments of Algorithms
1 and
3. Because line 12 in Algorithm
1 and Algorithm
3 limits tuple number to even numbers, the numbers of executions of the instructions after line 12 will be reduced to
$n/2$.
In Algorithm
1, lines 20–32 execute
$n/2$ times. Because we assume situations A–D happen averagely, lines 21–25 and lines 27–31 share
$n/2$ of lines 20–32; hence, lines 21–25 and lines 27–31 are executed
$\frac{(n/2)}{2}$ times, respectively. Lines 22 and 24 share
$\frac{(n/2)}{2}$ times of lines 21–24; therefore, lines 22 and 24 are executed
$\frac{((n/2)/2)}{2}$ times, respectively. Moreover, lines 22 and 24 both have two-line code, so we multiply
$\frac{((n/2)/2)}{2}$ times of lines 22 and 24 by two. Lines 28 and 30 are in the same way. For the same reason, we calculate the number of executions of every instruction between lines 33–45. Because we ignore cases in Table 3, lines 47, 49, 51, 53, 55, 57, and 59 will not be calculated.
The number of executions of total instructions in Algorithm
1 is
$1+n+n+n/2+n/2+n/2+n/2+n+5n/2+2(n/2+n/4+n/4+n/4+n/4+n/8+n/4)+n/2+(n/2)\mathit{TDB}=11n+3n/4+1+(n/2)\mathit{TDB}$, and moreover, its time complexity is
$O(n)$. Therefore, it is a linear time algorithm.
The number of executions of total instructions in Algorithm
3 is
$1+n+n+n/2+n/2+n/2+n/2+n+5n/2+n/2+n/2+(n/2)\mathit{TDB}=8n+n/2+1+(n/2)\mathit{TDB}$, and moreover, its time complexity is
$O(n)$. Therefore, it is also a linear time algorithm.
As mentioned above, time complexity of our algorithms in Algorithms
1 and
3 are both linear time algorithms. According to “Linear time is the best possible time complexity in situations where the algorithm has to sequentially read its entire input (Sudhan and Kalaiarasan,
2017)”, our technology reads the entire database sequentially and meets the linear time requirements; therefore, our proposed technique is not only efficient in hiding phase but also efficient in extraction and restoration phases.
5 Discussion and Conclusion
In this study, we proposed a reversible hiding technique for relational databases by using the LSB matching method. In the experiments, we proved that our technique meets data hiding requirements, and it not only enables to recover the raw data, but also maintains a high hiding capacity. Additionally, we analyse the complexity of our algorithms to demonstrate our technique is efficient. Therefore, according to Xie
et al. (
2016), our algorithms can be applied to big data databases. To the best of our knowledge, it is the first reversible hiding technique for relational databases. Furthermore, we want to discuss two issues:
-
1) Application: In our opinion, our technique is most suitable for statistical databases. Statistical databases (SDB) have an inference problem: an attacker may infer the correct data from known information and well-chosen queries (Tendick and Matloff,
1994); however, data perturbation can solve this problem. Data perturbation is a technique that adds noises into the sensitive data. Its method is to change data through mathematic formulas (such as adding and subtracting) (Adam and Worthmann,
1989; Taneja
et al.,
2014). After SDB passes above-mentioned preprocess, it transforms these data into a perturbed SDB (Adam and Worthmann,
1989; Taneja
et al.,
2014). The searchers only query the perturbed SDB, so they never get correct results. Therefore, it is hard for people to infer the correct data (Adam and Worthmann,
1989).
Because our technique must copy data into the same two data in the relational database, an attacker may doubt whether this database has confidential messages or not. Therefore, attribute ${A_{i2}}$ can be put into the perturbed SDB after hiding phases, i.e. regarding the hiding method as mathematic formulas and regarding ${A_{i2}}$ as perturbed data. Because ${A_{i2}}$ is in the perturbed SDB and ${A_{i}}$ is in the original SDB, it can prevent the original SDB from having an additional data, so the attacker does not doubt if the SDB has confidential messages. During extraction and restoration phases, confidential messages is extracted and raw data is recovered through attribute ${A_{i}}$ in the SDB and attribute ${A_{i2}}$ in the perturbed SDB.
-
2) Future work: Because our research is not robust enough to resist malicious attacks, it is just a data hiding technique for relational databases. In the future, we will strengthen the robustness in order to make our technique become watermarking relational databases.

