1 Introduction
In recent years, multi-criteria decision-making (MCDM) methods have been developed by many researchers and applied to many real-world problems (Keshavarz-Ghorabaee
et al.,
2018). The MCDM can be classified into multi-attribute decision-making (MADM) and multi-objective decision-making (MODM); the MADM is for evaluation, and the MODM is for design. In the MADM, alternatives are predefined. However, the MODM designs the best alternative by considering various constraints (Hwang and Yoon,
2012).
In the past decades, several MADM methods have been proposed and the most popular methods are Best-Worst Method (BWM) (Rezaei,
2015), Analytic Hierarchy Process (AHP) (Saaty,
1986), Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) (Hwang and Yoon,
1981), ELimination and Choice Expressing REality (ELECTRE) (Roy,
1990), VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) (Opricovic and Tzeng,
2004), and Evaluation based on Distance from Average Solution (EDAS) (Keshavarz Ghorabaee
et al.,
2015).
In decision-making processes, many elements should be considered simultaneously. Therefore, it is very important to have an appropriate approach to obtain unambiguous results. There are many examples in which pairwise comparison (PC) method can be used to draw the final result in a relatively easy way (Koczkodaj,
1993). Psychologists believe that comparing two items at a time is easier and more accurate than comparing all items simultaneously (Ishizaka and Labib,
2011). The first documented use of PC returns to Ramon Llull, a 13th-century mystic and philosopher (Koczkodaj
et al. 2016, 81). Condorcet (
1785), Fechner (
1860) and Thurstone (
1927) also used PC in their studies. However, MADM is one of the most famous fields that has used PC to rank criteria or alternatives (Bozóki
et al.,
2016) and Saaty (
1977;
1980) made the greatest impact in the popularization of the PC method by proposing Analytic Hierarchy Process (AHP) (Koczkodaj,
1993). The PC methods decompose problems into sub-problems and let experts discriminate between two items at a time. Consequently, problems can be solved easily (Brunelli and Fedrizzi,
2015). Using the PC is useful as it compels the decision maker to think about and analyse the situation more precisely and deeply (Kurttila
et al.,
2000). Since the comparison of two items is the simplest type of question for measuring the weights, using the PC has become an interesting topic to researchers (Kim
et al.,
2017).
BWM (Rezaei,
2015) is a MADM method which works based on a PC system. The most important advantages of the BWM are as follows: (1) it needs less PCs; (2) it leads to more consistency. Therefore, BWM presents more reliable results. In this method, the decision-maker identifies the best (most desirable) and the worst (least desirable) criteria. Then PCs should be obtained between each of these criteria (the best and worst) and the other criteria (Rezaei,
2015). So far, the BWM has been used in some studies (Rezaei
et al.,
2016,
2015; Salimi and Rezaei,
2016,
2018; Ren
et al.,
2017; Gupta
et al.,
2017; Rezaei
et al.,
2018). Rezaei (
2016) proposed interval analysis for the case of multiple optimal solutions for not-fully consistent comparison systems and when the problem contains more than three criteria. He also proposed a linear model of the BWM. The major difference between the BWM and other PC-based methods is that those methods use the PCM (Eq. (
1)) whereas the BWM uses pairwise comparison vectors (PCVs) (Eq. (
2)).
Recently, the use of some PC-based methods has gained more interest, because it is possible to compute the consistency ratio, which boosts the reliability of results. However, researchers have faced difficulties in using PCMs due to rank reversal and great number of comparisons, as well as the inappropriate consistency ratio in big PCMs. The BWM was proposed by Rezaei (
2015) to provide an accurate PC system with less comparisons. In addition to the possibility to compute the consistency ratio, the BWM decreases the number of comparisons to
$
2n-3$ and results in a better consistency ratio and accuracy of results.
So far, some researchers attempted to develop BWM in fuzzy environment. Guo and Zhao (
2017) extended BWM to fuzzy environment and compared it with BWM. Lo and Liou (
2018) proposed a hybrid model for failure mode and effect analysis. This study modifies the model of BWM according to the FBWM which was provided by Guo and Zhao (
2017); they applied the interval numbers with BWM to obtain risk priority numbers. Mou
et al. (
2016) proposed intuitionistic fuzzy multiplicative BWM (IFMBWM) with intuitionistic fuzzy multiplicative preference relations for group decision-making. Hafezalkotob and Hafezalkotob (
2017) proposed a method based on group and individual decisions supported on FBWM called GI-FBWM. The study considered a hierarchical decision framework and both democratic and autocratic decision making styles can be considered in the proposed method. Liu
et al. (
2018a) proposed a two-stage model for supplier selection of green fresh product. In this study, FBWM is applied for subjective criteria weights and Shannon entropy is applied for objective criteria weights. Finally, suppliers are ranked using fuzzy MULTIMOORA method. Aboutorab
et al. (
2018) combined the concept of Z-numbers with BWM and applied the proposed method in a supplier development problem.
Some researchers attempted to develop BWM base on rough numbers and some researchers applied rough BWM in their studies. Zavadskas
et al. (
2018) developed a rough SWARA approach and compared the obtained result with rough BWM and rough AHP to determine the weight values. The results showed the correlation of ranks using rough SWARA with the ranks of rough BWM and rough AHP was complete. Stević
et al. (
2017) proposed an approach based on rough BWM (RBWM) and rough SAW (RSAW) methods and applied the hybrid model to select wagons for internal transport of a logistics company. This study compares the obtained ranks using RBWM-RSAW with the obtained ranks using AHP-TOPSIS, AHP-MABAC, AHP-SAW, BWM-TOPSIS, BWM-MABAC, BWM-SAW, RAHP-RTOPSIS, RAHP-RSAW, RAHP-RMABAC, RBWM-RTOPSIS and RBWM-RMABAC. The results indicate that there is a high correlation between the ranks of the compared models. Stević
et al. (
2018) proposed an integrated model based on Rough BWM and Rough WASPAS methods. The model was applied to a location selection problem for the construction of roundabout. Through the sensitivity analysis the proposed model was compared with RBWM-RSAW, RBWM-RMABAC, RBWM-RVIKOR, RBWM-RMAIRCA, RBWM-RTOPSIS and RBWM-REDAS. The sensitivity analysis indicated that the model stability was verified. Liu
et al. (
2018b) combined rough number, the BWM and the VIKOR to solve a Supply chain partner selection problem under cloud computing environment. Pamučar
et al. (
2018) developed an approach based on interval-valued fuzzy-rough numbers (IVFRN). In this study, BWM and MABAC methods were combined and applied to evaluate firefighting aircraft. Through the sensitivity analysis, the proposed model was compared with the fuzzy and rough extension of the MABAC, COPRAS and VIKOR methods and showed a high degree of stability.
Several studies combined BWM and other MADM methods. Tian
et al. (
2018) combined the BWM and improved TOPSIS and developed a hybrid multi-criteria group decision-making (MCGDM) model in a green supplier selection problem. You
et al. (
2016) proposed a hybrid decision framework to solve MCGDM problems based on the BWM and ELECTRE III methods. Yadav
et al. (
2018) proposed a hybrid BWM-ELECTRE-based framework for effective offshore outsourcing adoption. In this study, having determined the weight values of offshore outsourcing enablers by employing BWM, the automotive case organizations were prioritized using ELECTRE approach. Amoozad Mahdiraji
et al. (
2018) applied the combination of interval BWM and fuzzy COPRAS to analyse key factors of environmental sustainability in Iranian contemporary architecture.
Keršuliene
et al. (
2010) developed Step-wise weight assessment ratio analysis (SWARA) to determine the weight values of the attributes. Although BWM and SWARA use different mathematical approaches, they are similar in some aspects. Identifying the best and the worst criterion in the BWM method is similar to the first step of the SWARA method. BWM and SWARA methods are more preferable than the AHP method which requires more PCs (Zolfani and Chatterjee,
2019). Zolfani
et al. (
2018) extended the classic SWARA method to improve the quality of decision making process. In this study, the reliability evaluation of experts’ opinion is incorporated into SWARA method. Zolfani and Chatterjee (
2019) compared the results of variability between the criteria priorities for SWARA and BWM in the sustainable housing material selection problem.
Apart from the aforementioned studies, other methods are proposed to determine the weight of the attributes. Zavadskas and Podvezko (
2016) proposed the Integrated Determination of Objective Criteria Weights (IDOCRIW) method to combine the weights yielded by the entropy and the Criterion Impact Loss (CILOS) methods to obtain aggregate criteria weights for objective evaluation of the data array structure. Vinogradova
et al. (
2018) proposed a method of weights’ recalculation, and the integration of various estimates into a single one.
Kocak
et al. (
2018) developed a quadratic model of Euclidean BWM and minimized the sum of the squared differences instead of maximum number of differences in BWM. However, the proposed model needs more computations in comparison with linear BWM.
The BWM provides an appropriate system to reflect DM preferences in final weights. However, for not fully-consistent comparison systems with more than three criteria, there may be multiple optimal solutions. Although multiple optimality may be desirable in some cases, in other cases, decision-makers prefer to have a unique solution. This research proposes new models which result in a unique solution. As the proposed model has less constraints in comparison with the previous models, we can mention that it involves less calculations. In Sections
2–
4, an overview of previous models is provided. In Section
5, we propose two models of the BWM. After that, a numerical example is presented in Section
6. Finally, Section
7 discusses the research conclusions.
6 Illustrative Example
When buying a car, a customer considers eight criteria including quality
$
({C_{1}})$, price
$
({C_{2}})$, comfort
$
({C_{3}})$, safety
$
({C_{4}})$, style
$
({C_{5}})$, speed
$
({C_{6}})$, fuel consumption
$
({C_{7}})$, and aftersale service
$
({C_{8}})$. In this example, the aim is to find the importance of criteria. The customer provides the best-to-others and others-to-worst pairwise comparison vectors as shown in Table
2.
Table 2
Best-to-others (BO) and others-to-worst (OW) pairwise comparison vectors.
| BO |
$
{C_{1}}$ |
$
{C_{2}}$ |
$
{C_{3}}$ |
$
{C_{4}}$ |
$
{C_{5}}$ |
$
{C_{6}}$ |
$
{C_{7}}$ |
$
{C_{8}}$ |
|
Best criterion:
$
{C_{1}}$
|
1 |
1 |
3 |
3 |
2 |
3 |
2 |
6 |
| OW |
Worst criterion:
$
{C_{8}}$
|
|
$
{C_{1}}$ |
|
|
|
|
|
6 |
|
|
|
$
{C_{2}}$ |
|
|
|
|
|
6 |
|
|
|
$
{C_{3}}$ |
|
|
|
|
|
2 |
|
|
|
$
{C_{4}}$ |
|
|
|
|
|
3 |
|
|
|
$
{C_{5}}$ |
|
|
|
|
|
4 |
|
|
|
$
{C_{6}}$ |
|
|
|
|
|
2 |
|
|
|
$
{C_{7}}$ |
|
|
|
|
|
3 |
|
|
|
$
{C_{8}}$ |
|
|
|
|
|
1 |
|
|
According to Table
2, both
$
{C_{1}}$ and
$
{C_{2}}$ are evaluated as the best criteria. When there are multiple best or worst criteria, one of them should be selected arbitrarily (Rezaei,
2015). Therefore, in this example,
$
{C_{1}}$ is selected as the best criterion. Moreover,
$
{C_{8}}$ is evaluated as the worst criterion by considering DM preferences. In this example, a 1 to 9 scale is used to define the amount of preferences.
Solving this example through Eq. (
4) yields
$
{\xi ^{\ast }}=0.4586$. This means that the PC system is not fully-consistent and we may have multiple optimal solutions. By solving Eqs. (
6) and (
7) for all the criteria, we can determine weight ranges of the criteria. Interval weights can be obtained by optimal weights of the criteria. Optimal interval weights of the criteria in the example are determined as follows (see also Fig.
1). By using such an interval analysis, the centre of intervals can be used to rank the criteria.
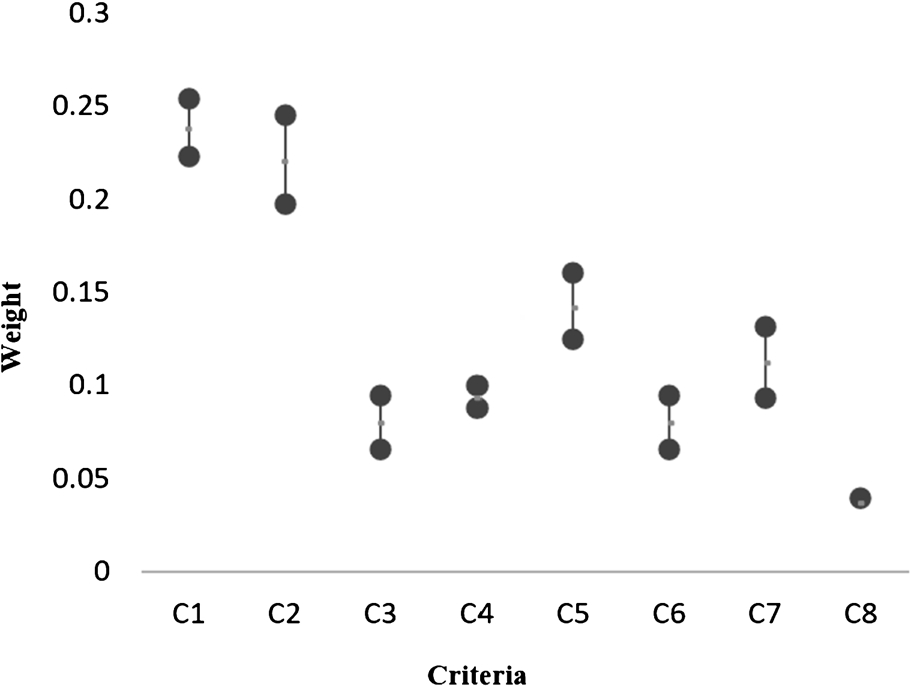
Fig. 1.
Optimal interval weights.
In some cases, DMs prefer to have a unique solution. This study proposes two models which result in a unique solution. Table
3 presents the results of application of the previous models and the proposed models to the example.
Table 3
Comparison of results of different models applied to the same data set.
| Criterion |
BWM |
Linear BWM |
Proposed nonlinear model |
Proposed linear model |
|
$
{C_{1}}$ |
0.2318 |
0.2308 |
0.2308 |
0.2400 |
|
$
{C_{2}}$ |
0.1994 |
0.2308 |
0.2308 |
0.2400 |
|
$
{C_{3}}$ |
0.0882 |
0.0839 |
0.0769 |
0.0800 |
|
$
{C_{4}}$ |
0.0912 |
0.0839 |
0.0769 |
0.0800 |
|
$
{C_{5}}$ |
0.1411 |
0.1259 |
0.1538 |
0.1200 |
|
$
{C_{6}}$ |
0.0882 |
0.0839 |
0.0769 |
0.0800 |
|
$
{C_{7}}$ |
0.1241 |
0.1259 |
0.1154 |
0.1200 |
|
$
{C_{8}}$ |
0.0359 |
0.0350 |
0.0385 |
0.0400 |
According to Table
2,
$
{C_{1}}$ and
$
{C_{2}}$ are of the same preference to the customer, since the preference of
$
{C_{1}}$ over
$
{C_{2}}$ is equal to 1. It means that
$
{C_{1}}$ and
$
{C_{2}}$ must have the same weight. The preference of
$
{C_{1}}$ over the worst criterion (
$
{C_{8}}$) equals to 6. Therefore, according to the both vectors, customer absolutely believes that
$
{C_{1}}$ and
$
{C_{2}}$ must have the same weight. After solving the BWM model, weights of the criteria are obtained as shown in the second column in Table
3. As the results show, the weight of
$
{C_{1}}$ is 0.2318 while the weight of
$
{C_{2}}$ is 0.1994, having a difference equal to 0.0324. As we mentioned before, we expected to reach the same weights for
$
{C_{1}}$ and
$
{C_{2}}$. However, the result was different. This condition may occur when we have multiple-optimality.
Except in the aforementioned issue, generally, Table
3 shows that the weights of criteria in all models are very close to each other. Table
4 also presents the distance from the centre of intervals which is 0.0612 for the BWM, 0.0668 for the linear BWM, 0.0559 for the proposed nonlinear model, and 0.0680 for the proposed linear model. According to the results, the solutions found by all the models are very close to the centre of intervals.
Table 4
Distances from the centre.
| Criterion |
Distance |
| BWM |
Linear BWM |
Proposed nonlinear model |
Proposed linear model |
|
$
{C_{1}}$ |
0.0064 |
0.0074 |
0.0074 |
0.0018 |
|
$
{C_{2}}$ |
0.0217 |
0.0097 |
0.0097 |
0.0189 |
|
$
{C_{3}}$ |
0.0082 |
0.0039 |
0.0031 |
0.0001 |
|
$
{C_{4}}$ |
0.0025 |
0.0098 |
0.0168 |
0.0137 |
|
$
{C_{5}}$ |
0.0016 |
0.0168 |
0.0112 |
0.0227 |
|
$
{C_{6}}$ |
0.0082 |
0.0039 |
0.0031 |
0.0001 |
|
$
{C_{7}}$ |
0.0117 |
0.0135 |
0.0030 |
0.0076 |
|
$
{C_{8}}$ |
0.0010 |
0.0019 |
0.0016 |
0.0031 |
| Sum |
0.0612 |
0.0668 |
0.0559 |
0.0680 |
To compare the proposed models with the existing models, the deviation of priority ratio from initial judgment can be calculated by sum of squared errors (SSE), as defined in Eq. (
14) (Mohtashami,
2014). According to Table
5, it is clear that the SSE value for the proposed nonlinear model (1.2547) is smaller than for the other models. Therefore, the proposed nonlinear model is superior to the existing models. The SSE value for the proposed linear model is also smaller than for the linear BWM. Thus, according to the results, we can conclude that the proposed models have a high level of accuracy.

