In this section, a sparse representation based multi-pose face recognition method is proposed which consists of three main steps:
The most important step in the proposed method is generating a virtual frontal view of a non-frontal face image. Since the proposed method learns view-dependent transformations to map the non-frontal face image to the frontal one, choosing the proper transformation needs the pose of the face image. Therefore, the first step of the proposed method is devoted to pose estimation. According to the estimated pose, a non-frontal to frontal view mapping is applied which generates a virtual frontal face image. Having the virtual frontal view in hand, SRC is used for the aim of face recognition. The following subsections explain these three steps of the proposed method in more details.
4.1 Pose Estimation Based on SRC
As mentioned earlier, prior knowledge of the pose of a face is an essential information in many face recognition techniques. It is often beneficial if the pose angle of the input face image can be estimated before recognition such as in modular PCA (MPCA) (Pentl
et al.,
1994) and eigen light-field (Gross
et al.,
2004). There are many efforts for automatic pose estimation in the literature. As the focus of this paper is on face recognition and not pose estimation, an interested reader is referred to Murphy-Chutorian and Trivedi (
2009) and Ding and Tao (
2016) as good surveys on face pose estimation.
It is obvious that two face images from different identities in the same pose are visually more similar than two face images of an identity in different poses. This can be used as a clue for face pose estimation aim, a face image in a specific pose can be estimated by a linear combination of face images of other subjects in the same pose. The proposed pose estimation method is based on the assumption that sparse representation coefficients of different identities in the same pose are closer than representation coefficients of images of the same identity in different poses. Therefore, using the sparse representation of unseen face image over training images of the same pose and repeating this for all poses, one can estimate the pose based on minimizing the reconstruction error on different poses. A similar idea has been used in Yu and Liu (
2014) where it is assumed that a face image in a specific pose cannot be approximated by a combination of face images in other poses.
Suppose there are
P classes of different poses
${A_{p}}$,
$p=1,\dots ,P$. The
p-th class
${A_{p}}=[{a_{p}^{1}},{a_{p}^{2}},\dots ,{a_{p}^{{n_{p}}}}]\in {\mathrm{\Re }^{(d{n_{p}})}}$ is called the view dictionary of pose
p that has
${n_{p}}$ training face images from different identities in this pose and
d is the dimension of each face image. Based on SR theory, every unseen face image
$y\in {\mathrm{\Re }^{d}}$ is expected to be expressed as a sparse representation of images in matrix
${A_{p}}$ in a particular pose. The sparse coefficients of image
y over the view dictionary
${A_{p}}$ is the
${\hat{x}_{p}}$ vector that can be obtained as follows:
where
λ is the regularization parameter as before. Therefore, face image
y is reconstructed based on different view dictionaries. The view dictionary that reconstructs the face image with minimum error determines the pose of the face image
y. In other words, the pose of face image
y is estimated based on minimizing the reconstruction error among all view dictionaries:
where
$\hat{p}$ is the estimated pose. Actually, this shows that
${A_{\hat{p}}}$ is the best view dictionary that can reconstruct the input face image from a linear combination of its set of face images. The proposed pose estimation algorithm is summarized in Algorithm
1. Figure
2 represents an example of the proposed pose estimation method where there are seven different poses (seven view dictionaries).

Algorithm 1
Sparse representation based pose estimation.

Fig. 2
An example of pose estimation based on sparse representation. (a) reconstructed input face image over 7 different view dictionaries ${A_{p}}$, $p=1,\dots ,7$ and (b) reconstruction error for each pose. Reconstruction error for 7-th pose is minimum and the input face image is supposed to be in this pose.
Figure
2(a) shows the input face image on the top and the 7-th reconstructed face images with respect to seven view dictionaries below that. As it is obvious, reconstructed image from the last dictionary
$({A_{7}})$ seems to be the most similar one to the input face image, where the reconstruction error plot in Fig.
2(b) confirms this consequence. Thus, the input face image is supposed to be in the last pose.
The proposed pose estimation method has some advantages over many other pose estimation methods. First, there is no assumption on the number of training face images in each pose and view dictionaries can have a different number of atoms. Also, no feature selection or 3D model of the face is required for pose estimation, so no image registration and heavy computation is used. However, the main shortcoming of the proposed pose estimation method is its accuracy drop in small pose intervals which will be discussed more in Section
5.2.
4.2 Virtual Frontal View Generation
In many face recognition methods, one of the key steps for achieving multi-pose face recognition is pose normalization or virtual frontal view generation. Obviously, a frontal face image contains the most details of the face which are beneficial for face recognition, compared to a non-frontal face image. In order to compensate for the loss of details in non-frontal views, one can try to generate a virtual frontal view from a non-frontal view. In this paper, this task is formulated as a general prediction framework which predicts a mapping from each non-frontal view to the frontal view, where the mapping is identity-independent. The purpose of this mapping is to estimate a frontal face image
${\hat{b}_{1}}\in {\mathrm{\Re }^{d}}$ given its non-frontal face image
${b_{p}}\in {\mathrm{\Re }^{d}}$ in pose
p. Modelling the virtual frontal view generation with linear mapping is as follows:
where
${V_{p}}(.)$ is the linear mapping function and
${W_{p}}$ is the linear mapping matrix for pose
p. Linear mapping function
${V_{p}}(.)$ can be achieved via a learning process. GLR and LLR (Chai
et al.,
2007) are general least square problems that use regression-based methods to find a good mapping. Another idea to find the mapping function is introduced in LSRR (Zhang
et al.,
2013) which assumes that the face images of one identity observed from different views share the same sparse representation coefficients over different view dictionaries. In other words, suppose
${f_{1}}$ and
${f_{2}}$ are two face images of one identity in poses
${p_{1}}$ and
${p_{2}}$ , respectively. The sparse representation coefficients of these two face images over view-dependent dictionaries related to
${p_{1}}$ and
${p_{2}}$ poses are supposed to be similar. Therefore, if sparse representation coefficients of a non-frontal face image of an identity are available over its view dictionary, these coefficients can be used to generate the virtual frontal view of that identity, using the frontal view dictionary. Consequently, considering face images of the
i-th identity, we have the following set of equations:
where
${A_{p}}$ is the view dictionary of pose
p,
${b_{p}^{i}}$ is the face image of identity
i in pose
p and
${e_{p}}$ is the reconstruction error in pose
p. The sparse representation coefficients
${x^{i}}$ are shared among all the
P views of the
i-th identity. These equations say that the face image from pose
p can be generated from sparse representation coefficients
${x^{i}}$ with the corresponding view dictionary
${A_{p}}$. Therefore, the key of virtual view generation lies in the recovery of the sparse representation coefficients
${x_{i}}$. The idea of sharing the sparse representation coefficients among different poses somehow reminds the idea used in Prince
et al. (
2008) where the authors assumed a face manifold and an identity space (latent space) and declared that the representation of each identity does not vary with pose. As another example, one can mention the research done in Sharma
et al. (
2012) which aims to find the sets of projection directions for different poses such that the projected images of the same identity in different poses are maximally correlated in the latent space.
Based on the discussion above, given training samples arranged in different view dictionaries
${A_{p}}$ $(p=1,\dots ,P)$, the non-frontal to frontal mapping function for input face images in pose
p (
${b_{p}}$s) can be obtained by first finding the sparse representation coefficients of
${b_{p}}$ on view dictionary of pose
p, then utilizing these coefficients with the frontal view dictionary
${A_{1}}$ as follows:
where
${\hat{x}_{p}}$ is the best vector of sparse representation coefficients of
${b_{p}}$ over view dictionary
${A_{p}}$,
λ is the regularization parameter as mentioned before and
${\hat{b}_{1}}$ is the virtual frontal view corresponding to the non-frontal view
${b_{p}}$.
It is worth noticing that the mapping in Eq. (
8) is based on two parameters, view dictionaries and sparse representation coefficients. As the sparse representation coefficients are obtained via an optimization problem based on a view dictionary, one of the factors that play an important role in high accuracy mapping is the selection of view dictionaries. These dictionaries can be simply made form training images of each pose or can be learned more effectively in a dictionary learning process. As training images are accompanied by identity label, using them as view dictionary atoms might not successfully generate a face image from a new identity. In other words, identity-independent view dictionaries are expected to be more efficient in generating face images from new identities. Therefore, one of the key steps for increasing the accuracy of the proposed method in obtaining the sparse representation coefficients and generating the virtual frontal view is to learn desirable identity-independent view dictionaries. The next subsection explains a supervised dictionary learning process to learn
${A_{p}}$s as efficient as possible.
4.3 Supervised View Dictionary Learning
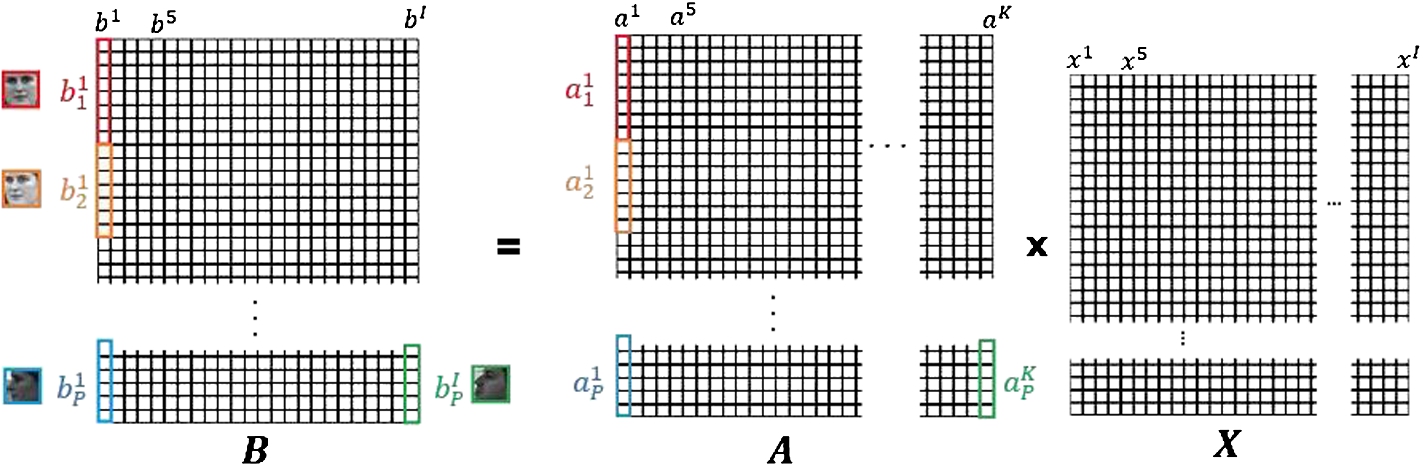
Fig. 3
Example of sparse dictionary learning. $B\in {\mathrm{\Re }^{(dP\times I)}}$ is the learning face images in P different poses for I identities, $A\in {\mathrm{\Re }^{(dP\times K)}}$ is the dictionary includes P different view dictionaries which each view dictionary can be extracted by separating d rows related to each pose, and $X\in {\mathrm{\Re }^{(K\times I)}}$ is the sparse representation matrix.
Suppose that
${b_{p}}$ and
${b_{1}}$ are two face images of one identity in non-frontal pose
p and frontal pose 1, respectively,
${\hat{x}_{p}}$ is the sparse representation of
${b_{p}}$ over view dictionary
${A_{p}}$, and
${\hat{x}_{1}}$ is the sparse representation of
${b_{1}}$ over view dictionary
${A_{1}}$. As mentioned in the previous section, view dictionaries
${A_{p}}$ and
${A_{1}}$ are called desirable if the sparse representations
${\hat{x}_{p}}$ and
${\hat{x}_{1}}$ are the same or at least close enough. So, the aim of this subsection is to learn view dictionaries that share similar sparse coefficients for face images of one identity in different poses. This is achieved via a supervised view dictionary learning process. By concatenating the
P equations in Eq. (
6), while omitting the identity parameter
i for simplicity, we have:
which states that the
P views, when concatenated together, should have the same sparse representation with respect to the concatenated view dictionary. Given the training dataset
${\{{b_{p}^{i}}\}_{p=1,\dots ,P}^{i=1,\dots ,I}}$, where
i is the index for identities and
p is the index for poses, the training set is rearranged by concatenating the
P views of each identity in
${\{{b^{i}}\}_{i=1,\dots ,I}}$ vector, where
${b^{i}}={[{b_{1}^{i}}{b_{2}^{i}}{b_{P}^{i}}]^{T}}\in {\mathrm{\Re }^{(dp\times 1)}}$ and
$B\in {\mathrm{\Re }^{(dP\times I)}}$ is the matrix made from concatenating face images of
I different identities. Now, the view dictionaries can be learned via the following minimization problem:
where
$\hat{A}={[{\hat{A}_{1}^{T}},{\hat{A}_{2}^{T}},\dots ,{\hat{A}_{P}^{T}}]^{T}}\in {\mathrm{\Re }^{(dP\times K)}}$ is the learned dictionary and
$\hat{X}=[{\hat{x}^{1}},{\hat{x}^{2}},\dots ,{\hat{x}^{I}}]\in {\mathrm{\Re }^{(K\times I)}}$ is the sparse coefficients matrix whose column
i is the sparse representation vectors of the training samples in
${b^{i}}$ and
K is the dictionary size. Eq. (
10) aims to jointly find the proper sparse representation coefficients and the dictionary. It describes face images from the ith identity (
${b^{i}}$) as the sparsest representation
${x^{i}}$ over dictionary
A. After
$\hat{A}$ is learned, the view dictionaries
${\{{\hat{A}^{p}}\}_{p=1,\dots ,P}}$ are obtained by splitting
$\hat{A}$ into
P parts, e.g. view dictionary of pose
p (
${\hat{A}_{p}}$) can be achieved by separating
d rows of
$\hat{A}$ that are corresponding to the
p-th pose (rows
$pd-d+1$ to
$dp$). Figure
3 demonstrates these matrices and the dictionary learning process visually.
In order to properly choose the dictionary size
K, it is worthy to remind some points on dictionary characteristics. Dictionary
$A\in {\mathrm{\Re }^{(dP\times K)}}$ is considered undercomplete if
$K<dP$ or overcomplete if
$K>dP$. When (
$K=dP$), dictionary is considered as a complete dictionary. From a representational point of view, a complete dictionary does not help in any improvement and is neglected. Undercomplete dictionaries are strongly related to dimensionality reduction. Principal component analysis is a famous example of this case where dictionary atoms have to be orthogonal. However, putting orthogonality constraint on dictionary atoms limits the choice of atoms which is the main disadvantage of undercomplete dictionaries. On the other side, overcomplete dictionaries do not have the orthogonality constraint, therefore, they allow for more flexible dictionaries and richer data representation (Elad,
2010).
Although all view dictionaries can be learned simultaneously using Eq. (
10), the learning process will be impractical for large dictionary sizes or high dimensional data. Consider a situation where each identity has images in 10 poses and each image has about 1000 pixels (a small 30×35 face image), so each column of dictionary has about 10000 entries. If the dictionary size is adjusted to 1000 atoms, the size of dictionary will be 10000×1000. Doing computation on a dictionary of this huge size is impractical because of memory and computational limitations. To dominate this problem, in this paper, pairwise dictionary learning is proposed, where each view dictionary is learned separately. In other words, in order to learn the view dictionary for pose
p, the training matrix will be
${B_{p}}\in {\mathrm{\Re }^{(2d\times I)}}$ where each column of
${B_{p}}$ is
${[{b_{p}^{i}}{b_{1}^{i}}]^{T}}\in {\mathrm{\Re }^{(2d\times 1)}}$ (face images of frontal pose and images of non-frontal pose
p). In this case, the optimization in Eq. (
10) results in
$\hat{A}\in {\mathrm{\Re }^{(2d\times K)}}$ where the first
d rows of
$\hat{A}$ can be considered as learned view dictionary for pose
p. It should be noted that view dictionaries are not learned simultaneously in pairwise dictionary learning. However, as training images in frontal pose are the same for learning all view dictionaries, it is expected that describing face images of one identity in different poses by these view dictionaries has similar sparse representation coefficients. Figure
4 shows the effect of dictionary learning on sparse representation of three face images of an identity in different poses. The first column shows the sparse coefficients when dictionary atoms are simply the training data in different poses while the second column shows sparse coefficients obtained based on learned dictionary. As expected, the representation coefficients of the three images shown in the second column are more similar compared to the ones in the first column. This observation confirms the effect of dictionary learning on unifying the sparse representation coefficients of face images of one identity in different poses. Also, the figure depicts the increase in sparsity of coefficients after dictionary learning, which is another aim of dictionary learning. Getting back to dictionary learning process in Eq. (
10), several dictionary learning methods have been proposed since now that can be divided into two groups: 1) unsupervised dictionary learning methods such as MOD (Engan
et al.,
1999) and K-SVD (Aharon
et al.,
2006) and 2) supervised dictionary learning methods such as SDL (Mairal
et al.,
2009) and LCKSVD (Jiang
et al.,
2013). The K-SVD method is introduced to efficiently learn an overcomplete dictionary and has been successfully applied to image restoration and image compression. K-SVD focuses on the representational power of the learned dictionary, but does not consider the discrimination capability of it. LCKSVD (Jiang
et al.,
2013) is a supervised extension of K-SVD that uses supervised information (labels) of training samples to learn a compact and discriminative dictionary. As LCKSVD has proved itself as a successful supervised dictionary learning method, it has been used here for learning view dictionaries. The objective function defined by LCKSVD is as follows:
where
$\| .{\| _{F}}$ is the Frobenius norm and
B,
A and
X are training data, dictionary and sparse coefficients matrices, respectively.
$Q=[{q^{1}},{q^{2}},\dots ,{q^{I}}]\in {\mathrm{\Re }^{(K\times I)}}$ is the discriminative sparse code of training samples in
B and is initialized based on the labels of training samples and desired labels of dictionary atoms. For example, if
i-th atom of dictionary has the same label as
j-th training sample, then
$Q(i,j)=1$, else
$Q(i,j)=0$.
T is a linear transformation matrix and the term
$\| Q-TX{\| _{F}^{2}}$ enforces the sparse coefficients
X to approximate the discriminative sparse codes
Q. This term enforces the samples from the same class to have very similar sparse representations. The first and second terms of Eq. (
11) are the reconstruction error and the discrimination power, respectively, where
α controls the contribution between these two terms. The implementation of LCKSVD is available by the LCKSVD authors and is used in this paper for solving Eq. (
11). For more details on LCKSVD, we refer the interested reader to Jiang
et al. (
2013).
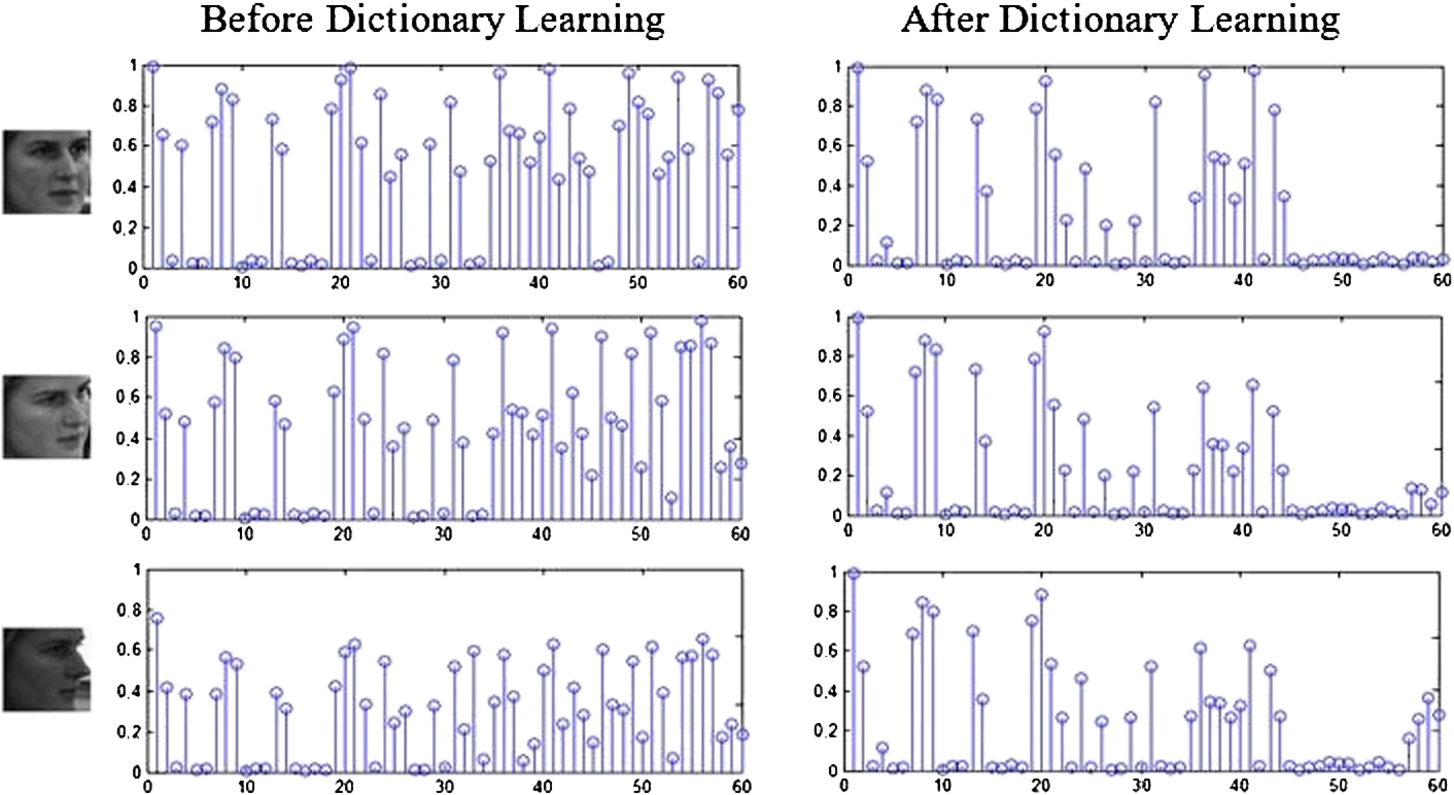
Fig. 4
Effect of dictionary learning on sparse representations of 3 different pose images of one identity. The first and second columns show the sparse representation of face images using training samples and the learned dictionary, respectively. As expected, representation coefficients in second column are more similar in different poses, while coefficients are sparser in each pose.
After obtaining view dictionaries, virtual frontal view generation can be done by first estimating the pose
$\hat{p}$ of the input face image
y by Algorithm
1, then finding
${\hat{x}_{\hat{p}}}$ as the sparse representation of
y over the learned view dictionary of the estimated pose. Finally, the virtual frontal view of
y is generated by multiplying the sparse representation
${\hat{x}_{\hat{p}}}$ to the learned view dictionary of frontal pose
${\hat{A}_{1}}$. The algorithm of virtual view generation is summarized in Algorithm
2 and an example of virtual view generation is shown in Fig.
5.

Algorithm 2
Virtual View Generation
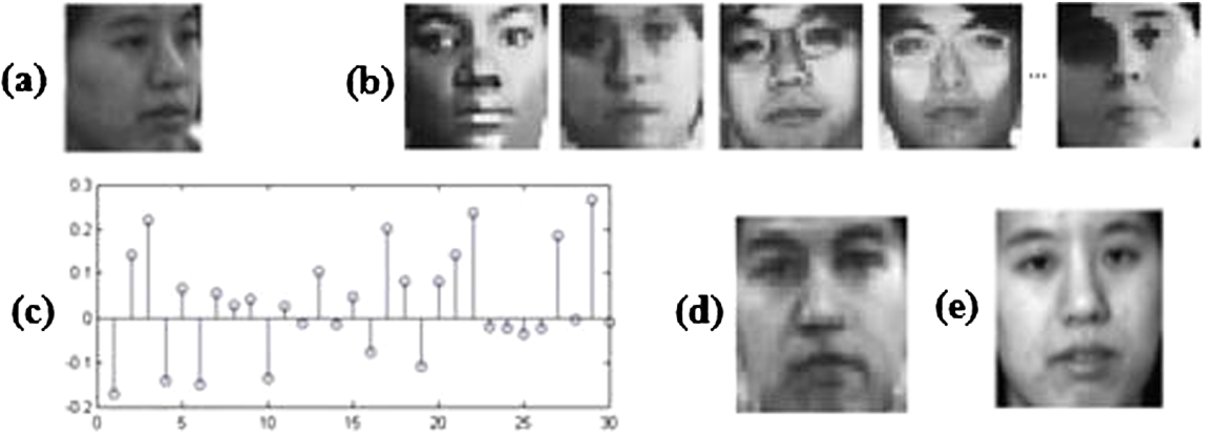
Fig. 5
Virtual frontal view generation. (a) non-frontal input face image ${y_{p}}$, (b) learned view dictionary for pose p (${\hat{A}_{p}}$), (c) sparse representation of ${y_{p}}$ over ${\hat{A}_{p}}$, (d) generated virtual frontal view ${\hat{y}_{1}}$, (e) actual frontal view of input face image ${y_{1}}$.

