1 Introduction
Clustering (Jain,
2010; Hartigan,
1975; Khemchandani and Pal,
2019) is an unsupervised learning process to partition a given data set into clusters based on similarity/dissimilarity functions, such that the data objects partitioned in the same cluster are as similar as possible, while those in different clusters are dissimilar at the same time. Currently, there have been various clustering methods that were proposed and applied in many areas (Olde Keizer
et al.,
2016; Benati
et al.,
2017; Truong
et al.,
2017; Pham
et al.,
2018; Motlagh
et al.,
2019; Borg and Boldt,
2016; Mokhtari and Salmasnia,
2015).
For crisp clustering method, like
k-means (MacQueen,
1967; Mehdizadeh
et al.,
2017) or hierarchical clustering method (Johnson,
1967), each data object can only be partitioned into one cluster. While fuzzy c-means (FCM) (Bezdek
et al.,
1984; Zhao
et al.,
2013) introduced the concept of membership degree so that each object can belong to two or more clusters with a certain membership degree value. FCM is the extension of hard
k-means clustering, and the rich information conveyed by the membership degree and fuzzifier in FCM further expanded its application areas. FCM algorithm was first proposed by Dunn and generalized by Bezdek (Dunn,
1973; Bezdek,
1981), and it has become a popular and widely used fuzzy clustering method in pattern recognition (Ahmed
et al.,
2002; Dembélé and Kastner,
2003; Park,
2009; Hou
et al.,
2007).
However, the fuzzifier, also known as the weighting exponent or fuzziness parameter in FCM, is an important parameter in FCM which can significantly influence the performance of FCM clustering (Pal and Bezdek,
1995). There have been considerable research efforts that focused on the selection of fuzzifier, and many suggestions have been proposed (Cannon
et al.,
1986; Hall
et al.,
1992; Shen
et al.,
2001; Ozkan and Turksen,
2004,
2007; Wu,
2012). However, there is still not one generally accepted criterion and few theoretical guides for the selection of fuzzifier in FCM (Fadili
et al.,
2001). In many cases, users subjectively select the value of fuzzifier while using FCM clustering.
In addition, the distributions of many data sets are not uniform in practical applications (Wu
et al.,
2012). It has been demonstrated that clustering performance is always affected by data distributions (Xiong
et al.,
2009; Wu
et al.,
2009c). In our previous work (Zhou and Yang,
2016), we have also found that FCM has the uniform effect similar to
k-means clustering. The clustering results of FCM can be significantly influenced by the cluster size distributions. Therefore, to improve the performance of FCM for data sets with different cluster size distributions, it is important to select the appropriate value of fuzzifier. In this study, a new fuzzifier selection criterion and a corresponding algorithm called CSD-m algorithm are proposed from the perspective of cluster size distribution. The cluster size distribution mainly refers to the variation of cluster sizes. First, we use the coefficient of variance (CV) to measure the variation of data in cluster sizes. Then, the values of DCV, which indicate the change of variation in cluster sizes after FCM clustering, are calculated iteratively with different fuzzifier values within an initial search interval. Finally, according to the minimum absolute value of DCV, the optimal value of fuzzifier is determined. Our experiments on both synthetic data sets and real-world data sets illustrate the effectiveness of the proposed criterion and CSD-m algorithm. The experimental results also reveal that the widely used fuzzifier value
$m=2$ is not optimal for many data sets, especially for data sets with large variation in cluster sizes.
The fuzzifier, denoted as
m in FCM, is an important parameter which can significantly influence the performance of FCM clustering. Currently, there have been considerable studies on fuzzifier selection. Bezdek proposed a range interval of fuzzifier,
$1.1\leqslant m\leqslant 5$, based on experience (Bezdek,
1981). Pal and Bezdek presented a heuristic criteria for the selection of optimal fuzzifier value, and the interval they suggested was
$[1.5,2.5]$ (Pal and Bezdek,
1995). They also pointed out that the median, namely
$m=2$, can be selected when there is no other specific constraints. Some studies (Cannon
et al.,
1986; Hall
et al.,
1992; Shen
et al.,
2001) presented the similar suggestion as the work of Pal and Bezdek (
1995). In addition, Bezdek studied the physical interpretation of FCM when
$m=2$ and pointed out that
$m=2$ was the best selection (Bezdek,
1976). The study of Bezdek
et al. further demonstrated that the value of
m should be greater than
$n/(n-2)$, where
n is the total number of sample objects (Bezdek
et al.,
1987). Based on their work of word recognition, Chan and Cheung suggested that the value range of
m should be
$[1.25,1.75]$ (Chan and Cheung,
1992). However, Choe and Jordan pointed out that the performance of FCM is not sensitive to the value of
m based on the fuzzy decision theory (Choe and Jordan,
1992). Ozkan and Turksen presented an entropy assessment for
m considering the uncertainty contained (Ozkan and Turksen,
2004). To obtain the uncertainty generated by
m in FCM, Ozkan and Turksen also identified the upper and lower values of
m as 1.4 and 2.6, respectively, (Ozkan and Turksen,
2007). Wu proposed a new guideline for the selection of
m based on a robust analysis of FCM, and suggested implementing FCM with
$m\in [1.5,4]$ (Wu,
2012).
In summary, there is still not one widely accepted criterion and little theoretical support for the selection of fuzzifier in FCM (Pal and Bezdek,
1995; Yu
et al.,
2004). In most practical applications, the value of fuzzifier is always subjectively selected by users, and
$m=2$ is the most common selection (Pal and Bezdek,
1995; Cannon
et al.,
1986; Hall
et al.,
1992; Shen
et al.,
2001). Indeed, this selection may not be always the optimal, and inappropriate selection of fuzzifier value can significantly affect the clustering results of FCM. Additionally, few of the above researches have focused on the cluster size distribution while studying the related issue of fuzzifier selection. The characteristics of cluster size distribution may have an impact on the performance of FCM clustering. Fuzzifier is a key parameter that influences the clustering results of FCM. Furthermore, in some studies, only the range intervals of empirical reference values were presented without specific criterion and method for the selection of optimal fuzzifer value in practical applications. Therefore, the motivation of this study is to explore the influence and measure the influence extent of fuzzifier value on FCM clustering results, and further investigate the fuzzifier selection from a cluster size distribution perspective. The main contributions of this study are as follows. First, the mechanism that fuzzifier influences the FCM clustering result is revealed. Second, we point out that the widely used fuzzifier value
$m=2$ is not optimal for many data sets with large variation in cluster sizes. Third, a criterion and a CSD-m algorithm for fuzzifier selection in FCM is presented from cluster size distribution perspective.
We note that, for a given data set, “data distribution” typically means many aspects of the characteristics, such as the shapes, densities and dimensions. While the focus of this study is the cluster size distributions of data sets. So we use cluster size distribution to represent the variation in cluster sizes of a data set.
The remainder of this paper is organized as follows. The FCM clustering algorithm is briefly reviewed in Section
2. In Section
3, we propose the fuzzifier selection criterion from cluster size distribution perspective and the corresponding algorithm called CSD-m algorithm. Experimental results and discussion are presented in Section
4. Finally, conclusions are made in Section
5.
2 FCM Clustering
FCM algorithm (Bezdek
et al.,
1984; Bezdek,
1981) starts with determining the number of clusters followed by guessing the initial cluster centres. Then every sample point is assigned a membership degree for each cluster. Each cluster centre’s point and corresponding membership degrees are updated iteratively by minimizing the objective functions until the stopping criteria are met. The stopping criteria mainly include the iterations
t reach the maximum number
${t_{\max }}$, or the difference of the cluster centres between two consecutive iterations is within a small enough threshold
ε, i.e.
$\| {v_{i,t}}-{v_{i,t-1}}\| \leqslant \varepsilon $. The objective function of FCM algorithm is defined as:
where
U is the membership degree matrix.
V represents the cluster centre’s matrix.
n is the total number of data objects in the data set.
c is the number of clusters.
m is the fuzzifier.
${\mu _{ij}}$ is the membership degree of the
jth data object
${x_{j}}$ to the
ith cluster
${C_{i}}$.
${v_{i}}$ is the cluster centre of
${C_{i}}$.
${d_{ij}^{2}}$ is the squared Euclidean distance between
${x_{j}}$ and the cluster centre
${v_{i}}$, and
${d_{ij}^{2}}=\| {x_{j}}-{v_{i}}{\| ^{2}}$.
In the iterative procedure, membership degree
${\mu _{ij}}$ and the cluster centres
${v_{i}}$ are updated by:
where
${\mu _{ij}}$ satisfies
The meanings of the symbols in Eq. (
2) to Eq. (
6) are the same as those in Eq. (
1).
The basic FCM algorithm is briefly reviewed as Algorithm
1.

Algorithm 1
Fuzzy c-means (FCM)
The flowchart of FCM algorithm can be shown in Fig.
1.
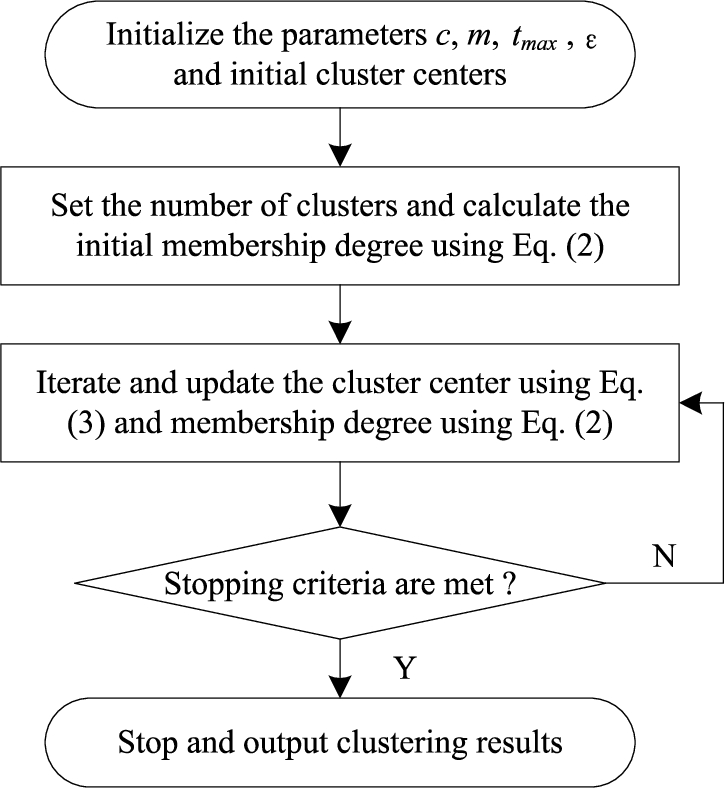
Fig. 1
Flow chart of FCM clustering.

