To assess risks, an expert needs to work on identifying types of threats. The list of threats is based on existing threats that create conditions for the entire information system to malfunction related to information security attributes (C – confidentiality, I – integrity, A – accessibility).
3.1 Brief Review of Methodology of an Integrated Delphic-Eckenrode’s Likert-Type Scale-Based Fuzzy Rating (Turskis et al., 2019)
The group decision-making processes are necessary to design and evaluate a set of different alternatives. One of the most important tasks is to reject those alternatives that do not meet lower bounds of the important criteria values. For a long time, a rigorous agreement was seen as a final group’s opinion. In most cases, a group of experts who make real-life decisions have no strict and steady opinion about the same criteria and alternatives. An agreement of the group is reached when the most dominant players agree with the criteria ratings and performances of the considered alternatives. Real-life problems’ modelling and solution lead the group of decision-makers to situations when models are based on vague logic. Besides, most often the models are based on the criteria rating in words. Such type of ratings cannot be replaced by the strict (crisp) numerical values. The fuzzy set theory allows decision takers to apply partially obtained information into the issue solving framework (Turskis
et al.,
2012). A fuzzy set is characterized by a membership (characteristic) function which assigns to each object a grade of membership ranging (Zadeh,
1965). Different types of membership functions are available. In this research, the most commonly used triangular membership function is used (Dubois and Prade,
1978). A fuzzy triangular number will be denoted as
$(\alpha ,\beta ,\gamma )$ (
α – lower value of the fuzzy number,
β – modal value of the fuzzy number,
γ – upper value of the fuzzy number).
It is required to identify the importance of the activities of the different process managers before starting to assess the critical challenges of workplace safety’s management, efficiency level of safety solutions and quality improvement. In order to achieve this, experts can use weighting methods for criteria. There are a lot of different subjective approaches for assessing weights: SWARA (Kersuliene
et al.,
2010; Keshavarz-Ghorabaee
et al.,
2018), FARE (FActor RElationship) (Ginevicius,
2011), and others.
Nominal group technique Delphi (Linstone and Turoff,
2002) is a useful tool for solving complicated problems which need expert data. It is a group decision-making process and includes idea generation, problem description, data assessment, and generation of feasible alternatives.
Likert scales are known as a tool for the measurement and assessment of attitudes. The reason for this is that the Likert scale is a straightforward tool to use and can be analysed effectively as interval or fuzzy scales (Allen
et al.,
2017).
Eckenrode (
1965) presented seminal work on criteria weights elicitation. Rating is sufficient for personal assessment, and it is especially useful for group decision making. It works well because it forces the expert to get clarity on his criteria and create a shared set of criteria. Eckenrode’s Rating method is selected and modified by applying the basics of fuzzy sets theory in this study.
Risk assessment for each information infrastructure and analysis of the adequacy of risk management measures are carried out by experts.
3.3 Selection of Criteria and Sub-Criteria
When solving problems by the MCDM method, first of all, a set of possible alternatives is formed, consisting of the CII. Next step is the selection of criteria and sub-criteria.
Criteria for risk assessment can be different. They depend on the infrastructure for which the risk is determined. In this case, the threats were taken as criteria. The experts determine the choice of threats aimed at the information infrastructure according to the Delphi method. The participants of the experts form a group, based on Sherwood
et al. (
2005). Then experts ranked and rated the impact of threats and probability of threats in the prevention of accidents at work. Based on the results, the following five threats that are most associated with cybersecurity were identified as criteria:
1) Health and safety threat (T1) – the threat to the personal health and safety of staff, customers and members of the population.
2) Technology threat (T2) – the threat of failure to plan, manage and monitor the performance of technology-related projects, product, services, processes, staff and delivery channels.
3) Information security threat (T3) – the threat of unauthorized disclosure or modification to information, or loss of availability of information, or inappropriate use of information.
4) Legal and regulatory compliance threat (T4) – the threat of failure to comply with the laws of the states in which business operations are carried out, or failure to comply with any regulatory, reporting, and taxation standards, or failure to comply with contracts, or failure of contracts to protect business interests.
5) Climate and weather threat (T5) – the threat of loss or damage caused by unusual climate conditions, including drought, heat, flood, cold, storm, and winds.
Each of the threats has its characteristics. According to Kosseff (
2018), it is necessary to promote “identification, confidentiality, and integrality of public and private information, systems, and networks”. Mena
et al. (
2018) focused on IoT inherent vulnerabilities and their implications to the fundamental information security challenges in confidentiality, integrity, and availability.
In this paper, the characteristics of the threats were taken as sub-criteria. It was proposed to choose sub-criteria, which focus on almost every aspect of security, i.e. protection of data from beginning to end. This work focuses on major six aspects of security, i.e. confidentiality, availability, integrity, direct losses, indirect losses, and criticality.
Thus, the following sub-criteria were chosen to solve the MCDM problem:
1) Loss of availability. Availability is the property of being accessible and usable upon demand by an authorized entity. Loss of availability can conclude performance degradation, short-term/long-term interruption, total loss (destruction).
2) Loss of confidentiality. Confidentiality is the property that information is not made available or disclosed to unauthorized individuals, entities, or processes. Confidentiality refers to keeping information secret from unauthorized entities (Sherman
et al.,
2018). Loss of confidentiality can lead to internal disclosure, external disclosure of information, and others.
3) Loss of integrity. Integrity is the property of protecting the accuracy and completeness of assets. Loss of integrity can conclude accidental modification, deliberate modification, incorrect results, incomplete results, etc.
Table 1
Weight ranking scale based on Immawan
et al. (
2018).
| Rating |
Description |
Definition |
| 10 |
Extremely dangerous |
Failure could cause the death of a person or infrastructure breakdown |
| 8–9 |
Very dangerous |
Failure could cause a significant injury or major infrastructure disruption with the interruption in service |
| 6–7 |
Dangerous |
Failure could cause a minor to moderate injury with a high degree of personal dissatisfaction or significant infrastructure issues requiring repairs |
| 5 |
Moderate danger |
Failure could cause a minor injury with some person dissatisfaction or significant infrastructure issues |
| 3–4 |
Low to moderate danger |
Failure could cause a very minor or no injury but annoys customers or results in minor infrastructure issues that can be overcome with minor modifications to the infrastructure or business |
| 2 |
Slight danger |
Failure could cause no injury, and the customer is unaware of the issue; however, the potential for minor injury exists |
| 1 |
No danger |
Failure causes no injury and has no impact on the infrastructure |
4) Direct losses are losses arising naturally, according to the usual course of things, from the breach of contract itself, and are therefore foreseeable and recoverable. Often these include financial costs.
5) Indirect losses are losses that arise from a particular circumstance of the case. Indirect losses, often referred to as “consequential losses”, are not inflicted by the peril itself but describe losses which were suffered as a result or consequence of the direct loss. For example, reputational risks.
6) Criticality is the quality, state, or degree of being of the highest importance. In RCM terms, criticality is based on the consequence of failure. It is an essential criterion for information infrastructures provided critical services.
3.4 The Importance of Threat Impact on CII
According to the analysis of severity (Lough
et al.,
2008), the importance of severity can be divided into five categories: insignificant (the client noticed a very slight failure), low (slight irritation of the client), medium (causes customer dissatisfaction, customer is annoyed), high (product does not work, client evils) and very high (the client is at risk, the safety rules are violated).
Table 2
Weight ranking scale for the impact of the threats on CII.
| Threat impact abbreviation |
Value |
Threat impact level |
Fuzzy triangular numbers |
| α |
β |
γ |
| ED |
10 |
Extremely dangerous |
0.9 |
1 |
1 |
| VD(H) |
9 |
Very dangerous (high level) |
0.8 |
0.9 |
1 |
| VD(M) |
8 |
Very dangerous (medium level) |
0.8 |
0.9 |
1 |
| D(H) |
7 |
Dangerous (high) |
0.6 |
0.7 |
0.8 |
| D(M) |
6 |
Dangerous (medium level) |
0.5 |
0.6 |
0.7 |
| MD |
5 |
Moderate danger |
0.4 |
0.5 |
0.6 |
| LM(H) |
4 |
Low to moderate danger (high level) |
0.3 |
0.4 |
0.5 |
| LM(M) |
3 |
Low to moderate danger (medium level) |
0.2 |
0.3 |
0.4 |
| SD |
2 |
Slight danger |
0.1 |
0.2 |
0.3 |
| ND |
1 |
No danger |
0 |
0.1 |
0.2 |
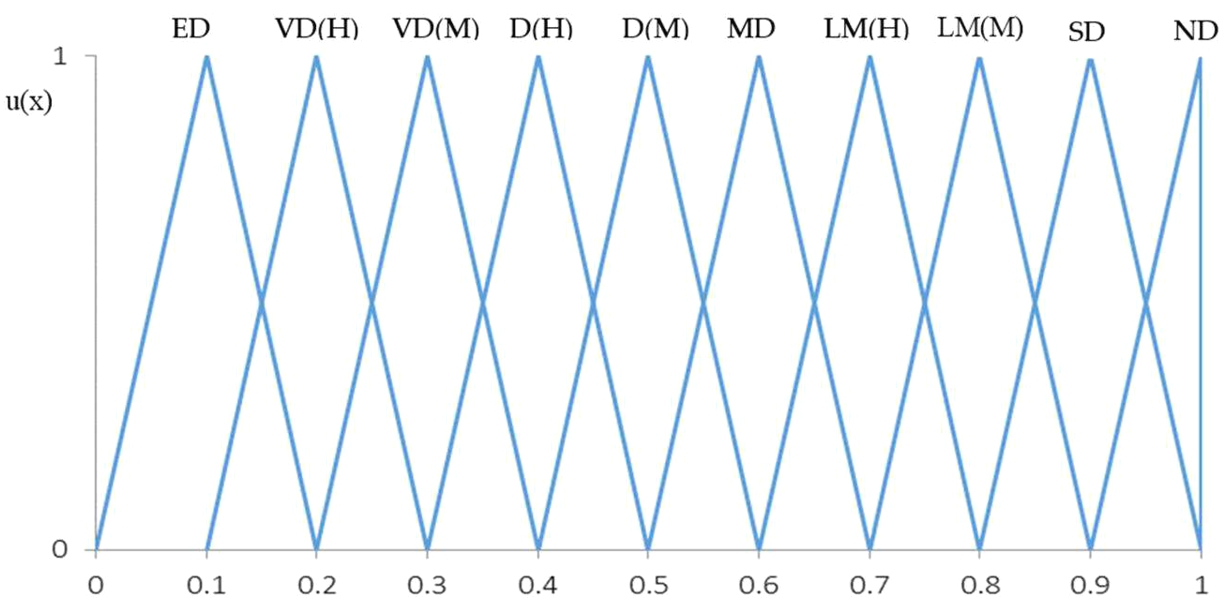
Fig. 4
Likert-type scale to determine the threat impact on CII.
At the same time, some methods of risk analysis apply a 10-point scale for ranking the severity of risks (Table
1).
The 10-level scale has more exact results of calculations. The weight depending on their importance determines further criteria. More critical criteria get higher weight values.
Based on the scale proposed in Table
1, the Likert-type scale is presented (Table
2, Fig.
4).
Rating: The raw rating assigned by the judge to each criterion, taking into account the sub-criteria, against the scale of 0 to 10 (10 most valuable) is treated as follows (Tables
3–
4):
where
${w_{cj}}$ – weight computed for criterion
c from the rating given by judge
j,
${p_{cj}}$ – rating given by judge
j to criterion
c, and
${w_{c}}$ is calculated as follows:
Table 3
Impact ofthe threats on CII lexical evaluation based on Likert-type scale.
| Impact of threats on CII |
Loss of availability experts |
… |
Criticality experts |
| ${E_{1}}$ |
${E_{2}}$ |
${E_{3}}$ |
${E_{4}}$ |
${E_{5}}$ |
… |
${E_{1}}$ |
${E_{2}}$ |
${E_{3}}$ |
${E_{4}}$ |
${E_{5}}$ |
| ${I_{1}}$ |
VD(M) |
VD(M) |
VD(H) |
VD(H) |
VD(H) |
… |
ED |
ED |
ED |
VD(H) |
ED |
| ${I_{2}}$ |
D(H) |
VD(M) |
D(M) |
D(M) |
D(H) |
… |
VD(H) |
VD(H) |
ED |
VD(H) |
VD(H) |
| ${I_{3}}$ |
D(M) |
D(H) |
D(H) |
D(H) |
D(M) |
… |
VD(M) |
VD(M) |
VD(M) |
VD(M) |
VD(M) |
| ${I_{4}}$ |
LM(H) |
LM(M) |
SD |
SD |
LM(M) |
… |
LM(H) |
MD |
D(M) |
LM(H) |
D(M) |
| ${I_{5}}$ |
D(M) |
VD(H) |
D(H) |
D(M) |
VD(M) |
… |
VD(M) |
D(H) |
D(M) |
MD |
MD |
Using rules of fuzzy arithmetic, the equations (
1) and (
2) are modified as follows:
where
${w_{j\alpha }}={\min _{k}}{y_{jk}}$,
$j=\overline{1,n}$,
$k=\overline{1,p}$, is minimum possible value of
j-th criterion,
${w_{j\beta }}={({\textstyle\prod _{k=1}^{p}}{y_{jk}})^{\frac{1}{p}}}$,
$j=\overline{1,n}$, is the most possible value of
j-th criterion and
${w_{j\gamma }}={\max _{k}}{y_{jk}}$,
$j=\overline{1,n}$,
$k=\overline{1,p}$, is the maximal possible value of
j-th criterion.
Table 4
Impact ofthe threats on CII expressed by fuzzy triangular numbers corresponding to the linguistic scale.
|
${E_{1}}$ |
${E_{2}}$ |
${E_{3}}$ |
${E_{4}}$ |
${E_{5}}$ |
|
α |
β |
γ |
α |
β |
γ |
α |
β |
γ |
α |
β |
γ |
α |
β |
γ |
| Loss of availability sub-criterion |
| ${I_{1}}$ |
0.7 |
0.8 |
0.9 |
0.7 |
0.8 |
0.9 |
0.8 |
0.9 |
1 |
0.8 |
0.9 |
1 |
0.8 |
0.9 |
1 |
| ${I_{2}}$ |
0.6 |
0.7 |
0.8 |
0.7 |
0.8 |
0.9 |
0.5 |
0.6 |
0.7 |
0.5 |
0.6 |
0.7 |
0.6 |
0.7 |
0.8 |
| ${I_{3}}$ |
0.5 |
0.6 |
0.7 |
0.6 |
0.7 |
0.8 |
0.6 |
0.7 |
0.8 |
0.6 |
0.7 |
0.8 |
0.5 |
0.6 |
0.7 |
| ${I_{4}}$ |
0.3 |
0.4 |
0.5 |
0.2 |
0.3 |
0.4 |
0.1 |
0.2 |
0.3 |
0.1 |
0.2 |
0.3 |
0.2 |
0.3 |
0.4 |
| ${I_{5}}$ |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
0.6 |
0.7 |
0.8 |
0.5 |
0.6 |
0.7 |
0.7 |
0.8 |
0.9 |
| Loss of confidentiality sub-criterion |
| ${I_{1}}$ |
0.3 |
0.4 |
0.5 |
0.1 |
0.2 |
0.3 |
0.2 |
0.3 |
0.4 |
0.2 |
0.3 |
0.4 |
0.1 |
0.2 |
0.3 |
| ${I_{2}}$ |
0.2 |
0.3 |
0.4 |
0.2 |
0.3 |
0.4 |
0.1 |
0.2 |
0.3 |
0.1 |
0.2 |
0.3 |
0.1 |
0.2 |
0.3 |
| ${I_{3}}$ |
0.2 |
0.3 |
0.4 |
0.2 |
0.3 |
0.4 |
0 |
0.1 |
0.2 |
0.2 |
0.3 |
0.4 |
0.1 |
0.2 |
0.3 |
| ${I_{4}}$ |
0.1 |
0.2 |
0.3 |
0 |
0.1 |
0.2 |
0.1 |
0.2 |
0.3 |
0.1 |
0.2 |
0.3 |
0.1 |
0.2 |
0.3 |
| ${I_{5}}$ |
0.1 |
0.2 |
0.3 |
0.1 |
0.2 |
0.3 |
0 |
0.1 |
0.2 |
0.1 |
0.2 |
0.3 |
0 |
0.1 |
0.2 |
| Loss of integrity sub-criterion |
| ${I_{1}}$ |
0.7 |
0.8 |
0.9 |
0.7 |
0.8 |
0.9 |
0.6 |
0.7 |
0.8 |
0.8 |
0.9 |
1 |
0.6 |
0.7 |
0.8 |
| ${I_{2}}$ |
0.5 |
0.6 |
0.7 |
0.5 |
0.6 |
0.7 |
0.3 |
0.4 |
0.5 |
0.3 |
0.4 |
0.5 |
0.3 |
0.4 |
0.5 |
| ${I_{3}}$ |
0.3 |
0.4 |
0.5 |
0.3 |
0.4 |
0.5 |
0.3 |
0.4 |
0.5 |
0.3 |
0.4 |
0.5 |
0.5 |
0.6 |
0.7 |
| ${I_{4}}$ |
0.1 |
0.2 |
0.3 |
0.1 |
0.2 |
0.3 |
0.1 |
0.2 |
0.3 |
0.1 |
0.2 |
0.3 |
0.2 |
0.3 |
0.4 |
| ${I_{5}}$ |
0.3 |
0.4 |
0.5 |
0.3 |
0.4 |
0.5 |
0.3 |
0.4 |
0.5 |
0.1 |
0.2 |
0.3 |
0.3 |
0.4 |
0.5 |
| Direct losses sub-criterion |
| ${I_{1}}$ |
0.7 |
0.8 |
0.9 |
0.7 |
0.8 |
0.9 |
0.6 |
0.7 |
0.8 |
0.8 |
0.9 |
1 |
0.6 |
0.7 |
0.8 |
| ${I_{2}}$ |
0.6 |
0.7 |
0.8 |
0.6 |
0.7 |
0.8 |
0.6 |
0.7 |
0.8 |
0.5 |
0.6 |
0.7 |
0.6 |
0.7 |
0.8 |
| ${I_{3}}$ |
0.5 |
0.6 |
0.7 |
0.5 |
0.6 |
0.7 |
0.3 |
0.4 |
0.5 |
0.3 |
0.4 |
0.5 |
0.5 |
0.6 |
0.7 |
| ${I_{4}}$ |
0.1 |
0.2 |
0.3 |
0.1 |
0.2 |
0.3 |
0.1 |
0.2 |
0.3 |
0.1 |
0.2 |
0.3 |
0.2 |
0.3 |
0.4 |
| ${I_{5}}$ |
0.3 |
0.4 |
0.5 |
0.3 |
0.4 |
0.5 |
0.3 |
0.4 |
0.5 |
0.1 |
0.2 |
0.3 |
0.1 |
0.2 |
0.3 |
| Indirect losses sub-criterion |
| ${I_{1}}$ |
0.8 |
0.9 |
1 |
0.7 |
0.8 |
0.9 |
0.6 |
0.7 |
0.8 |
0.7 |
0.8 |
0.9 |
0.8 |
0.9 |
1 |
| ${I_{2}}$ |
0.6 |
0.7 |
0.8 |
0.6 |
0.7 |
0.8 |
0.6 |
0.7 |
0.8 |
0.7 |
0.8 |
0.9 |
0.7 |
0.8 |
0.9 |
| ${I_{3}}$ |
0.3 |
0.4 |
0.5 |
0.5 |
0.6 |
0.7 |
0.3 |
0.4 |
0.5 |
0.7 |
0.8 |
0.9 |
0.3 |
0.4 |
0.5 |
| ${I_{4}}$ |
0.3 |
0.4 |
0.5 |
0.4 |
0.5 |
0.6 |
0.1 |
0.2 |
0.3 |
0.3 |
0.4 |
0.5 |
0.2 |
0.3 |
0.4 |
| ${I_{5}}$ |
0.5 |
0.6 |
0.7 |
0.3 |
0.4 |
0.5 |
0.5 |
0.6 |
0.7 |
0.3 |
0.4 |
0.5 |
0.3 |
0.4 |
0.5 |
| Criticality sub-criterion |
| ${I_{1}}$ |
0.9 |
1 |
1 |
0.9 |
1 |
1 |
0.9 |
1 |
1 |
0.8 |
0.9 |
1 |
0.9 |
1 |
1 |
| ${I_{2}}$ |
0.8 |
0.9 |
1 |
0.8 |
0.9 |
1 |
0.9 |
1 |
1 |
0.8 |
0.9 |
1 |
0.8 |
0.9 |
1 |
| ${I_{3}}$ |
0.7 |
0.8 |
0.9 |
0.7 |
0.8 |
0.9 |
0.7 |
0.8 |
0.9 |
0.7 |
0.8 |
0.9 |
0.7 |
0.8 |
0.9 |
| ${I_{4}}$ |
0.3 |
0.4 |
0.5 |
0.4 |
0.5 |
0.6 |
0.5 |
0.6 |
0.7 |
0.3 |
0.4 |
0.5 |
0.5 |
0.6 |
0.7 |
| ${I_{5}}$ |
0.7 |
0.8 |
0.9 |
0.6 |
0.7 |
0.8 |
0.5 |
0.6 |
0.7 |
0.4 |
0.5 |
0.6 |
0.4 |
0.5 |
0.6 |
A defuzzification should be applied before final decisions are made. The defuzzification is a process of producing a quantifiable result in crisp logic, given fuzzy logic, and corresponding membership degrees. A common and useful defuzzification technique is a centre of gravity. This method is selected in the case study (Turskis
et al.,
2019).
The experts were requested to rate the main threats according to linguistic significance scale. Finally, linguistic variables are converted to fuzzy numbers and ranks determined (Tables
3–
4, Fig.
5).
Fuzzy threat impact on CII values defuzzified as follows (Fig.
5).
The last stage is a calculation of a relative impact index (
$RI$) of each considered threat (Fig.
6):

