Abstract
This paper suggests a new fast colour image cipher to meet the increasing demand for secure online image communication applications. Unlike most other existing approaches using a permutation-substitution network, the proposed algorithm consists of only a single substitution part. The keystream sequence is generated from a 4-D hyperchaotic system, whose initial conditions are determined by both the secret key and the SHA-224 cryptographic hash value of the plain-image. Favoured by the avalanche effect of hash functions, totally different keystream sequences will be generated for different images. Consequently, desired diffusion effect can be achieved after only a single round of substitution operation, whereas at least two encryption rounds are required by the state-of-the-art permutation-substitution type image ciphers. We also demonstrate the computational efficiency of the proposed algorithm by comparing it with the AES encryption algorithm. A thorough security analysis is carried out in detail, demonstrating the satisfactory security of the proposed algorithm.
1 Introduction
The explosive growth in the amount of image data distributed over the Internet over the past decade has raised great concern about the protection of image information against unauthorized eavesdropping. Definitely, the most straightforward way is to use a cryptographic algorithm. Unfortunately, many of the existing studies have indicated that commonly used block ciphers, such as DES and AES, are not suitable for practical image encryption. This is because the security of these algorithms depends on the complexity of the algorithms, making them difficult to meet the demand for online communications when dealing with digital images characterized by bulk data capacity. Recently, chaos-based cryptography has suggested a promising way to deal with the intractable problems of fast and highly secure image encryption. Making use of the favourable characteristics such as extreme sensitivity to initial condition(s), ergodicity and long-term unpredictability, chaotic systems have demonstrated great potential for information, especially multimedia encryption. (Fridrich,
1998) proposed the first chaos-based image encryption scheme using iterative permutation and substitution operation. In the permutation stage, the pixels in the input image are rearranged in a pseudorandom manner, which leads to a great reduction in the correlation between neighbouring pixels. In the substitution stage, the pixel values are altered sequentially and the influence of each individual pixel is diffused to all its succeeding ones during the modification process. With such a structure, a minor change of the plain-image may result in a totally different cipher-image with several overall rounds of encryption. Following Fridrich’s pioneer work, a growing number of chaos-based image encryption algorithms and their improvements have been suggested. A brief overview of some major contributions is given below.
Conventionally, three area-preserving invertible chaotic maps, i.e. the cat map (Fu
et al.,
2013), the baker map (Fu
et al.,
2016), and the standard map (Wong
et al.,
2008), are widely used for image scrambling. Unfortunately, this kind of permutation strategy suffers from two main disadvantages: (1) the periodicity of discretized version of chaotic maps, and (2) only applicable to square images. To address these two drawbacks, Fu
et al. (
2011) suggested an image scrambling scheme using a chaotic sequence sorting mechanism. Unfortunately, this method takes a whole row/column of an image as the scrambling unit and results in weaker confusion effect compared with many of the schemes working on individual pixels. Inspired by the natural ripple-like phenomenon that distorts a reflection on a water surface, Wu
et al. (
2014) suggested a novel scrambling algorithm that shuffles images in an
n dimensional (
n D) space using wave perturbations. Chen
et al. (
2014) and Chen
et al. (
2015a) suggested image scrambling schemes using a pixel-swapping mechanism respectively. In their schemes, each pixel in the input image is swapped with another pixel chosen by keystream sequence generated from a chaotic system.
To better meet the challenge of online secure image communication, much research has been done on improving the efficiency of chaos-based image ciphers. For instance, (Xiang
et al.,
2007) investigated the feasibility of selective image encryption on a bit-plane. It’s concluded that only selectively encrypting the higher four bit-planes of an image can achieve an acceptable level of security. As only 50% of the whole image data are encrypted, the execution time is reduced. Wong
et al. (
2009) proposed a more efficient diffusion mechanism using simple table lookup and swapping techniques as a light-weight replacement of the 1-D chaotic map iteration. Following this work Chen
et al. (
2015b) presented an efficient image encryption scheme with confusion and diffusion operations being both performed based on a lookup table. The other advantage of their approach is that it can effectively tolerate the channel errors, which may lead to the corruption of cipher data. It has been demonstrated that images recovered from the damaged cipher data have satisfactory visual perception. Wang
et al. (
2011) suggested a mechanism for combining the permutation and diffusion stages. Compared with other existing schemes with separated permutation and diffusion stages, their proposed scheme reduces the image-scanning cost by half, thereby increasing the execution speed. Fu
et al. (
2012) proposed a fast image cipher using a novel bidirectional diffusion mechanism. Simulation results indicated that their scheme requires only one round of permutation and two rounds of substitution to satisfy the plaintext sensitivity requirement. Zhu
et al. (
2011), Fu
et al. (
2014), Zhang
et al. (
2016) and Chen
et al. (
2017) suggested chaos-based image ciphers using a bit-level permutation respectively. Owing to the substitution effect introduced in the permutation stage, the number of iteration rounds required by the time-consuming substitution procedure is reduced, and hence a shorter encryption time is needed. Chen
et al. (
2015c) proposed a method for obtaining diffusion keystream sequence from the permutation matrix, which is produced and preserved in the permutation stage. As no extra chaotic iteration and quantization is required in the diffusion procedure, the computational efficiency is thereby improved.
Through the exploration of above schemes, one can find that all these schemes can be thought of as the extensions of the Fridrich’s approach, where the permutation and substitution stages are indispensable. In this paper, we propose a novel fast colour image encryption algorithm consisting of only a single substitution part. The keystream sequence is generated from a 4-D hyperchaotic system, whose initial conditions are determined by both the secret key and the SHA-224 cryptographic hash value of the plain-image. As is known, a cryptographic hash function is extremely sensitive to an input message and a chaotic system is extremely sensitive to initial conditions. As a result, a small change in a plain-image can be diffused to the entire cipher-image after only a single round of substitution operation, whereas at least two encryption rounds are required by the state-of-the-art permutation-substitution type image ciphers. Besides, our proposed algorithm does not suffer from the key distribution problem as the hash value is not part of the secret key.
The remainder of this paper is organized as follows. Section
2 presents the architecture of the new image cipher. The detailed encryption algorithm is described in Section
3, followed by the implementation of SHA-224 hash function in Section
4. In Section
5, extensive analysis of the security of the encryption algorithm is carried out, and the diffusion performance of the encryption algorithm is compared with that of a typical permutation-substitution type image cipher. In Section
6, the speed performance of the proposed algorithm is measured and the results are compared with those of AES algorithm in CBC mode. Finally, conclusions are drawn in the last section.
2 Architecture of the New Image Encryption Algorithm
The architecture of the proposed image encryption algorithm is illustrated in Fig.
1. Compared with the widely studied permutation-substitution type image ciphers, the proposed algorithm consist of only a single substitution part. The substitution keystream sequence is extracted from the trajectory of a 4-D hyperhaotic system, whose initial conditions are determined by both the secret key and the SHA-224 cryptographic hash value of the plain-image. More specifically, the 224-bit hash value is split into four equal parts, and each part is involved in determining one of the four initial conditions of the hyperchaotic system. To analyse the diffusion efficiency improvement obtained from the above change, the diffusion mechanism of the permutation-substitution type image cipher is discussed first.
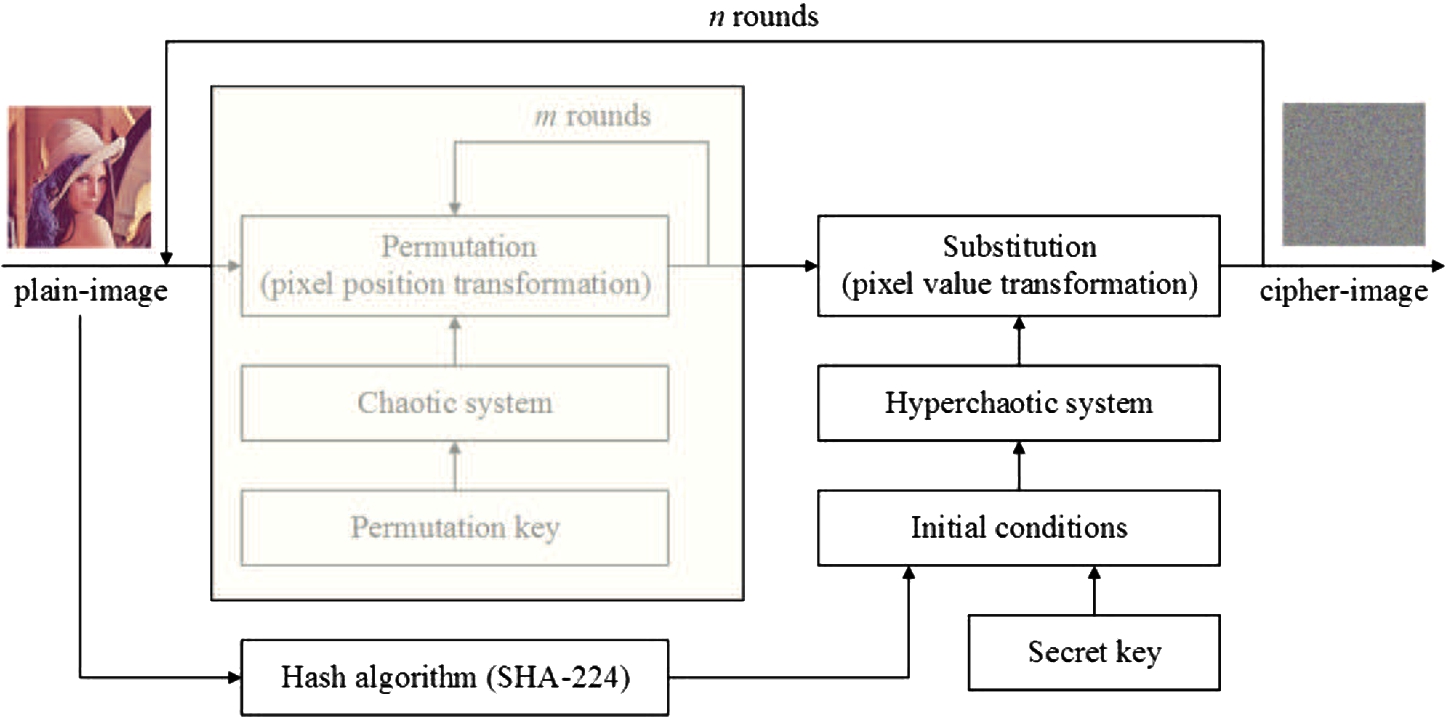
Fig. 1
Architecture of the proposed image encryption algorithm.
Generally, the diffusion operation is done from left to right and top to bottom. Consequently, we assume a worst case that two plain-images (
$M\times N$ pixels), (I) and (II), have only 1-bit difference at the last, lower-right pixel, as illustrated in Figs.
2(a) and (b). We suppose that the differential pixel is moved to
$(p,q)$ during the first round of permutation operation, as illustrated in Figs.
2(c) and (d). During the subsequent substitution operation, the pixel values are modified sequentially and the modification made to a particular pixel depends on both the keystream element and the accumulated effect of all the previous pixel values. Obviously, the influence of the differential pixel will be spread out to all its succeeding ones, as illustrated in Figs.
2(e) and (f). During the second round of permutation operation, the pixels containing the influence of the differential pixel are scattered over a wider area inside the intermediate cipher-image, and the subsequent substitution operation further increases the percentage difference between the two intermediate cipher-images. Generally, the influence of each individual pixel can be diffused over the whole cipher-image after at least three rounds of permutation-substitution operation.
It’s obvious that if desired diffusion effect can be achieved with fewer number of encryption rounds, the computational efficiency will be increased. Recently, some plaintext-dependent keystream generation mechanisms have been proposed to strengthen the robustness against chosen-plaintext attack and increase the diffusion intensity. Unfortunately, these schemes can only generate different keystream elements for differential pixels. As the substitution operation can only diffuse the influence of a pixel to its succeeding ones, only some of the pixels have increased their diffusion intensity. Experimental results show that many of these schemes may take two encryption rounds to achieve desired diffusion effect. Clearly, if two totally different keystream sequences can be generated for any two different images, the desired diffusion effect will be achieved after only a single encryption round, as illustrated in Figs.
3(c) and (d).
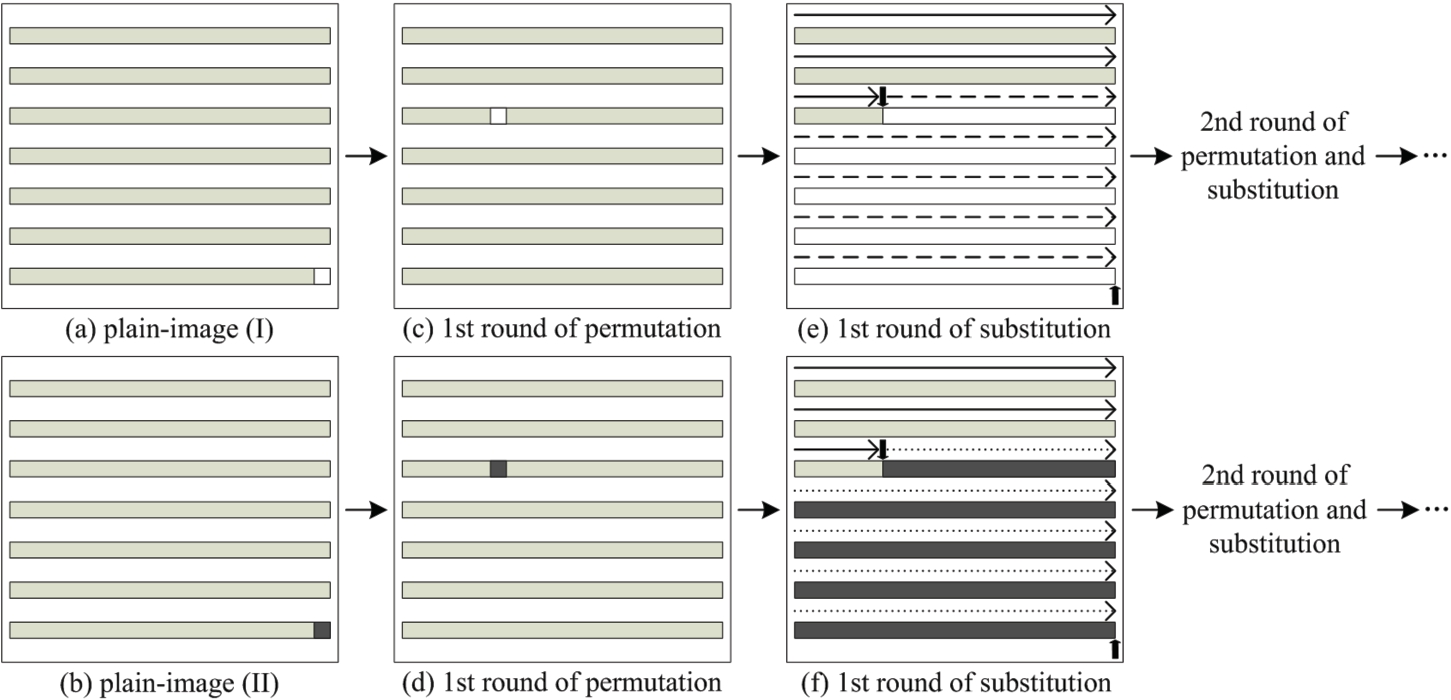
Fig. 2
Encryption process of permutation-substitution type image cipher.
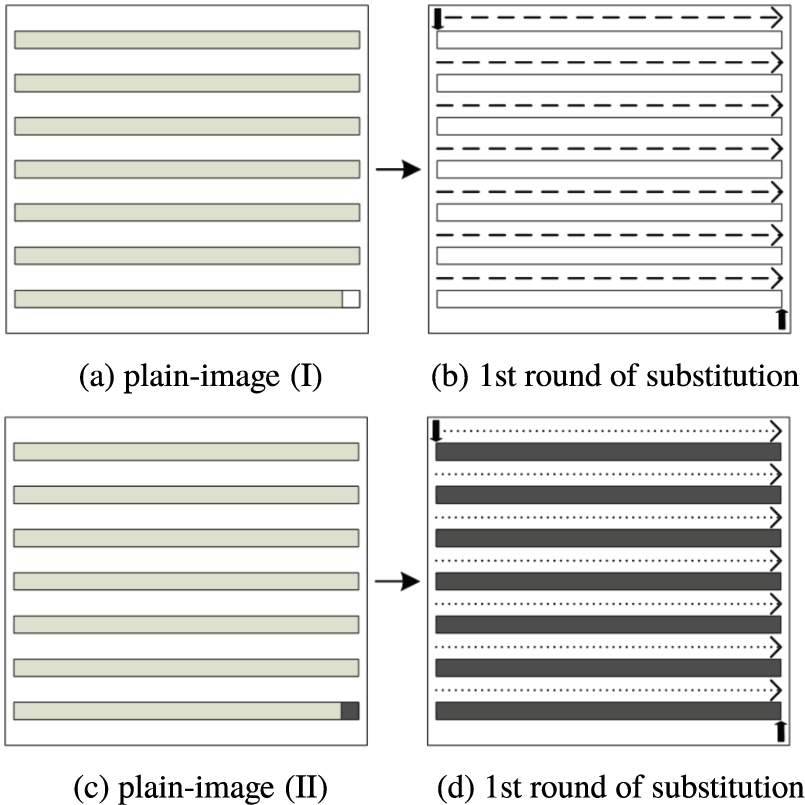
Fig. 3
Encryption process of our proposed cipher.
As is known, good hash functions, including the SHA-224, hold the following properties. 1) Every binary digit, bit, of input message data influences the content of its hash value. That is, any change to a message will almost surely result in a different hash value. 2) It is computationally infeasible to find a message that corresponds to a given message digest, or to find two different messages that produce the same message digest. Clearly, if the initial conditions of a chaotic system depend on the hash value of the input image as well as the secret key, a slight change of the plain-image can lead to a totally different keystream sequence. Besides, as the hash value is not part of the secret key, it can be transmitted in plaintext form together with the cipher-image. Therefore, our proposed algorithm does not suffer from the key distribution problem, a serious practical drawback of one-time pads.
Moreover, as the differential or diffused pixel(s) no longer need(s) to be transferred to different positions of the original or intermediate cipher-image, the permutation part can be removed, which further decreases the computational complexity. The detailed image encryption algorithm and the SHA-224 cryptographic hash function will be discussed in the next two sections.
3 Colour Image Encryption Using Hyperchaotic System
In the present paper, a hyperchaotic system (Li
et al.,
2005), which is formulated by introducing an additional state into the third-order generalized Lorenz equation, is employed to generate the substitution keystream sequence. The system is described by
where
${a_{11}}$,
${a_{12}}$,
${a_{21}}$,
${a_{22}}$,
${a_{33}}$ are the system parameters, and
k is the control parameter that determines the dynamical behaviour of the system. When parameters
${a_{11}}=-{a_{12}}=-35$,
${a_{21}}=7$,
${a_{22}}=12$,
${a_{33}}=-3$, and either
$0<k\leqslant 21.84$ or
$37.44<k\leqslant 41.84$, the system exhibits hyperchaotic behaviour. The projections of phase portrait of one typical case, with
$k=20$, are depicted in Fig.
4.
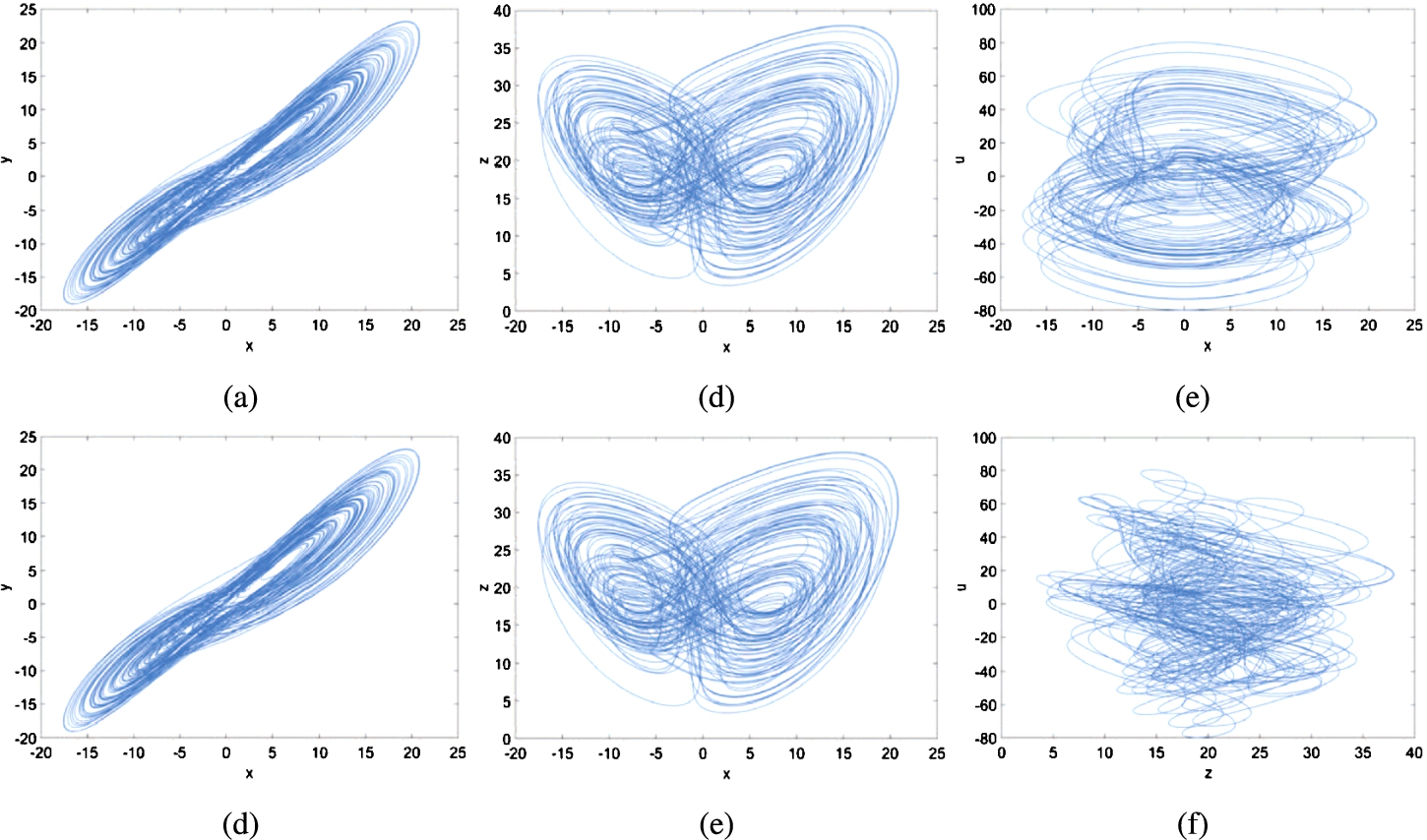
Fig. 4
Projections of phase portrait of system (1) with ${a_{11}}=-{a_{12}}=-35$, ${a_{21}}=7$, ${a_{22}}=12$, ${a_{33}}=-3$ and $k=20$. (a) x–y plane. (b) x–z plane. (c) x–u plane. (d) y–z plane. (e) y–u plane. and (f) z–u plane.
The secret key of the proposed encryption algorithm consists of four real numbers $\{{\mathit{subkey}_{x}},{\mathit{subkey}_{y}},{\mathit{subkey}_{z}},{\mathit{subkey}_{u}}\}$ corresponding to the four state variables of system (1). The value of each subkey can be chosen in a range a little wider than that of its corresponding state variable. Taking a 24-bit true colour image of size $H\times W$ as input, the detailed encryption algorithm is described as follows:
Step 1: Arrange the coloured subpixels in the input image to a one-dimensional byte array $\mathit{imgData}=\{{p_{0}},{p_{1}},\dots ,{p_{3\times W\times H-1}}\}$ in the order from left to right, top to bottom.
Step 2: Generate a chaotic sequence of length ${L_{cs}}=3\times W\times H$ by iterating system (1).
Step 2.1: Calculate the SHA-224 hash of $imgData$, and the result is denoted by ${\mathit{SHA}_{\mathit{img}}}$.
Step 2.2: Divide
${\mathit{SHA}_{\mathit{img}}}$ into four 56-bit parts, which are denoted by
${\mathit{SHA}_{\mathit{img}(p1)}}-{\mathit{SHA}_{\mathit{img}(p4)}}$, respectively, from which four real numbers between 0 and 1 can be obtained according to
where “
$\ll s$” denotes a left shift by
s bit.
Step 2.3: Set the initial conditions of system (1) according to
Step 2.4: Pre-iterate system (1) for
${T_{0}}$ times to avoid the harmful effect of transitional procedure, where
${T_{0}}$ is a constant. The system can be numerically solved by using fourth-order Runge–Kutta method, as given by
where
and the step size
h is chosen as 0.005.
Step 2.5: Continue to iteration for ${T_{i}}={L_{cs}}/4$ times. For each iteration, the current states $({x_{n}},{y_{n}},{z_{n}},{u_{n}})$ of the system(1) are in turn stored into array $\mathit{subSeq}=\{s{s_{0}},s{s_{1}},\dots ,s{s_{3\times W\times H-1}}\}$.
Step 3: Extract a substitution keystream sequence
$subKstr=\{s{k_{0}},s{k_{1}},\dots ,s{k_{3\times W\times H-1}}\}$ by quantifying
$\mathit{subSeq}$ according to
where
$abs(x)$ returns the absolute value of
x,
$\mathit{sig}(x,m)$ returns the
m most significant decimal digits of
x,
$\mathit{mod}(x,y)$ divides
x by
y and returns the remainder of the division, and
${G_{L}}$ is the number of gray levels in the input image (for a 24-bit RGB image,
${G_{L}}=256$). An
m value of 15 is recommended as all the state variables in our scheme are declared as double-precision type, which has 15 or 16 decimal places of accuracy.
Step 4: Encipher the coloured subpixels in
$\mathit{imgData}$ sequentially according to Eq. (
6).
where
${p_{n}}$ and
${c_{n}}$ are the currently operated plain-subpixel and the resulting cipher-subpixel, respectively, and ⊕ performs bit-wise exclusive OR operation.
As can be seen from the above description, each pixel in the original image is encrypted using XOR operation. Therefore, the decryption uses the same algorithm as encryption.
4 Implementation of SHA-224 Cryptographic Hash Function
As discussed above, the initial conditions of the employed hyperchaotic system are determined by both the secret key and the SHA-224 cryptographic hash value of the plain-image. In this section, the implementation of SHA-224 cryptographic hash function is briefly discussed.
SHA-224 may be used to hash a message, M, having a length of l bits, where $0\leqslant l\leqslant {2^{64}}$. The algorithm uses 1) a message schedule of sixty-four 32-bit words, 2) eight working variables of 32 bits each, 3) sixty-four constant 32-bit words, and 4) a hash value of eight 32-bit words. The final result of SHA-224 is a 224-bit message digest.
The words of the message schedule are labelled ${W_{0}},{W_{1}},\dots ,{W_{63}}$. The eight working variables are labelled a, b, c, d, e, f, g, and h. The sixty-four constant words are labelled, ${K_{0}^{(256)}},{K_{1}^{(256)}},\dots ,{K_{63}^{(256)}}$. These words represent the first thirty-two bits of the fractional parts of the cube roots of the first sixty-four prime numbers. In hex, these constant words are (from left to right)
| 428a2f98 |
71374491 |
b5c0fbcf |
e9b5dba5 |
3956c25b |
59f111f1 |
923f82a4 |
ab1c5ed5 |
| d807aa98 |
12835b01 |
243185be |
550c7dc3 |
72be5d74 |
80deb1fe |
9bdc06a7 |
c19bf174 |
| e49b69c1 |
efbe4786 |
0fc19dc6 |
240ca1cc |
2de92c6f |
4a7484aa |
5cb0a9dc |
76f988da |
| 983e5152 |
a831c66d |
b00327c8 |
bf597fc7 |
c6e00bf3 |
d5a79147 |
06ca6351 |
14292967 |
| 27b70a85 |
2e1b2138 |
4d2c6dfc |
53380d13 |
650a7354 |
766a0abb |
81c2c92e |
92722c85 |
| a2bfe8a1 |
a81a664b |
c24b8b70 |
c76c51a3 |
d192e819 |
d6990624 |
f40e3585 |
106aa070 |
| 19a4c116 |
1e376c08 |
2748774c |
34b0bcb5 |
391c0cb3 |
4ed8aa4a |
5b9cca4f |
682e6ff3 |
| 748f82ee |
78a5636f |
84c87814 |
8cc70208 |
90befffa |
a4506ceb |
bef9a3f7 |
c67178f2 |
The words of the hash value are labelled ${H_{0}^{(i)}},{H_{1}^{(i)}},\dots ,{H_{7}^{(i)}}$, which will hold the initial hash value, ${H^{(0)}}$, replaced by each successive intermediate hash value (after each message block is processed), ${H^{(i)}}$, and ending with the final hash value, ${H^{(N)}}$. SHA-224 also uses two temporary words, ${T_{1}}$ and ${T_{2}}$.
SHA-224 uses six logical functions, where each function operates on three 32-bit words, which are represented as
x,
y, and
z. The result of each function is a new 32-bit word.
where
$\wedge ,\oplus ,\lnot $ performs bitwise AND, XOR and complement operations, respectively,
${\mathit{ROTL}^{n}}(x)$ circularly left shifts
x by
n bits, and
${\mathit{SHR}^{n}}(x)$ right shifts
x by
n bits.
The detailed hash procedures are described as follows.
Step 1: Set the initial hash value,
${H^{(0)}}$, which shall consist of the following five 32-bit words, in hex:
Step 2: Pad the message. The purpose of this padding is to ensure that the padded message is a multiple of 512 bits. Suppose that the length of the message, M, is l bits. Append the bit “1” to the end of the message, followed by k zero bits, where k is the smallest, non-negative solution to the equation $l+1+K\equiv 448$ mod 512. Then append the 64-bit block that is equal to the number l expressed using a binary representation.
Step 3: Parse the message. The message and its padding are parsed into N 512-bit blocks, ${M^{(1)}},{M^{(2)}},\dots ,{M^{(N)}}$. As the 512 bits of the input block may be expressed as sixteen 32-bit words, the first 32 bits of message block i are denoted ${M_{0}^{(i)}}$, the next 32 bits are ${M_{1}^{(i)}}$, and so on up to ${M_{15}^{(i)}}$.
Step 4: Compute the hash value. Each message block, ${M^{(1)}},{M^{(2)}},\dots ,{M^{(N)}}$, is processed in order, using the following substeps. Notice that addition $(+)$ is performed modulo ${2^{32}}$.
For $i=1$ to N:
{
1. Prepare the message schedule, {
${W_{t}}$}:
2. Initialize the eight working variables,
a,
b,
c,
d,
e,
f,
g, and
h, with the
$(i-1)$st hash value:
4. Compute the
ith intermediate hash value
${H^{(i)}}$:
After repeating steps one through four a total of
N times (i.e. after processing
${M^{(N)}}$), the resulting 224-bit message digest of the message,
M, is obtained by truncating the final hash value,
$H(N)$, to its left-most 224 bits:
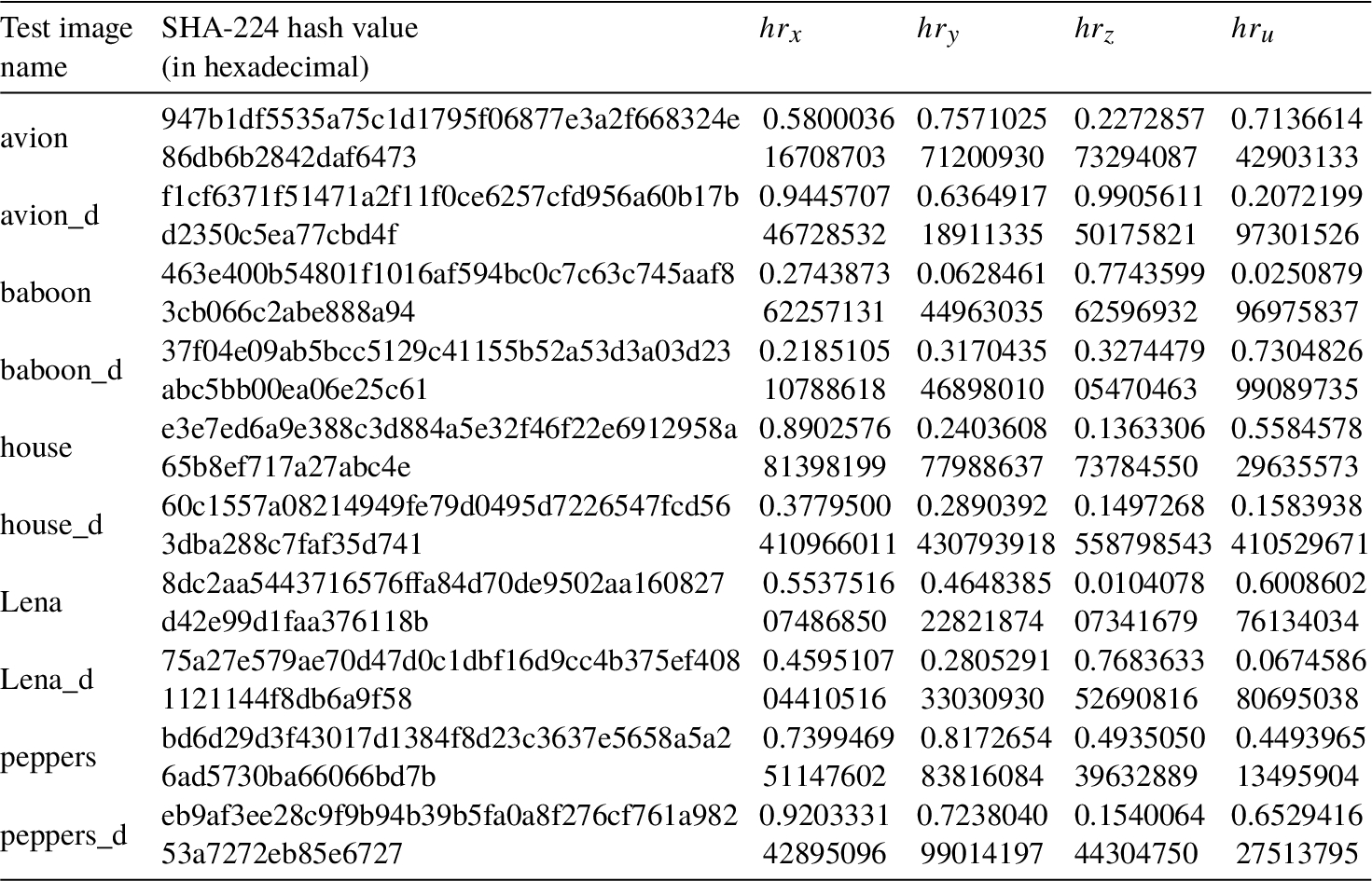
To evaluate the dependency of the initial conditions of the employed hyperchaotic system on input image, we first select five standard test images (512 × 512 pixels, 24-bit RGB colour) from the USC-SIPI image database. Then, we randomly choose a pixel in each test image and change its least significant bit, as illustrated in Table
1. A differential image is named by append a “_d” to the name of its original version. Finally, we calculate the SHA-224 hash values of all the original images and the revised ones, from which the four real numbers
$h{r_{x}},h{r_{y}},h{r_{z}}$, and
$h{r_{u}}$ are derived. The results are given in Table
2, from which it can be seen that changing 1-bit of the plain-image will lead to the trajectory of the hyperchaotic system starting from totally different initial conditions.
Table 1
Changes made to the original images.
| Test image name |
Colour component |
Pixel position $(x,y)$
|
Pixel |
value |
| Original |
Revised |
| avion |
blue |
(294, 305) |
172 |
173 |
| baboon |
red |
(511, 335) |
67 |
68 |
| house |
blue |
(403, 196) |
182 |
181 |
| Lena |
red |
(263, 67) |
102 |
103 |
| peppers |
blue |
(159, 496) |
151 |
150 |
Table 2
Numbers derived from the SHA-224 hash values of the original images and the revised ones.
5 Security Analysis
5.1 Key Size
In cryptography, key size or key length is the size measured in bits of the key used in a cryptographic algorithm. As is known, even if a symmetric cipher is currently unbreakable by exploiting structural weaknesses in its algorithm, it is possible to run through the entire space of keys in what is known as a brute force attack. As longer keys require exponentially more work to brute force search, the key length of an effective cryptosystem should be sufficiently long to make this line of attack impractical. Generally, cryptographic algorithms use keys with a length greater than 100 bits are considered to be “computational security” as the number of operations required to try all possible ${2^{100}}$ keys is widely considered out of reach for conventional digital computing techniques for the foreseeable future. As aforementioned, the secret key of the proposed algorithm consists of four independent floating-point numbers. A 64-bit double-precision type gives 53 bits of precision, and therefore the key length of the proposed algorithm is 4 × 53 = 212 bits, which is long enough to make exhaustive search impractical.
5.2 Chosen-Plaintext Attack
A chosen-plaintext attack is an attack model for cryptanalysis which presumes that the attacker can obtain the ciphertexts for arbitrary plaintexts. As is known, a chosen-plaintext attack is more powerful than known-plaintext attack. This is because the attacker can directly target specific terms or patterns without having to wait for these to appear naturally, allowing faster gathering of data relevant to cryptanalysis. Therefore, any cipher that prevents chosen-plaintext attacks is also secure against known-plaintext and ciphertext-only attacks. To carry out a chosen-plaintext attack on a XOR cipher, the simplest way is to input an all-zero (black) image, and the output is exactly the same as the keystream sequence. Obviously, the proposed encryption algorithm cannot be broken in such a way, because it never reuses a keystream sequence for encrypting different images, i.e. different keystream sequences are used for encrypting different images. Differential cryptanalysis is the most powerful chosen-plaintext attack that analyses how the differences in two plaintext messages affect the differences between the corresponding ciphertexts. To do this, an opponent may firstly create two plain-images with a slight difference, and then encrypt the two images using the same secret key. If some meaningful relationship between the plain-image and cipher-image can be found by comparing the two cipher images, the secret key may be determined with the help of some other analysis methods. Obviously, this kind of cryptanalysis may become impractical if a slight change in the plain-image can be effectively diffused to the entire cipher-image, i.e. changing one bit of the plain-image affects every bit in the cipher-image.
The diffusion effect of an image cryptosystem is usually measured using two criteria, i.e.
$\mathit{NPCR}$ (the number of pixel change rate) and
$\mathit{UACI}$ (the unified average changing intensity). The
NPCR is used to measure the percentage of different pixel numbers between two images. Let
${I_{1}}(i,j,k)$ and
${I_{2}}(i,j,k)$ be the
$(i,j)$th pixel in
kth colour channel (
k = 1, 2, 3 denotes the red, green, and blue colour channels, respectively) of two images
${I_{1}}$ and
${I_{2}}$, the
NPCR can be defined as:
where
$D(i,j,k)$ is defined as
The second criterion,
UACI is used to measure the average intensity of differences between the two images. It is defined as
Clearly, no matter how similar the two input images are, a good image cryptosystem procedure outputs with
$\mathit{NPCR}$ and
$\mathit{UACI}$ values ideally being equal to that of two random images, which are given by
and
For instance, the $\mathit{NPCR}$ and $\mathit{UACI}$ values for two random colour images in 24-bit RGB format (${G_{L}}=256$) are $99.609\% $ and $33.464\% $, respectively.
To evaluate the worst-case diffusion performance, we use the five test image pairs listed in Table
1. The two images in each image pair are encrypted using the same secret key. Table
3 gives the
NPCR and
UACI values for each ciphered image pair generated by the proposed algorithm and the conventional permutation-substitution type encryption algorithm. As can be seen from this table, to achieve the desired diffusion effect, the proposed scheme takes only a single round of encryption, whereas two more rounds are required by conventional permutation-substitution type encryption algorithm. Therefore, the proposed algorithm provides significantly superior computational efficiency.
Table 3
Results of NPCR and UACI tests.
|
No. of cipher rounds (proposed algorithm) |
No. of cipher rounds (conventional algorithm) |
| Test image name |
1 |
1 |
2 |
3 |
| NPCR |
UACI |
NPCR |
UACI |
NPCR |
UACI |
NPCR |
UACI |
| avion |
0.99604 |
0.33443 |
0.50649 |
0.00397 |
0.99604 |
0.33661 |
0.99618 |
0.33405 |
| baboon |
0.99612 |
0.33484 |
0.72392 |
0.00568 |
0.99619 |
0.33359 |
0.99620 |
0.33460 |
| house |
0.99616 |
0.33440 |
0.24593 |
0.01544 |
0.99625 |
0.33367 |
0.99610 |
0.33434 |
| Lena |
0.99607 |
0.33450 |
0.21977 |
0.00086 |
0.99532 |
0.32542 |
0.99615 |
0.33492 |
| peppers |
0.99615 |
0.33428 |
0.72565 |
0.00284 |
0.99594 |
0.33318 |
0.99614 |
0.33449 |
5.3 Statistical Analysis
5.3.1 Frequency Distribution of Pixel Values
A good image cryptosystem should flatten the frequency distribution of cipher-pixel values so as to make frequency analysis infeasible. That is, the redundancy of plain-image or the relationship between plain-image and cipher-image should not be observed from the cipher-image as such information has the potential to be exploited in a statistical attack. The frequency distribution of pixel values in an image can be easily determined by using histogram analysis. An image histogram is a graph showing the number of pixels in an image at each different intensity value found in that image. The histograms of the RGB colour channels of the “Lena” test image and its corresponding cipher-image are shown in Fig.
5. It’s clear from Figs.
5(l)–(n) that the pixel values in all the three colour channels of the resulting cipher-image are fairly evenly distributed over the whole intensity range, and therefore no information about the plain-image can be gathered through histogram analysis.
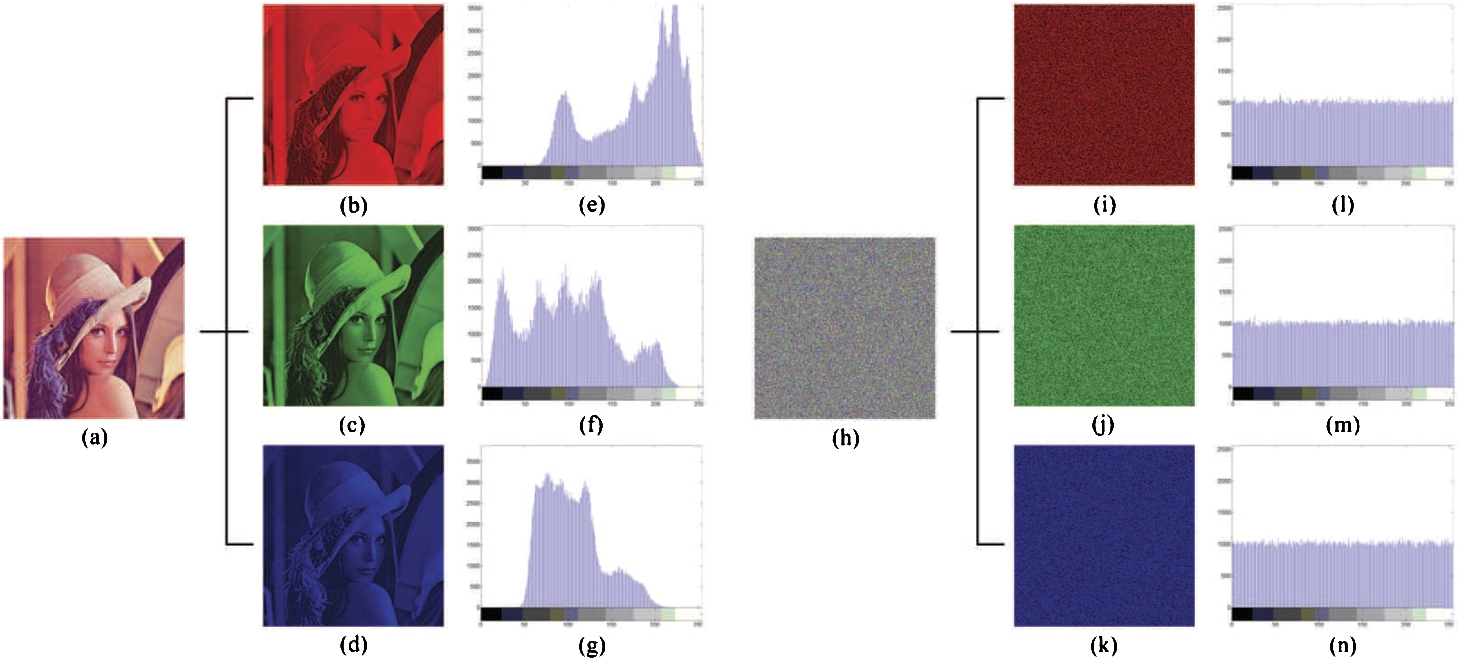
Fig. 5
Histogram analysis. (a) and (h) are the test image and its output cipher-image, respectively. (b)–(d) and (i)–(k) are the three colour channels of (a) and (h), respectively. (e)–(g) and (l)–(n) are the histograms of (b)–(d) and (i)–(k), respectively.
The distribution of pixel values can be further quantitatively determined by calculating the information entropy of the image. Information entropy, introduced by Claude E. Shannon in his classic paper “A Mathematical Theory of Communication”, is a key measure of the randomness or unpredictability of information content. The information entropy is usually expressed by the average number of bits needed to store or communicate one symbol in a message, as described by
where
S is a random variable with
N outcomes
$\{{s_{1}},\dots ,{s_{N}}\}$ and
$P({s_{i}})$ is the probability mass function of outcome
${s_{i}}$. It is obvious from Eq. (
13) that the entropy for a random source emitting
N symbols is
${\log _{2}^{N}}$. For instance, for a ciphered image with 256 colour levels per channel, the entropy should ideally be 8, otherwise there exists a certain degree of predictability which threatens its security.
The information entropies of the test images and their corresponding cipher-images are calculated, and the results are listed in Table
4. As can be seen from this table, the entropy of all the output cipher-images are very close to the theoretical value of 8. This means the proposed scheme produces outputs with perfect randomness and hence is robust against frequency analysis.
Table 4
Information entropies of the test images and their corresponding cipher-images.
| Test image name |
Information entropy |
| Plain-image |
Cipher-image |
| Avion |
6.663908 |
7.999799 |
| Baboon |
7.762436 |
7.999773 |
| House |
7.485787 |
7.999759 |
| Lena |
7.750197 |
7.999723 |
| Peppers |
7.669826 |
7.999741 |
5.3.2 Correlation Between Neighbouring Pixels
Pixels in an ordinary image are usually highly correlated with their neighbours either in horizontal, vertical or diagonal direction. However, an effective image cryptosystem should process cipher-images with sufficiently low correlation between neighbouring pixels. A scatter diagram is commonly used to qualitatively explore the possible relationship between two data sets. To plot a scatter diagram for image data, the following procedures are carried out. First, randomly select ${S_{n}}$ pairs of neighbouring pixels in each direction from the image. Then, the selected pairs are displayed as a collection of points, each having the value of one pixel determining the position on the horizontal axis and the value of the other pixel determining the position on the vertical axis.
Figs.
6(a)–(c) and (d)–(f) show the scatter diagrams for horizontally, vertically and diagonally neighbouring pixels in the red channel of the “Lena” test image and its corrsponding cipher-image with
${S_{n}}=5000$, respectively. Similar results can be obtained for the other two colour channels. As can be seen from Fig.
6, most points in (a)–(c) are clustered around the main diagonal, whereas those in (d)–(f) are fairly evenly distributed. The results indicate that the proposed scheme can effectively eliminate the correlation between neighbouring pixels in an input image.
To further quantitatively measure the correlation between neighbouring pixels in an image, the correlation coefficients
${r_{xy}}$ for the sampled pairs are calculated according to the following three formulas:
where
${x_{i}}$ and
${y_{i}}$ form the
ith pair of neighbouring pixels.
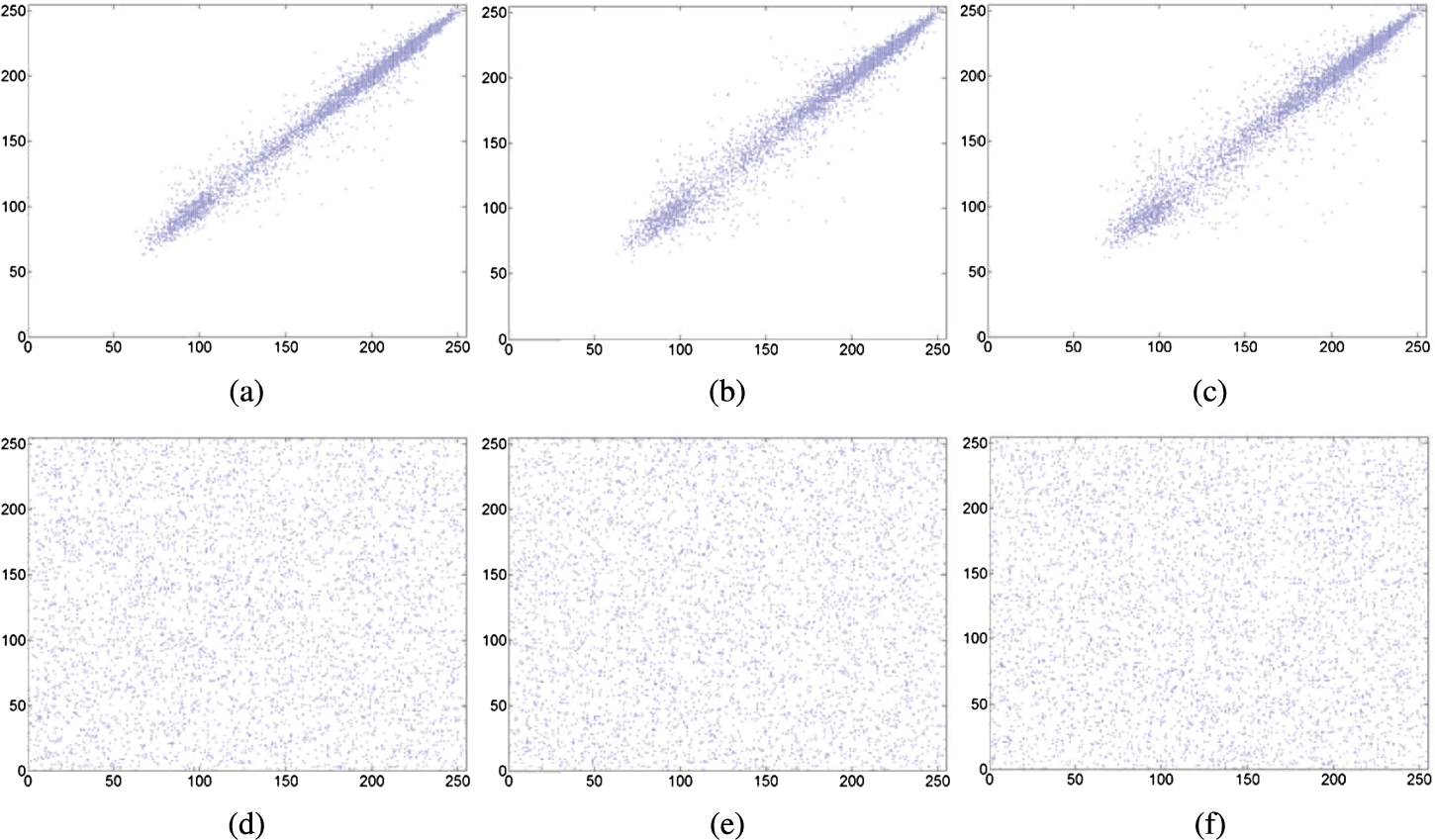
Fig. 6
Graphical analysis for correlation of neighbouring pixels. (a)–(c) and (d)–(f) are scatter diagrams for horizontally, vertically and diagonally neighbouring pixels in the red channel of the “Lena” test image and its output cipher-image, respectively.
Table
5 gives the calculated correlation coefficients for neighbouring pixels in the three colour channels of the five test images and their corresponding cipher-images. As can be seen from this table, the correlation coefficients for neighbouring pixels in all the three colour channels of the output cipher-images are practically zero, and it further supports the conclusion drawn from Fig.
6.
Table 5
Correlation coefficients between neighbouring pixels in the test images and their corresponding cipher-images.
| Test image name |
Direction |
Plain-image |
Cipher-image |
| R |
G |
B |
R |
G |
B |
| avion |
horizontal |
0.9575 |
0.9671 |
0.9316 |
0.0269 |
−0.0240 |
0.0259 |
|
vertical |
0.9728 |
0.9634 |
0.9658 |
−0.0122 |
0.0156 |
0.0307 |
|
diagonal |
0.9370 |
0.9336 |
0.9115 |
0.0045 |
0.0215 |
0.0141 |
| baboon |
horizontal |
0.8787 |
0.7757 |
0.8769 |
0.0027 |
−0.0022 |
−0.0092 |
|
vertical |
0.9291 |
0.8655 |
0.8995 |
−0.0383 |
-0.018 |
−0.0006 |
|
diagonal |
0.8671 |
0.7462 |
0.8314 |
−0.0221 |
−0.0074 |
−0.0215 |
| house |
horizontal |
0.9566 |
0.9526 |
0.9672 |
0.0222 |
0.0030 |
−0.0118 |
|
vertical |
0.9507 |
0.9333 |
0.9719 |
0.0243 |
0.0028 |
0.0183 |
|
diagonal |
0.9165 |
0.8988 |
0.9421 |
0.0034 |
0.0162 |
−0.0155 |
| Lena |
horizontal |
0.9896 |
0.9823 |
0.9585 |
−0.0026 |
0.0117 |
−0.0199 |
|
vertical |
0.9799 |
0.9680 |
0.9381 |
0.0163 |
−0.0226 |
−0.0154 |
|
diagonal |
0.9685 |
0.9566 |
0.9229 |
0.0120 |
−0.0178 |
0.0062 |
| peppers |
horizontal |
0.9667 |
0.9796 |
0.9672 |
0.0107 |
0.0081 |
−0.0176 |
|
vertical |
0.9633 |
0.9808 |
0.9678 |
0.0122 |
0.0002 |
−0.0076 |
|
diagonal |
0.9580 |
0.9671 |
0.9461 |
−0.0057 |
−0.0118 |
−0.0369 |
5.4 Key Sensitivity Analysis
Key sensitivity, a basic design principle of cryptographic algorithms, ensures that no information about the plaintext can be revealed even if there is only a slight difference between the decryption and encryption keys. To evaluate the key sensitivity property of the proposed scheme, the “Lena” test image is firstly encrypted using a randomly generated secret key: (
${x_{0}}=8.28751887014337$,
${y_{0}}=6.61047141256491$,
${z_{0}}=25.4548941736193$,
${u_{0}}=-42.9012685104726$), and the resulting cipher-image is shown in Fig.
7(a). Then the cipher-image is tried to be decrypted using five decryption keys with the first one exactly the same as the encryption key and the other four have only one-bit difference to each part of the encryption key, respectively, as given in Table
6. The resulting deciphered images are shown in Figs.
7(b)–(f), respectively, from which we can see that even an almost perfect guess of the key does not reveal any information about the original image. It can, therefore, be concluded that the proposed scheme fully satisfies the key sensitivity requirement.
Table 6
Decryption keys used for key sensitivity test.
| Figure |
Decryption key |
| 7(b) |
${x_{0}}=8.28751887014337$, ${y_{0}}=6.61047141256491$, |
|
${z_{0}}=25.4548941736193$, ${u_{0}}=-42.9012685104726$
|
| 7(c) |
$\underline{{x_{0}}=8.28751887014338}$, ${y_{0}}=6.61047141256491$, |
|
${z_{0}}=25.4548941736193$, ${u_{0}}=-42.9012685104726$
|
| 7(d) |
${x_{0}}=8.28751887014337$, $\underline{{y_{0}}=6.61047141256492}$, |
|
${z_{0}}=25.4548941736193$, ${u_{0}}=-42.9012685104726$
|
| 7(e) |
${x_{0}}=8.28751887014337$, ${y_{0}}=6.61047141256491$, |
|
$\underline{{z_{0}}=25.4548941736194}$, ${u_{0}}=-42.9012685104726$
|
| 7(f) |
${x_{0}}=8.28751887014337$, ${y_{0}}=6.61047141256491$, |
|
${z_{0}}=25.4548941736193$, $\underline{{u_{0}}=-42.9012685104727}$
|

Fig. 7
Results of key sensitivity test.
5.5 Robustness to Noise and Data Loss
In the real world, transmission errors are unavoidable, especially given the presence of noise in any communication channel, leading to the change of some pixels values. Besides, digital images may also lose data if they are corrupted due to intrusion. Consequently, an image encryption algorithm should have the robustness to resist noise and the data loss. As can be derived from Eq. (
6), the proposed algorithm does not suffer from the problem of “error propagation”, that is, a one-pixel error in the transmitted cipher-image would result in a one-pixel error in the reconstructed plain-image.
To demonstrate the robustness of the proposed algorithm against noise and data loss, we first encrypt the “Lena” test image using a randomly generated secret key, and the resulting cipher-image is shown in Fig.
8(a). Then we add four main types of noise, i.e. the Gaussian noise, the Poisson noise, the salt & pepper noise, and the speckle noise, to the cipher-image, and the results are shown in Figs.
8(b)–(e), respectively. Next we crop part of the cipher-image and the result is shown in Fig.
8(f). Finally, we reconstruct plain-images from Figs.
8(a)–(f), and the results are shown in Figs.
8(g)–(l), respectively. To quantitatively measure the quality of the reconstructed plain-images, their PSNR are calculated, and the results are given in Table
7. As can be seen from Fig.
8 and Table
7, when a cipher-image is with noise or data loss, our algorithm can still reconstruct the plain-image with a high visual quality. Therefore, it can be concluded that the proposed algorithm is robust against noise and data loss.

Fig. 8
Results of robustness analysis against noise and data loss. (a) cipher-image. (b) cipher-image with Gaussian noise (mean = 0 and variance = 0.01). (c) cipher-image with Poisson noise. (d) cipher-image with salt & pepper noise (density = 0.05). (e) cipher-image with speckle noise (mean = 0 and variance = 0.04). (f) cipher-image with data loss. (g)–(l) are reconstructed plain-images corresponding to (a)–(f), respectively.
Table 7
PSNR values for plain-images reconstructed from cipher-images with noise and data loss.
| Figure |
Fig. 8(h) |
Fig. 8(i) |
Fig. 8(j) |
Fig. 8(k) |
Fig. 8(l) |
| PSNR |
20.2106 |
27.1379 |
18.1460 |
18.7766 |
26.6073 |
6 Speed Performance
To demonstrate the efficiency of the proposed algorithm, we compare its performance with that of the AES algorithm, one of the most frequently used and most secure encryption algorithms available today. Tables
8–
10 show the time required by the proposed algorithm and the AES algorithm to encrypt/decrypt 24-bit true colour images of size 512 × 512, 1024 × 1024 and 2048 × 2048, respectively. The AES algorithm works in CBC mode and the performance of all its three versions (128-bit, 192-bit and 256-bit) are measured. All the algorithms have been implemented using C programming language on Windows 7 64-bit platform, and the tests have been done on a personal computer with an Intel i7-7700 3.6 GHz processor and 8 GB RAM. To make the comparison fair, we run each algorithm 10 times on each test image and compute the average running time. As can be seen from Tables
8–
10, the proposed algorithm is approximately three times faster than the simplest version of the AES algorithm, i.e. AES-128. Besides, it’s found that our algorithm takes less time to decrypt than encrypt. This is because the decryption procedure does not include the step of calculating the digest of the original image. It can therefore be concluded from these results that the proposed algorithm provides a good candidate for online secure image transmission over public networks.
Table 8
Time (in seconds) taken to encrypt/decrypt a 24-bit true colour image of size 512${^{\ast }}$512.
| Trial No. |
Proposed algorithm |
AES-128 |
AES-192 |
AES-256 |
| Encryption |
Decryption |
Encryption |
Decryption |
Encryption |
Decryption |
Encryption |
Decryption |
| 1 |
0.028 |
0.024 |
0.088 |
0.092 |
0.113 |
0.117 |
0.134 |
0.122 |
| 2 |
0.028 |
0.021 |
0.094 |
0.100 |
0.106 |
0.105 |
0.130 |
0.130 |
| 3 |
0.029 |
0.023 |
0.095 |
0.090 |
0.107 |
0.105 |
0.133 |
0.131 |
| 4 |
0.030 |
0.022 |
0.092 |
0.116 |
0.11 |
0.112 |
0.131 |
0.137 |
| 5 |
0.030 |
0.022 |
0.091 |
0.108 |
0.109 |
0.107 |
0.129 |
0.127 |
| 6 |
0.030 |
0.021 |
0.090 |
0.089 |
0.108 |
0.106 |
0.125 |
0.141 |
| 7 |
0.028 |
0.021 |
0.089 |
0.087 |
0.107 |
0.104 |
0.127 |
0.128 |
| 8 |
0.029 |
0.022 |
0.090 |
0.087 |
0.108 |
0.109 |
0.133 |
0.127 |
| 9 |
0.029 |
0.025 |
0.090 |
0.095 |
0.104 |
0.106 |
0.136 |
0.128 |
| 10 |
0.028 |
0.026 |
0.091 |
0.095 |
0.106 |
0.111 |
0.125 |
0.124 |
| Mean |
0.029 |
0.023 |
0.091 |
0.096 |
0.108 |
0.108 |
0.130 |
0.130 |
Table 9
Time (in seconds) taken to encrypt/decrypt a 24-bit true colour image of size 1024*1024.
| Trial No. |
Proposed algorithm |
AES-128 |
AES-192 |
AES-256 |
| Encryption |
Decryption |
Encryption |
Decryption |
Encryption |
Decryption |
Encryption |
Decryption |
| 1 |
0.115 |
0.085 |
0.363 |
0.355 |
0.430 |
0.439 |
0.495 |
0.508 |
| 2 |
0.114 |
0.097 |
0.358 |
0.396 |
0.427 |
0.432 |
0.500 |
0.491 |
| 3 |
0.114 |
0.085 |
0.354 |
0.351 |
0.429 |
0.429 |
0.494 |
0.496 |
| 4 |
0.117 |
0.087 |
0.363 |
0.374 |
0.424 |
0.435 |
0.499 |
0.497 |
| 5 |
0.117 |
0.085 |
0.370 |
0.352 |
0.426 |
0.439 |
0.495 |
0.492 |
| 6 |
0.117 |
0.089 |
0.368 |
0.364 |
0.424 |
0.449 |
0.494 |
0.500 |
| 7 |
0.115 |
0.091 |
0.364 |
0.352 |
0.423 |
0.437 |
0.496 |
0.500 |
| 8 |
0.114 |
0.088 |
0.358 |
0.363 |
0.431 |
0.429 |
0.503 |
0.509 |
| 9 |
0.116 |
0.096 |
0.364 |
0.377 |
0.427 |
0.440 |
0.502 |
0.505 |
| 10 |
0.113 |
0.089 |
0.359 |
0.366 |
0.430 |
0.444 |
0.501 |
0.518 |
| Mean |
0.115 |
0.089 |
0.362 |
0.365 |
0.427 |
0.437 |
0.498 |
0.502 |
Table 10
Time (in seconds) taken to encrypt/decrypt a 24-bit true colour image of size 2048${^{\ast }}$2048.
| Trial No. |
Proposed algorithm |
AES-128 |
AES-192 |
AES-256 |
| Encryption |
Decryption |
Encryption |
Decryption |
Encryption |
Decryption |
Encryption |
Decryption |
| 1 |
0.459 |
0.348 |
1.426 |
1.415 |
1.719 |
1.821 |
1.994 |
2.108 |
| 2 |
0.455 |
0.340 |
1.430 |
1.431 |
1.707 |
1.764 |
2.002 |
2.003 |
| 3 |
0.492 |
0.348 |
1.421 |
1.421 |
1.718 |
1.745 |
1.991 |
2.087 |
| 4 |
0.457 |
0.346 |
1.437 |
1.414 |
1.722 |
1.726 |
2.001 |
2.053 |
| 5 |
0.454 |
0.341 |
1.431 |
1.414 |
1.713 |
1.736 |
1.995 |
2.043 |
| 6 |
0.456 |
0.345 |
1.428 |
1.422 |
1.704 |
1.738 |
2.014 |
2.031 |
| 7 |
0.452 |
0.341 |
1.426 |
1.414 |
1.706 |
1.732 |
2.003 |
2.020 |
| 8 |
0.459 |
0.341 |
1.428 |
1.426 |
1.704 |
1.728 |
1.997 |
1.992 |
| 9 |
0.456 |
0.341 |
1.420 |
1.417 |
1.706 |
1.716 |
1.991 |
1.972 |
| 10 |
0.457 |
0.344 |
1.421 |
1.417 |
1.701 |
1.735 |
1.997 |
2.015 |
| Mean |
0.460 |
0.344 |
1.427 |
1.419 |
1.710 |
1.744 |
1.999 |
2.032 |
7 Conclusions
In this paper, we have proposed a fast and robust approach for image data protection. We first calculate the SHA-224 hash value of the original image, and then the hash value, together with the secret key, is used to generate the initial conditions of a 4-D hyperchaotic system. Subsequently, the hyperchaotic system is iterated for appropriate times to produce a keystream sequence used for the substitution operation. Due to the avalanche effect of hash functions, a slight change of the plain-image can lead to a totally different keystream sequence. Consequently, desired diffusion effect can be achieved with only a single round of substitution operation, whereas at least two encryption rounds are required by the state-of-the-art permutation-substitution type image ciphers. We have also demonstrated the computational efficiency of the proposed algorithm by comparing it with the AES encryption algorithm. Our theoretical analysis and experimental results have indicated that the proposed algorithm has a high security level, which can effectively resist all common attacks, such as brute force attack, statistical attack and differential attack. In conclusion, the proposed image encryption algorithm is particularly suitable for online applications.
Acknowledgements
This work was supported by the Fundamental Research Funds for the Central Universities (Nos. N150402004 and N171903003) and the National Nature Science Fundation of China (No. 61802055).
References
Chen, J.X., Zhu, Z.L., Fu, C., Yu, H. (2014). A fast image encryption scheme with a novel pixel swapping-based confusion approach. Nonlinear Dynamics, 77(4), 1191–1207.
Chen, J.X., Zhu, Z.L., Fu, C., Zhang, L.B., Zhang, Y. (2015a). An image encryption scheme using nonlinear inter-pixel computing and swapping based permutation approach. Communications in Nonlinear Science and Numerical Simulation, 23(1), 294–310.
Chen, J.X., Zhu, Z.L., Fu, C., Zhang, L.B., Zhang, Y. (2015b). An efficient image encryption scheme using lookup table-based confusion and diffusion. Nonlinear Dynamics, 81(3), 1151–1166.
Chen, J., Zhu, Z., Fu, C., Yu, H., Zhang, Y. (2015c). Reusing the permutation matrix dynamically for efficient image cryptographic algorithm. Signal Processing, 111, 294–307.
Chen, J., Zhu, Z., Zhang, L., Yang, B. (2017). Exploiting self-adaptive permutation-diffusion and DNA random encoding for secure and efficient image encryption.
Signal Processing,
142.
Fridrich, J. (1998). Symmetric ciphers based on two-dimensional chaotic maps. International Journal of Bifurcation and Chaos, 8(06), 1259–1284.
Fu, C., Lin, B.B., Miao, Y.S., Liu, X., Chen, J.J. (2011). A novel chaos-based bit-level permutation scheme for digital image encryption. Optics Communications, 284(23), 5415–5423.
Fu, C., Chen, J.J., Zou, H., Meng, W.H., Zhan, Y.F., Yu, Y.W. (2012). A chaos-based digital image encryption scheme with an improved diffusion strategy. Optics Express, 20(3), 2363–2378.
Fu, C., Meng, W.H., Zhan, Y.F., Zhu, Z.L., Lau, F.C., Chi, K.T., Ma, H.F. (2013). An efficient and secure medical image protection scheme based on chaotic maps. Computers in Biology and Medicine, 43(8), 1000–1010.
Fu, C., Huang, J.B., Wang, N.N., Hou, Q.B., Lei, W.M. (2014). A symmetric chaos-based image cipher with an improved bit-level permutation strategy. Entropy, 16(2), 770–788.
Fu, C., Wen, Z., Zhu, Z., Yu, H. (2016). A security improved image encryption scheme based on chaotic Baker map and hyperchaotic Lorenz system. International Journal of Computational Science and Engineering, 12(2–3), 113–123.
Li, Y., Tang, W.K., Chen, G. (2005). Hyperchaos evolved from the generalized Lorenz equation. International Journal of Circuit Theory and Applications, 33(4), 235–251.
Wang, Y., Wong, K.W., Liao, X., Chen, G. (2011). A new chaos-based fast image encryption algorithm. Applied Soft Computing, 11(1), 514–522.
Wong, K.W., Kwok, B.S.H., Law, W.S. (2008). A fast image encryption scheme based on chaotic standard map. Physics Letters A, 372(15), 2645–2652.
Wong, K.W., Kwok, B.S.H., Yuen, C.H. (2009). An efficient diffusion approach for chaos-based image encryption. Chaos, Solitons & Fractals, 41(5), 2652–2663.
Wu, Y., Zhou, Y., Agaian, S., Noonan, J.P. (2014). A symmetric image cipher using wave perturbations. Signal Processing, 102, 122–131.
Xiang, T., Wong, K.W., Liao, X. (2007). Selective image encryption using a spatiotemporal chaotic system. Chaos: An Interdisciplinary Journal of Nonlinear Science, 17(2), 023115.
Zhang, W., Yu, H., Zhao, Y.L., Zhu, Z.L. (2016). Image encryption based on three-dimensional bit matrix permutation. Signal Processing, 118, 36–50.
Zhu, Z.L., Zhang, W., Wong, K.W., Yu, H. (2011). A chaos-based symmetric image encryption scheme using a bit-level permutation. Information Sciences, 181(6), 1171–1186.

