3.1 Time-Horizon, Vessels, and Production Capacity
Let H be the set of days in the time-horizon, and let T be the set of types of vessels in the company’s fleet, where ${\Omega _{t}}$ represents the capacity of a vessel of type $t\in T$. For each $t\in T$, let $n=1,\dots ,{M_{t}}$ index the vessels of type t, and let ${O_{t}}$ and ${\mathit{CH}_{t}}={M_{t}}-{O_{t}}$ respectively, denote the number of company-owned vessels and the number of available vessels of this type that can be possibly chartered. The company-owned vessels are indexed by $n=1,\dots ,{O_{t}}$, while the chartered vessels are indexed by $n={O_{t}}+1,\dots ,{O_{t}}+{\mathit{CH}_{t}}\equiv {M_{t}}$. Accordingly, let ${\mathrm{\$ }_{t,n}}$ be the cost (in US dollars) of chartering a vessel n of type t, for each $n={O_{t}}+1,\dots ,{O_{t}}+{\mathit{CH}_{t}}$, and $t\in T$. Let ${\mathit{UT}_{t,n}}$ be the maximum number of days vessel n of type t can be used during the time-horizon, where this time restriction is typically needed for maintenance purposes. Let ${H^{t,n}}\subseteq \{1,\dots ,H\}$ be a subset of the time-horizon during which the ship n of type t will be available for use, where ${h_{1}^{t,n}}$ represents the first day in ${H_{}^{t,n}}$. A production capacity or a certain imposed supply quota for the product at the source is also specified, as given by Q.
3.2 Demand Structure and Penalty Functions
The demand structure of the problem is determined based on the following factors: (a) the storage capacity at the destination; (b) the initial level of each destination storage; (c) the rates of consumption at the destination; and (d) the production capacity at the source. The rates of consumption at a destination may vary due to seasonal considerations; however, we assume that this information is known a priori. For any given day of the time-horizon, there are minimum and maximum allowable limits imposed on the storage levels at the destinations, where certain agreed-upon penalties are incurred for violating these limits. At the beginning of the time-horizon, the storage level at the destination is given by w. This level may pertain to either a single storage unit or a collection of storage units at the destination; however, for the sake of modelling, we only deal with a combined aggregate storage level. Let SL${_{1}}$ and SL${_{2}}$ denote the minimum and maximum desired storage levels, respectively, at the client’s destination, which should be maintained to the extent possible in order to avoid penalties. Accordingly, let ${\Pi _{1}}>0$ and ${\Pi _{2}}>0$, respectively, denote the daily penalties for each shortage or excess unit at the destination, where ${\Pi _{1}}>{\Pi _{2}}$ is to emphasize the fact that shortage levels are more critical than excess levels. The permitted shortage and excess quantities at the destination with respect to the desired levels SL${_{1}}$ and SL${_{2}}$ are specified by the amounts ${A_{1}}$ and ${A_{2}}$, respectively. Let ${b_{1}}\equiv {\mathit{SL}_{1}}-{A_{1}}$ and ${b_{2}}\equiv {\mathit{SL}_{2}}+{A_{2}}$, and let $\mathit{UB}>{b_{2}}$ be a sufficiently large upper bound on the maximum allowable storage level on any given day of the time-horizon. Storage levels falling below ${b_{1}}$ or in excess of ${b_{2}}$ (up to $\mathit{UB}$), while permitted, are highly undesirable, and incur significantly greater penalties, respectively, given by ${\lambda _{1}}>{\Pi _{1}}$, and ${\lambda _{2}}>{\Pi _{2}}$ per unit.
Let ${R_{j}}$ denote the expected consumption rate at the destination on day j, for $j=1,\dots ,H$. The different daily consumption rates arise from possible seasonal changes during the time-horizon, as well as from client-specific considerations. Thus, the total cumulative consumption at the destination over the days $j=1,\dots ,h$ is given by ${\mathit{TC}_{h}}={\textstyle\sum _{j=1}^{h}}{R_{j}}$. The daily storage levels determine the overall penalty over the time-horizon, being given by the sum of Type I and Type II penalties as defined below, where ${S_{h}}$ denotes the storage level on day h and where ${\Pi _{1}}>0$, ${\Pi _{2}}>0$, ${\lambda _{1}}>{\Pi _{1}}$ and ${\lambda _{2}}>{\Pi _{2}}$ are as defined above.
Type I penalty: ${P_{I}}({S_{h}})={\Pi _{1}}$ maximum $\{0,({\mathit{SL}_{1}}-{S_{h}})\}$ if ${S_{h}}\in [{b_{1}},S{L_{1}}),$
$\hspace{54.06006pt}{P_{I}}({S_{h}})={\Pi _{2}}\hspace{2.5pt}\text{maximum}\hspace{2.5pt}\{0,({S_{h}}-S{L_{2}})\}\hspace{1em}\text{if}\hspace{2.5pt}{S_{h}}\in ({\mathit{SL}_{2}},{b_{2}}];\hspace{2.5pt}\text{and}$
Type II penalty: ${P_{\mathit{II}}}({S_{h}})=\left\{\begin{array}{l@{\hskip4.0pt}l}{\Pi _{1}}{A_{1}}+{\lambda _{1}}({b_{1}}-{S_{h}})\hspace{1em}& \text{if}\hspace{2.5pt}{S_{h}}\in [0,{b_{1}}),\\ {} {\Pi _{2}}{A_{2}}+{\lambda _{2}}({S_{h}}-{b_{2}})\hspace{1em}& \text{if}\hspace{2.5pt}{S_{h}}\in ({b_{2}},\mathit{UB}].\end{array}\right.$
Note that if
${S_{h}}\in [S{L_{1}},S{L_{2}}]$, then the storage level lies within the desired bounds and no penalty is induced. If
${S_{h}}\in [{b_{1}},{\mathit{SL}_{1}})\cup ({\mathit{SL}_{2}},{b_{2}}]$, then a Type I penalty is incurred based on the respective shortage or excess quantity. On the other hand, if
${S_{h}}\in [0,{b_{1}})\cup ({b_{2}},\mathit{UB}]$, then a relatively larger additional Type II penalty rate is imposed continuously beyond that of
${P_{I}}(.)$ to indicate the undesirabity of such a storage level on any given day of the time-horizon.
Proposition 1.
Let
where
Define the linear penalty function $P({S_{h}})={\Pi _{1}}{S_{2,h}}+{\Pi _{2}}{S_{4,h}}+{\lambda _{1}}{S_{3,h}}+{\lambda _{2}}{S_{5,h}}$, for $0\leqslant {S_{h}}\leqslant \mathit{UB}$. Then any minimization objective formulation that incorporates the term $P({S_{h}})$ defined above along with (
1)
and (
2)
will automatically enforce the sum of the Type I and Type II penalties ${P_{I}}({S_{h}})+{P_{\mathit{II}}}({S_{h}})$.
Proof.
See Proposition 1 in Sherali and Al-Yakoob (
2006a). □
Example.
The following simple example illustrates the Type I and Type II penalty structures. The various destinations storage levels associated with such penalties are illustrated in Fig.
1. Let
$H=45$, where the per unit Type I and Type II penalties are given by
$\{{\Pi _{1}}=100,{\Pi _{2}}=50\}$ and
$\{{\lambda _{1}}=400,{\lambda _{2}}=150\}$, respectively. Assume that on day
$h=1$ of the time horizon, the initial storage level at the destination is
$w=5000$. Then the storage level on day
h of the time horizon
$({S_{h}})$ is given by 5000 plus the total amount delivered to the destination from day 1 to day
h minus
${\mathit{TC}_{h}}$, where
${\mathit{TC}_{h}}$ denotes the total cumulative consumption at the destination over the days
$j=1,\dots ,h$. Let
${R_{j}}=500$ for
$j=1,\dots ,H$. Then
${\mathit{TC}_{h}}={\textstyle\sum _{j=1}^{h}}{R_{j}}=500h$, for
$j=1,\dots ,h$.
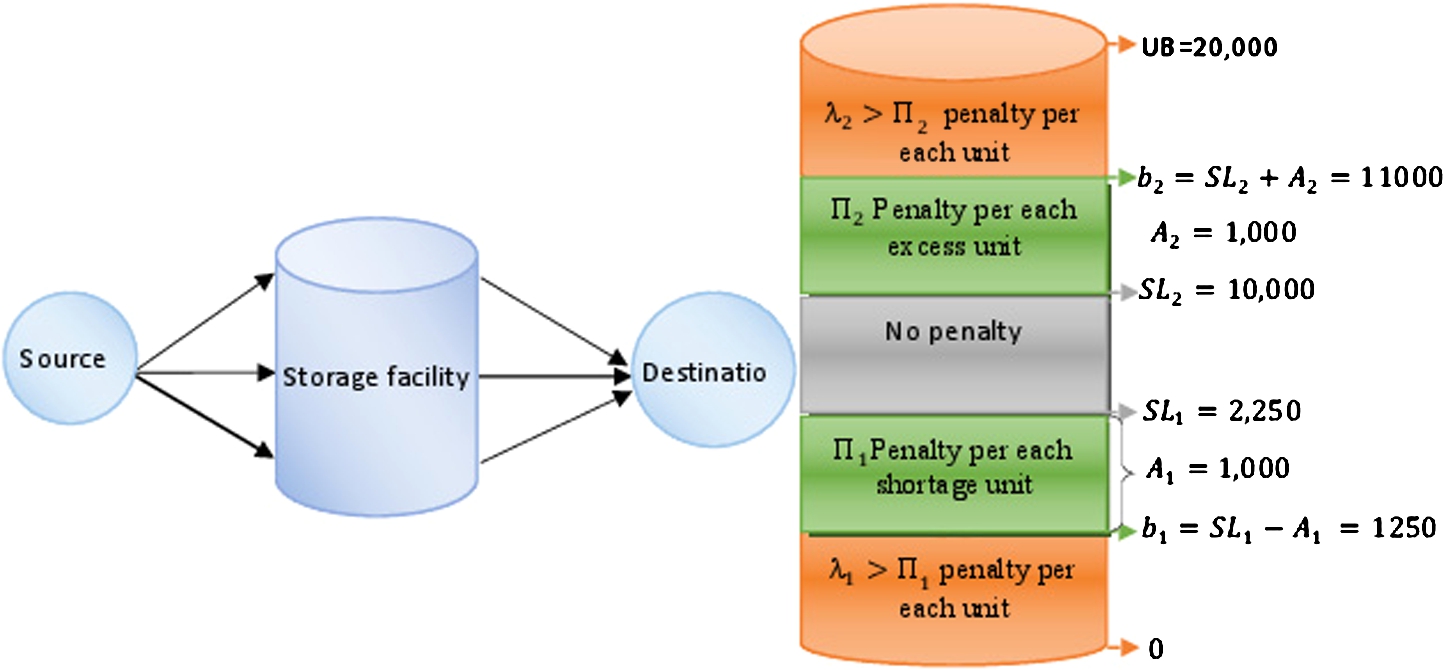
Fig. 1
Illustrative penalty structure.
Based on this information, we compute the incurred penalties for the days
$h=5$, 15, 22, 29, and 36, assuming that the total amount delivered to the destination on days
$h=5$, 15, 22, 29, and 36 are respectively given by 1000, 3000, 8000, 20000 and 25000. Note that,
${S_{5}}=3500$,
${S_{15}}=500$,
${S_{22}}=2000$,
${S_{29}}=10500$, and
${S_{36}}=12000$. The total Type I and Type II penalties incurred for each of the above five days, calculated based on Proposition
1, are given as follows:
3.3 Viable Trips, Average Speeds, and Transportation Costs
There are five permissible journey itineraries, denoted by ${J_{j}}$, for $j=1,\dots ,5$, as defined next. Let $i=1,2,3$ index the source, transshipment facility, and destination, respectively, and let $\mathit{SFD}=\{1,2,3\}$. Then the permissible journeys are given as follows:
${J_{1}}=(1,3,1)$: source → destination → source;
${J_{2}}=(1,2,1)$: source → transshipment facility → source;
${J_{3}}=(1,3,2)$: source → destination → transshipment facility;
${J_{4}}=(2,3,1)$: transshipment facility → destination → source;
${J_{5}}=(2,3,2)$: transshipment facility → destination → transshipment facility.
Let $J={\textstyle\bigcup _{j=1}^{5}}{J_{j}}$, which is composed of all permissible journeys. For $j=1,\dots ,5$, let ${J_{j}}=({p_{1}^{j}},{p_{2}^{j}},{p_{3}^{j}})$ characterize the itinerary of Journey ${J_{j}}$ as identified above, where ${p_{1}^{j}},{p_{2}^{j}}$, and ${p_{3}^{j}}$ respectively represent the loading, unloading, and termination points of Journey ${J_{j}}$, and let ${J_{j}^{1}}\equiv ({p_{1}^{j}},{p_{2}^{j}})$ and ${J_{j}^{2}}\equiv ({p_{2}^{j}},{p_{3}^{j}})$ denote the two sequential legs of this itinerary. For $i=1,2$, let ${I_{i}^{1}}$ be a subset of J such that i is the loading point of any journey in ${I_{i}^{1}}$. Hence, ${I_{1}^{1}}=\{{J_{1}},{J_{2}},{J_{3}}\}$ and ${I_{2}^{1}}=\{{J_{4}},{J_{5}}\}$. For $i=2,3$, let ${I_{i}^{2}}$ be a subset of J such that i is the intermediate point (unloading point) of any journey in ${I_{i}^{2}}$. Thus, ${I_{2}^{2}}=\{{J_{2}}\}$ and ${I_{3}^{2}}=\{{J_{1}},{J_{3}},{J_{4}},{J_{5}}\}$. For $i=1,2$, let ${I_{i}^{3}}$ be a subset of J such that i is the terminal point of any journey in ${I_{i}^{3}}$. Accordingly, ${I_{1}^{3}}=\{{J_{1}},{J_{2}},{J_{4}}\}$ and ${I_{2}^{3}}=\{{J_{3}},{J_{5}}\}$.
Remark 1.
We assume that partial loading/unloading is not allowed and that all journeys commence and terminate at either the source or the transshipment facility. Partial loading/unloading could, however, further enhance the overall operational efficiency and cost by allowing other types of journeys in the operation, and could be likewise handled in a similar fashion. We defer this for future research.
The average speed (knots per hour) of a vessel of type t is given by ${V_{t}^{F}}$ when the vessel is fully loaded, and ${V_{t}^{E}}$ when the vessel is empty. The permitted average daily utilization of a vessel of type t (in hours per day) is given by ${\mathit{DU}_{t}^{F}}$ when the vessel is fully loaded, and ${\mathit{DU}_{t}^{E}}$ when the vessel is empty. Let ${C_{t}^{\mathit{PU},F}}$and ${C_{t}^{\mathit{PU},E}}$ be the daily transportation costs associated with a vessel of type t when the vessel is fully loaded and empty, respectively. Note that ${C_{t}^{\mathit{PU},F}}$ and ${C_{t}^{\mathit{PU},E}}$ are calculated as the product of the vessel capacity ${\Omega _{t}}$ and the per unit transportation cost when the vessel is fully loaded and empty, respectively.
Next, we compute the cost associated with journeys in the set
J. For let, denote the distance (in knots) between
α and
β. For
$j\in \{1,\dots ,5\}$, let
$\mathit{TD}({J_{j}})$ be the total distance that a vessel travels to complete Journey
${J_{j}}$. Accordingly, we have
Let
${\mathit{ND}_{t}^{({p_{1}^{j}},{p_{2}^{j}})}}=\frac{\delta ({p_{1}^{j}},{p_{2}^{j}})}{{V_{t}^{F}}{\mathit{DU}_{t}^{F}}}$ and
${\mathit{ND}_{t}^{({p_{2}^{j}},{p_{3}^{j}})}}=\frac{\delta ({p_{2}^{j}},{p_{3}^{j}})}{{V_{t}^{E}}{\mathit{DU}_{t}^{E}}}$, where the former represents the average travel time (in days) required from point
${p_{1}^{j}}$ to point
${p_{2}^{j}}$, and the latter represents the average travel time (in days) required from point
${p_{2}^{j}}$ to point
${p_{3}^{j}}$. Also, let
${\mathit{ND}_{t}^{j}}={\mathit{ND}_{t}^{({p_{1}^{j}},{p_{2}^{j}})}}+{\mathit{ND}_{t}^{({p_{2}^{j}},{p_{3}^{j}})}}$.
Hence, the transportation cost of a vessel of type t that undertakes journey ${J_{j}}$ is given by ${C_{t,j}}={C_{t,j}^{F}}+{C_{t,j}^{E}}$, where ${C_{t,j}^{F}}={C_{t}^{\mathit{PU},F}}{\mathit{ND}_{t}^{({p_{1}^{j}},{p_{2}^{j}})}}$ and ${C_{t,j}^{E}}={C_{t}^{\mathit{PU},E}}{\mathit{ND}_{t}^{({p_{2}^{j}},{p_{3}^{j}})}}$ represent the total transportation cost for a vessel of type t when this vessel is fully loaded and empty, respectively.
It is worth mentioning that the transportation costs of vessels were assumed to be fixed and known
a priori in Sherali and Al-Yakoob (
2006a,
2006b). In contrast, in this paper, the transportation costs are fixed for the journeys that do not involve the transshipment facility; otherwise, these costs are functions of the location of the transshipment facility.

