1 Introduction
Multi-attribute decision making (MADM) is pervasive around us and as the aggregating information tends to be uncertain and vague, the fuzzy MADM is more and more popular (Yu,
2017; Rostamzadeh
et al.,
2017). Due to the superiority in expressing the imprecise and vague information, the hesitant fuzzy sets (HFSs) are regarded as one of the most efficient tool to deal with fuzzy MADM problems (Mu
et al.,
2015). Torra (
2010) originally introduced the hesitant fuzzy set (HFS), and Chen
et al. (
2013a,
2013b) extended the HFS to interval-valued hesitant fuzzy set (IVHFS) by using the interval to represent the membership. Since the IVHFS is more general than the HFS, we devote ourselves to this set and intend to investigate the information measures of it to solve MADM problems in this paper.
Chen
et al. (
2013a,
2013b) first introduced interval-valued hesitant fuzzy preference relations to describe uncertain evaluation information in group decision making (GDM) processes. They also presented some aggregation operators and defined the correlation coefficients for IVHFSs. Chen and Xu (
2014) further investigated the properties, operational laws and relationships of fundamental operations on IVHFS. Recently, Verma (
2017) also proposed four new operations on IVHFS and studied their properties and relations in details. Besides, Yang
et al. (
2017) proposed a new comparative law based on the possibility degree to compare interval-valued hesitant fuzzy elements (IVHFEs). Following Chen
et al.’s work, many researchers contributed to the IVHFS and applied it to various decision making problems. To our knowledge of the existing analyses of IVHFS in decision making, we summarize them to three categories. The first is based on the information measures (Chen
et al.,
2013a; Wei
et al.,
2014a,
2014b; Farhadinia,
2013; Jin
et al.,
2016b; Meng
et al.,
2016; Peng
et al.,
2017; Liu
et al.,
2018), the second is based on the aggregation operators (Wei
et al.,
2013; Zhang
et al.,
2014; Meng and Chen,
2014; He
et al.,
2016; Jin
et al.,
2016a) and the third is based on the preference, outranking or consensus relational models (Gitinavard
et al.,
2017; Zhang,
2016; Asan
et al.,
2018). Among which, the information measures take important occupations in the MADM. Some primary and classical decision making methods as EDAS (Evaluation based on Distance from Average Solution), TODIM (an acronym in Portuguese for Interactive Multi-Criteria Decision Making), TOPSIS (Technique for Order Preference by Similarity to Ideal Solution), VIKOR (Visekriterijumska Optimizacija I Kompromisno Resenje) and MOORA (Multi-Objective Optimization by Ratio Analysis) are all established on the basis of information measures. Therefore, in this paper, we mainly focus on this point and aim at improving the existing information measures for IVHFS. To date, such information measures as distance, similarity, entropy, cross-entropy and correlation coefficients for IVHFS have been proposed and applied in various MADM fields. Wei
et al. (
2014a,
2014b) proposed a variety of distance, similarity and correlation coefficients for IVHFSs. Farhadinia (
2013) discussed the distance, similarity and entropy measure for IVHFSs and the transformation techniques between each other. Besides, Farhadinia (
2015) also introduced the division and subtraction formulas for IVHFSs. Jin
et al. (
2016b) defined the entropy, similarity measures and cross-entropy for IVHFSs based on continuous ordered weighted averaging operator. Meng
et al. (
2016) defined several new correlation coefficients which do not need to consider the lengths of IVHFEs and the arrangement of their possible interval values. Peng
et al. (
2017) exploited some (weighted) distance measures for IVHFSs based on the COWA operator and used relative ratio to make the decision. Liu
et al. (
2018) developed the distance and similarity measures for IVHFSs and transferred distance to similarity by set-theoretic approach. Gitinavard
et al. (
2016) introduced a novel multi-criteria weighting and ranking model for IVHFS and applied it to location and supplier selection problems. Zhang and Xu (
2014) extended the TODIM to the IVHFS domain based on the defined measured functions and compared it with the TOPSIS (Zhang and Xu,
2013) to make the decision. Further, Fernández
et al. (
2015) introduced finite interval-valued hesitant fuzzy sets, defined a new order, entropy between them considering the fuzziness, lack of knowledge and hesitance and applied it in the business selection. Although numerous information measures have been defined for IVHFSs, in a further analysis of these measures, we classify them into two types. One is based on the closeness and the other is based on the linear relations or the variation tendency of IVHFSs. Because the distance, similarity and entropy can be transferred to each other (Farhadinia,
2013; Jin
et al.,
2016b), they are all equivalent in a sense and based on the closeness. Instead, correlation coefficient is based on the linear relations or the variation tendency. Therefore, we claim that these existing information measures are all one side of a coin in the real measures. They are not the real and actual measures between data.
As mentioned above, the existing information measures pay attention to either the closeness or the variation tendency of IVHFSs. None of them includes both sides. For this reason, the motivation of this paper is to develop a novel information measure of IVHFSs which considers both the closeness and the variation tendency factors to improve the existing ones. We attempt to explore this information measure by the grey relational analysis (GRA) of the IVHFSs. Comparing with other information measures, the GRA of the IVHFSs is relatively week. Therefore, another purpose of this paper is to enhance the GRA in the IVHFSs field. Actually, the traditional GRA of the fuzzy sets takes an important occupation in the fuzzy measure fields. It can measure the closeness of two fuzzy sets just like the distance, similarity and entropy measures. Many researchers focused on the GRA of fuzzy sets and proposed several approaches to solve decision making problems. Turskis and Zavadskas (
2010) used the additive ratio assessment method with grey numbers to multiple criteria analysis. Wei (
2011a,
2011b,
2011c) established a series of GRA methods to investigate the multiple attribute decision-making problems with intuitionistic fuzzy information, 2-tuple linguistic information and the dynamic hybrid multiple attribute decision information. Kong
et al. (
2011) presented a new algorithm based on GRA to discuss fuzzy soft set decision problems. Kuo and Liang (
2011) combined the concepts of VIKOR and GRA to present an effective fuzzy MCDM method. Zhang
et al. (
2011,
2013) and Guo (
2013) also developed the GRA method for solving MCDM problems with interval-valued triangular fuzzy numbers, intuitionistic trapezoidal fuzzy number and hybrid multiple attribute information respectively. Tang (
2015) and Li
et al. (
2015) proposed a novel fuzzy soft set approach in decision making based on GRA and Dempster-Shafer theory of evidence respectively. Liou
et al. (
2016) combined the DEMATEL (DEcision-MAking Trial and Evaluation Laboratory), ANP (Analytical Network Process) and COPRAS-G (COmplex Proportional ASsessment of alternatives with Grey relations) techniques together to make the decision with interval grey numbers. As to the HFSs domain, Li and Wei (
2014) established an optimization model based on GRA to get the weight vector of the HFSs criteria. Zang
et al. (
2017) proposed a grey relational projection method based on the distance measure between the interval-valued dual hesitant fuzzy elements. Although there are so many GRA methods for various types of fuzzy sets, none of them is special for IVHFSs. Furthermore, the existing GRA in the HFSs domain can not be directly transferred for IVHFSs. Even if they can be transferred through some techniques, the transferred GRA for IVHFSs from the existing methods is also one side of a coin just like the aforementioned distance, similarity and entropy measures. That is to say, the existing GRA methods for fuzzy sets only pay attention to the closeness between the fuzzy sets and neglect their variation tendency and relations. Obviously, these kinds of information measures are unreasonable. They can reflect only one aspect of the real measures. Sun
et al. (
2018) and Guan
et al. (
2018) presented a synthetic grey relational degree considering both sides by defining the slope grey relational degree, however, the slope grey relational degree can not be used for IVHFSs directly. Furthermore, the combination of synthetic grey relational degree is simple and can not reflect the influence of the whole index space of the grey theory. Nevertheless, what luck is that we can draw lessons from Sun
et al.’s notions and construct a novel synthetic grey relational degree as information measure for IVHFSs which takes both the closeness and the variation tendency factors into account. Consequently, in this paper, we commit ourselves to construct a novel synthetic grey relational degree for IVHFSs which can achieve the aforementioned two goals: (1) develop a novel information measure of IVHFSs which considers both the closeness and the variation tendency factors; (2) enhance the GRA in the IVHFSs field.
As debated above, the main contribution of this paper is the novel synthetic grey relational degree for IVHFSs. It consists of two aspects: the grey relational degree accounting for the closeness and the variation tendency. As to the grey relational degree describing the closeness, we can extend the traditional grey relational degree from HFSs to IVHFSs. We call it the closeness grey relational degree in this paper. And for the grey relational degree expressing the variation tendency, we do not transfer the slope grey relational degree of HFSs in Sun
et al. (
2018) to IVHFSs. Instead, we define a novel variation rate grey relational degree. We use the variation rate of the mean value of the interval membership to represent the variation tendency. We define two different variation rates of the mean value and use them to construct the variation rate grey relational degree. Based on the closeness and the variation rate grey relational degree, we further develop the novel synthetic grey relational degree which can reflect the influence of the whole index space better than (Sun
et al.,
2018).
The rest of the paper is as follows: Section
2 briefly reviews the concepts of IVHFSs and GRA theory. In Section
3, we extend the traditional grey relational degree from HFSs to IVHFSs and define the closeness grey relational degree for IVHFSs. We also propose the novel variation rate grey relational degree for IVHFSs in this section. Furthermore, we construct the synthetic grey relational degree with the help of the former two. In Section
4, we use the synthetic grey relational degree in MADM based on TOPSIS. In Section
5, a practical MADM problem is used to validate the synthetic grey relational degree. We also compare it with the similarity and correlation coefficient through a pattern recognition example. Finally, the paper ends with some concluding remarks and future challenges in Section
6.
3 GRA for IVHFSs
In this section, we firstly extend the traditional grey relational degree to the IVHFSs domain and form a closeness grey relational degree for IVHFSs. Subsequently, we propose the variation rate grey relational degree and further construct the synthetic grey relational degree.
3.1 Closeness Grey Relational Degree for IVHFSs
Definition 3.
For two IVHFSs on the fixed set
$X=\{{x_{1}},{x_{2}},\dots ,{x_{n}}\}$,
$\tilde{A}=\{\langle x,{\tilde{h}_{\tilde{A}}}({x_{i}})\rangle |{x_{i}}\in X,\hspace{0.1667em}i=1,2,\dots ,n\}$ and
${\tilde{B}_{j}}=\{\langle {x_{i}},{\tilde{h}_{{\tilde{B}_{j}}}}({x_{i}})\rangle |{x_{i}}\in X,\hspace{0.1667em}i=1,2,\dots ,n,\hspace{0.1667em}j=1,2,\dots ,m\}$ with
${\tilde{h}_{\tilde{A}}}({x_{i}})=\{{\tilde{\gamma }_{\tilde{A}i1}},{\tilde{\gamma }_{\tilde{A}i2}},\dots ,{\tilde{\gamma }_{\tilde{A}i{l_{\tilde{A}i}}}}\}$,
${\tilde{h}_{{\tilde{B}_{j}}}}({x_{i}})=\{{\tilde{\gamma }_{{\tilde{B}_{j}}i1}},{\tilde{\gamma }_{{\tilde{B}_{j}}i2}},\dots ,{\tilde{\gamma }_{{\tilde{B}_{j}}i{l_{{\tilde{B}_{j}}i}}}}\}$,
$i=1,2,\dots ,n$,
$j=1,2,\dots ,m$, then we extend the traditional grey relational coefficient to be the traditional grey relational coefficient between IVHFEs
${\tilde{h}_{\tilde{A}}}({x_{i}})$ and
${\tilde{h}_{{\tilde{B}_{j}}}}({x_{i}})$ as:
where
$d({\tilde{h}_{\tilde{A}}}({x_{i}}),{\tilde{h}_{{\tilde{B}_{j}}}}({x_{i}}))$ is the distance between IVHFEs
${\tilde{h}_{\tilde{A}}}({x_{i}})$ and
${\tilde{h}_{{\tilde{B}_{j}}}}({x_{i}})$, which can be calculated according to:
For more distance between IVHFEs, please refer to Wei
et al. (
2014a,
2014b), Farhadinia (
2013), Jin
et al. (
2016b), Peng
et al. (
2017), Liu
et al. (
2018). The traditional grey relational coefficient between IVHFEs describes the closeness of the IVHFSs data, so we also call it the closeness grey relational coefficient in this paper.
Remark 1.
In this paper, we assume the number of the membership in each IVHFE to be compared with is equal. For the moment, we do not discuss the unequal case. Actually, if the number of the membership in each IVHFE is different, we have to extend the shorter one until both of them have the same length when we compare them. We can extend them according to the optimistic or the pessimistic methods and some other rules.
Based on the closeness grey relational coefficient between IVHFEs, the closeness grey relational degree between IVHFSs
$\tilde{A}$ and
${\tilde{B}_{j}}$ is defined as:
If we take the weight into consideration and let the weight vector of
X be
$w={({w_{1}},{w_{2}},\dots ,{w_{n}})^{T}}$,
${\textstyle\sum _{i=1}^{n}}{w_{i}}=1$,
$i=1,2,\dots ,n$, then we extend the IVHFSs closeness grey relational degree to the weighted IVHFSs closeness grey relational degree as:
3.2 Variation Rate Grey Relational Degree for IVHFSs
In this section, we define the variation rate grey relational degree which can represent the variation tendency of IVHFSs. We use the variation rate of the mean value in the interval membership to represent this variation tendency. We define two different variation rates of the mean value and use them to construct the variation rate grey relational degrees.
For IVHFE
$\tilde{h}(x)=\{{\tilde{\gamma }_{1}},{\tilde{\gamma }_{2}},\dots ,{\tilde{\gamma }_{k}},\dots ,{\tilde{\gamma }_{l}}\}$ with interval membership
${\tilde{\gamma }_{k}}=[{\tilde{\gamma }_{k}^{L}},{\tilde{\gamma }_{k}^{U}}]$,
$k=1,2,\dots ,l$, the mean value of the interval membership in IVHFE can be represented by
With the help of the mean value sequence, we define two different variation rates of the mean value to represent the variation tendency of IVHFSs: the global variation rate and the local variation rate.
The global variation rate of the mean value is described as:
where
where
$\bar{m}({\tilde{\gamma }_{k}})$ is the mean of mean value of the interval membership.
The local variation rate of the mean value is described as:
where
With the help of these two different variation rates, we defined the variation rate grey relational degree as follows.
Definition 4.
For two IVHFSs on the fixed set
$X=\{{x_{1}},{x_{2}},\dots ,{x_{n}}\}$,
$\tilde{A}=\{\langle x,{\tilde{h}_{\tilde{A}}}({x_{i}})\rangle |{x_{i}}\in X,\hspace{0.1667em}i=1,2,\dots ,n\}$ and
${\tilde{B}_{j}}=\{\langle {x_{i}},{\tilde{h}_{{\tilde{B}_{j}}}}({x_{i}})\rangle |{x_{i}}\in X,\hspace{0.1667em}i=1,2,\dots ,n,\hspace{0.1667em}j=1,2,\dots ,m\}$ with
${\tilde{h}_{\tilde{A}}}({x_{i}})=\{{\tilde{\gamma }_{\tilde{A}i1}},{\tilde{\gamma }_{\tilde{A}i2}},\dots ,{\tilde{\gamma }_{\tilde{A}i{l_{\tilde{A}i}}}}\}$,
${\tilde{h}_{{\tilde{B}_{j}}}}({x_{i}})=\{{\tilde{\gamma }_{{\tilde{B}_{j}}i1}},{\tilde{\gamma }_{{\tilde{B}_{j}}i2}},\dots ,{\tilde{\gamma }_{{\tilde{B}_{j}}i{l_{{\tilde{B}_{j}}i}}}}\}$,
$i=1,2,\dots ,n$,
$j=1,2,\dots ,m$, the variation rate grey relational coefficient between the IVHFEs
${\tilde{h}_{\tilde{A}}}({x_{i}})$ and
${\tilde{h}_{{B_{j}}}}({x_{i}})$ is defined as:
where
${l_{Ai}}$ is the number of membership in
${\tilde{h}_{\tilde{A}}}({x_{i}})$,
where
${m^{\prime }}({\tilde{\gamma }_{\tilde{A}ik}})$ and
${m^{\prime }}({\tilde{\gamma }_{{\tilde{B}_{j}}ik}})$ are the variation rate of IVHFSs, which can be obtained in two ways: the global variation rate (
12) and the local variation rate (
15).
Based on the variation rate grey relational coefficient between the IVHFEs, the variation rate grey relational degree between the IVHFSs
$\tilde{A}$ and
${\tilde{B}_{j}}$ is defined as:
If we take the weight into consideration and let the weight vector of
X be
$w={({w_{1}},{w_{2}},\dots ,{w_{n}})^{T}}$,
${\textstyle\sum _{i=1}^{n}}{w_{i}}=1$,
$i=1,2,\dots ,n$, then we extend the variation rate grey relational degree between the IVHFSs to the weighted IVHFSs variation rate grey relational degree as:
3.3 Synthetic Grey Relational Degree for IVHFSs
Based on the closeness and the variation rate grey relational degree, we further construct the novel synthetic grey relational degree which takes into consideration both the closeness and the variation tendency factors.
Definition 5.
For two IVHFSs on the fixed set
$X=\{{x_{1}},{x_{2}},\dots ,{x_{n}}\}$,
$\tilde{A}=\{\langle x,{\tilde{h}_{\tilde{A}}}({x_{i}})\rangle |{x_{i}}\in X,\hspace{0.1667em}i=1,2,\dots ,n\}$ and
${\tilde{B}_{j}}=\{\langle {x_{i}},{\tilde{h}_{{\tilde{B}_{j}}}}({x_{i}})\rangle |{x_{i}}\in X,\hspace{0.1667em}i=1,2,\dots ,n,\hspace{0.1667em}j=1,2,\dots ,m\}$ with
${\tilde{h}_{\tilde{A}}}({x_{i}})=\{{\tilde{\gamma }_{\tilde{A}i1}},{\tilde{\gamma }_{\tilde{A}i2}},\dots ,{\tilde{\gamma }_{\tilde{A}i{l_{\tilde{A}i}}}}\}$,
${\tilde{h}_{{\tilde{B}_{j}}}}({x_{i}})=\{{\tilde{\gamma }_{{\tilde{B}_{j}}i1}},{\tilde{\gamma }_{{\tilde{B}_{j}}i2}},\dots ,{\tilde{\gamma }_{{\tilde{B}_{j}}i{l_{{\tilde{B}_{j}}i}}}}\}$,
$i=1,2,\dots ,n$,
$j=1,2,\dots ,m$, the synthetic grey relational coefficient between the IVHFEs
${\tilde{h}_{\tilde{A}}}({x_{i}})$ and
${\tilde{h}_{{\tilde{B}_{j}}}}({x_{i}})$ is defined as:
where
${\lambda _{1}},{\lambda _{2}}>0$, which indicate the importance of the closeness and the variation rate of the IVHFSs, respectively,
${\lambda _{1}}+{\lambda _{2}}=1$.
ξ and
ζ denote the resolution coefficient of the closeness and the variation rate,
$\xi ,\zeta \in [0,1]$.
${\tilde{h}^{\prime }_{\tilde{A}}}({x_{i}})$ and
${\tilde{h}^{\prime }_{{\tilde{B}_{j}}}}({x_{i}})$ are the variation rates of the mean value in the interval membership, which can be gotten in two ways: equations (
11) and equations (
14).
$d({\tilde{h}_{\tilde{A}}}({x_{i}}),{\tilde{h}_{{\tilde{B}_{j}}}}({x_{i}}))$ is the distance between IVHFEs
${\tilde{h}_{\tilde{A}}}({x_{i}})$ and
${\tilde{h}_{{\tilde{B}_{j}}}}({x_{i}})$ and
$d({\tilde{h}^{\prime }_{\tilde{A}}}({x_{i}}),{\tilde{h}^{\prime }_{{\tilde{B}_{j}}}}({x_{i}}))$ is the distance between the variation rate of IVHFEs
${\tilde{h}^{\prime }_{\tilde{A}}}({x_{i}})$ and
${\tilde{h}^{\prime }_{{\tilde{B}_{j}}}}({x_{i}})$.
$d({\tilde{h}_{\tilde{A}}}({x_{i}}),{\tilde{h}_{{\tilde{B}_{j}}}}({x_{i}}))$ can be calculated by equations (
7) and
$d({\tilde{h}_{\tilde{A}}}({x_{i}}),{\tilde{h}_{{\tilde{B}_{j}}}}({x_{i}}))$ can be calculated by:
Based on IVHFEs synthetic grey relational coefficient, the IVHFSs synthetic grey relational degree is defined as:
If we take the weight into consideration and let the weight vector of
X be
$w={({w_{1}},{w_{2}},\dots ,{w_{n}})^{T}}$,
${\textstyle\sum _{i=1}^{n}}{w_{i}}=1$,
$i=1,2,\dots ,n$, then we extend the IVHFSs synthetic grey relational degree to the weighted IVHFSs synthetic grey relational degree as:
Actually, we can use either the global variation rate of the mean value or the local variation rate of the mean value in constructing the synthetic grey relational degree, which are called global synthetic grey relational degree and local synthetic grey relational degree, respectively.
The IVHFSs synthetic grey relational degree takes the considerations of both the closeness and the variation tendency factors of IVHFSs together, which can better distinguish two IVHFSs than the existing fuzzy information measures.
The process of the construction of the IVHFSs grey relational degree is shown in Fig.
1.
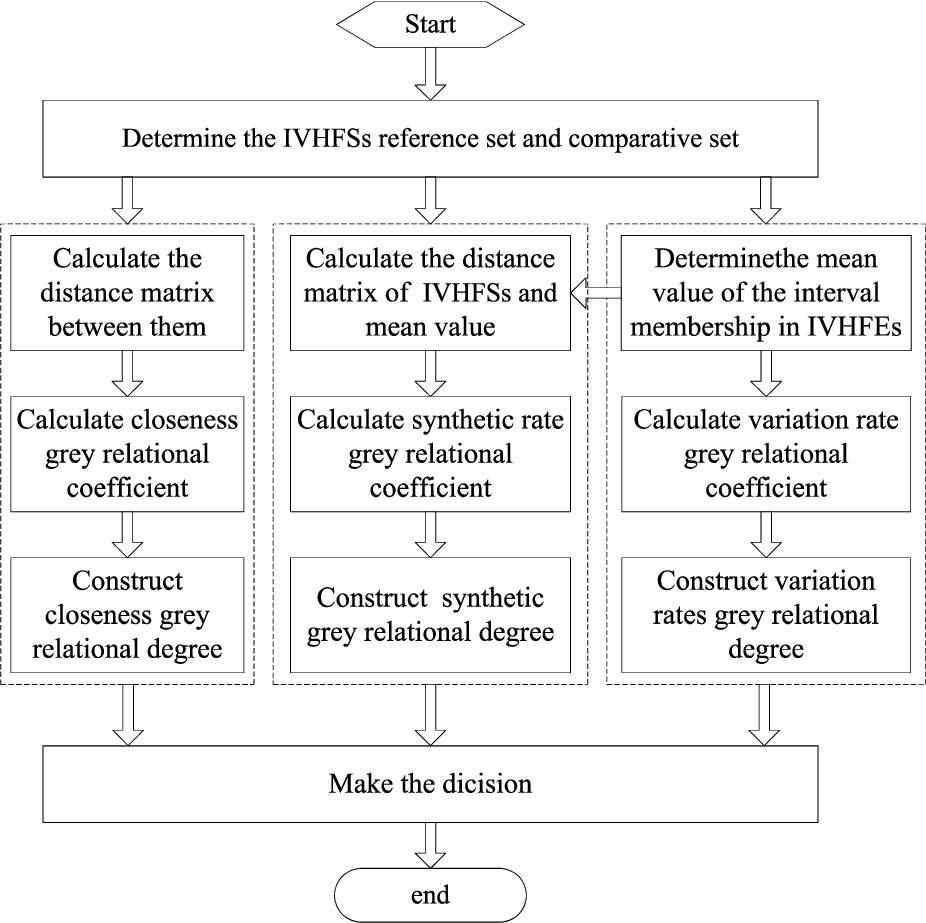
Fig. 1
The process of the construction of the IVHFSs grey relational degree.
4 The MADM Methodology with IVHFSs Information Based on the Grey Relational Degree
In this section, we investigate the MADM problems with IVHFSs information based on the synthetic grey relational degree and the TOPSIS method.
Suppose an interval-valued hesitant fuzzy MADM problem, that there are
m alternatives
${\tilde{A}_{i}}$ $(i=1,2,\dots ,m)$ to be evaluated, each alternative has
n interval-valued hesitant fuzzy attributes
${C_{j}}$ $(j=1,2,\dots ,n)$, denote
${h_{{\tilde{A}_{i}}}}({C_{j}})=\{{\gamma _{{\tilde{A}_{i}}1}},{\gamma _{{\tilde{A}_{i}}2}},\dots ,{\gamma _{{\tilde{A}_{i}}k}},\dots ,{\gamma _{{\tilde{A}_{i}}{l_{ij}}}}\}$ represent the interval-valued hesitant fuzzy information of the alternatives
${A_{i}}$ on the attribute
${C_{j}}$,
${l_{ij}}$ is the number of the membership values in
${h_{{\tilde{A}_{i}}}}({C_{j}})$, let
$w={({w_{1}},{w_{2}},\dots ,{w_{j}},\dots ,{w_{n}})^{T}}$ be the relative weight vector of the attribute, satisfying the normalization conditions:
$0\leqslant {w_{j}}\leqslant 1$ and
${\textstyle\sum _{j=1}^{n}}{w_{j}}=1$. Then all the interval-valued hesitant fuzzy information can be concisely expressed in matrix format as:
According to the process of TOPSIS, we express the steps of MADM with IVHFSs information based on the synthetic grey relational degree as follows:
Step 1: Determine the positive ideal solution (PIS) and the negative ideal solution (NIS) of each attribute in the normalized interval-valued hesitant fuzzy decision matrix to form the positive and the negative IVHFSs:
where
${h_{\tilde{A}}^{+}}({C_{j}})$ and
${h_{\tilde{A}}^{-}}({C_{j}})$ are the positive and the negative IVHFEs:
where
where
${\Omega _{b}}$ and
${\Omega _{c}}$ are related to benefit attribute and cost attribute,
${l_{j}^{+}}$ and
${l_{j}^{-}}$ are the number of the membership values in the positive and the negative IVHFEs, respectively,
${l_{j}^{+}}={l_{j}^{-}}$. We can use the comparative law in Chen and Xu (
2014) to calculate the maximum and the minimum value in equations (
29) and (
30).
Step 2: Calculate the IVHFSs positive and negative synthetic grey relational degrees between each alternative and the PIS and the NIS according to the process of the construction of the IVHFSs synthetic grey relational degree.
Step 3: Construct the relative closeness of the alternative
${\tilde{A}_{i}}$ $(i=1,2,\dots ,m)$ with respect to the ideal solution based on the calculated positive and negative IVHFSs synthetic grey relational degrees which is defined as:
Step 4: Rank the alternatives according to the decreasing order of their relative closeness. That is, the best alternative is the one with the greatest relative closeness to the ideal solution.
6 Conclusion
In this paper, we propose the synthetic grey relational degree of IVHFSs and use it to solve MADM problems with hesitant fuzzy information. We firstly apply the GRA theory to the IVHFSs and define the closeness grey relational degree. Since the closeness grey relational degree reflects the closeness of the data just like the distance, similarity and entropy information measures, we explore two novel variation rate grey relational degrees: the global and the local variation rate grey relational degrees. We use them to describe the variation rate of the data, which enhances the cognition of the traditional grey relational degree. Furthermore, we construct the synthetic grey relational degree with the help of the closeness and the variation rate. The synthetic grey relational degree combines both the merits of the former two grey relational degrees. It can measure not only the closeness but also the variation rate of the data, which is a novel information measure for IVHFSs. Based on the synthetic grey relational degree, we develop a MCDM process with the help of TOPSIS. We apply this notion in a real MCDM problem about the emergency management evaluation, which illustrates its validity. We also make a sensitivity analysis of the parameters in the synthetic grey relational degree. Based on the analysis, we conclude that the importance of the closeness and the variation rate of the IVHFSs ${\lambda _{1}}$ and ${\lambda _{2}}$ have obvious effect on the relative closeness while the resolution coefficients ξ and ζ have no obvious effect it. In addition, we compare the synthetic grey relational degree with 5 information measures: distance, correlation coefficient, traditional (closeness) grey relational degree, global variation rate grey relational degree and local variation rate grey relational degree, to show its advantages in discrimination and accuracy.
In the future, the notion of the construction of the synthetic grey relational degree is expected to be used in the information measures for other types of fuzzy sets. Furthermore, we will devote ourselves to other innovative information measures.

