1 Introduction
Atanassov (1986, 1989) proposed the concept of intuitionistic fuzzy sets (IFSs) based on fuzzy set by Zadeh (1965). Atanassov and Gargov (1989) and Atanassov (1994) defined interval-valued intuitionistic fuzzy sets (IVIFSs). The IFSs and IVIFSs have been investigated by many researchers (Bustince and Burillo, 1995; Atanassov et al., 2005; Ronald, 2015; Xu, 2007; Xu and Yager, 2006; Konwar and Debnath, 2017; Wu and Chiclana, 2014; Wang, 2017; Chen, 2011; Chen and Li, 2011; Chen, 2014, 2016; Chen and Chiou, 2015; Garg, 2016; Li, 2011; Zhao and Wei, 2013; Liu, 2017b; Zhang, 2017; Song and Wang, 2017; Ye, 2009, 2010; Wei and Zhao, 2012; Liu, 2017a). Recently, Cuong (2013) developed picture fuzzy set (PFS) and studied the properties and basic operations laws of PFS. Singh (2014) studied the correlation coefficients for PFSs. Son (2015) and Thong (2015) proposed several clustering algorithms with PFSs. Thong (2015) proposed a hybrid method between PF clustering and IF recommender systems. Wei (2016) proposed the cross-entropy for MADM problems with PFNs. Wei (2017a) investigated the picture fuzzy aggregation operators for MADM problems. Wei et al. (2016b) gave the projection models for MADM with picture fuzzy information. Thong and Son (2016b) considered the improvement of FCM on the PFSs. Thong and Son (2016a) proposed the Automatic Picture Fuzzy Clustering (AFC-PFS). Son (2016) proposed a generalized picture distance measure. Son (2017) proposed the generalized picture distance measures and association measures. Son et al. (2017) proposed the picture inference system (PIS). Son and Thong (2017) developed two hybrid forecast models with picture fuzzy clustering.
Many previous studies have captured the DMs’ attitudinal characters in the MADM problems (Gomes and Lima, 1992; Chen et al., 2012; Liu et al., 2014; Wu and Chiclana, 2014). In order to show the risk and uncertainty of the MADM problems simultaneously, more and more scholars have proposed some fuzzy TODIM approach (Konwar and Debnath, 2017; Fan et al., 2013), the intuitionistic fuzzy TODIM approach (Lourenzutti and Krohling, 2013; Krohling et al., 2013), Pythagorean fuzzy TODIM approach (Ren et al., 2016), multi-hesitant fuzzy linguistic TODIM approach (Wang et al., 2016; Wei et al., 2015), interval type-2 fuzzy sets-based TODIM method (Sang and Liu, 2016), intuitionistic linguistic TODIM method (Wang and Liu, 2017) and 2-dimension uncertain linguistic TODIM method (Liu and Teng, 2016). But until now, no research extend TODIM model for PFNs. Therefore, it is necessary to investigate this issue. The purpose of this paper is to expand TODIM model to MADM with PFNs to overcome this limitation. The rest of this paper is organized as follows. In Section 2, we introduce the concepts of PFNs and classical TODIM model. In Section 3 we develop the TODIM model for MADM with PFNs. In Section 4, an illustrative example for potential evaluation of emerging technology commercialization is pointed out and some comparative analysis is conducted. In Section 5 we conclude this paper.
2 Preliminaries
Some definitions of PFSs are introduced. The operations of PFNs are also provided as they will be utilized in the rest of the paper. At the same time, the process of traditional TODIM approach in decision making is also presented.
2.1 Picture Fuzzy Set Sets (PFSs)
Definition 1 (See Atanassov, 1986, 1989).
An IFS A in X is given by
where ${\mu _{A}}:X\to [0,1]$ and ${\nu _{A}}:X\to [0,1]$, where, $0\leqslant {\mu _{A}}(x)+{\nu _{A}}(x)\leqslant 1$, $\forall x\in X$. The number ${\mu _{A}}(x)$ and ${\nu _{A}}(x)$ represents, respectively, the membership degree and non- membership degree of the element x to the set A.
(1)
\[ A=\big\{\big\langle x,{\mu _{A}}(x),{\nu _{A}}(x)\big\rangle \hspace{0.1667em}\big|\hspace{0.1667em}x\in X\big\}\]Definition 2 (See Cuong, 2013).
A picture fuzzy set (PFS) A on the universe X is an object of the form
where ${\mu _{A}}(x)\in [0,1]$ is called the “degree of positive membership of A”, ${\eta _{A}}(x)\in [0,1]$ is called the “degree of neutral membership of A” and ${\nu _{A}}(x)\in [0,1]$ is called the “degree of negative membership of A”, and ${\mu _{A}}(x),{\eta _{A}}(x),{\nu _{A}}(x)$ satisfy the following condition: $0\leqslant {\mu _{A}}(x)+{\eta _{A}}(x)+{\nu _{A}}(x)\leqslant 1$, $\forall x\in X$. Then for $x\in X$, ${\pi _{A}}(x)=1-({\mu _{A}}(x)+{\eta _{A}}(x)+{\nu _{A}}(x))$ could be called the degree of refusal membership of x in X.
(2)
\[ A=\big\{\big\langle x,{\mu _{A}}(x),{\eta _{A}}(x),{\nu _{A}}(x)\big\rangle \hspace{0.1667em}\big|\hspace{0.1667em}x\in X\big\}\]If ${\pi _{A}}(x)=0$, then the picture fuzzy set reduces to the Atanassov’s IFSs theory (Atanassov, 1986, 1989). Thus, the Atanassov’s IFSs theory is a special form of the PFSs (Cuong, 2013).
Definition 3 (See Abdellaoui et al., 2017).
Definition 4 (See Wei, 2017a).
Wei (2018a) gave an order relation between two PFNs.
Definition 5 (See Wei, 2017a).
Let $\alpha =({\mu _{\alpha }},{\eta _{\alpha }},{\nu _{\alpha }})$ and $\beta =({\mu _{\beta }},{\eta _{\beta }},{\nu _{\beta }})$ be two PFNs, $S(\alpha )=\frac{1+{\mu _{\alpha }}-{\nu _{\alpha }}}{2}$ and $S(\beta )=\frac{1+{\mu _{\beta }}-{\nu _{\beta }}}{2}$ be the scores of α and β, respectively, and let $H(\alpha )={\mu _{\alpha }}+{\eta _{\alpha }}+{\nu _{\alpha }}$ and $H(\beta )={\mu _{\beta }}+{\eta _{\beta }}+{\nu _{\beta }}$ be the accuracy degrees of α and β, respectively, then if $S(\alpha )<S(\beta )$, then $\alpha <\beta $; if $S(\alpha )=S(\beta )$, then (1) if $H(\alpha )=H(\beta )$, then $\alpha =\beta $; (2) if $H(\alpha )<H(\beta )$, then $\alpha <\beta $.
Definition 6.
Let $\alpha =({\mu _{\alpha }},{\eta _{\alpha }},{\nu _{\alpha }})$ and $\beta =({\mu _{\beta }},{\eta _{\beta }},{\nu _{\beta }})$ be two PFNs, then the normalized Hamming distance between $\alpha =({\mu _{\alpha }},{\eta _{\alpha }},{\nu _{\alpha }})$ and $\beta =({\mu _{\beta }},{\eta _{\beta }},{\nu _{\beta }})$ is:
2.2 The TODIM Approach
Let $G=\{{G_{1}},{G_{2}},\dots ,{G_{n}}\}$ be the set of attributes, $w=({w_{1}},{w_{2}},\dots ,{w_{n}})$ be the weight vector of attributes ${G_{j}}$, where ${w_{j}}\in [0,1]$, $j=1,2,\dots ,n$„ ${\textstyle\sum _{j=1}^{n}}{w_{j}}=1$. Let $A=\{{A_{1}},{A_{2}},\dots ,{A_{m}}\}$ be a discrete set of alternatives. Suppose that $A={({a_{ij}})_{m\times n}}$ be a decision matrix, where ${a_{ij}}$ is the attribute value, given by an expert, for the alternative ${A_{i}}\in A$ with respect to the attribute ${G_{j}}\in G$, $i=1,2,\dots ,m$, $j=1,2,\dots ,n$. We define ${w_{jr}}={w_{j}}/{w_{r}}$ $(r,j=1,2,\dots ,n)$ are the relative weight of the attribute ${G_{j}}$ to ${G_{r}}$, and ${w_{r}}=\max \{{w_{j}}\mid j=12,\dots ,n\}$, and $0\leqslant {w_{jr}}\leqslant 1$. Then the traditional TODIM model includes the following steps:
-
Step 1. Normalize the $A={({a_{ij}})_{m\times n}}$ into $B={({b_{ij}})_{m\times n}}$.
-
Step 2. Compute the dominance degree of ${A_{i}}$ over each alternative ${A_{t}}$ for ${G_{j}}$:where
(6)
\[ \delta ({A_{i}},{A_{t}})={\sum \limits_{j=1}^{n}}{\phi _{j}}({A_{i}},{A_{t}})\hspace{1em}(i,t=1,2,\dots ,m)\]and the parameter values θ depict the attenuation factor of the losses. If ${b_{ij}}-{b_{tj}}>0$, then ${\phi _{j}}({A_{i}},{A_{t}})$ represents a gain; if ${b_{ij}}-{b_{tj}}<0$, then ${\phi _{j}}({A_{i}},{A_{t}})$ signifies a loss.(7)
\[ {\phi _{j}}({A_{j}},{A_{t}})=\left\{\begin{array}{l@{\hskip4.0pt}l}\sqrt{\frac{{w_{jr}}({b_{ij}}-{b_{tj}})}{{\textstyle\textstyle\sum _{j=1}^{n}}{w_{jr}}}},\hspace{1em}& if{b_{ij}}>{b_{tj}};\\ {} 0,\hspace{1em}& if{b_{ij}}={b_{tj}};\\ {} -\frac{1}{\theta }\sqrt{\frac{({b_{ij}}-{b_{tj}}){\textstyle\textstyle\sum _{j=1}^{n}}{w_{jr}}}{{w_{jr}}}},\hspace{1em}& if{b_{ij}}<{b_{tj}},\end{array}\right.\] -
Step 3. Compute the overall dominance of the alternative ${A_{i}}$ with the following formula:
(8)
\[\begin{array}{l}\displaystyle \phi ({A_{i}})=\frac{{\textstyle\textstyle\sum _{t=1}^{m}}\delta ({A_{i}},{A_{t}})-{\min _{i}}\big\{{\textstyle\textstyle\sum _{t=1}^{m}}\delta ({A_{i}},{A_{t}})\big\}}{{\max _{i}}\big\{{\textstyle\textstyle\sum _{t=1}^{m}}\delta ({A_{i}},{A_{t}})\big\}-{\min _{i}}\big\{{\textstyle\textstyle\sum _{t=1}^{m}}\delta ({A_{i}},{A_{t}})\big\}},\\ {} \displaystyle \hspace{1em}i=1,2,\dots ,m.\end{array}\] -
Step 4. Rank and select the best alternative by the overall values $\phi ({A_{i}})$ $(i=1,2,\dots ,m)$. The alternative with the minimum value is the worst. Inversely, the maximum value is the most desirable one.
3 TODIM Method for Picture Fuzzy MADM Problems
The following notations are utilized to show MADM problems with PFNs. Let $A=\{{A_{1}},{A_{2}},\dots ,{A_{m}}\}$ be a set of alternatives, and $G=\{{G_{1}},{G_{2}},\dots ,{G_{m}}\}$ be a set of attributes. Let $w=({w_{1}},{w_{1}},\dots ,{w_{1}})$ be the weight vector of attributes, where ${w_{j}}\in [0,1]$, $j=1,2,\dots ,n$, ${\textstyle\sum _{j=1}^{n}}{w_{j}}=1$. Suppose that $R={({r_{ij}})_{m\times n}}={({\mu _{ij}},{\eta _{ij}},{\nu _{ij}})_{m\times n}}$ be a picture fuzzy decision matrix, where ${\mu _{ij}}$ indicates the degree of positive membership, ${\eta _{ij}}$ indicates the degree of neutral membership, ${\nu _{ij}}$ indicates the degree of negative membership, ${\mu _{ij}}\in [0,1]$, ${\eta _{ij}}\in [0,1]$, ${\nu _{ij}}\in [0,1]$, ${\mu _{ij}}+{\eta _{ij}}+{\nu _{ij}}\leqslant 1$, $i=1,2,\dots ,m$, $j=1,2,\dots ,n$.
Then, we extend the TODIM model to solve the MADM problem with PFNs.
Firstly, we can obtain the relative weight of ${G_{j}}$ as:
where ${w_{r}}=\max \{{w_{j}}\mid j=1,2,\dots ,n\}$, and $0\leqslant {w_{jr}}\leqslant 1$.
We calculate the dominance of ${A_{i}}$ over alternative ${A_{t}}$ under attribute ${G_{j}}$:
where the parameter θ is the attenuation factor of the losses.
(10)
\[ {\phi _{j}}({A_{j}},{A_{t}})=\left\{\begin{array}{l@{\hskip4.0pt}l}\sqrt{\frac{{w_{jr}}d({r_{ij}},{r_{tj}})}{{\textstyle\textstyle\sum _{j=1}^{n}}{w_{jr}}}},\hspace{1em}& if{r_{ij}}>{r_{tj}};\\ {} 0,\hspace{1em}& if{r_{ij}}={r_{tj}};\\ {} -\frac{1}{\theta }\sqrt{\frac{d({r_{ij}},{d_{tj}}){\textstyle\textstyle\sum _{j=1}^{n}}{w_{jr}}}{{w_{jr}}}},\hspace{1em}& if{r_{ij}}<{r_{tj}}.\end{array}\right.\]In order to indicate the functions ${\phi _{j}}({A_{j}},{A_{t}})$ clearly, we depict it in a matrix under attribute of ${G_{j}}$ as:
where $j=1,2,\dots ,n$, then we can derive the overall dominance degree of the alternative ${A_{i}}$ over alternative ${A_{j}}$ by
Thus, by Eq. (13), the overall dominance matrix is:
(13)
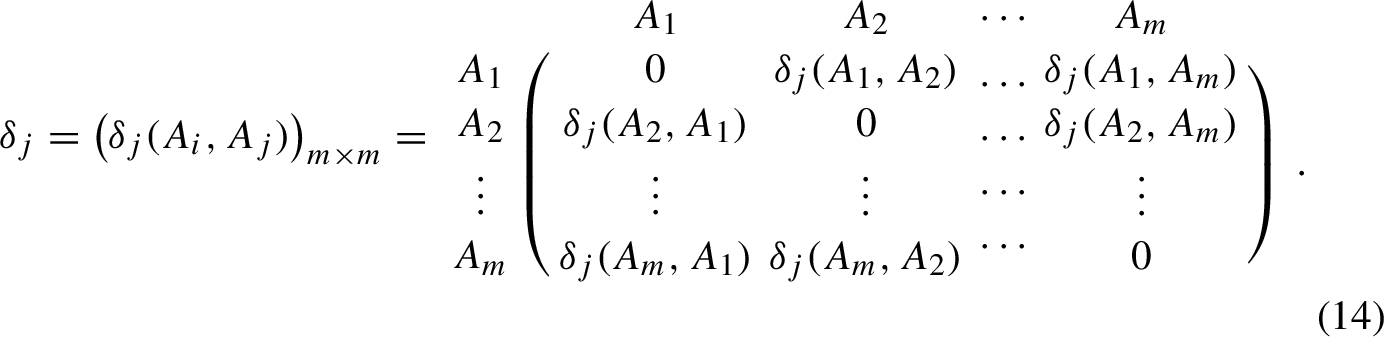
\[ \delta ({A_{i}},{A_{j}})={\sum \limits_{j=1}^{n}}{\phi _{j}}({A_{i}},{A_{t}}),\hspace{1em}i,t=1,2,\dots ,m.\]Finally, the overall value of ${A_{i}}$ is:
and rank all alternatives, the greater the overall value $\delta ({A_{i}})$ $(i=1,2,\dots ,m)$, the better the alternative ${A_{i}}$.
(15)
\[\begin{array}{l}\displaystyle \delta ({A_{i}})=\frac{{\textstyle\textstyle\sum _{t=1}^{m}}\delta ({A_{i}},{A_{t}})-{\min _{i}}\big\{{\textstyle\textstyle\sum _{t=1}^{m}}\delta ({A_{i}},{A_{t}})\big\}}{{\max _{i}}\big\{{\textstyle\textstyle\sum _{t=1}^{m}}\delta ({A_{i}},{A_{t}})\big\}-{\min _{i}}\big\{{\textstyle\textstyle\sum _{t=1}^{m}}\delta ({A_{i}},{A_{t}})\big\}},\\ {} \displaystyle \hspace{1em}i=1,2,\dots ,m,\end{array}\]4 Numerical Example and Comparative Analysis
4.1 Numerical Example
With the rapid development of science and technology, the social life, national politics, the economy and the culture has also taken significant changes. Some theory in the traditional single field has been unable to guide the new practice. The new complex issues that appear in people’s social practice can’t be resolved by relying on the knowledge, theories and tools in a single field. Transdisciplinary research of emerging technologies appears on the scene. Evaluating transdisciplinary research of emerging technologies has important theoretical and practical significance. Thus, we shall give a numerical example for potential evaluation of emerging technology commercialization with PFNs. There are five possible emerging technology enterprises (ETES) ${A_{i}}$ $(i=1,2,3,4,5)$ to select. The expert selects four attributes to assess the five possible ETES: (1) ${G_{1}}$ is the human resources and financial conditions; (2) ${G_{2}}$ is the industrialization infrastructure; (3) ${G_{3}}$ is the technical advancement; (4) ${G_{4}}$ is the development of science and technology. The five possible ETES ${A_{i}}$ $(i=1,2,3,4,5)$ are to be assessed with PFNs according to four attributes (whose weighting vector $w={(0.2,0.1,0.3,0.4)^{T}}$), as listed as follows.
\[ R=\left(\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c@{\hskip4.0pt}c}(0.89,0.08,0.03)& (0.42,0.35,0.18)& (0.08,0.89,0.02)& (0.80,0.11,0.05)\\ {} (0.23,0.64,0.11)& (0.03,0.82,0.13)& (0.73,0.15,0.08)& (0.73,0.10,0.14)\\ {} (0.52,0.26,0.05)& (0.04,0.85,0.10)& (0.68,0.26,0.06)& (0.43,0.13,0.25)\\ {} (0.74,0.16,0.10)& (0.02,0.89,0.05)& (0.08,0.84,0.06)& (0.85,0.09,0.05)\\ {} (0.68,0.08,0.21)& (0.05,0.87,0.06)& (0.13,0.75,0.09)& (0.65,0.05,0.02)\end{array}\right).\]
In the following, we utilize the approach developed for potential evaluation of emerging technology commercialization of five possible ETEs.
Firstly, since ${w_{4}}=({w_{1}},{w_{2}},{w_{3}},{w_{4}})$, then ${G_{4}}$ is the reference attribute and ${w_{r}}=0.4$. Thus, ${w_{1r}}=0.50$, ${w_{2r}}=0.25$, ${w_{3r}}=0.75$ and ${w_{4r}}=1.00$. Then, we can calculate the dominance degree of the candidate ${A_{i}}$ over each candidate ${A_{t}}$ under ${G_{j}}$ $(j=1,2,3,4)$. Let $\theta =2.5$, we get:
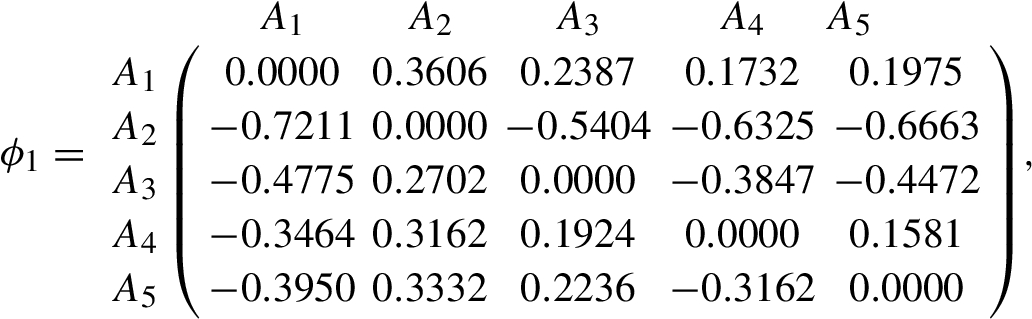
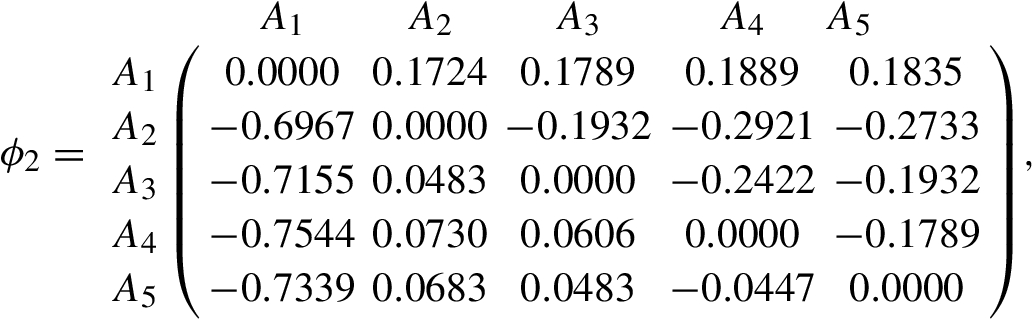
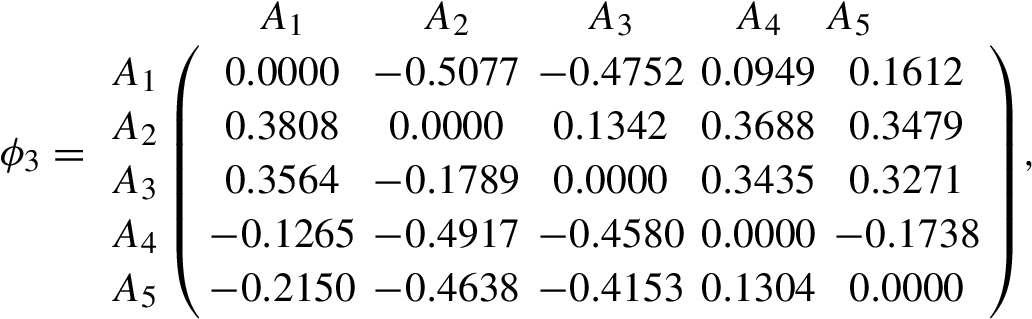
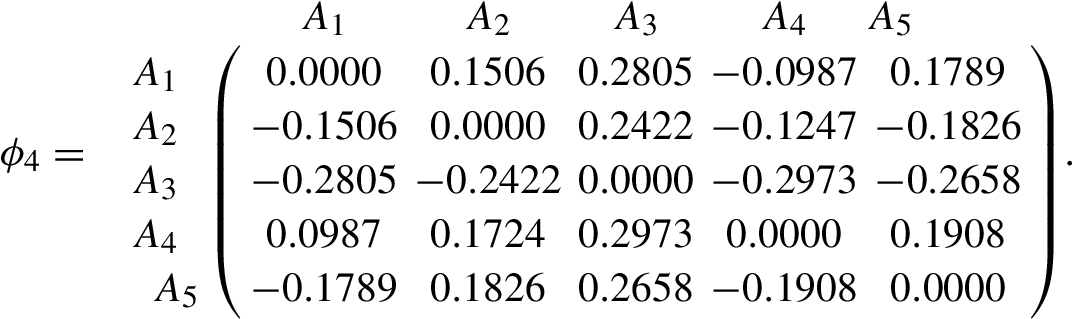
Secondly, by Eq. (13), and the overall dominance matrix is:
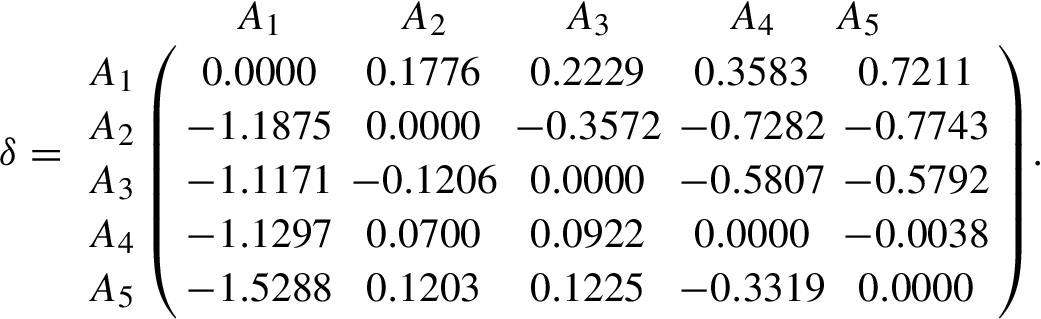
Then, we can obtain $\delta ({A_{i}})$ $(i=1,2,3,4,5)$ by Eq. (14):
Finally, the order is: ${A_{1}}\succ {A_{4}}\succ {A_{5}}\succ {A_{3}}\succ {A_{2}}$, and thus the best ETE is ${A_{1}}$.
4.2 Comparative Analysis
Then, we compare our method with picture fuzzy weighted averaging (PFWA) operator and picture fuzzy weighted geometric (PFWG) operator proposed by Wei (2017a) as follows:
Definition 7.
(See Wei, 2017a.) Let ${a_{ij}}=({\mu _{ij}},{\eta _{ij}},{\nu _{ij}})$ be a collection of PFNs, $w={({w_{1}},{w_{2}},\dots ,{w_{n}})^{T}}$ be the weight vector of ${a_{ij}}$ $(j=1,2,\dots ,n)$, and ${w_{j}}>0$, ${\textstyle\sum _{j=1}^{n}}{w_{j}}=1$, then
(16)
\[\begin{aligned}{}{r_{i}}=& ({\mu _{i}},{\eta _{i}},{\nu _{i}})\\ {} =& {\mathit{PFWA}_{w}}({r_{i1}},{r_{i2}},\dots ,{r_{im}})={\underset{j=1}{\overset{n}{\bigoplus }}}({w_{j}}{r_{ij}})\\ {} =& \Bigg(1-{\prod \limits_{j=1}^{n}}{(1-{\mu _{ij}})^{{w_{i}}}},{\prod \limits_{j=1}^{n}}{({\eta _{ij}})^{{w_{i}}}},{\prod \limits_{j=1}^{n}}{({\nu _{ij}})^{{w_{i}}}}\Bigg),\end{aligned}\](17)
\[\begin{aligned}{}{r_{i}}=& ({\mu _{i}},{\eta _{i}},{\nu _{i}})\\ {} =& {\mathit{PFWG}_{w}}({r_{i1}},{r_{i2}},\dots ,{r_{im}})={\underset{j=1}{\overset{n}{\bigotimes }}}{({r_{ij}})^{{w_{j}}}}\\ {} =& \Bigg({\prod \limits_{j=1}^{n}}{({\mu _{ij}})^{{w_{i}}}},1-{\prod \limits_{j=1}^{n}}{(1-{\eta _{ij}})^{{w_{i}}}},1-{\prod \limits_{j=1}^{n}}{(1-{\nu _{ij}})^{{w_{i}}}}\Bigg).\end{aligned}\]The calculating results are shown in Table 1.
Table 1
The aggregating results of the ETEs by the PFWA (PFWG).
| PFWA | PFWG | |
| ${A_{1}}$ | (0.6880,0.2170,0.0390) | (0.3840,0.5363,0.0521) |
| ${A_{2}}$ | (0.6216,0.2020,0.1120) | (0.4211,0.3729,0.1154) |
| ${A_{3}}$ | (0.5121,0.2218,0.1077) | (0.4042,0.3270,0.1431) |
| ${A_{4}}$ | (0.6547,0.2482,0.0607) | (0.2801,0.5696,0.0632) |
| ${A_{5}}$ | (0.5008,0.1647,0.0561) | (0.3131,0.4816,0.0858) |
Table 2
The score values of the ETEs.
| PFWA | PFWG | |
| ${A_{1}}$ | 0.8245 | 0.6664) |
| ${A_{2}}$ | 0.7548 | 0.6529 |
| ${A_{3}}$ | 0.7022 | 0.6305 |
| ${A_{4}}$ | 0.7970 | 0.6084 |
| ${A_{5}}$ | 0.7223 | 0.6137 |
Table 3
Ordering of the ETEs.
| Ordering | |
| PFWA | ${A_{1}}>{A_{4}}>{A_{2}}>{A_{5}}>{A_{3}}$ |
| PFWG | ${A_{1}}>{A_{2}}>{A_{3}}>{A_{4}}>{A_{1}}$ |
From Table 4, it can be seen that two methods have the same best ETE ${A_{1}}$ and two methods’ ranking results are slightly different.
Essentially, these two approaches are discrepant for consideration of the DMs’ psychological behaviours. The PFWA and PFWG operators based on the approaches can’t depict the DMs’ psychological behaviours under risk. The picture fuzzy TODIM model can reasonably show the DMs’ psychological behaviours under risk.
Furthermore, we compare our proposed method with picture fuzzy cross-entropy (Wei, 2016), picture fuzzy projection models (Wei et al., 2016b), generalized picture fuzzy distance measure (Son, 2016), similarity measures for picture fuzzy sets (Wei, 2018b) and cosine similarity measures for picture fuzzy sets (Wei, 2017c) as shown in Table 4.
Table 4
Ordering of the ETEs by using different methods.
| Ordering | |
| Picture fuzzy cross-entropy (Wei, 2016) | ${A_{1}}>{A_{4}}>{A_{2}}>{A_{5}}>{A_{3}}$ |
| Picture fuzzy projection models (Wei et al., 2016b) | ${A_{1}}>{A_{2}}>{A_{3}}>{A_{4}}>{A_{1}}$ |
| Generalized picture fuzzy distance measure (Son, 2016) | ${A_{1}}>{A_{4}}>{A_{2}}>{A_{3}}>{A_{5}}$ |
| Similarity measures for picture fuzzy sets (Wei, 2018b) | ${A_{1}}>{A_{4}}>{A_{2}}>{A_{5}}>{A_{3}}$ |
| Cosine similarity measures for picture fuzzy sets (Wei, 2017c) | ${A_{1}}>{A_{4}}>{A_{2}}>{A_{5}}>{A_{3}}$ |
5 Conclusion
In this paper, we expand the TODIM model for MADM with the PFNs. Firstly, the definition, comparative method and distance of PFNs and the calculating steps of the traditional TODIM model are introduced. Then, the extended TODIM model is developed to solve MADM problems in which the attribute values are in the PFNs, and its important characteristic is that it can fully depict the decision makers’ bounded rationality. Finally, an example for potential evaluation of emerging technology commercialization is considered to verify the developed model and a comparative analysis is also given. In subsequent works, more and more models with PFNs need to be investigated in uncertain decision making and risk analysis (Zeng et al., 2016; Wei et al., 2018a; Wei, 2017b; Merigo and Casanovas, 2009; Wei and Wei, 2018; Wei and Lu, 2018b; Zeng, 2017; Wei and Lu, 2017; Wei et al., 2018b; Gao et al., 2018a, 2018b; Tang and Wei, 2018; Wei and Lu, 2018a; Wei et al., 2016a; Wei and Zhang, 2018; Wei et al., 2018c; Wang et al., 2018).
