1 Introduction
It is well known that due to living in the digital era, we meet digitized signals daily, regardless of our occupation and personal interest. As capability to speak represents a crucial human characteristic, which separates humans from other living beings, speech signal takes high place in digital signal processing. Therefore, digital processing of speech signal has always occupied interest and a lot of research was conducted, for the purpose of representing speech signal with the smaller bit rate, while preserving sufficient quality (Jayant and Noll,
1984; Kondoz,
2004; Chu,
2003; Sayood,
2017; Rabiner and Schafer,
1978). Speech signal coding implies the application of a data compression technique to digitized speech signal samples, by using certain amount of bits per sample (Gibson,
2016). The goal is to achieve high quality, by using fewer bits per sample possible. Speech signal coding plays a crucial role in any technology used for speech transmission, as: voice over Internet protocol (VOIP), digital cellular communications, and any system working with digitized speech (Chu,
2003). Latest expansion in software applications, which offer functionality of voice and video communication, further emphasizes on speech coding, for the purpose of more efficient usage of the available data transmission bandwidth. By lowering the bit rate, we also lower the objective quality of the signal, so that signal compression always presents a compromise between the desired signal quality and the available bandwidth for transmission, or memory for storing the output signal. Different speech coding standards require fulfilling certain conditions regarding bit rate and signal quality (Chu,
2003).
This paper presents a novel waveform speech signal coding algorithm, based on differential coding scheme. Waveform coding is suitable for application in speech signal coding, and it is known that this type of coding can provide the highest level of speech signal quality (Jayant and Noll,
1984; Kondoz,
2004; Chu,
2003). One of the most familiar and commonly used, simple waveform coder is defined by the G.711 standard (ITU-T,
1972). G.711 coder is known as Pulse Code Modulation (PCM), with two basic types,
μ-law and
A-law. As PCM utilizes 8 bits per sample, a lot of research was performed for reducing the bit rate, while preserving original quality of the input signal (Kondoz,
2004; Gibson,
2016). Along with the bit rate, modifications and improvements have been done in the usage of available frequency bands (ITU-T,
2008). For instance, ITU-T, Recommendation G.711.1 allows implementation in narrowband and wideband speech signal coding, with sample frequency up to 16 kHz and bit rate ranging from 64 to 90 kbit/s. Since the used bit rate has significant impact on overall algorithm performance, certain techniques have been introduced to lower the bit rate, like linear prediction technique (Jayant and Noll,
1984; Kondoz,
2004; Chu,
2003). Linear prediction implies that the value of the current input signal sample can be represented as a linear combination of the previous samples. The earliest system which implemented this technique was Differential Pulse Code Modulation (DPCM), where prediction has been implemented for calculating the error (difference) signal (Jayant and Noll,
1984; Suma,
2012). Difference signal is obtained by subtracting the input signal sample from its predicted value. The main benefit of implementing differential coding is that the obtained difference signal is characterized by smaller variance and lower dynamic amplitude range. This means that the difference signal is more convenient for coding than the original input signal, regardless of the applied coding scheme type. Simplicity and benefits from implementing differential coding maintains this and related techniques interesting for exploitation and motivate researchers to consider it when designing new solutions and algorithms. For instance, in Uddin
et al. (
2016), a low bit rate speech signal coding algorithm with the implementation of DPCM has been analysed, and it has been shown that differential coding is suitable for application in coding of correlated speech signals. Predictive coding, which utilizes correlation as well, has been recently implemented in designing a LPC-Based Fronthaul Compression Scheme (Ramalho
et al.,
2017,
2018), designed to compress LTE signal, by means of predictive and Huffman coding. The compression system from Ramalho
et al. (
2017,
2018) is characterized by low computational complexity and low latency, while preserving high output signal quality. Microcontroller implementation of DPCM and ADPCM in speech signal compression has also been recently presented in Sarade (
2017), and it has been shown how ADPCM can take advantage of correlated signals to achieve more efficient signal compression compared to DPCM technique.
Further implementing the adaptation techniques into DPCM resulted in ADPCM (Adaptive DPCM) algorithm, which exploits correlation between the input signal samples and reduces the bit rate required for coding (Jayant and Noll,
1984). Adaptation is most commonly implemented as forward or backward adaptation (Jayant and Noll,
1984; Kondoz,
2004; Chu,
2003; Sayood,
2017). Adaptive quantization has wide area of implementation, as it represents a simple method for increasing the objective quality of the output signal. It is successfully applied in speech coding (Suma,
2012; Dinčić
et al.,
2016), image and video coding (Ortega and Ramchandran,
1995), as well as in wireless sensor networks (Fang and Li,
2008). In this paper, we combine adaptive quantization with simple differential coding to perform high quality speech coding. The algorithm is convenient for improvements by implementing more complex differential coding and quantization techniques. As we design a low complexity algorithm, this is left to future research.
The coding algorithm developed in this research is based on the backward adaptive technique, so it does not require transmission of the side information. This allows the developed coding algorithm to be used in the cases when small delay is required, without increasing the bit rate, as is the case of using forward adaptation, where transmission and coding of the side information is required. The goal is to achieve high quality output speech signal, which would meet the G.712 Recommendation for a high-quality speech coding (ITU-T,
2001), by using a low bit rate. Speech signal can be modelled with Gaussian or Laplacian probability density function (p. d. f.) (Kondoz,
2004). The algorithm we propose considers both models of the input signal p. d. f. and as will be shown, in the case of the Gaussian distribution it provides higher quality of the output signal for each value of the compression factor
μ. Eventually, for achieving high performance of the proposed algorithm, it is important to determine the support limit of the quantizer in the specific manner to minimize the signal distortion (Na and Neuhoff,
2001), which we also take into account in designing our quantizer.
The rest of the paper is organized as follows. Section
2 describes the support limit determination for the Gaussian source model. In Section
3, the basic principles of differential coding are described. The description of the novel differential speech signal coding algorithm is presented in Section
4, while the results of its application are presented and discussed in Section
5. Finally, Section
6 is devoted to conclusions.
2 Support Limit Determination for the Quasilogarithmic Quantizer of Gaussian Source
In designing speech signal coding algorithm, input signal has to be modelled by some probability distribution function (PDF). It is well known that speech signal can be successfully modelled by Gaussian (normal) distribution (Jayant and Noll,
1984; Kondoz,
2004; Chu,
2003; Sayood,
2017). PDF for a random variable with the Gaussian distribution with mean value denoted by
α and variance by
${\sigma ^{2}}$ is defined as Jayant and Noll (
1984):
Without loss of generality, we can assume that information source is memoryless Gaussian source with mean value equal to zero. PDF of thus defined Gaussian source is given by:
Quantization is a significant part in the digitalization process. A quantizer is defined as the structure of encoder and decoder (Jayant and Noll,
1984). Role of a quantizer is to perform mapping of the input signal amplitudes into the group of permitted amplitudes. An
N-level scalar quantizer
Q is defined by mapping
Q:
$R\in Y$, where
R represents a set of real numbers, while
$Y\equiv {y_{1}},{y_{2}},{y_{3}},\dots ,{y_{N}}\subset R$, is a set of representation levels that makes the code book of size
$|Y|=N$ (Jayant and Noll,
1984). Scalar quantizer divides a set of real numbers into
N cells
${R_{i}}=({t_{i-1}},{t_{i}}]$,
$i=1,\dots ,N$, where
${t_{i}}$,
$i=0,1,\dots ,N$ are decision thresholds of the quantizer, defined as
$Q(x)={y_{i}}$,
$x\in {R_{i}}$. In practice, during the process of scalar quantization, the region of an input signal is divided into granular and overload regions, which are separated by the support region thresholds
$-{t_{N-1}}$ and
${t_{N-1}}$. Minimum and maximum support region thresholds define the support region of the quantizer
$[-{t_{N-1}},{t_{N-1}}]$, which has a high influence on the total distortion of the quantizer (Jayant and Noll,
1984; Na and Neuhoff,
2001; Na,
2004). In order to determine the optimal support region, we implement an iterative numerical method for determining the support region thresholds. Optimal support limit can be found by minimizing the total distortion. In the case of quasilogarithmic quantizer and an input signal modelled with Gaussian source, with mean value equal to zero and variance
${\sigma ^{2}}=1$, granular distortion is defined by Jayant and Noll (
1984):
where
μ represents the compression factor. In the case of implementing larger compression factors, as is the case with the quantizer defined with the G.711 standard, where
$\mu =255$, (
$\mu \gg 1$) the term of the equation
$\frac{1}{{\mu ^{2}}}$ tends towards zero, so that Eq. (
3) can be approximated as:
For a quantizer with a support region threshold
${t_{N-1}}$ and input signal modelled by Gaussian PDF of zero mean and unit variance, overload distortion can be calculated as Na and Neuhoff (
2001):
The total distortion represents the sum of the granular and the overload distortion
$D={D_{g}}+{D_{o}}$. Minimizing the distortion in relation to the
${t_{N-1}}$ is performed as:
From Eq. (
6) we can obtain the optimal support limit, which is iteratively calculated by:
For the purpose of increasing the algorithm speed, we use only two iterations and obtain the result near the optimal one, where optimality refers to the solution of Eq. (
6). The initial values are chosen intuitively, as it is known that the iterative procedure converges to the same output for different initial values. Table
1 shows the convergation of support limit values, when different starting values are chosen.
Table 1
Support limit convergation for different starting values chosen.
|
R bit rate |
Compression factor μ
|
Starting value ${t_{N-1}}$
|
1st iteration |
2nd iteration |
3rd iteration |
|
|
3 |
4.3869 |
4.1760 |
4.2028 |
|
|
3.5 |
4.3001 |
4.1869 |
4.2014 |
| 6 |
255 |
4 |
4.2264 |
4.1963 |
4.2002 |
|
|
4.5 |
4.1622 |
4.2046 |
4.1991 |
|
|
5 |
4.1052 |
4.2122 |
4.1981 |
As already stated, in this research we have chosen to implement quasilogarithmic quantizer to perform input signal quantization. It represents a good choice, especially in the case of adaptive quantization, where we can easily adjust the quantizer by changing the compression factor. Also, a quasilogarithmic quantizer can be defined by the closed form formulas, which makes the design and analysis simple. Quasilogarithmic quantizer performs signal compression by applying a compressor function defined by Jayant and Noll (
1984):
By finding and implementing the optimal support limit and choosing the appropriate compression factor, we obtain a simple and efficient quantizer, which combined with the differential coding and backward adaptation technique is capable to provide a high quality output signal.
3 Theoretical Background of Differential Coding
Signals in nature are often correlated, meaning that the successive samples have values similar to a certain extent (Jayant and Noll,
1984; Chu,
2003). Wideband speech signal, sampled at 16 kHz, can be considered to be a correlated source, which can be practically examined by calculating the correlation coefficient of a real speech signal. For an input signal
$x[n]$,
$n=1,\dots ,M$, with the length of
M samples, the correlation coefficient can be calculated by:
Differential coding (DPCM) exploits the correlation of the successive samples of the input signal to reduce the redundancy of the input. It is based on quantizing the difference (prediction-error) signal
$e[n]$, which is obtained by subtracting the input signal
$x[n]$ from the signal prediction
${x_{p}}[n]$ formed between the actual value of the current sample and predicted value of the previous sample (Jayant and Noll,
1984; Chu,
2003). Prediction is commonly performed by implementing linear prediction, in which current sample is predicted as a linear combination of the previously quantized samples (Jayant and Noll,
1984; Makhoul,
1975; Markel and Gray,
2013). The number of previous samples used in prediction represents the order of a predictor. Function of the
k-th order linear predictor is defined as:
where
${a_{l}}$,
$l=1,2,\dots ,k$ are the prediction coefficients, while
$\hat{x}[n-1]$ represents the previously quantized input signal samples. The main benefit of differential approach is that prediction-error signal has smaller variance and dynamic amplitude range, which makes it more suitable for quantization (Suma,
2012). Quantizing prediction-error signal enables us to achieve higher SQNR for a given resolution, or equally given number of quantization levels
N.
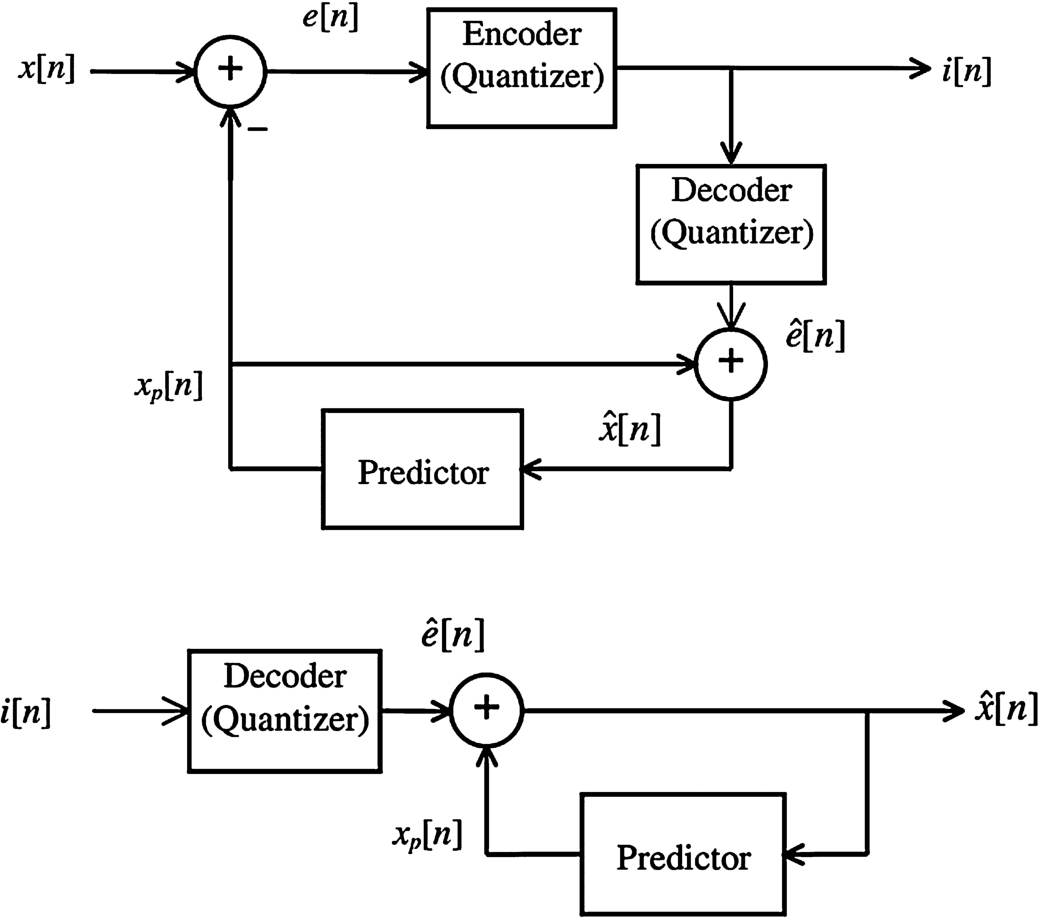
Fig. 1
DPCM encoder (top) and decoder (bottom).
DPCM encoder and decoder are presented in Fig.
1. Output of the encoder are indices
$i[n]$, by which the decoder obtains quantized prediction error, which is used in forming the quantized input. The thus defined DPCM system has been successfully implemented in speech (Jayant and Noll,
1984; Ortega and Ramchandran,
1995), image coding (Zschunke,
1977), as well as in ECG signal coding (Peric
et al.,
2013a). We implement DPCM principles in designing a speech coding algorithm presented in this paper. The combination of differential coding and backward adaptation provides a simple and efficient coding scheme without increasing the bit rate used. The contribution of this research lies also in the optimal quantizer design with utilization of correlation in speech signal coding. This enables us to obtain high quality output signal, while implementing the simplest differential coding. The following section describes the design and implementation of the algorithm we propose.
4 Algorithm for Differential Adaptive Coding of Speech Signal
Designing a speech coding algorithm is not a simple task, since a speech coding algorithm has to comply with the following Chu (
2003):
-
1. Use low bit rate;
-
2. Provide high output signal quality;
-
3. Be robust in a wide area of possible speakers and languages;
-
4. Have low computational complexity and low coding delay.
We have chosen to implement low complexity coding techniques with the possibility of using small frame sizes. This enables the algorithm to be implemented when small delay is required, as is the case in real time speech communication or package transmission of data. Since the coding algorithm includes encoder and decoder, both blocks will be described in steps separately. The purpose of the encoder is to convert the input signal into a form convenient for transmission and to send the encoded bit-stream to transmission channel as indices (Jayant and Noll,
1984). The designed algorithm encoder is described in the following.
As we implement backward adaptation technique, the first frame of the input signal does not have the required information for this process, as there was no information before. This is overcome by implementing PCM encoder (ITU-T,
1972) to the first frame of the input signal. As the same bit rate was implemented for all frames, the usage of PCM encoder for the first frame cannot significantly degrade the overall quality of the output, while it provides the initialization of the algorithm. The first encoded frame is used for accessing the statistical information required for the backward adaptation process, which is based on the previous, encoded frame. In the following steps, we calculate and implement the statistical data from the previous frame for coding the current one. Firstly, we calculate the correlation coefficient, starting from the second frame. The correlation coefficient used for coding the current
jth frame can be determined with the implementation of Eq. (
9) as:
where
L represents the total number of the input signal frames,
M is the total number of samples in the frame, while
$x[n]$ and
$x[n+1]$ denote the current and the next sample of the current input signal frame, respectively. The next parameter used is the variance of the previously quantized frame, defined by:
where
${\eta ^{(j-1)}}=\frac{1}{M}{\textstyle\sum _{n=1}^{M}}{\hat{x}^{(j-1)}}[n]$,
$j=2,\dots ,L$ represents the mean value of the quantized
$(j-1)$th signal frame.
Difference signal frame is formed in sample by sample manner, as:
The next step is to calculate difference frame variance, which is defined by:
The last step of encoding is the application of the designed adaptive quasilogarithmic quantizer
$({Q_{ad}})$ to the difference signal sample:
where the adaptive quantizer has the support region threshold defined by:
where
${t_{N-1}}$ is obtained from Eq. (
7). Thus defined adaptive support region thresholds contain information about the input signal, as in the case of implementing backward adaptation and differential coding represents the information about the previously quantized difference signal frame. In this manner, by implementing few simple calculations we adapt the quantization process to the input signal and its statistics and obtain better signal compression. Finally, the output of the described encoder is sent through the channel as binary information
$(I)$. The encoded values are received and decoded for the purpose of reconstructing the input signal.
Decoding represents an inverse process to encoding, with the purpose of extracting the input signal from its encoded representation. The first frame of the input signal is decoded by applying the PCM decoder (ITU-T,
1972). By reconstructing the first frame, we are able to extract the data required for decoding the following one. As in the encoding procedure, firstly we extract the correlation coefficient of the previous frame, by implementing Eq. (
11). The next statistical parameter from the previous frame used is the variance, calculated by implementing Eq. (
12). When we have the information about the previous frame variance, we can apply the inverse quantization to obtain the difference signal sample:
Actual input signal sample can be reconstructed as:
This step completes the decoding procedure, as we obtain the values of the quantized input signal samples.
The encoding algorithm can be presented as a series of the following steps:
From the second to the last frame (for $j=2,\dots ,L$) the following steps repeat:
The decoding procedure is performed by applying the following steps:
From the second to the last frame the following is repeated:
-
Step 2. Output frames are fed to the frame buffer.
-
Step 3. Information about the previous frame correlation coefficient and variance is extracted.
-
Step 4. Output signal sample is obtained from the quantized difference signal, quantized previous sample and from the correlation coefficient of the previously quantized frame (Eq. (
18)).
-
Step 5. Samples are fed to the output frame buffer, where we have reconstructed signal samples.
By performing quantization, we introduce an irreversible error due to rounding the current values of the input signal to the representation levels. This error is named quantization error and it can be expressed by distortion, which is commonly defined as the average value of a mean-squared error (Jayant and Noll,
1984). Eqs. (
3)–(
5) define theoretical distortion for the quasilogarithmic quantization of Gaussian source. In the case of applying algorithm in real input signal coding, distortion can be calculated by:
where
S represents the total number of the input signal samples. Thus defined distortion with input signal power determines signal to quantization noise ratio, an objective signal quality measure, used in this paper (Jayant and Noll,
1984):
5 Numerical Results and Analysis
This section presents the numerical results of applying the proposed algorithm in speech signal coding. In addition, we observe the theoretical characteristics of the basic coding schemes implemented in differential speech signal coding, to show the improvements which are results of the algorithm design. As we implement quasilogarithmic quantization, firstly we analyse the theoretical performance of the quasilogarithmic quantizer. This represents the case when quantization is performed only by applying quasilogarithmic quantization, with 6 bits per sample and the usage of different compression factors. Speech signal is modelled with the Gaussian distribution with zero mean and unit variance, as it has been assumed in the proposed algorithm design. Additionally, we show the theoretical performance of the quasilogarithmic quantizer in the case of using Laplacian distribution with zero mean and unit variance for modelling a speech signal. In the case of using Laplacian distribution, optimal support limit of quasilogarithmic quantizer can be defined as Jayant and Noll (
1984):
The total distortion of the quasilogarithmic quantizer designed for the Laplacian source can be calculated by Kondoz (
2004), Peric
et al. (
2013b):
We show the results for the case of using smaller compression factor values, ranging from 2 to 50, as our algorithm implements adaptive quantization and it is expected that it will have the best performance in this range of compression factors. Fig.
2 shows the benefits of modelling speech signal with Gaussian source, as the quasilogarithmic quantizer designed for Gaussian source provides better theoretical SQNR characteristics.
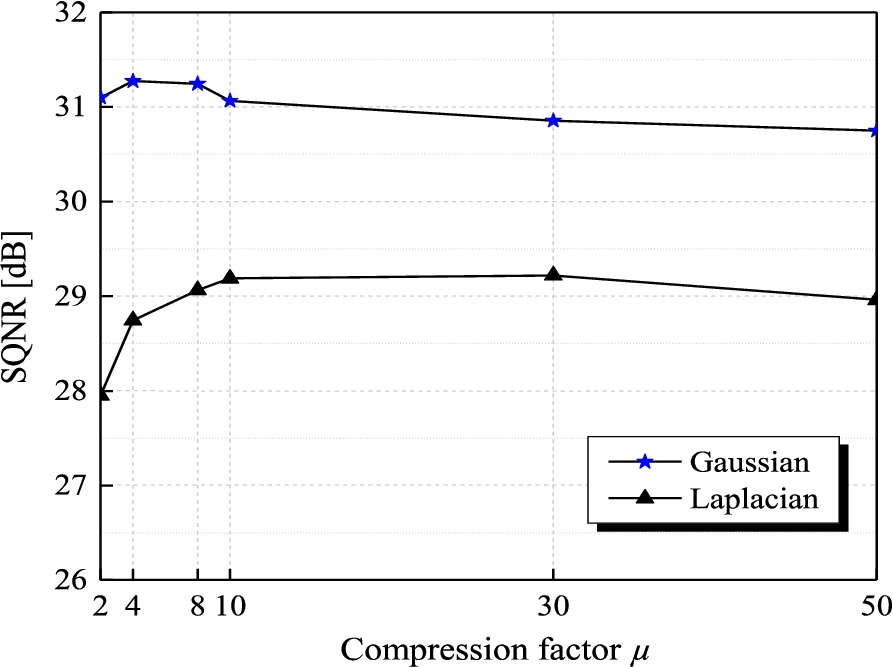
Fig. 2
Theoretical dependence of SQNR on compression factor for the quasilogarithmic quantizer that is designed for Gaussian vs. Laplacian source models for speech signal.
The figure shows that the highest theoretical SQNR value in the case of using Gaussian model is obtained for the compression factor equal to 4 and it amounts to around 31.3 dB. When using Laplacian model, maximum is obtained in the case when compression factor is equal to 10, and it amounts to around 29.2 dB. One can notice that the theoretical maximum in SQNR is greater when using Gaussian source model, and the gain amounts to 2.1 dB. For higher compression factor values SQNR characteristics are in steady decline, while the gain is obtained for all compression factor values. This confirms the benefits of modelling speech signal with the Gaussian distribution.
In order to evaluate the performance of the proposed coding algorithm, an experiment was also conducted. The input signal has been a 15 seconds long sequence of a male speech signal, sampled at 16 kHz. The objective quality measure used in the experiment is SQNR, expressed in dB. Along the performance of the proposed algorithm, we analyse the performance of the algorithm without using adaptive quantization and PCM scheme. The advantage of implementing adaptive quantization is observed through the obtained gain in SQNR, especially for lower compression factor values. Comparison with PCM indicates significantly higher objective output signal quality obtained with the implementation of the proposed algorithm.
Table 2
Experimentally obtained SQNR for the proposed algorithm with comparison.
|
R bit rate |
Frame size |
Compression factor μ
|
SQNRPCM [dB] |
SQNRNON-AD [dB] |
SQNRAD [dB] |
|
|
10 |
24.0995 |
3.7499 |
35.7590 |
|
|
20 |
24.0995 |
7.4873 |
36.3638 |
|
|
30 |
24.0995 |
9.7586 |
36.4615 |
| 6 |
40 |
40 |
24.0995 |
11.3872 |
36.4439 |
|
|
50 |
24.0995 |
12.6633 |
36.4267 |
|
|
100 |
24.0995 |
16.5379 |
36.0445 |
|
|
255 |
24.0995 |
21.2701 |
35.2108 |
By observing Table
2, one can notice that the proposed algorithm (SQNR
AD) satisfies the G.712 Recommendation, by using 6 bits per sample for coding, as it provides SQNR greater than 34 dB (ITU-T,
2001), for all values of compression factor implemented. Additionally, the proposed algorithm provides gain in SQNR from 11.1 to about 12.36 dB, when compared to PCM. We should point out that PCM uses fixed compression factor, equal to 255, so SQNR in the column has a single value. The constant gain in SQNR of more than 10 dB, compared to the widely used PCM, confirms that the proposed coding algorithm provides high quality output speech signal. The version of the differential algorithm without implementing adaptive quantization provides lower objective quality of the output signal, for all values of the compression factor used (SQNR
NON-AD). When we use smaller compression factors, the non-adaptive quantizer is not suitable for application, while for the adaptive version of the algorithm it provides approximately constant performance for different compression factor values. In the case of using compression factor equal to 255, the gain in SQNR is close to 14 dB in favour of the proposed differential speech coding algorithm with adaptive quantization, when compared to non-adaptive version, while the gain amounts to about 11 dB, in comparison to the PCM.
Furthermore, we can compare our results with the results obtained in earlier researches, by using similar or greater complexity coding schemes, where some of them also comply with the G.712 Recommendation. Table
3 shows the comparative results obtained by implementing DPCM with uniform quantization and the second order predictor (Suma,
2012), providing SQNR of about 30 dB, while using 6 bits per sample. One can notice that the proposed algorithm provides gain in SQNR of about 6.5 dB, compared to the case of implementing the basic DPCM coding scheme for the same bit rate. This gain is somewhat justified by the more suitable design of our quantizer. It is also justified by the fact that we have processed the wideband speech signal, which is more correlated compared to the narrowband speech signal processed in Suma (
2012). Additionally, Table
3 shows the performance of the fixed and adaptive companding quantizer with variable-length codeword Perić
et al. (
2013c) and transform coding with forward adaptive quantization (Tancic
et al.,
2016). In both cases, SQNR obtained is greater than 34 dB, while it is achieved by using around 6.5 bits per sample. The algorithm proposed in this paper overreaches SQNR of the compared coding schemes by using around 0.5 bits per sample less for coding. We can easily estimate the performance of the proposed algorithm for the case of using 6.5 bits per sample. This could be done by obtaining the SQNR performance for the case of using 7 bits per sample and by finding the mean value of this value and the one obtained in the case of using 6 bits per sample from Table
3. The estimated SQNR performance of the proposed algorithm for 6.5 bits per sample amounts to about 39.51 dB. This shows that in the case of using the same bit rate, the proposed algorithm provides gain in SQNR from 4.3 dB to 4.9 dB, when compared to the aforementioned coding schemes.
Table 3
Comparative SQNR performance of coding schemes which comply with the G. 712 Recommendation.
| Bit ratea
|
SQNRa [dB] |
Bit rateb
|
SQNRb [dB] |
Bit ratec
|
SQNRc [dB] |
Bit rate (proposed) |
SQNRAD [dB] (proposed) |
| 6 |
30 |
6.5 |
35.143 |
6.52 |
34.603 |
6 |
36.46 |
The experimental results of applying the proposed algorithm to a real speech signal and comparative results shown in Tables
2 and
3, confirm the suitability of the proposed algorithm to be implemented in speech signal coding.
6 Conclusion
This paper has presented a simple, differential wideband speech signal coding algorithm, with the implementation of backward adaptation technique. The algorithm implements low complexity signal coding techniques and provides high quality output speech signal, while using low bit rate. By implementing differential coding, instead of common waveform coding of input signal samples, we perform quantization on the difference signal, which has lower amplitude dynamics and, as shown, is more suitable for performing quantization. The difference signal has been quantized by the backward adaptive quasilogarithmic quantizer, whose design has been presented in this paper. By inspecting the theoretical performance of the quasilogarithmic quantizer, we have demonstrated the advantages of modelling the input signal with Gaussian distribution, since in that case SQNR overreaches the results of using Laplacian distribution to model the input signal. The experimental results have shown the benefits of implementing adaptive quantization and differential speech coding. Moreover, the experimental results have shown that the proposed algorithm can satisfy the G. 712 Recommendation for high-quality speech coding, in the case of using 6 bits per sample for coding. Comparative results of the proposed algorithm with similar complexity speech coding schemes have confirmed that the proposed algorithm can be successfully implemented in speech signal coding.

