1 Introduction
Video surveillance technology has been widely used for monitoring situation or postmortem analysis. Different applications focus on various kinds of objects in video sequences. In public places, e.g. squares, railway stations, etc., video surveillance technology can be used to detect and analyse abnormal situations. In this kind of scenarios, pedestrians are of most interest. Comparing to individual movement, crowd motion is much more important and harder to track.
Crowd is a unique group of individuals or something that involves community or society. Crowd can be described in a general term, the behaviour of the crowds has a collective characteristic such as ‘an angry crowd’ and ‘a peaceful crowd’. In ‘an angry crowd’ we have to identify its behaviour. Various tasks for detecting crowd behaviour can be defined such as crowd density estimation, crowd behaviour identification, crowd motion, crowd tracking. Good reviews of crowd behaviour situations are given in Sjarif et al. (2012), Li et al. (2015), Yogameena and Nagananthini (2017).
Crowds react to their surroundings; they may also actively cause certain situations when abnormal event happens. In abnormal case crowd can quickly move in one direction or run in different directions. We will not consider in this paper crowd moving in one direction. We will concentrate our attention to crowd aggregation and crowd dispersion. When these behaviours happen, they usually mean abnormal or even urgent event happens. So, in this paper, we will consider a crowd abnormal behaviour as crowd aggregation and dispersion.
Identifying crowd behaviours in videos has been proved challenging. In traditional way, one could segment objects of interests from the background and track their movements separately (Cheriyadat and Radke, 2008; Hu et al., 2013). But in crowded situations, this is difficult due to severe occlusions (Junior et al., 2010). In recent years, there have been great improvements in the study of Convolutional Neural Network (CNN), thus some works used CNN for crowd behaviour analysis. Shao et al. (2016) presented Slicing-CNN for crowd video understanding. Zhang et al. (2016) proposed a method using optical flow and CNN to recognize crowd events on video. Ravanbakhsh et al. (2017) employed Fully Convolutional Network and optical flow to obtain the complementary information of both appearance and motion patterns. There are some other CNN-based methods that have been proposed for crowd video analysis, e.g. (Cheung et al., 2016; Zhao et al., 2016; Shao et al., 2017). Some works which also require training adopted other training techniques. Andrade et al. (2006) presented a method combining optical flow and unsupervised feature extraction based on spectral clustering and Multiple Observation Hidden Markov Model (MOHMM) training for abnormal events detection in crowds and correctly distinguished blocked exit situation from normal crowd flow. Wang et al. (2016) presented a feature descriptor called hybrid optical flow histogram and performed training on normal behaviour samples through sparse representation, they detected change of speed in different directions of a movement as abnormal behaviour for every frame. Mehran et al. (2009) proposed abnormal crowd behaviour detection method based on social force model, it could distinguish abnormal frames from normal frames. Methods with training stage usually need mass data to train certain behaviour model and it is not easy to create that kind of data set with professional and accurate labels. Some works which don’t require training have also been published. Hu et al. (2008) proposed a method to learn crowd motion pattern based on sparse optical flows and clustering, and neighbourhood graph was used to measure the similarity and proximity of flow vectors. They didn’t further identify crowd behaviours. Chen and Shao (2014) proposed a method for detection and localization of crowd escape anomalous behaviours in video surveillance systems, they used energy of optical flow to detect abnormality and divergent centre to indicate corresponding location. Ali and Shah (2007) presented a framework in which Lagrangian Particle Dynamics is used for the segmentation of high density crowd flows and detection of flow instabilities. An interesting approach for moving object detection based on partitioning a video into blocks of equal length and detecting objects in the first and last frames of the block is proposed in Kustikova and Gergel (2016). Solmaz et al. (2012) proposed a method to identify five crowd behaviours including blocking, lane, bottleneck, ring/arch and fountainhead based on stability analysis through Jacobian matrix. This paper considered abnormal crowd behaviour, based on using an optical flow and it is much closer to our research.
Among aforementioned works, optical flow is widely used for motion analysis because of its ability to treat crowd as single entity and thus avoid individual tracking. Instead of using basic optical flow (Lucas and Kanade, 1981; Farnebäck, 2003; Horn and Schunck, 1981; Tao et al., 2012) directly, we use integral optical flow (Chen et al., 2017) to analyse crowd motion. Ali and Shah (2007), Solmaz et al. (2012) also integrate basic optical flow over time in similar ways, but the reason of using integral optical flow in our work is to separate background and foreground and obtain intensive motion region. Several works, e.g. Mehran et al. (2009), Ali and Shah (2007), Solmaz et al. (2012), create dynamical system and perform particle advection along with optical flow to emulate crowd motion, while our method only uses start position and end position of pixels in certain time period to perform motion analysis.
In this paper, we present a novel method based on integral optical flow to identify crowd aggregation and crowd dispersion in videos which should be captured by stationary cameras in public places. The main contributions of our work are as follows: 1) Identifying specific crowd behaviours in public places where pedestrians are the main moving objects. 2) Instead of being inspired by particle advection from fluid dynamics, our method is from the perspective of geometry. We focus on geometric structure formed by crowd motion in certain time period. This straightforward idea makes our method simpler than other methods. 3) Taking advantage of the accumulative effect of integral optical flow. Random motion of background is reduced in integral optical flow, thus separating foreground from background becomes much easier. Our method doesn’t require training, it can be used for situation monitoring and analysis, or as a component of comprehensive systems. We apply our method on simulated videos and real word videos and get good results. Experimental results show that our method outperforms state-of-the-art methods.
2 Integral Optical Flow
Optical flow provides a way letting one study pixel motion at different time. There exist several methods for computing optical flow, these methods differ in basic theory and mathematic method. Some of the methods only compute optical flow for certain set of pixels, e.g. Lucas and Kanade (1981), while others compute optical flow for all pixels in the frame, e.g. Farnebäck (2003), Horn and Schunck (1981), Tao et al. (2012). In this paper method in Farnebäck (2003) is used to find dense optical flow.
Basic optical flow only records displacement vector of pixels between two consecutive frames. Taking into account the very short time interval between them, it is hard to distinguish foreground from background due to motion of background. Generally background moves randomly, e.g. back and forth or circularly. In short time this kind of character doesn’t show, but after a long enough time, it will reveal itself thus help identifying foreground. Integral optical flow is an intuitive idea that accumulate optical flows for several consecutive frames. Along with the accumulation, displacement vectors of background become small, while those of foreground keep growing.
For description convenience, we use ${I_{t}}$ to denote t-th frame of video I and ${I_{t}}(p)$ to denote pixel at position p in ${I_{t}}$ throughout the remainder of this paper. Let ${\mathit{OF}_{t}}$ denote basic optical flow of ${I_{t}}$ and ${\mathit{IOF}_{t}^{\mathit{itv}}}$ denote integral optical flow of ${I_{t}}$, where $\mathit{itv}$ is the frame interval parameter used to compute integral optical flow. ${\mathit{IOF}_{t}^{\mathit{itv}}}$ is a vector field which records accumulated displacement information in time period of $\mathit{itv}$ frames for all pixels in ${I_{t}}$. For any pixel ${I_{t}}(p)$, its integral optical flow ${\mathit{IOF}_{t}^{\mathit{itv}}}(p)$ can be determined as follows:
where ${p_{t+i}}$ is the position in ${I_{t+i}}$ of the pixel.
3 Proposed Method
3.1 General Scheme
Our method considers three factors to identify crowd behaviours: motion intensity, quantity and motion direction of pixels moving toward and away from certain regions. First we define basic motion structures of crowd aggregation and crowd dispersion. Based on integral optical flow, we then define four motion maps to describe pixel motions at each position, i.e. statistical analysis of quantity and motion direction of pixels moving toward or away from each position. After that, we introduce regional motion indicators to analyse motion at region-level, which is appropriate for crowd behaviour identification. At last, we use threshold segmentation to identify above-mentioned crowd behaviours. General scheme of our method is shown in Fig. 1.
3.2 Definition of Crowd Behavior
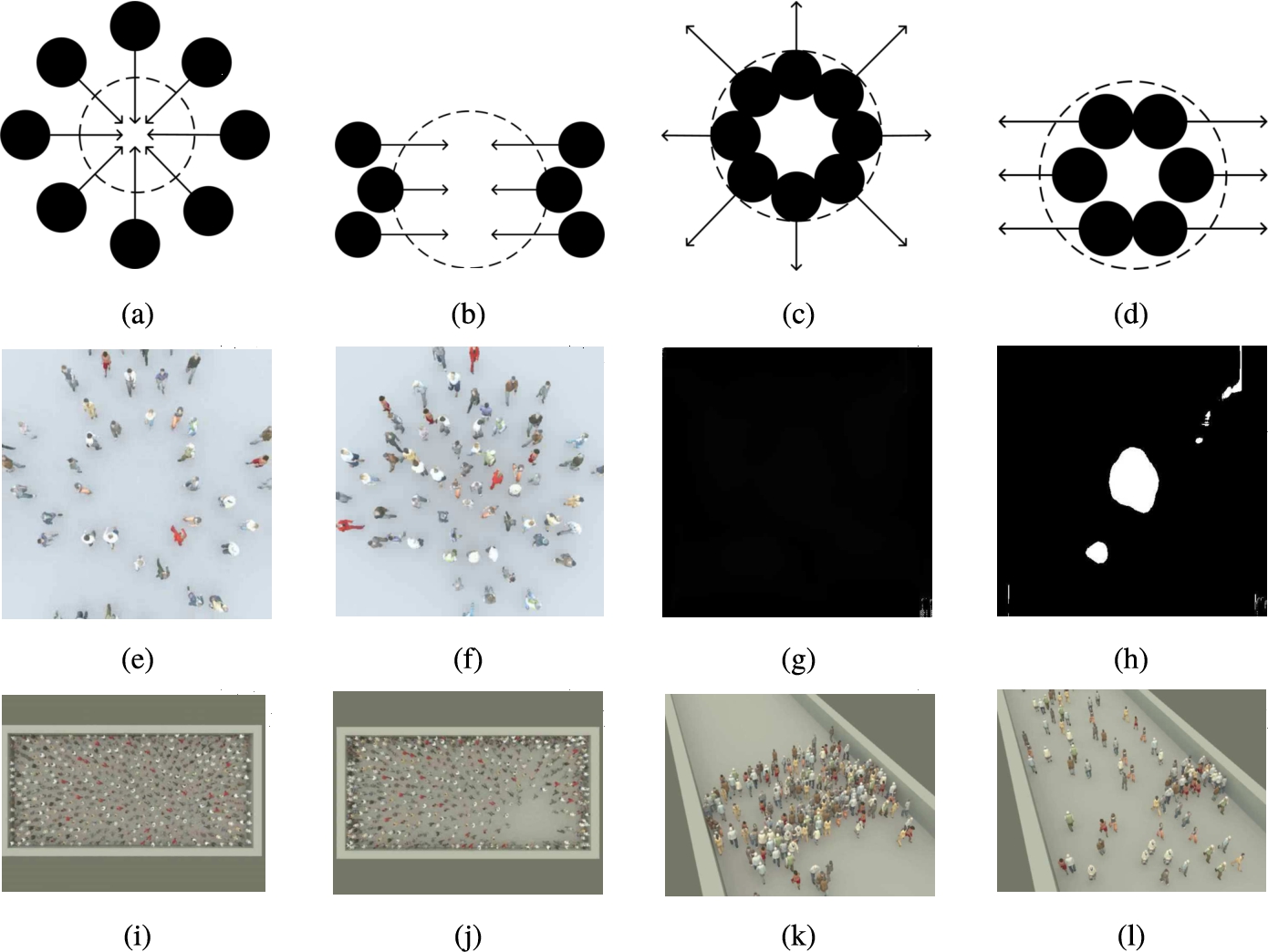
Fig. 2
Diagram of crowd aggregation and crowd dispersion. (a) basic structure of typical crowd aggregation; (b) basic structure of crowd aggregation with fewer motion directions; (c) basic structure of typical crowd dispersion; (d) basic structure of crowd dispersion with fewer motion directions; (e), (f) crowd aggregate from all directions; (g), (h) crowd aggregate from two opposite directions; (i), (j) crowd disperse in all directions; (k), (l) crowd disperse in two opposite directions. In (a), (b), (c) and (d), a black solid circle represents a group of people, a dotted circle represents a certain region and arrows show motion directions.
Human behaviours reflect one’s emotion which can be affected by surroundings. Individual behaviours may not be reliable for indicating things happening around, but behaviours of crowd in public places are very reliable indicators. From human nature point of view, people react rapidly to urgent events, thus their motions become fast on video. For example, when people see something dangerous, they get away from the corresponding region in order to prevent getting hurt. Crowds not only react to their surroundings, they may also create emergencies. When conflict is going to happen between two groups of people, e.g. fans of two football clubs, they tend to approach each other rapidly. There are many other situations causing these crowd behaviours.
Definition 1 (Crowd aggregation).
Many people move rapidly toward a certain region from different directions. In typical crowd aggregation as shown in Fig. 2(a), people are from all directions symmetrically. But in real situations, that is not necessary. It depends on characteristic of the public place where people are and at which stage the corresponding event is. For example, if two groups of people decide to attack each other after some sort of plan or emotion accumulation, aggregation like Fig. 2(b) is more likely to happen. In general, three rules are proposed to identify crowd aggregation: 1) many people move toward a certain region from elsewhere; 2) they move fast; 3) there are at least two moving directions and they are more or less symmetrical.
Definition 2 (Crowd dispersion).
Many people move rapidly away from a certain region in different directions. Usually it means something urgent or dangerous happens and people run in different directions to get away, like it is shown in Fig. 2(c). But unless it is too crowded that people stand shoulder by shoulder, they don’t necessarily move in all directions, although their motion directions are still more or less symmetrical. Situation like Fig. 2(d) can also happen when two groups of people retreat from a conflict. In general, three rules are proposed to identify crowd dispersion: 1) many people move away from a certain region to elsewhere; 2) they move fast; 3) there are at least two moving directions and they are more or less symmetrical.
3.3 Statistical Motion Analysis at Position-Level
Crowd behaviours are related to regions spatially. As a region comprises several adjacent positions, before looking into those behaviours, one should describe motion at each position clearly. Basic optical flow and integral optical flow record basic information of motions, i.e. starting position and ending position of pixels, thus for each position in the frame, not only number of pixels passing through can be counted, their comprehensive moving directions can also be computed.
3.3.1 Pixel Motion Path
Definition 3 (Motion path of a pixel).
Suppose ${I_{t}}(p)$ moves to q in ${I_{t+itv}}$, then position sequence $(p,q)$ is called simple motion path of pixel ${I_{t}}(p)$ in the time period from ${I_{t}}$ to ${I_{t+itv}}$. Suppose ${p_{0}},{p_{1}},\dots ,{p_{n-1}}(n\geqslant 2,{p_{0}}=p,{p_{n-1}}=q)$ are positions computed through Digital Differential Analyzer (DDA) for line segment $pq$, then position sequence $({p_{0}},{p_{1}},\dots ,{p_{n-1}})$ is called interpolative motion path of pixel ${I_{t}}(p)$ in the time period from ${I_{t}}$ to ${I_{t+itv}}$.
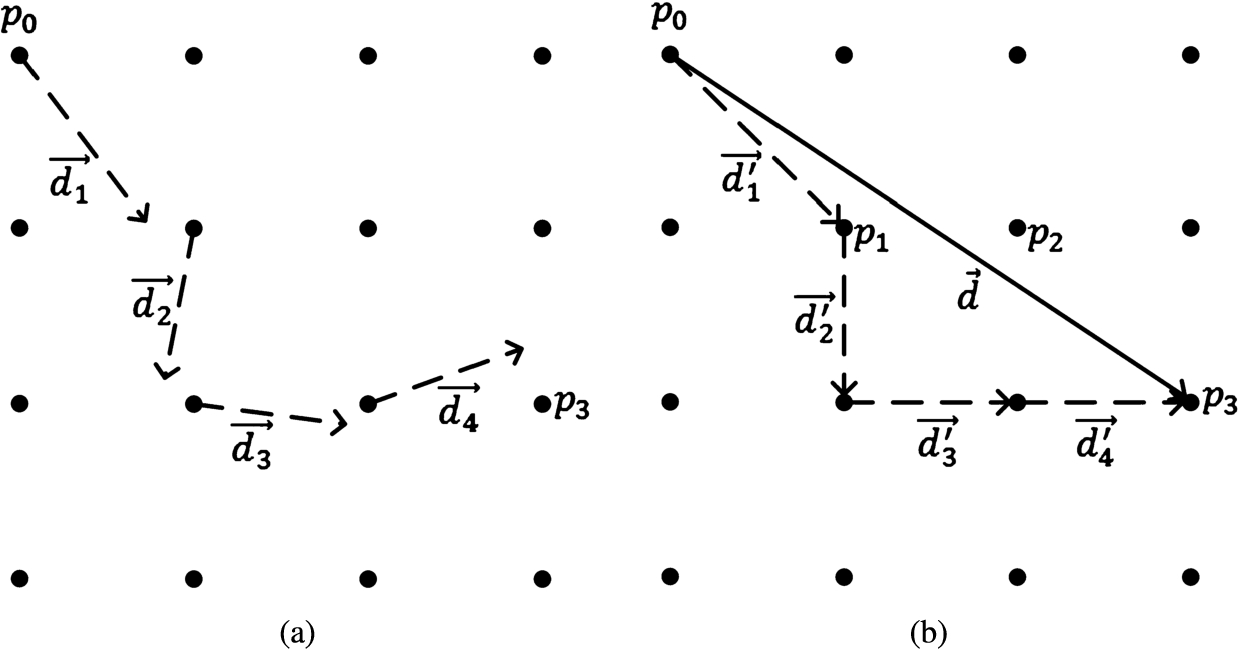
Fig. 3
An example of pixel motion path. (a) displacement vectors of pixel ${I_{t}}({p_{0}})$ in basic optical flows; (b) displacement vector of ${I_{t}}({p_{0}})$ in integral optical flow and its motion path. Dotted arrows represent displacement vectors in basic optical flows and their integer versions, the solid arrow represents displacement vector in integral optical flow, solid circles represent positions.
From integral optical flow, motion of a pixel in given time period can be determined. For example, in Fig. 3(a), one pixel in ${I_{t}}$ with original position ${p_{0}}$ moves to position ${p_{3}}$ after four frames in ${I_{t+4}}$; $\vec{{d_{1}}},\vec{{d_{2}}},\vec{{d_{3}}},\vec{{d_{4}}}$ are displacement vectors of the pixel extracted from basic optical flows $O{F_{t}},O{F_{t+1}},O{F_{t+2}},O{F_{t+3}}$, respectively, $\vec{{d^{\prime }_{1}}},\vec{{d^{\prime }_{2}}},\vec{{d^{\prime }_{3}}},\vec{{d^{\prime }_{4}}}$ in Fig. 3(b) are their integer versions for computing integral optical flow; $\vec{d}=\vec{{d^{\prime }_{1}}}+\vec{{d^{\prime }_{2}}}+\vec{{d^{\prime }_{3}}}+\vec{{d^{\prime }_{4}}}$ is the displacement vector of the pixel extracted from integral optical flow ${\mathit{IOF}_{t}^{4}}$. Here we call position sequence $({p_{0}},{p_{3}})$ simple motion path of the pixel in time period from frame ${I_{t}}$ to frame ${I_{t+4}}$. When we need to describe the motion more precisely, position sequence $({p_{0}},{p_{1}},{p_{2}},{p_{3}})$ can be used as interpolative motion path of the pixel in the same time period.
For statistical motion analysis, only pixels which actually move should be considered. Thus for each position, only motion path whose starting position is different from its ending position should be taken into account.
Definition 4 (Effective motion path of a position).
Suppose $({p_{0}},{p_{1}},\dots ,{p_{n-1}})$ is a motion path of ${I_{t}}({p_{0}})$, where $n\geqslant 2,{p_{0}}\ne {p_{n-1}}$, then $({p_{0}},{p_{1}},\dots ,{p_{n-1}})$ is called an effective motion path of ${p_{i}}$ $(0\leqslant i<n)$. Here $({p_{0}},{p_{1}},\dots ,{p_{n-1}})$ can be a simple motion path or an interpolative motion path depending on which type of motion path is used for motion analysis. All effective motion paths of ${p_{i}}$ $(0\leqslant i<n)$ form its effective motion path set (EMP set).
3.3.2 Motion Maps
Comprehensive motion direction of pixels in a region can be easily obtained or computed thus help determine whether the pixels move in the same direction or in symmetrical directions. But without knowing their destinations, one can hardly say it is a motion of aggregation or dispersion. Therefore in this section, motion maps are defined and created to describe motions in a frame from the point of view of positions instead of pixels.
Definition 5 (Motion maps).
A map with a scalar value at each position indicating number of pixels moving toward the corresponding position is called in-pixel quantity map (IQ map); A map with a scalar value at each position indicating number of pixels moving away from the corresponding position is called out-pixel quantity map (OQ map); A map with a vector at each position indicating comprehensive motion of pixels moving toward the corresponding position is called in-pixel comprehensive motion map (ICM map); A map with a vector at each position indicating comprehensive motion of pixels moving away from the corresponding position is called out-pixel comprehensive motion map (OCM map).
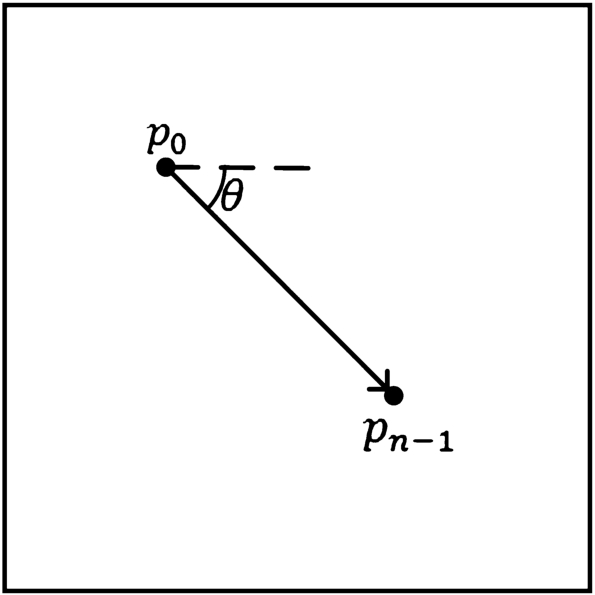
Fig. 4
An effective motion path starting from ${p_{0}}$ and ending at ${p_{n-1}}$ where $n\geqslant 2$ and the corresponding displacement vector in integral optical flow is $\overrightarrow{{p_{0}}{p_{n-1}}}$.
Let’s take a look at a single effective motion path. Assume $({p_{0}},{p_{1}},\dots ,{p_{n-1}})$ is an effective motion path as shown in Fig. 4, vector $\overrightarrow{{p_{0}}{p_{n-1}}}$ is the corresponding displacement vector in integral optical flow. In order to compute contributions of pixel quantity and comprehensive motion of this path for every position in it, we use the normalized vector of $\overrightarrow{{p_{0}}{p_{n-1}}}$, because it carries information of both pixel number and motion direction. The normalized vector of $\overrightarrow{{p_{0}}{p_{n-1}}}$ can be computed as follow:
where ${\vec{v}_{\mathrm{norm}}}$ is the normalized vector, $|\overrightarrow{{p_{0}}{p_{n-1}}}|$ is the magnitude of $\overrightarrow{{p_{0}}{p_{n-1}}}$. If the angle between ${\vec{v}_{\mathrm{norm}}}$ and x-axis is θ, then
Note that $|{\vec{v}_{\mathrm{norm}}}|=1$ indicates pixel number for a single effective motion path, four values can be computed for any position ${p_{i}}$ $(0\leqslant i<n)$ in the path:
where ${w_{\mathrm{in}}},{w_{\mathrm{out}}}$ are weights to indicate the degree or percentage of coming and leaving of the corresponding pixel at the position and ${w_{\mathrm{in}}}+{w_{\mathrm{out}}}=1$. There is a simple way to determine ${w_{\mathrm{in}}}$ and ${w_{\mathrm{out}}}$ based on distance:
where ${p^{\prime }_{i}}$, which is rounded to ${p_{i}}$ in the process of generating interpolative motion path, is the intersection of line segment ${p_{0}}{p_{n-1}}$ and the underlying grid.
(2)
\[ {\vec{v}_{\mathrm{norm}}}=\frac{\overrightarrow{{p_{0}}{p_{n-1}}}}{|\overrightarrow{{p_{0}}{p_{n-1}}}|}\]In general, let ${S_{t}}(p)$ denote EMP set of position p at the time of ${I_{t}}$, ${\mathit{IQ}_{t}},{\mathit{OQ}_{t}},{\mathit{ICM}_{t}},{\mathit{OCM}_{t}}$ denote IQ map, OQ map, ICM map and OCM map of ${I_{t}}$, respectively, then values at position p on these maps at the corresponding time can be computed as follows:
where ${s_{\mathrm{in}}}(a,p),{s_{\mathrm{out}}}(a,p),{\vec{v}_{\mathrm{in}}}(a,p),{\vec{v}_{\mathrm{out}}}(a,p)$ are computed according to Eqs. (4)–(7).
After above four motion maps for time of ${I_{t}}$ have been created, important characteristics of pixel motions at that time will be revealed by these maps.
In conclusion, positions with big values on IQ map and small vector magnitudes on ICM map are positions at which pixels tend to aggregate; positions with big values on OQ map and small vector magnitudes on OCM map are positions at which pixels tend to disperse.
-
(1) Positions with bigger value on IQ map are positions to which more pixels move;
-
(2) Positions with bigger value on OQ map are positions from which more pixels leave;
-
(3) Positions with smaller vector magnitude on ICM map are positions to which pixels move in more symmetrical directions;
-
(4) Positions with smaller vector magnitudes on OCM map are positions from which pixels leave in more symmetrical directions.
3.4 Regional Motion Analysis
It makes more sense to analyse motions at region-level when studying crowd behaviours. In this section, meaningful indicators are defined and computed for regions of interest, these indicators will be used to identify crowd aggregation and crowd dispersion.
3.4.1 Intensive Motion Region
Motion intensity is a major factor for detecting urgent events. It is appropriate to use average displacement of pixels to represent motion intensity in a region.
Definition 6 (Regional motion intensity).
Average of displacement vector magnitudes extracted from integral optical flow for pixels in a certain region. Let r denote a certain region, $M{I_{t}}(r)$ denote regional motion intensity of r at the time of ${I_{t}}$, then it can be computed as follow:
where n is position number in r, ${\mathit{IOF}_{t}^{\mathit{itv}}}(p)$ is displacement vector of ${I_{t}}(p)$ extracted from integral optical flow. Any region with a high enough regional motion intensity is considered an intensive motion region. Identification of intensive motion region is the precondition of further process, i.e. crowd behaviour identification.
(14)
\[ M{I_{t}}(r)=\frac{1}{n}\sum \limits_{p\in r}\big|{\mathit{IOF}_{t}^{\mathit{itv}}}(p)\big|,\]3.4.2 Regional Motion Analysis Based on Motion Maps
IQ map and OQ map can be used to obtain quantities of pixels moving toward and away from a certain region, respectively. Since region size will be considered further in crowd behaviour identification, whether to use sum or average here doesn’t matter.
Definition 7 (Regional in-pixel relative quantity).
Average of values on IQ map at positions in a certain region.
Definition 8 (Regional out-pixel relative quantity).
Average of values on OQ map at positions in a certain region.
Let r denote a certain region, ${\mathit{IRQ}_{t}}(r)$ and ${\mathit{ORQ}_{t}}(r)$ denote regional in-pixel relative quantity and regional out-pixel relative quantity of r at the time of ${I_{t}}$, respectively, then
where n is position number in r, ${\mathit{IQ}_{t}}(p)$ and ${\mathit{OQ}_{t}}(p)$ are values at position p on IQ map and OQ map at the time of ${I_{t}}$, respectively.
By comparing ${\mathit{IRQ}_{t}}(r)$ with ${\mathit{ORQ}_{t}}(r)$, one can know whether more pixels move toward a certain region than pixels move away from it or vice versa. This is important when identifying possible crowd aggregation and crowd dispersion.
Definition 9 (Regional in/out indicator).
Regional in-pixel relative quantity divided by regional out-pixel relative quantity.
Let r denote a certain region, ${\mathit{IOI}_{t}}(r)$ denote regional in/out indicator of r at the time of ${I_{t}}$, then
${\mathit{IOI}_{t}}(r)>1$ means more pixels move toward r while ${\mathit{IOI}_{t}}(r)<1$ means more pixels move away from r.
According to Definition 5 and Eqs. (10)–(13), it can be concluded that $\frac{{\mathit{IQ}_{t}}(p)}{|{\mathit{ICM}_{t}}(p)|}\geqslant 1$ and $\frac{{\mathit{OQ}_{t}}(p)}{|{\mathit{OCM}_{t}}(p)|}\geqslant 1$. The equal sign in each inequality works when and only when pixels move in exactly the same direction. When motion directions become more symmetrical, value of the left side of each inequality becomes bigger. These kinds of useful properties shall keep invariant for regions thus help identify crowd behaviours.
Definition 10 (Regional in-pixel symmetry).
Regional in-pixel relative quantity of a certain region divided by magnitude of average vector in that region on ICM map.
Definition 11 (Regional out-pixel symmetry).
Regional out-pixel relative quantity of a certain region divided by magnitude of average vector in that region on OCM map.
Let r denote a certain region, ${\mathit{IS}_{t}}(r)$ and ${\mathit{OS}_{t}}(r)$ denote regional in-pixel symmetry and regional out-pixel symmetry of r at the time of ${I_{t}}$, respectively, then where n is position number in r.
Here we have ${\mathit{IS}_{t}}(r)\geqslant 1$ and ${\mathit{OS}_{t}}(r)\geqslant 1$ with the equal signs work when corresponding pixels move in exactly the same direction. The bigger ${\mathit{IS}_{t}}(r)$ or ${\mathit{OS}_{t}}(r)$ is, the more symmetrically the corresponding pixels move.
3.5 Identifying Crowd Behaviours
Methods proposed in this paper apply to identifying crowd behaviours from videos captured by stationary camera and with foreground mainly consisting of pedestrians. Videos captured by Closed Circuit Television (CCTV) in public places normally have these characteristics.
As described in Section 3.2, crowd aggregation and crowd dispersion are good indicators of abnormal or urgent events. When trying to identify these behaviours, lower limits of region size and regional motion intensity and thresholds for pixel quantity and motion direction should be properly determined according to specific purposes in different applications. One proper way to determine these parameters, which we adopt in our experiments, is to perform statistical analysis of videos which contain crowd aggregation or crowd dispersion, especially for the same scene.
We may have different types of regions of interest. Sometimes only several certain regions are of interest, other times the whole scene needs to be monitored. For the first case, indicators of Definitions 6–11 can be computed only for certain regions; for the second case, a sliding window should be moved through each position which is treated as the centre of a region. There are basically no restrictions on region shape, though normally self-symmetric regions should be used, e.g. squares, rectangles, circles, etc. Since the first case is just a special case of the second and much easier, we will just discuss the second case.
Square region will be used and its centre will represent the region. Let r denote a certain square region, c denote the centre position of r, then we have $M{I_{t}}(c)=M{I_{t}}(r)$, ${\mathit{IRQ}_{t}}(c)={\mathit{IRQ}_{t}}(r)$, ${\mathit{ORQ}_{t}}(c)={\mathit{ORQ}_{t}}(r)$, ${\mathit{IOI}_{t}}(c)={\mathit{IOI}_{t}}(r)$, ${\mathit{IS}_{t}}(c)={\mathit{IS}_{t}}(r)$, ${\mathit{OS}_{t}}(c)={\mathit{OS}_{t}}(r)$. Thus $M{I_{t}},{\mathit{IRQ}_{t}},{\mathit{ORQ}_{t}},{\mathit{IOI}_{t}},{\mathit{IS}_{t}},{\mathit{OS}_{t}}$ can be seen as maps and are called regional motion intensity map (MI map), regional in-pixel relative quantity map (IRQ map), regional out-pixel relative quantity map (ORQ map), regional in/out indicator map (IOI map), regional in-pixel symmetry map (IS map) and regional out-pixel symmetry map (OS map), respectively. Regional versions of ICM map and OCM map, called regional in-pixel comprehensive motion map (RICM map) and regional out-pixel comprehensive motion map (ROCM map), respectively, can also be created to show how symmetrically pixels move toward and away from a region. Let ${\mathit{RICM}_{t}}$ and ${\mathit{ROCM}_{t}}$ denote RICM map and ROCM map, respectively, then ${\mathit{RICM}_{t}}(c)={\mathit{RICM}_{t}}(r)=\frac{1}{n}{\textstyle\sum _{p\in r}}{\mathit{ICM}_{t}}(p)$, ${\mathit{ROCM}_{t}}(c)={\mathit{ROCM}_{t}}(r)=\frac{1}{n}{\textstyle\sum _{p\in r}}OC{M_{t}}(p)$, where n is position number in r.
3.5.1 Identification of Crowd Aggregation
According to Definition 1 and the three rules, crowd aggregation is identified in region r if $M{I_{t}}(r),{\mathit{IRQ}_{t}}(r),{\mathit{IOI}_{t}}(r)$ and ${\mathit{IS}_{t}}(r)$ meet thresholds. Let ${t_{11}}$ denote threshold for MI map, ${t_{12}}$ denote threshold for IRQ map, ${t_{13}}$ denote threshold for IOI map, ${t_{14}}$ denote threshold for IS map when identifying crowd aggregation, then if the following conditions are met, one can conclude that crowd aggregation is going to happen in region r at the time of ${I_{t}}$.
Here ${t_{13}}>1$ and ${t_{14}}>1$.
3.5.2 Identification of Crowd Dispersion
According to Definition 2 and the three rules, crowd dispersion is identified in region r if $M{I_{t}}(r),{\mathit{ORQ}_{t}}(r),{\mathit{IOI}_{t}}(r)$ and ${\mathit{OS}_{t}}(r)$ meet thresholds. Let ${t_{21}}$ denote threshold for MI map, ${t_{22}}$ denote threshold for ORQ map, ${t_{23}}$ denote threshold for IOI map, ${t_{24}}$ denote threshold for OS map when identifying crowd dispersion, then if the following conditions are met, one can conclude that crowd dispersion is going to happen in region r at the time of ${I_{t}}$.
Here $0<{t_{23}}<1$ and ${t_{24}}>1$.
4 Results and Discussion
The proposed methods are tested on some videos in Agoraset and several real world videos. Agoraset is a dataset dedicated to researchers working on crowd video analysis. It was described in Allain et al. (2012), Courty et al. (2014) and can also be found in https://www.sites.univ-rennes2.fr/costel/corpetti/agoraset/Site/Scenes.html. There are totally eight scenes in Agoraset, among which SCENE 5: Dispersion (Dispersion from a given point), SCENE 7: Sideway (Two flows are going in opposite directions) and SCENE 8: Crossing (Four groups of people are meeting in the middle of the scene) contain at least one of the two types of crowd behaviour and are therefore used for testing.
4.1 Explanations About the Experiments
In order to describe crowd motion precisely, especially to determine whether they move symmetrically or not, the window size for computing basic optical flow should be about or a little smaller than the size of a person on video. Except for SCENE 7, there are two types of view for videos in Agoraset: top view and perspective view. In top view video, size of a person almost doesn’t change during motion. In perspective view video, size of a person becomes bigger when that person moves closer to the camera. Therefore, window size for computing optical flow is determined according to the size of a person away from the lens for perspective view video.
Munsell colour system is referenced to display integral optical flow. Different colours mean different motion directions (Fig. 5). For example, when a pixel moves right, then it will be red in the colour image of integral optical flow. In the meantime, colour purity depends on magnitude of displacement vector, the bigger the purer.
Images transformed from other intermediate results will be selectively shown based on the type of crowd behaviour to be identified. Transformation methods for these results are listed as follows:
Finally, masks of different colours are mixed with original video to show certain crowd behaviours are identified. Green and blue are used for crowd aggregation and crowd dispersion, respectively. We also use red mask to indicate simple directional motion in Section 4.4. Note that only centre position of a region will be marked when certain crowd behaviour is identified in that region. In top view of SCENE 8 ($512\times 512$, 25 fps), four group of people are meeting in the middle of the scene. Interpolative motion path is used for motion analysis. When identifying crowd aggregation, it is important to know that motion intensity inside the aggregation region is probably small. $itv=20$ is frame interval parameter for computing integral optical flow, size of square region used to identify crowd behaviour is $101\times 101$. ${t_{11}}=10$, ${t_{12}}=3.0$, ${t_{13}}=1.5$, ${t_{14}}=4$ are thresholds for MI map, IRQ map, IOI map, IS map, respectively. Here ${t_{13}}=1.5$ means number of pixels moving toward a candidate region should be relatively at least 1.5 times of number of pixels moving away from the region.
-
(1) IQ map, OQ map, MI map, IRQ map, ORQ map, IOI map, IS map and OS map are transformed into grey images.
-
(2) ICM map, OCM map, RICM map and ROCM map are transformed into colour images in the same way as integral optical flow is transformed. Lighter colours mean pixels move more symmetrically or less pixels are moving.
-
(3) MI map, IRQ map, ORQ map, IOI map, IS map and OS map are segmented using thresholds and shown as binary images with white indicating specific thresholds are met.
4.2 Crowd Aggregation
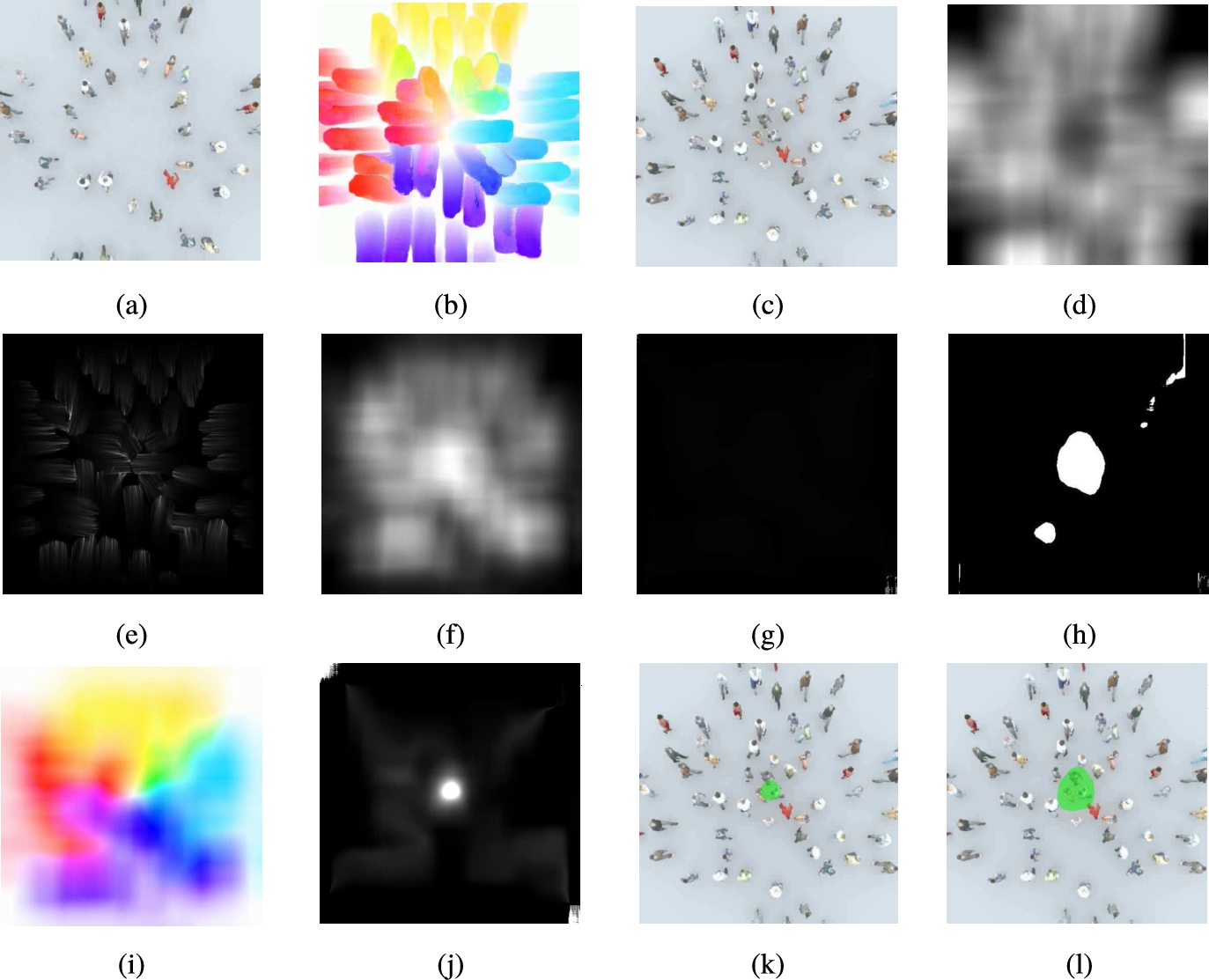
Fig. 6
Experimental results of crowd aggregation identification using interpolative motion path (top view of SCENE 8). (a) ${I_{t}}$; (b) colour image of ${\mathit{IOF}_{t}^{20}}$; (c) ${I_{t+20}}$; (d) grey image of $M{I_{t}}$; (e) grey image of ${\mathit{IQ}_{t}}$; (f) grey image of ${\mathit{IRQ}_{t}}$; (g) grey image of ${\mathit{IOI}_{t}}$; (h) segmentation result of ${\mathit{IOI}_{t}}$; (i) colour image of ${\mathit{RICM}_{t}}$; (j) grey image of ${\mathit{IS}_{t}}$; (k) crowd aggregation identification result of ${I_{t}}$; (l) crowd aggregation identification result of ${I_{t}}$ with only ${t_{14}}$ changed to 2.
As shown in Fig. 6(a) and 6(c), the crowd starts to aggregate at the centre of the scene. The integral optical flow in Fig. 6(b) clearly shows their motion trend. Because interpolative motion path is used, the slender greyish-white trails in Fig. 6(e) mean values are very big at corresponding positions on IQ map. There are some noises at the lower right corner of IOI map causing most of Fig. 6(g) is black, but segmentation result in Fig. 6(h) shows there are more pixels moving toward than moving away from around the centre and some other places. Figure 6(i) shows pixels move symmetrically around the centre with light colours. Figure 6(j) shows their symmetrical motion directions much clearer. Final result is shown in Fig. 6(k) with green mask at the centre of regions in which crowd aggregation is happening. In order to get better visual result, the result is mixed with ${I_{t+20}}$ instead of ${I_{t}}$. When restriction on the symmetry of motion directions is relaxed, more regions are identified as shown in Fig. 6(l).
Fig. 7
Experimental results of crowd aggregation identification using interpolative motion path (perspective view of SCENE 8). (a) ${I_{t}}$; (b) ${I_{t+20}}$; (c) crowd aggregation identification result of ${I_{t}}$; (d) crowd aggregation identification result of ${I_{t}}$ with only ${t_{14}}$ changed to 2.
${\mathit{IS}_{t}}$ which stands for symmetry of motion directions is a decisive factor in this example. This doesn’t mean motion intensity or pixel quantity can be ignored. For perspective view of SCENE 8 ($512\times 512$, 25 fps, angle of view: 30), same parameters are used and results are shown in Fig. 7.
Fig. 8
Experimental results of crowd aggregation identification using interpolative motion path (SCENE 7). (a) ${I_{t}}$; (b) ${I_{t+20}}$; (c) crowd aggregation identification result of ${I_{t}}$; (d) crowd aggregation identification result of ${I_{t}}$ with only ${t_{14}}$ changed to 2.
In SCENE 7 ($640\times 480$, 30 fps, angle of view: 54.43), two group of pedestrians walk rapidly toward each other in two opposite directions. With the same parameters used above, results are shown in Fig. 8.
4.3 Crowd Dispersion
In top view of SCENE 5 ($640\times 480$, 30 fps), the crowd disperse from the lower right part of a square with walls. As the crowd disperse, motion intensity inside the corresponding region reduces, so later dispersion won’t be able to be detected unless increasing region size or reducing threshold for MI map. Interpolative motion path is used for motion analysis. $itv=20$ is frame interval parameter for computing integral optical flow, size of square region used to identify crowd behaviour is $101\times 101$. ${t_{21}}=10$, ${t_{22}}=2.0$, ${t_{23}}=0.8$, ${t_{24}}=4$ are thresholds for MI map, ORQ map, IOI map, OS map, respectively.
Fig. 9
Experimental results of crowd dispersion identification using interpolative motion path (top view of SCENE 5). (a) ${I_{t}}$; (b) colour image of ${\mathit{IOF}_{t}^{20}}$; (c) ${I_{t+20}}$; (d) grey image of $M{I_{t}}$; (e) grey image of ${\mathit{OQ}_{t}}$; (f) grey image of ${\mathit{ORQ}_{t}}$; (g) grey image of ${\mathit{IOI}_{t}}$; (h) segmentation result of ${\mathit{IOI}_{t}}$; (i) colour image of ${\mathit{ROCM}_{t}}$; (j) grey image of ${\mathit{OS}_{t}}$; (k) crowd dispersion identification result of ${I_{t}}$; (l) crowd dispersion identification result of ${I_{t}}$ with only ${t_{24}}$ changed to 2.
As shown in Fig. 9(a) and 9(c), the crowd starts to disperse from the lower right part of the square. The integral optical flow in Fig. 9(b) clearly shows their motion trend. Because the dispersion happens near the bottom wall and pedestrians are stopped by the wall, thus symmetry of motion directions is affected, Fig. 9(j) shows the distortion. But combining with other segmentation results, this problem can be solved. Dispersion centre is clearly shown in Fig. 9(b), 9(e), 9(i). Final result is shown in Fig. 9(k) with blue mask at the centre of regions in which crowd dispersion is happening. Figure 9(l) shows result with symmetry restriction relaxed.
For perspective view of SCENE 5 ($640\times 480$, 30 fps, angle of view: 54.43), same parameters are used as above and results are shown in Fig. 10.
Fig. 10
Experimental results of crowd dispersion identification using interpolative motion path (perspective view of SCENE 5). (a) ${I_{t}}$; (b) ${I_{t+20}}$; (c) crowd dispersion identification result of ${I_{t}}$; (d) crowd dispersion identification result of ${I_{t}}$ with only ${t_{24}}$ changed to 2.
In SCENE 7, which is already used for crowd aggregation identification experiment, two groups of pedestrians continue their motion after aggregation, thus causing crowd dispersion later. Same parameters are used as above. As shown in Fig. 11(a) and 11(b), the crowd is blocked on the right side, therefore there is a much smaller area marked on the right side in identification result shown in Fig. 11(c). When restriction on symmetry of motion directions is relaxed, area around the centre where more pedestrians move upside than those move downside is marked as shown in Fig. 11(d).
4.4 Crowd Behaviour Identification on Real World Videos
We also test our method on real world videos downloaded from YouTube. Figure 12(a) shows that a team of South Korean police move fast in one direction to help the front police in a riot control exercise. Figure 12(b) shows the police and the protesters approach each other with the police occupying the position first. Figure 12(c) shows that the police who are confronting with the protesters start to extend their formation and the protesters start to retreat. The video shakes thus background motion is a little intensive, but with proper thresholds we still manage to get good results. Figure 12(d) shows that prisoners move fast in a Mexican prison riot, the blue area shows some of the prisoners start to disperse to dodge something thrown toward them (a white object in the red circle) from the dark area between the two buildings. Figure 12(e) shows many Marathon runners run along a U-shape street.
4.5 Comparison with State-of-the-Art Methods
To the best of our knowledge, most of the non-training works published only detected abnormal behaviours or events, they didn’t identify specific crowd behaviours. Solmaz et al. (2012) proposed a method to identify five crowd behaviours including crowd dispersion and aggregation. Therefore our method is to be compared with this method.
It is important to notice that definitions in Solmaz et al. (2012) are not the same as ours, although some of those definitions are similar to ours to some extent. In the comparison, we take blocking and bottleneck in Solmaz et al. (2012) as crowd aggregation, and fountainhead as crowd dispersion. To estimate performance, we first generate ground truth manually, then count total number, correctly identified number, missed number and misidentified number of corresponding structure defined in Section 3.2 of each crowd behaviour. Table 1 shows the results.
As shown in Table 1, our method outperforms method in Solmaz et al. (2012). However, we have to point out that the definitions of crowd behaviour used here are in favour of our method. As a matter of fact, generally accepted definitions of crowd behaviour are not present yet, these can only be obtained through more researchers’ work in computer vision and related fields. We believe that, for abnormal or urgent event detection, it is important not to miss identification of related crowd behaviours. In our experiment, we choose thresholds in order to achieve this goal. The relatively high misidentified number is an apparent side effect of our choice.
Table 1
Crowd behaviour identification results.
| Crowd behaviour | Total | Proposed method | (Solmaz et al., 2012) | ||||
| Correctly identified | Missed | Misidentified | Correctly identified | Missed | Misidentified | ||
| Crowd aggregation | 27 | 25 | 2 | 7 | 20 | 7 | 6 |
| Crowd dispersion | 37 | 34 | 3 | 11 | 27 | 10 | 9 |
4.6 Discussion
-
(1) Although we can get good results for jittering videos through changing thresholds in some cases, but that is not universal, thus our method should be applied to stable videos generally. In different applications thresholds for motion intensity, quantity and motion direction of pixels should be set depending on the scene and specific purposes.
-
(2) Frame interval parameter for computing integral optical flow affects determination of threshold for motion intensity. With bigger frame interval parameter, more intensive motion field will be obtained, thus threshold for motion intensity should be bigger for the same situation monitoring application. Let ${t_{s}}$ denote threshold for motion intensity, e.g. ${t_{11}}$ in identification of crowd aggregation and ${t_{21}}$ in identification of crowd dispersion, $\mathit{itv}$ denote frame interval parameter, then when determining ${t_{s}}$ for the same task the following relation should hold: where α is a constant for the specific task.
-
(3) Region size is another parameter that affects determination of threshold. If number of people in the moving crowd is important regardless of how large area they occupy, then if bigger region is used, threshold for pixel quantity should be smaller. Let ${t_{q}}$ denote threshold for pixel quantity, e.g. ${t_{12}}$ in identification of crowd aggregation and ${t_{22}}$ in identification of crowd dispersion, s denote area of region that is used, then when determining ${t_{q}}$ for the same task the following relation should hold: where β is a constant for the specific task. If crowd density is important, then ${t_{q}}$ stays the same when region size is changed.
5 Conclusion
In urgent event monitoring or analysing applications, it is important to detect abnormal or urgent events as soon as possible. People react rapidly to these events happening around them, therefore certain types of crowd behaviours are reliable indicators for urgent events. In this paper, we have defined two types of crowd behaviours: crowd aggregation and crowd dispersion and presented a method to identify these behaviours at their early stage. Our method mainly consists of the following steps: integral optical flow computation, position-level motion analysis, region-level motion analysis and threshold segmentation. The accumulative effect of integral optical flow is taken advantage of to separate background and foreground and obtain intensive motion regions which are usually of interest. Pixel motion intensity, quantity and motion direction in regions are together used to describe motions and identify crowd behaviours. The effectiveness of our method has been demonstrated and confirmed by experimental results.
