1 Introduction
Real life problems are involved in multiple factors with complex relationships. To deal with these problems, we should apply a realistic point of view which considers the facts that problems need multi-valued assessments instead of binary ones. Education has been playing an important role in governmental and personal dimensions and a fair evaluation of students has traditionally been something of an Achilles heel for the education systems. In recent years, this has led governments to improve education systems and encouraged researchers to explore new educational tools and methods. For example, No Child Left Behind (NCLB) was an U.S. Congress Act to expand public education, which activated many researchers to design decision making frameworks and develop practical education models (Mandinach
et al.,
2006; Wohlstetter
et al.,
2001; Wayman,
2005). Later, the rise of social networks led American researchers to apply social network data and data mining in education (Romero and Ventura,
2010; Daly,
2012; Romero and Ventura,
2013).
In the absence of government endorsement or support, academicians have also developed different methods to make valuable contribution toward improving evaluation in education. Using appropriate mathematical modelling and sophisticated methods of artificial intelligence, researchers have conducted many researches from student project evaluation using fuzzy TOPSIS (Pejic
et al.,
2013) to measuring the real knowledge of examinees through calculating of Amo-Salas
et al. (
2014) and automated essay evaluation (Zupanc and Bosnic,
2015).
Evaluation methods in education are mainly classified into two main categories: evaluation of lecturers by students and evaluation of students by lecturers. To our knowledge, the latter one is mostly focused and frequently studied by researchers. Among infrequent lecturer evaluation studies, Hristova and Sotirova (
2008) used generalized net model to algorithmization of multifactor method to assess teaching quality at universities. Chu (
1990) applied a multi-criteria decision making model to grade teachers. The potential of fuzzy logic techniques to evaluate academic performance (Kakani
et al.,
2016) drew some researchers to develop fuzzy methods for educational evaluation. Considering the framework of Chu’s (
1990) study, Othman (
2016) established fuzzy rules in the form of If-Then to discriminate lecturers of 5 courses by 35 respondent students. Liu (
2015) applied multi attribute decision making method using intuitionistic fuzzy information to measure the effectiveness of teaching in foreign language courses.
To better the evaluation of students by lecturers, Hameed
et al. (
2016) proposed to exploit fuzzy sets and replace the sharp criteria of traditional evaluation of students with fuzzy ones. Sakthivel
et al. (
2013) applied fuzzy numbers and fuzzy rules using Mamdani fuzzy decision technique to infer the performance of students. Johanyak and Kovacs (
2014) used fuzzy arithmetic operations to evaluate student assignments and developed a software tool to support the user. To evaluate the English academic writing, Chai
et al. (
2015) developed a peer assessment method which establishes a combination of a Per-C and a fuzzy ranking algorithm that uses fuzzy preference relations. Identifying 20 evaluators/experts from different schools and using 5 linguistic expressions including very poor, poor, average, good, and very good, Salunkhe
et al. (
2016) evaluated the performance of 237 secondary school students using fuzzy classification based on fuzzy similarity relation. Li
et al. (
2015) applied preference-based fuzzy numbers and TOPSIS method to assess the development levels of higher vocational education.
Many evaluation methods for classical detailed exam questions have been developed using fuzzy logic. Chang and Sun (
1993) proposed a fuzzy assessment method of junior high school students. Chiang and Lin (
1994) applied fuzzy theory to teaching assessment. Biswas (
1995) developed fuzzy evaluation method (fem) and generalized fuzzy evaluation method (gfem). Law (
1996) focused on the precision, i.e. correctness and falseness, of the scores. This method presented a systematic approach to aggregate scores and produced linguistic grading.
Chen and Lee (
1999) extended Biswas’s (
1995) method and proposed two new methods. These methods used a fuzzy model to calculate each question’s score by linguistic terms, then evaluator achieves a final score for the student. They claimed that their methods were faster and fairer than Biswas’s. Ma and Zhou (
2000) proposed a student-centered method to assess students themselves. Students and lecturers should determine a couple of criteria through brainstorming, and then weigh the criteria. Finally, this approach forms an evaluation matrix for each student. Based on the eigenvectors and using fuzzy envelopes, they allocate a letter grade for each student.
Wang and Chen (
2006) extended Biswas’s (
1995) and Chen and Lee’s (
1999) methods. The authors used fuzzy numbers as the degrees of confidence of the evaluator. Then,
α-cuts of these fuzzy evaluations and arithmetic operations between
α-cuts evaluate the answerscripts of students. Wang and Chen (
2008) presented a new evaluation method using type-2 fuzzy sets. They considered the degree of optimism of evaluator and provided a more flexible and intelligent method. Ibrahim and Kim (
2009) also considered importance, complexity, and difficulty to evaluate the answerscripts of the students. They developed a fuzzy controller by Mamdani’s max-min inference mechanism and center of gravity defuzzification method to assist the evaluation process. Chen and Wang (
2009) applied interval-valued fuzzy sets to evaluate the answerscripts. These intervals are between zero and one and the similarity of interval-valued fuzzy marks and a standard interval-valued fuzzy sets are used for evaluation of students. This method provides more stable evaluations than Biswas’s (
1995) method.
Fuzzy rules and fuzzy reasoning methods are widely focused by researchers like Darwish (
2016) who applied fuzzy rules to evaluate student performance. Baba
et al. (
2015) developed a rule-based assessment system based on a fuzzy group decision support system (FGDSS). Using fuzzy numbers and fuzzy rules, Kakani
et al. (
2016) developed an evaluation method calculating the degree of confidence and the degree of satisfaction of the evaluator which measure the confidence of examiner in assigning the marks and the satisfaction of examiner by given answers. Akbay
et al. (
2016) created a fuzzy rules-based system to maximize the achievement of secondary school students through finding the optimal sleeping hours and study time. Bai and Chen (
2008a) proposed a new evaluation method using three criteria including difficulty, importance, and complexity, to develop fuzzy rules and fuzzy reasoning system. Later, Bai and Chen (
2008b) developed a fuzzy rule-based method which automatically constructs grade membership functions. Their method regarded three types of grade membership functions, namely lenient-type grades, normal-type grades, and strict-type grades for students’ evaluation. Chen and Li (
2011) extended Ibrahim and Kim’s (
2009) method by considering accuracy, time rate (i.e. time consumed by a student to solve a question divided by a predefined maximum time), difficulty, complexity, answer-cost, and importance as fuzzy rules of their models.
The extensions of fuzzy sets and fuzzy prediction techniques are also considered by academicians (Rodriguez
et al.,
2012,
2014; Xu,
2007; Herrera
et al.,
2009; Chiclana
et al.,
2001; Zeng
et al.,
2016; Cabrerizo
et al.,
2015; Urena
et al.,
2015; Yu
et al.,
2017; Morente-Molinera
et al.,
2015). In order to increase the quality and consistency of assessment of students’ answer scripts, Hameed
et al. (
2016) applied interval type-2 fuzzy sets and fuzzy inference system to achieve higher transparency. Parmar and Kumbharana (
2015) developed a text pattern recognition method to automatically evaluate multiple choice question (MCQ) with one word answer or fill in blank type question. To predict the performance of students, Arora and Saini (
2016) implemented a user-friendly personalized performance monitoring system based on a hybrid fuzzy neural network model using 760 samples. Considering two grouping criteria: (1) the understanding levels of the students and (2) the interest levels of the students, both with respect of the topics of a given course, Yannibelli
et al. (
2016) proposed a steady-state evolutionary algorithm for building well-balanced teams and enhance students’ performance.
Measuring the knowledge of examinees in MCQ exams is a challenging problem, which affects the evaluation process during the preparation of questions and choices by examiner, selection of the correct choice by examinee, and the scoring by examiner. Classical MCQs cannot generally detect the differences between the knowledge of examinees accurately, e.g. an examinee with medium level of knowledge and an examinee with less than medium level of knowledge can be evaluated as equal examinees through classical MCQs. These tests provide a strict structure for examinees to select one of the choices. This choice would be the correct answer and other choices are considered as false answers. This structure of MCQs has been criticized for encouraging surface learning and unfair evaluation (Hameed,
2016). However, we believe that crisp structure of classical MCQs cannot evaluate the students properly, and fuzzy sets can improve this evaluation. Fuzzy sets have been recently applied to the evaluation of MCQs. Shahbazova and Kosheleva (
2014) proposed fuzzy multiple choice quizzes, in which a student explicitly describes his/her degree of confidence in each possible answer. However, the practicability of this fuzzy approach is low since it is based on logarithm and entropy calculations which require many parameters such as integration constants. Fahim and Dehghankar (
2014) proposed a fuzzy MCQ considering a degree of correctness for semi-correct choices to award partial knowledge of examinees. Rather than just selecting a particular choice, examinees are supposed to provide test-givers with the information on the reason why they think other choices are distractors. The idea of correctness degree provides fairer evaluation but writing further explanation on answer sheets complicates the evaluation process. Hameed (
2016) also developed a fuzzy MCQ evaluation system using linguistic variables, Gaussian membership functions with fixed mean and variable variance or standard deviation for fuzzification of inputs, and Mamdani’s fuzzy inference system. Although this system can automatically and fairly discriminate examinees, the complexity of fuzzifying inputs and running the Fuzzy Logic Toolbox of MATLAB complicates the usage of this system.
Our literature review shows that most of the fuzzy evaluation studies are focused on detailed examination rather than MCQs. Those rarely developed fuzzy MCQ provide poor performance or results mainly because of their complexity and impractical structure. In this study, we present a new evaluation method through MCQs to achieve more accurate and fairer evaluation which can be easily used by examiners. Here, we propose five approaches to measure the performance of examinees in multiple choice exams. Two main approaches are punishing approach (PA) and awarding approach (AA). The third one is a mixed approach (MA) which is the arithmetic mean of the AA and PA (Fahmi and Kahraman,
2015). Classical approach (CA) defuzzifies examinees’ answers and provides defuzzified evaluation. Finally, joint approach (JA) combines above-mentioned approaches and provides the terminal evaluation.
The rest of the paper is organized as follows. In Section
2, a brief background, required definitions of fuzzy sets, and our proposed approaches are presented. Section
3 is devoted to the application of the proposed fuzzy MCQ examination and the simulation of the proposed approaches. In Section
4, the results of the application are discussed. Lastly, the conclusion and future works are provided in Section
5.
2 Fuzzy Sets and Fuzzy Examination
Zadeh (
1965) proposed fuzzy sets and defined a membership degree for each member of a fuzzy set. This value is not restricted to be zero and one; however, values between zero and one are also considered as degrees of membership. Fuzzy logic enables us to judge fairly by providing values between zero and one as membership degrees of a particular set. Using degrees of membership afford fuzzy sets to deal with uncertainty in a proper manner. Examination involves the uncertainty of examiners and examinees. Fuzzy examination considers the uncertainty of examinees and examiners and evaluates examinees using fuzzy sets. In the following part, required definitions of fuzzy sets are presented.
Definition 1.
Cardinality of a fuzzy set
$\tilde{A}$ expressed as a sum of the values of the membership function of
$\tilde{A}$.
Definition 2.
α-cut of a fuzzy set
$\tilde{A}$ is given by
Definition
1 is used in all the proposed approaches to calculate their total scores, while Definition
2 is only used in the classical approach to defuzzify the evaluations.
There are two main structural differences between classical and proposed MCQs. First, during preparation of questions, examiner should assign an adequate degree of correctness for each choice of questions, i.e. each choice embeds a degree of correctness and the most correct choice accompanies the full score for the question. Second difference is that our proposed MCQ obliges examinees to assign a degree of reliability to all choices of a particular MCQ, where the summation of these reliability degrees must be equal to one. Two main fuzzy approaches, AA and PA, as well as MA, CA, and JA are presented below.
2.1 Awarding Approach
During preparation of questions, examiner should assign an adequate degree of correctness for each choice of the questions, i.e. each choice embeds a degree of correctness and the most correct choice accompanies the full score for the question. We call it “awarding” because the overall summation of the scores is mostly higher than overall summation of scores of classical approach. The degree of correctness of the choice with the highest degree of reliability is considered as the awarding score (AS) of the question. This approach is based on the fact that a student should not collect any score when he/she assigns equal reliability degrees to all choices of a question. If two or more choices are assigned equal reliability degrees by examinee, examinee will be awarded zero $\mathit{AS}$.
The main point in AA is how to find an appropriate degree of correctness for the choices. Examiners are aware about the prevalent mistakes of examinees and they generally consider examinees’ possible mistakes while designing questions. These possible mistakes could be the most regular mistakes of examinees such as logical, understanding, calculation error, and weak analysis of the question or choices.
In AA, we suggest to utilize the expertise of examiners in designing of MCQs. The basic assumption is that one choice is the most correct answer and the other choices include common mistakes of examinees. Examiner should specify a suitable degree of correctness for the choices according to the correctness of the answer and write them on the dotted lines. For example, consider following MCQ from the topics of Engineering Economics course.
In how many years will X accumulate to $3X$ with 8 percent interest rate, compounded monthly?
.....a) Less than 3 years
.....b) Around 70 years
.....c) 14 to 15 years
.....d) 13 to 14 years
The solution of this question is as follows:
As you see, Choice
d is the most correct choice and embeds the full score. However, other choices are prepared based on the most common mistakes of students. Choice
a considers the confusion between present worth factor
$(P/F)$ and sinking fund factor
$(A/F)$, and the semi-mistaken solution will be as follows:
Another examinee may confuse the nominal or effective interest rate (8 percent) and the coefficient of accumulated money (
3). This results the following semi-mistaken solution:
This answer is represented by Choice b. Though without calculation of effective interest rate, the answer would be 70.34, which Choice b implies as well.
An examinee may unintentionally forget to calculate the effective interest rate beforehand. In this case, he/she would do following calculations and select Choice
c as the most correct answer.
Choice c considers a regular mistaken solution, i.e. using the nominal interest rate instead of effective interest rate. The most correct solution must be found by using effective interest rate, but a misunderstanding or a calculation error can confuse examinee. While this solution is not completely correct, we believe that the examinees should be awarded for their semi-mistaken solution. Among aforementioned choices, d is the most correct answer. We assign a degree of correctness for Choices a, b, and c, which should be assigned by examiner.
In general, the maximum reliability degree assigned by the student is represented by Eq. (
1):
where
${r_{j}}$ is the reliability degree of choice
j and
n is the number of choices in each question.
Then the
$\mathit{AS}$ becomes
where
${t_{z}}$ is the degree of correctness of choice
z.
The total score
${\mathit{TS}_{A}}$ that a student will collect from all the questions based on AA is calculated by Eq. (
3):
where
k is the number of questions.
Consider the correctness degrees of the choices are as written on the upper right hand side of each choice. Imagine a student forgets to calculate effective interest rate and follows the second above-written solution. Then, he/she may assign following reliability degrees:
0.00
...... a) Less than 3 years 0.25
0.00
...... b) Around 70 years 0.25
0.90
...... c) 14 to 15 years 0.40
0.10
...... d) 13 to 14 years 1.00
Using Eqs. (
1) and (
2),
${r_{\max }}$ and
$\mathit{AS}$ of this examinee will be as follows:
2.2 Punishing Approach
After assignment of reliability degrees to each choice of the question by examinee, we consider them to find the punishing score (PS). The word “punishing” predicates PS’s lesser scores than the scores of classical approach. In this approach, the score of a particular question is calculated using the proposed formula of
$\mathit{PS}$ as follows:
where
n is the number of choices;
${\mathit{RTC}_{j}}$ is the reliability of the most correct choice
j; and
${\mathit{ROC}_{i}}$ stands for the reliabilities of other choices.
The total score of punishing approach (
${\mathit{TS}_{P}}$) that a student will collect from all the questions is calculated by Eq. (
5):
where
k is the number of questions.
For instance, consider before-mentioned MCQ.
0.00
...... a) Less than 3 years
0.00
...... b) Around 70 years
0.90
...... c) 14 to 15 years
0.10
...... d) 13 to 14 years
Based on the assigned reliability degrees, the
$\mathit{PS}$ will be as follows:
As you see, examinee’s doubt about the correctness of Choice
d and partially relying on Choice
c punished him/her by a dramatical reduction of
$\mathit{PS}$; however,
$\mathit{AS}$ equals the reliability degree of the most correct choice which is 0.4 in the question above. The formula of
$\mathit{PS}$ (Eq.
5) reaches the highest score when the most correct choice is assigned maximum reliability degree (equals one) and other choices are assigned zero reliability degree. Any other reliability assignment reduces the
$\mathit{PS}$ of the particular question. Therefore, it is obvious that the
$\mathit{PS}$ of a question is always equal or less than classical score.
2.3 Mixed Approach
MA is the arithmetic mean of
$\mathit{PS}$ and
$\mathit{AS}$. The outcome of MA is logically close to the result of classical multiple choice. Mixed score (MS) is as follows:
The total score
${\mathit{TS}_{M}}$ that a student will collect from all the questions based on MA is calculated by Eq. (
7):
where
k is the number of questions.
2.4 Classical Approach
This approach denotes to the classical MCQ tests. In our proposed test, examinee is supposed to assign a degree of reliability for each choice and it is not possible to select a single choice like common MCQs. Therefore, using Definition
2, we assume that the most reliable choice whose degree of reliability is greater than 0.5 is the correct answer, if the examination was a common MCQ test. Otherwise, the examinee gets no score from the particular question. In this regard, classical approach is indeed a defuzzification method which provides a crisp score (0 or 1) for each question and enables examiner to compare fuzzy scores with classical scores (CS). To obtain
$\mathit{AS}$, Eq. (
8) is used:
The total score
${\mathit{TS}_{C}}$ that a student will collect from all the questions based on classical approach is calculated by Eq. (
9):
where
k is the number of questions.
In the before-mentioned example, the maximum reliability degree, corresponding correctness degree and
$\mathit{AS}$ are
2.5 Joint Approach
Table 1
Students’ scores (out of 100).
| Student number |
${\mathit{TS}_{P}}$ |
${\mathit{TS}_{A}}$ |
${\mathit{TS}_{M}}$ |
${\mathit{TS}_{C}}$ |
${\mathit{TS}_{J}}$ |
| 1 |
49.786 |
62.308 |
56.047 |
46.154 |
44.919 |
| 2 |
27.584 |
46.154 |
36.869 |
23.077 |
25.708 |
| 3 |
62.846 |
80.000 |
71.423 |
76.923 |
60.310 |
| 4 |
63.161 |
68.462 |
65.811 |
61.538 |
60.261 |
| 5 |
51.792 |
61.538 |
56.665 |
53.846 |
50.506 |
| 6 |
53.462 |
64.615 |
59.038 |
53.842 |
51.300 |
| 7 |
38.251 |
53.846 |
46.049 |
38.462 |
37.266 |
| 8 |
35.769 |
55.385 |
45.577 |
38.462 |
35.207 |
| 9 |
65.000 |
77.692 |
71.346 |
69.231 |
61.829 |
| 10 |
42.200 |
80.000 |
61.100 |
53.846 |
36.876 |
| 11 |
40.264 |
47.692 |
43.978 |
46.154 |
41.215 |
| 12 |
39.183 |
66.154 |
52.668 |
38.462 |
35.515 |
| 13 |
29.324 |
42.308 |
35.816 |
30.769 |
30.068 |
| 14 |
33.635 |
42.308 |
37.971 |
30.769 |
31.997 |
| 15 |
37.861 |
36.154 |
37.007 |
30.769 |
32.934 |
| 16 |
21.674 |
43.077 |
32.375 |
15.385 |
20.338 |
| 17 |
41.354 |
50.000 |
45.677 |
38.462 |
38.811 |
| 18 |
37.895 |
54.615 |
46.255 |
38.462 |
36.899 |
| 19 |
37.895 |
54.615 |
46.255 |
38.462 |
36.899 |
| 20 |
49.742 |
61.538 |
55.640 |
61.538 |
50.377 |
| 21 |
48.198 |
66.923 |
57.561 |
53.846 |
46.028 |
| 22 |
22.088 |
50.000 |
36.044 |
30.769 |
25.033 |
| 23 |
39.439 |
53.077 |
46.258 |
38.462 |
37.833 |
| 24 |
42.308 |
51.538 |
46.923 |
38.462 |
38.948 |
| 25 |
67.769 |
91.538 |
79.654 |
69.231 |
58.734 |
All above-mentioned approaches are involved in calculation of the joint score of examinees. The main shortcoming of classical MCQs is that examiner cannot find out whether the selected choice is selected intentionally or randomly. This approach enables the examiner to differentiate knowingly or randomly selection of the choices by considering the degree of sureness of the examinees during reliability assignment. Term A of Eq. (10) calculates the difference between ${\mathit{TS}_{P}}$, ${\mathit{TS}_{A}}$, ${\mathit{TS}_{M}}$, and ${\mathit{TS}_{C}}$. This difference represents the sureness of examinee in answering the questions, i.e. if an examinee is sure about his/her learnt knowledge, he/she will gain close scores in AA, PA, MA, and CA. In this case, the coefficient will be close to 1. Otherwise, if an examinee is not sure about his/her learnt knowledge, he/she will gain distinct scores, and accordingly the coefficient will be less than 1. Term B of Eq. (10) refers to the weighted mean of ${\mathit{TS}_{P}}$, ${\mathit{TS}_{A}}$, ${\mathit{TS}_{M}}$, and ${\mathit{TS}_{C}}$. The total score using joint approach (${\mathit{TS}_{J}}$) is as follows:
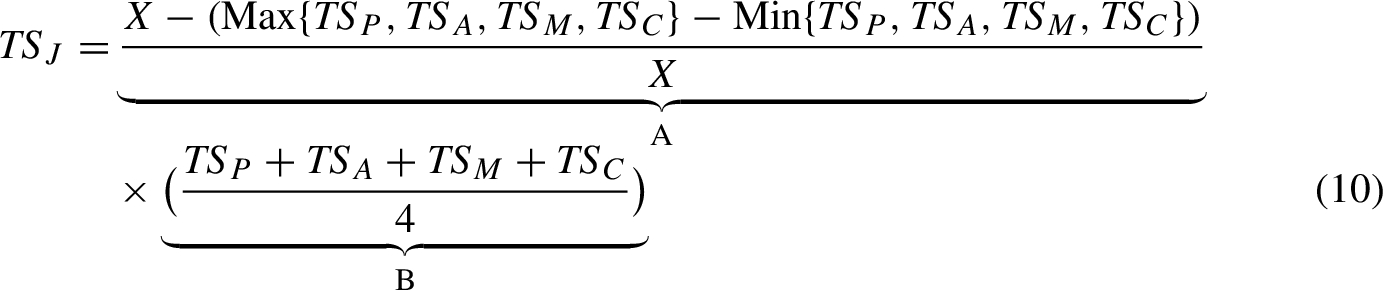
where X is the full score of the exam and which is equal to 100 in our study.
3 Application and Graphical Illustrations
We gave three exams in the Engineering Economics course of the BSc program in Industrial Engineering at the Istanbul Technical University. In the first exam, we applied AA and CA. Then, in the second and third exams, we added PA, MA, and JA. Here, the total scores of the exam and the corresponding ranking of students are presented in Tables
1 and
2, respectively. These tables distinctly represent the differences and similarities between the scores and rankings of different approaches.
Table 2
Students’ ranking.
| PA |
AA |
MA |
CA |
JA |
| 25 |
25 |
25 |
3 |
9 |
| 9 |
10 |
3 |
25 |
3 |
| 4 |
3 |
9 |
9 |
4 |
| 3 |
9 |
4 |
4 |
25 |
| 6 |
4 |
10 |
20 |
6 |
| 5 |
21 |
6 |
10 |
5 |
| 1 |
12 |
21 |
6 |
20 |
| 20 |
6 |
5 |
5 |
21 |
| 21 |
1 |
1 |
21 |
1 |
| 24 |
5 |
20 |
1 |
11 |
| 10 |
20 |
12 |
11 |
24 |
| 17 |
8 |
24 |
12 |
17 |
| 11 |
19 |
23 |
17 |
23 |
| 23 |
18 |
19 |
7 |
7 |
| 12 |
7 |
18 |
19 |
19 |
| 7 |
23 |
7 |
18 |
18 |
| 19 |
24 |
17 |
8 |
10 |
| 18 |
17 |
8 |
23 |
12 |
| 15 |
22 |
11 |
24 |
8 |
| 8 |
11 |
14 |
13 |
15 |
| 14 |
2 |
15 |
15 |
14 |
| 13 |
16 |
2 |
22 |
13 |
| 2 |
13 |
22 |
14 |
2 |
| 22 |
14 |
13 |
2 |
22 |
| 16 |
15 |
16 |
16 |
16 |
Using Eq. (
11), the Spearman rank correlation coefficients between any two approaches have been calculated and recorded in Table
3.
Table 3
Spearman rank correlation coefficients.
|
PA |
AA |
MA |
CA |
JA |
| PA |
1 |
0.096154 |
0.181538 |
−0.20462 |
−0.03385 |
| AA |
|
1 |
0.192308 |
−0.01615 |
0.106923 |
| MA |
|
|
1 |
−0.37615 |
0.148462 |
| CA |
|
|
|
1 |
−0.30769 |
| JA |
|
|
|
|
1 |
Table
3 indicates that there is not a strong correlation between the approaches, which means that each approach has a different point of view to the evaluation of examinees. The largest negative correlation exists between MA and CA while the largest positive correlation is between AA and MA. The least negative correlation is between AA and CA while the least positive correlation is between PA and AA.
We simulate the results of the proposed approaches using randomly generated numbers in MATLAB. First, the matrix of answer key is formed based on the answer key of the exam, i.e. the correctness degrees of the choices. Later, using the matrix of answer key and the uniformly distributed random numbers, we obtained random reliability degrees to form a matrix of answers. As shown in Fig.
1, by doing arithmetic operations on both answer key and answer matrices, random results of AA, PA, CA, MA, and JA in 100 iterations are attained.
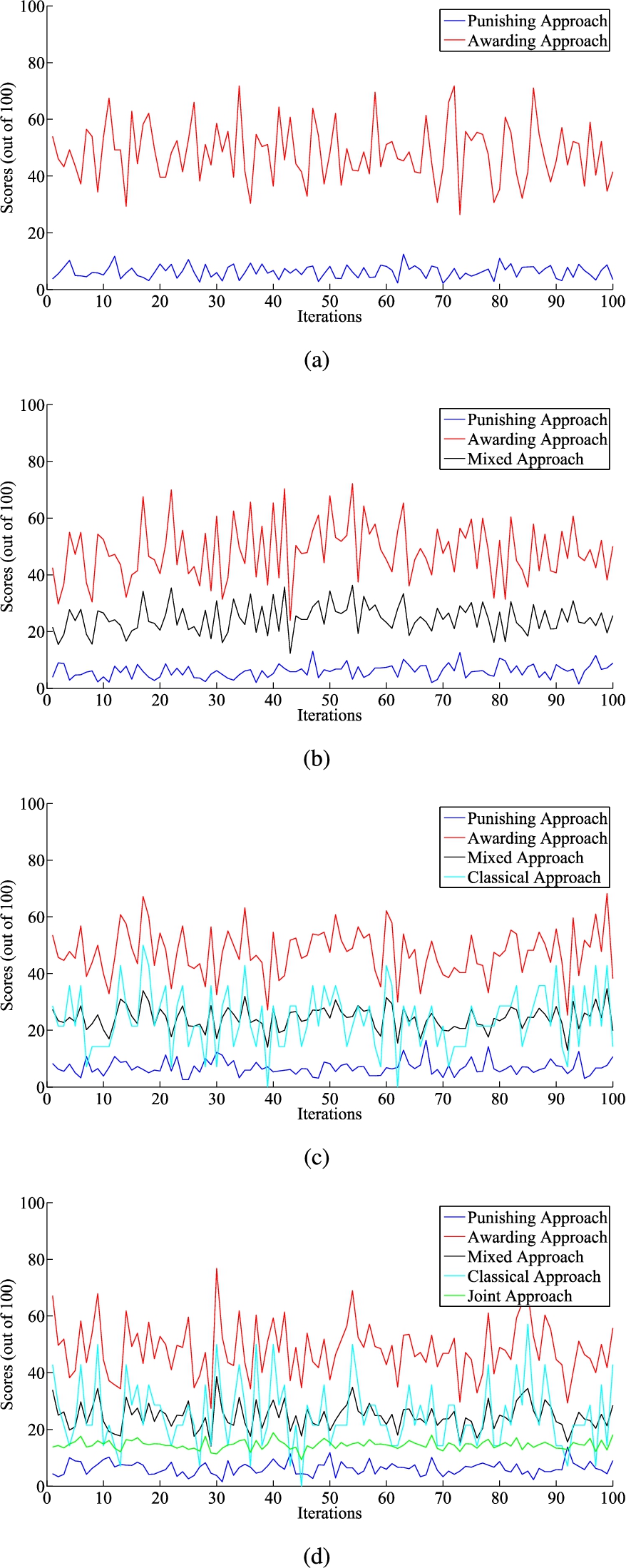
Fig. 1
Simulations of the exam results using random numbers.
In Fig.
1, the simulation of the exam’s results is depicted using randomly generated numbers. As shown in Fig.
1(a), blue graph or punishing results are lesser than red graph or awarding results in almost all the iterations. The simulation of AA, PA, and CA are presented in Fig.
1(b). Obviously, the red graph or the simulations of AA are greater than PA and CA, and black graph or mixed results are mostly between AA and PA. The simulations of AA, PA, MA, and CA are also gathered together in Fig.
1(c). The graphs of MA and CA, i.e. cyan and black graphs are overlapped in most of the iterations. This shows the close results of MA and CA. In Fig.
1(d), green colored graph or joint results are also added. This graph represents that although JA is a weighted arithmetic mean of AA, PA, MA, and CA, as JA simulation by random numbers is generally positioned somewhere at the middle of other approaches. Especially, it is generally lower than CA and higher than PA. This can imply that the JA is neither similar to CA nor like PA. It’s remarkable that JA does not behave like CA, and is able to punish examinees who randomly assign the reliability degrees for the choices.
4 Discussion
Table 4
LSD posthoc test.
| Approach (I) |
Approach (J) |
Mean difference (I–J) |
Standard error |
Significance level |
95% confidence interval |
| Lower bound |
Upper bound |
| 1 |
2 |
−15.32228∗
|
3.71925 |
0.000 |
−22.6861 |
−7.9584 |
|
3 |
−7.66108${^{\ast }}$
|
3.71925 |
0.042 |
−15.0249 |
−0.2972 |
|
4 |
−1.47628 |
3.71925 |
0.692 |
−8.8401 |
5.8876 |
|
5 |
2.10676 |
3.71925 |
0.572 |
−5.2571 |
9.4706 |
| 2 |
3 |
7.66120∗
|
3.71925 |
0.042 |
0.2973 |
15.0251 |
|
4 |
13.84600∗
|
3.71925 |
0.000 |
6.4821 |
21.2099 |
|
5 |
17.42904∗
|
3.71925 |
0.000 |
10.0652 |
24.7929 |
| 3 |
4 |
6.18480 |
3.71925 |
0.099 |
−1.1791 |
13.5487 |
|
5 |
9.76784* |
3.71925 |
0.010 |
2.4040 |
17.1317 |
| 4 |
5 |
3.58304 |
3.71925 |
0.337 |
−3.7808 |
10.9469 |
We applied SPSS software to compare the total scores of different approaches. Statistical analyses are used to check if there is a significant difference among the total scores of punishing, awarding, mixed, classical, and joint approaches. Analysis below are the outputs of the analysis of variance (ANOVA) of the scores, where the assumptions of ANOVA are satisfied in the analysis. In order to obtain the differences between each pair of approaches, LSD post-hoc tests are applied to the one-way ANOVA. Table
4 presents the multiple comparisons of the results of post-hoc tests. In Table
4, I and J represent the numbers of the approaches, which 1, 2, 3, 4, and 5 represent
${\mathit{TS}_{P}}$,
${\mathit{TS}_{A}}$,
${\mathit{TS}_{M}}$,
${\mathit{TS}_{C}}$, and
${\mathit{TS}_{J}}$ respectively.
The multiple comparisons demonstrate significant difference between all the scores of the five approaches, except the differences between PA and CA ($p=0.692$), PA and JA ($p=0.572$), MA and CA ($p=0.099$), and CA and JA ($p=0.337$). Hence, the approaches of exception pairs have equal means. PA and CA have close total scores because a large number of students in the exam assigned equal reliability degree for each choice, e.g. 0.25 for four choices. This decreased the ${\mathit{TS}_{C}}$ of the students and approached the results of CA and PA. Additionally, the reason of equal means of PA and JA is that examinees who randomly assign the reliability degrees decreased the difference between ${\mathit{TS}_{P}}$ and ${\mathit{TS}_{J}}$. The results of other pairs of approaches, i.e. MA and CA, as well as CA and JA can be compared similarly.
The scatter plot of
${\mathit{TS}_{A}}$,
${\mathit{TS}_{P}}$,
${\mathit{TS}_{M}}$,
${\mathit{TS}_{C}}$, and
${\mathit{TS}_{J}}$ provides a deep insight into the total scores of students which is shown in Fig.
2. These total scores show that
${\mathit{TS}_{A}}$ of examinees is almost higher than the total scores of other approaches, and
${\mathit{TS}_{P}}$ is lower than the total scores of other approaches.
In Fig.
2, some students like number 4, 6, 11, and 15 have close scores with variances equal to or less than 10 points fluctuating between 60 and 70, 50 and 70, 40 and 50, and 30 and 40, respectively. These results imply that although they are positioned in different levels of knowledge, close scores of each of them uncover their similar sureness about their knowledge and assigned reliability degrees. However, Students number 10, 12, 22, and 25 have gained distinct scores in different approaches fluctuating by at least 25 points which are between 30 and 80, 30 and 70, 20 and 50, and 55 to 95.
The result comparison between Student 6 and Student 10 represents that Students 6 has greater joint score than Students 10, although their classical scores are almost equal. The compact set of scores of Student 6 shows that (s)he is neither unnecessarily awarded by AA nor dramatically punished by PA. But distinct scores of Student 10 reveals that (s)he is neither gratuitously awarded by AA nor drastically punished by PA. This means that Student 6 is surer on her/his knowledge in comparison with Student 10.
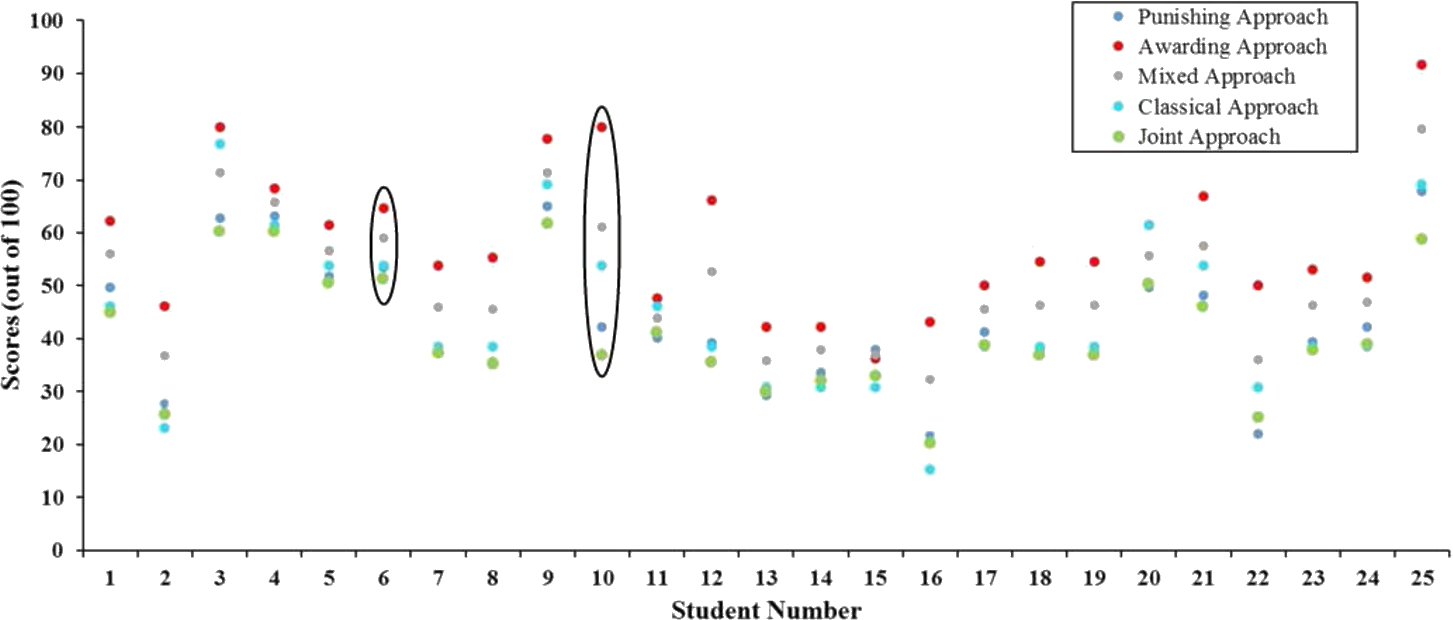
Fig. 2
Scatter plot of students’ scores.
According to Fig.
2, we can state whoever achieves high total scores is knowledgeable, however, sureness is a different criterion. Knowledgeable examinees do not necessarily achieve close total scores in the five approaches, and examinees are not necessarily knowledgeable and sure simultaneously. Some examinees are sure about their knowledge and they are not trapped in the random assignment of reliability degrees for the choices. On the other hand, some examinees are not sure about their knowledge and assign reliability degrees for the choices in an unsure way. PA catches this type of examinees and leads to a low score in PA, however, AA assigns a high score for these examinees. Regardless of their level of knowledge, they are not sure about their knowledge. Finally, JA considers the knowledge and sureness of examinees at the same time. This approach can reveal any unsure assignment of reliability degree which might be considered as fully correct answer in classical MCQ tests. Consequently, JA is authorized to punish any unsureness of examinee in their choice evaluation process.
If students were to be ranked based on CA, Student 10 would be superior to Student 6 with a tiny margin. However, our proposed approaches, specifically JA which aggregates the scores, uncover the real knowledge of students. Table
2 shows the ranking difference between CA and JA in details. While Student 6 is the 5th and Student 10 is 17th in the ranking of JA, they are respectively 6th and 7th in the ranking of CA. Whilst CA is obviously incapable of evaluating properly, proposed approaches, particularly JA, provide fairer scores and ranking.
5 Conclusion
In this study, we challenge the fairness of classical MCQs and propose a modified structure for MCQs with novel evaluation method to find fairer results and ranking of students. Proposed method is based on fuzzy logic and consists of five approaches, namely punishing, awarding, mixed, classical, and joint. These approaches are applied to evaluate students through MCQs. Two primary approaches, AA and PA, could perfectly deal with the uncertainty embedded in the examinees’ evaluation of the choices. AA and PA regard the uncertainty of examinees and examiners to properly score the examinees, and then fairly rank them. Close AA, PA, MA, and CA results also represent the sureness of the examinee about their knowledge. While classical MCQs cannot perceive that the questions are answered surely, the proposed JA, which is a combination of other approaches, can provide an intelligent scoring method and reveal both knowledge and sureness of examinees. Accordingly, the ranking of students using this approach is fairer than CA, which can overcome the most important shortcoming of the classical MCQs, i.e. the random selection of the choices.
The main drawback of our proposed evaluation method is that it forces examinees to assign reliability degree which can take more period of their time during exam. It can also confuse examinees how to deal with the new structure of MCQs. So that examinees should be clearly informed about the structure of our MCQs. Despite new evaluation methods like Shahbazova and Kosheleva (
2014) or Hameed
et al.’s (
2016) which consist complex mathematics including logarithmic operations and interval type-2 fuzzy sets, the preparation and scoring of the proposed MCQs can be conducted easily and quickly. In addition, although Fahim and Dehghankar’s (
2014) study is logically similar to our proposed method, the time consuming process of answering and scoring of their method is eliminated in the proposed method.
These intelligent approaches do not equalize the examinees’ knowledge like crisp MCQs. They can improve the quality of knowledge measurement considering sureness of examinees in the examinations. Consequently, the results and ranking of examinees by using our proposed five approaches are more precise and fairer than classical MCQs. This method not only can be used by lecturers and teachers to accurately evaluate their students, but also can be applied by large institutes or organizations to fairly assess their examinees. This can be conducted by computerizing the proposed method by creating a graphical user interface and analysis tools. Future studies can focus on categorization of questions based on the examiner’s evaluation criteria, and by weighing criteria to evaluate the examinees. As future work, extensions of fuzzy sets such as type-2 fuzzy sets, intuitionistic fuzzy sets, or hesitant fuzzy sets can be investigated to check against our current baseline evaluations.

