In this paper, we developed two new adaptive IABC versions. The first is adaptive improved ABC that uses adaptive parameter control and the second is self-adaptive improved ABC that uses self-adaptive parameter control. In adaptive parameter control, strategic parameter values are updated based on the behaviour of the algorithm in the running phase, namely feedbacks from the searching process. On the other hand, in self-adaptive parameter control, the strategic parameters become a part of solution array and thus mutate. Appropriate parameter values help to have good solutions and ensure that good candidate solutions are selected; thus these appropriate parameter values can be handed down to the forthcoming population (Eiben
et al.,
1999). Hence, it is different from adaptive parameter control. Parameters are involved in evolutionary progress and their values are tried to be improved.
3.1 Adaptive IABC (AIABC) Algorithm
AIABC tries to increase performance by making online updates for m and p strategic parameters having a direct effect on the performance of IABC through adaptive parameter control. In adaptive parameter control, strategic parameters are updated according to the feedbacks to be obtained in the search process during the performance of the algorithm. With this approach, the algorithm will become adaptive to the problem and it will be ensured that it displays good performance in high dimensional optimization problems.
In this version, randomly generated candidate values of
m and
p parameters are kept in two separate arrays (
mArray and
pArray). In onlooker bee stage, the values in the array are used in turn for
m and
p parameters. If the best solution found so far has changed by using
m and
p values, these successful
m and
p values are kept in two separate arrays (
sMarray and
sParray). Figure
1 shows the relations of these four arrays. When all candidate values in
sMarray and
sParray are used, re-initialization of these arrays is made by using random values beside the ones in
sMarray and
sParray. By this it means, it is aimed to achieve good parameter values through the utilization of successful experiences in different stages of the problem during the performance of the algorithm. The pseudo-code of AIABC can be seen in Algorithm
4. The proposed modifications are presented in italic form in the Algorithm
4.
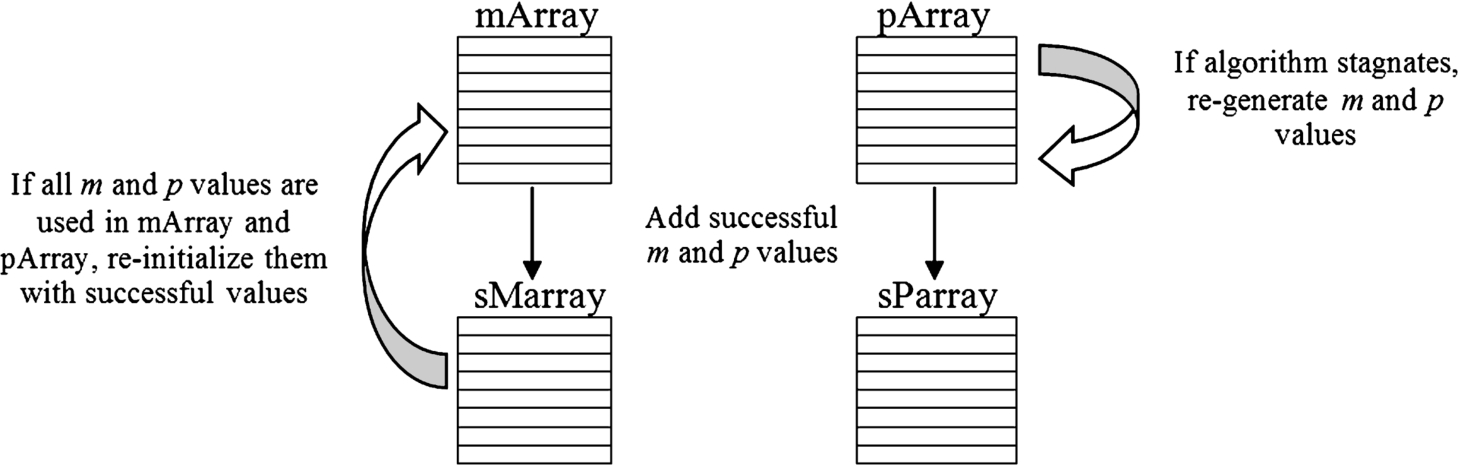
Fig. 1
Re-generation and re-initialization of arrays holding the values of m and p parameters in AIABC algorithm.

Algorithm 4
The Adaptive Improved ABC (AIABC) Algorithm.
The method developed to update the online values of
m and
p parameters is realized through the determination of new values by utilizing previous successful experiences during the performance of the algorithm. There are arrays including the possible ranges for each parameter (
mArray for
m and
pArray for
p).
Each array includes values as many as
maxCount. The process begins with
$\mathit{cnt}=1$, which is used as a counter. Before each employed bee stage, values are determined as
$m={m_{i}^{\mathit{cnt}}}$,
$p={p_{i}^{\mathit{cnt}}}$. In employed bee stage, the algorithm continues its performance with these values. If the best-so-far solution is improved further,
m and
p values used in that cycle are transferred to
${\mathit{sMarray}_{i}}$ and
${\mathit{sParray}_{i}}$. When
cnt counter reaches to
maxCount value representing the size of arrays, re-initialization process is started for
mArray and
pArray. In the re-initialization process,
mArray and
pArray are updated by taking values randomly selected within the adaptively adjusted ranges or by taking from a certain number of successful values in
${\mathit{sMarray}_{i}}$ and
${\mathit{sParray}_{i}}$. The selection mechanism is controlled randomly by using re-initialization probability value (
RP).
RP is increased gradually in the running of algorithm and thus, successful
m and
p values can be selected more than random values in later iterations. Moreover, when all the elements of
mArray and
pArray are used but successful arrays are still empty, the stagnation is detected. This time,
mArray and
pArray are re-initialized with new random values by utilizing the ranges of parameters adaptively.

Algorithm 5
Adaptive Parameter Control Procedure in AIABC Algorithm.
Determination of the possible range of
m parameter properly will also have a positive effect on the performance of the algorithm. For instance, it is detected that the high values for
m may have a negative effect on the performance of the algorithm specifically for high dimensional functions (Liao
et al.,
2013; Aydın,
2015). Therefore, the range of these parameters is adjusted adaptively while algorithm is running.
In the first random initialization, the range of
m is kept
$[1,2]$. In the following initializations, an adaptive approach is applied in the determination of the range of
m parameter. If all elements of
mArray and
pArray are used and any of them is not transferred to
sMarray and
sParray in onlooker bee stage and the stagnation is detected, range of
m parameter is changed. If the range of
m is between 1 and
$D\ast \mathit{factor}$ (
$\mathit{LARGE}$ strategy), it is changed to between 1 and 2 (
$\mathit{SMALL}$ strategy). On the contrary, when the range of
m is between 1 and 2, it is changed to 1 and
$D\ast \mathit{factor}$ after stagnation. The initial value of
$\mathit{factor}$ variable is 0.1 and is increased by 0.1 after each stagnation. When this variable reaches 1, it is then reduced to 0.1 again. In other words, the maximum value of
m is 10% of the problem dimension in the first stage; it is increased by 10% after each stagnation. When range of
m parameter reaches to problem dimension, it is then reduced to 10% of the problem dimension again. Moreover, in each stagnation of the algorithm,
$\mathit{mArray}$ and
$\mathit{pArray}$ are re-initialized according to the range determined above. So, values leading to stagnation are changed. The whole process of adaptive parameter control procedure mentioned here is presented in Algorithm
5.
3.2 Self-Adaptive IABC (SaIABC) Algorithm
In the self-adaptive parameter control (Eiben
et al.,
1999), parameters to be controlled are encoded to solution chromosome as gene in evolutionary algorithms while they are encoded as a new dimension to the solution vector in SaIABC (Fig.
2).
m and
p parameters are added to each candidate solution as two new dimensions. If in the employed and onlooker bee search equations, these dimension values can be modified just as the dimensions of the problem and
m and
p values can be changed. Therefore, the control of these parameters depends on the algorithm itself.
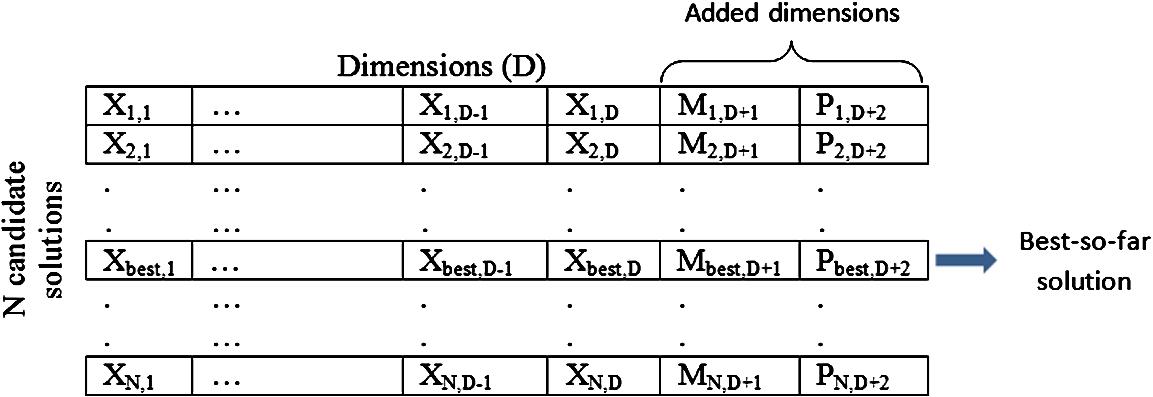
Fig. 2
New structure of solution arrays in SaIABC algorithm.
SaIABC algorithm uses values found in two additional dimensions of the best-so-far solution as m and p values for each iteration. Search equations in employed and onlooker bee stages are performed according to these parameter values. The range of m parameter is as well adjusted adaptively as in AIABC. The only difference is determination of algorithm stagnation. Here, if the algorithm cannot improve the best-so-far solution at some consecutive iterations (i.e. 25 iterations), this means algorithm stagnates and changes the strategy from LARGE to SMALL or vice versa.

