Abstract
In recent years, the growth of marine traffic in ports and their surroundings raise the traffic and security control problems and increase the workload for traffic control operators. The automated identification system of vessel movement generates huge amounts of data that need to be analysed to make the proper decision. Thus, rapid self-learning algorithms for the decision support system have to be developed to detect the abnormal vessel movement in intense marine traffic areas. The paper presents a new self-learning adaptive classification algorithm based on the combination of a self-organizing map (SOM) and a virtual pheromone for abnormal vessel movement detection in maritime traffic. To improve the quality of classification results, Mexican hat neighbourhood function has been used as a SOM neighbourhood function. To estimate the classification results of the proposed algorithm, an experimental investigation has been performed using the real data set, provided by the Klaipėda seaport and that obtained from the automated identification system. The results of the research show that the proposed algorithm provides rapid self-learning characteristics and classification.
1 Introduction
The maritime industry is one of the main sectors in Europe. Over 90% of the European Union external trade goes by sea, and more than 3.7 billion tonnes of freight per year are loaded and unloaded in the European Union seaports. This sector is one of the most important areas of human activity, and it is one of the most dangerous. Nowadays, the navigation technology is highly developed: the vessels are considerably bigger, faster and safer, and the staff is more professional. As the traffic becomes more intense, to prevent maritime incidents also becomes more difficult. The growth of marine traffic in ports and their surroundings raises the traffic and security control problems and increases the workload for traffic control operators. The huge numbers of vessels make the process of abnormal movement detection time-consuming and error-prone for human analysts (Will
et al.,
2011).
Analysing and finding anomalies within marine traffic data is a complex task. The scientific community is actively working on the development of algorithms for modelling the regular maritime traffic in ports and surroundings, to optimize the human resources and to improve safety at sea and security in navigation. Anomaly detection or abnormal movement detection is one of many techniques available for improving the safety and security in this domain. The obtained knowledge can help in interpreting suspicious movements by providing additional information to traffic control operators. Anomalies are patterns in data that do not conform to a clear notion of normal behaviour. Anomalies are detected as conflicts between the vessel’s registered live data and the history-based potential data. Anomalies are defined as deviations from the normal state. Detection of these differences can be treated as a classification problem: given a set of observations, they must be classified as normal or abnormal (Riveiro
et al.,
2008a). Various types of anomalies in a maritime domain are presented in Martineau and Roy (
2011).
The increasing marine traffic enhances the amount of data. Therefore most of the existing methods for abnormal movement detection in maritime traffic are not suitable for massive data processing. They can hardly be applied in the decision support system because of the high computational cost. To this end, rapid self-learning algorithms for the decision support system have to be developed to detect the abnormal movement in intense marine traffic areas. An effective information system for marine traffic monitoring should be able to combine human-based monitoring and machine learning possibilities to interpret huge amounts of data, thus enabling an efficient and accurate detection of abnormal vessel behaviour at seaport surroundings.
The paper is structured as follows. In Section
2, the related works on the abnormal movement detection in marine traffic and the state-of-the-art solutions are reviewed. Section
3 introduces a new method based on the integration of self-organizing map and virtual pheromone for real-time abnormal movement detection. The experimental results of the proposed method and a comparative analysis are demonstrated in Section
4. The last section concludes the paper.
2 Related Works
Recent developments in the abnormal movement detection in marine traffic are discussed in this section. Over the past few years, the number of studies that address the use of anomaly detection in maritime traffic is increasingly growing. The solution of this problem has employed a variety of methods including neural networks (Perera
et al.,
2012), Naive Bayes classifier (Zhen
et al.,
2017), Gaussian Processes (Smith
et al.,
2014; Kowalska and Peel,
2012), Support Vector Machines (Handayani
et al.,
2013). The authors of Zissis
et al. (
2016) present the results of employing machine learning methods and neural networks as a basis for accurate predicting of a vessel’s behaviour with an emphasis on the solution practicality. The rule-based fuzzy expert system introduced by Jasinevicius and Petrauskas (
2008) takes into account the ship type, persons on board, and the riskiness of cargos for abnormal movement detection. The proposed algorithm can be used by decision makers at different stages of maritime awareness and port security evaluation. The authors in Alessandrini
et al. (
2016) demonstrate how different methodologies, such as data mining, information fusion and visual analytics, enable the automatic detection of structured anomalies, understanding of activities at sea and the analysis of their trends over time. This kind of knowledge can provide new possibilities for improving the safety of navigation.
In Mascaro
et al. (
2014) the detection of vessel movement anomalies by using the data mining in Bayesian networks is presented. The authors have found that the learned networks examine data and verify results quite easily, despite a significant number of variables involved. The experimental results have shown that the Bayesian Networks are a promising tool for detecting anomalies in vessel tracks. Another data mining approach, based on the Bayesian networks, is presented in Johansson and Falkman (
2007). The main advantages of the approach are that it is possible to handle the missing values in the data set and to include the human expert knowledge into the model due to the graphical representation of the model. The drawbacks of the Bayesian network include the sensitivity of the performance to modelling assumptions and the high computational cost. The authors in Lane
et al. (
2010) have proposed a general Bayesian network-based method, which can identify five abnormal ship behaviours: deviation from standard routes, unexpected activity of automated identification system (AIS), unexpected arrival at port, close approach, and specific zone entry.
The example of a semi-supervised method for detecting the maritime traffic anomaly is presented in Rhodes
et al. (
2005). The method provides continuous on-the-fly learning that benefits from but does not depend on, the operator’s interaction. The proposed system self-organizes to discover common events versus anomalous and can adapt to changing situations.
A clustering-based maritime traffic anomaly detection model was proposed in Liu
et al. (
2015). The algorithm for abnormal movement detection is based on three division distances: Absolute Division Distance, Relative Division Distance, and Cosine Division Distance. However, the expert human interaction is needed while setting movement trajectory thresholds.
In the paper Osekowska
et al. (
2013), a novel approach to anomaly detection in maritime traffic, based on the theory of potential fields, is presented. An advantage of this method is the ability to create a normal traffic model, based on the traffic history, without a need for expert knowledge. Anomalies are identified as a lack of normal behaviour.
The increasing marine traffic enhances the amount of data, so new algorithms have to be developed to detect the abnormal movement in intense marine traffic areas. In Kowalska and Peel (
2012), Gaussian Processes Combined with Active Learning have been used for maritime anomaly detection. Gaussian Processes can be applied to large data sets for accurate anomaly detection. A knowledge discovery system, based on the genetic algorithm (GeMASS), was proposed in Chen
et al. (
2014). GeMASS was developed to analyse a large volume of real-time streaming data and to generate up-to-date knowledge in a dynamic fashion. Based on the knowledge obtained, the system screens vessels for anomalies in real-time.
Despite a significant amount of research, this area has not yet been completely explored and keeps a place for developing new algorithms while solving abnormal vessel movement detection in marine traffic data.
3 Integration of a Self-Organizing Map and a Virtual Pheromone
3.1 Clustering with SOM
The self-organizing map (SOM) is a neural network-based method that is trained in an unsupervised way using a competitive learning (Kurasova and Molytė,
2011; Dzemyda
et al.,
2012). A distinctive characteristic of this type of neural networks is that they can be used for both visualization and clustering of multidimensional data. The most important property of SOM can be utilized for many tasks, such as reduction of the amount of data, speeding up of learning nonlinear interpolation and extrapolation, generalization, and efficient compression of information (Kohonen
et al.,
1996). SOM is one of the most analysed neural networks, that is learned in an unsupervised manner. In our case, SOM represents a set of neurons, connected to one another via a rectangular topology. The rectangular SOM is a two-dimensional array of neurons
$W={w_{ij}},\hspace{2.5pt}i=1,\dots ,k,\hspace{2.5pt}j=1,\dots ,s$. Here
k is the number of rows, and
s is the number of columns. Each element of the input observation vector is connected to every individual neuron in the rectangular structure. Any neuron is entirely defined by its location on the grid by its specific index at the row
i and the column
j, and by its weight (so-called code book) vector. After SOM training, the data are presented to SOM and the winning neuron for each data vector are found. The winning neuron is the one to which the Euclidean distance of the input data vector is the shortest. In such a way, the data vectors are distributed on SOM, and some data clusters can be observed.
The results of a SOM map depend on the selected learning parameters. Learning rates and neighbourhood functions
${h_{ij}}$ are the necessary parameters that influence the results. The neighbourhood function determines how strongly the neurons are connected to each other and influences the training result of SOM. Therefore, it is important to choose the proper neighbourhood function. There are different kinds of neighbourhood functions: bubble, Gaussian, Cut Gaussian (Vesanto
et al.,
2000; Liu
et al.,
2006), heuristic (Dzemyda,
2001), Mexican hat (Kohonen,
1982), triangular (Kohonen,
1982), rectangular (Kohonen,
1982) and others. In this research, we have compared five neighbourhood functions: Gaussian, triangular, cut Gaussian, bubble, Mexican hat and its influence on the classification results obtained by the modified SOM method. These functions are presented in Table
1, where
${d_{ij}}$ is a distance between the current observation vector and the winning neuron,
${\eta _{ij}}$ is the neighbourhood radius,
F is a step function:
$F(x)=0$, if
$x<0$ and
$F(x)=1$, if
$x\geqslant 0$.
Table 1
Neighbourhood functions.
| Gaussian |
${h_{ij}}(t)=\exp \Big(-\frac{{d_{ij}^{2}}}{2{({\eta _{ij}}(t))^{2}}}\Big)$ |
| Bubble |
${h_{ij}}(t)=F({\eta _{ij}}(t)-{d_{ij}})$ |
| Cut Gaussian |
${h_{ij}}(t)=\exp \Big(-\frac{{d_{ij}^{2}}}{2{({\eta _{ij}}(t))^{2}}}\Big)F({\eta _{ij}}(t)-{d_{ij}})$ |
| Triangular |
${h_{ij}}(t)=\left\{\begin{array}{l@{\hskip4.0pt}l}1-\frac{|{d_{ij}}|}{{\eta _{ij}}(t)},\hspace{1em}& \text{if}|{d_{ij}}|\leqslant {\eta _{ij}}(t)\\ {} 0,\hspace{1em}& \text{otherwise}\end{array}\right.$ |
| Mexican hat |
${h_{ij}}(t)=\Big(1-\frac{{d_{ij}^{2}}}{{({\eta _{ij}}(t))^{2}}}\Big)\exp \Big(-\frac{{d_{ij}^{2}}}{2{({\eta _{ij}}(t))^{2}}}\Big)$ |
As mentioned before, the learning rate also influences the results of SOM. Usually, linear, inverse-of-time, and power series learning rates are used for the SOM training (Stefanovic and Kurasova,
2014,
2011). In this research, the learning rate is constant and equal to 0.5, both the initial neighbourhood radius and the radius decay parameter are set to
$-0.1$.
3.2 Classification by Using a Virtual Pheromone Concept
The application areas of SOM are data clustering and graphical result presentation. To use the gathered knowledge about clusters and with a view to classify observations, we exploit the biologically-inspired notion of a virtual pheromone. The idea is based on the observations of ant colonies. To mark the way to the food source, the ants use a chemical substance called pheromone. Other ants follow the pheromone trail to reach the discovered food source. Pheromone evaporates in time, and the trail on the road slowly disappears. The ants must continually travel by the same route to strengthen the evaporating pheromone trail.
In the proposed approach, the training process of a modified SOM method is the same as the original one except that the virtual pheromone intensity value is introduced in the last epoch. The epoch of the SOM network is completed when all possible pairs of vectors from the training data set are shown to SOM. Further, taking into account the number of vectors that were assigned to the same cluster, it can be calculated how this cluster represents a majority. To count the number of vectors in the cluster, it is necessary to assign the vectors from the training data set to winning neurons.
In the beginning, each winning neuron has its pheromone value intensity of which is equal to the cluster size of this neuron. The value of a pheromone mark Q is calculated as follows: when the winning neuron is selected, the pheromone intensity is increased by one, i.e. the pheromone mark is attached to the neuron. Thus, the more observation vectors are assigned to the same winning neuron, the higher its virtual pheromone intensity is.
In order to adjust the pheromone evaporation procedure, after each SOM network re-training, the virtual pheromone intensity value
${\tau _{ij}}$ is updated according to the formula (Yingying
et al.,
2003; Venskus
et al.,
2015):
where
${\tau _{ij}}$ is a virtual pheromone intensity;
${t_{1}}$ is the previous state of the virtual pheromone intensity;
${t_{2}}$ is the recent state of the virtual pheromone intensity. The parameter
ρ represents a virtual pheromone intensity evaporation speed (
$0<\rho <1$). In the formula, similarly to the ant colony system, the pheromone trail will evaporate unless it is renewed within a particular time. The intensity evaporation is slower than its renewal process.
The pheromone intensity threshold used for abnormal movement detection is calculated using the validation data set. The precision and sensitivity of the algorithm can be adjusted by changing the threshold value. To adjust the threshold, the classification error cost function has been optimized according to:
Here
$J(\Theta )$ is a classification error rate by choosing Θ as a threshold value;
${\mathit{PPV}_{\Theta }}$ is a classification precision;
${\mathit{TPR}_{\Theta }}$ is a classification sensitivity;
${\beta _{\mathit{PPV}}}$ and
${\beta _{\mathit{TPR}}}$ are the influence of classification parameters on the classification error cost function;
${\mathit{TP}_{\Theta }}$ is the count of true positive (assigned to an abnormal state) observations;
${\mathit{FP}_{\Theta }}$ is a false positive (assigned to a false abnormal state);
${\mathit{TN}_{\Theta }}$ is a true negative (assigned to a normal state);
${\mathit{FN}_{\Theta }}$ is a false negative (assigned to a false normal state). The gradient descent method has been used to find a local minimum of the function depicted by equation (
2).
When it is necessary to obtain a new observation state, the vector representing this state is assigned to a winning neuron of the SOM network. Thus, a winning neuron should be found for each new observation, and the classification is performed according to its pheromone value. The marine traffic observation is classified as normal if the pheromone value is greater than the threshold value, or abnormal if less.
3.3 Method Description
As mentioned before, the combination of a self-organizing map and a virtual pheromone is proposed to classify events for abnormal movement detection in maritime traffic. It is important to identify whether the observation data show the abnormal vessel behaviour and to react accordingly. Therefore, creating and testing the algorithm, the trained SOM neural network is transferred to a system where it classifies real time data, based on the existing network settings without additional re-training. However, as the amount of new data increases, in order to ensure a high classification accuracy, there is a necessity to re-train the network periodically. The re-training process of the neural network is run by adding new observation data to the training set.
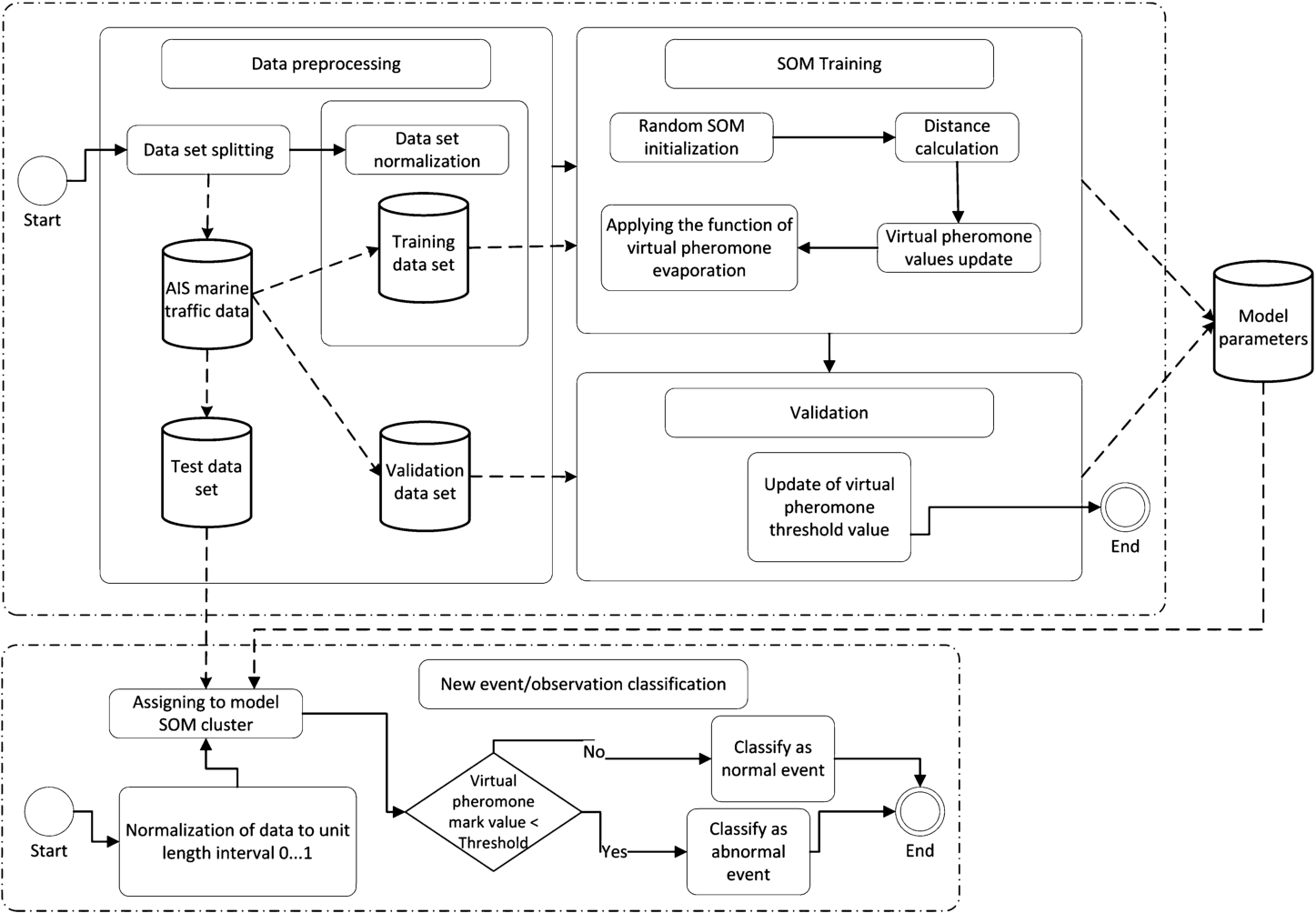
Fig. 1
Integration of a self-organizing map and a virtual pheromone.
A general scheme of the proposed algorithm (SOM_Pheromone) is presented in Fig.
1. Its implementation steps are described as follows:
-
• Data processing. The data filtering is applied in order to reject repeated and erroneous data, then the data set is divided into three subsets: training, validation and testing.
-
• Normalization of the training data set. Each observation attribute is normalized to interval 0 and 1.
-
• SOM network training. Each winning neuron has its pheromone intensity value which is equal to the number of data vectors assigned to the winning neuron. The virtual pheromone value is calculated in the last epoch. During the SOM re-training process, the function of the virtual pheromone intensity evaporation is applied.
-
• Tuning of the pheromone threshold using validation data. The sensitivity and precision of the algorithm are adjusted by changing the threshold value. After the SOM network training, the threshold value of the pheromone intensity for abnormality detection is chosen with respect to the minimum and maximum values of pheromones. To adjust the optimal threshold, the classification error rate function has been used (see Eq. (
2)).
-
• Testing of the algorithm using test data. The test data set is normalized to interval 0 and 1. Further, the test data observations are classified as normal or abnormal by taking into account the SOM network parameters and pheromone values obtained in the training step.
-
• Classification of new marine traffic observations. The classification of new data in real time is based on the resulting network settings without additional SOM training.
3.4 Maritime Anomaly Detection Using Self-Organizing Maps and a Gaussian Mixture Models
A comparison of the obtained results of the proposed algorithm with other similar methods has been carried out. Another SOM-based algorithm for abnormal movement detection in marine traffic is presented in Riveiro (
2011), Riveiro
et al. (
2008a). This anomaly detection method (SOM_GMM) is a combination of SOM and Gaussian Mixture Models (GMM). The implementation steps of the algorithm is as follows:
-
• Division of the available data sets. The available vessel traffic data from the area of interest are divided into three sets: 50% – a training data set for SOM learning, 30% – a validation/adjustment data set for a pheromone intensity threshold calculation, and 20% – a test data set for classification results evaluation.
-
• Pre-processing of the training data set. During the pre-processing, all the duplicate data vectors are filtered out.
-
• Normalization of the training data set. Each attribute has been normalized into the range of 0 and 1.
-
• SOM calculation. The learning process of SOM is influenced by several parameters: a shape of the grid is square, the learning rate was set to 0.5, the weight range was set to 0.5, the Gaussian neighbourhood function was used, both the initial neighbouring radius and the radius decay parameter were set to −0.1.
-
• Covariance matrix calculation. For each map neuron, the covariance matrix of all input vectors which have to correspond to a winning neuron is calculated.
-
• Calculation of prior probabilities. For each SOM cluster the n-dimensional Gaussian probability density function has been calculated. The mean of each density function corresponds to the weights of the SOM neuron vector, and the variance is given by dispersion of training data.
-
• GMM calculation. GMM is calculated by summing all Gaussian distributions of each SOM cluster.
-
• Adjustment of the $P(H=\text{normal})$ likelihood value on validation data set.
In Riveiro (
2011), a division of the anomaly detection process into on-line and off-line subprocesses has been proposed. The on-line data processing refers to the analysis of incoming data in real-time, the off-line processing relates to the establishment of normal models from the training data and rules used during the on-line detection process. The method, presented in Riveiro (
2011), Riveiro
et al. (
2008b), is based on two assumptions: unusual events have to be sufficiently different from the normal events in order to be detectable; the training set should be free from unusual events. The same assumptions and conditions were met while carrying out the experiments described in Section
4.
4 Experimental Investigation
The performance of the proposed algorithm has been compared with the performance of the algorithm presented in Riveiro
et al. (
2008b). The purpose of the proposed algorithm is to classify the events in maritime traffic in order to identify the abnormal vessel movement. Anomalies are defined as deviations from normality, and they are patterns in data that do not conform to the notion of normal behaviour. Given a set of observations, they must be classified as normal or abnormal. The proposed algorithm can classify the events on-line using the previously obtained knowledge. The usage of a virtual pheromone concept adds additional knowledge to the re-training process of the SOM network and influence the classification accuracy. However, this paper takes under consideration only a part of the re-training process, i.e. covers only the first stage of the SOM network training without the re-training procedure, while the goal of the research is to evaluate the proposed algorithm and to determine the optimal learning parameters.
The clustering results of the SOM network depend on the selected learning parameters. Intending to evaluate the influence of the SOM network parameters on the anomalies classification accuracy, the experiments have been done with different neighbourhood functions (see Table
1). The size of the SOM network (grid dimension) and its influence on the classification results were also considered. To validate the classification results of the modified SOM network with the experimentally determined learning parameters, similar experiments were carried out using three data sets, described in Table
2.
4.1 Description of the Analysed Data Sets
Data from the region of medium maritime traffic at the Klaipeda seaport were selected for a comparative algorithm analysis. Marine traffic data were taken from the marine traffic monitoring system (AIS) which provides multidimensional vessel movement data (see Table
3). Meteorological data for the relevant time period were provided by the Lithuanian meteorological service. Three data sets were used for the experiments: Cargo Vessels, Passenger vessels, Tugs and Pilot vessels (see Table
2).
| Data set |
Total items |
Abnormal items |
Normal items |
| Cargo vessels |
138242 |
3362 |
134890 |
| Passenger vessels |
43879 |
2914 |
40965 |
| Tugs and Pilot vessels |
50372 |
2306 |
48066 |
Data sources:
-
• AIS Maritime traffic data were obtained from the UHF receiver, controlled by administration of Klaipeda Maritime Safety. Its WGS84 coordinates are 55${^{\circ }}$43′36″N, 21${^{\circ }}$4′36″E.
-
• Meteorological data were obtained from the Klaipeda Hydrometeorological Station of Lithuanian Hydrometeorological Service.
Data set limitations:
-
• Geographical region: Klaipeda State Seaport and its environs. Region sampling was limited to WGS84 latitude values from ${55.7^{\circ }}$ to ${55.814^{\circ }}$ and longitude values from ${20.55^{\circ }}$ to ${21.13^{\circ }}$.
-
• The data sample was filtered by the type of a cargo ship, i.e. the data of this ship type were used for further analysis.
-
• The period taken for analysis was from January 1, 2016 to February 29, 2016.
-
• Meteorological measurements were taken twice a day at 10 a.m. and 5 p.m. The meteorological measurement obtained at 10 a.m. was assigned to the time range from 1:30 a.m. to 1:30 p.m., while the measurement obtained at 5 p.m. was assigned to the time range from 1:30 p.m. to 1:30 a.m.
Data set splitting:
-
• The training set consists of 50% of the data set which is free from abnormal traffic events.
-
• The validation set consists of 30% of the data set items. The data vectors of the set are labelled by an expert into the classes: normal traffic and abnormal traffic. To test and compare the algorithms abnormal data were used as well:
-
– deviation from the route southwards,
-
– deviation from the route northwards,
-
– approaching the shore unacceptably close (Melnrage beach),
-
– approaching the shore unacceptably close (Oil quay),
-
– slow movement at the sea gate to the port,
-
– drift at the sea gate to the port,
-
– a stop in the prohibited area in the port,
-
– movement through the port gates during the storm,
-
– getting too close to the shore during the storm.
-
• Test set consists of 20% of the data set that contained both normal and abnormal observations.
Table 3
Structure of a data vector.
| Feature Id |
Feature name |
Feature name |
Description type |
Data |
| 1 |
Longitude |
AIS |
Vessel longitude in WGS84 coordinate system, indicating the number of seconds in decimal format |
Float |
| 2 |
Latitude |
AIS |
Vessel latitude in WGS84 coordinate system, indicating the number of seconds in decimal format |
Float |
| 3 |
Heading |
AIS |
Direction of vessel movement, indicating the azimuth in degrees |
Integer |
| 4 |
Speed |
AIS |
Vessel speed in knots |
Integer |
| 5 |
Wind direction |
Meteo |
Wind direction, indicating the azimuth in degrees |
Integer |
| 6 |
Wind speed |
Meteo |
Wind speed, m/s |
Integer |
| 7 |
Wave direction |
Meteo |
Wave direction, indicating the azimuth in degrees |
Integer |
| 8 |
Wave height |
Meteo |
Wave height in meters |
Integer |
4.2 Selection of a Neighbourhood Function
The modified SOM network was trained, using different neighbourhood functions in order to establish which has the best impact on the classification results. The experiments have been performed with the Cargo Vessels data set, using the following learning parameters for the SOM network training: a shape of the grid is square; grid dimension is
$20\times 20$. The experimental results, presented in Table
4, show that using the Mexican hat neighbourhood function the best classification accuracy is obtained (marked in bold in Table
4). The results were compared with the classification accuracy obtained by other methods: a combination of SOM and Gaussian mixture models (SOM_GMM), introduced in Riveiro
et al. (
2008b), and classification carried out by experts. To ensure correctness of the results, additional experiments were carried out with different grid dimensions. An example of the influence of the neighbourhood function on the classification accuracy with SOM grid dimension
$25\times 25$ is presented in Table
5. In all further experiments, the Mexican hat neighbouring function is used.
Table 4
Influence of the neighbourhood function on the classification accuracy when the SOM grid dimension is $20\times 20$.
|
Neighbourhood function |
TP |
FP |
TN |
FN |
Precision |
Sensitivity |
| Expert |
|
1681 |
0 |
27167 |
0 |
1 |
1 |
| SOM_GMM |
Gaussian |
1489 |
81 |
27086 |
192 |
0.948 |
0.886 |
| SOM_Pheromon |
Gaussian |
1477 |
68 |
27099 |
204 |
0.956 |
0.879 |
|
Triangular |
1241 |
122 |
27045 |
440 |
0.911 |
0.738 |
|
Bubble |
1454 |
68 |
27099 |
227 |
0.955 |
0.865 |
|
Cut Gaussian |
1479 |
65 |
27102 |
202 |
0.958 |
0.880 |
|
Mexican hat |
1509 |
51 |
27116 |
172 |
0.967 |
0.898 |
Table 5
Influence of the neighbourhood function on the classification accuracy when the SOM grid dimension is $25\times 25$.
|
Neighbourhood function |
TP |
FP |
TN |
FN |
Precision |
Sensitivity |
| Expert |
|
1681 |
0 |
27167 |
0 |
1 |
1 |
| SOM_GMM |
Gaussian |
1495 |
80 |
27087 |
186 |
0.949 |
0.889 |
| SOM_Pheromone |
Gaussian |
1491 |
59 |
27108 |
190 |
0.962 |
0.887 |
|
Triangular |
1288 |
117 |
25948 |
1495 |
0.917 |
0.463 |
|
Bubble |
1455 |
63 |
27104 |
226 |
0.955 |
0.865 |
|
Cut Gaussian |
1498 |
55 |
27112 |
183 |
0.958 |
0.866 |
|
Mexican hat |
1512 |
50 |
27117 |
169 |
0.968 |
0.899 |
4.3 Dependence of the Classification Accuracy on the SOM Grid Dimension
The comparison of the classification results obtained by the proposed algorithm (SOM_Pheromone) and the SOM_GMM algorithm is presented in Table
6. The experiments have been performed using the Cargo Vessels data set. All the experiments have been performed under the same conditions with the same parameters by increasing the SOM network grid dimension from
$10\times 10$ to
$40\times 40$ by step 5. By comparing the obtained results in Table
6, it can be concluded that using the SOM_Pheromone algorithm for teh Cargo Vessels data set, the classification accuracy is better than that of SOM_GMM (the best results are marked in bold for each grid dimension). Another conclusion from the obtained results is that the optimal size of the SOM grid for the SOM_Pheromone and SOM_GMM is
$25\times 25$.
The experiment was repeated with the Passenger vessels data set and the Tugs and Pilot vessels data set. The classification results are presented in Tables
7 and
8. The learning parameters for the SOM network training are the same as in the previous experiment, the grid size of SOM is
$25\times 25$. The experimental results, presented in Table
7, show that, using the SOM_Pheromone algorithm, the best classification accuracy (marked in bold in Tables
7 and
8) is achieved.
Figure
2 presents the visualization results of the Passenger vessels data set, obtained using the SOM_Pheromone algorithm with
$25\times 25$ SOM size. The sign ’∘’ represents the neurons whose pheromone value is greater than the threshold value and those neurons classify the maritime traffic as normal. The sign ‘×’ represents the neurons whose pheromone value is less than the threshold value, and the maritime traffic is classified as abnormal. The sign ‘▲’ represents the real traffic data of three passenger vessels.

Fig. 2
Visualization results of the Passenger vessels data set, obtained using the SOM_Pheromone algorithm.
Table 6
Influence of the SOM grid dimension on the classification accuracy of SOM_Pheromone and SOM_GMM algorithms.
| Grid dimension |
SOM_Pheromone |
SOM_GMM |
| Precision |
Sensitivity |
Precision |
Sensitivity |
| $10\times 10$ |
0.919 |
0.773 |
0.867 |
0.780 |
| $15\times 15$ |
0.933 |
0.814 |
0.921 |
0.834 |
| $20\times 20$ |
0.967 |
0.898 |
0.948 |
0.886 |
| $25\times 25$ |
0.968 |
0.899 |
0.949 |
0.889 |
| $30\times 30$ |
0.961 |
0.897 |
0.948 |
0.888 |
| $35\times 35$ |
0.948 |
0.893 |
0.932 |
0.877 |
| $40\times 40$ |
0.918 |
0.886 |
0.919 |
0.875 |
Table 7
Classification results of the Passenger vessels data set (normal states: 8193, abnormal states: 1457).
| Method |
TP |
FP |
TN |
FN |
Precision |
Sensitivity |
| SOM_GMM |
1314 |
17 |
8176 |
143 |
0.987 |
0.902 |
| SOM_Pheromone |
1328 |
18 |
8175 |
123 |
0.987 |
0.911 |
Table 8
Classification results of the Tugs and Pilot vessels data set (normal states: 12298, abnormal states: 1153).
| Method |
TP |
FP |
TN |
FN |
Precision |
Sensitivity |
| SOM_GMM |
971 |
9 |
12289 |
182 |
0.991 |
0.842 |
| SOM_Pheromone |
978 |
9 |
12289 |
175 |
0.991 |
0.848 |
5 Conclusions and Future Works
In this paper, the modified SOM algorithm for marine vessel movement data classification into normal and abnormal classes is presented. The modification is achieved by incorporating virtual pheromone intensity calculations at the last epoch of model training. Further, during the model validation stage, the pheromone intensity threshold is established by applying a gradient descent method. The authors have investigated the dependence of the network neighbouring function on the classification results and found that the best classification accuracy is achieved using the Mexican hat neighbouring function. Next, the influence of different SOM grid dimensions on the classification results of both SOM_Pheromone and SOM_GMM algorithms has been investigated. The results show that:
-
• Both algorithms start losing precision when the grid dimensions are larger than $25\times 25$.
-
• Both algorithms achieved the best precision using grid dimension $25\times 25$.
-
• The proposed SOM_Pheromone modification outperforms the SOM_GMM algorithm.
The conclusions mentioned above have been confirmed by classifying the other two data sets: Passenger vessels and Tugs and Pilot vessels. For the future work these aspects of the proposed SOM_Pheromone algorithm need to be investigated more in detail:
-
• The modification needs to be verified on other seaport data.
-
• SOM grid dimension dependency on the sea region size should also be investigated.
-
• Investigation of the virtual pheromone evaporation function using different re-training strategies.

