Abstract
The popularity of sharing data through cloud services has increased these days. As a result, the security of data sharing has become an important issue. The security mechanism has to ensure that the shared data would not be intercepted or altered by illegal members during transmission. A data sharing scheme for cloud services is proposed in this paper to achieve the following four security requirements: 1) forward secrecy and backward secrecy, 2) source authentication, 3) data integrity, and 4) confidentiality. In addition, message recovery is applied to improve the efficiency of encryption and signature computation. The computation cost is reduced by computing a common key for all data. Thus, the data owner only needs to encrypt the shared data once before sending it in this proposed scheme.
1 Introduction
Cloud service has become a trend nowadays. There are three common cloud service architectures (Ghazia and Masood,
2012): Software as a Service (SaaS), Platform as a Service (PaaS), and Infrastructure as a Service (IaaS). SaaS provides applications as a service from the web without needing the user to download or install software at the user’s end. The cloud applications can be accessible through a thin client interface, such as a web browser or a program interface. The consumer does not need to manage or control the cloud infrastructures such as network, servers, operating systems, storage, or even individual application capabilities. Salesforce is an example of SaaS in the area of Customer Relationship Management (CRM), which is an approach to managing a company’s interaction with current and potential future customers.
PaaS offers platform as a service where clients can develop systems or applications. It provides the client to deploy their systems or applications onto the cloud infrastructure supported by the provider. The client does not manage or control the cloud infrastructures such as network, servers, operating systems, or storage. However, the client has the ability to control the deployed applications and possibly configuration settings using the application-hosting mode. Examples of PaaS are Google App Engine and Windows Azure.
IaaS offers physical or virtual machine as a service to the client. It provides processing, storage, networks, and fundamental computing resources to the client. And thus the client can deploy the software, which includes operating systems and applications. The consumer does not need to manage or control the cloud infrastructure but has control over operating systems, storage, and deployed applications. An example of IaaS is Amazon EC2.
Although the above cloud services provide convenient and flexible way to utilize resources, security is considered one of the most important open issues in cloud computing as reported by International Data Corporation (IDC) (Almorsy
et al.,
2011), which is an American market research, analysis and advisory company for information technology and telecommunications. An increasing security concern in cloud is the possibility of unintended resource sharing with competitors or malicious users due to insecure channels. Therefore, it is critical to ensure the confidentiality and integrity of the data in cloud services.
Data sharing is a widely used cloud service, and the examples are Google Drive and Dropbox. To address the security concerns mentioned above, we proposed a data sharing scheme which satisfies the following four security requirements: 1) forward secrecy and backward secrecy to ensure even if the encryption key is leaked, no one can decrypt the data; 2) source authentication to verify whether the data is send by the data owner; 3) data integrity to verify whether the data has been altered by attackers or not; 4) confidentiality to make sure that the data cannot be read by illegal members.
To achieve source authentication, data integrity, and confidentiality, we applied Lin and Yang’s source authentication scheme (Lin and Yang,
2012) to propose the data sharing scheme. However, using their scheme for the source authentication has some security problems as follows. Once a receiver can decrypt a data, and then the receiver can decrypt every data encrypted by the same data owner because the encryption key is in the same finite field of elliptic curve. As a result, Lin and Yang’s scheme cannot achieve the forward secrecy and backward secrecy. On the other hand, Lin and Yang’s source authentication scheme has large computation costs. This is because the data needs to be encrypted according to the number of receivers. If the number of receivers becomes large, then the computation costs are greatly increased.
To solve the above problems, we propose a new data sharing scheme for cloud services using message recovery in this paper. We compute the encryption key by using bilinear pairing and adding a random number before the encryption key is computed to achieve the forward secrecy and backward secrecy. In addition, we reduce the computation costs by using a common key for all data which has to be encrypted. Moreover, the proposed scheme only has to encrypt the shared data once regardless the number of the receivers. According to our computation analysis, the computation cost of the proposed scheme is less than those of the related works. Therefore, the proposed scheme is very efficient for the data sharing in cloud services.
The rest of the paper is organized as follows. Section
2 presents the preliminaries, including introductions of message recovery, elliptic curve cryptosystem, bilinear pairing, and security requirements. Section
3 describes the proposed data sharing scheme. The security and computation cost analysis is presented in Section
4. Finally, Section
5 concludes the paper.
2 Preliminaries
2.1 Message Recovery
Message recovery concept is first proposed by Nyberg and Ruppel (
1993). They showed that if the message encryption and digital signature computation can be done together, the sender only has to transmit a set of cipher text to achieve both authentication and encryption. The receivers can authenticate the data of the sender by checking whether the recovered message makes sense or not, and only the legal receiver has the key to correctly recover the original data. Thus, the message recovery scheme can encrypt the original message and generate its digital signature at the same time.
Lin and Chang (
2008) used this concept to propose a new digital signature scheme for linearly hierarchical organization. In Lin and Yang’s (
2012) scheme, the elliptic curve cryptosystem is applied to improve the computation efficiency of source authentication. The parameters used in Lin and Yang’s scheme are defined as follows:
p is a large prime number,
g is a point on the elliptic curve in the finite field
$\mathit{GF}(p)$, where
$g\in {Z_{p}}$;
${M_{i}}$ is the message in packet
i, where
i is the packet’s sequence number;
${k_{i}}$ is a random number for the
ith packet, and
$H(.)$ is a one-way hash function;
$\mathit{GF}(p)\to R$.
$({y_{s}},{x_{s}})$ is the public and private key pair for the sender, where
${y_{s}}={x_{s}}\times g\hspace{0.2em}\mathrm{mod} \hspace{0.2em}p$;
$({y_{{r_{j}}}},{x_{{r_{j}}}})$ is the public and private key pair for the receiver
j, where
${y_{{r_{j}}}}={x_{{r_{j}}}}\times g\hspace{0.2em}\mathrm{mod} \hspace{0.2em}p$.
In Lin and Yang’s scheme, when the sender wants to send a message, and the sender has to generate the information set
$({r_{i}},{s_{i}},i)$ using the following equations:
where
${({k_{i}}\times i\times {y_{{r_{j}}}})_{x}}$ is the
x-coordinate of the point
P.
${r_{i}}\equiv {m_{i}}+H({R_{i}})\hspace{0.2em}\mathrm{mod} \hspace{0.2em}p,$ and
After the information set
$({r_{i}},{s_{i}},i)$ is generated, it is sent to the receivers. When the receivers receive the information set, each receiver will authenticate the sender and check the integrity of the message. Each receiver computes
${r^{\prime }_{i}}$ by using its private key with the equation below:
${m_{i}}\equiv {r_{i}}-H({R_{i}})\hspace{0.2em}\mathrm{mod} \hspace{0.2em}p$, and
The recovered message will be meaningless if the sender or the receiver is illegal. That is, this scheme can achieve both source authentication and message encryption at the same time. However, there are two disadvantages in their scheme. First, their scheme cannot satisfy the forward secrecy and backward secrecy. According to the equations presented above, if a receiver’s public key is in the finite field of elliptic curve, the receiver can decrypt any data encrypted by the sender. This is a big problem when it applies to data sharing in cloud services because the malicious receiver can access the confidential data in this scenario. Second, when the sender wants to send a message to more than one receiver, the sender has to encrypt the message once for each receiver. This causes the high computation cost problem.
2.2 Bilinear Pairing and Some Problems
To achieve the higher efficiency and security, the bilinear pairing (Miller,
1986; Koblitz,
1987) is applied to the group signature schemes and ID-based encryption schemes (Zhang
et al.,
2004; Joux,
2002; Barreto
et al.,
2002; Bonehand and Franklin,
2001). Let
${G_{1}}$ be a cyclic additive group and
${G_{2}}$ be a cyclic multiplicative group of prime order
p. The bilinear pairing
$\widehat{e}:{G_{1}}\times {G_{1}}\to {G_{2}}$ has the following three properties (Lin
et al.,
2010).
-
1. Bilinearity: for all
${g_{1}},{g_{2}},{g_{3}}\in {G_{1}}$ and
$a,b\in {Z_{q}^{\ast }}$,
and
-
2. Non-degeneracy: There exists ${g_{1}},{g_{2}}\in {G_{1}}$, such that $\widehat{e}({g_{1}},{g_{2}})\in {G_{2}}$.
-
3. Computability: ${g_{1}},{g_{2}}\in {G_{1}}$, $\widehat{e}({g_{1}},{g_{2}})$ can be computed in polynomial time.
Suppose the following problems relating to bilinear pairing.
-
1. Discrete Logarithm Problem (DLP) (Lin
et al.,
2010): for
$Y=nX$ and
$n\in {Z_{q}^{\ast }}$; given
$X,Y\in {G_{1}}$; compute
n.
-
2. Decision Diffie–Hellman Problem (DDHP): for $X\in {G_{1}}$ and $a,b,c\in {Z_{q}^{\ast }}$; given $X,aX,bX,cX$; determine whether $c=ab\hspace{0.2em}\mathrm{mod} \hspace{0.2em}q$ holds or not.
-
3. Computational Diffie–Hellman Problem (CDHP): given $X,aX,bX$; compute $abX$ where $X\in {G_{1}}$ and $a,b\in {Z_{q}^{\ast }}$.
According Lin
et al. (
2010), the DLP is supposed to be the hard problem is
${G_{1}}$ and
${G_{2}}$ in this paper.
2.3 Security Requirements
Cloud service offers many benefits; it enables users to share their data with anyone on the cloud. However, the security, privacy, and integrity of the cloud services are the main challenges (Hay
et al.,
2011). To address these challenges, we propose a scheme in this paper that can satisfy the four security requirements as defined in Wang and Wu (
2005) as follows.
-
1. Forward secrecy and backward secrecy: forward secrecy says if the decryption key is leaked, the receivers cannot recover any data by the previous encryption key except when the data owner allows. Similarly, backward secrecy says when a data is shared with a new receiver, the new receiver cannot recover any of the previous data using the new decryption key unless the data owner allows.
-
2. Source authentication: to avoid impersonation attacks, the sender should provide a way for the receivers to authenticate whether the data is sent from the legal sender.
-
3. Data integrity: the data might be intercepted and altered by attackers when the data is transmitted through an unsecure channel; therefore, the accuracy of the data should be confirmed by the receivers after recovering the data.
-
4. Confidentiality: to avoid eavesdropping when the data is in transmission through an unsecure channel, the confidentiality is also an important requirement in data sharing.
3 The Proposed Scheme
Table 1
The notations used in the proposed scheme.
| Notations |
Descriptions |
| M |
Shared data in the cloud service |
| n |
Sequence number of the shared data |
| k |
Random number, $k\in {Z_{p}^{\ast }}$
|
| r |
Random number for the shared data, $r\in {Z_{p}^{\ast }}$
|
| ${H_{1}}()$ |
Hash function, ${H_{1}}():{\{0,1\}^{\ast }}\to {G_{1}}$
|
| ${H_{2}}()$ |
Hash function, ${H_{2}}():{\{0,1\}^{\ast }}\to \{0,1\}$
|
| ${G_{1}}$ |
A cyclic additive group of a large prime order p
|
| ${G_{2}}$ |
A cyclic multiplicative group of a large prime order p
|
| $\widehat{e}$ |
Bilinear mapping, $\widehat{e}:{G_{1}}\times {G_{1}}\to {G_{2}}$
|
| x |
Master key, $g\in {Z_{p}^{\ast }}$
|
| g |
Generator of ${G_{1}}$
|
| ${P_{i}}$ |
The public key of cloud storage service member, ${P_{i}}={H_{1}}({\mathit{ID}_{i}})\in {G_{1}}$
|
| ${S_{i}}$ |
The private key of cloud storage service member, ${S_{i}}=x{P_{i}}\in {G_{1}}$
|
In the proposed scheme, M is the data shared in the cloud service, n is the shared data’s sequence number, and r is a random number which is chosen by the data owner for the shared data. The proposed scheme consists of three phases: (1) the Setup Phase, (2) the Initialization Phase, and (3) the Verification Phase. The three phases are described below. The notations used in the proposed scheme are listed as follows:
The setup phase: suppose the group size is
n. CA determines two hash functions
${H_{1}}(.):{\{0,1\}^{\ast }}\to {G_{1}}$ and
${H_{2}}(.):{\{0,1\}^{\ast }}\to \{0,1\}$, an additive cyclic group
${G_{1}}$ of order
q, where
q is a large prime number, a multiplicative group
${G_{2}}$ of the same order, one bilinear mapping
$\widehat{e}$, a generator
g of
${G_{1}}$, and a master key
$x\in {Z_{q}^{\ast }}$. Then, CA computes
$w=x\times g$ and generates the key pair (
${P_{i}}$,
${S_{i}}$) for every member in the cloud service, where
${P_{i}}={H_{1}}({\mathit{ID}_{i}})\in {G_{1}}$, and
${S_{i}}=g{P_{i}}\in {G_{1}}$. After that, CA sends
$({G_{1}},{G_{2}},\widehat{e},{H_{2}},{P_{i}},{S_{i}},g,q)$ through a secure channel to every member who registers on the cloud service. Figure
1 illustrates the steps of the setup phase.
The initialization phase: when the data owner
i wants to share his data with other members on the cloud service; the data owner creates a set
G to store the public keys of the members whom the data will be shared with, e.g.
$G=\{{P_{j}},{P_{k}},\dots ,{P_{n}}\}$. Then the data owner
i performs the following initialization phase.
-
1. Select two random numbers $k,r\in {Z_{q}^{\ast }}$.
-
2. Compute a parameter $Q=k{\textstyle\prod _{l=i}^{n}}{P_{l}}$.
-
3. Compute a session key $K=\widehat{e}(Q/{P_{i}},{S_{i}})$.
-
4. Compute $z\equiv r\times g\hspace{0.2em}\mathrm{mod} \hspace{0.2em}q$.
-
5. Compute $R\equiv n\times z\hspace{0.2em}\mathrm{mod} \hspace{0.2em}q$.
-
6. Compute $m\equiv M+(r\times n\times K\times g)\hspace{0.2em}\mathrm{mod} \hspace{0.2em}q$.
-
7. Compute $v\equiv m+{H_{2}}(R)\hspace{0.2em}\mathrm{mod} \hspace{0.2em}q$.
-
8. Compute $u\equiv (r-{S_{i}}\times v)\times g\hspace{0.2em}\mathrm{mod} \hspace{0.2em}q$.
-
9. Share
$v,u,n,Q$ on the cloud service. The above steps are shown in Fig.
2.
The verification phase: when the member
j of the cloud service wants to read data shared by data owner
i, the following verification phase is performed.
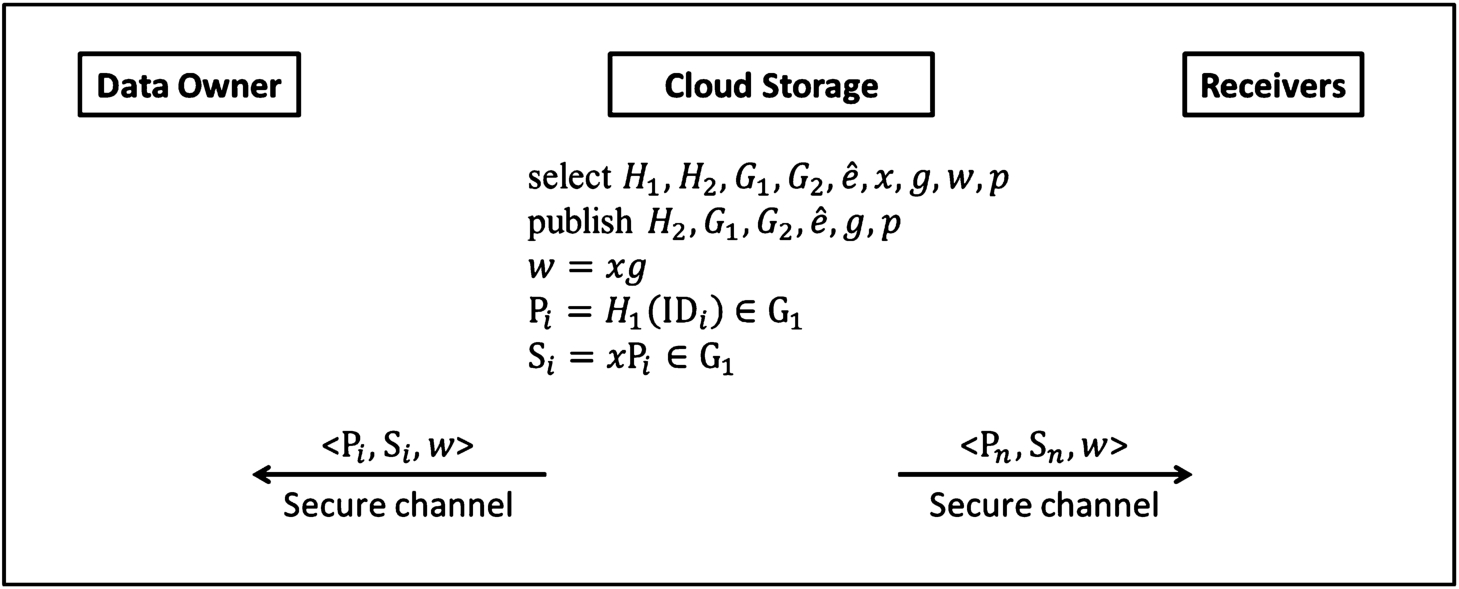
Fig. 1
The steps of the setup phase.
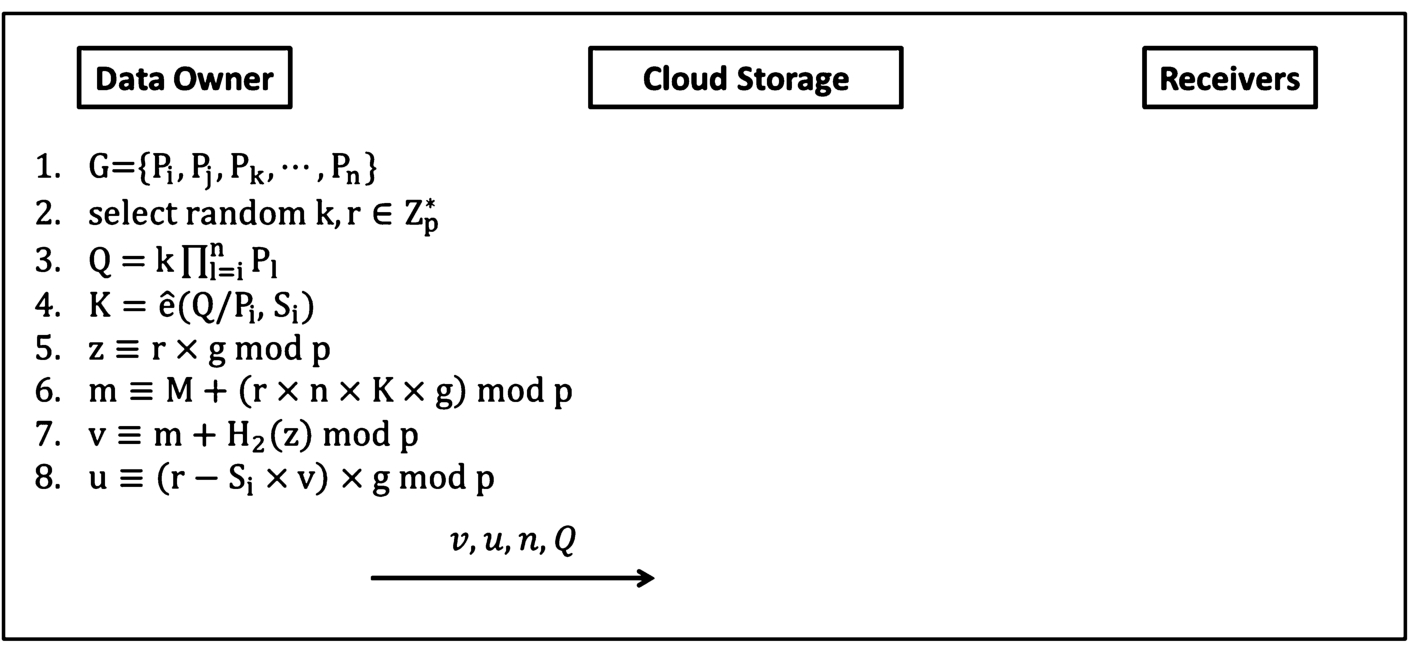
Fig. 2
The steps of the initialization phase.
4 Analyses
In this section, we give the security and computation cost analyses as follows.
4.1 Security Analysis
Forward secrecy and backward secrecy: the encryption key is computed by $K=\widehat{e}(Q/{P_{i}},{S_{i}})$, where $Q=k{\textstyle\prod _{l=i}^{n}}{P_{l}}$. The parameter k is selected randomly in every session in the proposed scheme. Due to the discrete logarithm problem (DLP), k is hard to be computed. Therefore, neither previous members nor new entrants can compute other keys except the session they are involved in. As a result, forward secrecy and backward secrecy are achieved in this proposed scheme.
Source authentication: when a legal member wants to authenticate the data, the member can compute
$z\equiv u+v\times {P_{i}}\times w\hspace{0.2em}\mathrm{mod} \hspace{0.2em}q$. Assume an attacker attempts to impersonate the legal data owner, then the attacker uses its public key
${P_{a}}$ to compute its private key
${S_{a}}$ and
${u_{a}}\equiv (r-{S_{a}}\times v)\times g\hspace{0.2em}\mathrm{mod} \hspace{0.2em}q$. Then, the attacker uploads
$(v,{u_{a}},n,Q)$ to the cloud service. When a receiver recovers the data send by the attacker, the following equations are used:
The receiver can verify whether the data is from the legal data owner by determining if the result,
M, is meaningless or not.
Data integrity: legal members can verify the integrity of the data using the following equations:
and
According to the equations above, if the sequence number
n is altered to
a, or
v is altered to
${v_{a}}$ by an attacker during transmission; the recovered data will become meaningless. When a legal member decrypts a packet, the member has to compute
R by
z and get
m by computing
R. As a result, without the right sequence number and the original
m, the recovered data will be meaningless.
Confidentiality: besides the integrity of data, data confidentiality is also considered in the proposed scheme. Data should be recoverable only by the members whom the data owner wants to share with. If an attacker tries to recover the data using the following equations without the correct private key or the random number
r, the recovered message will be meaningless.
and
With regard to the privacy and the security in cloud storage service, the security requirements of the proposed scheme is compared with Zhao
et al.’s and Han
et al.’s scheme in Table
2. As Table
2 shows, the proposed scheme and Han
et al.’s scheme can achieve forward secrecy and backward secrecy, authentication of the data source, integrity of the data, and the confidentiality of the data. However, Zhao
et al.’s scheme cannot satisfy the source authentication requirement.
Table 2
The comparisons of security requirements.
| Security requirements |
| Schemes |
Zhao et al. (2010) scheme |
Han et al. (2013) scheme |
The proposed scheme |
| Forward secrecy and |
Yes |
Yes |
Yes |
| backward secrecy |
| Source authentication |
No |
Yes |
Yes |
| Data integrity |
Yes |
Yes |
Yes |
| Confidentiality |
Yes |
Yes |
Yes |
4.2 Computation Cost Analysis
In the aspect of computational cost analysis, the proposed scheme is compared with Zhao
et al.’s scheme and Han
et al.’s scheme in Table
3.
${T_{A}}$ is the time complexity of point addition,
${T_{B}}$ is the time complexity of bilinear paring,
${T_{M}}$ is the time complexity of real number multiplication, and
${T_{E}}$ is the time complexity of exponential operation. There is no exponential operation in the proposed scheme; therefore, it is obvious that the proposed scheme is more efficient than the scheme proposed by Han
et al.
Table 3
Comparison of time complexity.
| Computational costs |
| Schemes |
Zhao et al. (2010) scheme |
Han et al. (2013) scheme |
The proposed scheme |
| Data owner |
$15{T_{A}}$ |
$6{T_{B}}+8{T_{E}}$ |
$(n+10){T_{A}}+{T_{B}}+2{T_{M}}$ |
| Receiver |
$2{T_{A}}$ |
$2{T_{B}}+4{T_{E}}$ |
$8{T_{A}}+{T_{B}}$ |
| Cloud storage |
$3{T_{A}}$ |
$2{T_{B}}+{T_{E}}$ |
$2{T_{A}}$ |
| PKG |
– |
$5{T_{B}}+11{T_{E}}$ |
– |
5 Conclusions
In this paper, we proposed a new data sharing scheme for cloud services. In the aspect of security, we achieved authentication of data source as well as data integrity and confidentiality. Furthermore, forward secrecy and backward secrecy are satisfied by using bilinear pairing to compute a common encryption key. In the aspect of efficiency, we use the concept of message recovery to address the problem that signed information might be lost during transmission. This approach also reduces the computation cost without using any exponential operation. Moreover, we compute a common key for every data to reduce the encryption time. Although the computation cost of the proposed scheme is higher than Zhao et al.’s scheme, but Zhao et al.’s scheme cannot achieve the security requirement of source authentication. Therefore, the proposed scheme is more secure and more efficient than the related works.

