Abstract
An adaptive multi-rate wideband (AMR-WB) speech codec with a sampling rate of 16 kHz is known as one of the speech codecs employed in handheld devices that support 4G mobile communication systems. When applied to smartphones, it provides a superior speech quality relative to conventional speech codecs. Nonetheless, a major disadvantage is that an algebraic codebook search occupies a significant computational load in an AMR-WB encoder. In other words, the high computational complexity accounts for the high power consumption on a smartphone battery. This paper presents an improved version of depth-first tree search (DF) algorithm as a means to considerably reduce the complexity of an algebraic codebook search in an AMR-WB speech codec. This proposed search algorithm firstly involves the choice of a specified number of candidate pulses according to a pulse contribution ranking. Subsequently, a DF search is performed on the candidate pulses for a set of best pulses. Consequently, the target of the search and computational complexity reduction can be reached as expected. With a well maintained speech quality, this proposal demonstrates a search performance superiority over a DF and a global pulse replacement approach. Furthermore, with DF as a benchmark, a computational load reduction above 73% is reached in all coding modes.
1 Introduction
Due to the double advantage of low bit rate and high speech quality, the algebraic code-excited linear-prediction (ACELP)-based speech coding technique (Adoul
et al.,
1987; Laflamme
et al.,
1991; Salami
et al.,
1998; Bessette
et al.,
2002) is the type of technique most widely used to digital speech communication systems, and is adopted in a great number of speech codec standards, such as G.723.1, G.729 (ITU-T Recommendation and 729,
1996), G.729.1 (ITU-T Recommendation and 1,
2006; Geiser
et al.,
2007) in International Telecommunication Union (ITU), adaptive multi-rate narrowband (AMR-NB) (3GPP TS 26.090,
2012a) and wideband (AMR-WB) (3GPP TS 26.190,
2012b; Ojala
et al.,
2006; Varga
et al.,
2006) in the 3rd Generation Partnership Project (3GPP). Among such protocols, an AMR-WB speech codec with a 16 kHz sampling rate is applied to 4G mobile communication system as a way to remarkably improve the speech quality of a smartphone.
An AMR-WB codec is a multi-mode speech codec with 9 wideband speech coding modes with bitrates of 23.85, 23.05, 19.85, 18.25, 15.85, 14.25, 12.65, 8.85 and 6.6 kbps. ACELP is developed as an excellent speech coding technique, but a price paid is a high computational complexity required in an AMR-WB codec, particularly much higher than in an AMR-NB one. Using an AMR-WB speech codec, the speech quality of a smartphone can be improved, but at the cost of high power consumption on a smartphone battery.
In an AMR-WB encoder, a depth-first tree search (DF) algorithm is performed for the purpose of an algebraic codebook search, and a DF search is found to occupy a significant computational load in various speech coding modes. A brief literature survey on the complexity reduction in algebraic codebook search is given as follows. An attempt is made to decrease the number of the candidate positions in a candidate scheme for fast ACELP search (Chen
et al.,
2002). As presented in Park
et al. (
2002), the least significant pulse is replaced in an iterative manner. Developed on the basis of Park
et al. (
2002), a global pulse replacement (GPR) (Lee
et al.,
2003), is adopted by G.729.1 (ITU-T Recommendation and 1,
2006). An iteration-free pulse replacement (IFPR) (Lee
et al.,
2007) method and a number of previously published reduced candidate mechanism (RCM) based search algorithms (Yeh and Su,
2012; Chu
et al.,
2014; Ku
et al.,
2014) are proposed to further reduce the search complexity in an efficient way. In addition, the issue of computational complexity reduction has been addressed in literature, as presented in Tsai and Yang (
2006).
As can be found in literature, a continuous effort has been made to address the issue of computational complexity reduction for an AMR-WB speech codec. A major motivation behind this is to meet the energy saving requirement on handheld devices, e.g. smartphones, for an extended operational time period.
This improved algebraic codebook search algorithm is a combined use of the RCM approach (Yeh and Su,
2012) and a DF algorithm. An RCM approach requires to locate 2–6 candidate pulses of each track, as a prerequisite, in an algebraic codebook search at 12.65 kbps and higher AMR-WB modes. In this context, there is no way to reduce the search complexity using RCM. For this sake, a specified number of candidate pulses are located out of each track in advance of a search task, and then the scope of DF search for a set of best pulses is confined within all the candidate pulses. In this manner, the search complexity can be reduced significantly, and the mechanism of the candidate pulse determination will be detailed herein.
This paper is outlined as follows. The coding criterion of algebraic codebook search in AMR-WB is briefly reviewed in Section
2. Presented in Section
3 is an efficient approach for the purpose of search complexity reduction. Experimental results are demonstrated and discussed in Section
4. This work is summarized at the end of this paper.
2 Algebraic Codebook Search in AMR-WB
In AMR-WB speech codec, the algebraic codebook structures corresponding to nine coding modes with bit rates of 23.85, 23.05, 19.85, 18.25, 15.85, 14.25, 12.65, 8.85 and 6.60 kbps are given in 3GPP TS 26.190 (
2012b). The codebook is structured using an interleaved single-pulse permutation (ISPP) scheme, where each pulse is with an amplitude of +1 or −1. As can be found, a codebook contains 2 tracks, each with 32 pulse positions, in the 6.60 kbps mode, and a nonzero pulse is located. In contrast, a codebook has 4 tracks in the remaining eight coding modes with bit rates of 8.85–23.85 kbps, and 16 pulse positions are assigned to each track. Subsequently, 1–6 nonzero pulses are located according to the specified coding mode.
The optimal codevector
${\mathbf{c}_{k}}=\{{c_{k}}(n)\}$ is thus found by minimizing the mean squared weighted error between the original and the synthesized speeches (Bessette
et al.,
2002), defined as
where
x denotes the target vector,
g a scaling gain factor, and
H a lower triangular convolution matrix. It can be shown that the optimal codevector is the one maximizing the term
${Q_{k}}$ (Bessette
et al.,
2002; 3GPP TS 26.190,
2012b):
where
$\mathbf{d}={\mathbf{x}^{\mathrm{T}}}\mathbf{H}$, the correlation function, is expressed as
where
$h(n)$ is the impulse response of the weighted synthesis filter,
L is the speech subframe size. The correlations of
$h(n)$ are contained in the symmetric matrix
$\boldsymbol{\Phi }={\mathbf{H}^{\mathrm{T}}}\mathbf{H}$, where the entries are given by
In an attempt to locate the optimal vector, (
2) is evaluated repeatedly and a full search is performed for
${N_{\mathrm{FS}}}$ number of times, given as
where
${N_{\mathrm{T}}}$ represents the number of tracks,
${N_{\mathrm{p}}}$ the number of pulse positions assigned to each track, and
${N_{\mathrm{s}}}({T_{i}})$ the number of optimal pulses that need to be located in track
i. Taking the 12.65 kbps mode in 3GPP TS 26.190 (
2012b) as an instance,
${N_{\mathrm{T}}}=4$,
${N_{\mathrm{p}}}=16$,
${N_{\mathrm{s}}}({T_{i}})=2$ for all
i, meaning that it requires as many as
${({C_{2}^{16}})^{4}}$ full searches that is an impractically large load to implement. For this sake, a DF algorithm is employed in AMR-WB for search load reduction.
Table 1
Depth-first tree search complexity in AMR-WB.
| Mode (kbit/s) |
Number of levels in tree search |
Number of no search levels |
Tested combinations in remaining levels (NTested) |
Iteration (NIter) |
Total searches (NIter × NTested) |
| 23.85 |
12 |
2 |
$(2+2+3+4+5+6+7+8+8+8)\times 16$ |
1 |
848 |
| 23.05 |
12 |
2 |
$(2+2+3+4+5+6+7+8+8+8)\times 16$ |
2 |
1696 |
| 19.85 |
9 |
2 |
$(2+3+4+5+6+7+8)\times 16$ |
3 |
1680 |
| 18.25 |
8 |
2 |
$(4+4+6+6+8+8)\times 16$ |
3 |
1728 |
| 15.85 |
6 |
2 |
$(4+6+8+8)\times 16$ |
4 |
1664 |
| 14.25 |
5 |
1 |
$(4+6+8+8)\times 16$ |
4 |
1664 |
| 12.65 |
4 |
1 |
$(4+8+8)\times 16$ |
4 |
1280 |
| 8.85 |
2 |
0 |
$(4+8)\times 16$ |
4 |
768 |
| 6.60 |
1 |
0 |
$32\times 32$ |
1 |
1024 |
As listed in Table
1, the number of levels in a tree search is evaluated as one-half the total number of nonzero pulses. In other words, there are 2 nonzero pulse contained in each level, and a search is conducted on consecutive levels to locate a pair of best nonzero pulses. The search scope in each level is confined to 2 neighbouring tracks, say,
$({T_{0}},{T_{1}})$,
$({T_{1}},{T_{2}})$,
$({T_{2}},{T_{3}})$,
$({T_{3}},{T_{0}})$. A pulse is located until a set of best pulses is found. Besides, 3 parameters are specified for each speech coding mode. The first parameter, designated as the number of no search level, refers to the number of levels where a set of best pulses is specified directly, meaning that there is no need to perform any search task. The second, termed as
NTested, refers to the test combinations in the remaining levels, and the third, denoted by
NIter, represents the number of iterations. Accordingly, the total number of searches is given as
NIter ×
NTested.
A DF search is illustrated with the example of 12.65 kbps mode. The goal is to locate the desired 8 best pulses, according to which there are 4 levels involved in a tree search. As the first step, a set of best pulses is specified directly, not by way of search, in level 1. Subsequently, respective numbers of searches are performed over the remaining levels, as specified in Table
1, i.e.
$4\times 16$,
$8\times 16$,
$8\times 16$, such that the best pulses for each level are located. In this manner, it requires 4 iterations to get the search done, that is, a total of
$4\times (4\times 16+8\times 16+8\times 16)=1280$ searches are required. In short, the DF search accounts for a significant computational load in the AMR-WB encoder operation. Besides, two existing methods, the GPR and RCM approaches, will be discussed in this section.
2.1 The GPR Search Approach
The GPR approach is derived from the least important pulse replacement approach (Park
et al.,
2002). In order to prevent the termination of the pulse replacement procedure without finding the best codevector in the GPR algorithm, except for the only track that contains the least important pulse, all the tracks are searched for a new pulse. That is, the new pulse is sought by replacing each pulse in each track with a new one so that the (2) associated with a new codevector is maximized. On the ground that the variation in (2) is always maximized during the replacement procedure, the codevector approaches the best solution rapidly as this procedure is repeated. When the value of
${Q_{k}}$ once reaches the upper bound, the search procedure is then terminated. Furthermore, the average number of searches, required by the GPR approach, is represented as
where
R represents the iteration number. For instance,
${N_{\mathrm{T}}}=4$,
${N_{\mathrm{p}}}=16$,
${N_{\mathrm{s}}}({T_{i}})=4$ for all
i in the 18.25 kbps mode, that is, the initial
${Q_{k}}$ is evaluated and the initial codevector is firstly yielded with one search. Subsequently, it requires 192 searches to seek the new pulse during the first pulse replacement procedure and requires an average of 180 during the second. Therefore, the GPR approach requires 193 searches in the first iteration
$(R=1)$, 373 in the second
$(R=2)$, 553 in the third
$(R=3)$, and so on.
2.2 The RCM Search Approach
Ahead of a search task, the number of candidate pulses in each track is reduced for the purpose of search complexity reduction. This is done in this work according to the contribution of individual pulses. It is that in each track a pulse sorting is made by the contribution thereof in descending order as the first step, and then the top M pulses are chosen as the candidate pulses for a full search.
In Yeh and Su (
2012), the contribution made by individual pulses is given as (
2), that is, a higher value of
${Q_{k}}$ reflects a higher contribution. In consideration of merely a single pulse contribution, the number of nonzero pulses in the codevector
${\mathrm{c}_{k}}$ is reduced to 1. Therefore, (
2) can be simplified into (
7), where the numerator of (
7) is derived from (
2) and (
3), and the denominator of (
7) is derived from (
2) and (
4), respectively. Just as in (
2), a higher value of
${Q_{k}^{i}}$ represents a higher contribution of the
ith pulse. This RCM approach is presented as an algorithm below.
Algorithm 1: The RCM search procedure.
Sort the pulses in each track in a descending order by individual pulse contribution evaluated as (
7).
Determine the value of M, and select the top M pulses in each track as the candidate pulses.
Search for the best pulses over all the combinations of the candidate pulses through a full search by means of (
2).
Terminate a searching task at the moment the combination of the best pulses is done.
Furthermore, the number of searches required in RCM is represented as
where
M represents the number of candidate pulses specified. Taking the 12.65 kbps mode as an instance,
${N_{\mathrm{T}}}=4$,
${N_{\mathrm{p}}}=16$,
${N_{\mathrm{s}}}({T_{i}})=2$ for all
i, meaning that it requires
${({C_{2}^{M}})^{4}}$ searches, i.e. 1 296 searches for
$M=4$ and 50 625 for
$M=6$. It is obvious that there is no way to reduce the search load using RCM at 12.65 kbps and higher AMR-WB modes.
3 Proposed Search Algorithm
Using a combination of RCM and DF approaches, an improved depth-first tree search (IDFT) is presented in this section as a way to reach the goal of search complexity reduction. This is done by means of a reduction in the number of candidate pulses contained in each track ahead of a DF search, and the reduction is made according to the contribution made by each pulse, but with a different criterion to evaluate individual pulse contribution than in RCM. Hence, this section firstly refers to the contribution made by a single pulse, and then details a search algorithm.
3.1 Analysis on the Contribution Made by an Individual Pulse
It is an issue of our interest whether there exists a correlation between the contribution made by a single pulse in each track and the best codevector via a DF search. More precisely, is there a probability that a pulse with a higher contribution in a track is more likely to serve as a component of the determined best codevector, i.e. a best pulse. The AMR-WB criterion Bessette
et al. (
2002); 3GPP TS 26.190 (
2012b) is treated as a measure of the contribution made by a single pulse in this work, that is,
where
${r_{\mathrm{LTP}}}(n)$ denotes the residual signal after a long term prediction,
${E_{\mathrm{d}}}={\mathbf{d}^{\mathrm{T}}}\mathbf{d}$ and
${E^{\mathrm{r}}}={\mathbf{r}_{\mathrm{LTP}}^{\mathrm{T}}}{\mathbf{r}_{\mathrm{LTP}}^{\phantom{\mathrm{T}}}}$ represent the energy of
$d(n)$ and
${r_{\mathrm{LTP}}}(n)$, respectively, and
α is a coding mode-dependent constant, i.e.
$\alpha =2$ for 6.6 and 8.85 modes;
$\alpha =1$ for 12.65, 14.25 and 15.85 modes;
$\alpha =0.8$ for 18.25 mode;
$\alpha =0.75$ for 19.85 mode; and
$\alpha =0.5$ for 23.05 and 23.85 modes. The value of
$b(n)$ varies in tandem with the contribution of the
nth pulse.
Moreover, a hit probability is defined here as
where
$\mathit{NH}({T_{t}},n)$ represents the times that the
nth ranked pulse in terms of contribution on track
${T_{t}}$ acts as one of the best pulses via the DF search,
TSF the total number of testing subframes,
${N_{\mathrm{T}}}$ the number of tracks, and
${N_{\mathrm{p}}}$ the number of pulses contained in each track.
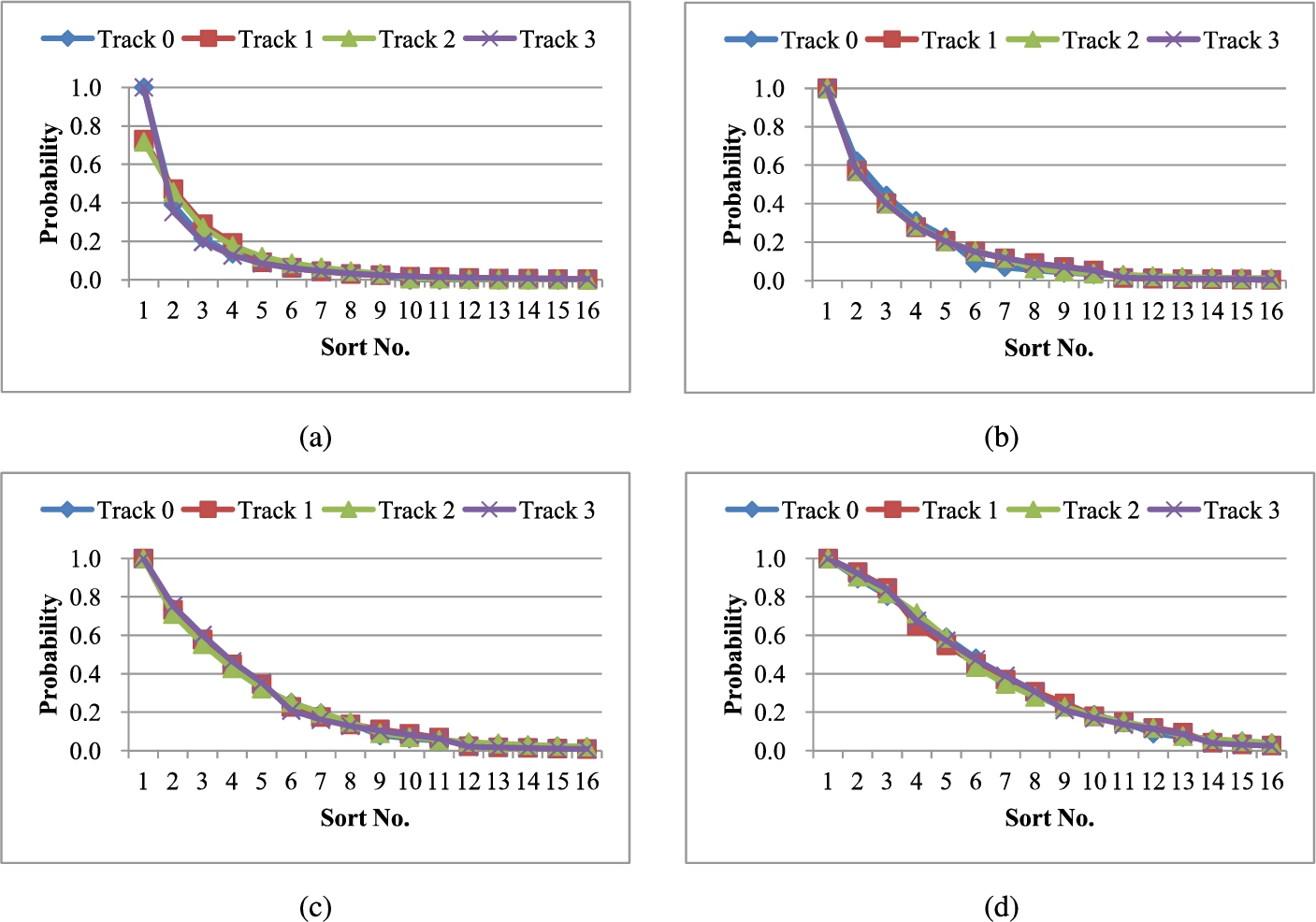
Fig. 1
Probability of a sorted pulse hitting an optimal pulse among tracks in (a) 12.65, (b) 15.85, (c) 18.25, and (d) 23.85 kbps modes.
Presented in Fig.
1 are the curves of four coding mode-dependent statistics according to (
10), that is, the probability that a sorted pulse hits one of the best pulses among tracks in 12.65, 15.85, 18.25, and 23.85 kbps modes. There are a total of 89,020 subframes, i.e.
$\mathit{TSF}=89\hspace{0.1667em}020$, in a Chinese-language speech database. As given in Fig.
1, the value of
$b(n)$ is positively correlated to the hit probability in each track, that is, a pulse with a high value of
$b(n)$ is more likely to be one of the best pulses on the corresponding track. Taking the 15.85 kbps mode as an instance, there are 3 best pulses waiting to be located from each track, and the one with the maximum value of
$b(n)$ in each track is specified as one of them (3GPP TS 26.190,
2012b). Hence, there is a 100% hit probability for such pulse, and the hit probability in each track numbers 3, since there exist three best pulses in each track during a search task. As indicated, the hit probability decreases with the pulse contribution ranking.
Hence, the presumption, as referred to at the beginning of this subsection, is validated accordingly. In this context, pulses with a high contribution can be chosen as candidate pulses as a way to reduce the search complexity significantly.
3.2 Improved Depth-First Tree Search Method
Based on the analysis in Section
3.1, the IDFT search strategy is proposed for the purpose of search complexity reduction. This approach is decomposed into following steps. Firstly,
$b(n)$ is evaluated as the contribution made by pulse
n, and then pulses contained in each track are sorted in terms of contribution in a descending order. Subsequently, the first
M $(1\leqslant M\leqslant 16)$ ranked pulses are treated as candidate pulses. Then, a DF search is performed on all the candidate pulses, and the pulse combination with the maximum value of
${Q_{k}}$, as given in (
2), is the desired best vector. Finally, this proposal is presented as an algorithm below.
Algorithm 2: The IDFT search procedure.
Apply (
9) to evaluate the individual pulse contribution, following which all the pulses in associated tracks are sorted by contributions.
Specify the value of M, and select the first M ranked pulses in each track as the candidate pulses.
Search for the best pulses among all the candidate pulses through a DF search by means of (
2).
Terminate the search process the moment the combination of the best pulses is acquired.
4 Experimental Results
There are two experiments conducted in this work. The first is a search complexity comparison among various search approaches. The second is that various approaches are compared with ITU-T P.862 perceptual evaluation of speech quality (PESQ) ITU-T Recommendation and 862 (
2001) as an objective measure of speech quality. The test objects are those selected out of a Chinese-language speech database, containing 1 694 syllables out of 50 sentences for a duration over 445 s and 89 020 subframes.
For the brevity of the following discussion, the proposed IDFT approach with M candidate pulses is abbreviated as IDFT-M, $1\leqslant M\leqslant 16$. For instance, IDFT-1 symbolizes the one with merely a candidate pulse extracted out of each track. Similarly, the GPR approach with R repetitions is designated as GPR-R.
Table 2
Search complexity comparison among various methods and coding modes.
| Method |
Search complexity and CS (%) in different coding mode (kbit/s) |
| 23.85 |
23.05 |
19.85 |
18.25 |
15.85 |
14.25 |
12.65 |
| DF (Benchmark, 0%) |
848 |
1696 |
1680 |
1728 |
1664 |
1664 |
1280 |
| GPR (CS, %) |
$R=1$ |
71.58 |
85.79 |
87.68 |
88.83 |
90.56 |
91.89 |
91.17 |
|
$R=2$ |
44.46 |
72.23 |
76.10 |
78.41 |
81.97 |
84.65 |
83.52 |
|
$R=3$ |
17.33 |
58.67 |
64.52 |
68.00 |
73.38 |
77.40 |
75.86 |
|
$R=4$ |
−9.79 |
45.11 |
52.95 |
57.58 |
64.78 |
70.16 |
68.20 |
|
$R=5$ |
−36.91 |
31.54 |
41.37 |
47.16 |
56.19 |
62.92 |
60.55 |
| Proposed (CS, %) |
$M=5$ |
– |
– |
– |
89.93 |
87.98 |
85.34 |
83.75 |
|
$M=6$ |
– |
– |
85.89 |
84.38 |
81.49 |
78.37 |
76.88 |
|
$M=7$ |
86.20 |
86.20 |
79.29 |
77.43 |
73.56 |
69.95 |
68.75 |
|
$M=8$ |
79.95 |
79.95 |
72.32 |
69.10 |
65.87 |
61.78 |
59.38 |
|
$M=9$ |
73.00 |
73.00 |
64.29 |
61.81 |
57.21 |
52.64 |
48.75 |
|
$M=10$ |
65.68 |
65.68 |
56.43 |
53.82 |
47.60 |
44.71 |
42.50 |
Table 3
PESQ values comparison among various methods.
| Method |
Mean |
STD |
Drop (%) |
Mean |
STD |
Drop (%) |
|
|
12.65 kbit/s mode |
15.85 kbit/s mode |
| DF |
4.048 |
0.119 |
Benchmark |
4.112 |
0.121 |
Benchmark |
| GPR |
$R=1$ |
3.964 |
0.111 |
2.075 |
4.012 |
0.106 |
2.432 |
|
$R=2$ |
4.016 |
0.114 |
0.791 |
4.060 |
0.111 |
1.265 |
|
$R=3$ |
4.033 |
0.120 |
0.371 |
4.096 |
0.119 |
0.389 |
|
$R=4$ |
4.035 |
0.117 |
0.321 |
4.110 |
0.118 |
0.049 |
|
$R=5$ |
4.035 |
0.114 |
0.321 |
4.117 |
0.118 |
-0.122 |
| Proposed |
$M=5$ |
4.018 |
0.116 |
0.741 |
4.057 |
0.109 |
1.338 |
|
$M=6$ |
4.031 |
0.118 |
0.420 |
4.078 |
0.111 |
0.827 |
|
$M=7$ |
4.039 |
0.111 |
0.222 |
4.097 |
0.113 |
0.365 |
|
$M=8$ |
4.038 |
0.122 |
0.247 |
4.100 |
0.116 |
0.292 |
|
$M=9$ |
4.039 |
0.116 |
0.222 |
4.105 |
0.114 |
0.170 |
|
$M=10$ |
4.039 |
0.115 |
0.222 |
4.104 |
0.124 |
0.195 |
|
|
18.25 kbit/s mode |
23.85 kbit/s mode |
| DF |
4.147 |
0.120 |
Benchmark |
4.164 |
0.120 |
Benchmark |
| GPR |
$R=1$ |
4.028 |
0.106 |
2.870 |
4.050 |
0.116 |
2.738 |
|
$R=2$ |
4.080 |
0.111 |
1.616 |
4.104 |
0.110 |
1.441 |
|
$R=3$ |
4.122 |
0.117 |
0.603 |
4.133 |
0.115 |
0.744 |
|
$R=4$ |
4.134 |
0.121 |
0.313 |
4.152 |
0.118 |
0.288 |
|
$R=5$ |
4.143 |
0.121 |
0.096 |
4.164 |
0.122 |
0.000 |
| Proposed |
$M=5$ |
4.037 |
0.110 |
2.653 |
– |
– |
– |
|
$M=6$ |
4.084 |
0.109 |
1.519 |
3.972 |
0.102 |
4.611 |
|
$M=7$ |
4.111 |
0.119 |
0.868 |
4.059 |
0.110 |
2.522 |
|
$M=8$ |
4.123 |
0.118 |
0.579 |
4.101 |
0.110 |
1.513 |
|
$M=9$ |
4.134 |
0.119 |
0.313 |
4.126 |
0.112 |
0.913 |
|
$M=10$ |
4.137 |
0.121 |
0.241 |
4.141 |
0.116 |
0.552 |
Firstly, listed in Table
2 is a comparison on the search complexity, that is, the number of searches performed and those required in the evaluation of
${Q_{k}}$ defined in (
2). The proposed IDFT search is performed among the first
M ranked pulses on a condition that
M be greater than the number of best pulses in each track. Table
2 firstly gives the number of searches required in a DF approach as a benchmark, and then gives relative search complexity change expressed in percentage form, i.e. computational saving (CS), in GPR and the proposed IDFT approaches for comparison purposes. A high value of CS reflects a high search complexity reduction, while a negative sign indicates a search complexity higher than in the DF case.
With DF as a benchmark, a noticeable computational saving is demonstrated, and the aim of search load reduction is achieved as expected by this proposal. It is noted that a CS above 50% can be reached for $M\leqslant 8$. Nevertheless, a comparison on speech quality must be made for a complete performance assessment of this presented search algorithm.
Table
3 gives a PESQ comparison, including the mean and the standard deviation (STD), in the 12.65, 15.85, 18.25 and 23.85 kbps modes. With DF as a benchmark, a minus sign in the comparison represents a superior PESQ relative to the benchmark. As pointed out in Yeh and Su (
2012), a subjective speech quality can be well maintained even though there is a slight drop in PESQ.
Table 4
Overall performance comparison among various methods.
|
Method |
Mode (kbit/s) |
|
23.85 |
18.25 |
15.85 |
12.65 |
| DF |
PESQ |
4.164 |
4.147 |
4.112 |
4.048 |
|
Search load |
848 |
1728 |
1664 |
1280 |
| GPR |
The optimum choice of R
|
3 |
3 |
3 |
2 |
|
PESQ |
4.133 |
4.122 |
4.096 |
4.016 |
|
Search load |
701 |
553 |
443 |
211 |
|
CS (%) |
17.33 |
68.00 |
73.38 |
83.52 |
| IDFT |
The optimum choice of M
|
9 |
7 |
6 |
5 |
|
PESQ |
4.126 |
4.111 |
4.078 |
4.018 |
|
Search load |
229 |
390 |
308 |
208 |
|
CS (%) |
73.00 |
77.43 |
81.49 |
83.75 |
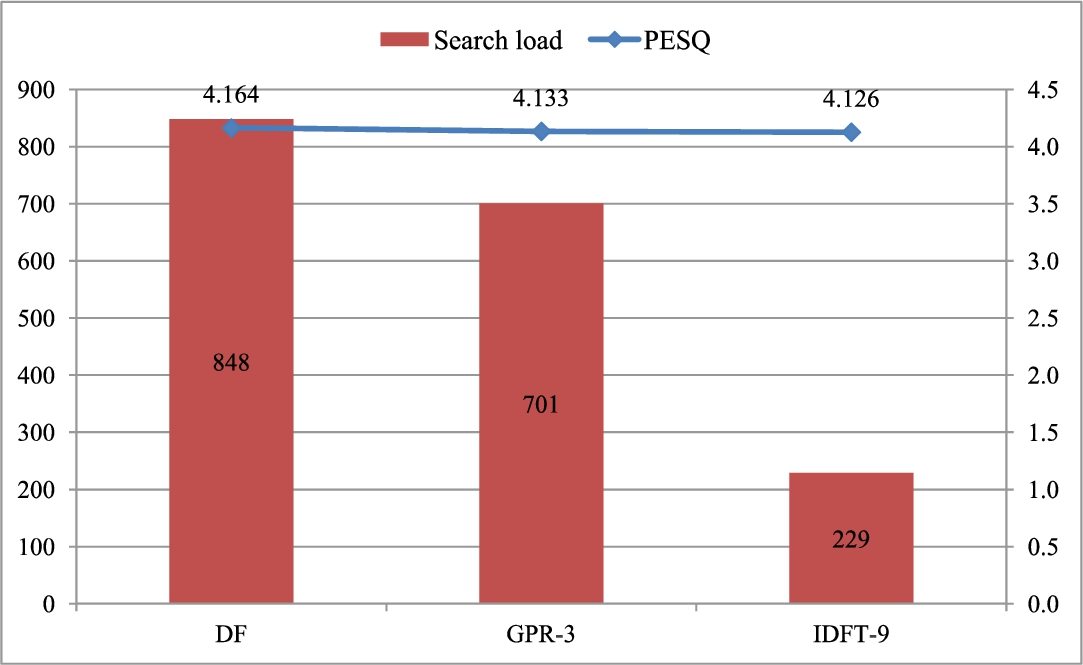
Fig. 2
Overall performance comparison in 23.85 kbps coding mode.
A rearrangement of Tables
2 and
3 gives Table
4. As listed in Table
4, on a condition of PESQ drop stays below 1% as compared with the DF case, the best choice of
R in GPR and
M in IDFT are respectively tabulated in various modes, and a performance comparison in the 23.85 kbps coding mode is presented in a graphic form as Fig.
2. The overall performance superiority is demonstrated with a well maintained high speech quality and a computational load reduction beyond 73%. A noticeable superiority over GPR is particularly seen in a high bit rate coding mode.
5 Conclusions
An improved depth-first tree search approach is presented in this work as an efficient means to enhance the search performance of an algebraic codebook search when applied to an AMR-WB speech codec. This improved version of depth-first tree search algorithm is presented as a way not merely to well maintain a high speech quality but also to achieve the aim of complexity reduction in algebraic codebook search. It offers a search performance superiority over a DF and a GPR counterpart. It is worth noting that with DF as a benchmark, a search load reduction beyond 73% is seen in all the coding modes on a condition that PESQ drop stays below 1%.
Furthermore, this improved AMR-WB speech codec can be adopted to improve the VoIP performance on a smartphone. As a consequence, the energy efficiency requirement is achieved for an extended operation time period due to computational load reduction.
Acknowledgements
This research was financially supported by the Ministry of Science and Technology under grant number MOST 104-2221-E-167-025, Taiwan, Republic of China.
References
Adoul, J.-P., Mabilleau, P., Delprat, M., Morissette, S. (1987). Fast CELP coding based on algebraic codes. In: Proceedings of International Conference on Acoustics, Speech, and Signal Processing, pp. 1957–1960.
Bessette, B., Salami, R., Lefebvre, R., Jelínek, M., Rotola-Pukkila, J., Vainio, J., Mikkola, H., Järvinen, K. (2002). The adaptive multirate wideband speech codec (AMR-WB). IEEE Transactions on Speech and Audio Processing, 10(8), 620–636.
Chen, F.-K., Yang, J.-F., Yan, Y.-L. (2002). Candidate scheme for fast ACELP search. IEE Proceedings – Vision, Image and Signal Processing, 149(1), 10–16.
Chu, C.P., Yeh, C.Y., Hwang, S.H. (2014). An efficient search strategy for ACELP algebraic codebook by means of reduced candidate mechanism and iteration-free pulse replacement. Information Technology and Control, 43(2), 183–187.
Geiser, B., Jax, P., Vary, P., Taddei, H., Schandl, S., Gartner, M., Guillaume, C., Ragot, S. (2007). Bandwidth extension for hierarchical speech and audio coding in ITU-T Rec. G.729.1. IEEE Transactions on Audio, Speech, and Language Processing, 15(8), 2496–2509.
ITU-T Recommendation, 729, G. (1996).
Coding of speech at 8 kbit/s using conjugate-structure algebraic-code-excited linear-prediction (CS-ACELP).
ITU-T Recommendation, 862, P. (2001).
Perceptual evaluation of speech quality (PESQ): an objective method for end-to-end speech quality assessment of narrow-band telephone networks and speech codecs.
ITU-T Recommendation, 1, G. (2006).
G.729 based Embedded Variable bit-rate coder: an 8–32 kbit/s scalable wideband coder bitstream interoperable with G.729.
Ku, N.Y., Yeh, C.Y., Hwang, S.H. (2014). An efficient algebraic codebook search for ACELP speech coder. EURASIP Journal on Audio, Speech, and Music Processing, 2014, 1–9.
Laflamme, C., Adoul, J.-P., Salami, R., Morissette, S., Mabilleau, P. (1991). 16 kbps wideband speech coding technique based on algebraic CELP. In: Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing, pp. 13–16.
Lee, E.D., Lee, M.S., Kim, D.Y. (2003). Global pulse replacement method for fixed codebook search of ACELP speech codec. In: Proceedings of Second IASTED International Conference on Communications, Internet and Information Technology, pp. 372–375.
Lee, E.D., Yun, S.H., Lee, S.I., Ahn, J.M. (2007). Iteration-free pulse replacement method for algebraic codebook search. Electronics Letters, 43(1), 59–60.
Ojala, P., Lakaniemi, A., Lepanaho, H., Jokimies, M. (2006). The adaptive multirate wideband speech codec: system characteristics, quality advances, and deployment strategies. IEEE Communications Magazine, 44(5), 59–65.
Park, H.C., Choi, Y.C., Lee, D.Y. (2002). Efficient codebook search method for ACELP speech codecs. In: Speech Coding, 2002, IEEE Workshop Proceedings, pp. 17–19.
Salami, R., Laflamme, C., Adoul, J.-P., Kataoka, A., Hayashi, S., Moriya, T., Lamblin, C., Massaloux, D., Proust, S., Kroon, P., Shoham, Y. (1998). Design and description of CS-ACELP: a toll quality 8 kb/s speech coder. IEEE Transactions on Speech and Audio Processing, 6(2), 116–130.
Tsai, S.-M., Yang, J.-F. (2006). Efficient algebraic code-excited linear-predictive codebook search. IEE Proceedings – Vision, Image and Signal Processing, 153(6), 761–768.
Varga, I., De Lacovo, R.D., Usai, P. (2006). Standardization of the AMR wideband speech codec in 3GPP and ITU-T. IEEE Communications Magazine, 44(5), 66–73.
Yeh, C.Y., Su, Y.J. (2012). Reduced candidate mechanism for an algebraic code-excited linear-prediction codebook search. IET Communications, 6(17), 2864–2869.
3GPP TS 26.090 (2012a).
Adaptive Multi-Rate (AMR) speech codec; transcoding functions. 3GPP TS 26.090.
3GPP TS 26.190 (2012b).
Adaptive Multi-Rate – Wideband (AMR-WB) speech codec, transcoding functions. 3GPP TS 26.190.

