1 Introduction
Globalization and expansion of the industries cause many environmental problems such as climate change, noise, and air pollution (Haque and Sharif,
2021). The automobile industry is one of the leading contributors worsening environmental issues in terms of a large proportion of greenhouse gases, especially carbon dioxide emission from vehicles (Hu
et al.,
2021). To protect the environment, the use of the green products that consume green energy is very important (Neizari
et al.,
2017). In this manner, hybrid vehicles have become popular and reshaped the automobile industry (Soon
et al.,
2013). Hybrid vehicles which are environmentally friendly products have many features to make significant contributions to the reduction of environmental problems. They consume less power and consequently produce less carbon dioxide than other non-hybrid vehicles (Neizari
et al.,
2017; Pielecha
et al.,
2020). Their engine powers are supported by a small internal combustion engine and a batteries’ bank during the acceleration (Suppes and Storvick,
2016; Wang
et al.,
2023a). Namely, they combine both a gasoline-powered engine and an electric motor (Cekerevac,
2025). In addition, some types of hybrid vehicles use solar and wind power to store electricity (Neizari
et al.,
2017). On the other hand, hybrid vehicle investments are very important for the country’s economy. Thanks to these investments, carbon emissions can be reduced, new job opportunities can be created to solve the unemployment problem, and the trade volume of many companies in the supply chain can increase. In summary, these investments have a great impact both environmentally and economically (Eti
et al.,
2025).
Especially in recent years, factors such as the increase in awareness about global warming and the environment, the decrease in the advantage of diesel and even its ban in some countries have started to direct users to hybrid vehicles. While a similar trend draws attention in Türkiye, it is observed that sales are increasing rapidly. In addition to individual customers, private companies, especially companies that want to reduce their carbon footprint, public institutions and fleets have started to turn to hybrid vehicles.
The fact that hybrid vehicles are becoming increasingly popular around the world is also reflected in the sales statistics. Hybrid vehicles captured 3.2% of the light vehicle market in 2013 and 5.5% in 2021 (Bureau of Transportation Statistics,
2024). In 2021, global hybrid vehicle sales reached 834,000 units while Toyota has sold over 16 million hybrids since 1997. Hybrid vehicles accounted for 18.75% of European new vehicle sales in 2020 and 4.4% of US new vehicle sales in 2021. The statistics demonstrate that hybrid vehicle sales have been increasing globally, with particularly strong growth seen in Europe and the United States. Also, China’s hybrid vehicle sales reached 172,000 units during the first half of 2021 alone (Gitnux Editorial Team,
2024).
Driver wages, fuel, automotive components and service costs increased significantly from 2021 to 2023 in Türkiye. When fuel costs of commercial or service vehicles were compared between 2021 and 2023, an increase of at least 3 times (300%) was observed. This situation reveals how important savings and improvements are for the environment and the economy (Tütüncü
et al.,
2023). According to TUIK data, while 5,980 hybrid cars were registered in 2023, this number increased to 12,941 in 2024. The share of hybrid vehicles in total registrations is 11.4% in Türkiye (Türkiye Statistical Institute,
2025). The global hybrid vehicle market size was evaluated at 156.97 billion $ in 2023. It is estimated that the hybrid vehicle sector will exhibit a compound annual growth rate of 26.03% from 2024 to 2032 (Market Research Future,
2025).
The decision to purchase a hybrid vehicle requires rigorous analysis since there are many hybrid vehicle alternatives with almost similar hybrid features. Selecting and purchasing a proper hybrid vehicle is a classical Multi Criteria Decision Making (MCDM) problem including conflicting quantitative and qualitative criteria such as hybrid type, powertrain features, price, safety, and reliability. Most of these criteria are evaluated with human judgments which cannot be quantified precisely. In other words, it is not easy to give the exact values to the criteria weights and performances of the alternatives under each criterion. In the literature, such problems have been solved by the fuzzy set theory developed by Zadeh (
1965) (Zhang
et al.,
2016). Many methods and theories have been proposed based on fuzzy set theory to process imprecision and uncertainty. However, the basic component of fuzzy sets is only a degree of membership. Atanassov (
1986) generalized the idea of Zadeh (
1965) to Intuitionistic Fuzzy (IF) sets. IF sets use both membership and non-membership degrees and the sum of them is less than one (Jamkhaneh and Nadarajah,
2015). The membership, non-membership and hesitancy functions are the main elements of IF sets (Onar
et al.,
2015; Ali
et al.,
2023; Asif
et al.,
2025). A fuzzy set is also an IF set. The sum of the membership and non-membership degrees is one. But the sum of two degrees can be less than one. It means that there is a certain uncertainty in the membership or non-membership decision. IF set is a suitable tool for such situations (Jamkhaneh and Nadarajah,
2015). Then, IVIF sets were developed by Atanassov and Gargov (
1989). Membership and non-membership function values of IVIF sets are defined as intervals rather than a single number (Li,
2011; Zhang
et al.,
2016). Some authors have argued that an IVIF set is more powerful, practical and flexible tool to cope with fuzziness and uncertainty than the other types of IF set (Chen
et al.,
2011; Onar
et al.,
2015). They have a strong ability to express uncertainty in terms of membership, non-membership, and hesitation degrees (Fan and Xiao,
2020).
This paper contributes to hybrid vehicles selection and IVIF sets integrated with Analytic Hierarchy Process (AHP) and Multi-Attributive Border Approximation Area Comparison (MABAC) methods. The presented approach handles the uncertainty and fuzziness in the problem under the IF environment. IF sets are used for incomplete and incompletely defined data since they include uncertainty. So, it provides more consistent results. With the help of IF sets, the situations where fuzzy sets cannot respond or are insufficient are handled efficiently (Tuğrul and Citil,
2022). On the other hand, the presented approach utilized the IVIF numbers that are tools of IF sets. Both membership and non-membership degrees are in interval format in IVIF numbers. There are some advantages and disadvantages of using IVIF numbers instead of fuzzy numbers or IF numbers in the decision-making process and therefore in the MCDM methods used;
i) Fuzzy set considers only membership degree, IF set considers both membership and non-membership degree. The type of membership value is fixed real-valued for fuzzy set and IF set. IVIF set also considers both membership and non-membership degree with interval format. ii) In fuzzy set, the parameter value is not precise; in IF set, it is more precise; and in IVIF set it is most precise. iii) Hesitation degree cannot find out in fuzzy set, while it can find out in IF set and IVIF set. iv) Boundaries are fixed in fuzzy set and IF set but there is interval valued fixed boundaries in IVIF set. v) The accuracy and efficiency are low in fuzzy set, average in IF set and high in IVIF set. vi) Fuzzy set measures the belongingness only. IF set measures both the belongingness and nonbelongingness. IVIF set measures both the belongingness and nonbelongingness in interval format. vii) For robust and effective decision-making, fuzzy set is suitable, IF set is more suitable, IVIF set is the most suitable. viii) Computational method is very easy with fuzzy set, easy with IF set and little complex with IVIF set (Ouyang and Guo,
2018; Wan and Dong,
2020; Chen
et al.,
2022; Mandal
et al.,
2024).
In order to utilize all the advantages of the IVIF sets mentioned above and to effectively quantify the uncertainty in the decision-making process and to provide consistent results to the decision makers, a decision-making approach based on AHP and MABAC methods in which IVIF numbers are processed is proposed in this study. Although fuzzy MABAC method has been already integrated with fuzzy AHP to analyse MCDM problems in different fields, they have not been used together under IVIF environment. To the best of our knowledge, there is not any research that integrates IVIF AHP process into IVIF MABAC for the hybrid vehicle selection. The strength of these integrated methods is that, despite the subjectivity and vagueness in the structure of the evaluation process, they can be easily understood and applied.
IVIF AHP is used for determining the hybrid vehicles selection criteria weights. AHP has some outstanding features compared to other subjective weighting methods, and it is suitable for the structure of the problem sought to be solved in this study. It does not require dependencies between criteria as in other methods. It is easy in terms of calculation steps, and effective solutions can be obtained by making pairwise comparisons in determining the criteria weights (Perçin,
2022). In addition, the method is easily adaptable to the IVIF environment. When viewed from this aspect, there are no dependencies between the criteria in the problem of the current study. Also, the number of criteria is relatively low in terms of dragging decision makers into inconsistency. When all these situations are evaluated, performing AHP method and its extension to IVIF sets are appropriate for this study. On the other hand, IVIF MABAC is used for ranking hybrid vehicles alternatives. The main advantages of MABAC method can be listed as having a simple computation process, ability to assign criteria weights, being suitable for the problems with uncertain data, and ability to integrate with different uncertainty theories (Xue
et al.,
2016; Patel and Chang,
2024). Considering the advantages of both AHP and MABAC methods, it is thought that their extensions under IVIF context are suitable for the problem sought to be solved in this study. By this way, experts’ assessments and opinions are evaluated under IVIF environment, and an approach based on group decision making is performed to overcome subjectivity. On the other hand, IVIF extensions of these methods have been used individually in the literature for different applications. These studies are discussed in the second section. However, to the best of our knowledge, IVIF AHP and IVIF MABAC methods are used together for the first time, and are also proposed for the first time for the solution of the hybrid vehicle selection problem. AHP and MABAC methods can be used as decision making methods in various fields. It has been discovered that AHP and MABAC methods have the highest level of agreement between analytical and experimental results when used together (Kumar
et al.,
2025). One of the most preferred MCDM methods is AHP, and a relatively new distance-based alternative ranking method is MABAC (Büyüközkan
et al.,
2021b). These two methods have similar applications to the selection process. The advantage of using the AHP and MABAC methods together is that it requires less numerical computation and helps to evaluate the most appropriate alternatives when there is a disagreement about the relative relevance of the criteria (Salman
et al.,
2023).
Motivation, novelties and contributions of the study can be summarized as follows:
-
• Ensuring the world’s limited energy supply and environmental sustainability with the climate crisis is one of the most important and critical challenges of recent times and constitutes the motivation of this study. One solution to these problems is the use of hybrid or electric vehicles. From this point of view, the main topic of this study, hybrid vehicle selection, is important in terms of providing a scientific and effective solution to this problem.
-
• The aim of this study is to solve the hybrid vehicle selection problem. For this aim, the novel decision-making approach including two MCDM methods (AHP and MABAC), which has been widely applied in different fields in the literature, is proposed. The novel contribution of this study is to represent a combination of these methods in order to produce a hybrid model. Moreover, it is proposed to use the extensions of these methods in IVIF environment. With this characteristic, this study is the first in terms of employing IVIF AHP and IVIF MABAC methods in the hybrid vehicle selection area. In both methods, expressing judgments in IVIF numbers allows dealing with inherent uncertainties and ambiguities in the decision-making process more decisively, making them well suited for such multi-criteria analyses. It also leads to more reliable and efficient decisions.
-
• IVIF AHP differs from classical AHP in that decision makers’ judgments are expressed as IVIF numbers. This not only clarifies the uncertainty in the decision-making process but also helps decision makers to more easily present their statements in terms of membership, non-membership, and hesitation degrees. In other words, by using IVIF numbers in the AHP method, decision makers can perform optimistic and pessimistic evaluations. In this way, the results obtained are thought to be more efficient and reliable.
-
• Despite many successful applications of AHP in which the data in the problem are precisely expressed, there is a gap in the literature regarding the calculation of the criteria weights for hybrid vehicle selection in IVIF environment. The gap filled by this study will provide a guide to the applicability of the AHP method in complex and contradictory real-world applications.
-
• The main aim of IVIF MABAC is to find the best alternative and the alternative ranking by processing approximation areas, ideal and anti-ideal alternatives like classical MABAC. However, presenting evaluations with linguistic variables to this process and expressing these evaluations with IVIF numbers led to the resolution of ambiguity and to express the thoughts of decision makers more accurately. This generally resulted in the process being concluded with more effective and accurate decisions.
-
• Sensitivity analysis is provided to test the effects of changing criteria weights on the alternative rankings. Results show that IVIF MABAC method is not sensitive in terms of criteria weights in ranking hybrid vehicle alternatives. Similarly, the study offers a comparative study covering IVIF WASPAS and IVIF TOPSIS methods. The results obtained from these methods support the results obtained from the methods proposed in the study. In short, from the comparative and sensitivity analysis performed, it is thought that the proposed method can produce quite robust results.
-
• In general, this study aims to provide a practical decision-making tool to all parties interested in the automotive industry, such as consumers, researchers, policy makers by helping hybrid vehicle alternatives meet specific sustainability goals.
-
• As a result, in this study, a new solution based on IVIF AHP and IVIF MABAC methods has been proposed for the hybrid car selection problem, which is a popular topic today. This study provides quantitative analysis to understand the criteria for the hybrid vehicles market. Considering all the contributions listed above, it is thought that the proposed solution methodology can be used for complex decision problems and problems where decision makers are active.
The organization of this paper is summarized as follows. Literature review about MCDM studies for hybrid vehicle selection and AHP-MABAC applications under intuitionistic fuzzy environment is given in the next section. In the third section, methodology is introduced, and IVIF sets, IVIF AHP and IVIF MABAC are explained in this section. Then, a case study related with hybrid vehicle selection is represented. Sensitivity and comparative analyses are also included in the same section. After discussion section, conclusion and recommendations are provided in the last section.
4 Application
A real case study is presented to demonstrate the implementation process and effectiveness of IVIF AHP and IVIF MABAC methods in this section. It is related to hybrid vehicle selection. A company in Türkiye wants to expand their vehicle fleet by purchasing new hybrid vehicles. First, the management of the company assigns a decision team including four department’s managers (decision makers; DM
1, DM
2, DM
3 and DM
4). The mission of the decision team is to rank the hybrid vehicle alternatives and to select the most proper hybrid vehicle. The management is asked to assess the decision makers in the decision team in terms of knowledge in hybrid technology and purchasing process. The assessments as linguistic terms are given in Table
4. They are transformed to IVIFNs, and Eqs. (
13)–(
14) are used to find the decision makers’ weights given in Table
8. Although all decision makers in the decision team have almost the same weight, the highest and the least importances are given to DM
1 and DM
4, respectively.
After computing the decision makers’ weights, the first task of the decision team is the determination of the expectations of their company from purchasing decisions. Then, they determine the selection criteria that fit the company’s needs and expectations. After making necessary interviews, examining on sites and reviewing the related literature five selection criteria are considered. They are vehicle price (C1), fuel consumption (C2), carbon dioxide emission (C3), engine and transmission (C4), and reliability (C5). The decision team interviews with the vehicle company, one of the pioneers of hybrid technology, and determines five vehicle models (A1, A2, A3, A4 and A5) that have hybrid technology.
The selection process begins with finding criteria weights by IVIF AHP method. For this aim, each decision maker constructs a pairwise comparison matrix on the criteria by using linguistic terms in Table
5. Their comparisons are processed directly, in other words, no preprocessing is performed. The information in pairwise matrices obtained from decision makers through face-to-face interviews is subjective and reflects the personal opinions of the decision makers. The four pairwise comparison matrices are shown in Table
9. They are transformed to IVIFNs and each decision maker’s pairwise comparison matrices on criteria are aggregated using Eq. (
15). The same procedure is repeated for group IVIF judgment matrix. Aggregated IVIF judgment matrix of DM
1 and group IVIF judgment matrix are shown in Table
10. After checking the consistency ratios of all IVIF judgment matrices, it is seen that their CRs are less than 0.10 so they are considered as consistent. By applying Eqs. (
17)–(
18), criteria weights are computed and shown in Table
11. Actually, it can be said that each of the criteria has almost similar weights. However, it is found that C
1, C
2, C
3 are the most important criteria and C
4 and C
5 are the least important criteria. Namely, C
1, C
2, C
3 are more important than other criteria with a very small difference.
Table 8
The decision makers’ weights.
| DMk
|
DM1
|
DM2
|
DM3
|
DM4
|
| Linguistic terms |
EQ |
VQ |
VQ |
Q |
| ${\lambda _{k}}$ |
0.262 |
0.252 |
0.252 |
0.233 |
Table 9
Pairwise comparison matrix of decision makers.
|
${C_{\textit{1}}}$ |
${C_{\textit{2}}}$ |
${C_{\textit{3}}}$ |
${C_{\textit{4}}}$ |
${C_{\textit{5}}}$ |
| DM1
|
| ${C_{\textit{1}}}$ |
EI |
MMI |
SMI |
MMI |
MMI |
| ${C_{\textit{2}}}$ |
|
EI |
|
SMI |
MMI |
| ${C_{\textit{3}}}$ |
|
SMI |
EI |
SMI |
MMI |
| ${C_{\textit{4}}}$ |
|
|
|
EI |
|
| ${C_{\textit{5}}}$ |
|
|
|
MMI |
EI |
| DM${_{\text{2}}}$
|
| ${C_{\textit{1}}}$ |
EI |
|
|
|
|
| ${C_{\textit{2}}}$ |
MMI |
EI |
|
|
|
| ${C_{\textit{3}}}$ |
SMI |
SMI |
EI |
SMI |
MMI |
| ${C_{\textit{4}}}$ |
MMI |
MMI |
|
EI |
|
| ${C_{\textit{5}}}$ |
MMI |
MMI |
|
MMI |
EI |
| DM${_{\text{3}}}$
|
| ${C_{\textit{1}}}$ |
EI |
EI |
|
MMI |
MMI |
| ${C_{\textit{2}}}$ |
|
EI |
|
MMI |
SMI |
| ${C_{\textit{3}}}$ |
MMI |
MMI |
EI |
MMI |
SMI |
| ${C_{\textit{4}}}$ |
|
|
|
EI |
MMI |
| ${C_{\textit{5}}}$ |
|
|
|
|
EI |
| DM${_{\text{4}}}$
|
| ${C_{\textit{1}}}$ |
EI |
|
|
MMI |
|
| ${C_{\textit{2}}}$ |
SMI |
EI |
MMI |
SMI |
MMI |
| ${C_{\textit{3}}}$ |
MMI |
|
EI |
SMI |
MMI |
| ${C_{\textit{4}}}$ |
|
|
|
EI |
|
| ${C_{\textit{5}}}$ |
MMI |
|
|
MMI |
EI |
Table 10
Aggregated judgment matrix of DM1 and group judgment matrix.
|
${DM_{\text{1}}}$ |
Group |
| ${C_{\textit{1}}}$ |
$([0.217,0.543],[0.021,0.457])$ |
$([0.198,0.561],[0.045,0.439])$ |
| ${C_{\textit{2}}}$ |
$([0.195,0.584],[0.043,0.416])$ |
$([0.196,0.572],[0.049,0.428])$ |
| ${C_{\textit{3}}}$ |
$([0.217,0.574],[0.039,0.426])$ |
$([0.209,0.553],[0.035,0.447])$ |
| ${C_{\textit{4}}}$ |
$([0.164,0.601],[0.069,0.399])$ |
$([0.163,0.578],[0.059,0.422])$ |
| ${C_{\textit{5}}}$ |
$([0.162,0.615],[0.044,0.385])$ |
$([0.167,0.573],[0.045,0.427])$ |
| $CR$ |
0.088 |
0.088 |
Table 11
Criteria weights.
|
${C_{\textit{1}}}$ |
${C_{\textit{2}}}$ |
${C_{\textit{3}}}$ |
${C_{\textit{4}}}$ |
${C_{\textit{5}}}$ |
| ${w_{j}}$ |
0.2000 |
0.2005 |
0.2002 |
0.1996 |
0.1998 |
The selection process continues with determining the best hybrid vehicle among all hybrid vehicles alternatives by performing IVIF MABAC method. For this aim, each decision maker evaluates the performances of different alternatives under various criteria using Table
7. As in the IVIF AHP, the information regarding the evaluation of alternatives based on the criteria for IVIF MABAC is subjective and reflects the personal opinions of the decision makers. As in the IVIF AHP, the decision maker’s evaluation related to alternatives on criteria are processed directly, in other words, no preprocessing is performed. The decision matrices in linguistic terms are shown in Table
12. They are transformed to IVIFNs, and all individual decision matrices are aggregated to obtain group IVIF decision matrix. Eq. (
21) is performed, and results are shown in Table
13. The weighted group IVIF decision matrix is calculated by using Eq. (
23), and it is shown in Table
14. For this calculation, the criteria weights shown in Table
11 are considered. The border approximation area on the criteria is calculated by using Eq. (
24), and the border approximation area vector is formed and shown in Table
15. The Euclidean distance of each alternative from the border approximation area are calculated by performing Eq. (
12). Distance matrix between alternatives and the border approximation area is formed by doing necessary operations. The elements of Table
16 are used for finding the values of criteria functions for all hybrid vehicle alternatives. According to the values in Table
17, the ranking order of the hybrid vehicle alternatives is stated as A
1–A
2–A
3–A
5–A
4. The best alternative is A
1 since it has the highest score value.
Table 12
Decision matrices of decision makers.
|
${C_{\textit{1}}}$ |
${C_{\textit{2}}}$ |
${C_{\textit{3}}}$ |
${C_{\textit{4}}}$ |
${C_{\textit{5}}}$ |
| DM${_{\text{1}}}$
|
| ${A_{\textit{1}}}$ |
H |
VH |
VH |
MH |
H |
| ${A_{\textit{2}}}$ |
VH |
H |
H |
H |
H |
| ${A_{\textit{3}}}$ |
M |
M |
ML |
VH |
VH |
| ${A_{\textit{4}}}$ |
MH |
H |
MH |
MH |
H |
| ${A_{\textit{5}}}$ |
MH |
MH |
M |
H |
VH |
| DM${_{\text{2}}}$
|
| ${A_{\textit{1}}}$ |
MH |
M |
H |
ML |
VH |
| ${A_{\textit{2}}}$ |
H |
MH |
MH |
M |
H |
| ${A_{\textit{3}}}$ |
ML |
MH |
L |
H |
H |
| ${A_{\textit{4}}}$ |
M |
H |
M |
ML |
MH |
| ${A_{\textit{5}}}$ |
M |
ML |
ML |
MH |
H |
| DM${_{\text{3}}}$
|
| ${A_{\textit{1}}}$ |
MH |
H |
H |
ML |
H |
| ${A_{\textit{2}}}$ |
H |
H |
H |
M |
MH |
| ${A_{\textit{3}}}$ |
L |
M |
ML |
VH |
VH |
| ${A_{\textit{4}}}$ |
ML |
MH |
MH |
ML |
H |
| ${A_{\textit{5}}}$ |
M |
MH |
MH |
MH |
VH |
| DM${_{\text{4}}}$
|
| ${A_{\textit{1}}}$ |
H |
H |
VH |
MH |
MH |
| ${A_{\textit{2}}}$ |
VH |
MH |
VH |
MH |
M |
| ${A_{\textit{3}}}$ |
M |
M |
M |
H |
VH |
| ${A_{\textit{4}}}$ |
MH |
ML |
H |
MH |
H |
| ${A_{\textit{5}}}$ |
MH |
H |
H |
H |
H |
Table 13
Group IVIF decision matrix.
|
${C_{\textit{1}}}$ |
${C_{\textit{2}}}$ |
${C_{\textit{3}}}$ |
${C_{\textit{4}}}$ |
${C_{\textit{5}}}$ |
| ${A_{\textit{1}}}$ |
$([0.716,0.755],[0.142,0.174])$ |
$([0.790,1.000],[0.000,0.000])$ |
$([0.858,1.000],[0.000,0.000])$ |
$([0.470,0.574],[0.317,0.426])$ |
$([0.803,1.000],[0.000,0.000])$ |
| ${A_{\textit{2}}}$ |
$([0.858,1.000],[0.000,0.000])$ |
$([0.720,0.756],[0.140,0.170]$ |
$([0.797,1.000],[0.000,0.000])$ |
$([0.627,0.651],[0.237,0.291])$ |
$([0.705,0.726],[0.165,0.192])$ |
| ${A_{\textit{3}}}$ |
$([0.387,0.411],[0.487,0.570])$ |
$([0.527,0.560],[0.336,0.440])$ |
$([0.331,0.382],[0.517,0.598])$ |
$([0.860,1.000],[0.000,0.000])$ |
$([0.881,1.000],[0.000,0.000])$ |
| ${A_{\textit{4}}}$ |
$([0.513,0.594],[0.300,0.406]$ |
$([0.681,0.714],[0.173,0.200])$ |
$([0.640,0.690],[0.203,0.264])$ |
$([0.470,0.574],[0.317,0.426])$ |
$([0.762,0.778],[0.119,0.132])$ |
| ${A_{\textit{5}}}$ |
$([0.552,0.612],[0.284,0.388])$ |
$([0.608,0.675],[0.214,0.276])$ |
$([0.585,0.628],[0.257,0.316])$ |
$([0.716,0.755],[0.142,0.174])$ |
$([0.860,1.000],[0.000,0.000])$ |
Table 14
The weighted group IVIF decision matrix.
|
${C_{\textit{1}}}$ |
${C_{\textit{2}}}$ |
${C_{\textit{3}}}$ |
${C_{\textit{4}}}$ |
${C_{\textit{5}}}$ |
| ${A_{\textit{1}}}$ |
$([0.223,0.245],[0.677,0.705])$ |
$([0.269,1.000],[0.000,0.000])$ |
$([0.324,1.000],[0.000,0.000])$ |
$([0.119,0.157],[0.795,0.843])$ |
$([0.277,1.000],[0.000,0.000])$ |
| ${A_{\textit{2}}}$ |
$([0.323,1.000],[0.000,0.000])$ |
$([0.225,0.247],[0.674,0.701])$ |
$([0.274,1.000],[0.000,0.000])$ |
$([0.179,0.189],[0.750,0.782])$ |
$([0.216,0.228],[0.697,0.719])$ |
| ${A_{\textit{3}}}$ |
$([0.093,0.100],[0.866,0.894])$ |
$([0.139,0.152],[0.804,0.848])$ |
$([0.077,0.092],[0.876,0.902])$ |
$([0.325,1.000],[0.000,0.000])$ |
$([0.346,1.000],[0.000,0.000])$ |
| ${A_{\textit{4}}}$ |
$([0.134,0.165],[0.786,0.835])$ |
$([0.205,0.222],[0.704,0.725])$ |
$([0.185,0.209],[0.726,0.766])$ |
$([0.119,0.157],[0.795,0.843])$ |
$([0.249,0.260],[0.654,0.667])$ |
| ${A_{\textit{5}}}$ |
$([0.148,0.172],[0.777,0.828])$ |
$([0.171,0.202],[0.734,0.773])$ |
$([0.161,0.180],[0.762,0.794])$ |
$([0.222,0.245],[0.677,0.705])$ |
$([0.325,1.000],[0.000,0.000])$ |
Table 15
Border approximation area matrix.
|
${C_{\textit{1}}}$ |
${C_{\textit{2}}}$ |
${C_{\textit{3}}}$ |
${C_{\textit{4}}}$ |
${C_{\textit{5}}}$ |
| G |
$[0.168,0.234],[0.710,0.755]$ |
$[0.197,0.279],[0.653,0.691]$ |
$[0.183,0.322],[0.619,0.657]$ |
$[0.179,0.258],[0.680,0.725]$ |
$[0.279,0.568],[0.363,0.377]$ |
Table 16
Distance matrix of the alternatives from the border approximation area.
|
${C_{\textit{1}}}$ |
${C_{\textit{2}}}$ |
${C_{\textit{3}}}$ |
${C_{\textit{4}}}$ |
${C_{\textit{5}}}$ |
| ${A_{\textit{1}}}$ |
0.041 |
0.598 |
0.569 |
−0.102 |
0.339 |
| ${A_{\textit{2}}}$ |
0.649 |
−0.024 |
0.566 |
−0.057 |
−0.295 |
| ${A_{\textit{3}}}$ |
−0.130 |
−0.129 |
−0.218 |
0.624 |
0.341 |
| ${A_{\textit{4}}}$ |
−0.068 |
−0.042 |
−0.095 |
−0.102 |
−0.257 |
| ${A_{\textit{5}}}$ |
−0.059 |
−0.071 |
−0.122 |
0.025 |
0.340 |
Table 17
Ranking of alternatives.
| Alternative |
${S_{i}}$ |
Rank |
| ${A_{\textit{1}}}$ |
1.445 |
1 |
| ${A_{\textit{2}}}$ |
0.839 |
2 |
| ${A_{\textit{3}}}$ |
0.488 |
3 |
| ${A_{\textit{4}}}$ |
−0.563 |
5 |
| ${A_{\textit{5}}}$ |
0.113 |
4 |
4.1 Sensitivity Analysis
In this study, criteria weights are calculated with the IVIF AHP method. As it is known, the AHP method is one of the subjective methods, in other words, the criteria weights are based on the opinions of decision makers. When the decision makers or their opinions change, the criteria weights change accordingly. Therefore, in this part of the study, sensitivity analysis is carried out to determine how sensitive the IVIF MABAC method is to changes in decision makers’ weights and criteria weights. To analyse this, firstly the decision makers’ weights are changed. 5 different cases are generated and the ranking of the hybrid vehicle alternatives is obtained by considering these weights. The weights of the decision makers and the rankings obtained are given in Table
18. The first case is the weights obtained by using the entropy method in the previous section. In this case, the four decision makers’ weights are quite close to each other. The other cases assume that there is only one decision maker in the decision problem. The hybrid vehicle alternative ranking result of the first case is A
1–A
2–A
3–A
5–A
4. This ranking is the same as the ranking where the first decision maker is effective alone (Case 2). This is due to the fact that the weight of the first decision maker is slightly more than the weights of other decision makers in the weights found by entropy. However, when we look at the cases where other decision makers are effective alone, it is observed that the ranking changes. This situation shows the sensitivity of the decision makers in the alternative ranking.
Table 18
Different cases for decision makers’ weights.
| Cases |
Decision makers’ weights |
Ranking |
| Case 1 |
$(0.262,0.252,0.252,0.233)$ |
A1–A2–A3–A5–A4
|
| Case 2 |
$(1,0,0,0)$ |
A1–A2–A3–A5–A4
|
| Case 3 |
$(0,1,0,0)$ |
A1–A2–A3–A4–A5
|
| Case 4 |
$(0,0,1,0)$ |
A3–A5–A2–A1–A4
|
| Case 5 |
$(0,0,0,1)$ |
A2–A1–A3–A5–A4
|
For the analysis of criteria weights, different 21 cases are firstly created regarding the criteria weights. All cases including different criteria weights are presented in Table
19. The first case is the solution given in the application section and the values obtained from IVIF AHP. In cases between Case 2 and Case 6, values of 0.30, 0.25, 0.20, 0.15, and 0.10 are taken into account as criteria weights. The cases where each criterion has the highest and lowest weight are taken into account. In cases between Case 7 and Case 11, the highest criterion weight is 0.40, and equal weight (0.15) is used in other criteria. In cases between Case 12 and Case 16, the lowest criterion weight is 0.08, while other criteria are assigned equal weight (0.23). Finally, in cases between Case 17 and Case 21, the highest criterion weight is 0.9, while other criteria are assigned equal weight (0.025).
Table 19
Different cases for criteria weights.
| Cases |
Criteria weights |
Cases |
Criteria weights |
| Case 1 |
$(0.20,0.20,0.20,0.19,0.19)$ |
Case 12 |
$(0.08,0.23,0.23,0.23,0.23)$ |
| Case 2 |
$(0.30,0.25,0.20,0.15,0.10)$ |
Case 13 |
$(0.23,0.08,0.23,0.23,0.23)$ |
| Case 3 |
$(0.25,0.30,0.20,0.10,0.15)$ |
Case 14 |
$(0.23,0.23,0.08,0.23,0.23)$ |
| Case 4 |
$(0.15,0.10,0.30,0.20,0.25)$ |
Case 15 |
$(0.23,0.23,0.23,0.08,0.23)$ |
| Case 5 |
$(0.10,0.15,0.25,0.30,0.20)$ |
Case 16 |
$(0.23,0.23,0.23,0.23,0.08)$ |
| Case 6 |
$(0.20,0.15,0.10,0.25,0.30)$ |
Case 17 |
$(0.900,0.025,0.025,0.025,0.025)$ |
| Case 7 |
$(0.40,0.15,0.15,0.15,0.15)$ |
Case 18 |
$(0.025,0.900,0.025,0.025,0.025)$ |
| Case 8 |
$(0.15,0.40,0.15,0.15,0.15)$ |
Case 19 |
$(0.025,0.025,0.900,0.025,0.025)$ |
| Case 9 |
$(0.15,0.15,0.40,0.15,0.15)$ |
Case 20 |
$(0.025,0.025,0.025,0.900,0.025)$ |
| Case 10 |
$(0.15,0.15,0.15,0.40,0.15)$ |
Case 21 |
$(0.025,0.025,0.025,0.025,0.900)$ |
| Case 11 |
$(0.15,0.15,0.15,0.15,0.40)$ |
|
|
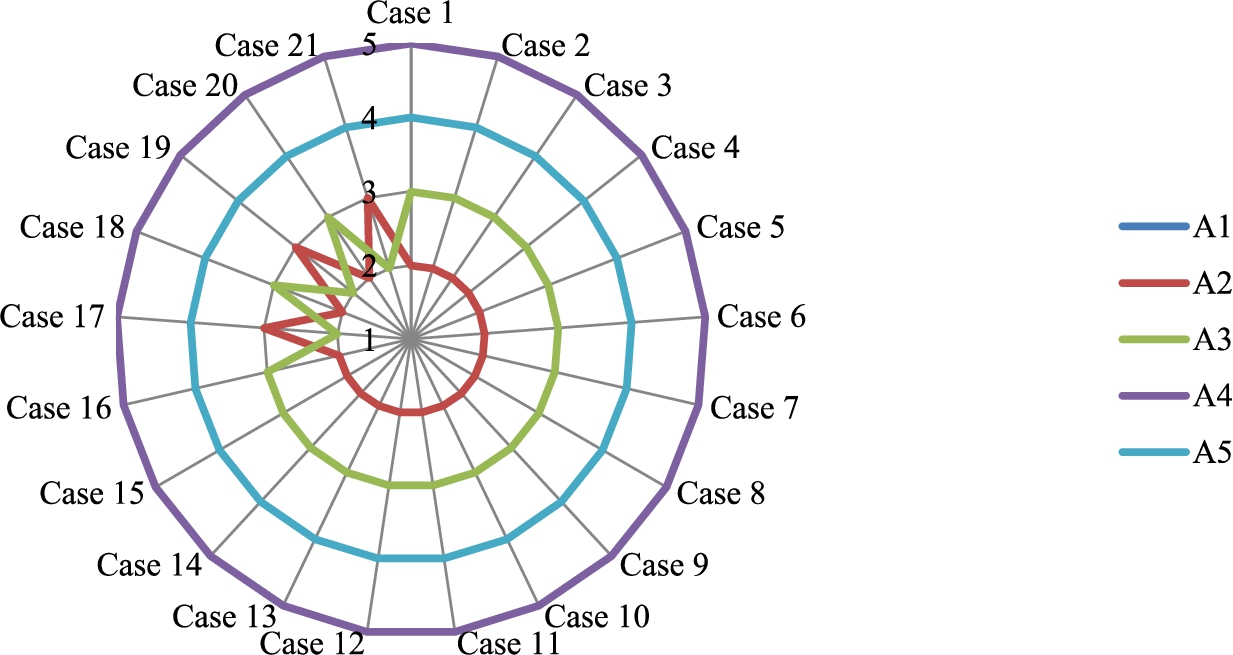
Fig. 2
Ranking results of different weight cases.
The problem given in the application section with the different criteria weights given in Table
19 is solved with the IVIF MABAC method, and rankings for hybrid vehicle alternatives are obtained. These rankings are given in Fig.
2. When Fig.
2 is examined, it is observed that there is no change in the ranking of hybrid vehicle alternatives. According to these results, we can say that the IVIF MABAC method is not sensitive in terms of criteria weights in ranking hybrid vehicle alternatives. This can be explained by the fact that the criteria weights are not very different from each other in all 16 cases. Considering all the situations, the change in the criteria weights is not too big, at most +20% and at least −12%. Therefore, the fact that the rankings do not change shows that the method is not very sensitive to small changes. When the criteria weights are close to each other, the best alternative is A
1 and the worst alternative is A
4. This situation is an advantage for decision makers in that they can consider the same ranking if they do not change the criteria weights too much. The fact that there is no change in the rankings despite a very large change in the criteria weights can be considered a negative situation. However, it is not possible to say this for the current situation. In order to analyse this situation, Case 17–Case 21 are generated, giving each criterion much more weight than the others. It has been observed that there are changes in the rankings in these cases. This is important in terms of showing that the method is sensitive to major changes.
4.2 Comparative Analysis
In this part of the study, in order to see the advantage of the proposed method, the results derived by IVIF MABAC method are compared with the results obtained by IVIF WASPAS and IVIF TOPSIS methods. The application steps of Abdullah
et al. (
2020) and Mishra and Rani (
2018) are applied for IVIF TOPSIS and IVIF WASPAS methods, respectively. The lambda value for IVIF WASPAS method is assumed as 0.5.
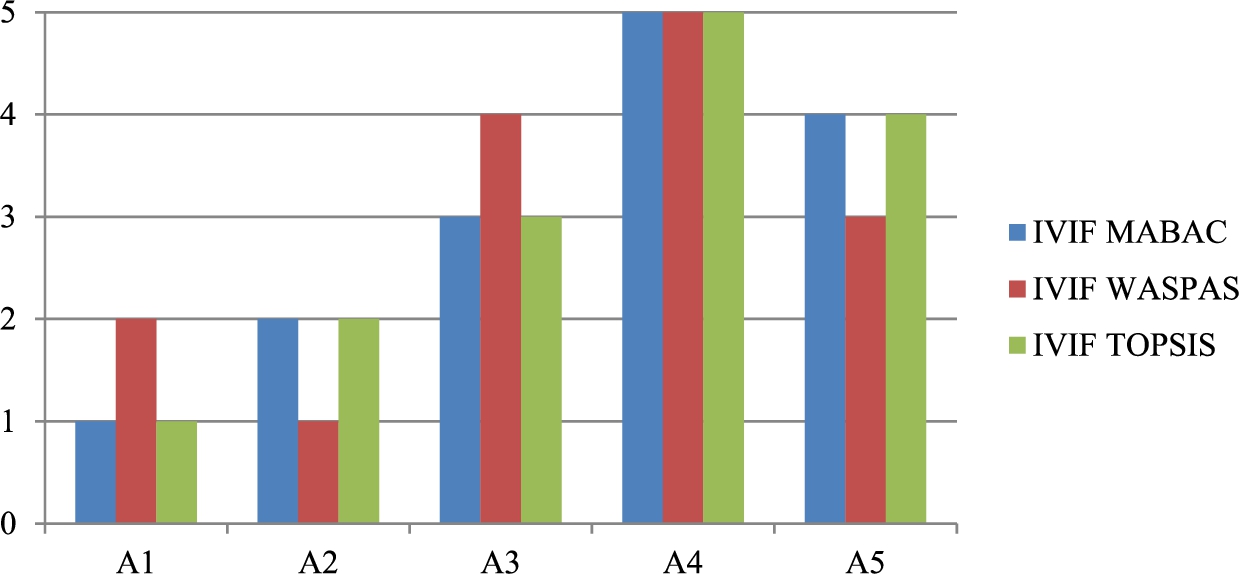
Fig. 3
Ranking results of three MCDM methods.
The results are shown in Fig.
3. The ranking obtained by the IVIF MABAC method is the same as the ranking obtained by the IVIF TOPSIS method, but slightly different from the ranking obtained by the IVIF WASPAS method. When Fig.
3 is examined, it is seen that the
${A_{1}}$ ranks first in the IVIF MABAC and IVIF TOPSIS methods, but ranks second in the ranking according to the IVIF WASPAS method. Similar interpretations can be made for other alternatives. To prove this better, the Pearson correlation coefficient between the methods is calculated. The correlation coefficient between IVIF MABAC and IVIF TOPSIS is 100%. This shows that both methods produce the same ranking of alternatives. On the other hand, the correlation coefficient value between IVIF MABAC and IVIF WASPAS methods is found to be 80%. This can be considered a relatively high value. When we look more closely at the alternative ranking of both methods, the difference is in the alternatives A
1, A
2, A
5 and A
3. For example, alternatives A
1 and A
2 rank first and second in IVIF MABAC method, while they rank second and first in the IVIF WASPAS method. A similar situation can also be applied to A
3 and A
5 alternatives. The last ranked alternative (A
4) remains unchanged in both methods. The computed crisp final scores of A
2 and A
1 are very close to each other, namely 0.873 and 0.867, respectively. These similarities in alternative rankings suggest that the IVIF MABAC method produces adequate and satisfactory results for current application. However, it should be noted that these rankings may change as the weights assigned to the criteria and decision makers change.
These three methods are also compared with respect to the time complexity as Aytaç Adalı and Tuş (
2023), Alkahtani
et al. (
2019), Aytaç Adalı
et al. (
2023), and Rani
et al. (
2021) performed in their studies. Considering there are
m alternatives and
n criteria,
IVIF MABAC method requires 4mn operations for the decision matrix, 4mn operations for the weighted decision matrix, 4n operations for border approximation area matrix, mn operations for Euclidean distances of each alternative, 2mn+n operations for distance matrix, and m operations for the ranking of the alternatives. In this manner, the time complexity of IVIF MABAC method is 11mn+5n+m.
IVIF-WASPAS method requires 4mn operations for the decision matrix, 4mn+2m(n−1)+2m operations for relative weight according to WSM (Weighted Sum Model), 4mn+2m(n−1)+2m operations for relative weight according to WPM (Weighted Product Model), 12m operations for total relative importance and m operations for the ranking of the alternatives. So, the time complexity of IVIF-WASPAS method is 16mn+13m.
IVIF-TOPSIS method requires 4mn operations for the decision matrix, 4mn operations for the weighted decision matrix, 4n+m operations for determining the positive and negative ideal solutions, and m operations for the ranking of the alternatives. The time complexity of IVIF-TOPSIS method is 8mn+8n+3m. According to this computational complexity analysis for these three methods, IVIF-WASPAS method shows the worst performance in terms of the number of operations. Although IVIF-TOPSIS method has a minimum number of operations, the operations performed to find positive and negative ideal solutions are much more complex than the operations performed to find the distance matrix in the IVIF MABAC method. In this respect, IVIF MABAC method can be considered as an alternative method to the IVIF-TOPSIS method.
5 Discussion
The global vehicle market is transforming from traditional vehicles to electric vehicles due to environmental and economic reasons. The fact that electric vehicles have zero carbon emissions and offer a more affordable option in the face of rising fuel prices naturally increases the interest in these vehicle models. On the other hand, the cost of purchasing a fully electric vehicle is quite high at first. For this reason, hybrid vehicles, which are a more environmentally friendly option than diesel and gasoline vehicles and a more affordable option than electric vehicles, have become very popular in recent years. Hybrid vehicles offer an ideal alternative for users who are undecided about switching to a fully electric vehicle or want to make a more affordable choice.
In this study, a new approach is presented by using IVIF AHP and IVIF MABAC, two MCDM methods together, so that decision makers can choose the most suitable hybrid car alternatives with various criteria. Criteria taken into account in the study are vehicle price, fuel consumption, carbon dioxide emission, engine and transmission, and reliability. Hybrid vehicles allow to go longer with less fuel. The fact that gasoline and diesel fuels are expensive directs users to hybrid vehicles. For this reason, hybrid vehicle prices are more expensive than traditional cars. Hybrid vehicles increase fuel efficiency by combining gasoline and electric engines. In this way, it consumes less fuel and causes less harm to the environment. With the use of electric motors, hybrid vehicles provide low emissions. This contributes to reducing air pollution. In hybrid vehicles, the engine and transmission wear out less because the gasoline engine is used less. This ensures a longer life of the vehicle. Hybrid vehicles are as reliable as gasoline-powered cars. They have been around for about two decades, so the tech is tried and tested.
In the evaluation performed with IVIF AHP, the importance that consumers attach to the determined criteria has been revealed. The importance levels of the criteria are very close to each other. This shows that decision makers attach equal importance to the determined criteria. Taking into account the situations where the criteria weights may differ from each other over time or by different decision makers, a sensitivity analysis is made and the ranking of the alternatives is examined with IVIF MABAC. When the criteria weights are close to each other, the best alternative is A1 and the worst alternative is A4. For this reason, it is very important for both decision makers and companies selling hybrid vehicles in the automotive industry to know which hybrid vehicle the decision makers will choose according to the degree of importance they attach to the criteria.
It should be kept in mind that the results of this study should not be generalised. The methods used are subjective methods. The weights assigned to the criteria used reflect the opinions of the 4 decision makers participating in the study. Similarly, the performance values of the hybrid vehicle alternatives under the criteria reflect the opinions of the decision makers. In other words, the decision matrix consists of the opinions of the decision makers is subjective. When the decision makers change, both the criteria weights and the rankings of the hybrid vehicle alternatives change. However, what is emphasized here is that the decision-making tool based on IVIF AHP and IVIF MABAC methods gives effective results in the hybrid vehicle selection problem. This is demonstrated by the results of the sensitivity and comparative analyses and by the fact that the results are found satisfactory by the decision makers. The IVIF environment is able to effectively analyse the uncertainty in the decision-making problem. From all these perspectives this study will help the decision makers and firms to understand the major criteria impacting hybrid electric vehicles market trends and develop strategy accordingly. At the same time, an effort has been made to provide a user-friendly and effective decision-making tool that helps in hybrid vehicle selection.
6 Conclusion and Recommendations
With the increase in the population in the world, human activities and movements have increased. In order to meet the increasing human mobility, transportation and transportation vehicles have become even more important. The transportation vehicles also have brought environmental problems such as noise, pollution, etc. Hybrid vehicles have been seen as a solution to reduce environmental impacts, and become very popular in the market. Namely, hybrid vehicles are preferred in terms of being fuel-efficient and producing less green gas than ordinary vehicles. The selection and purchasing process of hybrid vehicles require analytical thinking for the consumers. Because they do not only consider greenhouse gas emission but also consider other criteria like vehicle cost, reliability, vehicle performance, etc. So, in this paper, the hybrid vehicle selection problem of a company operated in Türkiye is handled as an MCDM problem. The two MCDM methods, IVIF AHP and IVIF MABAC, are applied to rank and select the best hybrid vehicle alternative. This problem is solved under the IF environment. IF numbers are more suitable in real problems than the crisp numbers in terms of expressing human judgment and preferences and modelling uncertainty in subjective judgments. In this paper, decision makers’ weights, selection criteria weights and performances of hybrid vehicle alternatives with respect to each criterion are expressed as IVIFNs. The IVIF AHP is utilized to find the hybrid vehicle selection criteria weights. Five criteria (price, fuel consumption, carbon dioxide emission, engine and transmission, and reliability) are considered by the decision team. It is found that the selection criteria weights are almost the same. For this case, it can be said that the emission of carbon dioxide is not only a determining criterion for the purchase of hybrid vehicles. Namely, other criteria like cost are as important as the environmental criterion in the hybrid selection process. IVIF MABAC is utilized to rank hybrid vehicle alternatives and select the best hybrid vehicle. Among the five alternatives, A1 is selected as the best hybrid vehicle. In IVIF MABAC method, there is no necessity to represent the necessary information with crisp data. The problem is solved by the decision makers’ judgments. In this way, the magnitude of the problem may also increase because the problems of finding exact data and forming decision matrix including crisp data are eliminated. In IVIF MABAC method, other IVIF distances may be used instead of IVIF Euclidean method and the effects of distance measure may be analysed. Decision makers are the main parts of both two MCDM methods. Their judgments and evaluations are considered in parallel with their weights.
The methodology in this paper is useful as a decision-making tool for the managers in better understanding the hybrid vehicle selection problem theoretically. Qualitative data in the problem is handled so uncertainty in the structure of the problem is modelled. However, the proposed methodology or the resulting solutions have some limitations. IVIF AHP method depends on pairwise comparison scale. As the number of levels in the hierarchy of the decision problem and the number of elements to be compared increase, the problem becomes more complex, which causes loss of time. Criteria affecting hybrid vehicle selection are limited to price, fuel consumption, carbon dioxide emission, engine and transmission, reliability and the number of alternatives is limited to five in this study. However, there are also criteria other than these main criteria that affect the choice of hybrid car. When the number of criteria and alternatives are increased, using the AHP method may be disadvantageous as it requires much more time and effort. Because pairwise comparisons will increase and computational difficulties will arise. The consistency of weight in AHP may not be derived for different fuzzy numbers. Moreover, AHP does not take into account the dependencies and interrelationships between criteria (Moslem
et al.,
2023). So, newly developed methods such as ANP, BWM, LBWA, FUCOM and DIBR, which eliminate the number of pairwise comparisons, can be used to reduce the limitations of the AHP method in solving more complex problems. In case there are many interconnected criteria and alternatives, the advantages of these newly developed methods instead of the AHP method can be used.
The other limitations of the study are as follows. IVIF AHP and IVIF MABAC methods are subjective. An IVIF number is used to cope with uncertainty and improve uncertainty in evaluating criteria and possible alternatives. The number of criteria and alternatives are selected as the decision maker preferences to solve such problems (Mandal
et al.,
2024). Determining the importance of the criteria and evaluating the alternatives on the basis of each criterion depends entirely on the linguistic expressions of the decision makers. Although this is an advantage under uncertainty and incomplete information, this is a disadvantage if the decision makers are not experts in their field. Decision makers have a significant influence on the decision. If decision makers make wrong evaluations, it may cause the decision to be wrong. This means that the order of the alternatives will not always be correct. The score and accuracy functions are used only to measure the IVIF numbers and rank them according to the score value. The ranking of the alternative may be different depending on the criteria. As a result, it is difficult to compare the performance of alternatives on many criteria objectively. Any uncertain situation may not be measured by the single real-valued membership and non-membership function in the IF set. Also, the exact belonging of an element cannot be obtained in the IVIF set (Mandal
et al.,
2024).
For future studies, these methods may be used for other selection problems in different areas such as facility location selection, supplier selection, material selection, personnel selection, etc. The usage of IVIF sets has been deemed sufficient in this study in terms of capturing the complexity in the problem. However, in cases that cover all types of missing data and are insufficient to represent real situations, type-2 IVIF sets may be used. Similarly, other fuzzy extensions like neutrosophic or Fermatean sets of these methods may be applied for handling uncertainty. Pythagorean fuzzy sets, which are useful expansion of IF sets (Asif
et al.,
2025), may be used. On the other hand, criteria weights obtained from IVIF AHP are used in this study. These weights are also subjective weights. In further studies, subjective weights may be calculated using different methods. In addition, objective weight calculation methods may also be evaluated, and results may be compared. Different selection criteria and alternatives may be added or changed.

