1 Introduction
MCDM (“multiple-criteria decision-making”) is an integral part of decision science and operation research, dealing with problems characterized by multiple, often conflicting criteria. It is a complex process that involves evaluating, prioritizing, and selecting the best alternative from a set of available options (Gal et al., 2013). Ranking in MCDM is a crucial step where alternatives are ordered based on their performance across various criteria. Over the years, numerous methods have been developed to address the challenges of MCDM, each with its unique approach to handling the intricacies of multi-dimensional decision spaces (Sahoo and Goswami, 2023). These methods range from traditional techniques like the AHP (“analytical hierarchy process”) and the TOPSIS (“technique for order preference by similarity to ideal solution”), to more recent methods like CRADIS (“compromise ranking of alternatives from distance to ideal solution”) and WISP (“weighted sum-product”).
Amidst the diverse landscape of ranking methods in MCDM, Yazdani et al. (2019) proposed a ranking methodology called CoCoSo (“combined compromise solution”) for MCDM to rank the alternatives based on the criteria. This method provides an overview of possible compromise solutions to a decision-maker. This method aggregates the weights of the compared sequences of alternatives using the multiplication rule and weighted power of distance methods. Next, the ranking index is calculated as a cumulative aggregate of three measures for every given alternative. Finally, the aggregated alternatives are sorted in descending order to provide the final ranking of the alternatives. After the inception of CoCoSo (Yazdani et al., 2019), many researchers actively utilized the method for different decision applications in areas such as nano science (Barua et al., 2019; Kharwar et al., 2022; Panchagnula et al., 2023), sustainability science (Das and Chakraborty, 2022; Dwivedi and Sharma, 2022; Ghasemi et al., 2022; Stanujkic et al., 2020; Phurksaphanrat and Panjavongroj, 2023), automobile industry (Kumar et al., 2022), medical diagnostics (Tripathi et al., 2023), and alike. The summarized view of these studies is presented in Table 1.
Table 1
Some applications of the CoCoSo method.
| Source | Type of fuzzy used | Methodology | Application |
| Wen et al. (2019a) | Probabilistic fuzzy linguistic term set | SWARA, CoCoSo | Clinical decision support systems – Selection of cold chain logistics management of medicine |
| Wen et al. (2019b) | Hesitant fuzzy linguistic term set | An extended CoCoSo where subordinate compromise scores and the subjective and objective weights of criteria are considered simultaneously | Selection of suitable third-party logistic service supplier in supply chain finance. |
| Banihashemi et al. (2021) | Triangular fuzzy numbers | CoCoSo | Investigating the environmental impacts of construction projects |
| Mishra et al. (2021) | Hesitant fuzzy sets | CoCoSo | Ranking sustainable third-party reverse logistic providers |
| Rani et al. (2021) | Single-valued neutrosophic fuzzy set | SWARA, CoCoSo | Renewable energy resource selection problem |
| Deveci et al. (2021) | Triangular fuzzy numbers | An extended CoCoSo using logarithmic and power heronian function | Real-time traffic management systems |
| Peng et al. (2021) | Interval-valued fuzzy soft set | CRITIC, CoCoSo | Intelligent healthcare management evaluation |
| Demir et al. (2022) | Triangular fuzzy numbers | FUCOM, CoCoSo | Sump development in urban areas |
| Qiyas et al. (2022) | Logarithmic picture fuzzy set | CoCoSo | Drug selection for COVID-19 |
| Ghoushchi et al. (2022) | Spherical fuzzy set | SWARA, CoCoSo | Evaluation of wind turbine failure modes |
| Ghoushchi et al. (2023) | Spherical fuzzy set | Best-worst method, CoCoSo | COVID-19 infodemic management strategies evaluation |
| Wang et al. (2023) | T-spherical fuzzy sets | An extension of the CoCoSo method based on frank softmax aggregation operator | Multi-attribute group decision-making |
| Zhang and Wei (2023) | Spherical fuzzy sets | CoCoSo, D-CRITIC | Location selection of electric vehicle charging station |
| Su et al. (2023) | Pythagorean fuzzy set | CoCoSo | Identifying technical challenges of blockchain technology for sustainable manufacturing paradigm |
| Tešić et al. (2023) | Crisp sets | BMO, DIBR II, CoCOSo | Assault boat selection for military operations |
| Krishankumar et al. (2024) | Double hierarchy hesitant fuzzy linguistic term set | CRITIC, EBM, CoCoSo | Selection for storage methods for storing hydrogen |
| Haseli et al. (2024) | Fuzzy ZE-numbers | BCM, CoCoSo | Evaluation of options to handle transportation crisis in 2026 world cup |
| Razzaq et al. (2024) | Picture fuzzy soft set | CRITIC, CoCoSo | Supplier selection under uncertainty in Industry 4.0 |
Note: CoCoSo – Combined compromise solution; SWARA – Stepwise weight assessment ratio analysis; ANOVA – Analysis of variance; CRITIC – Criteria importance through inter-criteria correlation; FUCOM – Full consistency method; D-CRITIC – Distance correlation CRITIC; BMO – Bonfferoni mean; DIBR II – Defining interrelationships between ranked criteria II; EBM – Evidence-based Bayesian method; BCM – Base criterion method.
Table 1 shows that the CoCoSo method is gaining attention in diverse MCDM fields/applications for ranking alternatives/options. Further, the simplicity and elegance of the method help managers/policymakers quickly adopt this technique for rational choice selection or decision-making. Some inferences that can be drawn from Table 1 are: (i) CoCoSo is popular with different fuzzy variants; (ii) CoCoSo is utilized in many different decision applications; and (iii) experimentation for the stability of CoCoSo is still unexplored, and there is high scope in this line of research as it facilitates researchers in the utilization of the method effectively.
1.1 Motivations and Contributions
From the inferences gained by the review, certain research gaps are determined such as (i) stability as a performance metric is not well explored for CoCoSo ranking method; (ii) specifically, alternative and criteria based adequacy tests are rarely conducted to investigate the stability/rank reversal phenomenon of the approach; and (iii) inclusion of partial adequacy test result is lacking in the existing studies. The stability of the CoCoSo method is experimented by using the adequacy test that observes the effect on ranking order when alterations are made to alternatives and criteria. Junior et al. (2014) utilized this method in their study of comparing AHP and TOPSIS in the fuzzy context. This method evaluates the performance by inclusion or exclusion of alternatives and criteria. In the case of the alternatives, an additional alternative, a repetition of one of the existing alternatives, was inserted into the decision matrix. For testing criteria, an additional criterion, a repetition of one of the existing criteria, was inserted into the decision matrix. The CoCoSo method has been applied to this newly generated decision matrix for alternatives and criteria. The rank values of the results of the original decision matrix and the newly generated decision matrix were compared to analyse the stability of the CoCoSo method.
By gaining motivation from the inferences/gaps provided above, the authors attempt to demystify CoCoSo in terms of its stability to support researchers in MCDM with better understanding of the scope and utility of the popular method, which is considered as the main objective of this study. Specific contributions are presented, such as:
-
• Stability of the CoCoSo method is realized in the fuzzy context by conducting a comprehensive simulation study with matrices simulated randomly by Python in various dimensions;
-
• Later, partial stability of the CoCoSo method is realized in the fuzzy context by considering partial pass condition in the simulation study;
-
• Finally, inferences are provided with respect to the CoCoSo method based on the simulation results to aid researchers in utilizing the ranking approach for future decision problems.
These contributions attempt to understand the stability and/or partial stability of the popular CoCoSo method in the fuzzy context, which is a novel proposition of this research and to the best of authors’ knowledge, such a study on the CoCoSo approach is conducted for the first time and this study aims to support/help researchers better understand the stability aspect (rank reversal behaviour) of the CoCoSo approach.
The paper is structured as follows. Section 2 explains the methodology of the CoCoSo method and the adequacy test. Section 3 describes the experiment done on the CoCoSo method. Section 4 provides the results obtained from this experiment and draws some discussion and insights. Section 5 concludes the paper and directs attention to future work.
2 Methodology
In this section, we delve into the comprehensive methodology employed for the CoCoSo and its associated adequacy tests. The CoCoSo method is a versatile decision-making approach characterized by the use of weighted matrices to evaluate alternatives against predefined criteria, employing both scalar and power approaches. To ensure the method’s reliability and effectiveness, it is subjected to testing under uncertain preference conditions. This section outlines the step-by-step application of the CoCoSo method, emphasizing the scalar and power approaches, followed by a detailed examination of the adequacy tests. These tests, conducted through the creation of children’s matrices and subsequent rank value comparisons, provide a robust evaluation of the CoCoSo method’s suitability and accuracy in diverse decision-making scenarios.
2.1 CoCoSo Method
The CoCoSo method was applied using the scalar and power approach. This method was applied with biased and unbiased weights for the criteria. Main reason for selecting CoCoSo method is that it is a fairly recent approach developed by Yazdani et al. (2019) and utilized by many reseachers for MCDM. Further, the method works on the principle of considering multiple compromise solutions in an integrated fashion, which provides certain level of rationale to experts in ranking alternatives. Thus, investigating the stability aspect of the method would help experts/researchers in their choice of choosing an appropriate approach for ranking alternatives. In the future, researchers can explore the stability of other approaches such as COPRAS (“complex proportional assessment”), MARCOS (“measurement alternatives and ranking according to compromise solution”), MABAC (“multi-attributive border approximation area comparison”), ARAS (“additive ratio assessment”), and VIKOR (“viekriterijumsko kompromisno rangiranje”) as well. The procedure for the CoCoSo method is shown in the following steps:
Step 1: Consider a decision matrix ${X_{ij}}$ defined in equation (1) having m alternatives and n criteria. The order of this matrix is $m\times n$:
(1)
\[ {X_{ij}}=\left[\begin{array}{c@{\hskip4.0pt}c@{\hskip4.0pt}c@{\hskip4.0pt}c}{x_{11}}\hspace{1em}& {x_{12}}\hspace{1em}& \cdots \hspace{1em}& {x_{1n}}\\ {} {x_{21}}\hspace{1em}& {x_{22}}\hspace{1em}& \cdots \hspace{1em}& {x_{2n}}\\ {} \cdots \hspace{1em}& \cdots \hspace{1em}& \cdots \hspace{1em}& \cdots \\ {} {x_{m1}}\hspace{1em}& {x_{m2}}\hspace{1em}& \cdots \hspace{1em}& {x_{mn}}\end{array}\right].\]
Step 2: Consider a weight vector ${w_{j}}$ defined in equation (2) which contains the weights for the n criteria. The order of this vector is $1\times n$:
Please note that if biased weights are used, the values of ${w_{j}}$ should be unequal, or if unbiased weights are used, the values of ${w_{j}}$ should be equal to the reciprocal of the number of criteria n defined in Step 1.
Step 3: The CoCoSo method can be applied using the scalar or power approach. For the matrix ${X_{ij}}$ defined in equation (1) using the weight vector ${w_{ij}}$ defined in equation (2), if the scalar approach is used, determine the weighted matrix $W{X_{ij}}$ using equation (3), or if you are using the power approach, determine the weighted matrix $W{X_{ij}}$ using equation (4). The order of this matrix is $m\times n$.
Step 4: Determine the multi-stage compromise solution for the matrix $W{X_{ij}}$ defined in equation (3) or equation (4) using equations (5)–(7). Each equation yields an $m\times 1$ vector:
where $w{x_{ij}}$ is the value of the matrix in the ith and jth position, and $\min (.)$ & $\max (.)$ are the minimum and maximum operators, respectively.
(5)
\[\begin{aligned}{}& {T_{1}}={\sum \limits_{i=1}^{m}}\frac{w{x_{ij}}}{{\textstyle\textstyle\sum _{j=1}^{n}}{x_{ij}}},\end{aligned}\]2.2 Adequacy Test
The adequacy test has been applied to both alternatives and criteria. The procedure for the adequacy tests is shown in the following steps:
Step 1: Construct children’s matrices for every matrix on which the CoCoSo method was applied. The children’s matrices should be created by repeating the alternatives or the criteria.
Step 2: Apply the CoCoSo method on each of the children matrices generated.
-
• For a matrix with dimension $m\times n$, m children matrices will be generated by repeating the alternative. Every children matrix generated should have only one unique alternative repeated.
-
• For a matrix having dimension $m\times n$, there will be n children matrices generated by repeating the criteria. Every children matrix generated should have only one unique criterion repeated.
Step 3: Compare the rank values of the original matrix and the children’s matrices by sorting the values in descending order. The comparison can be made in the following two methods:
The PASS and FAIL percentages can be calculated with equations (9) and (10). The PASS COUNT and FAIL COUNT are numerical values denoting the number of matrices that have passed and failed the adequacy test, respectively.
-
• The second method is the Partial method which will give the PASS, PARTIAL PASS, and the FAIL percentage of the CoCoSo method.
-
– If the rank values of all the children’s matrices equal the original matrix, then the matrix has passed the adequacy test.
-
– For all of the children’s matrices, if the first rank value is equal to the first rank value of the original matrix, the matrix has partially passed the adequacy test.
-
– Else, it has failed the adequacy test.
-
The PASS percentage, PARTIAL PASS percentage, and FAIL percentage can be calculated with equations (11)–(13). The PASS COUNT, PARTIAL PASS COUNT, and FAIL COUNT are numerical values denoting the number of matrices that have passed, partially passed, and failed the adequacy test, respectively.
(11)
\[\begin{aligned}{}& \mathrm{PASS}\hspace{0.1667em}\% =\frac{\mathrm{PASS}\hspace{2.5pt}\mathrm{COUNT}}{\mathrm{PASS}\hspace{2.5pt}\mathrm{COUNT}+\mathrm{PARTIAL}\hspace{2.5pt}\mathrm{PASS}\hspace{2.5pt}\mathrm{COUNT}+\mathrm{FAIL}\hspace{2.5pt}\mathrm{COUNT}}\times 100,\end{aligned}\](12)
\[\begin{aligned}{}& \mathrm{PARTIAL}\hspace{2.5pt}\mathrm{PASS}\hspace{0.1667em}\% \\ {} & \hspace{1em}=\frac{\mathrm{PARTIAL}\hspace{2.5pt}\mathrm{PASS}\hspace{2.5pt}\mathrm{COUNT}}{\mathrm{PASS}\hspace{2.5pt}\mathrm{COUNT}+\mathrm{PARTIAL}\hspace{2.5pt}\mathrm{PASS}\hspace{2.5pt}\mathrm{COUNT}+\mathrm{FAIL}\hspace{2.5pt}\mathrm{COUNT}}\times 100,\end{aligned}\]3 Experiment
The study presented herein strategically examines the performance and scalability of the CoCoSo method with an unequivocal focus on matrices of varying sizes generated randomly with fuzzy values. Matrices of dimensions $5\times 6$, $7\times 8$, $8\times 9$, and $9\times 12$ were meticulously generated to assess the CoCoSo method’s proficiency.
This method’s scalability was rigorously tested by fabricating 300 matrices for each size. The total number of matrices was subsequently increased by 300 in each experimental run until the test was conducted on a substantial 3000 matrices of each size. For every matrix in each experimental run, the CoCoSo method as presented in Section 2.1 was applied to these generated matrices.
In the context of alternatives and criteria, the total and partial adequacy tests, as elaborated in Section 2.2, were implemented on these matrices. Each experimental run yielded decisive results in the form of pass percentage, fail percentage, and partial-pass percentage. The results and discussions from all the runs have been exhaustively tabulated and summarized in Section 4.
4 Results and Discussion
This section analyses CoCoSo’s performance under various conditions, including the use of both scalar and power approaches, as well as the application of unbiased and biased weights. The results offer a deep insight into the stability and robustness of the CoCoSo method when faced with alterations in alternatives and criteria. Notably, the inclusion of partial pass percentages sheds light on scenarios where the top-ranked alternative maintains its position despite significant modifications. These findings provide invaluable insights for researchers and decision-makers seeking to apply the CoCoSo method effectively in diverse contexts, offering a clearer understanding of its performance and stability characteristics.
4.1 CoCoSo Method Using the Scalar Approach and Unbiased Weights
Figures 1 and 2 summarize the results of applying the CoCoSo method using the scalar approach with unbiased weights. The criteria for unbiased weights and the scalar approach of the CoCoSo method can be referred from Step 2 and Step 3 of Section 2.1, respectively.
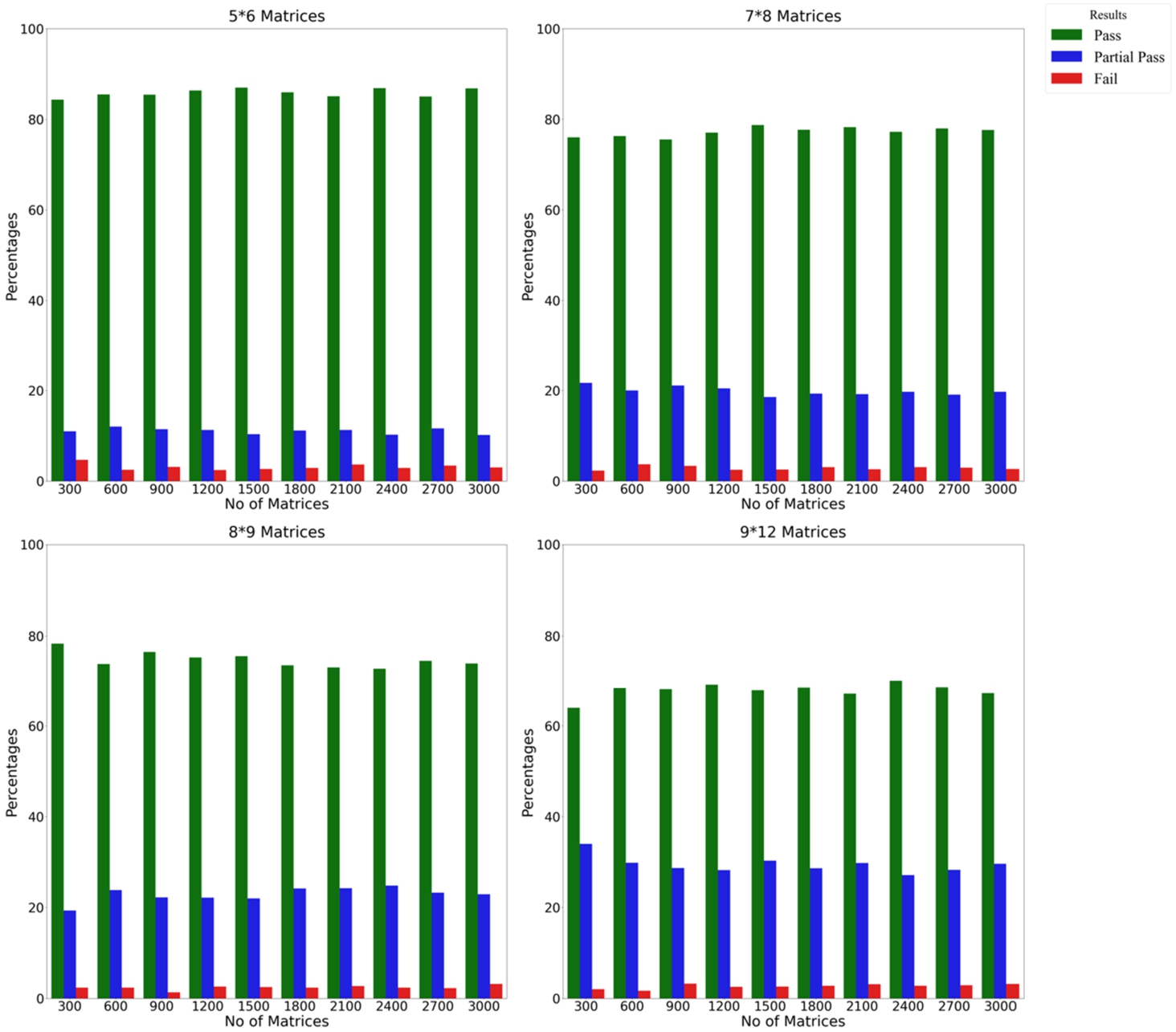
Fig. 1
Results of the experiment on the CoCoSo method using the scalar approach and unbiased weights by repeating alternatives.
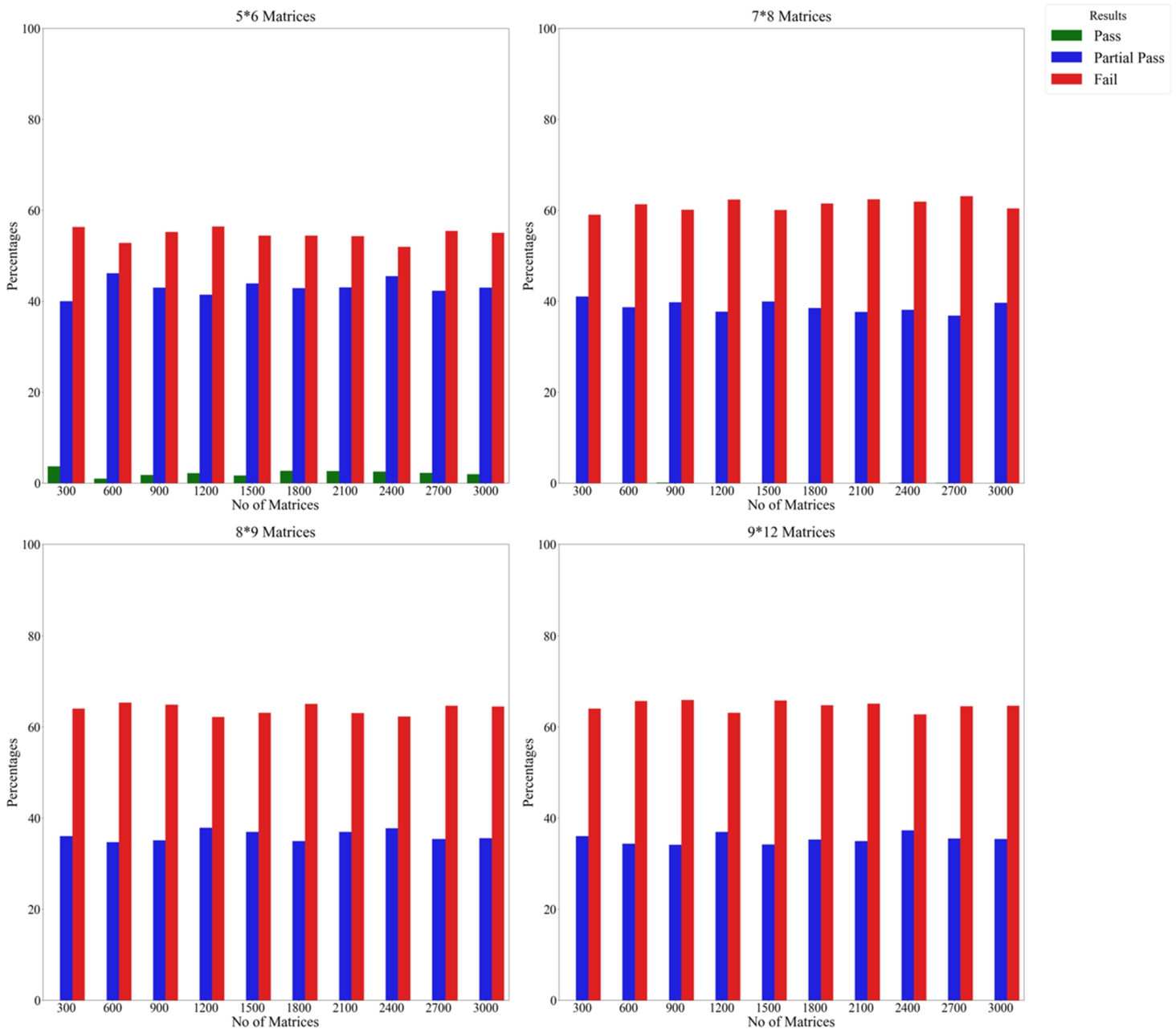
Fig. 2
Results of the experiment on the CoCoSo method using the scalar approach and unbiased weights by repeating criteria.
Figures 1 and 2 present the pass, fail, and partial pass percentages for various simulated matrices of different sizes. This affords a comprehensive understanding of the CoCoSo method, significantly illuminating its workings for its more efficient application by future researchers. Key insights can be confidently drawn: (i) CoCoSo exhibits a commendable level of stability when alternative adjustments are contrasted with criteria changes; (ii) with the expansion of matrix dimensions, the pass rate experiences variability in response to both alternative and criteria modifications; (iii) however, fluctuations in the matrix sets do not yield decisive conclusions about the pass and fail rates; (iv) notably, the incorporation of partial pass in the process of criteria alteration substantially diminishes the fail rate. This confirms that there are situations where the top-ranking alternative sustains its position, regardless of significant alterations made to alternatives and criteria.
4.2 CoCoSo Method Using Power Approach and Unbiased Weights
Figures 3 and 4 summarize the results of applying the CoCoSo method using the power approach with unbiased weights. The criteria for unbiased weights and the power approach of the CoCoSo method can be referred to from Step 2 and Step 3 of Section 2.1, respectively.
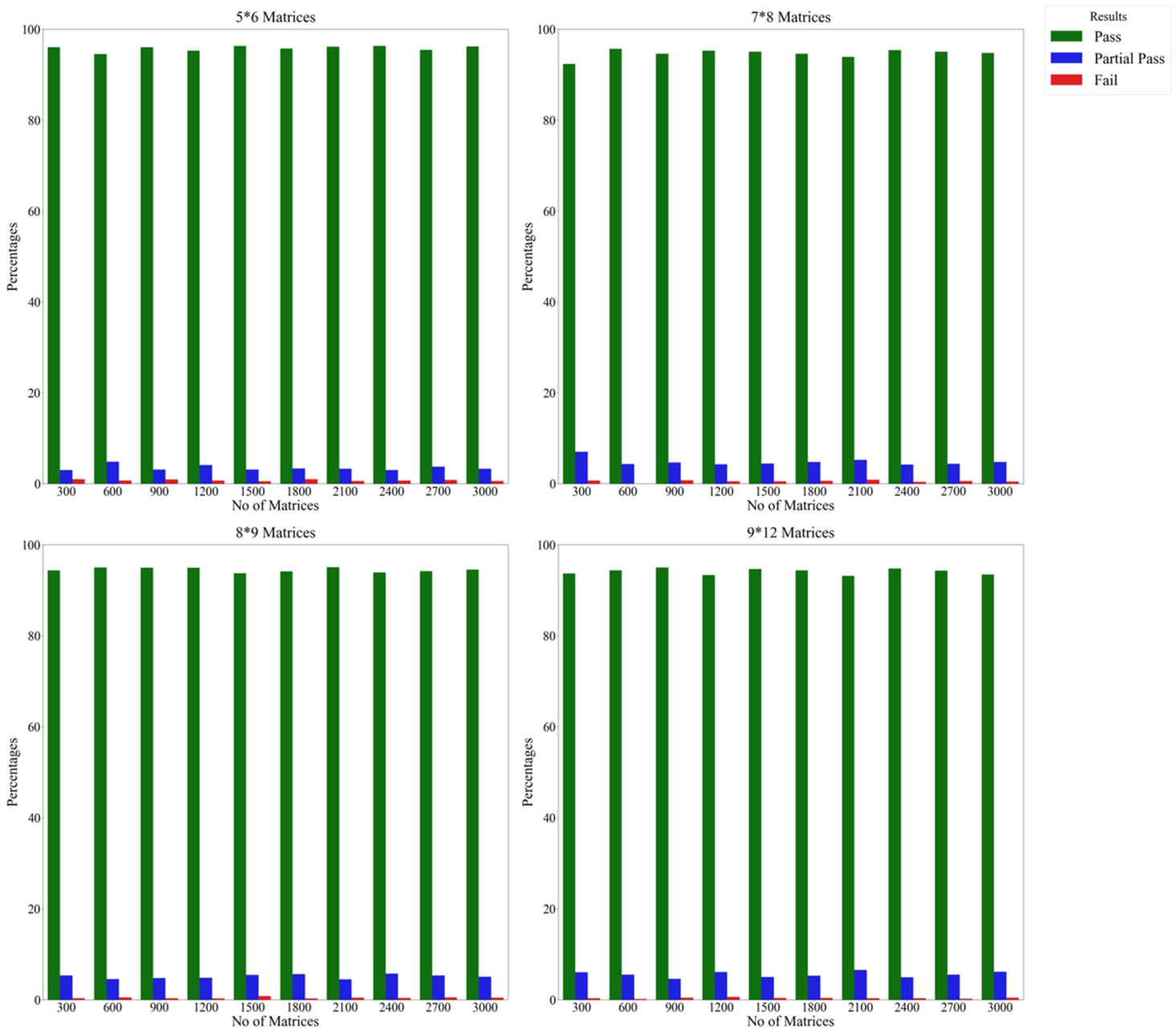
Fig. 3
Results of the experiment on the CoCoSo method using the power approach and unbiased weights by repeating alternatives.
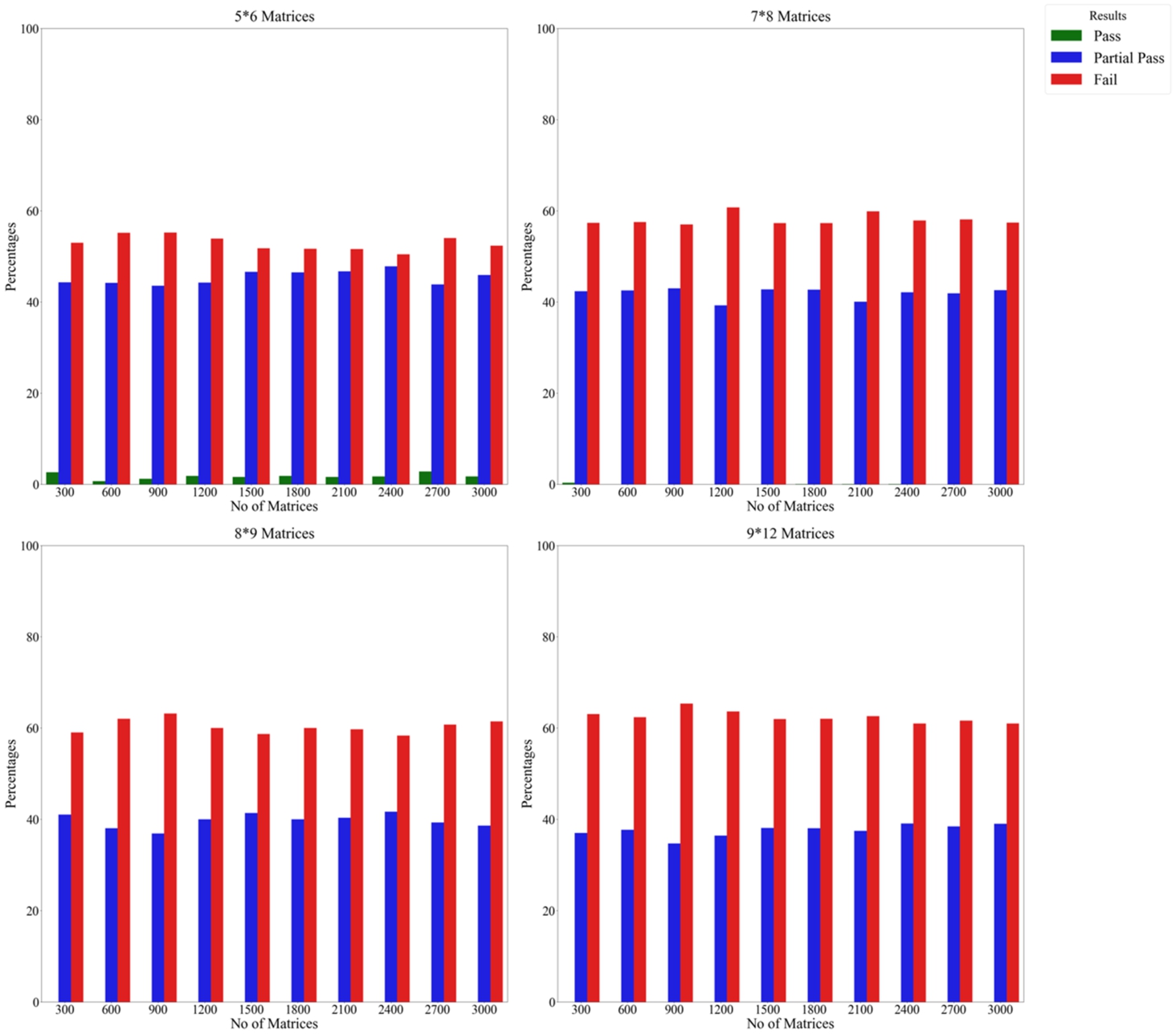
Fig. 4
Results of the experiment on the CoCoSo method using the power approach and unbiased weights by repeating criteria.
Figures 3 and 4 offer the stability outcomes associated with the CoCoSo method when employing the power approach and unbiased weight condition. It is unequivocally evident that modifications regarding alternatives have a diminished impact on the method’s stability, resulting in an increased stability value and a decrease in failure instances. These results demonstrate that when a partial pass is factored in, the failure rate plummets dramatically, signalling an elevated level of stability. We can confidently deduce the following: (i) substantial adjustments to the criteria have a profound impact on the stability of the CoCoSo method, triggering a rank reversal phenomenon, and (ii) the partial pass score is notably high relative to substantial changes to criteria, affirming that in a majority of cases, the top-ranked alternative retains its standing even after significant alterations to the criteria are executed.
4.3 CoCoSo Method Using Scalar Approach and Biased Weights
Figures 5 and 6 summarize the results of applying the CoCoSo method using the scalar approach with biased weights. The criteria for biased weights and the scalar approach of the CoCoSo method can be referred to from Step 2 and Step 3 of Section 2.1, respectively.
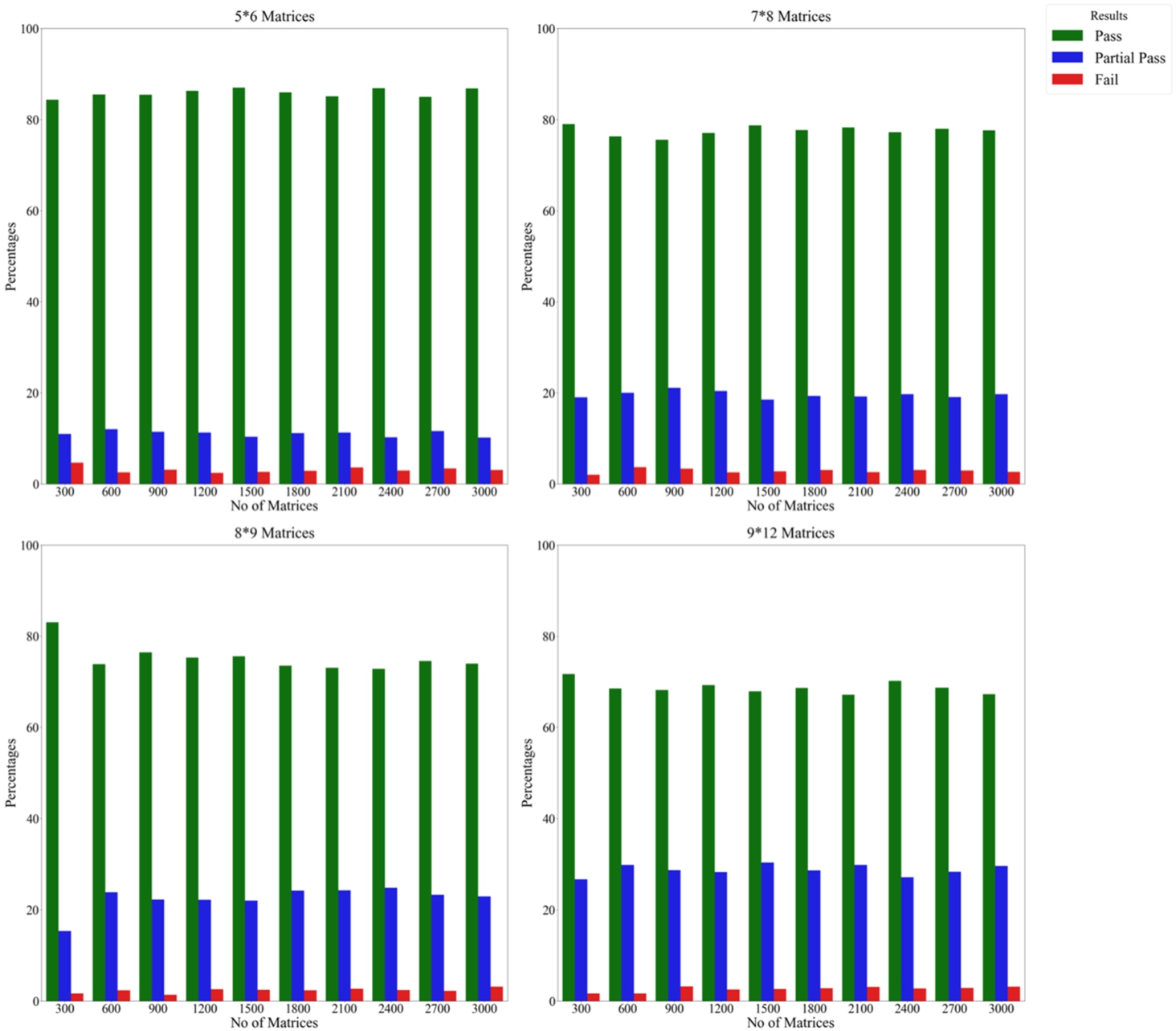
Fig. 5
Results of the experiment on the CoCoSo method using the scalar approach and biased weights by repeating alternatives.
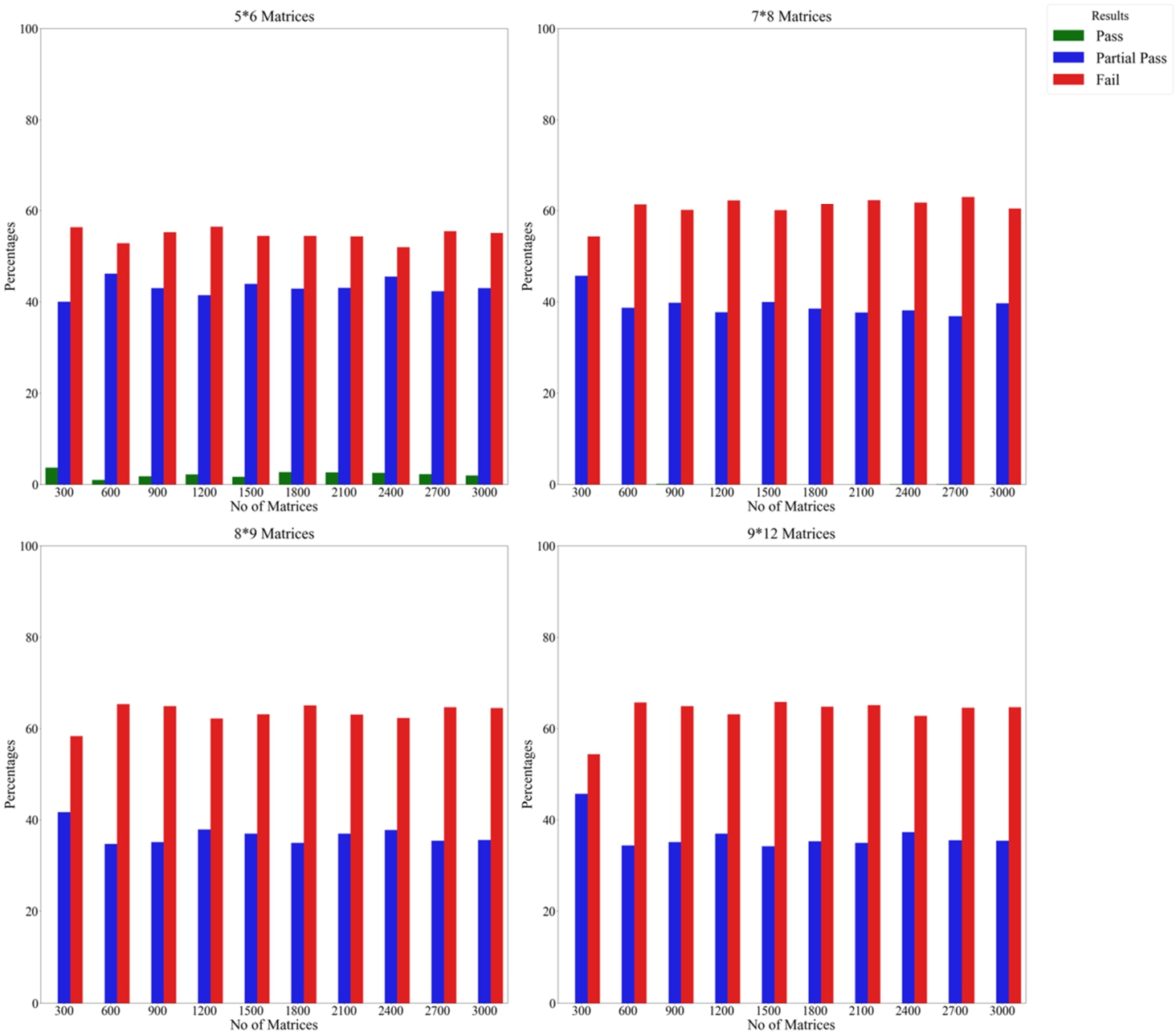
Fig. 6
Results of the experiment on the CoCoSo method using the scalar approach and biased weights by repeating criteria.
Figures 5 and 6 outline the percentages for pass, fail, and partial pass across different sizes of simulated matrix sets, offering a comprehensive perspective of the CoCoSo method using a scalar approach and biased weights. It is worth noting that the findings presented here strongly resemble those detailed in Fig. 1 and Fig. 2. From this set of results, we can observe that (i) the CoCoSo method maintains a satisfactory stability level when alternative changes are compared with criteria modifications; (ii) the pass percentage exhibits volatility with the increase in matrix dimensions regarding both alternative and criteria changes; (iii) changes in matrix sets do not provide an apparent effect on the percentages of pass and fail; (iv) however, incorporating a partial pass in the criteria modification process significantly cuts down the failure rate, suggesting instances where the highest-rated alternative retains its rank even after substantial changes to alternatives and criteria are implemented.
4.4 CoCoSo Method Using Power Approach and Biased Weights
Figures 7 and 8 summarize the results of applying the CoCoSo method using the power approach with biased weights. The criteria for biased weights and the power approach of the CoCoSo method can be referred to from Step 2 and Step 3 of Section 2.1, respectively.
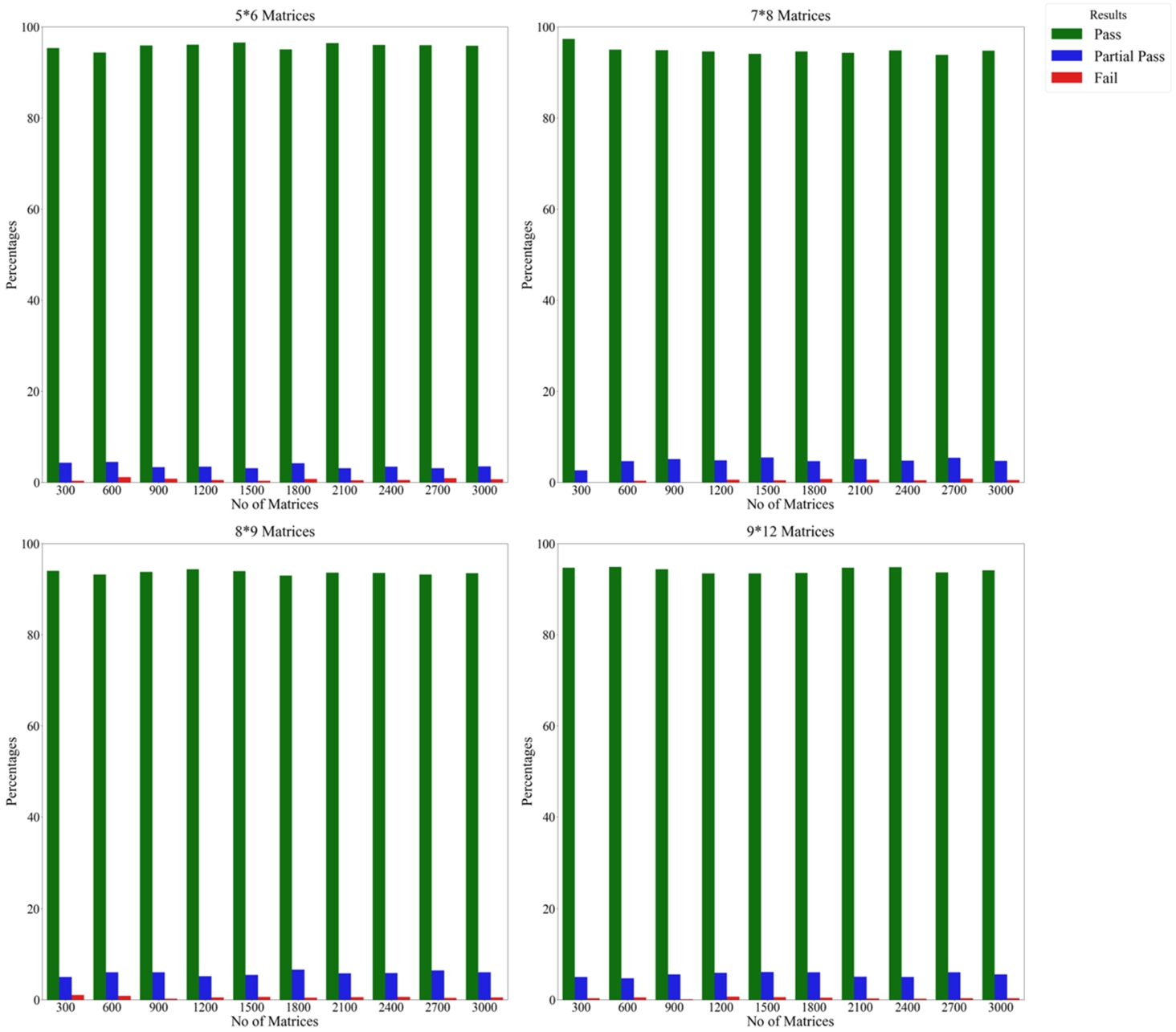
Fig. 7
Results of the experiment on the CoCoSo method using the power approach and biased weights by repeating alternatives.
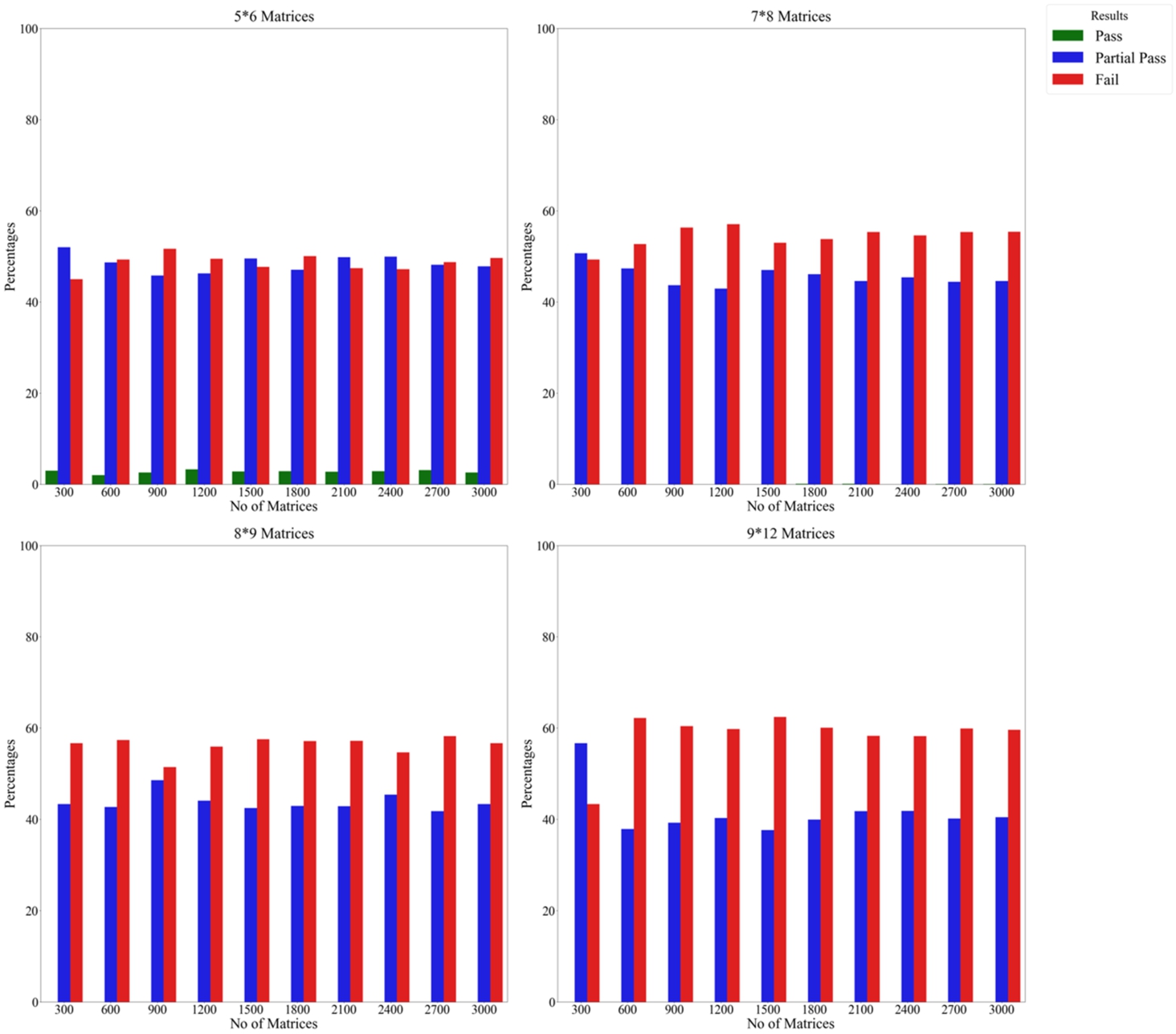
Fig. 8
Results of the experiment on the CoCoSo method using the scalar approach and biased weights by repeating criteria.
Figures 7 and 8 present the stability outcomes of the CoCoSo method when applied with the power approach and biased weight condition. From this, we can deduce that alterations related to alternatives have a minimal impact on the method’s stability, leading to a higher stability value and fewer failures. The data suggest that including partial pass results in a substantial drop in failure rate, signifying enhanced stability. It is essential to point out that the findings here exhibit a weak similarity to those in Fig. 3 and Fig. 4. The following points can be drawn: (i) substantial modifications to the criteria impact the CoCoSo method’s stability, resulting in the phenomenon of rank reversal, and (ii) the partial pass score is noticeably high in relation to substantial criteria modifications, indicating that in numerous cases, the top-rated alternative maintains its rank even after extensive criteria changes are implemented.
4.5 Feature-Based Comparison
A feature based comparison of proposed work with earlier works is also performed to clearly understand the unique proposition of the developed work. For this purpose, works such as Rani and Mishra (2022), Stanujkic et al. (2021), Liu and Han (2022), and Mathew et al. (2020) are compared with the proposed framework to understand the efficacy of the model in Table 2.
From Table 2, it must be noted that these models follow compromise strategy and/or considers functions that provides relative benefits based on diverse ranking approaches and they are actively utilized for ranking in the decision process. Some key features are considered based on which the comparison is provided and from the comparison it is clear that the proposed work is innovative and supports value addition to the ranking process in decision-making by demystifying the properties of the ranking scheme.
5 Conclusion
This paper mainly focuses on exploring the stability aspect of CoCoSo ranking method that is a recent ranking approach based on the principle of compromise solutions. A simulation experiment with multiple matrices of varying dimensions are considered as data in the fuzzy context and the stability metric is determined by adopting the procedures of adequacy test and partial adequacy test. Criteria weights are directly assigned for the simulation experiment and the test is conducted by varying both alternatives, as well criteria. Percentage of pass, partial pass, and fail are determined from the experiment.
Results infer that the ranking approach is stable with respect to alternative alteration compared to criteria alteration. But, the partial stability indicates that the method can also manage changes in criteria. Some impact/insights that are inferred are (i) CoCoSo is a suitable approach from the alternative’s point-of-view; (ii) from the criteria’s point-of-view, it is seen that there are stability issues; (iii) but partial pass, which is assigned when the top rank alternative’s position remains intact even after sufficient changes are made to criteria, indicates that CoCoSo is a good choice for criteria variation also; and (iv) finally, the experimental findings based on simulation provides a comprehensive understanding of the ranking method. Some implications are: (i) stakeholders can gain better understanding of the CoCoSo approach and utilize the ranking approach for rational decision-making; (ii) simulation based experiments offer flexibility to experiment with multiple data in different context, which may become difficult in case of other experiment forms such as empirical study and so on; (iii) the choice of CoCoSo approach from the compromise ranking category for such an exploration will provide motivation to researchers to explore other ranking methods as well; and (iv) finally, the construct of the experiment via Python provides a sense of efficient analysis of the rank reversal phenomenon of CoCoSo, which in turn offers clarity on the stability metric of the method.
Table 2
Feature-based comparison of the proposed model with other extant models.
| Parameter | Proposed model | Rani and Mishra (2022) | Stanujkic et al. (2021) | Liu and Han (2022) | Mathew et al. (2020) |
| Input | Fuzzy number | Single-valued neutrosophic number | Crisp number | Crisp number | Interval-type 2 number |
| Stability from alternatives’ perspective | Considered | Not considered | Not considered | Not considered | Not considered |
| Stability from criteria’s perspective | Considered | Not considered | Not considered | Not considered | Not considered |
| Partial stability from alternatives’ perspective | Considered | Not considered | Not considered | Not considered | Not considered |
| Partial stability from criteria’s perspective | Considered | Not considered | Not considered | Not considered | Not considered |
| Simulation experiment | Performed | Not performed | Not performed | Not performed | Not performed |
Some limitations are: (i) criteria weights are not determined methodically; (ii) experiment is conducted with the classical fuzzy set and not advanced variants; and (iii) finally, large number of alternatives and criteria are not considered, but only the commonly adopted dimensions from the literatures are utilized. In the future, plans are made to address the limitations of the study by considering objective/subjective approaches with no prior information or partial information; utilize different orthopair variants, hesitation variants, neutrosophic variants and alike; and extend the matrix dimension for large scales. Also, we can extend the simulation experiment to different interval fuzzy and probability variants. Further plans are made to extend the study/test experiment to different ranking methods from compromise, utility, and outranking categories. Finally, plans are made to assess the performance of different frameworks developed by researchers in the literatures by integrating different decision approaches.
