1 Introduction
As AI technology has created more attractive application scenarios in the social network domain (Leung,
2023; August
et al.,
2020), not only the number of netizens but also their activity on multiple digital platforms has increased rapidly (Kuo
et al.,
2021). That is followed by the emergence of a large amount of online public opinion events, widely disseminated across different platforms (Akhter
et al.,
2021). On the one hand, online public opinion plays a significant role on the policy making process, since it contains lots of valuable netizens’ demand and attitude information (Xiao and Wong-On-Wing,
2021; Li
et al.,
2022b; Lili
et al.,
2020). On the other hand, sometimes the policy itself will also cause heated discussion of online public opinions, that is defined as the policy(-focused) public opinion (Wang
et al.,
2019).
Moreover, the phenomena of public opinion inversion has aroused wide attention in both academic and industrial fields (Yuan
et al.,
2017; Tan and Hua,
2019). The public opinion inversion refers to netizens’ attitude, emotions or points of view quickly reversed in the opposite direction over time (Zhang
et al.,
2023; Yang,
2023), which is proved to be the result of the synergistic evolution between multiple subjects in the dissemination of public opinion (Zhao
et al.,
2023; Ai
et al.,
2023; Zhu,
2023). It can be seen that the time attribute is an important dimension in observing the state of public opinion, while different observation time intervals (temporal scales) might lead to obtain different netizens’ features. In particular, for the policy-focused public opinion, some key observation time points, like the promulgation time of relevant policies, have a more significant impact on public opinion. Therefore, in order to manage online public opinion, it is crucial to timely and accurately identify netizens’ features following dynamic observation time.
The variable-scale data analysis theory (VSDA) (Wang and Gao,
2022) is used to study the influence of different types of observation scales on decision-making results, by simulating the scale transformation process of decision makers. The framework of VSDA could be classified into main three stages. Firstly, select a single scale data set for scale transformation from the multi-scale data model. Then (taking the clustering data analysis task as an example) perform the cluster analysis on the current single scale data model, and evaluate the satisfaction of the clustering results. Finally, iteratively adjust the observation scale of single scale data model according to the evaluation results, until all the divided clusters meet the satisfaction standard of management scenarios (Wang and Gao,
2021a).
Since different data types (such as spatial data (Radosevic
et al.,
2023), numerical data (Wang and Wang,
2021), categorical data (Lee and Jung,
2021), binary data (Shati
et al.,
2023), etc.) are suitable for different data structures, the structure representation model of different observation scales in the VSDA (i.e. the scale space model) also has different connection modes between multiple scale hierarchies (Wang and Gao,
2022). Although Wang and Gao (
2021b) propose a variable-scale dynamic clustering method that is capable of describing the timeliness characteristics of time-related observation scales (like the material inventory data of aerospace project), its numerical scale space model could only reflect the single perspective that the latest period data provides more significance during the decision-making process. It is unable to meet the jointly observation requirements of multiple time intervals and key time points on the management of policy-focused public opinion.
Therefore, this paper studies the feature identification problem of public opinion considering the multiple observation time intervals and policy time points simultaneously, based on the variable-scale data analysis theory. The main contributions of our research are summarized as follows:
-
• In order to characterize the multi-level analysis requirements of time dimensions for the policy-focused public opinion management, the temporal scale space model is established to describe all the candidate temporal observation scales, which are organized following the time points of relevant policy promulgation (policy time points).
-
• According to the proposed temporal scale space model above, the multi-scale temporal data model is established to represent netizens’ different behaviours in the dissemination of public opinion under every temporal observation scale, instead of just keeping one maximum value of the original time series in the research work (Wang and Gao,
2021b).
-
• A temporal variable-scale clustering method (T-VSC) is put forward. Compared to the traditional variable-scale dynamic clustering method for numerical data, the proposed T-VSC enables to combine the subjective attention of decision-makers and objective timeliness of public opinion data together during the scale transformation process for netizens’ demand feature identification.
The paper is organized as follows. Section
2 introduces the previous research works, including public opinion management and variable-scale clustering methods. Section
3 presents the main part methodology of our research in detail. A case study on the real public opinion dataset of the double-reduction education policy is described in Section
4. The paper is concluded in the last Section.
3 Research Methods
Since the variable-scale data analysis theory (VSDA) has the advantage of modelling the multi-level decision analysis needs (Wang
et al.,
2022), this section studies the feature identification problem of policy-focused public opinion while considering different types of data.
In order to describe the relation between multiple observation time intervals and key time points simultaneously, the temporal scale space model is established in Definition
1.
Definition 1 (Temporal scale space model).
Given a time series
$\textit{TS}=({v_{t1}},{v_{t2}},\dots ,{v_{tn}})$ of observation ruler (dimension)
${A^{\lambda }}$, and
${v_{t}}$ represents the value at time
t, the temporal scale space model of
${A^{\lambda }}$ is Temporal-
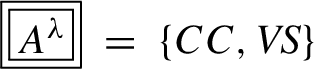
, where the concept chain
$CC=\{{\textit{CH}_{k}^{\lambda }}|\hspace{0.1667em}0\leqslant k\leqslant m\}$ and
${\textit{CH}_{k}^{\lambda }}$ is the kth observation scale of
${A^{\lambda }}$, the value space
$\textit{VS}=\{{V_{kt}^{\lambda }}|\hspace{0.1667em}{V_{kt}^{\lambda }}=f({v_{(t-k):(t+k)}})\wedge (k+1\leqslant t\leqslant n-k)\}$, if
t is the policy time point (Observation time point); otherwise,
${V_{kt}^{\lambda }}=f({v_{(t-k):t}})\wedge (k+1\leqslant t\leqslant n)$,
f is the maximum information function, i.e.
$f({v_{(t-k):(t+k)}})$ means get the maximum value of
$\textit{TS}$ in the time window
$[t-k,t+k]$.
According to Definition
1, the temporal scale space model has the following properties: (1) The lower level temporal observation scale in the concept chain is partially ordered at the higher level scale; (2) The scale values in value space follow the partial order relationship between the scale hierarchies to which they belong.
Taking the public opinion on the double-reduction education policy as an example, the data collection process is shown in Section
4.1 in detail. Since there was an influential double-reduction relevant policy promulgated in March 2023, the above policy time point gains more attention from policymakers and the public. Moreover, combining the data timeliness requirement (that the latest period data earns more significance on the decision-making process, Wang and Gao,
2021b), March and November are the two key observation time points for netizens’ feature identification. Hence, according to the Definition
1, the temporal scale space model could be built (see Fig.
2). It can be seen that with the increase of the time observation scale, the number of observation scale value in the value space becomes smaller and gathers two key points towards Mar. and Nov., showing a double-peak pattern.
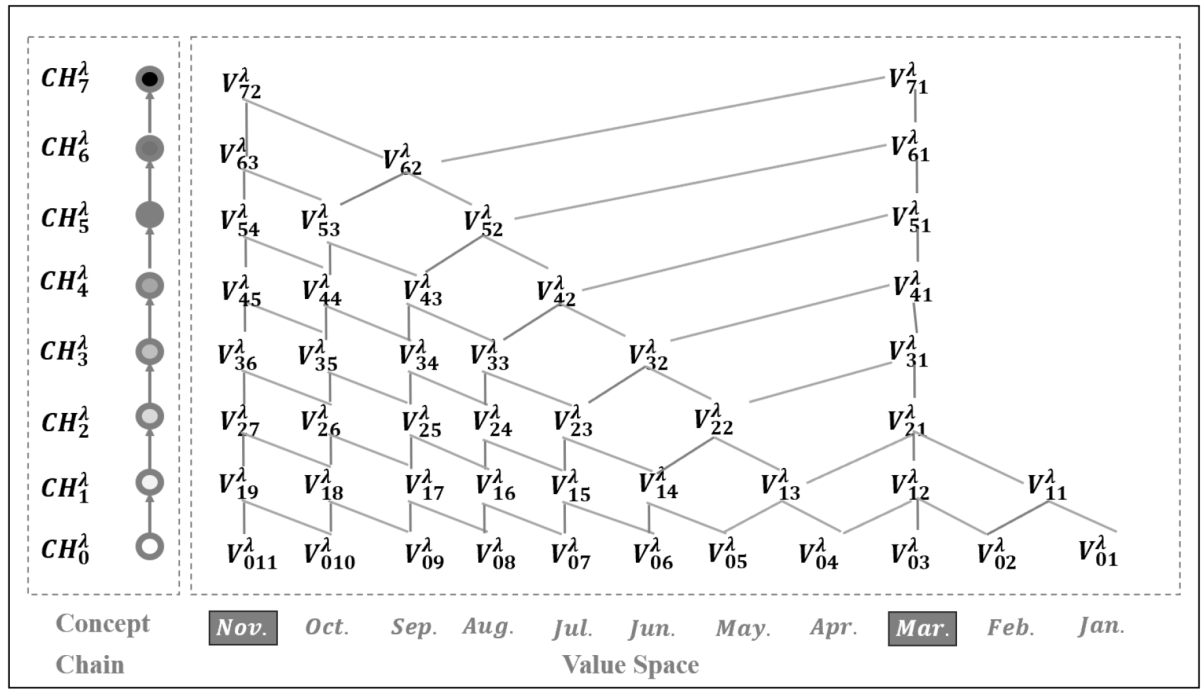
Fig. 2
Example: The temporal scale space model.
According to the construction procedures of traditional scale space model (Wang and Gao,
2022), the temporal scale space model could be built mainly through three stages below.
On the first stage, determine all the candidate temporal scale hierarchies (time intervals) and clarify the key time points for the specific management scenario. For example, the basic (lowest) observation scale
${\textit{CH}_{0}^{\lambda }}$ in Fig.
2 is equal to the initial monthly interval in the double-reduction education policy case, while the adjacent higher scale
${\textit{CH}_{1}^{\lambda }}$ means the last two months.
On the second stage, correlate scale values according to the scale hierarchies from low to high, and follow the order of key time points within the same scale level, which could be broken down into three steps. (1) Extract the maximum value within the observation time interval at the latest time point, that is November in Fig.
2. (2) Extract the maximum value within the observation time interval at other key time points in a chronological order from far to near, that is March in Fig.
2. (3) Extract the maximum value within the observation time interval of the remaining time points in a chronological order from near to far.
At the last stage, reduce the current temporal scale space model from the high scale hierarchy to the low level, until its peak number is the same as the number of key time points.
Compared to the traditional numerical scale space model in the research of Wang and Gao (
2021b), the proposed temporal scale space model keeps the scale hierarchies of the latest observation time intervals, while also emphasizes the influence of policy time points on netizens’ participation behaviour in the public opinion dissemination, which provides a kind of problem-solving space (Allen and Simon,
1972) for the subsequent variable scale data analysis process.
After establishing the temporal scale space model, the multi-scale temporal data model is proposed in Definition
2, in order to comprehensively present various netizens’ behaviour in the dissemination of public opinion under every temporal observation scale.
Definition 2 (Multi-scale temporal data model).
Let Temporal-${D^{S}}=(\mathcal{U},{\mathcal{A}^{S}},{\mathcal{V}^{S}},f)$ represent the multi-scale temporal data model, where $\mathcal{U}=\{{x_{1}},{x_{2}},\dots ,{x_{p}}\}$ is the object set (universe), ${\mathcal{A}^{S}}=\{{A^{1}},{A^{2}},\dots ,{A^{r}}\}$ represents the observation attribute (observation ruler) set, where at least one attribute within ${\mathcal{A}^{S}}$ has multiple temporal scales in its temporal scale space, i.e. $\exists {A^{\lambda }}$, $CC({A^{\lambda }})=\langle {\textit{CH}_{0}^{\lambda }},{\textit{CH}_{1}^{\lambda }},\dots ,{\textit{CH}_{m}^{\lambda }}\rangle ({A^{\lambda }}\in {\mathcal{A}^{S}})$, $f:\mathcal{U}\times {\mathcal{A}^{S}}\to {\mathcal{V}^{S}}$ is the information function, and ${\mathcal{V}^{S}}\in \textit{VS}({A^{\lambda }}),{A^{\lambda }}\in {\mathcal{A}^{S}}$.
Hence, compared to the traditional multi-scale numerical data model in Table
1, the multi-scale temporal data model could represent netizens’ different behaviour under every temporal observation scale (like the various behaviour features
${V_{0i}^{\lambda }}$ $(i=1,2,\dots ,11)$ on the basic observation scale
${\textit{CH}_{0}^{\lambda }}$ in Fig.
2), instead of just keeping one maximum value of the original time series.
According to the temporal scale space model (Temporal-

) and multi-scale temporal data model (Temporal-
${D^{S}}$), the mechanism of the temporal scale transformation (Temporal-
ST) is proposed in Fig.
3.
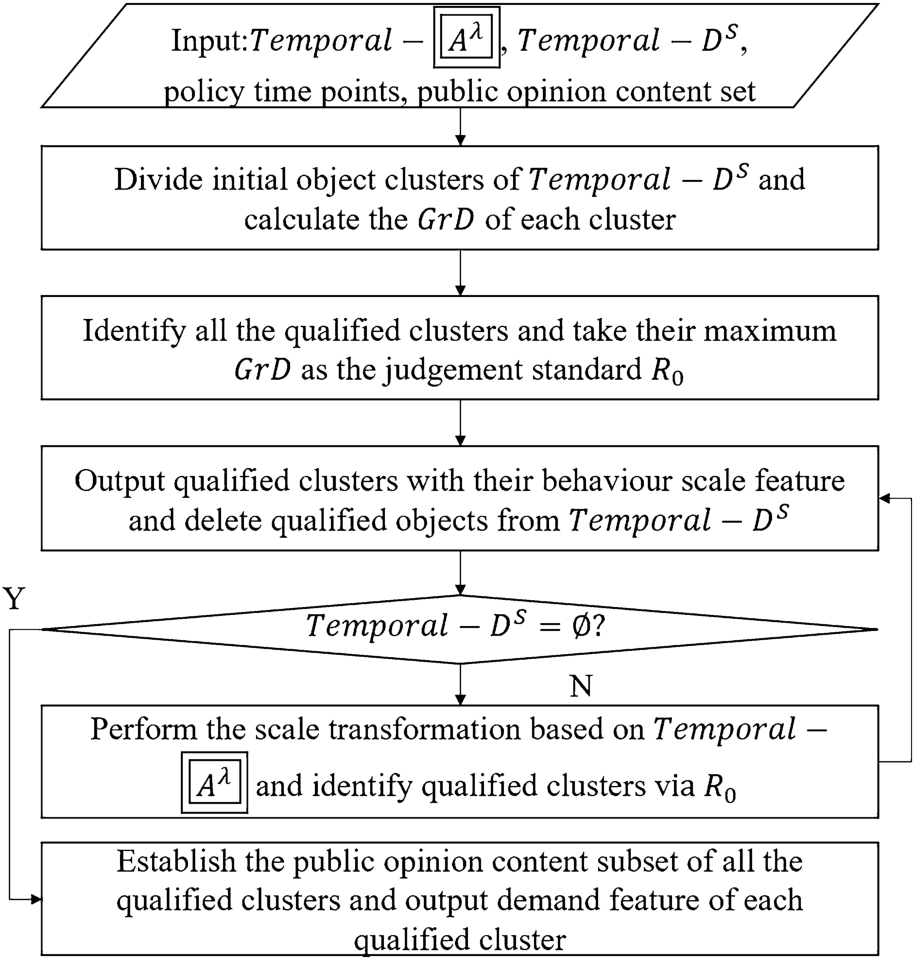
Fig. 3
The mechanism of the temporal scale transformation (Temporal-ST).

Algorithm 1
Temporal variable-scale clustering (policy time points, Temporal-

, Temporal-
${D^{S}}$, initial evaluation dimension
${A^{\lambda }}$, public opinion content set) // Temporal-
${D^{S}}=(\mathcal{U},{\mathcal{A}^{S}},{\mathcal{V}^{S}},f)$ is the multi-scale temporal data model of all the netizens; Temporal-

(
${A^{\lambda }}\in {\mathcal{A}^{S}}$) are the temporal scale space model of netizens’ behaviour observation rulers (while the data collection process is shown in Section
4.1 in detail).
In order to achieve the public opinion management for different types of netizens, the temporal scale transformation mechanism starts with the initial clustering process on the basic temporal scale of Temporal-
${D^{S}}$, which aims to obtain netizen clusters with similar behaviour feature. The measurement granular deviation
GrD (see Eq. (
1)) is utilized to evaluate whether the scale feature of each cluster satisfies decision requirements. According to the variable-scale data analysis theory (see Section
2.2), the satisfaction judgement standard of granular deviation is specified as the maximum granular deviation value of initial qualified clusters which are determined by decision makers. Hence, all the clusters with larger granular deviation are unqualified clusters and need further scale transformation.
For the scale transformation process, such as improving the scale hierarchy from the lower level to higher level, let different observation values of qualified objects’ equivalence classes on the target level be the equivalent interval (Wang and Gao,
2022) and replace it with the intermediate value. And then iteratively perform clustering for the remaining objects based on the Temporal-

.
According to the temporal scale transformation mechanism
Temporal-
ST, a temporal variable-scale clustering method (T-VSC) is put forward, and the calculation steps are shown in Algorithm
1.
The time complexity of the method T-VSC is $O(t(\varphi +p))$, where t is the time complexity of the meta clustering method, $\varphi =\min (p,{m^{r}})$, p is the number of netizens, r is the number of observation rulers of netizens’ behaviour and m is the maximum number of temporal scale hierarchies in one ruler.
5 Conclusions
In this paper, we address the feature identification problem for the management of policy-focused public opinion. According to the variable-scale data analysis theory, the research starts from establishing the temporal scale space model considering the influence of the data timeliness and key observation time points on netizens’ feature identification process. The multi-scale temporal data model is established with the aim to represent netizens’ different behaviours in the dissemination of public opinion on the basis of the temporal scale space model.
After proposing the temporal scale transformation mechanism, a temporal variable-scale clustering method (T-VSC) is put forward. Compared to the traditional numerical variable-scale clustering method, the proposed T-VSC enables to combine the subjective attention of decision-makers and objective timeliness of public opinion data together during the scale transformation process. The efficiency of the proposed method T-VSC is verified by 48552 real public opinion data on the double-reduction education policy from the Sina Weibo platform. Experimental results indicate that the proposed T-VSC method could divide netizens that participating in the dissemination of policy-focused public opinion into clusters with low behavioural granularity deviation on the satisfied observation time scales, and identify the differentiated demand feature of each netizen cluster at policy time points.
In the future, we will keep studying the real-time decision-making constraint in intelligent management scenarios on the mechanism of temporal scale transformation process.


 , Temporal-
, Temporal- (
(